Anomalous Brownian motion discloses viscoelasticity in the ear’s mechanoelectrical-transduction apparatus

Abstract

The ear detects sounds so faint that they produce only atomic-scale displacements in the mechanoelectrical transducer, yet thermal noise causes fluctuations larger by an order of magnitude. Explaining how hearing can operate when the magnitude of the noise greatly exceeds that of the signal requires an understanding both of the transducer’s micromechanics and of the associated noise. Using microrheology, we characterize the statistics of this noise; exploiting the fluctuation-dissipation theorem, we determine the associated micromechanics. The statistics reveal unusual Brownian motion in which the mean square displacement increases as a fractional power of time, indicating that the mechanisms governing energy dissipation are related to those of energy storage. This anomalous scaling contradicts the canonical model of mechanoelectrical transduction, but the results can be explained if the micromechanics incorporates viscoelasticity, a salient characteristic of biopolymers. We amend the canonical model and demonstrate several consequences of viscoelasticity for sensory coding.

The development of experimental and analytical tools has made possible high-resolution studies of the mechanical properties of biological macromolecules on time scales ranging from the picosecond fluctuations of single amide bonds in proteins, through the submillisecond dynamics of ion-channel gating and enzyme catalysis, to the much slower events involved in cell division and motility (1,2). These studies reveal that the energy landscapes in proteins are complex and that the associated hierarchy of time scales produces nonexponential temporal correlations (3,4). The absence of a single characteristic time scale implies stochastic processes with memory and therefore distinct from simple diffusion.

Auditory physiology offers a unique perspective on biological micromechanics. The conversion of a sound’s energy into an electrical signal in the ear is a molecular event that involves an ion channel linked mechanically to a gating spring, an elastic element whose tension is modulated by sound. The weakest sounds that we can hear extend the gating spring by less than a nanometer (5,6). Under these conditions, separating the signal from the intrinsic thermal noise is a formidable task, but one facilitated by the periodic structure of most sounds. Although random fluctuations are known to dominate hair-bundle kinematics and to influence signal detection through stochastic resonance (7), their origin and statistical properties have remained obscure. In this work we have experimentally characterized the random fluctuations of hair bundles by dual-beam differential interferometry, a technique that has allowed us to make large-bandwidth, high-resolution measurements of the nanometer-scale thermal motions of stereocilia in living hair bundles from the inner ear. We have interpreted the measurements by introducing a theoretical framework that incorporates viscoelasticity and the known principles of anomalous stochastic processes into the traditional model of mechanotransduction.

Results

Subdiffusion in the Thermal Motion of Hair Bundles.

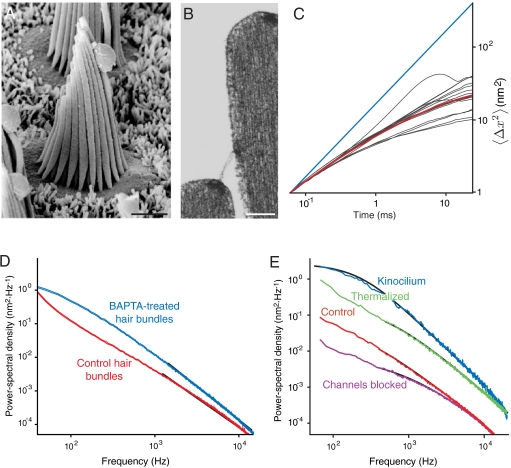
A hair bundle is a mechanosensitive organelle that comprises an array of closely spaced, rigid, cylindrical stereocilia protruding from the upper surface of a hair cell (Fig. 1A). Each stereocilium tapers and becomes more compliant near its base, where it bends when a mechanical stimulus deflects the hair bundle. As the stereocilia slide with respect to one another while preserving a constant separation, the mechanical energy contained in this mode of motion is efficiently captured and delivered to the mechanosensitive ion channels by obliquely oriented tip links (8) (Fig. 1B). Other structural polymers between the stereocilia are stretched negligibly during small hair-bundle deflections because they are oriented not obliquely but perpendicularly to the sliding stereocilia; they are engaged only during very large deflections to protect hair bundles from mechanical damage (9).

Fig. 1.

Subdiffusive movement of the hair bundle. (A) A scanning electron micrograph depicts a hair bundle from the bullfrog’s sacculus. The axis of mechanosensitivity corresponds to the plane of the illustration; the direction of excitatory mechanical stimulation is to the right. The scale bar represents 2 μm. (B) A transmission electron micrograph portrays the tops of two stereocilia joined by an obliquely oriented tip link, which is thought to be attached at its lower insertion to two transduction channels. The scale bar represents 100 nm. (C) A plot of a hair bundle’s mean square displacement demonstrates that an intact bundle performs subdiffusion. The values of 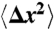for 16 hair cells are shown in gray and their average in red. For comparison, ordinary diffusion defined by the relation 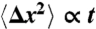is indicated by a blue reference line. (D) The average power spectrum (red) from the 16 intact hair bundles in (C) displays a limiting slope near -1.75 (underlying black line). Cutting the tip links with BAPTA in 11 cells yields a spectrum (blue) with a slope near -2 (underlying black line) characteristic of ordinary diffusion. The shaded areas represent 99% confidence intervals obtained by bootstrapping. (E) The power spectrum of a hair bundle at thermal equilibrium after treatment with NaN₃ (green) displays subdiffusion. A fit with the Mittag-Leffler function (underlying black line) yields a coefficient of α = 0.77. The power spectra of another hair bundle also display subdiffusion, both when its channels are intact (red, α = 0.69) and when they are blocked with 5 mM amiloride (magenta, α = 0.74). The difference in the magnitudes of the fluctuations between the two hair bundles results primarily from differences in the positions of the laser beams. By contrast, the spectrum for a single kinocilium (blue) accords with ordinary diffusion; the coefficient for fitting a Mittag-Leffler function is α = 0.96.

Because a hair bundle’s position is directly coupled to the tension in its tip links, thermal fluctuations in these links and the associated channels must reciprocally cause the bundle to move randomly (SI Appendix, section 1). One might expect this mechanical noise to resemble the overdamped motion of a Brownian particle in a quadratic potential: the drag force provides the coupling to the fluid and the elastic connections constitute a harmonic well. Brownian motion in a quadratic potential has three related salient characteristics. The mean square displacement at short times grows linearly with time as

[1]

the positional autocorrelation function decays exponentially with time; and the power spectrum is Lorentzian with a high-frequency slope in logarithmic coordinates of -2. These behaviors are characteristic of systems in which the mechanisms governing energy dissipation are distinct from those of energy storage (10).

We examined the statistics of thermal fluctuations of hair bundles with the techniques of passive microrheology (11), which are noninvasive and extend over a broad frequency range to high frequencies inaccessible to the existing active methods (12). The experiments disclosed that the thermal motion of a hair bundle differs from the expectation for an overdamped particle in a potential well. The mean square displacement grew sublinearly with time, so α < 1 (Fig. 1C). The autocorrelation function exhibited power-law behavior and the power spectrum displayed a high frequency slope less negative than -2 (Fig. 1D). The thermal motion of a living hair bundle is therefore likely to represent subdiffusion, an hypothesis that we subjected to several additional tests.

The observed statistics of hair-bundle motion are consistent with an equilibrium, time-reversible, Gaussian process in the frequency range from 100 Hz to 10 kHz (SI Appendix, section 2, and Figs. S1 and S2). The fluctuations may reflect nonequilibrium processes at even lower frequencies and inertial forces at still higher frequencies (13). We excluded the possibility that instrumental noise affected the high-frequency portion of the measured spectra by quantifying its power and by including it in our data analysis. Both approaches indicated that additive noise was negligible (SI Appendix, Figs. S3 and S4). Anomalous, fractional Brownian motion satisfies the Gaussian property and can generate subdiffusion (14). When coupled to an elastic element, the process becomes mean reverting–it drifts toward its average value with time–and provides a good phenomenological explanation of the hair bundle’s high-frequency motion. Fractional Brownian motion has been used in the form of a generalized Langevin equation to explain subdiffusive fluctuations within single protein molecules (4, 15, 16). What viscoelastic models and what arrangement of coupled biomechanical components can explain the data from hair cells?

Effect of Disrupting Gating Springs on Subdiffusion.

If fluctuations in gating springs underlie a hair bundle’s subdiffusion, then removing the springs should restore ordinary diffusion. To test this prediction, we disconnected the gating springs with the Ca²⁺ chelator bis(2-aminophenoxy)ethane tetraacetic acid (BAPTA), which severs the bonds between the cadherin-23 and protocadherin-15 dimers that form a tip link (17). This intervention switched the scaling from subdiffusive to ordinary (Fig. 1D). In contrast, subdiffusion persisted when we applied the protease subtilisin, which is known to remove basal links and shaft connectors, lateral structural polymers that are not coupled to the channels and are not stretched appreciably during small hair-bundle deflections. A similar result ensued when we arrested metabolism and brought ten hair cells to thermodynamic equilibrium with poisons that block oxidative phosphorylation and glycolysis (Fig. 1E; SI Appendix, section 2). The fluctuations likewise remained subdiffusive in six cells after we blocked the mechanotransduction channels, whose effective gating viscosity could affect the noise spectrum (18), with the chemically unrelated compounds amiloride (Fig. 1E) and gentamicin (19). This result indicates that reverse electromechanical transduction is not responsible for subdiffusion.

To test whether BAPTA or any of the other drugs caused hair-bundle damage, we used a dual-beam laser interferometer directed at the opposite edges of the hair bundle (20) and established that after the pharmacological treatments the stereociliary movements remained coherent, ruling out gross rearrangements of bundle geometry as the cause of the cessation of subdiffusion. Moreover, in line with previous observations (21, 22), damaged hair bundles that became incoherent produced a broad spectrum of subdiffusive behaviors regardless of any pharmacological treatments. In damaged hair bundles, unlike functional ones, individual stereocilia displayed relative motions as large as several nanometers that certainly engaged various structural polymers. Because viscoelasticity is a generic property of polymers, in a damaged hair bundle the structural polymers could produce subdiffusion independently of the gating springs and even in their absence. We therefore experimented only on hair bundles displaying a coherence of at least 0.9 between 100 Hz and 10 kHz. These experiments emphasize the importance of the control for coherence, which requires the use of a dual-beam interferometer and is impossible with a single-beam instrument.

Hair-Bundle Motion as a Fractional Brownian Process.

To extract summary statistics from the experimental data, we used a model based on fractional Brownian motion. Differential equations invoking fractional derivatives to describe anomalous scaling entered the physics literature in the context of rheology as an expedient to describe phenomenologically the linear responses of viscoelastic materials (23). The autocorrelation function of a fractional Brownian process in a harmonic potential is given by the Mittag-Leffler function (15). An integer-order Brownian process exhibits exponential autocorrelation, so the Mittag-Leffler function reduces to the exponential as a special case when the scaling exponent α equals unity.

After fitting the Mittag-Leffler function by maximum likelihood to experimental power spectra over the frequency range 400–10,000 Hz (SI Appendix, section 2), we determined the scaling exponents, whose deviation from unity characterized the anomalous character of hair-bundle diffusion (Fig. 1E). As expected for ordinary diffusion in a potential well (Eq. 1), α = 0.98 ± 0.01 (mean ± standard deviation) for 11 cells treated with BAPTA and α = 1.02 ± 0.02 for four individual stereocilia and kinocilia disconnected from their bundles (Fig. 1 D and E). By contrast, α = 0.85 ± 0.05 for six cells with blocked channels, α = 0.85 ± 0.01 for three cells treated with subtilisin, α = 0.80 ± 0.04 for ten deenergized cells, and α = 0.71 ± 0.03 for 16 untreated hair bundles. These pharmacological results show that removing a hair bundle’s structural polymers, disrupting cellular metabolism, or blocking the mechanotransduction channels does not suppress hair-bundle subdiffusion, but disconnecting the gating springs does.

To buttress these pharmacological results, we projected all the power spectra onto the first two principal components of a kernel principal-components analysis. This approach demonstrated two clusters: isolated cilia and hair bundles without gating springs on the one hand, and control cells, thermalized cells, and cells with blocked channels on the other (SI Appendix, Fig. S5). We conclude that the high-frequency thermal fluctuations that agitate the mechanoelectrical-transduction apparatus belong to the class of subdiffusive processes with a fractional time dependence.

Viscoelastic Gating-Spring Model.

Having established the fractional nature of a significant portion of the power spectrum of hair bundles, we sought a microscopic model to explain our data. The macroscopic phenomenon of fractional diffusion over a finite set of time scales can be modeled effectively by the superposition of a finite series of simple viscoelastic modes. To explain the data, we therefore incorporated viscoelastic components into a gating-spring model that meets three criteria: the behavior at high frequencies should be subdiffusive; the application of drugs that block the channels should retain subdiffusivity; and severing the tip links should yield ordinary diffusion. Because of the highly coherent motion of the hair bundle (20), we can model its deflection from equilibrium by a single variable X(t) that corresponds to the displacement of a point at the top of either the short or the long edge of the bundle. The shearing of the stereocilia with respect to each other is then proportional to X(t) and the dynamics is determined by the sum of the forces acting on all the stereocilia.

The topological arrangement of the stereocilia is that of a parallel mechanical circuit. The damping force owing to the fluid and the elastic restoring force from the stereociliary pivots sum linearly to contribute a total damping force 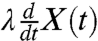and a total elastic restoring force kX(t) (SI Appendix, Fig. S6A). There are two distinct ways in which additional viscoelastic modes can be introduced. The modes can lie in series with the mechanotransduction channels, such that the force across the viscoelastic components and the channels is identical (SI Appendix, Fig. S6B). Alternatively, the modes can occur in parallel, in which case the displacement is shared (SI Appendix, Fig. S6C). Because the application of BAPTA abolishes subdiffusion by cutting the tip links, which are in series with the channels, the viscoelastic elements probably lie in series with the channels. Neglecting for the present the details of the parallel arrangement (SI Appendix, section 3), we therefore focus on the consequences of a serial arrangement.

The transduction channels’ rates of opening and closing are determined by the tension in the tip links, which depends on the viscoelastic properties of the tip-link complex. Even without knowing the molecular composition of the viscoelastic components, we could effectively model their fractal behavior through mode decomposition (SI Appendix, section 3). Motivated by the possibility that the source of subdiffusion is a polymer, we used the mode structure of the worm-like chain to approximate fractional behavior with α = 3/4 (SI Appendix, section 4). In this configuration–which is not unique–we found that summing over the first three modes was sufficient to explain our data and was indistinguishable from summations including additional modes. The model satisfied our three requirements: high-frequency subdiffusion, subdiffusive channel block, and reversion to ordinary diffusion upon tip-link scission.

Linear Noise Approximation.

Thermodynamic equilibrium and linearization of the dynamics about a fixed point allow us to approximate analytically the linear response and power-spectral density of a hair bundle and its channels. For two thermodynamic variables, bundle position X(t) and number of open channels n, the linear response matrix χ of the system in the linear noise approximation (SI Appendix, section 3) is given by

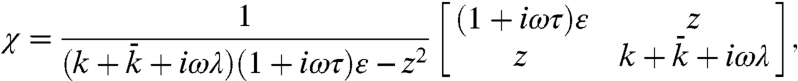[2]

in which the stiffnesses k and 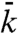are respectively the elastic contributions of the stereociliary pivots and the sum of the viscoelastic responses of the channel complexes in the bundle’s frame of reference. The force associated with opening a channel through its gating distance d is 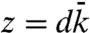, thermal fluctuation of the number of open channels contributes the constant ε, and the mean open time of the channels is τ. By the fluctuation-dissipation theorem (SI Appendix, section 1), the power-spectral density follows from the imaginary part of the linear response,

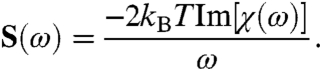[3]

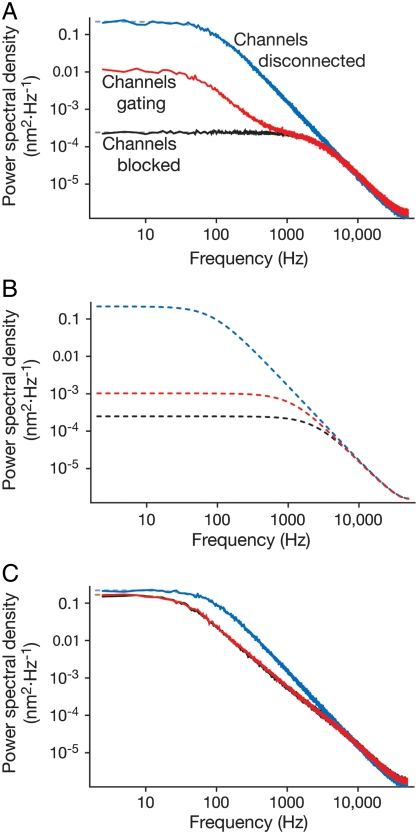
The fluctuation power spectrum of the bundle position X(t) is determined by component S_XX of matrix S. Calculations based on the linear noise approximation agree well with the results of simulations (Fig. 2 A and C). Both approaches demonstrate the effect of channel clatter and the fact that it is masked by the inclusion of series viscoelastic elements. The linear noise approximation facilitates the search for parameter values to fit the model to data, allows us to take limits, and clarifies the relationship between bundle motion and channel response.

Fig. 2.

The effect of viscoelasticity on mechanotransduction: channel clatter. (A) In the canonical gating-spring model, which lacks viscoelasticity, channel clatter has a significant impact on the noise spectrum for a mean open time of τ = 1.26 ms. (B) The response is also significantly affected by channel clatter when τ = 12.6 ms. Both the magnitude and the frequency spectrum of the phenomenon change with the mean open time. To emphasize the effect of the channels, the gating-spring stiffness was set to κ = 2,000 μN·m^-1, higher than the value of 800 μN·m^-1 usually employed. (C) A viscoelastic component in series with each channel masks the channels’ viscosity. Blocking the channels does not significantly change the power spectrum. The fitted parameter values were κ = 2,000 μN·m^-1, κ₁ = 130 μN·m^-1, ξ₁ = 650 nN·s·m^-1, d = 3.5 nm, and p_open = 0.2 (SI Appendix, Fig. S7, Eq. S14, and section 3). The damping of the hair bundle owing to water was set at λ = 130 nN·sm^-1 and the stereociliary stiffness at k = 70 μN·m^-1. (A and C) additionally establish a close correspondence between numerical estimates (solid) and approximate theoretical curves (dashed). The numerical estimates stemmed from an average of 100 simulations of 50 channels for 400 ms. The theoretical curves were computed using the linear noise approximation; (B) shows only an approximation.

Channel Clatter.

In the canonical gating-spring model the channels are coupled tightly to hair-bundle motion, so their fluctuations and the associated phenomenological viscosity should be apparent in the data (18). In the absence of viscoelasticity, we accordingly expect differences in the power spectra with channels blocked (SI Appendix, Eq. S20) and unblocked (SI Appendix, Eq. S19). With series viscoelasticity included in the model, the difference between the spectra shrinks appreciably (Fig. 2C). That we observe less viscosity than expected from the channels can be explained as a consequence of series viscoelasticity. In the series model and at high frequency, the gating-spring component of the tip-link complex places an upper limit on the stiffness of the complex, and hence on the frequency at which the channels couple effectively to the hair bundle (Fig. 2). Fitting the data (Fig. 1E), we estimate this stiffness to be at least 2 mN·m^-1, a value consistent with a recent estimate of the tip-link stiffness (24) at 50 mN·m^-1.

Frequency Selectivity from Viscoelastic Relaxation.

Mechanotransduction channels are force detectors that measure hair-bundle position by sensing the tension in gating springs. From the perspective of signal transduction, it is the channels’ response rather than the bundle’s movement that ultimately matters. Adding viscoelastic elements in series with the channels–that is, generalizing the gating spring to gating viscoelasticity–introduces a dynamic high-pass filter of the force and hence of the input signal. In combination with the low-pass filter set by the corner frequency of the hair bundle as a whole, transduction channels can therefore display resonant sensitivity to a stimulus and demonstrate a degree of frequency selectivity. Note that viscoelastic relaxation differs in a number of ways from Ca²⁺-dependent channel reclosure or fast adaptation (25). Whereas the latter might increase the tension, viscoelastic relaxation reduces the tension in the gating springs, allowing the channels to close. This behavior accords with that of a postulated relaxation element (26, 27).

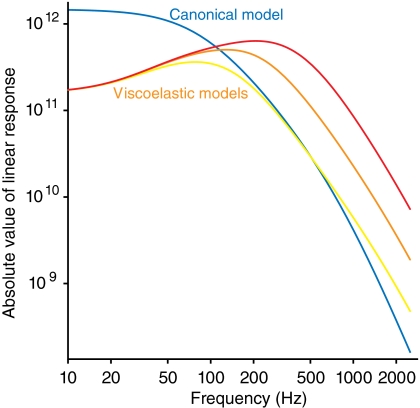
The components of matrix χ (Eq. 2) determine the linear response of the bundle and the channels to external forces. Just as bundle fluctuations are affected by channel clatter, the channels are gated not only by thermal forces applied directly to them but also by external forces impinging on the bundle. This behavior is of course necessary to allow the transduction of external stimuli. The response of channels to bundle motion, 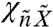, exhibits a peak in the frequency domain indicative of frequency selectivity (Fig. 3). This resonance, which can be tuned to a range of specific frequencies, is present neither in the bundle’s displacement alone nor in the canonical model. It is a consequence of the viscoelasticity that has potential implications for signal transduction. Signals in a specific range of frequencies are preferentially transduced by the channels, whereas noise at other frequencies is suppressed, yielding an improved signal-to-noise ratio.

Fig. 3.

The effect of viscoelasticity on mechanotransduction: frequency resonance. In the viscoelastic model, resonance appears in the response of channels to a force applied to the hair bundle. Varying the channels’ mean open time τ alters the peak of the linear response. Three values of τ are shown: τ = τ₀ = 1.26 ms (yellow), τ = τ₀/2 (orange), and τ = τ₀/4 (red). The response of the canonical model is shown for comparison (blue).

Comparing Theory and Experiment with Viscoelastic Moduli.

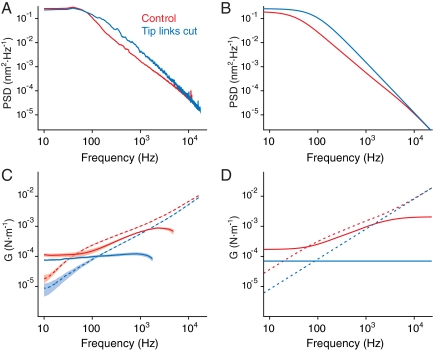
To extend the parallel between our theory and the experiments, we compared the frequency scaling of the power spectra and of the viscoelastic moduli of a real hair bundle with those from the extended model (Fig. 4; SI Appendix, section 3). The frequency scaling of the hair bundle’s viscoelastic modulus was obtained directly from the data using techniques common in microrheology (SI Appendix, section 2). The modeled results fit the viscoelastic moduli and power spectra of actual hair bundles before and after BAPTA application: unambiguously viscoelastic and subdiffusive when the mechanoelectrical-transduction apparatus is intact, the motion becomes regularly diffusive after the gating springs have been disconnected (Fig. 4).

Fig. 4.

Comparison of the extended model with experimental results. (A) Power spectra portray the responses of an actual hair bundle in a control preparation (red) and after the tip links have been severed by BAPTA (blue). (B) The power spectra predicted for the series viscoelastic model accord with the experimental results. The parameter values used to fit this experimental power spectrum are listed in the caption of Fig. 2. (C) The complex viscoelastic modulus can be determined from measurements of a hair bundle’s thermal fluctuations and provides a valuable alternative view of the rheological properties. Because we set the geometric factor to identity, the resulting quantity, a proxy for the modulus and a visualization of the linear response function, is a complex spring constant with units of newtons per meter. The real part of the modulus (continuous lines), which represents the hair bundle’s elasticity, is shown under control conditions (red) and after scission of the tip links by BAPTA (blue). The corresponding imaginary part of the modulus (dotted lines) reflects the hair bundle’s viscosity. The shaded areas represent 95% confidence intervals obtained by bootstrapping. (D) The complex modulus predicted for an extended model with series viscoelasticity resembles the observations under both experimental conditions.

Discussion

We have combined the traditional methods of hearing research with the modern techniques of materials science, particularly the experimental and analytical tools of passive microrheology, to examine mechanotransduction. We have characterized the statistical properties of the internal mechanical noise in the mechanoelectrical-transduction apparatus and determined the frequency dependence of the associated viscoelastic moduli. Through modeling we have then explored the consequences of those properties for sensory transduction, which we discuss in the following paragraphs.

A general implication of viscoelasticity in series with the mechanically sensitive channels is that it changes the nature of the mechanical noise experienced by the transduction apparatus. Because each channel is equipped with a viscoelastic element serving both as a noise generator and as a mechanical filter, fluctuations in the currents carried by different channels are decorrelated and can be averaged. The second benefit of this arrangement is that series viscosity can implement the release mechanism for fast adaptation. When coupled with negative stiffness, this mechanism can provide amplification (28). The third consequence involves masking the high phenomenological viscosity of the channels, which in the presence of viscoelasticity has little effect on hair-bundle motion. This phenomenon renders hair-bundle drag only a few times the minimum imposed by hydrodynamics alone (29), rather than the hundredfold the minimum expected if channel viscosity were to dominate (18). The fourth potential benefit is that viscoelasticity endows the mechanotransduction complex with frequency resonance. The relationship of this phenomenon to other resonant properties of a hair bundle remains to be investigated. Finally, we note that gating-spring viscoelasticity may be based on the mode structure of a worm-like chain, which is nonlinear. In principle even a small gating swing of the mechanotransduction channel can significantly decrease the effective stiffness of the gating spring and produce the gating compliance required for signal amplification by the hair bundle. In contrast, to achieve the same softening of a linear linkage necessitates an unrealistically large conformational change of the channel’s gate that surpasses the size of a typical ion channel (30). Viscoelasticity of the mechanotransduction apparatus may therefore be key for the ear’s sensitivity. Verifying this conjecture experimentally would require single-molecule assays on isolated gating springs or perhaps very fast mechanical measurements from hair bundles in which adaptation is blocked.

It is not surprising that a hair bundle manifests viscoelasticity, for biopolymers and their complexes with lipid membranes are intrinsically viscoelastic. It is noteworthy, however, that introducing in the model as few as three additional mechanical modes, arranged either in series or in parallel with a mechanotransduction channel, suffices to replicate the experimental results. This result implies that viscoelasticity is a robust feature of the mechanoelectrical-transduction apparatus and that its physiological consequences are independent of the details of the molecular implementation.

Methods

Experimental Methods.

The experimental procedures were approved by the Institutional Animal Care and Use Committee of The Rockefeller University. Sacculi were dissected from adult bullfrogs (Rana catesbeiana) and maintained in oxygenated saline solution containing 120 mM NaCl, 2 mM KCl, 1 mM CaCl₂, 10 mM D-glucose, and 5 mM Hepes at pH 7.3. After a 30–60 min digestion at 20–25 °C in 1 mg·mL^-1 collagenase (type XI, Sigma Chemical Co.), each sensory epithelium was separated from the underlying connective tissue, the otolithic membrane was removed, and the epithelium was folded along its line of mirror symmetry and secured against the bottom of an experimental chamber by a golden electron-microscopic grid. Laser interferometry was used to measure hair-bundle motions with subnanometer spatial and submillisecond temporal resolution (20, 29, 31). Data were acquired simultaneously with two independent laser beams, low-pass filtered at 20 kHz, and sampled at 10 μs intervals. The multitaper method (32) was used for spectral analysis in Matlab (MathWorks).

Maximum-Likelihood Fit of Data.

Model spectra were fit to data with a maximum-likelihood procedure (SI Appendix, section 2). Each standard error was approximated as the square root of the inverse of the Hessian matrix of the negative log-likelihood. Power spectra were estimated using the multitaper method.

Estimating Viscoelastic Moduli.

The fluctuation-dissipation theorem links a viscoelastic material’s shear modulus with its equilibrium power spectrum (SI Appendix, section 1). Moduli were estimated by two different methods (SI Appendix, section 2).

Mode Decomposition and Simulation.

The bundle’s response to stereociliary and thermal forces can effectively be decomposed into a series of viscoelastic modes (SI Appendix, Fig. S6). This network of simple modes combined with the nonlinear channels formed the basis for our analytical approximation and numerical simulations. We used Langevin simulations of the nonlinear channels and the viscoelastic modes in equilibrium to capture the nonlinear effects of the channels, to verify the quality of our linear noise approximation, and to compare the model directly to experimental data (SI Appendix, section 3).