Sheet-Like White Matter Fiber Tracts: Representation, Clustering, and Quantitative Analysis

Abstract

We introduce an automated and probabilistic method for subject-specific segmentation of sheet-like fiber tracts. In addition to clustering of trajectories into anatomically meaningful bundles, the method provides statistics of diffusion measures by establishing point correspondences on the estimated medial representation of each bundle. We also introduce a new approach for medial surface generation of sheet-like fiber bundles in order too initialize the proposed clustering algorithm. Applying the new method to a population study of brain aging on 24 subjects demonstrates the capabilities and strengths of the algorithm in identifying and visualizing spatial patterns of group differences.

Introduction

Analysis of diffusion-weighted MR imaging enables in vivo study of human brain integrity to assess the neurodegeneration and de-myelination of white matter fiber tracts. Developing computational tools to extract quantitative information from diffusion MRI is, therefore, of great interest to the clinical community. Early methods for quantitative DTI analysis were based on the analysis of scalar diffusion measures, either within a region of interest (ROI) or at each acquired voxel. More recent variants incorporate tractography models to increase specificity. In [4], ROIs are constructed based on identified tracts, whereas TBSS [11] aligns subjects based on tract skeletons onto which scalar measures are then projected. However, these methods still suffer from some limitations. The former does not preserve the local variations and the latter ignores tract orientation and thus cannot always distinguish between adjacent tracts.

To overcome these limitations, recent tract-based quantitative methods analyze diffusion measures for a group of trajectories that belong to the same fiber tract and report the statistics along a descriptive model (e.g., tract skeleton) [9,7,15]. These methods have two main components: clustering and model construction. Within a single subject, clustering of fiber trajectories into groups that correspond to macroscopic fiber tracts (bundles), greatly improves the quality of tract-based analysis as it eliminates outlier trajectories [7,13]. Across subjects, clustering ensures that the measurements are performed on the same tract in all subjects. By building a representative geometric model for each bundle (e.g., a medial curve), these methods provide a reference system for quantitative analysis of diffusion measures along the clustered trajectories. Statistics of these measures projected onto the medial model typically have lower variance across subjects and result in higher statistical power compared with voxel-wise analysis. On the other hand, unlike ROI-based methods, tract-oriented analysis allows studying of local variation along the bundle, as dimensionality reduction is constrained to the directions perpendicular to the model.

Most tract-based methods proposed so far are limited to tubular-shaped tracts, such as the cingulum bundle (CB), which can be represented by medial curves [1,9,7]. Although this one-dimensional model has been successfully used for population studies [9,8], important tracts such as the body of the corpus callosum (CC) and the rostral part of corticospinal tract (CST) are not tubular and two-dimensional models are more appropriate for these sheet-like bundles. A medial representation for sheet-like fiber bundles has previously been proposed in [15] but that method used manual clustering of fiber trajectories in the group-averaged tensor data. Our method, by contrast, incorporates automatic clustering of the trajectories extracted in the subject space.

In this paper, we address problems of probabilistic clustering, geometric modeling, and quantitative analysis of sheet-like fiber bundles. Clustering is achieved by solving a mixture model on the distances between fiber trajectories and bundle medial surfaces. A novel composite distance measure incorporates spatial distance and orientation difference between trajectories. To our knowledge, this paper is the first to address the probabilistic clustering of sheet-like bundles. We also present a novel method for generating the medial surface models of such bundles. Statistics of diffusion measures for a bundle of interest are achieved by establishing point correspondences between trajectories and medial surface model. We demonstrate the proposed method by identifying spatial patterns of group differences between 12 young and 12 elderly subjects in a brain aging study for the right CST (rCST) and CC as examples of sheet-like tracts.

Method

Our method has three main steps: initial medial surface generation, clustering with surface evolution, and quantitative analysis, as detailed in the next subsections.

2.1 Orientational Medial Surface Generation

For each sheet-like fiber tract, a medial surface model is constructed as a triangular mesh. For each vertex in the mesh, we store the orientation of fiber trajectories at that location. Each vertex is thus described by a tuple (μ, ε), where μ ∈ ℝ³ is its location and ε ∈ ℝ³ is the local fiber orientation. This orientational medial surface is generated from a binary tract segmentation in an atlas or in a reference subject and serves as the initial tract model, which is then evolved by the clustering algorithm.

Yushkevich et al. [14] used a Voronoi skeleton as an initial parametric medial model, which was then fitted to the binary segmentation of the structure using a deformable model. Here, we leverage the fact that sheet-like fiber tracts are thin-walled shapes and propose an alternative approach. The method is based on the chordal axis transform (CAT) [10], wherein the chordal (i.e., medial) surface of a thin-wall-ed shell structure is estimated by connecting the mid-planes of its tetrahedral mesh elements [5].

Figure 1 illustrates the steps to estimate the medial surface of CC. Starting with the binary segmentation (Fig. 1a), which can be supplied by an atlas of fiber tracts [12], we first extract the surface mesh (Fig. 1b) using the marching cubes algorithm [6]. We then construct a single-layer volumetric hexahedral mesh (Fig. 1c), using the publicly available IA-FEMesh [3]. From the single-layer hexahedral mesh, we generate the chordal surface mesh by connecting the patches of each hexahedron mid-plane. This requires the cut direction to be determined. For each hexahedron, we first identify the two facing facets that are not shared with other hexahedrons. The cut is the mid plane between these two facets. This leads to a quadrilateral surface mesh, represented as a QuadEdgeMesh structure [2], which is then triangulated (Fig. 1d) to facilitate the use of InsightToolkit (ITK) libraries. Optionally, mesh smoothing and decimation are performed to increase the quality of the chordal mesh. Finally, we add orientation information at each point on the surface by storing the principal eigenvector of the diffusion tensor at that point, computed from the atlas or reference subject tensor volume.

Figure 1. Steps to estimate the medial surface of a fiber tract.

(a) Binary segmentation of the tract from an atlas [12], (b) surface mesh generation using marching cubes algorithm, (c) single-layer volumetric hexahedral mesh generation, and (d) the CAT-based medial surface estimation.

2.2 Trajectory-Surface Distance Measure

Each trajectory (i.e., every streamline produced by tractography) is treated as a uniformly-sampled 3-D curve, which is mapped from the subject space into the template space, for example via an affine transformation computed by image registration. Each sample on a trajectory is represented by its coordinate, r ∈ ℝ³, and its unit-length local orientation e ∈ ℝ³ . A trajectory is a collection of these samples, i.e., (r_i, e_i) = [(r_ij, e_ij)]_j=1,…,J(i) where J(i) is the number of samples on the i-th trajectory. We calculate the trajectory’s local orientation at each point from its 3-D representation. Alternatively, the principal diffusion eigenvector can be used as e_ij, but explicit vector re-orientation is then needed when the trajectories are mapped into the reference space.

Each cluster (i.e., each fiber bundle) is represented by a medial surface, initially generated as described in the previous subsection and evolved throughout the algorithm. For each trajectory, distances to all cluster medial surfaces are calculated. We define the distance measure between the i-th trajectory and the k-th cluster medial surface representation as a combination of Euclidean distance and orientation dissimilarity. The Euclidean distance can be calculated efficiently by constructing a distance map from each cluster medial surface. For each trajectory-surface pair, the spatial distance measure is $d_E\left(r_i,{\mu }_k\right)=\frac{1}{J(i)}\sum D_k\left(r_{ij}\right)$, where D_k (x) is the value of the Euclidean distance map for cluster k at point x.

Orientation dissimilarity is calculated from the angle between the local orientation of the trajectory points and the orientation stored for their corresponding points on the medial surface. The point correspondences are obtained by generating a Voronoi diagram, L_k (x), for each cluster medial representation, which provides the index of the closest sample on the k-th cluster medial surface for a given point x in the space. In an ideal point correspondence, the local orientation of a trajectory point and its closest point on the medial surface should match. The orientation dissimilarity between trajectory i and cluster medial representation k is defined as

$$d_O\left(e_i,{\epsilon }_k\right)=\frac{1}{J(i)}\sum \left(1-u\left(\mid \langle e_{ij},{\epsilon }_{k,L_k\left(r_{ij}\right)}\rangle \mid -\tau \right)\right),$$ (1)

where ε_k,Lk(rij) is the orientation at the corresponding sample on the k-th cluster medial representation to the point r_ij, u (·) is the unit step function, and τ is the threshold of acceptable misorientation, i.e., a user-defined minimum bound on the cosine of the angle between each closest-point pair. We define the combined dissimilarity measure, d_ik, between trajectory i and cluster k as

$$d_{ik}=d_E\left(r_i,{\mu }_k\right)+{\lambda }_{ik}{d}_O\left(e_i,{\epsilon }_k\right),$$ (2)

where λ_ik is a weight factor to correct for the scale difference between the orientation dissimilarity and the distance. Here, we simply set λ_ik =d_E(r_i, μ_k).

2.3 Probabilistic Clustering

The trajectories in a subject can be clustered based on their calculated distances to each cluster medial representation. To this end, we follow the gamma mixture model approach proposed in [7]¹. Assuming that each d_ik is drawn from a gamma distribution, we estimate the unknown parametersand the expected value of the hidden data, which indicates the membership probabilities. Specifically, p_ik denotes the membership probability of trajectory i to cluster k.

An Expectation Maximization formulation has been described in detail in [7] for both maximum-likelihood and maximum-posterior estimation of the mixture-model parameters given the observed data (i.e., d_ik). The clustering algorithm is an iterative process that alternates between parameter estimation and medial surface evolution. At each iteration, once the EM part has converged, the cluster medial surfaces are updated based on the new membership probabilities assigned to the trajectories by the EM formulation. Each point on the medial surface is updated as the weighted average of the corresponding points on the trajectories that belong to that cluster. Note that due to partial overlap and fiber tractography errors, it is possible to have trajectories that belong to a given cluster but contain portions that do not resemble the shape of the tract. To exclude these portions, we use a threshold on the mis-orientation between the trajectory points and the corresponding points on the medial surface, i.e.,

$${\mu }_{kj}=\frac{\sum p_{ik}{w}_{\mathit{ikj}}{r}_{i,n_{ik}\left(j\right)}}{\sum p_{ik}{w}_{\mathit{ikj}}}$$ (3)

where w_ikj =1 − u (〈e_i,nik(j), ε_kj〉 − τ). Here, n_ik (·) is the reverse lookup function on L_k (x), which returns the closest corresponding sample on the i-th trajectory to a given index on the medial representation of k-th cluster, and t is the same mis-orientation threshold as in Eq. (1). After each vertex on the mesh has been updated, the mesh is regularized by a Laplacian smoothing filter, available in ITK.

The output of the clustering algorithm is the probabilistic assignment of the trajectories to each cluster and medial representations of all clusters. Outliers are identified as those trajectories that receive membership likelihood lower than a user-specified threshold from all clusters, and these are removed from further processing.

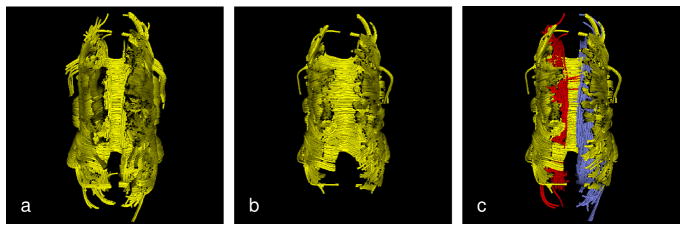
To demonstrate the importance of using orientation information in the clustering, Fig. 2 shows the clustering of CC trajectories seeded from the ROI shown in Fig. 1a and the initial medial surface shown in Fig. 1d. When orientation information is not used (Fig. 2a) some of the CB trajectories are falsely assigned to the CC cluster. These trajectories are removed as outliers when orientation information is used (Fig. 2b). In Fig. 2c clustering of the same input trajectories is performed with three initial centers, adding initial medial curves for the left and the right CBs. Note that the same EM formulation works for clustering of tubular bundles given 3D curves as the initial medial representations. Figure 3 shows the clustered trajectories of rCST in a single subject and compares visually the match between the variation of FA along the clustered trajectories with the computed average value over the estimated medial surface.

Figure 2. The importance of orientation information for successful clustering.

Clustering of the trajectories seeded from the ROI in Fig. 1a: (a) When orientation information is not used, some CB trajectories are falsely assigned to CC. (b) These trajectories are removed as outliers when orientation information is used. (c) Orientation information enables successful clustering of CB trajectories that are spatially close to CC but differ in shape.

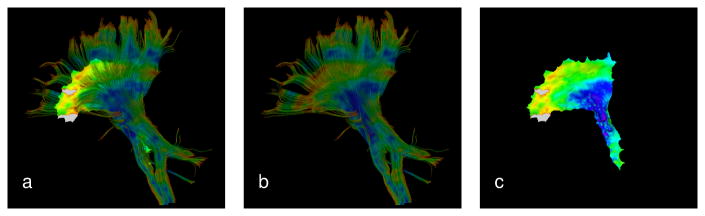
Figure 3. Projection of scalar measures onto the cluster medial surface enables reduction in the dimensionality without loss of spatial information.

Shown here is FA distribution in the rCST of a single subject. The clustered trajectories and the medial surface are shown together in (a) to aid the visual comparison, and separately in (b) and (c) to reveal more details. Note that we used the corticospinal ROI defined in [12] which specifies a region substantially smaller than what is spanned by the trajectories. Portions of the medial surface that do not have any contribution from the trajectories are shown in gray.

Experiments and Results

To demonstrate the capabilities of the proposed approach, we performed a preliminary population study to quantify how the integrity of white matter fiber tracts is affected in normal aging. Data were acquired from 12 young (age=25.5±4.34) and 12 elderly (age=77.67±4.94) healthy subjects. Echo-planar DWI data was acquired with slice thickness of 2.5mm, fifteen unique diffusion directions with b=860s/mm², along with 5 baseline scans with b=0. Images were corrected for eddy-current and B0 distortions, and tensors were estimated using the Teem library.

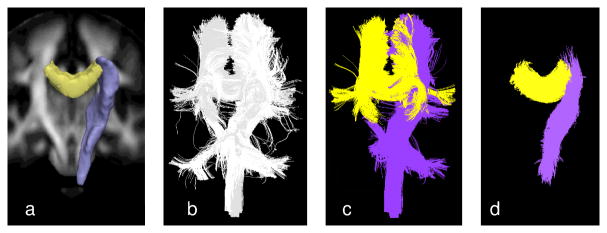
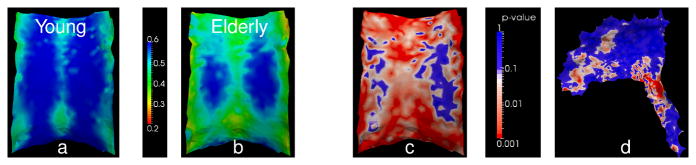
The labeled tracts in the ICBM atlas² were mapped to each subject space to seed the tractography by applying the transformation computed from pairwise affine registration on the FA volumes of the subject and the atlas using CMTK’s registration tool³. Streamline tractography was performed using 3D Slicer, seeded from the mapped labeled regions of CC and rCST (Fig. 4a), and terminated when an FA value less than 0.15, or maximum curvature of 0.8 was reached. The quantitative parameters of interest, such as FA, were computed at each point on the trajectories and stored for subsequent analysis. Subject-specific trajectories were then back-transformed into the atlas space as shown in Fig. 4b. Given the orientational medial surfaces of CC and rCST as initial surfaces, trajectories were successfully clustered by the proposed EM algorithm (Fig. 4c) with minimum-likelihood threshold of 0.02 for outlier rejection and the orientation threshold of τ=0.85 (allowing approximately 30 degrees mis-orientation). Once the trajectories of all 24 subjects were clustered, for each subject diffusion measure means were calculated for each vertex on the estimated medial surface of the bundle. For subject s, let I_s be the set of trajectory indices i that originate from that subject. The weighted mean of the feature of interest for subject s at the j-th point on the k-th cluster medial surface was calculated as ${\overline{f}}_{kj}^s=\frac{\sum p_{ik}{w}_{\mathit{ikj}}{f}_{i,n_{ik}\left(j\right)}}{\sum p_{ik}{w}_{\mathit{ikj}}}$, where f_i,nik(j) is the feature sample at the closest corresponding point on trajectory i. At each point j on every cluster k we performed group comparisons using the per-subject feature values ${\overline{f}}_{kj}^s$. For each vertex on the medial surface, we performed a two-sample Welch’s t-test, assuming unequal variances, to calculate the statistical significance of the group differences. Since we perform tractography in subject image space, as opposed to group-average tractography (e.g., [15]), our method can identify the regions in which a given subject does not contribute to the statistics as shown in Fig. 3 (regions in gray), adding to the reliability of the quantitative analysis. The proposed framework also enables the user to control the extent of coherence in the bundle of interest through probabilistic label assignments from the clustering. Moreover, in the quantitative analysis step, the user has control over inclusion of contributing points in the final statistics by adjusting a threshold of acceptable local orientation difference between the corresponding points. Threshold adjustment capability is important for reliable statistical analysis, because definition of tracts can be indefinite and subjective. Through visual inspection as shown in Fig. 4d, the user can be confident of the region on which the derived statistics are based. Fig. 5 illustrates the final medial representations of body of CC, colored by the average FA of 12 young subjects (Fig. 5a) and 12 elderly subjects (Fig. 5b). In these visualizations, one easily observes the local variation of the diffusion measure over the medial surface and differences between the group means. Figs. 5c and 5d demonstrate the results of our statistical analysis of FA for CC and CST. In general, we observed lower FA and higher diffusivity in the elderly group than the young group, which is consistent with findings in earlier diffusion MRI studies on aging.

Figure 4. Group clustering of sheet-like bundles.

(a) Body of CC and rCST as defined in the ICBM atlas, (b) trajectories of 24 subjects transformed to the ICBM space, (c) successful clustering of CC and rCST; trajectories that belong to other fiber tracts such as CB and pons have been correctly excluded. (d) Portions of the clustered trajectories which meet the maximum mis-orientation threshold of 30 degrees, and therefore contribute to the final statistics on the estimated medial surfaces.

Figure 5. Example of group-difference statistics.

Each point on the medial representation of CC is colored with the weighted average FA over all corresponding points on the clustered trajectories for (a) young and (b) elderly group. The results clearly show the spatial variation of FA along the cluster and lower FA in the elderly population. The corresponding p-value for the group difference in FA is shown in (c) for CC and (d) right CST. Red corresponds to regions with high statistical significance (p ≤ 0.001).

Conclusion

This work is the extension and generalization of [7] and enables probabilistic clustering and quantitative analysis of sheet-like tracts, either in a single subject or in a population, while still supporting tubular bundles. We also propose a novel method for estimating the orientational medial surface of bundles, which then serve as initial tract models in the proposed clustering scheme. Here, we start from segmentation provided in the ICBM atlas but the method is general and could instead have been started from a manually segmented region in a reference subject. Our experiments demonstrate the strengths of the presented method in computing the spatial summary statistics of diffusion measures on the medial representations of white matter fiber tracts.