A three-dimensional color space from the 13th century

Abstract

We present a new commentary on Robert Grosseteste’s De colore, a short treatise that dates from the early 13th century, in which Grosseteste constructs a linguistic combinatorial account of color. In contrast to other commentaries (e.g., Kuehni & Schwarz, Color Ordered: A Survey of Color Order Systems from Antiquity to the Present, 2007, p. 36), we argue that the color space described by Grosseteste is explicitly three-dimensional. We seek the appropriate translation of Grosseteste’s key terms, making reference both to Grosseteste’s other works and the broader intellectual context of the 13th century, and to modern color spaces.

1. BACKGROUND

Robert Grosseteste (c.1175—1253), bishop of Lincoln, was a theologian, scientist, pastor, and politician. Our forthcoming, related publication [1] presents a new edition of and commentary on one of Grosseteste’s scientific works, the De colore. Here we discuss the De colore from a modern perspective on color and color vision.

The De colore was composed, probably, in the mid-1220s. It is a dense text of fewer than 400 words but one that presents a number of deep puzzles and challenges. It has received relatively little study and yet forms an important element within Grosseteste’s “scientific” canon. To understand the De Colore, it is important to consider the context in which it was written. The development of scientific thought in the 13th century drew together many different schools, as the development of natural science and the scientific method progressed hand-in-hand with theological discussion of creation. Ideas of reason and rationality were highly prized, with an overarching belief in a universe that is ordered and whose order would become clear through careful observation.

Grosseteste himself was fascinated with the physical world and its phenomena, particularly that of light. His writings are informed both by the theological traditions he inherited and by the classical tradition of Plato and especially Aristotle (including his Arabic commentators whose writings became available in Latin during the 13th century). Yet, as we show, Grosseteste moves far beyond the classical authors in the sophistication of his conceptual framework for color. In the De colore, Grosseteste conceives and deploys terminology in a way that assumes very tight definitions, but he avoids linking those definitions to explicit color terms. Instead, he uses his precise terminology to construct an abstract geometric space within which he enumerates exact mathematical combinatorics of color.

2. OUR RATIONALE

Our discussion of the De colore is part of a larger research project that aims to develop and apply a new collaborative methodology for the interpretation of medieval scientific thought between 1100 and 1400. The scientific writing of Grosseteste is complex and intricate and its explication requires collaboration between medievalists and scientists. The surviving manuscripts are difficult to transcribe, and the 13th century saw substantial development of Latin terminology, so any translation must also be sensitive to the dynamics of this evolution. Although the De colore contains no explicit reference to Grosseteste’s other works on light and color (e.g., the De luce and the De iride), their presence in the background of his thought is vital for the interpretation of the De colore. Thus, historical and literary analyses are critical components to understanding the conceptual achievement of the De colore, but a great deal more is to be gained by drawing on our contemporary understanding of color and mathematical approaches that are commensurate with Grosseteste’s own methodology. The De colore is a technical text, and some terminology drawn from contemporary color science proves very useful in discussing the issues that Grosseteste confronts in his text. To do so is not to admit any form of anachronistic projection of a modern scientific framework onto the achievements of a 13th century mind; rather it is to employ all the tools at our disposal to think ourselves back toward what Grosseteste perceived his task to be, and what he accounted as progress toward its completion.

3. COLOR RESIDES IN A CONTINUOUS COMBINATORIAL SPACE

The writings of Aristotle were hugely influential in 13th century scientific thought. From the mid-12th century a huge scholarly effort was devoted to the translation of Aristotle’s scientific corpus new to the West. These were made mostly from Arabic translations of the Greek originals, and as a result, often included not only Aristotle’s texts but also commentaries by preeminent Arabic thinkers, such as Ibn Rushd (known in the West as Averroes). Aristotle rejected Plato’s idea that sight is accomplished via an extramissive ray, instead conceiving of sight as passive and intromissive, and as the action of elemental color on the eye [2]. He identified seven “species” of color existing naturally in the world that could be arranged in a line from white to black [3]. Aristotle proposed that all other colors were derived by mixture of the seven fundamental species. A later anonymous work from the Peripatetic School, the De coloribus, was long-believed to have been written by Aristotle himself, since it systematically describes colors according to the elemental admixture theory of Aristotle’s De sensu et sensato. The De coloribus identifies three things that generate colors: “the light, the medium through which the light is seen, such as air and water, and thirdly the colors forming the ground, from which the light happens to be reflected“ [4]. Any link between the seven fundamental species of color and the three things that generate colors remains obscure in these texts.

In his De colore, Grosseteste opens by introducing the phenomenon of color as a property of light and matter: “Color is light incorporated in a diaphanous medium.” Grosseteste then identifies three bipolarities, each of which is labeled with two extremal terms. Two bipolarities belong to the description of light independent of the medium carrying it, and one arises only by reference to properties of the medium through which the light is passing. The medium can be purum or impurum. The light can be either clara or obscura, and either multa or pauca. The three pairings are used consistently and without variation throughout the text. In the following analysis, we use Grosseteste’s Latin terms without translation. For, as we shall see, the appropriate translation is not immediately obvious.

Grosseteste identifies whiteness with light that is clara and multa incorporated in a medium that is purum, and blackness with light that is obscura and pauca incorporated in a medium that is impurum. By identifying whiteness with the positive poles of his three qualities and blackness with the negative poles, or poles of absence, Grosseteste makes a conceptual link with an Aristotelian one-dimensional axis. His triplet of bipolar terms, however, suggests three separate qualities of color, described by three axes of variation. But, if the text were to stop here, the structure of Grosseteste’s space would remain ambiguous. The subsequent paragraphs of the De colore are critical to understanding the dimensionality of the space in which Grosseteste conceives color to be engendered.

Having identified three bipolar qualities that give rise to color, the text continues, “It also follows from this statement that there are seven colors close to whiteness (no more, no fewer) …” In explaining the move from three qualities to seven colors, Grosseteste provides an impressive mathematical discussion of color enumeration. For, in the De colore, the “seven colors close to whiteness” result not from a close sequence of descent but from the combinatorics of three bipolar qualities. There are eight different combinations that can be made by choosing one pole from each quality (in mathematical notation, 8 = 2³). One of these combinations has already been identified with white, so seven (i.e., 2³ – 1) remaining combinations constitute the other available colors. Grosseteste goes to great pains to work through the calculation in detail, counting the combinations resulting from varying first one, then two, then finally all three of the independent qualities of light and the medium in which it is embodied. In Grosseteste’s text the geometric space is, of course, described in linguistic rather than algebraic terms given the period of composition. However, Grosseteste effectively describes the binomial co-efficients, $\left(\genfrac{}{}{0ex}{}{3}{1}\right)$ , $\left(\genfrac{}{}{0ex}{}{3}{2}\right)$, and $\left(\genfrac{}{}{0ex}{}{3}{3}\right)$, which contribute three, three, and one combination, respectively. Once the geometric space is recognized, a structure of stark clarity emerges from the apparently dense language.

In a second, impressively mathematical move, Grosseteste then extends the discrete combinatorial space of his first enumeration into a fully continuous three-dimensional space: “However, in any of the colors in the middle the degrees of intensification and diminution are infinite.” [1] This statement opens a short section in which he elaborates, paralleling the stylistic approach in which he repeats and extends the idea of combinatorics earlier in the text, to reinforce the concept of continuity by pointing out its consequence within the areas of the color space close to whiteness, close to blackness, and “in the middle.” The attentive reader is left with a careful construction of a three-dimensional conceptual space of color that possesses particular extrema of qualities at its poles, and an explicit recognition of an infinite continuity of colors between them. Contemporary readers of this account with a geometrical turn of mind will already have perceived that Grosseteste’s structure can be thought of in an abstract cubic geometry, an idea that we develop below.

4. TRANSMISSION OF GROSSETESTE’S THREE-DIMENSIONAL SCHEME

A. Errors in Textual Transmission

The text of the De colore appears in 11 different manuscripts, copied from the late 13th to the early 16th century. It is quite normal to find discrepancies between manuscripts, since errors arise during transcription. In preparing our critical edition of the De colore we have been able to gain access to all 11 manuscripts, and have therefore been able to reach new conclusions about the textual transmission of the De colore. There are two particularly interesting examples of textual corruption, which we summarize here since they provide insight into the almost universal failure of modern editors and commentators to appreciate Grosseteste’s three-dimensional scheme.

Analysis of textual variants in the 11 manuscripts of the De colore suggests a major textual split between the two earliest witnesses, dated toward the end of the 13th century, and the remaining nine examples, copied between the 14th and 16th centuries. The supremacy of the early manuscripts is confirmed by the fact that they preserve key elements of Grosseteste’s color-theory.

After enumerating the seven colors close to whiteness, Grosseteste states that there are also seven color directions emanating from blackness. In later manuscripts, on which Baur [7] based his 1912 edition of the De colore, this is summarized as a total of nine colors between white and black. However, in earlier manuscripts we see the more logical summary that since seven colors are connected to each extreme, there are 14 intermediate colors, plus white and black, giving a total of 16. The mistake is likely to have arisen from a straightforward transcription error—where the Arabic numerals 1 and 4 were mistaken for the roman numeral IX and transcribed as novem, the Latin word for nine.

The second transmission error is more interesting from a methodological perspective. We initially started working from later manuscripts that we now know to be in the untrustworthy branch of transmission. However, because of our analysis of the scientific and conceptual content of Grosseteste’s work, we believed that a word was missing in the manuscripts we had available, and we predicted that we would find this missing word in the earliest manuscript from Madrid, which we subsequently did. Later manuscripts omit the adjective obscura in the definition of “blackness.” But, if three extremal qualities were needed for the creation of “whiteness,” i.e., light that is clara and multa incorporated in a medium that is purum, the opposite extremes of the same number of axes are necessary for the creation of “blackness,” i.e., light that is obscura and pauca incorporated in a medium that is impurum.

These errors are not trivial. Grosseteste’s scheme relies on accurate navigation through a geometric, combinatorial space, which he achieves through deployment of precisely defined linguistic labels and careful enumeration of bipolar combinations. If either of these mechanisms of exposition are corrupt they interfere with the correct understanding of Grosseteste’s theory on color creation.

B. A Populist Account

A large section of the De colore appears (unattributed) in an encyclopedia, compiled around 1245, in Paris, by Batholomaeus Anglicus—Bartholomew the Englishman. This encyclopedia, the De proprietatibus rerum (On the properties of things) gives a condensed version of the De colore, which was later translated into Middle English in the 14th century by John Trevisa (1398-9) [5] and further altered and shortened by Batman (1582) [6]. The surviving account of the generation of seven colors from three qualities is as follows (Batman, p. 389):

And while meane [intermediate] colour may abate, then in this wise is generation of three colours, if one abideth alone, the other two abate: and so of white commeth 7 colours.

It is not surprising that the subtlety of Grosseteste’s account of a color space with three dimensions was lost. The contemporary popularity and durable influence of encyclopedists may well have hampered transmission of Grosseteste’s intellectual contribution.

C. Recent Accounts of the De Colore

The first modern edition of the De colore was published by Ludwig Baur in 1912 [7]. Baur, it seems, was unaware of the earliest manuscript, from Madrid, and his account closely follows an early printed version (1514) [8] of a Venice manuscript, which we now know to be at least three times removed from the original [1], and to contain several errors. Few modern scholars discuss the De colore in any detail. In his article on the scientific writings of Grosseteste, Dales [9] provides an almost complete translation of the main sections of the treatise, based on the Baur edition. The corrupt text obscures Grosseteste’s exposition of a combinatorial space, and the dimensionality of his framework for color is therefore missed. Eastwood [10] uses a summary of the color scheme of De colore, which Grosseteste provides in the related but later text De iride (On the Rainbow). Eastwood identifies Grosseteste’s enumeration of the combinations of three bipolar qualities to give six colors in addition to white and black. However, he then maps the six possibilities on to specific colors, without justification, and fails to capture the concept of three axes of variation that give rise to a continuous three-dimensional space of color. A later discussion by Parkhurst and Feller [11] does argue that the color space that Grosseteste describes is indeed a three-dimensional color solid. First, they say, the seven intermediate colors are “all midway between light and dark” (p.g. 225), which by geometric arguments necessitates rotating them away from the one-dimensional Aristotelian scale. Second, they appeal to statements in Grosseteste’s other writings which propose that propagation of “species” follows geometric laws. Third, they note that Grosseteste refers to “figures” which other modern commentators, notably Crombie, have shown to mean three-dimensional figures [12]. Based on this somewhat circumstantial evidence, they sketch (their Fig. 14) a color solid, with a color-circle sandwiched between two conical figures, one with white at the apex, and the other inverted with black at the apex. This interpretation has not been universally adopted, however. A more recent study of the De colore from Kuehni and Schwarz [13] draws Grosseteste’s color scale as a linear one (p. 36).

5. EXPLORING GROSSETESTE’S COLOR SPACE

A. Descriptions of the Physical World and Descriptions of Human Experience

The language of modern color science is strict in its separation of terms that describe physical stimuli and terms that describe human experience. For example, lightness is the perceptual correlate of reflectance (the proportion of light reflected from a surface), and brightness is the perceptual correlate of luminance (the amount of visible light that comes to the eye from a surface). Reflectance and luminance can be measured using physical devices and accepted tabulations of the relative luminous efficiency of the eye; lightness and brightness describe the subjective experiences of the observer. This conceptual framework of physical, physiological, and psychological descriptions will not have been available to Robert Grosseteste. Yet his account speaks to the relationship between the physical and the psychological. He describes the physical manipulations of light and of the diaphanous medium that generate colors. However, his primary method of color measurement will have been visual observation. To identify the bipolarities as separate manipulations of color at least implies that they describe axes of variation that are nondegenerate in perceptual terms. It would be an anachronism to impose our separation of physical and perceptual accounts on a 13th century writer such as Grosseteste, but the language of modern color science brings a useful rigor to the interpretation of his account of color, in the same way that mathematical nomenclature serves to frame the discussion of his formalism.

B. Human Color Perception

The properties of the cone photoreceptors in the retinal mosaic impose a fundamental constraint on human color perception. Metamerism—the prediction that two lights that evoke the same triplet of L-, M-, and S-cone quantal catches will be indistinguishable, even though they may differ in wavelength content—implies that the three-dimensional space of cone quantal catches is exhaustive in describing the gamut of color experience [14]. This is true under certain limited conditions of observation in which a small patch of light is seen in isolation against a black surround, as if through an aperture [15]. However, if we consider regions of extended spatial extent, descriptions of color perception become more complex, not least because of retinal inhomegeneities [16,17]. One important distinction arises between color perception of objects, and of the materials from which they are made, which is categorically different from the perception of isolated lights or surfaces presented in aperture mode [18]. Object colors have additional qualitative dimensions: they can appear glossy or matte; rough or smooth; cloudy or transparent, for example. The neural processes that identify these higher qualities are relatively poorly understood [19].

C. Grosseteste’s Color Space and Modern Constructions

Modern color spaces (e.g., Fig. 1) fall into two broad categories: (i) Cartesian spaces whose axes represent independent primaries, such that an arbitrary colored light can represented within the space according to the combination of primary lights required to produce a metamer; and (ii) a coordinate transform of such spaces that recognizes the special status of the achromatic direction (in which the ratio of primaries is unchanging). Examples of the first category are the RGB space common in computer graphics [Fig. 1a], and the LMS cone space that uses the spectral sensitivities of the L-, M- and S-cones as its primaries. Examples of the second category are a Cartesian space whose axes span the achromatic, red-green and blue-yellow dimensions [Fig. 1c], or a space in which the plane perpendicular to the achromatic axis is described in polar coordinates, with the radial axis representing saturation and the azimuthal angle representing hue [Fig. 1d].

Fig. 1.

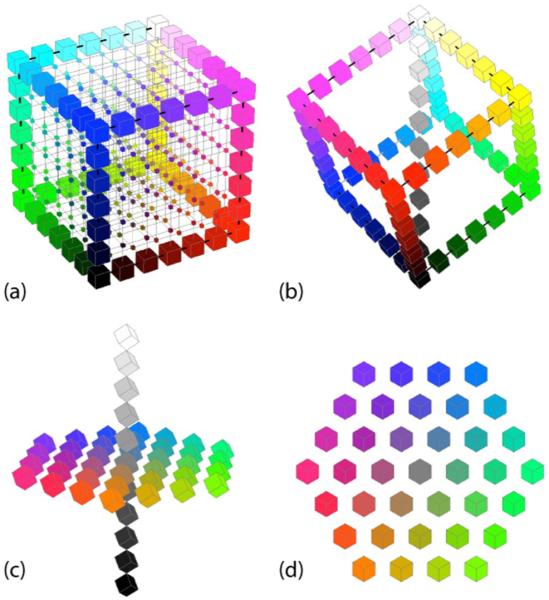
(a) RGB color space; (b) a rotation of the RGB space, in which the achromatic axis (R = G = B) is vertically aligned; (c) achromatic axis and a chromatic plane, spanned by a red-green and a blue-yellow axis; (d) chromatic plane, showing variation in hue (azimuthally) and saturation (radially).

Is it possible to map the color-space of the De colore onto any of these modern constructions? The question arises because of the apparent commensurability between the color-space envisaged by Grosseteste, and that imposed by human trichromacy, at least in terms of dimension. Is it possible that this correspondence could have arisen from careful observation on Grosseteste’s part? Or is it coincidental? Grosseteste sees several distinct colors in the world, and for six or seven of them he has focal color names. He also knows conceptually that three bipolarities are needed to enumerate eight things, perhaps following the tradition of Aristotelian physics to classify elements by the presence of absence of particular properties, or perhaps likening variations in color to variations in spatial position described within the three-dimensional structure of the physical world and its geometric “figures.” In this interpretation, the motivation for identifying three bipolar qualities is purely one of mathematical convenience, and it requires no insight into the three-dimensionality of our perceptual experience of color.

We probe these alternatives by considering possible interpretations of the axes of variation that Grosseteste identifies. It is possible that Grosseteste may have been using three axes of variation as a means to present the concept of a volumetric space, without attaching any further significance to the axes themselves. However, this interpretation fails to motivate the labelling of the axes and the explicit association of the (perceptual) terms whiteness and blackness with the triplets of clara-multa-purum and obscura-pauca-impurum, respectively. Furthermore, although Grosseteste introduces his color space through abstract geometric arguments, the treatise concludes with a paragraph suggesting that those skilled in the principles of optics can appreciate his arguments through experience. For, if they know how to manipulate the three qualities he identifies, “through skill they can show visibly, as they wish, all kinds of colors” [1]. This account is a firm indication that the axes of variation that Grosseteste identified were envisaged by him as real physical qualities with perceptual correlates.

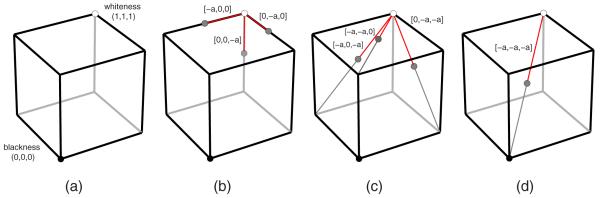
Our examination of the De colore leads us to suggest that Grosseteste’s axes of color variation might be imagined in a Cartesian sense [Fig. 2]. For simplicity we illustrate this using the unit cube, where the origin (0,0,0) is arbitrarily associated with blackness (obscura-pauca-impurum) and the coordinate (1,1,1) is associated with whiteness (clara-multa-purum). Grosseteste’s exposition of the seven colors descending from whiteness describes the seven displacements from the (whiteness) coordinate (1,1,1) toward the other corners of the cube. Following Grosseteste’s categorization of these displacements, the first set of three correspond to decreasing exactly one quality while keeping the others fixed, and can be defined by the Cartesian vectors [−α,0,0], [0,−α,0], [0,0,−α], where a is a scalar quantity between 0 and 1 indicating the magnitude of the displacement. These vectors correspond to the edges of the cube [Fig. 2b]. The second set of three, notationally [−α,−α,0], [−α,0,−α], [0,−α,−α],correspond to decreasing two of the qualities while keeping one fixed. These vectors correspond the diagonals along faces of the cube [Fig. 2c]. Finally, the vector [−α,−α,−α] corresponds to the decrease of all three qualities at once, and corresponds to the main diagonal of the cube [Fig. 2d]. Although this geometric construction is exactly equivalent to Grosseteste’s logic, and provides us with a way to understand the conceptual leap made in the De colore away from the Aristotelian linear series of degrees from whiteness to blackness, we have no direct evidence that allows us to impute to Grosseteste the idea of a cubic color space. He offers little direct indication that abstract geometrical spaces were employed as conceptual tools in the 13th century. A strong geometric constraint on Grosseteste’s color space is the identification of “whiteness” with coordinate (1,1,1), labeled as clara-multa-purum. It is important to note, however, that Grosseteste is quite specific in his language of whiteness (albedo) rather than white (albus), and that whiteness itself incorporates various degrees.

Fig. 2.

(a) Cubic representation of the geometry described in the De colore, with whiteness at the corner (111) and blackness at the corner (000). (b) Three vectors identified by reduction of one of the three qualities. (c) Three vectors identified by simultaneous reduction of two of the three qualities. (d) Vector identified by simultaneous reduction of all three qualities.

D. Qualitative Interpretation of Grosseteste’s Key Terms

It is striking that in a treatise known by the title De colore, Grosseteste includes no color terms, nor does he provide examples of materials with diagnostic color. In one interpretation of De colore, in which Grosseteste’s account reflects a straightforward mathematical convenience of relating eight colors to combinations of three bipolar qualities, this silence is inevitable since there is no scheme by which to identify particular patterns of bits to particular colors, except in the case of blackness and whiteness. Alternatively, the failure to identify specific color terms is equally to be expected if Grosseteste were describing a three-dimensional perceptual space in which the bipolarities identified subjective axes of color variation, like hue and saturation.

Grosseteste provides no explicit definition of the bipolar axes of color variation that he describes, except in the case of multa-pauca, where he elaborates, writing, “I do not say that multa light is light diffused through a large expanse; rather, I say that multa light is gathered as if in a point when a concave mirror is positioned facing the sun and light falling over the whole surface of the mirror is reflected towards the center of the sphere of the mirror…” [1].

So, it is tempting to relate the multa-pauca dimension to variation in the intensity of light, without a change in its chromatic quality. However, in the 13th century, focusing light with a mirror would modify not only the intensity of light at a point but also its wavelength content since the reflectance of the mirror is unlikely to be spectrally flat. So, in practical terms, the primary effect of intensification of light would be accompanied by spectral changes and isochromatic manipulation of intensity would have been difficult to achieve. Nevertheless, since Grosseteste is so explicit in the De colore that multa refers to light focused at a point, we pursue this possible mapping to see how far it can take us. By identifying multa-pauca with an achromatic intensity axis, the remaining two-dimensional subspace spanned by clara-obscura and by purum-impurum (identified as a bipolar property of the medium in which light is embodied), must, if a mapping is indeed possible, correspond to the chromatic (i.e., hue and saturation) subspace of color perception.

It is initially compelling to associate one of the dimensions identified by Grosseteste to saturation, for saturation terminates at a locus of points associated with an achromatic percept (whiteness or grayness depending on intensity). The hazy, indistinct colors close to the central achromatic axis might be described as obscura, “obscure” or dim, and the distinct hues at the perimeter as clara, “clear” or bright (e.g., Fig. 1d). The terms used by Grosseteste in the De colore to identify dimensions of color variation also appear in other of his texts, particularly in the De luce (On Light) and the De iride (On the Rainbow). Some support for the association of clara-obscura with an axis of saturation is suggested by Grosseteste’s use of obscura elsewhere to refer to the impression created by inclusion of scattering particles, like smoke, into a medium. This by itself would desaturate perceived color. The remaining axis of purum-impurum would then be identified with hue. This interpretation, however, produces unresolvable contradictions. In the De colore both the axes of clara and purum terminate at the locus of whiteness. Desaturated colors are perceptually close to white and associated with cloudiness, which would present things in the opposite sense from the axis of progression in the De colore. Furthermore, white light is a mixture of at least two components of different wavelength composition. Although white is a “unique hue” in perceptual terms—appearing phenomeno-logically pure and uncontaminated by other hues—mixing components of different hues can produce white light. In a modern color space this relationship is shown geometrically by arranging hues in a color wheel around a central achromatic point. The hue circle could be unwrapped and arranged linearly, but then Grosseteste’s space would not capture all hues, since the linear arrangement of hue cannot also terminate in black and white.

So, if we abandon the direct association of clara-obscura with saturation, perhaps the association of multa-pauca with intensity can be rescued if both clara-obscura and purum-impurum carry elements of hue and saturation. Certainly, the scattering particles that Grosseteste associates with the term obscura would also generically contain pigment; while purum-impurum, which is explicitly identified as a property of the “diaphanous medium” in which color is embodied, might be identified with a nonscattering pigment or “stain.” If impura and obscura had separable influences on wavelength content, they would effectively give two independent chromatic axes, which might span the chromatic plane [Fig. 1c]. Still we are left with the fundamental difficultly that according to the De colore whiteness is located where all three axes of variation are at their positive extremes: if Grosseteste intended to accommodate the full gamut of hue variation in his scheme, this is inconsistent with only two axes to carry variation in hue, if additionally both of these terminate at the white point.

Perhaps instead the three axes of variation would be better interpreted as identifying three primary lights. As we hinted above, the association of multa-pauca with a pure achromatic axis is implausible on practical grounds. Multa might move along a yellow-white axis as sunlight or candlelight was intensified to the point of burning. The idea that multa-pauca may itself carry a component of hue is supported by reference to the related treatise the De iride, which probably postdates the De colore [1]. When the apparent colors are eventually mentioned toward the end of the text of the De iride it is the intensification and diminution of light by refraction that is supposed to generate the spectrum of hues across the rainbow. The one example given is the relation of blue shades to pauca. Since yellow and blue are complementary colors, a shadow cast in candlelight can appear bluish [20]. Furthermore, variation between direct sunlight and indirect skylight (often seen in shadows) traces out a perceptually significant line in color space, between unique yellow and unique blue [20]. If clara-obscura and purum-impurum are identified with two other independent primary lights, Grosseteste has a direct recipe for mixing colors within a color cube analogous to the RGB cube mentioned above. Reference to another of Grosseteste’s writings, Dictum 141, lends some support to this interpretation, at least for purum-impurum since Grosseteste discusses explicitly how “pure” sunlight is incorporated within glass, so taking on the colored nature of that material. In that Dictum 141 Grosseteste deploys several color terms—green, yellow and red.

It is possible that, on examination, Grosseteste is not extending the dimensionality of Aristotle’s color-line at all, but merely incorporating the ideas of “cloudiness” or “transparency” (or a combination of these) within the concept of “color.” Perhaps the departure from Aristotle really consists of a move from discussing the appearance of colored lights (in “aperture” mode) to discussing the appearance of colored materials (in “object” mode). This corresponds to quite a different dimensional extension of a color line.

An important clue regarding this suggestion is found within the opening statement: “color is light incorporated in a diaphanous medium.” One possibility identified above is that obscura-clara might relate to “cloudiness” or “translucency,” thus broadening Grosseteste’s definition of “color” beyond that of pure colorimetry, to include other aspects of materially embodied perception of light. Some difficulties arise with this interpretation since the quality of translucency, within the context of the obscura-clara axis, is identified in the De colore as a property of light itself, rather than a property of the medium. If obscura-clara described for Grosseteste the quality of translucency, it is difficult to see why the explicit association between purum-impurum and the medium would not have been extended by Grosseteste also to obscura-clara.

6. CONCLUSION

Robert Grosseteste in his short treatise the De colore creates an explicitly three-dimensional abstract space of color. He replaces Aristotle’s linear arrangement of colors between white and black by a scheme in which colors are generated from whiteness (and symmetrically from blackness) by the independent adjustment of three qualities. He painstakingly leads the reader through an explicit combinatorial exercise, identifying 2³ - 1 unique directions from whiteness along which color can vary. The space is continuous, with infinite degrees of intensification or diminution along each of the directions he identifies. He introduces this space through abstract reasoning, but in the closing paragraph he refers to technical expertise in manipulating light and materials to generate all possible colors. The basis for his choice of three-dimensions is not clear, but one possibility is that it is motivated by the number of independent operations by which light could be manipulated within materials. Whether Grosseteste actually carried out such manipulations, or just conceived of them, is a tantalizing question, coming as it does from an era that saw the first stirrings of ideas that later led to the experimental method. We pursue a number of possible interpretations of Grosseteste’s color axes. While it is possible to generate some plausible mappings to modern color terminology, it is also true that such mappings are achieved only by forcing interpretations onto the text. The De colore is probably best interpreted as a conceptual theater in which specific manipulations of color can be played out, rather than an equivalent of any modern color space, although the three-dimensionality of Grosseteste’s color space is beyond question.