Optimal study design for pioglitazone in septic pediatric patients

Abstract

The objective was to demonstrate the methodology and process of optimal sparse sampling pharmacokinetics (PK). This utilized a single daily dose of pioglitazone for pediatric patients with severe sepsis and septic shock based upon adult and minimal adolescent data. Pioglitazone pharmacokinetics were modeled using non-compartment analysis WinNonlin Pro (version 5.1) and population kinetics using NONMEM (version 7.1) with first order conditional estimation method (FOCE) with interaction. The initial model was generated from single- and multiple-dose pioglitazone PK data (15 mg, 30 mg, and 45 mg) in 36 adolescents with diabetes. PK models were simulated and overlaid upon original data to provide a comparison best described by a single compartment, first order model. The optimal design was based on the simulated oral administration of pioglitazone to three groups of pediatric patients, age 3.8 (2–6 years), weight 14.4 (7–28 kg); age 9.6 (6.1–11.9 years), weight 36.5 (28.1–48 kg) and age 15.5 (12–17 years,) weight 61.6 (48.1–80 kg). PFIM (version 3.2) was used to evaluate sample study size. Datasets were compiled using simulation for each dose (15, 30 and 45 mg) for the potential age/weight groups. A target dose of 15 mg daily in the youngest and middle groups was considered appropriate with area under the curve exposure levels (AUC) comparable to studies in adolescents. The final optimal design suggested time points of 0.5, 2, 6 and 21 h for 24 h dosing. This methodology provides a robust method of utilizing adult and limited adolescent data to simulate allometrically scaled, pediatric data sets that allow the optimal design of a pediatric trial. The pharmacokinetics of pioglitazone were described adequately and simulated data estimates were comparable to literature values. The optimal design provided clinically attainable sample times and windows.

Introduction

There is a fundamental need to incorporate size and physiological based information while modeling data in a systematic fashion that will be applicable for use with pharmacologic and therapeutic compounds that children are exposed to. In pediatric pharmacology, particularly with respect to the approach of optimal design, pharmacokinetic (PK) data is rarely if ever readily available, particularly for a specific age group or condition. Adult data, and in some cases, adolescent data is frequently available but typically reported only as summary statistics rather than actual population level data. In order to be useful to the study of pediatrics, that data must be appropriately scaled as well as address the increased variability typically seen in pediatric populations.

This approach allows the reduction of the risk associated with obtaining data for the sake of collecting data in these populations. While models have been advanced for some pediatric applications, they can lack sufficient numbers or generalizability to be clinically relevant and applicability to the wider pediatric population. The development of well-designed clinical trials, utilizing optimal design and trial simulation holds the promise of providing more relevant data. A systematic application of design techniques for sample size calculation, sampling times for PK studies, effectiveness outcome measurements during the study, and drug-drug interactions can lead to improved clinical trial outcome.

This manuscript demonstrates the process of simulating adult data from available summary data, allometrically scaling that data and accounting for the increased variability associated with pediatric populations in order to utilize those results to optimally design a pediatric clinical trial with sparse sampling techniques. As an example of this methodology, a pediatric clinical trial utilizing pioglitazone, a peroxisome proliferator-activated receptor-c (PPAR-c) agonist, to potentially reduce inflammation in the treatment of pediatric sepsis is described.

Pioglitazone is primarily known as a thiazolidinedione antidiabetic agent which increases insulin sensitivity [1]. The PPAR-c agonists also inhibit monocyte inflammatory cytokines [2] and are involved in the regulation of the sepsis-induced inflammatory response. PPAR-c ligands exert anti-inflammatory effects in experimental models of sepsis and improve survival [3–5]. Specifically, treatment with PPAR-c ligands reduce neutrophil infiltration in the lung, colon, and liver and reduce cytokine production [6–8]. It is proposed that the use of thiazolidinediones may show benefit in reducing the inflammatory process associated with severe sepsis in pediatric patients. Sepsis is associated with high rates of morbidity and mortality in children and adults, the mortality rate increases with age from 10% in children to 38% in the elderly population [9, 10]. Sepsis is a continuum of clinical entities, from the systemic inflammatory response syndrome (SIRS), sepsis, severe sepsis, and septic shock which can lead to multiple organ dysfunction syndrome (MODS) and death [11].

Pioglitazone is well absorbed after oral administration and extensively metabolized by hydroxylation and oxidation to three active metabolites, M-II, M-III and M-IV. M-III and M-IV also contribute to the lowering of plasma glucose [12]. The safety and efficacy in children is relatively unknown and there have been limited studies in adolescents [1, 12]. In studies to date, age and gender have not been reported to significantly affect the pharmacokinetics of pioglitazone. Studies in patients with renal failure have concluded that no adjustment is needed to the starting dose, since elimination is primarily hepatic [1]. The clinical pharmacokinetics of pioglitazone have been reported following clinical trials in healthy subjects. Peak concentrations in plasma are achieved approximately 1.5 h (range 0.5–3 h), with doses ranging from 2 to 60 mg. In single oral dosing in adults the maximum plasma concentration (C_max) and the area under the curve (AUC) increased linearly with dose, with C_max ranging from 101 to 3500 ng/ml [13]. Following repeated dosing, there was no dependency between dose and time on the absorption of pioglitazone.

The primary objective of this study was to demonstrate the techniques that allow the design of a single daily dose pharmacokinetic study for pediatric patients. We focused on the specific example of sepsis using a sparse sampling strategy for pioglitazone. We utilized a population PK modeling and simulation with variability estimates and significant covariates based upon adult and limited adolescent data.

Methods

Non-compartmental analysis

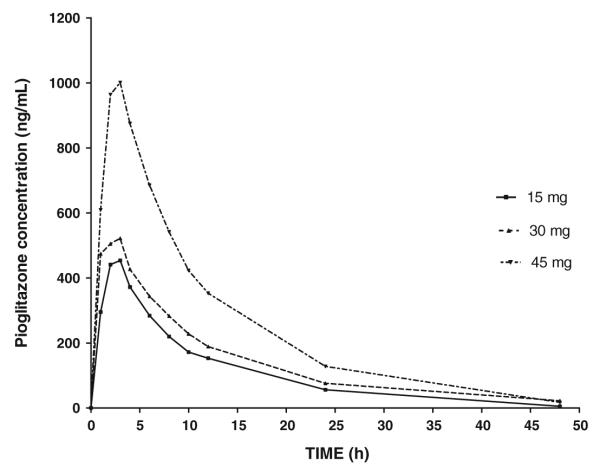
WinNonlin Pro (version 5.1, Pharsight, Mountain View, CA) was used to determine the PK parameter estimates for a single 15, 30 or 45 mg dose from Christensen et al. [12] Using a non-compartmental approach (NCA) the following was determined for a single 15 mg dose, half-life, 7.94 h and C_max, 454 ng/ml (Fig. 1, Table 1). The NCA provided estimates for total drug exposure and AUC that were consistent with the literature.

Fig. 1.

Time-concentration profiles (n = 12) from Christensen et al. [16] study following a single dose of 15 mg (bottom line), 30 mg (middle line) and 45 mg (top line) (0–48 h)

Table 1.

Comparison of PK estimates for a single dose between the literature reported values and simulated values for 15, 30 and 45 mg

	Half-life (h) mean (range)	Cmax (ng/ml) mean (range)	AUC0–24 (ng h/ml) mean (range)
Christensen et al. [16]
15 mg	8–9 (4–17)a	478 (333–886)	4506 (2849–7522)
30 mg	8–9 (4–17)a	587 (120–1225)	5618 (1076–8868)
45 mg	8–9 (4–17)a	1053 (701–1715)	10438 (6297–16897)
Simulated PK
15 mg	7.9 (4.9–11.5)b	498 (357–870)	4933 (2534–8094)
30 mg	8.3 (5.29–13.3)	629 (343–1156)	5563 (2134–9142)
45 mg	9.3 (5.18–16.95)	1087 (589–1743)	10663 (4784–20134)

^aReported half-life mean (range) for single dose (15, 30, 45 mg)

^bEstimated half-life mean (range) for single dose (15 mg)

Population pharmacokinetic analysis

Non-linear mixed effects modeling (NONMEM, version 7.1, ICON Dev. Soln., Ellicott City, MD) with PDx-Pop® (version 4.10, 2007 ICON Dev. Soln., Ellicott City, MD) interfaced with Xpose® (version 4.0, release 6, update 1) was used to perform the pharmacokinetic analyses. NONMEM was used with first order conditional estimation method (FOCE) with interaction algorithm.

The mean concentration data for each pioglitazone dose was available from Christensen et al. data were obtained from adolescents with type 2 diabetes following a single daily dose (15, 30 and 45 mg) (Fig. 2). Using NONMEM, the concentration time profiles were simulated for various doses based upon the PK parameters obtained from [12]. Simulation data were used to obtain n = 20 for each the following doses, 15, 30 and 45 mg. Inter-individual variability and residual variability were estimated. The PK parameters were oral clearance (CL/F), oral volume of distribution (V_d/F) and absorption rate constant (k_a). A one-compartment PK model with first order absorption was used to describe the data. Two compartment models were tested, but the one-compartment model performed better, providing a much lower objective function value and standard error, the final estimates also more closely match those reported in the literature.

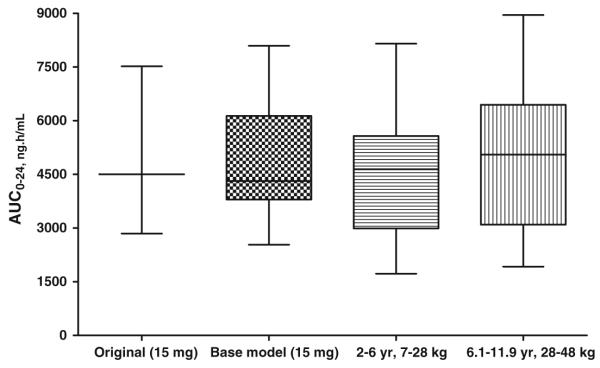
Fig. 2.

AUC₂₄ estimates (ng h/ml) from Christensen et al. [16] study following a single 15 mg dose compared to estimates obtained from the base PK model and allometric scaled models

A base model applied to the concentration data available from Christensen et al. estimated pioglitazone CL/F at 3.03 l/h, V_d/F was 0.112 l and k_a, 1.53 h. In comparison the base model applied to the simulated data estimated CL/F 3.36 l/h, V_d/F 0.196 l and k_a, 1.54 h. Inter-individual variability was estimated at 82.3 CV% for CL/F, 71.3 CV% for V_d/F and 31.5 CV% for k_a. The estimates obtained from the model applied to the simulated data were consistent with estimates reported in the literature [1, 12]. It was anticipated that inter-individual variability would be higher in a pediatric population [14]; therefore individual variability was set at 50% for k_a (as opposed to 27% in adolescents [12]). The residual variability was 13.5 CV% and 0.316 ± SD for the base model.

Subjects

The study aimed to investigate the administration of pioglitazone as a single daily dose therapy in a pediatric population with severe sepsis and septic shock. Due to the large variation in age and weights observed in pediatric populations, 3 groups divided by age and weight were derived. The cutoffs used to defined the 3 different age groups was in accordance with the guidelines outlined by the FDA [15]. Data related to weight and age were obtained from retrospective analysis of patients admitted to the Cincinnati Children’s Hospital Medical Center (CCHMC) Pediatric Intensive Care Unit (PICU) with sepsis and the Center for Disease Control clinical growth charts for children [16]. Datasets were compiled for each separate dose (15, 30 and 45 mg) for the potential age/weight groups under investigation. In total 9 separate datasets were created and included the following: Group 1 age 3.8 (2–6 years), weight 14.4 (7–28 kg); Group 2 age 9.6 (6.1–11.9 years), weight 36.5 (28.1–48 kg) and Group 3 age 15.5 (12–17 years,) weight 61.6 (48.1–80 kg). Each dataset contained 20 individuals and 200 observations. The datasets, which utilized allometric scaling, did not account for the potential for obesity and a maximum weight of 80 kg was utilized. The optimal dose and required study recruitment numbers were also determined for the 3 groups.

Covariate analysis

The population PK base model was used to evaluate the effect of weight and age and other covariates on the pharmacokinetics of pioglitazone. Along with weight and age, height and gender was also included in the covariate analysis. This information was obtained from the retrospective PICU database. Length of stay and mortality score were also tested, but as all the data from the PICU came from confirmed septic patients; sepsis could not be tested as a dichotomous covariate. PK parameters were allometrically scaled in the model according to the covariate of interest, in the simulated individual results obtained using the following Eq. 1 based upon original subject data.

$${\text{Param}}_i={\text{Param}}_{\text{typical}}\cdot {\langle \frac{{\mathrm{Cov}}_i}{{\mathrm{Cov}}_{\text{refvalue}}}\rangle }^{\text{allometric},\text{exponent}}$$ (1)

where Param_i is the PK parameter for the ith individual, Paramtypical is the typical population value. Cov_i is the specific individual covariate and Covrefvalue is the value of the covariate that is used as a reference. The “allometric exponent” is the allometric exponent that defines the relationship between the PK parameter and the covariate.

Following covariate modeling, body weight was the only covariate identified as having a statistically significant effect on CL/F and V_d/F in the population PK model. Age was not identified as having a statistically significant effect. Along with the potential influence of age, the influence of maturation of clearance and renal function were also considered as potential covariates. Age is typically used to describe maturation of clearance. The inclusion of a quantitative model to describe maturation varies depending on the population under investigation [17]. Maturation of clearance was not included in the model as elimination is primarily hepatic (CYP2C8 and CYP3A4) with no clear maturation of these pathways beyond the age of 1–2 years, therefor by the age of the individuals that were simulated, this should not be a contributing factor [1, 18]. CYP2D6 has been associated with polymorphism on the variability of the pharmacokinetics of some drugs [14, 17, 18]. However, CYP2D6 is suggested to only play a minor role in the PK of pioglitazone.

Another approach to scaling the PK parameters was a theoretical approach that fixed the allometric exponent to its theoretical values [14]. In pediatric dosing, theoretical scaling of models is considered more conservative and preferable as the covariate distribution used to develop population PK models may not include the low body weight ranges or age ranges specific to pediatric populations. Allometric size modeling is a mechanistic approach, by fixing the power exponent to a specific value it allows improved investigated of secondary covariate effects from the effect of size [17, 19].

Determining dose

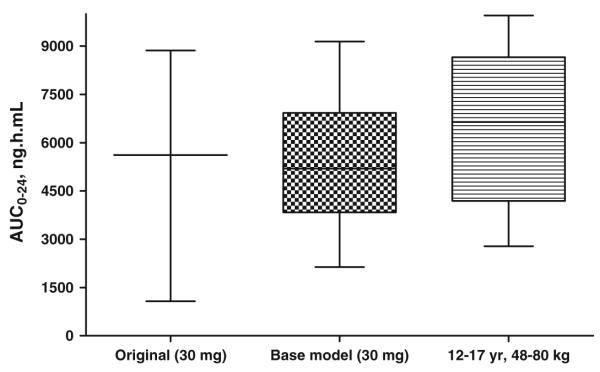
Using allometric scaling, pediatric dosing can be determined from adult doses [17,19]. With an approximate age range of 2–6 years, weight range 10–23 kg, the percentage of adult dose required is estimated as 23–43.5%. The fraction of adult dose using an allometric scaled model is estimated at ’. In order to predict the target exposure levels for pioglitazone in relation to therapeutic response and safety, NONMEM, was used to predict AUC using the base population PK model and the allometric scaled model. AUC was used to compare estimates between the original data and estimates from the developed models by using box and whisker plots. This provided a comparison between the smallest observation (sample min), lower quartile (25th), median (50th), upper quartile (75th), and largest observation (sample max). These values were compared to those reported in the literature [12]. It was found that the estimates produced in the base model were comparable to the reported AUC and as expected the AUC estimated in the allometric scaled model was slightly higher. For example the mean (range) estimated AUC (ng h/ml) reported by Christensen et al. was 4506 (2849–7522) compared to 4933 (2534–8094) from the base model; 4407 (1725–8153) in the 2–6 years, 7–28 kg model and 5105 (1925–8953) for the 6.1–11.9 years, 28.1–48 kg model. In comparison to the 15 mg dose, the mean AUC estimate for 30 and 45 mg dose was high higher (Fig. 3). The mean (range) estimated AUC (ng h/ml) form the base PK model was 5563 (2134–9142) and 6557 (2784–9953) in the 12–17 years, 48.1–80 kg compared with the estimations from Christensen et al. of 5618 (1076–8868).

Fig. 3.

AUC₂₄ estimates (ng h/ml) reported by Christensen et al. [16] following a single 30 mg dose compared to estimates obtained from the base PK model and allometric scaled model

Although the proposed study is in pediatric patients with severe sepsis or septic shock, it is worth noting that for type 2 diabetes mellitus, the initial dosage of pioglitazone is 15 or 30 mg orally once daily without regard to meals. If the patient has an inadequate response to pioglitazone, the dose may be increased in 15 mg increments up to 45 mg orally once daily. The maximum recommended dosage of pioglitazone in adults is 45 milligrams once daily. To date, safety and effectiveness of pioglitazone has not been established in pediatric patients. (Prod Info ACTOS(R) oral tablets, 2008).

A target dose of 15 mg daily in those aged 2–6 years (7–28 kg) and 6.1–11.9 years (28.1–48 kg) was considered appropriate to result in exposure levels (AUC) of pioglitazone comparable to the 15 mg dose level in adolescents as reported by Christensen et al. Generally, the dose required in infancy (<1 year) to achieve a set target concentration is greater than in older children. This is because clearance is nonlinearly related to weight [17]. A target dose of 15 mg is also proposed due to the available formulations of pioglitazone; 15 mg, 30 mg and 45 mg. Use of this dose (15 mg) will reduce the potential to introduce variability and error by requiring modification of the existing formulation, as tablets will not have to be broken. In the older proposed age group of 12–18 years (48.1–80 kg), a target dose of 30 mg daily was predicted to provide equivalent exposure. Although age is specified here in relation to choice of dose, it should be noted that estimates for AUC and other PK estimates have been based primarily on weight. Therefore, in the case where a subject is aged 13 years but has a body weight of less than 48 kg, they should be dosed at the lower dose of 15 mg. The dosing determined in the study for the ages of 2–6 years with weight 7–28 kg and [28 kg proposed 15 mg. In the age ranges 6.1–11.9 years and 12–17 years for weights less than 48 kg a dose of 15 mg was suggested. For those with a weight over 48 kg and less than 80 kg, a dose of 30 mg was proposed.

Consideration should also be given to the potential need for dose adjustment in severe sepsis and septic shock. Drug distribution may be altered as tissue perfusion is reduced in less vital organs such as the kidney and the skin. Changes in tissue perfusion and capillary permeability in sepsis are highly variable, often resulting in different dosage requirements within and between individuals [20]. Septic patients tend to have an increased volume of distribution and large inter-patient variability in clearance. The volume of distribution then decreases as the patient’s condition improves. During severe illness, usual dosages (mg/kg) of some drugs have been shown to result in lower than expected peak concentrations, thus necessitating administration of larger doses [21].

Optimal design strategy

Population PK modeling and optimal sampling strategies used WinPOPT (version 1.2, 2008)[22], as described by Fig. 4 to evaluate and to determine an optimal sampling strategy in a pediatric population. WinPOPT is specifically designed for optimizing sampling strategies for nonlinear mixed effects models [23–25]. WinPOPT is a windows interface and provides extensibility to the Population Fisher Information Matrix (PFIM) application. The design was also evaluated in PFIM 3.2 [26], an R function for evaluation and optimization of population designs based on the Population Fisher Information Matrix of nonlinear mixed effects models. For the given population PK model, PK parameter estimates, dose and optimal sampling times, the effects of between subject variation and sample size on precision of PK parameter estimates were investigated.

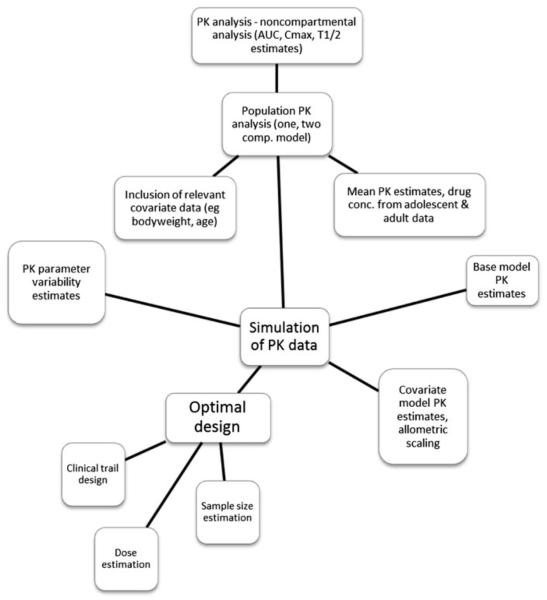
Fig. 4.

Flow diagram showing methods used in study design. Where PK is pharmacokinetic; AUC is area under the curve; T1/2 is half-life; C_max is maximum plasma concentration

The optimal sampling analysis was performed using a priori information for the PK parameter estimates as determined using the one-compartment PK model with first order absorption from the simulated data and estimates reported in the literature [1, 12]. An optimal design approach was used to maximize the PK study information in pediatric patients while minimizing the number of blood samples required and the volume of blood collected for the study. Typically, one sample is required for each PK parameter that is to be estimated by the PK model. Therefore, a minimum of 3 sampling time points was required to produce reasonable concentration time-profiles.

Determining sample size

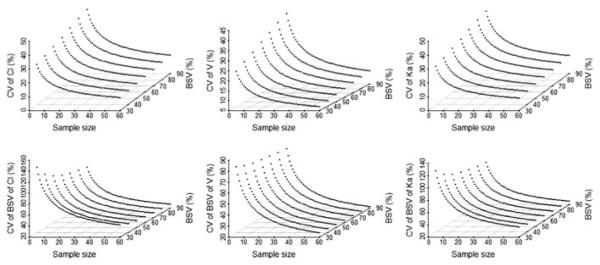
It is proposed that the selection of sample size in pediatric studies should be based on the PK parameters with defined acceptable estimates for precision (P.R. Jadhav, Personal communication). In pediatric studies, when using a power equation to determine sample size or sampling, a 20% CV in the parameter of interest has been proposed as the quality standard [27]. Figure 5 shows the CV and SE of PK parameter estimates with BSV ranging from 30 to 90% at sample sizes of 5–60 patients. It was estimated that the number of subjects needed to achieve 20% CV for PK parameters for different age groups were as follows. Group 1 18 subjects for (2–6 years, 15 mg, 50% BSV), to 24 subjects for (2–6 years, 15 mg, 80% BSV) (Fig. 5); Group 2 13 subjects for (6.1–11.9 years, 15 mg, 50% BSV) to 20 subjects for (6.1–11.9 years, 15 mg, 80% BSV); and Group 3 6 subjects for (12–17 years, 30 mg, 50% BSV), to 20 subjects for (12–17 years, 30 mg, 80% BSV).

Fig. 5.

Using PFIM estimates obtained relating to sample size required for 2–6 years 15 mg. Where CV is coefficient of variation; BSV is between subject variability, CL is clearance; V_d is volume of distribution and Ka is absorption rate constant

For each age/weight group and each dosing range it can be seen that with increasing variability more subjects are required to achieve the required accuracy. Assuming the primary PK parameter CL/F is associated with C50–B80% variability in a pediatric population, then the estimated sample size required to achieve the quality standard is a minimum of 6–13 subjects dependent on the age/weight group. If the variability of the parameter is C80–B90%, then the ideal sample size is 20–24 subjects in the 2–6, 6.1–11.9 and 12–17 years age groups are required (P.R. Jadhav, Personal communication) [27].

Optimization of design

The main design variables were the sampling times applied to each tested design option. The dose was set at 15 or 30 mg per 24 h. The design for optimal sampling times was continuous over the potential range of 0–24 h. The numbers of subjects evaluated were, Group 1 (n = 18–24), Group 2 (n = 13–20) and Group 3 (n = 6–20). As outlined above, the PFIM application was used to evaluate and determine appropriate sample size numbers for each group. The total number of samples per subject was initially fixed to 3, the same number as the number of fixed effect parameters. The smallest allowable time between consecutive sampling times was fixed at 0.5 h.

The optimal design strategy was tested for each of the best final three allometric scaled models for the three age/weight groups, Group 1 and Group 2 received 15 mg and Group 3 received 30 mg. Following evaluation of the study design and review of the FIM determinant and criterion, standard errors for the PK parameters were reviewed. SE% less than 50% for the fixed effects parameters were used to assess the utility of the design. Designs with SE% over 50% for the fixed effects parameters were considered poor designs. Sampling windows were estimated around each of the sampling times to allow for the design to be applied more easily to clinical practice.

Evaluation of this design found reasonable SE (defined as B20–30%) for the fixed effect parameters. Group 1, n = 18, initial sampling times were: 0.5 fixed, 1.5 and 3.5 h. Timing for the initial sample was fixed to occur after 30 min postdose due to a potential lag-time in absorption. As pioglitazone is administered orally, a longer time should exist between the time the drug is administered and when the first sample is taken to account for absorption. Therefore, a fixed initial sampling time was set at 30 min post dose. Group 1, n = 24, produced lower SE% compared to n = 18, suggesting the optimal design should include at least 24 subjects. Group 2 showed the same trend with n = 20 producing lower SE estimates. For group 3 with a dose of 3 mg, the trend was the same as seen for group 1 and 2, however, the SE% estimates for generally higher for all fixed effect parameters. Given these results it was decided to evaluate all further optimal designs using n = 20. Following optimization of the final sampling times (0.5, 1.5, and 3.5 h) the sampling windows for Group 1, 2 and 3 were estimated and found to be similar. There was little distinction between proposed designs for Groups 1 and 2.

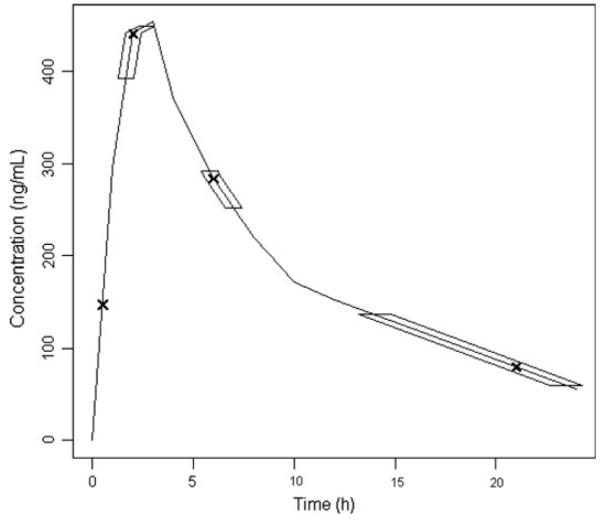
The initial design, which was constrained to 3 sampling times, did not produce a later sampling time (trough). Therefore the constraint was removed and additional sampling times were evaluated. Following further optimization, which included a fixed sampling time at 30 min post dose, the design proposed 4 sampling times as outlined in Fig. 6. To further evaluate the proposed sampling times, the design was optimized using simulated annealing which is considered to have more rigorous convergence properties compared to an exchange algorithm. It was found that the optimal sampling times were not much different from those provided by use of the exchange algorithm, 0.5, 2.2, 6.5 and 20.5 h. However, for clinical convenience the proposed sampling times have been rounded to the nearest hour or half-hour. The upper and lower boundaries for the marginal sampling windows were 1 h 40 min–2 h 40 min, 5 h 50 min–7 h and 14 h–23 h 30 min (Fig. 6).

Fig. 6.

Final proposed optimal design sampling times at 0.5, 2, 6 and 21 h (design included a 0.5 h fixed sample time, no upper time constraint and no limit on number of sample times). Sampling windows were suggested as follows for each optimal sample time: 2 h (1 h 40 min–2 h 40 min); 6 h (5 h 50 min–7 h); 21 h (14 h–23 h 30 min)

There was no significant difference in the sampling times and windows proposed by the optimization for any of the age/weight groups. Group 3 provided slightly wider sampling times but for clinical convenience and to reduce confusion it is suggested that the sampling times and windows used should be the same for all age/ weight groups. It is proposed that sampling within these windows will yield a design that is clinically attainable and provided reasonable estimates for the PK parameters of interest.

Discussion

This methodology relies upon the systematic and stepwise implementation of a variety of pharmacokinetic and optimal design tools to propose a design for a single daily dose of pioglitazone in pediatric patients with severe sepsis or septic shock using a sparse sampling strategy. This required the utilization population PK modeling and simulation, variability estimates and evaluation of significant covariates. The study was undertaken using a D-optimal design approach and suggested sampling times were 0.5, 2, 6 and 21 h for a single 24 h dose. The optimal design produced precise parameter estimates and resulted in a clinically attainable and practical sampling strategy. The design also provided suggestions for sampling windows to provided flexibility in the clinical setting and for undertaking the study in a pediatric population.

Achievement of the objective of this study, allows for application of this approach to be generalized to other datasets by increasing the amount and quality of informative data available. Once existing adult data has been appropriately adapted, it forms the basis upon which a clinical trial can be simulated in silico to allow potential problems to be addressed before the clinical trial is run. Data subsequently generated from the actual clinical trial can be used to validate the model and further refine the simulation for larger, more definitive clinical trials. This will lead to better designed clinical trials from which funding agencies and investigators will be more able to answer the clinical research question. For patients and families this means fewer samples will be required in a pharmacokinetic study and fewer study visits. The impact of optimal design and trail simulation will significantly improve the safety and ultimately the ability to conduct trails. The ability to conduct efficient clinical trials will build more extensive data sets that will allow further refinement for even safer studies to be designed.

Pediatric patient PK data are limited in general and there are no PK studies in children treated with pioglitazone. This study therefore utilized simulation techniques to generate data appropriate for children. This allowed consideration to be given to estimate variability and those covariates, which are significant in a pediatric population, namely weight and age. Currently there are no data available on the pharmacokinetics of pioglitazone in septic patients. Furthermore, because sepsis is a continuum of clinical entities ranging from the SIRS to sepsis, severe sepsis and septic shock the pharmacokinetics of pioglitazone may change depending on the physiologic state of the patient. Therefore it is unknown if sepsis will be a significant covariate in relation to the pharmacokinetics of pioglitazone.

Prior information was obtained from a study undertaken in adolescents with type 2 diabetes. This allowed for some comparison in the PK estimates and associated variability of pioglitazone. The inter-individual variability in drug exposure as measured by the AUC was reported to be dose dependent, with inter-individual variability of an AUC 50% at lower doses and 30–35% at higher doses in the adolescent study. AUC was dose proportional, at 15 mg, 4474 ng h/ml, 30 mg, 7845 ng h/ml and with 45 mg dose, 11370 ng h/ml. CL/F for a 15 mg dose, 3.23 (1.08) l/h, 30 mg, 5.53 (5.39) l/h and 45 mg dose, 3.92 (1.19) l/h (16). There was a reasonable correlation between the simulated data parameter and AUC estimates compared to those reported in the literature.

As this is the first proposed study of pioglitazone for use in the treatment of sepsis in children aged 2–12 years of age, it is possible the design may need to be modified. Although the proposed dosing strategy and sampling design is expected to result in adequate exposure, it is suggested that an interim PK analysis following the availability of concentration data from a minimum of 3 subjects should be performed for each of the three age/weight groups. Individual Bayesian PK estimates should be derived using the data and concentration–time profiles used to evaluate the study design performance. Assessment of the PK parameters as predicted by the concentration–time profiles will help to determine safety and whether dose adjustment or sampling time adjustment is necessary.

Application of this methodology relies upon limited data utilizing a combination of technique, which provides initial design parameters. This technique establishes a starting point based upon efficient usage of pharmacometric techniques. However, it is not intended nor is it appropriate to assume that this type of information is sufficient to make dosage or treatment recommendations. Clearly, the accuracy of the original data is reflected in the outcome of the optimal design process. Nothing can replace reevaluation of the design once data from the population of interest becomes available.

Conclusions

The pharmacokinetics of pioglitazone were described and simulated data estimates were comparable to those outlined in the literature. The D-optimal designed strategy provided clinically attainable sample times and windows. The final proposed optimal design suggested sampling times were at 0.5, 2, 6 and 21 h for a single 24 h dose. As pioglitazone has not previously been used in the treatment of sepsis in the 1–18 year old patient, the potential risks of the dosing schedules will need to be individually assessed and evaluated.

This type of methodology is useful across the spectrum of pediatric clinical research as well as within any subpopulation (age, developmental level or condition) in which the extrapolation of existing data is necessary prior to initiating studies of that group. Taken together, the techniques described provide a starting point from which actual data in the given subpopulation can be collected, which can then be used to further refine the pharmacometrics and expansion of existing knowledge.