Abstract
Background
Enumeration of chemical graphs satisfying given constraints is one of the fundamental problems in chemoinformatics and bioinformatics since it leads to a variety of useful applications including structure determination of novel chemical compounds and drug design.
Results
In this paper, we consider the problem of enumerating all tree-like chemical graphs from a given set of feature vectors, which is specified by a pair of upper and lower feature vectors, where a feature vector represents the frequency of prescribed paths in a chemical compound to be constructed. This problem can be solved by applying the algorithm proposed by Ishida et al. to each single feature vector in the given set, but this method may take much computation time because in general there are many feature vectors in a given set. We propose a new exact branch-and-bound algorithm for the problem so that all the feature vectors in a given set are handled directly. Since we cannot use the bounding operation proposed by Ishida et al. due to upper and lower constraints, we introduce new bounding operations based on upper and lower feature vectors, a bond constraint, and a detachment condition.
Conclusions
Our proposed algorithm is useful for enumerating tree-like chemical graphs with given upper and lower bounds on path frequencies.
Introduction
Development of novel drugs is one of the major goals in chemoinformatics and bioinformatics. To achieve this purpose, it is important not only to investigate common chemical properties over chemical compounds having common structural patterns [1-3] but also to study methods of enumerating chemical structures satisfying given constraints. The enumeration of chemical structures has a long history. Actually, Cayley [4] considered the enumeration of structural isomers of alkanes in the 19th century. Applications for the enumeration of chemical compounds include structure determination using mass-spectrum and/or NMR-spectrum [5,6], virtual exploration of chemical universe [7,8], reconstruction of molecular structures from their signatures [9,10], and classification of chemical compounds [11].
In the field of machine learning, the pre-image problem [12,13] has been studied. In this problem, a desired object is computed as a feature vector in a feature space, and then the feature vector is mapped back to the input space, where this mapped back object is called a pre-image. The definition of the feature vectors based on the frequency of labeled paths [14,15] or small fragments [11,16] has been widely used. Akutsu and Fukagawa [17] formulated the graph pre-image problem as the problem of inferring graphs from the frequency of paths of labeled vertices, which corresponds to the pre-image problem, and proved that the problem is NP-hard even for planar graphs with bounded degrees [17]. Nagamochi [18] proved that a graph determined by frequency of paths with length 1 can be found in polynomial time if any.
To enumerate tree-like chemical graphs, Fujiwara et al. [19] proposed a branch-and-bound algorithm which consists of a branching procedure based on the tree enumeration algorithm due to Nakano and Uno [20,21] and bounding operations designed by the path frequency and the atom-atom bonds. In addition, to reduce the size of search trees, Ishida et al. [22] introduced a new bounding operation, called the detachment-cut, based on the result by Nagamochi [18]. Implementations of the algorithm proposed by Ishida et al. [22] are available at a web server (http://sunflower.kuicr.kyoto-u.ac.jp/tools/enumol/) for enumerating tree-like chemical graphs with given path frequency. However, an instance with constraint which is specified by one feature vector admits no solution in many cases. Therefore, it is needed to introduce a more relaxed constraint than a single feature vector to obtain some solutions in the tree-like chemical graph enumeration problem.
In this paper, we are given a set of feature vectors, which is specified by a pair of upper and lower feature vectors, and enumerate all tree-like chemical graphs satisfying one of the vectors. It seems that this can be done by simply applying the algorithm proposed by Ishida et al. to each single feature vector in the given set. However, this method will take much computation time because in general there are many feature vectors in a given set. We propose a new exact branch-and-bound algorithm for the problem so that all the feature vectors in a given set are handled directly.
Methods
Preliminaries and problem formulation
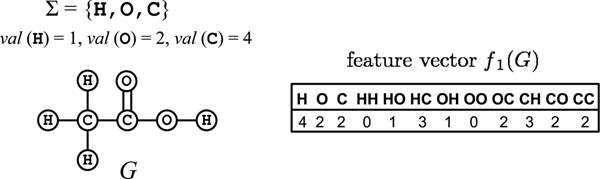
A graph is called a multigraph if multiple edges (i.e., edges with the same end vertices) are allowed; otherwise it is called simple. A path P is a sequence v0, e1, v1, e2, v2, …, ek, vk of distinct vertices vi (i = 0, …, k) and edges ej that join vj – 1 and vj (j = 1, …, k). Without confusion we may write P = (v0, v1, …, vk). The length |P| of path P is defined to be k, i.e., the number of edges. Assume that a set Σ = {ℓ1,ℓ2, …,ℓs} (i.e., chemical elements) is given. Let each label ℓ be associated with a valence val( ℓ) ∈ ℤ+. A multigraph G is called Σ-labeled if each vertex v has a label ℓ(v) ∈ Σ, and is called (Σ, val)-labeled if, in addition, the degree of each vertex v is val(ℓ(v)), i.e., the valence of the element ℓ(v). We regard chemical compounds as (Σ, val )-labeled, self-loopless, and connected multigraphs, where vertices and labels represent atoms and elements, respectively. For a path P = (v0, v1, …, vk), we call ℓ(P) = ℓ(v0), ℓ(v1), …, ℓ(vk) the label sequence of P. Given a label sequence t, let #t denote the number of paths P with ℓ(P) = t in a graph, where multiple edges with the same end-vertices are treated as a single edge and paths are considered to be “directed.” The feature vector fK(G) of level K(∈ ℤ+) of G is defined to be the vector whose entry fK(G)[t] (|t| ≤ K) represents #t. See Fig. 1 for an example.
Figure 1.
A chemical compound and its feature vector. An illustration of a (Σ, val)-labeled multitree G and its feature vector f1(G). Notice that multiple edges with the same end-vertices are treated as one edge, where #OC = #CO = 2.
Let deg(v; G) denote the degree of a vertex v in a graph G. The tree-like chemical graph enumeration problem with given one feature vector can be formulated as follows [19].
Enumeration of Tree-like chemical graphs with given Path Frequency (ETPF)
Given a set Σ of labels, a valence function val : Σ → ℤ+ and a feature vector g of level K, find all (Σ, val)-labeled multitrees T such that fK(T) = g and deg(v;T) = val(ℓ(v)) for all vertices v ∈ V(T).
Observe that a large number of chemical compounds contain a high proportion of hydrogens. Based on this fact, another model can be considered in the problem ETPF by removing all hydrogen atoms. These two different models were proposed by Fujiwara et al. [19] and Ishida [23].
In this paper, we consider the problem of enumerating all tree-like chemical graphs based on given upper and lower feature vectors because we want to relax the feature vector constraint in the problem ETPF. For feature vectors g1 and g2 of level K, we define g1 ≤ g2 to be g1[t] ≤ g2[t] for any label sequence t (|t| ≤ K). The problem of enumerating tree-like compounds from given two feature vectors can be formulated based on the problem ETPF as follows (see Fig. 2 for an illustration).
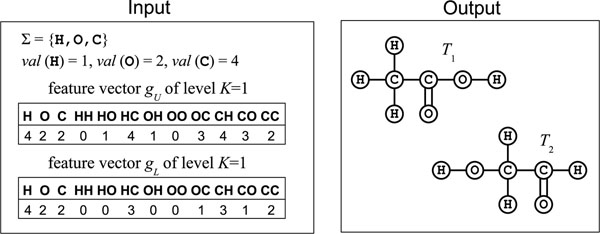
Figure 2.
An instance of ETULF. An instance of ETULF with upper and lower feature vectors, which admits two different solutions.
Enumeration of Tree-like chemical graphs with given Upper and Lower bounds on path Frequencies (ETULF)
Given a set Σ of labels, a valence function val : Σ → ℤ+ and feature vectors gU and gL of level K (gL ≤ gU), find all (Σ, val)-labeled multitrees T such that gL ≤ fK(T) ≤ gU and deg(v;T) = val(ℓ(v)) for all vertices v ∈ V(T).
For the problem ETULF, we assume that gL(ℓ) = gU(ℓ) for an atom type ℓ ∈ Σ, where g(L) denotes the entry in g that corresponds to a label sequence L (thus g(ℓ) specifies the number of vertices of label ℓ) and that gL(L) ≤ gU(L) for any label sequence L (|L| ≥ 2).
Note that the number n of vertices is given by Σℓ∈Σg(ℓ). To solve the problem ETULF, we start with an empty graph, and repeatedly extend the current tree T by appending a new vertex with each label ℓ ∈ Σ to obtain a valid tree (a tree that does not violate any constraints on output trees) one by one until we get n vertices. In order to avoid duplicate outputs, we follow the branch-and-bound framework of Fujiwara et al. [19], which first defines a canonical representation for isomorphic trees, and then lists them using the algorithm of Nakano and Uno [20,21] (the branching operation) discarding invalid trees with some bounding operations. Since we cannot directly use the bounding operation proposed by Ishida et al. [22] due to upper and lower constraints, we introduce some new bounding operations.
Canonical representation of trees and the branching operation
In this section, we explain a canonical representation of trees introduced by Fujiwara et al. [19] and the branching operation based on the canonical representation.
First of all, we introduce a root of a tree based on the following theorem.
Theorem 1 (Jordan [24]) For any tree with n′ vertices, either there exists a unique vertex v* such that each subtree obtained by removing v* contains at most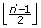
vertices, or there exists a unique edge e* such that both of the subtrees obtained by removing e* contain exactly
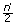vertices.
Such a vertex v* and an edge e* in Theorem 1 are called unicentroid and bicentroid, respectively. Either unicentroid or bicentroid is called as centroid. Note that there exists a bicentroid only for an even n′. Since a case of bicentroid is similar to a case of unicentroid, now we only explain a case of unicentroid.
Next we introduce a canonical representation of trees that must be unique up to isomorphism. Let T be a tree of n vertices rooted at a vertex v0 (which is not necessarily its unicentroid). Suppose that it is embedded in the plane as an ordered tree, where v0 is located at the top part. Without loss of generality, let v0, v1, …, vn – 1 be indexed by the depth-first search (DFS) that starts from v0 and visits vertices from the left to the right. Define the depth d(v) of a vertex v to be the length of the (unique) path from v0 to v in T. The depth-label sequence of T (L(T)) is defined to be
 |
Given an arbitrary order of labels, we define the order of depth-label sequences as follows. For any T1 and T2, we denote L(T1) >L(T2) if L(T1) is lexicographically larger than L(T2). Then the canonical representation of a rooted tree is defined by the largest depth-label sequence among all its plane embeddings. Actually this is equivalent to the left-heavy plane embedding [20,21].
Thus our branching task is to list all centroid-rooted left-heavy trees with n vertices and m (= |Σ|) labels. Following the scheme [20,21], we define a parent-child relation between two left-heavy trees. The parent P(T) of a left-heavy tree T is obtained from T by removing its rightmost leaf. Clearly P(T) is still left-heavy In this way, we can define a family tree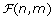
of left-heavy trees whose leaves are exactly what we want to obtain.
Therefore we only need to enumerate the (leaf) nodes of 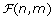. This can be done by starting from the empty tree (the root node of 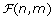) and repeatedly appending a new leaf to some appropriate place on the rightmost path of the current tree. Our branching operation employs the algorithm of Nakano and Uno [20,21], which extends the current tree T (i.e., finds a child of T) in constant time [19].
Bounding operations
In this section, we explain how to check the validity of the current tree T. If we can conclude that T and all its descendants are not valid, then we can discard T. Our bounding operation discards T if at least one of the following criteria is violated:
(C1) The root of T remains the centroid of an output (the centroid constraint);
(C2) deg(v;T) ≤ val(l(v)) for all v ∈ V(T) (the valence constraint);
(C3) fK(T) ≤ gU, and |T| = n and gL ≤ fK(T) (the feature vector constraint);
(C4) T can be extended to a connected and loopless tree with n vertices (the detachment constraint);
(C5) T can have a descendant which has an appropriate number of multiple bonds (the multiplicity constraint).
(C1) and (C2) are the same as the work by Fujiwara et al. [19] and not difficult to check. (C3) and (C4) are different from the work by Fujiwara et al. [19] and Ishida et al. [22] due to upper and lower constraints. (C5) is a new bounding operation that we propose in this paper. In the following three subsections, we will discuss three bounding operations resulting from (C3), (C4), and (C5), called as feature-vector-cut, detachment-cut, and multiplicity-cut, respectively.
Feature-vector-cut procedure
In the problem ETULF, we cannot use the bounding operation proposed by Fujiwara et al. [19] directly due to upper and lower feature vectors, but we can introduce a bounding operation based on upper and lower feature vectors by modifying Fujiwara et al.’s work slightly.
Let T denote a current tree, fK(T) denote the feature vector of T, gu denote a given upper feature vector, and gL denote a given lower feature vector. By the feature vector constraints in the problem ETULF, we check the following condition.
 |
(1) |
If T violates (1), then we discard T.
In addition, if |T| = n, then we check the following condition based on the constraint of upper and lower feature vectors.
 |
(2) |
If T violates (2), then we discard T.
Detachment-cut procedure
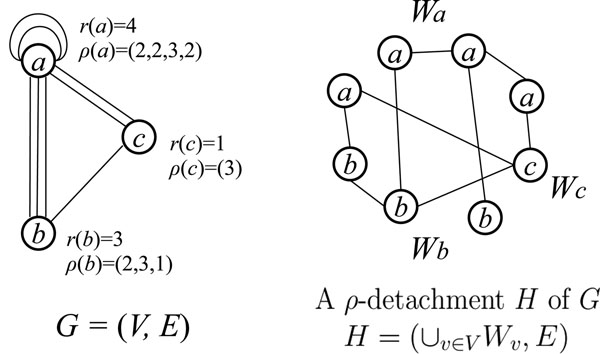
This subsection describes the definition of detachment [18] and a new bounding operation based on it for the problem ETULF. Let G be a multigraph that may have self-loops, which represents the graph obtained from a chemical graph H by contracting the vertices with the same label into a single vertex, where each vertex in G corresponds a label in H (note that we do not eliminate any edges in H in contracting vertices to obtain G). A process of regaining H from G is described as follows. Given a function r : V(G) → ℤ+, an r-detachment H of G is a multigraph obtained from G by splitting each vertex v ∈ V(G) into a set of r(v) copies of v, denoted by Wv = {v1, v2 …, vr(v)}, so that each edge {u, v} ∈ E(G) joins some vertices ui ∈ Wu and vj ∈ Wv. Hence an r-detachment H of G is not unique in general. A self-loop {u, u} in G may be mapped to a self-loop {ui,ui} or a non-loop edge {ui,uj} in a detachment H of G. Note that, for all vertex pairs {u, v} ∈ V(G), the number of edges between subsets Wu and Wv in H is equal to that of edges between vertices u and v in G.
To obtain a chemical graph H as an r-detachment H of G, we need to specify the degree of vertices (with the same label) in H. For a function r : V(G) → ℤ+, an r-degree specification is a set ρ of vectors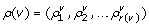 
for v ∈ V(G) such that
 |
which is necessary for all the edges incident to vertex v in G to be assigned to split vertices vi ∈ Wv completely. An r-detachment H of G is called a ρ-detachment if each v ∈ V satisfies
 |
which is a requirement that each vertex vi in H must have the prescribed degree 
. Figure 3 illustrates a ρ-detachment H for a graph G = (V, E) with V = {a, b, c}, a function r with r(a) = 4, r(b) = 3, r(c) = 1, and a degree specification ρ with ρ(a) = (2, 2, 3, 2), ρ(b) = (2, 3, 1), ρ(c) = (3). The next theorem gives a characterization of a multigraph G that admits a connected and loopless ρ-detachment.
Figure 3.
A multigraph and a ρ-detachment. A multigraph G and a ρ-detachment H of G.
Theorem 2 (Nagamochi [18]) Let G = (V, E) be a multigraph, r : V → ℤ+ and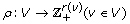 
. Then G has a connected and loopless ρ-detachment H if and only if the following hold:
 |
where r(X) = Σ v∈ Xr(v), c(G′) denotes the number of connected components of a graph G′, G – X denotes the graph obtained from a graph G by removing the vertices in X together with all edges incident to vertices in X, and d(A, B; G) denotes the number of edges (u, v) ∈ E with u ∈ A and v ∈ B.
Ishida et al. [22] proposed a bounding operation for the problem ETPF based on Theorem 2. However, we cannot use the bounding operation proposed by Ishida et al. for the problem ETULF due to upper and lower constraints. We now describe our new bounding operation based on detachments for the problem ETULF. The new bounding operation, called detachment-cut tests whether the current multitree T has a multitree that is consistent with given path frequencies among its descendants in the family tree, based on the difference between the feature vector fK(T) and the input feature vectors gU and gL.
Let ℓ1, ℓ2, …, ℓs be input labels and gU, gL : Σ≤ K + 1 → ℤ+ be feature vectors. Let r0, …, rh be the vertices in the rightmost path to which a new leaf can be appended and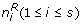 
denote the number of vertices rj (0 ≤ j ≤ h) with ℓ(rj) = ℓi. For each label sequence t, #t denotes the number of paths P in T with ℓ(P) = t. From gU, gL, and T, we define new feature vectors 
and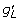 
of level K = 1 to be
 |
 |
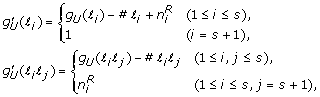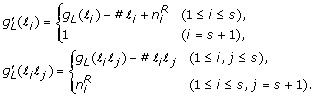We next introduce a vertex with a new label ℓs+1 of valence h + 1 (for example, label A in Fig. 4), a graph GU = (VU, EU) with a vertex set VU = {v1, …, vs, vs+1 | ℓ(vi) = ℓi, 1 ≤ i ≤ s + 1} and edge set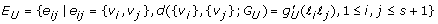 
, and a graph GL = (VL,EL) with a vertex set VL = {v1, …, vs, vs+1 | ℓ(vi) = ℓi, 1 ≤ i ≤ s + 1} and edge set 
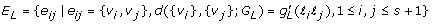. Note that d({vi}, {vj}; G) means a multiplicity of the edge {vi,vj} in a graph G. The function r and degree specification ρ are defined to be
 |
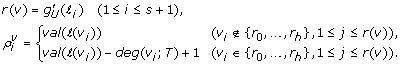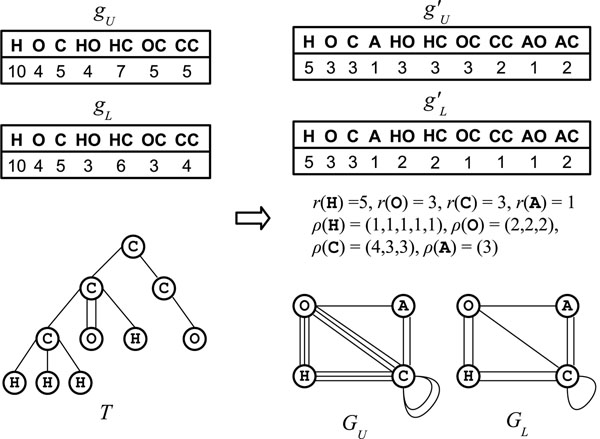
Figure 4.
Detachment-cut. Bounding operation by detachment-cut, where vectors gU(ℓ, ℓ′), gL(ℓ, ℓ′),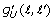 
, and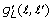 
are defined for unordered pairs {ℓ, ℓ′} and those with value=0 are omitted in the tables.
Using GU, GL, r, and ρ, we can check if a current multitree T violates (C4). We need to check whether none of the following two conditions is violated.
(a)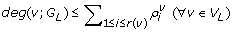 
.
(b) r(X) + c(GU – X) – d(X, VU; GU) ≤ 1 (∀X ⊆ VU, X ≠ ∅).
In the first condition, we check whether the number of the rest of bonds is large enough to satisfy the lower feature vector constraint. In the second condition, we check whether T has a connected and loopless descendant based on GU and Theorem 2.
Multiplicity-cut procedure
This subsection describes a new bounding operation based on multiplicity for the problem ETULF. Let g(ℓ) be the number of vertices with label ℓ ∈ Σ that are obtained from given the feature vector. Now we assume that g(ℓ) for all ℓ ∈ Σ are fixed in the problem ETULF. Then we can calculate the number of edges in output trees in the problem ETULF. Let n be the number of vertices in output trees. If we treat a multiple edge as a set of single edges, the number of edges em in an output tree is given by:
 |
On the other hand, if we treat a multiple edge as a simple one, the number of edges es in an output tree is equal to n – 1 due to the tree-like constraint. Now we consider
 |
which means that only M edges are used to construct multiple bonds in an output tree. Note that M ≥ 0. We calculate M from an input of the problem ETULF before the enumeration algorithm starts.
Let T = (V, E) be a multitree, and me denote the multiplicity of e ∈ E. The multiplicity M(T) of T is defined to be
 |
Now we describe the multiplicity-cut based on M(T) and M.
Let T be the current rooted multitree in the branching operation, M(T) be the multiplicity of T, RP(T) = (r0, r1, …, rk) be the rightmost path of T, Ti be the new rooted multitree obtained by appending a new leaf p to a vertex ri (0 ≤ i ≤ k), and RP(Ti) be the rightmost path of Ti . The rightmost path RP(Ti) of Ti is updated by appending p to the end of RP(T) when a new leaf p is appended to ri, that is, RP(Ti) = (r0, r1,…, ri, p). Then we can determine the multiplicities of the edges {(rj, rj – 1), j = k, k – 1, …, i + 1} due to the valence constraint, at the same time, we update M(Ti). We denote the multiplicity of an edge (rj, rj – 1) in Ti by Mul(rj, rj – 1 | Ti). When we update the multiplicity of the edge (rj,rj – 1), M(Ti) is updated as follows:
 |
By the definition of M, a valid multitree Ti satisfies
 |
(3) |
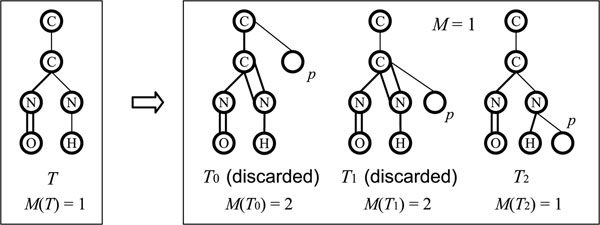
If Ti violates (3), then we discard Ti . See Fig. 5 for an illustration of this.
Figure 5.
Multiplicity-cut. An illustration of the multiplicity-cut procedure, where M = 1.
Results
This section reports the experimental results of our algorithm. First of all, we mention that the problem ETULF can be solved by applying the algorithm proposed by Ishida et al. [22] to each single feature vector in a given set of feature vectors, i.e., the problem ETULF can regard as a set of the problem ETPF. Then we call an algorithm for the problem ETULF based on the algorithm proposed by Ishida et al. RepEnum (Repeated Enumeration). On the other hand, we call our algorithm SimEnum (Simultaneous Enumeration). It is to be noted that RepEnum is one of the fastest tools to enumerate tree-like chemical structures from a given molecular formula (i.e., feature vector with K = 0) [22] and, to our knowledge, there does not exist any other available tool to enumerate chemical structures from a given feature vector based on path frequency (i.e., feature vector with general K).
Now we compare the performances of two algorithms, SimEnum and RepEnum, and we also compare the performances of two algorithms, SimEnum including multiplicity-cut and SimEnum not including multiplicity-cut. We have tested the algorithm SimEnum for some widths between upper and lower feature vectors. Tests were carried out on a PC with CPU AMD Athlon Dual Core Processor 5050e using instances based on some chemical compounds selected from the KEGG LIGAND database [25] (http://www.genome.jp/ligand/). Note that we treat a benzene ring contained in these compounds as a new virtual atom of valence six.
We define w ∈ ℤ+ to be a width between upper and lower feature vectors. From a feature vector g, we construct two feature vectors gU and gL as follows. For each entry a > 0 of g, let gU be the upper feature vector, where each entry aU is given by a + w and gL be the lower one, where each entry aL is given by max{0, a – w}. Note that if w = 0, then an instance for the problem ETULF is equivalent for the problem ETPF.
Table 1 and Additional file 1 show the results of the comparison. We find that the algorithm RepEnum cannot solve all the problems with K = 2 within the time limit since the number of feature vectors in a given set is exponentially increasing with K. On the other hand, Table 1 shows that the algorithm SimEnum can solve the problem much faster for a larger K. This shows that the algorithm SimEnum runs significantly faster than the algorithm RepEnum. It is also seen that RepEnum can only examine a very small portion of feature vectors in most cases. Additional file 1 shows that the algorithm SimEnum including multiplicity-cut runs faster than the algorithm SimEnum not including multiplicity-cut for almost all of the instances. This shows that the multiplicity-cut operation works well to improve enumeration efficiency.
Table 1.
Comparison of previous method and our method
| Entry Formula | SimEnum | RepEnum | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| n | K | w | fv | time (s) | nodes | solutions | time (s) | nodes | solutions | solved | |
| 1 | 1 | 36 | 1037.04 | 177,074,686 | 414,890 | 163.32 | 44,340,488 | 414,890 | 729 | ||
| 2 | 1 | 318 | 2.97 | 392,246 | 44 | T.O. | 2,381,360,000 | N.F. | 65,909,572 | ||
| 3 | 1 | 334 | 1.22 | 145,213 | 2 | T.O. | 3,293,260,000 | N.F. | 96,860,588 | ||
| C00062 | 26 | 4 | 1 | 353 | 0.33 | 34,539 | 1 | T.O. | 2,780,050,000 | N.F. | 81,766,176 |
| C6H14N2O4 | 5 | 1 | 371 | 0.24 | 20,361 | 1 | T.O. | 1,561,230,000 | N.F. | 45,918,529 | |
| 6 | 1 | 385 | 0.25 | 15,166 | 1 | T.O. | 569,590,000 | N.F. | 16,752,647 | ||
| 7 | 1 | 396 | 0.18 | 14,547 | 1 | T.O. | 79,870,000 | N.F. | 2,349,117 | ||
| 1 | 1 | 36 | T.O. | 377,260,000 | N.F. | T.O. | 413,000,000 | N.F. | 460 | ||
| 2 | 1 | 318 | 7.24 | 845,760 | 25 | T.O. | 1,442,760,000 | N.F. | 70,175,902 | ||
| 3 | 1 | 331 | 2.81 | 307,151 | 7 | T.O. | 3,316,970,000 | N.F. | 195,115,882 | ||
| C03343 | 37 | 4 | 1 | 347 | 1.03 | 99,945 | 1 | T.O. | 2,494,780,000 | N.F. | 146,751,764 |
| C16H22O4 | 5 | 1 | 364 | 0.98 | 87,600 | 1 | T.O. | 1,050,480,000 | N.F. | 61,792,941 | |
| 6 | 1 | 382 | 0.76 | 60,194 | 1 | T.O. | 315,820,000 | N.F. | 18,577,647 | ||
| 7 | 1 | 399 | 0.57 | 42,538 | 1 | T.O. | 41,450,000 | N.F. | 2,438,235 | ||
| 1 | 1 | 38 | T.O. | 157,320,000 | N.F. | T.O. | 200,490,000 | N.F. | 1,388 | ||
| 2 | 1 | 326 | 37.59 | 1,940,295 | 238 | T.O. | 2,911,390,000 | N.F. | 66,167,954 | ||
| 3 | 1 | 348 | 1.71 | 60,792 | 3 | T.O. | 2,673,940,000 | N.F. | 60,771,363 | ||
| C07178 | 46 | 4 | 1 | 371 | 0.35 | 14,248 | 1 | T.O. | 1,925,490,000 | N.F. | 43,761,136 |
| C21H28N2O5 | 5 | 1 | 392 | 0.27 | 10,866 | 1 | T.O. | 743,940,000 | N.F. | 16,907,727 | |
| 6 | 1 | 3110 | 0.27 | 10,680 | 1 | T.O. | 93,880,000 | N.F. | 2,133,636 | ||
| 7 | 1 | 3125 | 0.24 | 9,276 | 1 | T.O. | 19,270,000 | N.F. | 437,954 | ||
| 1 | 1 | 35 | T.O. | 382,470,000 | N.F. | T.O. | 552,290,000 | N.F. | 61 | ||
| 2 | 1 | 316 | T.O. | 211,800,000 | N.F. | T.O. | 530,930,000 | N.F. | 10,451,912 | ||
| 3 | 1 | 327 | 1395.13 | 144,244,042 | 206 | T.O. | 3,314,260,000 | N.F. | 194,956,470 | ||
| C03690 | 61 | 4 | 1 | 341 | 121.36 | 11,332,363 | 4 | T.O. | 2,392,530,000 | N.F. | 140,737,058 |
| C24H38O4 | 5 | 1 | 357 | 83.70 | 6,978,557 | 2 | T.O. | 958,650,000 | N.F. | 56,391,176 | |
| 6 | 1 | 375 | 40.11 | 2,923,819 | 1 | T.O. | 298,600,000 | N.F. | 17,564,705 | ||
| 7 | 1 | 392 | 16.50 | 1,096,128 | 1 | T.O. | 38,670,000 | N.F. | 2,274,705 | ||
Comparison of SimEnum and RepEnum for the problem ETULF.
Note:
(1) C00062, C03343, C07178, and C03630 are the chemical compounds in the KEGG LIGAND database, respectively;
(2) n is the number of vertices in an instance preprocessed by replacing each benzene ring with a new atom having six valences;
(3) K is the level of given feature vectors;
(4) w is the width for constructing upper and lower feature vectors;
(5) fv is the number of feature vectors in a given set;
(6) “time (s)” is the CPU time in seconds;
(7) T.O. means “time over” (the time limit is set to be 1,800 seconds);
(8) “nodes” is (the sum of) the number of nodes of family trees that are traversed;
(9) “solutions” is the number of all possible solutions;
(10) “solved” is the number of feature vectors which the algorithm RepEnum solved in the time limit; and (11) N.F. means “not found.”
Table 2 shows the results on the performance for varying width w for the problem ETULF. The search space in the problem ETULF is exponentially increasing with w. However, it seems that the number of search nodes and computation time are not exponentially increasing with w. This suggests that the algorithm SimEnum works efficiently for the large search space in the problem ETULF.
Table 2.
Comparison of varying width
| Entry Formula | SimEnum | |||||
|---|---|---|---|---|---|---|
| n | K | w | time (s) | nodes | solutions | |
| 2 | 0 | 0.51 | 55,196 | 6 | ||
| 2 | 1 | 3.58 | 400,501 | 44 | ||
| 2 | 2 | 7.58 | 835,509 | 503 | ||
| C00062 | 26 | 2 | 3 | 10.84 | 1,163,548 | 2,351 |
| C6H14N2O4 | 2 | 4 | 12.55 | 1,349,057 | 5,430 | |
| 2 | 5 | 13.29 | 1,431,075 | 9,852 | ||
| 2 | 50 | 14.31 | 1,537,496 | 25,425 | ||
| 2 | 0 | 0.34 | 35,952 | 9 | ||
| 2 | 1 | 8.39 | 845,760 | 25 | ||
| 2 | 2 | 48.27 | 4,815,369 | 41 | ||
| C03343 | 37 | 2 | 3 | 149.83 | 14,781,738 | 305 |
| C16H22O4 | 2 | 4 | 377.01 | 37,435,878 | 40,732 | |
| 2 | 5 | 639.68 | 63,459,180 | 106,870 | ||
| 2 | 50 | 1118.75 | 110,703,034 | 510,079 | ||
| 2 | 0 | 2.33 | 111,781 | 16 | ||
| 2 | 1 | 46.81 | 2,246,578 | 238 | ||
| 2 | 2 | 96.52 | 4,715,072 | 1,375 | ||
| C07178 | 46 | 2 | 3 | 152.18 | 7,420,060 | 6,824 |
| C21H28N2O5 | 2 | 4 | 179.42 | 8,744,563 | 19,180 | |
| 2 | 5 | 199.66 | 9,677,513 | 29,891 | ||
| 2 | 50 | 255.01 | 12,292,587 | 54,861 | ||
| 5 | 0 | 19.50 | 1,482,017 | 2 | ||
| 5 | 1 | 220.14 | 16,063,569 | 5 | ||
| 5 | 2 | 439.12 | 33,037,741 | 32 | ||
| C03690 | 61 | 5 | 3 | 684.88 | 52,207,745 | 178 |
| C24H38O4 | 5 | 4 | 1024.96 | 78,509,554 | 349 | |
| 5 | 5 | 1285.55 | 98,762,291 | 615 | ||
| 5 | 50 | T.O. | 136,835,134 | N.F. | ||
Comparison of the performance for varying w for the problem ETULF.
Here, we briefly discuss practical values on K and w though we do not have concrete evidence and these values depend on target classes of chemical compounds. It is suggested from the results on similar feature vectors [9,10,15] that K between 3 to 10 should be used. Though there is no previous result on w, it is seen from Table 2 that w cannot be large because there may exist too many solutions. Therefore, w less than 4 should be used.
Conclusions
We considered the problem of enumerating all tree-like chemical graphs from a given set of feature vectors, which is specified by upper and lower feature vectors based on frequencies of paths, and proposed a new exact branch-and-bound algorithm. Our experimental results show that our algorithm outperforms the naive algorithm based on a previous method. In comparison to the algorithm based on Ishida et al. [22], our algorithm can greatly reduce the number of search nodes and the computation time and enumerate all the feasible solutions in many instances.
However, the search space of the problem ETULF is much larger than that of the problem ETPF due to upper and lower constraints and in fact there are many search nodes for solving the problem ETULF by our algorithm. One of the future works is to improve the bounding operations, or introduce a new bounding operation. Actually, in the feature-vector-cut mentioned in subsection , information of a lower feature vector gL is only used if |T| = n. Another future work is to develop a web server that implements our proposed algorithm. Generalization of the proposed techniques for other types of kernel functions and other problems is also left as a future work.
Competing interests
The authors declare that they have no competing interests.
Author’s contributions
HN gave the basic idea based on discussions with TA and MS. MS developed and implemented the algorithms, and carried out the experiments. MS, HN, and TA authored and approved the manuscript.
Supplementary Material
Comparison of multiplicity-cut Comparison of SimEnum including multiplicity-cut and SimEnum not including multiplicity-cut for the problem ETULF. Note: (1) “add multiplicity-cut” is the algorithm SimEnum including multiplicity-cut; and (2) “no multiplicity-cut” is the algorithm SimEnum not including multiplicity-cut.
Contributor Information
Masaaki Shimizu, Email: masaaki@amp.i.kyoto-u.ac.jp.
Hiroshi Nagamochi, Email: nag@amp.i.kyoto-u.ac.jp.
Tatsuya Akutsu, Email: takutsu@kuicr.kyoto-u.ac.jp.
Acknowledgements
This work was partially supported by Grant-in-Aid #22240009 from Mext, Japan.
This article has been published as part of BMC Bioinformatics Volume 12 Supplement 14, 2011: 22nd International Conference on Genome Informatics: Bioinformatics. The full contents of the supplement are available online at http://www.biomedcentral.com/1471-2105/12?issue=S14.
References
- Bytautas L, Klein DJ. Chemical combinatorics for alkane-isomer enumeration and more. Journal of Chemical Information and Computer Sciences. 1998;38:1063–1078. doi: 10.1021/ci980095c. [DOI] [Google Scholar]
- Bytautas L, Klein DJ. Formula periodic table for acyclic hydrocarbon isomer classes: combinatorially averaged graph invariants. Physical Chemistry Chemical Physics. 1999;1:5565–5572. [Google Scholar]
- Bytautas L, Klein DJ. Isomer combinatorics for acyclic conjugated polyenes: enumeration and beyond. Theoretical Chemistry Accounts. 1999;101:371–387. doi: 10.1007/s002140050455. [DOI] [Google Scholar]
- Cayley A. On the analytic forms called trees with applications to the theory of chemical combinations. Reports British Association for the Advancement of Science. 1875;45:257–305. [Google Scholar]
- Buchanan BG, Feigenbaum EA. DENDRAL and Meta-DENDRAL: their applications dimension. Aritificial Intelligence. 1978;11:5–24. doi: 10.1016/0004-3702(78)90010-3. [DOI] [Google Scholar]
- Funatsu K, Sasaki S. Recent advances in the automated structure elucidation system, CHEMICS. Utilization of two-dimensional NMR spectral information and development of peripheral functions for examination of candidates. Journal of Chemical Information and Computer Sciences. 1996;36:190–204. doi: 10.1021/ci950152r. [DOI] [Google Scholar]
- Fink T, Reymond JL. Virtual exploration of the chemical universe up to 11 atoms of C, N, O, F: assembly of 26.4 million structures (110.9 million stereoisomers) and analysis for new ring systems, stereochemistry, physicochemical properties, compound classes, and drug discovery. Journal of Chemical Information and Computer Sciences. 2007;47:342–353. doi: 10.1021/ci600423u. [DOI] [PubMed] [Google Scholar]
- Mauser H, Stahl M. Chemical fragment spaces for de novo design. Journal of Chemical Information and Computer Sciences. 2007;47:318–324. doi: 10.1021/ci6003652. [DOI] [PubMed] [Google Scholar]
- Faulon JL, Churchwell CJ, Jr DPV. The signature molecular descriptor. 2. Enumerating molecules from their extended valence sequences. Journal of Chemical Information and Computer Sciences. 2003;43:721–734. doi: 10.1021/ci020346o. [DOI] [PubMed] [Google Scholar]
- Hall LH, Dailey ES. Design of molecules from quantitative structure-activity relationship models. 3. Role of higher order path counts: path 3. Journal of Chemical Information and Computer Sciences. 1993;33:598–603. doi: 10.1021/ci00014a012. [DOI] [Google Scholar]
- Deshpande M, Kuramochi M, Wale N, Karypis G. Frequent substructure-based approaches for classifying chemical compounds. IEEE Transactions on Knowledge and Data Engineering. 2005;17:1036–1050. [Google Scholar]
- Bakir GH, Weston J, Schölkopf B. Learning to find pre-images. Advances in Neural Information Processing Systems. 2003;16:449–456. [Google Scholar]
- Bakir GH, Zien A, Tsuda K. Learning to find graph pre-images. Lecture Notes in Computer Science. 2004;3175:253–261. doi: 10.1007/978-3-540-28649-3_31. [DOI] [Google Scholar]
- Kashima H, Tsuda K, Inokuchi A. Marginalized kernels between labeled graphs. Proceedings of the Twentieth International Conference on Machine Learning, AAAI Press. 2003. pp. 321–328.
- Mahé P, Ueda N, Akutsu T, Perret JL, Vert JP. Graph kernels for molecular structure-activity relationship analysis with support vector machines. Journal of Chemical Information and Modeling. 2005;45:939–951. doi: 10.1021/ci050039t. [DOI] [PubMed] [Google Scholar]
- Byvatov E, Fechner U, Sadowski J, Schneider G. Comparison of support vector machine and artificial neural network systems for drug/nondrug classification. Journal of Chemical Information and Computer Sciences. 2003;43:1882–1889. doi: 10.1021/ci0341161. [DOI] [PubMed] [Google Scholar]
- Akutsu T, Fukagawa D. Inferring a graph from path frequency. Lecture Notes in Computer Science. 2005;3537:371–392. doi: 10.1007/11496656_32. [DOI] [Google Scholar]
- Nagamochi H. A detachment algorithm for inferring a graph from path frequency. Algorithmica. 2009;53:207–224. doi: 10.1007/s00453-008-9184-0. [DOI] [Google Scholar]
- Fujiwara H, Wang J, Zhao L, Nagamochi H, Akutsu T. Enumerating treelike chemical graphs with given path frequency. Journal of Chemical Information and Modeling. 2008;48:1345–1357. doi: 10.1021/ci700385a. [DOI] [PubMed] [Google Scholar]
- Nakano S, Uno T. Generating colored trees. Lecture Notes in Computer Science. 2005;3787:249–260. doi: 10.1007/11604686_22. [DOI] [Google Scholar]
- Nakano S, Uno T. Efficient generation of rooted trees. NII Technical Report NII-2003-005E. 2003.
- Ishida Y, Zhao L, Nagamochi H, Akutsu T. Improved algorithms for enumerating tree-like chemical graphs with given path frequency. Genome Informatics. 2008;21:53–64. [PubMed] [Google Scholar]
- Ishida Y. Improved algorithms for enumerating tree-like chemical graphs with given path frequency. Master thesis of Graduate School of Informatics in Kyoto University. 2008. [PubMed]
- Kvasnicka V, Pospichal J. Constructive enumeration of acyclic molecules. Collect Czech Chem Commun. 1991;56:1777–1802. doi: 10.1135/cccc19911777. [DOI] [Google Scholar]
- Kanehisa M, Goto S, Furumichi M, Tanabe M, Hirakawa M. KEGG for representation and analysis of molecular networks involving diseases and drugs. Nucleic Acids Res. 2010;36:D355–D360. doi: 10.1093/nar/gkp896. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Comparison of multiplicity-cut Comparison of SimEnum including multiplicity-cut and SimEnum not including multiplicity-cut for the problem ETULF. Note: (1) “add multiplicity-cut” is the algorithm SimEnum including multiplicity-cut; and (2) “no multiplicity-cut” is the algorithm SimEnum not including multiplicity-cut.