Abstract
Chemical exchange saturation transfer (CEST), arising from the generally mobile groups, and magnetization transfer (MT) contrast arising from immobile protons, have enjoyed wide popularity recently in MRI applications. It is often difficult to separate genuine CEST signatures from MT effects, which are asymmetric with respect to the water resonance. A two-pool model for magnetization transfer (MT) is established fully based on Provotorov’s theory of saturation, and then extended to the situation of simultaneous two-frequency rf irradiation. Numerical simulations and experimental results demonstrate that two-frequency rf irradiation can flatten out MT asymmetry when both frequency components lie within the spectrum of an MT pool. Based on this result, we propose a strategy to isolate chemical exchange saturation transfer (CEST) contrast from MT asymmetry contrast by using the two-frequency rf irradiation technique.
1. Introduction
Magnetization transfer (MT) is in general a macroscopic phenomenon in which two distinct pools of nuclear spins exchange their magnetic polarizations. In the field of magnetic resonance imaging (MRI), MT indicates a specific phenomenon: one of the two pools consists of water protons, the amount of which is present in large excess in tissues and organs, and the other consists of protons associated with solid-like macromolecules, between which there can exist either a physical exchange or a magnetization exchange via relaxation pathways such as NOE [1–3].
The term, chemical exchange saturation transfer (CEST), is used when MT is caused by chemical exchange, especially between water protons and exchangeable solute protons [4–6]. In tissues and organs, CEST may occur together with MT, which makes the quantitative measure of CEST difficult. In principle, CEST can be distinguished from conventional MT by its frequency selectivity: CEST may occur in a very narrow range of frequencies, which can be selectively irradiated, compared with MT happening over a wide range of frequencies. It is not trivial, however, to separate the two effects if an asymmetry in MT exists. Such cases are very common in tissues [7, 8].
In previous work [9, 10], it was demonstrated that one can achieve uniform saturation of a strongly-coupled spin system by simultaneously irradiating at two different frequencies that lie within its spectral range broadened by dipolar couplings. If the MT exchange processes occur on a timescale that is slower than the rate of saturation, the two-frequency rf irradiation may uniformly saturate those protons belonging to macromolecules in tissues and organs. As a result, the magnetization of water protons diminishes through MT exchange processes. Consequently, the MT effect becomes independent of the frequency positions of the saturating rf irradiation. On the other hand, due to the frequency selectivity of CEST agents, two-frequency rf irradiation does not significantly alter CEST dynamics. Therefore, an unencumbered extraction of CEST contrast can be expected.
In this work, we establish a two-pool model for MT based on Provotorov’s theory of saturation and extend the model to describe the dynamics under simultaneous two-frequency rf irradiation. Through numerical and experimental studies, we show that two-frequency rf irradiation can make the MT effect uniform and that it is possible to isolate CEST from MT asymmetry effects. Finally, a novel two-frequency CEST scheme is proposed, which will be useful for the quantification of CEST contrast.
2. Two-pool model under two-frequency rf irradiation
Provotorov’s thermodynamic theory has been used to describe the dynamics of a strongly coupled spin system under weak rf irradiation [12, 13], i.e., when the strength of the rf Hamiltonian is much smaller than the Zeeman and dipolar Hamiltonians. By treating the weak rf irradiation as a perturbation, the master equation can be solved by iteration to the second order under the assumption that the density operator is described at all times by a quasi-equilibrium form ρ(t) = (1/2N) [1 + βS(t)ω0Sz − βd(t)
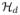 ], where βS and βd are respectively the Zeeman and dipolar inverse spin temperatures, ω0 is the resonance frequency, and
], where βS and βd are respectively the Zeeman and dipolar inverse spin temperatures, ω0 is the resonance frequency, and
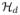 is the dipole-dipole interaction Hamiltonian. By introducing the spin and dipolar polarizations PS = (2/N)〈Sz〉 and Pd = (2/N)(〈
is the dipole-dipole interaction Hamiltonian. By introducing the spin and dipolar polarizations PS = (2/N)〈Sz〉 and Pd = (2/N)(〈
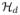 〉/ωloc), one can obtain a set of first-order coupled differential equations as follows [11]:
〉/ωloc), one can obtain a set of first-order coupled differential equations as follows [11]:
| (1) |
and
| (2) |
where 〈O〉 ≡ tr{Oρ}, , Δ ≡ ω0 − ω is the frequency difference between the resonance frequency ω0 and the frequency ω of the weak rf irradiation, , ω1(≪ ωloc) is the amplitude of the weak rf irradiation, gS(Δ) is the normalized absorption line shape for a spin S, T1,S and T1,d are the spin-lattice relaxation times for the Zeeman and dipolar reservoirs, respectively, and PS,0 is the thermal equilibrium polarization. Eqs. (1) and (2) are valid in both the rotating and laboratory frames.
To build a two-pool model for MT, one can add an additional Zeeman polarization PI without any dipolar reservoirs attached, representing protons in bulk water, for example. Following the same procedure leading to Eq. (1), it is easy to show that the spin polarization follows a kinetic equation
| (3) |
Notice that Eq. (3) is written in the laboratory frame and valid if ω1 ≪ ω0 and the changes in PS and Δ are small on a time scale of the spin-spin relaxation time T2 or the inverse of the line width. In the rotating frame, the perturbation approach cannot be applied because there is only the rf term in the spin Hamiltonian. In addition, Eq. (3) has been derived without any assumptions about the form of g(Δ). It is straightforward to check that Eq. (3) gives exactly the same steady state as the Bloch equations with a Lorentzian line shape gLorentz(Δ) = (T2/π)[1 + (ΔT2)2]−1.
A two-pool model for MT can be established by combining Eqs. (1), (2), and (3) and adding exchange terms. It is customary to assume that the exchange between the two pools is a first-order process. The equations
| (4) |
| (5) |
and
| (6) |
can be used to describe MT phenomena. By setting Pd = 0, one obtains the relevant expressions for the description of CEST phenomena. Notice that Δ is measured from the resonance of spin I and that the chemical shift of spin S is imbedded in the line shape function gS(Δ).
With additional irradiation frequencies, we cannot take recourse of a rotating frame in which the Hamiltonian is time-dependent, so the description of the dynamics becomes more complicated. On the other hand, it was shown that the accomodation of additional weak rf irradiation was rather straightforward in the laboratory frame [9]. If the differences between irradiation frequencies is much larger than the amplitudes of the rf fields, the cross effect caused by the simultaneous existence of two rf fields can be shown to be negligible, and each frequency contributes to the kinetics in the same way as in Eqs. (1) and (2) or Eq. (3). Therefore, the kinetic equations for a two-pool model for MT with a dipolar reservoir and under two-frequency rf irradiation will be given by:
| (7) |
| (8) |
and
| (9) |
where the primed symbols W′ and Δ′ are the transition rate and the offset for the second rf irradiation at ω′. Likewise, CEST under two-frequency rf irradiation can be described by Eqs. (7) and (8) with Pd = 0.
By setting dPI/dt = dPS/dt = dPd/dt = 0, Eqs. (7), (8), and (9) give the steady-state solutions PI,∞, PS,∞, and Pd,∞:
| (10) |
| (11) |
and
| (12) |
where and .
3. Numerical Study
Eqs. (4), (5), and (6) can now be solved numerically to check whether they produce a proper two-pool model. Two different examples are investigated, depending on the spectral parameters given to spin S. Let us call them the MT and CEST cases.
The simulation parameters were chosen as follows. The relaxation times for spin I, T1,I = 5 s and T2,I = 1 s, were set to be similar to those of the water proton NMR signal in the chondroitin sulfate (CS) solution used in the experimental study (Section 4). The same T1 relaxation time was used for spin S, i.e., T1,S = T1,I, because the concentration of spin S was set to be small: The initial and equilibrium polarizations PI,0 and PS,0 were assumed to be 0.99 and 0.01. Therefore, it may be assumed that the major relaxation mechanism for spin S is due to the fluctuating dipolar field from spin I, which makes the T1 relaxation times similar. The resonance frequency of spin S was set to be 1500 Hz, which is the frequency offset measured from the resonance frequency of spin I. If the external static magnetic field is 11.74 T, this value of 1500 Hz is close to the chemical shift (3.2 ppm) of amide protons relative to the water signal in cartilage [14, 15].
The line shape of spin I was assumed to be Lorentzian. For the CEST case, the line shape of spin S was also set to Lorentzian with T2,S = 1 s. The exchange rates kI→S and kS→I were set to 1 s−1 and 99 s−1, respectively. They are 3 to 5 times higher than the reported chemical exchange rates of amide protons [5, 6], so the CEST effect was exaggerated in our simulation. For the MT case, we assumed that spin S had a Gaussian line shape with ωloc = 2π × 1000 Hz or . The exchange rates kI→S and kS→I were set to 0.01 s−1 and 0.99 s−1, respectively, to produce the Z spectra similar with those of the CEST case. They are about 10% of the reported proton exchange rates of gelatin [16].
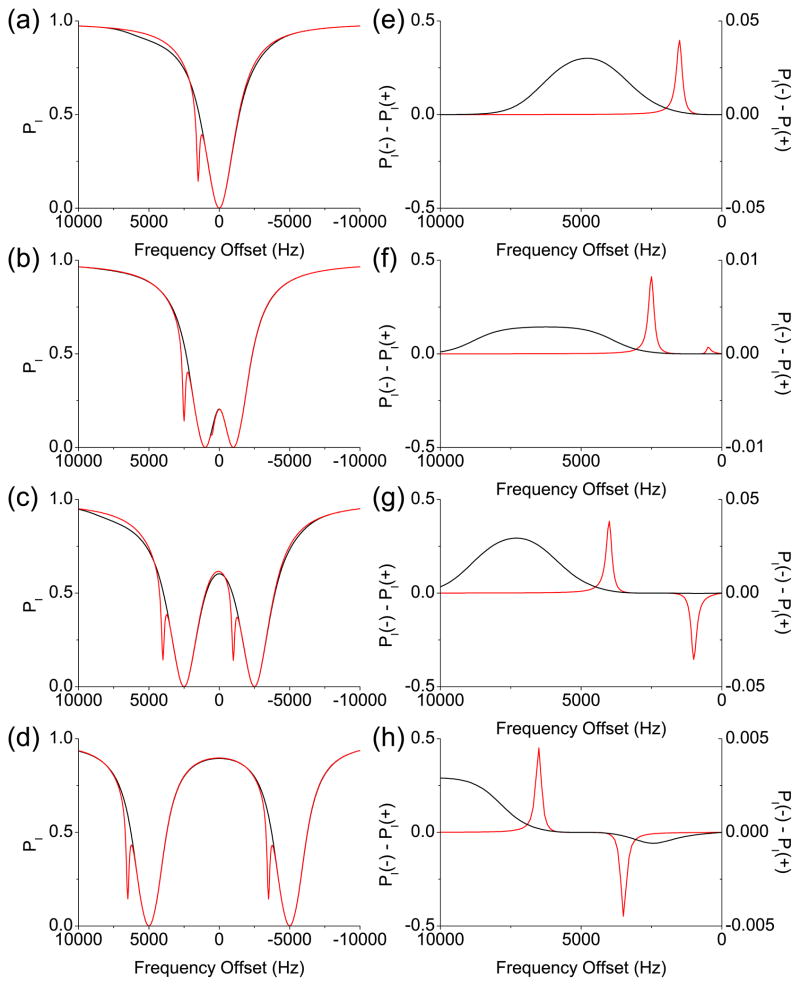
In Fig. 1(a), the numerically calculated PI after a 5 s-long rf irradiation with ω1/2π = 100 Hz are plotted against the frequency offsets of the rf irradiation, which are the so-called Z spectra. And Fig. 1(e) shows the asymmetries of the Z spectra, which were obtained by subtracting PI’s at the positive frequency offsets from PI ’s at the corresponding negative frequency offsets: PI(−Δ) − PI(+Δ). The MT and CEST cases are presented as black and red lines, respectively. In Fig. 1(a), two Z spectra are very similar except for the spike at 1500 Hz due to the CEST effect. In our simulation, the CEST and MT effects were so small that the only visually perceptible contribution to the Z spectra was the direct saturation of spin I. However, the asymmetry curves reveal the difference more clearly, as seen in Fig. 1(e).
Figure 1.
Simulated Z spectra and asymmetry curves from the two-pool model based on Provotorov’s theory. The black and red lines represent the MT and CEST cases, respectively. (a) Z spectra after 5 s-long single-frequency rf irradiation. (b)–(d) Z spectra after 5 s-long two-frequency rf irradiation. The distance between the two frequency components is (b) 2 kHz, (c) 5 kHz, and (d) 10 kHz, respectively. (e)–(h) The asymmetry curves corresponding to (a)–(d). The scales for the asymmetry curve from the MT case are separately indicated on the right.
In Figs. 1(b)–(d), the Z spectra of spin I after a 5 s-long two-frequency rf irradiation with the rf amplitudes and the distance between the two frequency components |Δ − Δ′ | = 2π× 2000 Hz, 5000 Hz, and 10000 Hz, respectively, are plotted against the central frequency offsets (Δ + Δ′)/2. So PI at f0 in the Z spectra resulted from the two-frequency rf irradiation at f0 + f and f0 − f, where f ≡ |Δ − Δ′ |/2. The asymmetries of the Z spectra were also calculated against the central frequency offset (Δ + Δ′)/2 as and are shown in Figs. 1(f)–(h).
With two-frequency rf irradiation, the Z spectrum is expected to have two dips due to the direct saturation of spin I as each frequency component independently sweeps the resonance of spin I, which is clearly shown in Figs. 1(b)–(d). For the CEST case, there are two more dips due to the CEST from spin S to spin I. When the distance between the two frequency components is smaller than twice the chemical shift difference between spins I and S, the two CEST dips will reside on the same side with respect to zero frequency, although one of them may be buried in one of the major dips due to the direct saturation as seen in Fig. 1(b). The corresponding asymmetry curve will have two CEST peaks with one sign as seen in Fig. 1(f). If the distance between the two frequency components is larger than twice the chemical shift difference, the two CEST dips will reside on opposite sides around zero frequency as seen in Figs. 1(c) and (d). These two CEST dips will contribute to the corresponding asymmetry curve as positive and negative peaks, as seen in Figs. 1(g) and (h).
For the MT case, the Z spectra with two-frequency rf irradiation, shown in Figs. 1(b)–(d), look like a simple duplication of the Z spectrum with the single-frequency rf irradiation. However, when the corresponding asymmetry curves are evaluated, there are cases in which only one asymmetry peak appears at the larger frequency offsets, as seen in Figs. 1(f) and (g). The flat regions at the smaller frequency offsets in the asymmetry curves in Figs. 1(f) and (g) can be explained by the uniform saturation of spin S when both frequency components lie within the spectrum of spin S, hence resulting in the uniformity of the MT effect. The MT asymmetry peak appears when the frequency offset is large enough such that only one frequency component touches the spectrum of spin S, and MT is no longer uniform. If the distance between the two frequency components is too large such that only one frequency component lies within the spectrum of spin S at all the frequency offsets, the asymmetry curve will have positive and negative peaks similar to the CEST case, as seen in Fig. 1(h).
When comparing the Z spectra shown in Figs. 1(b)–(d) to each other, one notices that PI also depends on the distance between the two frequency components: PI is bigger when the distance between the two frequency components is larger. The major contribution to this dependence would be the direct saturation effect. The uniformity of the MT effect can be checked only when the direct saturation effect is removed, which is done for paired frequency offsets in the asymmetry curve.
While the two-pool model established here accounts for MT and CEST separately, the results can be projected to the mixed (CEST + MT) case to some extent if the exchange rate between MT and CEST pools is much smaller than the individual MT or CEST exchange rates. Given that the bulk water pool is typically much larger than either the MT or CEST pool, in practice this assumption is often valid. In such a case, our simulation results imply that two-frequency rf irradiation can isolate CEST effects when it flattens out the asymmetry caused by the MT effects.
4. Experiments
The Z spectra under single- and two-frequency rf irradiations were obtained from CS solution, gelatin, and a bovine cartilage piece. These samples were chosen to respectively represent the CEST, MT, and mixed (CEST + MT) cases. All NMR experiments were performed using a Bruker Avance 500 MHz NMR spectrometer equipped with a broadband observe (BBO) probe, of which the outer saddle coil was used for proton NMR experiments. To reduce radiation damping effects, the probe was detuned to 508 MHz. Depending on the exact tuning and matching conditions, the duration of the 360° pulse was between 230 μs and 264 μs.
The CS solution was prepared in a 5 mm o.d. NMR tube by dissolving a CS sodium salt from bovine cartilage, purchased from Sigma-Aldrich, in a 50:50 H2O/D2O solution to give a concentration of 1% wt. The spin-lattice and spin-spin relaxation times for the water protons peak were measured to be 5.8 sec and 880 ms, respectively. The Z spectra were obtained with a 2 s-long rf irradiation followed by a 5° reading pulse. The amplitude of the 2 s-long rf irradiation (γB1/2π) was 100 Hz, and each experiment was repeated twice with alternating the phase of the rf irradiation in order to kill residual transverse magnetization. The recycle delay was set to 40 sec. Two-frequency rf irradiation was implemented by cosine pulses with the modulation frequencies from 1 kHz to 4 kHz, each of which consisted of 100,000 digitized steps. For example, the cosine pulse with the modulation frequency of 1 kHz had 50 digitized steps per cycle. The amplitude of the cosine pulses was set to 200 Hz, so each frequency component had the amplitude of 100 Hz. The frequency of the single-frequency rf irradiation or the center frequency of the cosine pulses were stepped from −4500 Hz to 4500 Hz at intervals of 100 Hz.
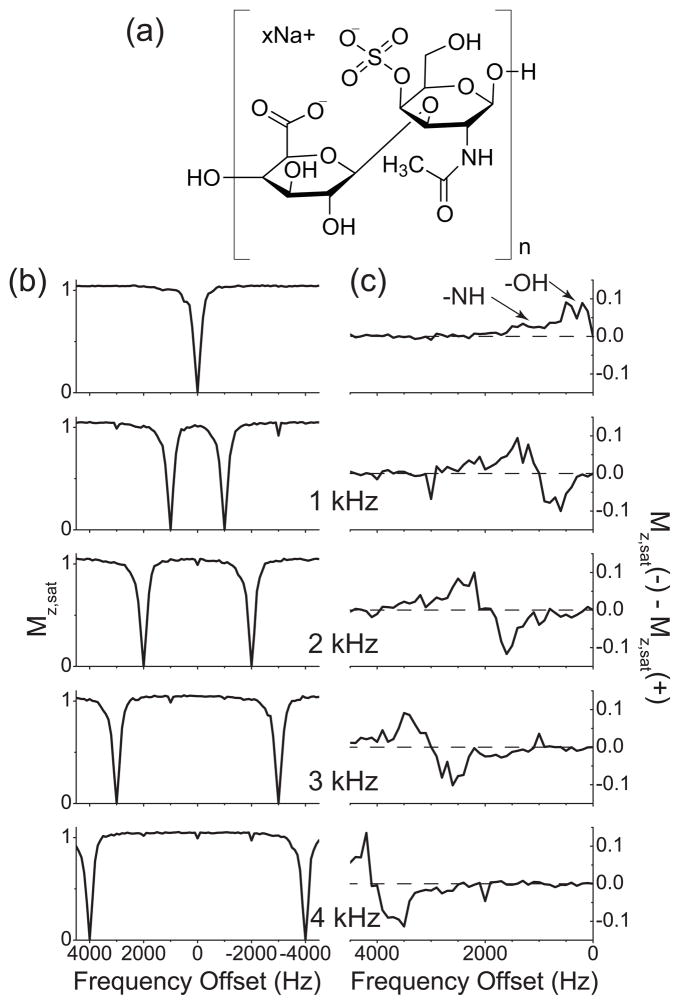
The Z spectra measured from the CS solution and their asymmetry curves are shown in Fig. 2. There are two groups of exchangeable protons (-NH and -OH) and two non-exchangeable MT sites (CH and N-acetyl residues) in the CS molecule (Fig. 2(a)), which give a broad positive bump spanning from 0 Hz to 1500 Hz in the asymmetry curve obtained with single-frequency rf irradiation (See Fig. 2(c), in which the two exchangeable sites are assigned.) [14, 15]. And with two-frequency rf irradiation, those CEST sites were scanned two times during the measurement of the Z spectra (Fig. 2(b)) and appeared as one negative and one positive peaks in the asymmetry curves (Fig. 2(c)), as expected from the numerical study in Section 3.
Figure 2.
Z spectra and their respective asymmetry curves of water protons in 1% CS solution. (a) The chemical structure of the disaccharide unit of a CS chain, composed of N-acetylgalactosamine and glucuronic acid. (b) Z spectra measured with (b0) the single-frequency rf irradiation and cosine pulses with the modulation frequencies 1 kHz, 2 kHz, 3 kHz, and 4 kHz. (c) The corresponding asymmetry curves calculated from the Z spectra shown in (a). The modulation frequencies of cosine pulses are indicated. The dashed line represents the zero asymmetry baseline.
For gelatin sample, gelatin powder (type B, from bovine skin, purchased from Sigma-Aldrich) was dissolved in heated water, then cooled down to the room temperature in order to obtain the gel state. The concentration of gelatin was 15% wt, and the gel was put into a 3 mm o.d. NMR tube. which was placed in a 5 mm o.d. NMR tube filled with D2O. This separation from D2O was necessary because the water proton resonance peak was distorted and proper shimming of the sample was not possible when the deuterium lock was operating with gelatin prepared in a mixture of H2O and D2O. This effect could perhaps be related to the MT mechanism in gelatin. The spin-lattice and spin-spin relaxation times of the water proton peak were 2 sec and 100 ms, respectively. The relaxation delay was set to 20 sec. The single-frequency and two-frequency rf irradiations were applied for 0.5 sec and followed by a 5° reading pulse. For two-frequency rf irradiations, cosine pulses with modulation frequencies from 1 kHz to 6 kHz were used, each of which consisted of 50,000 digitized steps (i.e., there were 100 digitized steps per cycle in the cosine pulse with the modulation frequency of 1 kHz). The frequency of the single-frequency rf irradiation and the center frequencies of the cosine pulses were varied from −8000 Hz to +8000 Hz at intervals of 100 Hz.
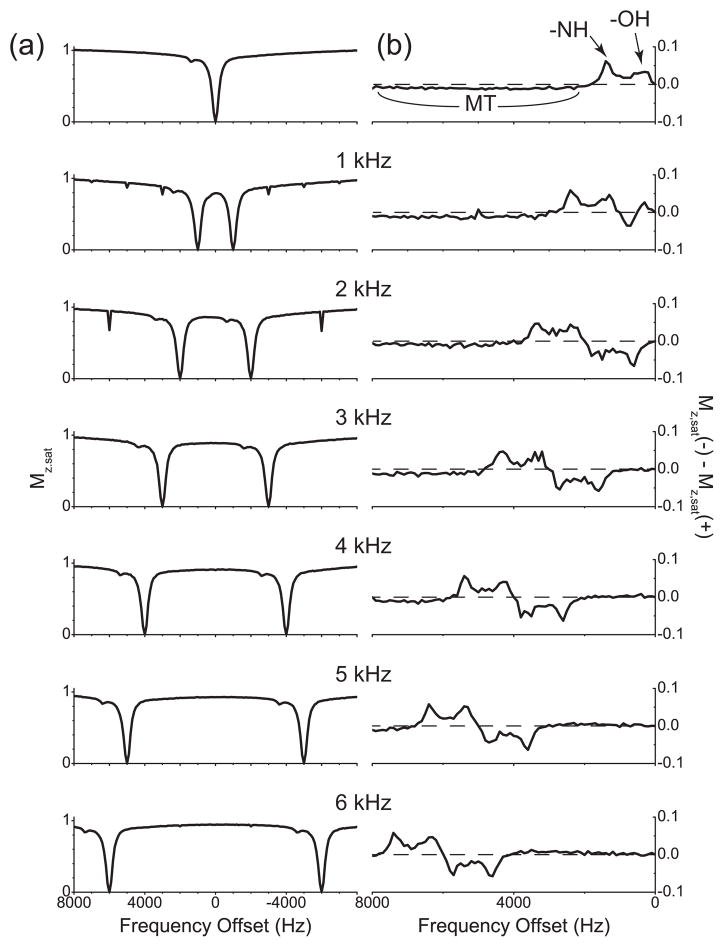
Interestingly, the Z spectrum of gelatin, obtained with single-frequency rf irradiation, revealed a narrow spike at 1400 Hz or 2.8 ppm downfield from the water protons resonance (Fig. 3(a)), which may indicate that gelatin contain some exchangeable protons [16]. When the asymmetry curve is plotted, there exist two narrow positive peaks between 0 Hz and 2000 Hz, and the asymmetry clearly stays negative beyond 2000 Hz, which suggests that the MT effect is not symmetric around the water resonance and that this MT pool should have its center frequency on the upfield side of the water protons resonance. In Fig. 3(b), the two CEST peaks are assigned and the range where the asymmetry curve stays negative is indicated as ‘MT’. The Z spectra obtained with cosine pulses or two-frequency rf irradiation (Fig. 3(a)) showed two dips due to direct saturation of water protons together with the narrow spike duplicated. Compared with the Z spectra from the CS solution, the Z spectra from gelatin showed less signal intensity of water protons, which is an indication of MT between water protons and protons in gelatin.
Figure 3.
Z spectra and their respective asymmetry curves of water protons in gelatin. (a) Z spectra measured with the single-frequency rf irradiation and cosine pulses with the modulation frequencies 1 kHz, 2 kHz, 3 kHz, 4 kHz, 5 kHz, and 6 kHz. (b) The corresponding asymmetry curves calculated from the Z spectra shown in (a). The modulation frequencies of cosine pulses are indicated. The dashed line represents the zero asymmetry baseline.
The corresponding asymmetry curves were plotted in Fig. 3(b). As expected, the narrow spike at 1400 Hz produced two peaks, one negative and one positive, in the asymmetry curves. For some cosine pulses, for example, when the modulation frequency was 3 or 4 kHz, the asymmetry was zero around the zero frequency until the negative peak appeared, as with the MT case of the numerical study in Section 3. By contrast, when the cosine pulses with larger modulation frequencies, say, 5 or 6 kHz, were applied, it can be seen that the asymmetry curves deviated from zero and moved to the positive direction before the negative peak appeared. This deviation is exactly the opposite of the broad negativeness observed in the asymmetry curve from single-frequency rf irradiation, which suggests that the situation is more like the CEST case and that the distance between two frequency components may be larger than the spectral range of the protons causing this MT effect.
A bovine articular cartilage piece was cut from a frozen patella, without bone segment, and placed in phosphate buffered saline solution for an hour. The cartilage piece was then blotted dry and put into a 3 mm o.d. NMR tube with Fluorinated oil (Fluorinert, FC-84, Oakwood) filling the void spaces for protection and reduction of susceptibility artifacts. Like the gelatin sample, the 3 mm o.d. NMR tube was placed in a 5 mm o.d. tube filled with D2O for the deuterium lock. The spin-lattice and spin-spin relaxation times for water protons were measured to be 4.2 sec and 80 ms, respectively. For the Z spectra, the same pulse sequence parameters were used as the CS solution.
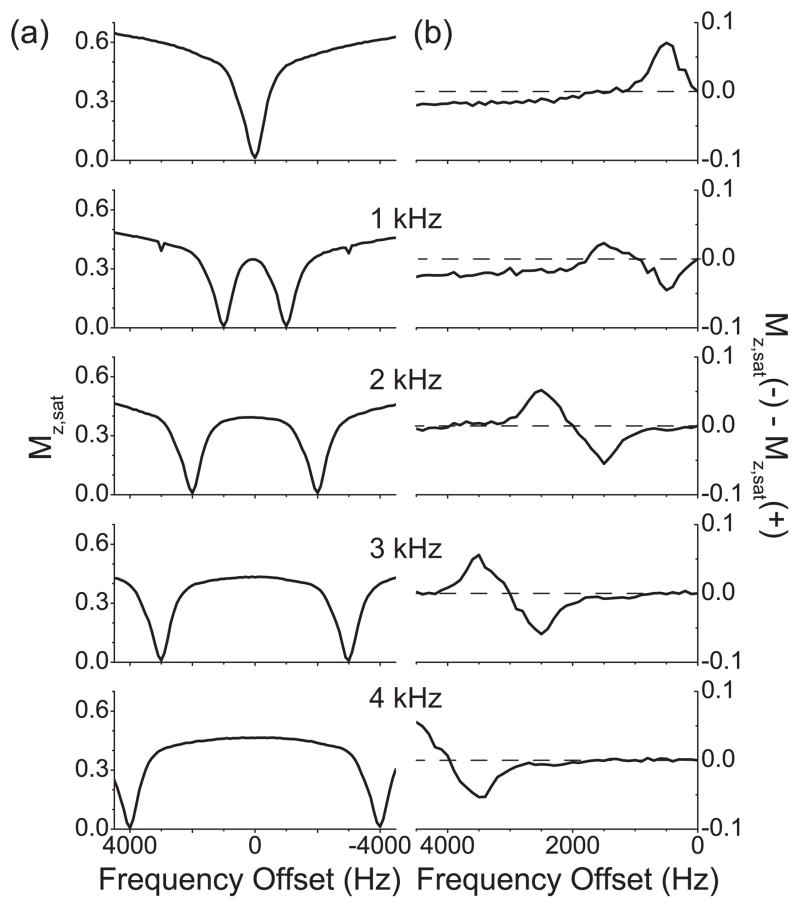
The Z spectrum obtained with single-frequency rf irradiation (Fig. 4(a)) shows a single dip around the zero frequency offset and much less intensity of water protons for all the frequency offsets compared with the CS and gelatin samples, which may be evidence for prevailing MT effects. Cartilage should have some exchangeable protons [14], which are barely seen in the Z spectrum. However, the corresponding asymmetry curve (Fig. 4(b)) clearly shows one narrow peak around 500 Hz or 1 ppm, can be assigned to CEST between water and -OH protons. At larger frequency offsets the curve converts into a broad negative baseline offset, which can be interpreted as large MT asymmetry effects.
Figure 4.
Z spectra and their respective asymmetry curves of the water protons in a bovine articular cartilage tissue sample. (a) Z spectra measured with the single-frequency rf irradiation and cosine pulses with the modulation frequencies 1 kHz, 2 kHz, 3 kHz, and 4 kHz. (b) The corresponding asymmetry curves calculated from the Z spectra shown in (a). The modulation frequencies of cosine pulses are indicated. The dashed line represents the zero asymmetry baseline.
The Z spectra obtained with cosine pulses (Fig. 4(a)) showed that the signal intensities of water protons became visibly smaller even when any of the two frequency components were not directly saturating the water protons. The corresponding asymmetry curves (Fig. 4(b)) showed that the asymmetry remained zero when the frequency offsets were small and until the negative peak appeared. Note that the integral of the asymmetry peak due to CEST became smaller with two-frequency rf irradiations as compared with single-frequency rf irradiation. When normalized to the integral of the asymmetry peak with single-frequency rf irradiation, the integrals of the negative asymmetry peaks were 0.55, 0.77, 0.92, and 0.87 for the cosine pulses with the modulation frequencies of 1 kHz, 2 kHz, 3 kHz, and 4 kHz, respectively. The negative peaks were chosen for this comparison, because they appear at smaller frequency offsets, where MT contributions are supposed to be minimal, as seen from the numerical studies (Section 3). If the areas of the negative asymmetry peaks from the cosine pulses with the modulation frequencies of 2 kHz, 3 kHz, and 4 kHz are taken into consideration, the average area is 0.85, and the standard deviation is 0.06. The area from the cosine pulse with the modulation frequency of 1 kHz was not included because it is exceptionally smaller, which could be caused by the simultaneous saturation of different CEST and NOE sites in cartilage [15].
5. Discussion
The kinetic equation for a spin without any dipolar reservoirs attached, Eq. (3), was derived in the laboratory frame, in which the condition for a perturbation approach, ω1 ≪ ω0, can be found. In contrast to the condition ω1 ≪ ωloc for Eqs. (1) and (2), which compares the strength of a perturbation with the spectral width of the dipolar reservoir, there is no such condition for Eq. (3). Therefore, it appears that Eq. (3) is still valid even if the amplitude of the applied rf field ω1 is larger than the spectral linewidth. For example, Eq. (3) predicts the same steady-state solutions, regardless of the value of ω1, as the Bloch equations (where the lineshape is Lorentizan). On the other hand, in the case when the applied magnetic field causes the Larmor precession of the magnetization vector, and consequently large and fast changes in the spin state, Eq. (3) may not be applied unless such Larmor precession is suppressed quickly enough. Such may be the case, for example, when a given system has fast transverse relaxation [17].
Previously, general line shape functions have been incorporated into the MT formalism via the Bloch equations [17]. In subsequent work, the kinetic equation for the dipolar reservoir was added [18]. The resulting equations are in accord with Eqs. (4)–(6), therefore the expansions of the MT formalism based on earlier work would not be affected [19–21]. The big advantage of deriving Eqs. (4)–(6) based on the Provotorov thermodynamic theory is that it provides a very simple conceptual framework with analytical results under approximations, which are satisfied in most cases. As for the uniform saturation under simultaneous two-frequency rf irradiations, it involves dipolar interactions between spins, which cannot be described by the Bloch formalism. By contrast, it is straightforward to incorporate two or more simultaneous rf irradiations with the Provotorov approach [9].
As a test for a mixed (CEST + MT) case, a sample of CS dissolved in agarose gel was also tested. However, the MT effect from agarose gel was symmetric, which means that two-frequency rf irradiation may not be required to isolate the CEST effects.
The uniformity of the MT effect is expected to occur as long as the two frequency components simultaneously touch the spectrum of spin S. From our gelatin experiment, for example, the asymmetry peak was produced at smaller frequency offsets when the modulation frequency was as large as 5 or 6 kHz (Fig. 3(b)), which indicates that only one frequency was within the spectral range of MT, and consequently uniformity of the MT effect was not achieved. In practice, it will be useful to determine the optimal distance between the two frequency components for a given sample, in order to insure the uniformity of the MT effect.
Cosine modulated pulses were used to apply two rf frequencies symmetrically around their center frequencies. They were implemented as digitized shapes with 50,000 steps for 0.5 s-long pulses and 100,000 steps for 2 s-long pulses. This number of steps should be large enough to approximate a continuous time variation of the rf amplitudes even at the highest modulation frequency for the given pulse duration. However, the experimental results showed spikes in the Z spectra at multiples of the modulation frequencies of the cosine pulses. For example, big spikes were observed especially at triple the modulation frequencies, which likely arised from digitization and truncation errors.
A practical constraint with the implementation of two-frequency rf irradiation by a digitized cosine pulse is that there is a limit on the maximum number of digitized steps in a shaped pulse on the spectrometer. Therefore, for a given distance between two frequency components, there exists a limit on the longest pulse duration. If implemented on an in vivo MRI scanner, one would, however, be limited to a larger degree by the specific absorption rate.
TWO-FREQUENCY CEST
Our numerical simulations and experiments presented here suggest that it is possible to separate CEST effects from MT effects with two-frequency saturation. When the MT effect is made uniform by two-frequency rf irradiation, only CEST effects contribute to the asymmetry of the Z spectra. As with conventional CEST contrast, the effect of direct saturation of water can be addressed by irradiating a given system at the opposite side of the water spectrum and subtracting the results. Therefore, so-called two-frequency CEST contrast can be estimated by combining two two-frequency rf irradiations: Their irradiation frequencies are pair-wise symmetric with respect to the resonance frequency of water protons, and one of the four frequency positions is located on the resonance frequency of an exchangeable proton. More efficient uniform saturation of MT effects can be performed by choosing the two frequency positions on opposite sides around the center frequency of the protons responsible for the MT effect [9]. These positions, however, may not in general be known directly because the spectra are often overlapped by the strong water signal. The positions may be estimated, however, through Z spectra.
Summarizing the above argument, the two-frequency CEST can be written in a compact form as CESTtwo freq(Δ1, Δ2) = Mz,sat(Δ1, Δ2) − Mz,sat(−Δ1, −Δ2), where Δ1,2 are the frequency positions measured from the resonance frequency of water protons and should be such that both frequencies simultaneously touch the spectrum of the protons which contribute to the MT effects, Δ1 is the chemical shift of an exchangeable proton measured from the resonance frequency of water protons. To avoid any interference due to the proximity of the two frequency positions and the possibility of simultaneous touch on multiple CEST sites, Δ2 may be chosen to be more than 5 or 6 ppm away from the water resonance, thus being outside of the typical range of proton chemical shifts [22].
Recently, a scheme using saturation with frequency alternating rf irradiation was developed to separate the CEST effect of the amide proton transfer (APT) from direct saturation of water protons and MT effects [23]. The method is based on the observation, that under saturation conditions when complete amide proton saturation is achieved, the APT effect becomes independent of the applied rf power, and the direct water saturation and MT effects vary mostly linearly with rf power. In order to isolate the APT effect, one then performs three measurements, with the off-resonant irradiations at the amide proton frequency, the opposite frequency, and both these frequencies simultaneously. A subsequent linear combination of the results is performed to separate the direct saturation from MT contributions. The method should work in the presence of B0 inhomogeneity under the assumption that the bandwidth of the applied rf power is broad enough that complete amide proton saturation can be maintained. This approach, however, relies on the linearity of MT effects, under multifrequency rf irradiation. We have highlighted earlier that under simultaneous two-frequency rf irradiation saturation happens in general much faster and more uniformly than when using a single frequency (at double the power). Therefore, the linearity assumption is not of general validity. As shown in this work, however, two-frequency rf irradiation offers other opportunities for separating CEST and MT asymmetry in such cases.
6. Conclusion
A two-pool model for MT and CEST has been established based on Provotorov’s theory of saturation, and the effects of two-frequency rf irradiation on MT and CEST were investigated. If the two frequency components simultaneously touch the broad spectrum of protons in macromolecules, the magnetization of those protons can be uniformly saturated over a broad spectrum, and the MT effect on the water protons can be made uniform. Therefore, one can remove the MT asymmetry, which may exist when single-frequency rf irradiation is applied. The spectrum of a CEST agent, on the other hand, is typically very narrow so that two-frequency rf irradiation merely duplicates the CEST effect. Based on this distinction between MT and CEST effects under two-frequency rf irradiation, we propose a novel two-frequency CEST scheme, which can isolate CEST effects from the MT effects and will be useful to quantify CEST contrast.
Acknowledgments
We acknowledge funding from the US National Science Foundation under Grant No. CHE0957586, and from the National Institutes of Health under Grant No. R21AR055724 and K25AR060269. The experiments were performed in the Shared Instrument Facility of the Department of Chemistry, New York University, supported by the US National Science Foundation under Grant No. CHE0116222.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Wolff SD, Balaban RS. Magnetization transfer contrast (MTC) and tissue water proton relaxation in vivo. Magn Reson Med. 1989;10:135–144. doi: 10.1002/mrm.1910100113. [DOI] [PubMed] [Google Scholar]
- 2.Henkelman RM, Stanisz GJ, Graham SJ. Magnetization transfer in MRI: a review. NMR Biomed. 2001;14:57–64. doi: 10.1002/nbm.683. [DOI] [PubMed] [Google Scholar]
- 3.Leibfritz D, Dreher W. Magnetization transfer MRS. NMR Biomed. 2001;14:65–76. doi: 10.1002/nbm.681. [DOI] [PubMed] [Google Scholar]
- 4.Ward KM, Aletras AH, Balaban RS. A New Class of Contrast Agents for MRI Based on Proton Chemical Exchange Dependent Saturation Transfer (CEST) J Magn Reson. 2000;143:79–87. doi: 10.1006/jmre.1999.1956. [DOI] [PubMed] [Google Scholar]
- 5.Zhou J, van Zijl PCM. Chemical exchange saturation transfer imaging and spectroscopy. Prog Nucl Magn Reson Spectrosc. 2006;48:109–136. [Google Scholar]
- 6.van Zijl PCM, Yadav NN. Chemical exchange saturation transfer (CEST): What is in a name and what isn’t? Magn Reson Med. 1011;65:927–948. doi: 10.1002/mrm.22761. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Pekar J, Jezzard P, Roberts DA, Leigh JS, Frank JA, McLaughlin AC. Perfusion imaging with compensation for asymmetric magnetization transfer effects. Magn Reson Med. 1996;35:70–79. doi: 10.1002/mrm.1910350110. [DOI] [PubMed] [Google Scholar]
- 8.Hua J, Jones CK, Blakeley J, Smith SA, van Zijl PC, Zhou J. Quantitative description of the asymmetry in magnetization transfer effects around the water resonance in the human brain. Magn Reson Med. 2007;58:786–793. doi: 10.1002/mrm.21387. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Lee JS, Khitrin AK, Regatte RR, Jerschow A. Uniform saturation of a strongly coupled spin system by two-frequency irradiation. J Chem Phys. 2011;134:234504-1–234504-6. doi: 10.1063/1.3600758. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Lee JS, Khitrin AK. Pseudopure state of a twelve-spin system. J Chem Phys. 2005;122:041101-1–041101-3. doi: 10.1063/1.1850456. [DOI] [PubMed] [Google Scholar]
- 11.Lee JS, Khitrin AK. Thermodynamics of adiabatic cross polarization. J Chem Phys. 2008;128:114504-1–041101-6. doi: 10.1063/1.2839436. [DOI] [PubMed] [Google Scholar]
- 12.Provotorov BN. Magnetic-resonance saturation in crystals. Zh Eksperim i Teor Fiz. 1961;41:1582–1591. [Google Scholar]
- 13.Goldman M. Spin Temperature and Nuclear Magnetic Resonance in Solids. Clarendon; Oxford: 1970. [Google Scholar]
- 14.Ling W, Regatte RR, Schweitzer ME, Jerschow A. Characterization of bovine patellar cartilage by NMR. NMR Biomed. 2008;21:289–295. doi: 10.1002/nbm.1193. [DOI] [PubMed] [Google Scholar]
- 15.Ling W, Regatte RR, Navon G, Jerschow A. Assessment of glycosaminoglycan concentration in vivo by chemical exchange-dependent saturation transfer (gagCEST) Proc Natl Acad Sci USA. 2008;105:2266–2270. doi: 10.1073/pnas.0707666105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Traoré A, Foucat L, Renou JP. 1H NMR studies: dynamics of water in gelatin. Eur Biophys J. 2000;29:159–164. doi: 10.1007/s002490000078. [DOI] [PubMed] [Google Scholar]
- 17.Henkelman RM, Huang X, Xiang QS, Stanisz GJ, Swanson SD, Bronskill MJ. Quantitative interpretation of magnetization transfer. Magn Reson Med. 1993;29:759–766. doi: 10.1002/mrm.1910290607. [DOI] [PubMed] [Google Scholar]
- 18.Morrison C, Stanisz G, Henkelman RM. Modeling magnetization transfer for biological-like systems using a semi-solid pool with a super-lorentzian line shape and dipolar reservoir. J Magn Reson B. 1995;108:103–113. doi: 10.1006/jmrb.1995.1111. [DOI] [PubMed] [Google Scholar]
- 19.Portnoy S, Stanisz GJ. Modeling pulsed magnetization transfer. Magn Reson Med. 2007;58:144–155. doi: 10.1002/mrm.21244. [DOI] [PubMed] [Google Scholar]
- 20.Cercignani M, Barker GJ. A comparison between equations describing in vivo MT: The effects of noise and sequence parameters. J Magn Reson. 2008;191:171–183. doi: 10.1016/j.jmr.2007.12.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Li AX, Hudson RHE, Barrett JW, Jones GK, Pasternak SH, Bartha R. Four-pool modeling of proton exchange processes in biological systems in the presence of MRI-paramagnetic chemical exchange saturation transfer (PARACEST) agents. Magn Reson Med. 2008;60:1197–1206. doi: 10.1002/mrm.21752. [DOI] [PubMed] [Google Scholar]
- 22.Levitt MH. Spin dynamics: Basics of nuclear magnetic resonance. John Wiley & Sons; Chichester: 2001. [Google Scholar]
- 23.Scheidegger R, Vinogradov E, Alsop DC. Amide proton transfer imaging with improved robustness to magnetic field inhomogeneity and magnetization transfer asymmetry using saturation with frequency alternating RF irradiation. Mang Reson Med. 2011;66:1275–1285. doi: 10.1002/mrm.22912. [DOI] [PMC free article] [PubMed] [Google Scholar]