Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2013 Apr 1.
Published in final edited form as: J Electromyogr Kinesiol. 2011 Dec 29;22(2):286–293. doi: 10.1016/j.jelekin.2011.12.002

Effects of loading on maximum vertical jumps: selective effects of weight and inertia

Bojan Leontijevic 1, Nemanja Pazin 1, Predrag R Bozic 1,2, Milos Kukolj 1, Dusan Ugarkovic 1, Slobodan Jaric 3
PMCID: PMC3288269  NIHMSID: NIHMS344092  PMID: 22209596

Abstract

A novel loading method was applied to explore selective effects of externally added weight (W), weight and inertia (W+I), and inertia (I) on maximum counter-movement jumps (CMJ) performed with arm swing. Externally applied extended rubber bands and/or loaded vest added W, W+I, and I corresponding to 10–40% of subjects' body mass. As expected, an increase in magnitude of all types of load was associated with an increase in ground reaction forces (GRF), as well as with a decrease in both the jumping performance and power output. However, of more importance could be that discernible differences among the effects of W, W+I, and I were recorded despite a relatively narrow loading range. In particular, an increase in W was associated with the minimal changes in movement kinematic pattern and smallest reduction of jumping performance, while also allowing for the highest power output. Conversely, W+I was associated with the highest ground reaction forces. Finally, the lowest maxima of GRF and power were associated with I. Although further research is apparently needed, the obtained finding could be of potential importance not only for understanding fundamental properties of the neuromuscular system, but also for optimization of loading in standard athletic training and rehabilitation procedures.

Keywords: force; power, performance, pattern, countermovement jump

INTRODUCTION

In general, the muscular system is loaded by the weight (W) and inertia (I) of its own body segments, but sometimes also by the loads and other external forces acting upon it. While the direction of I force is determined by the direction of acceleration in the 3-dimensional space, the direction of the acting W is always vertical. Therefore, the lines of action of W and I forces are collinear only when human body (together with occasionally added external load) accelerates in vertical direction, such as in vertical jumps. As a consequence, the scalar equation that represents the vertical component of the ground reaction force (GRF) exerted over time t during vertical jumping is:

GRF(t)=m[g+a(t)], (eq. 1)

where m is the body mass, g is gravity acceleration, and a(t) acceleration of the body in upward direction. Note that the product of m and g corresponds to the body weight (W = m g) which is constant over time, while the product of m and a(t) corresponds to the inertial force [I(t) =m a(t)] which changes over time depending upon the body acceleration. The same equation also applies to the vertical component of the external force acting upon other body movements performed in other directions. In general, the movements performed predominantly in the vertical direction, such as vertical jumps, seem to be predominantly affected by W, whereas walking and running is predominantly loaded by limb I (i.e., resistance to acceleration and deceleration of the limbs; McMahon, 1984, Teunissen et al., 2007).

Its is well known that manipulation of external weights inevitably affects the kinematic and kinetic pattern, dynamic output (e.g., power and momentum), as well as the overall efficiency of the muscular system (Cormie et al., 2011a, b, Frost et al., 2010). However, it still remains unclear whether and to which extent the particular components of external loads (i.e., W and I) have selective affect on the aforementioned variables in complex human movements. A number of previous studies have been focused upon the optimum loading regarding the minimization of the energy expenditure (Teunissen et al., 2007) and maximization of output (Bevan et al., 2010, Cormie et al., 2007c, Lund et al., 2004, Markovic and Jaric, 2007, Nuzzo et al., 2010). Manipulation of external constant force in vertical direction that mimics change in W allowed for formulation of the Maximum Dynamic Output Hypothesis suggesting that for the lower limb muscles the optimal load for maximizing the power and momentum production could be the subject's own body (Jaric and Markovic, 2009). However, only the horizontal walking and running have been explored regarding the selective effects of W on movement kinematic and kinetic patterns and the results were rather inconclusive (Chang et al., 2000, De Witt et al., 2008, Teunissen et al., 2007). However, previous studies neither explored the effect of I, nor focused on movements performed at least partly in vertical direction where the effects of W could be at least comparable to the effect of I. Finally, excluding some single-joint tasks (see further text for details), the selected effects of W and I on maximum performance movements have been mainly neglected.

In addition to the theoretical aspects discussed above, discerning the effect of external W and I on human movements could also be important from practical perspective. The exercise with external loading has been routinely used to enhance performance in both athletes and various clinical populations subjected to rehabilitation procedures. By far the most frequently applied type of load in athletic training, rehabilitation, and testing has been the addition of external weights either directly or through various pulleys (Anderson et al., 2008, Cavagna et al., 1972, Chang et al., 2000, Cormie et al., 2007b, De Witt et al., 2008, McBride et al., 1999, Wallace et al., 2006, Wilson et al., 1993). Therefore, the movements performed were inevitably loaded by both W and I of the applied loads. Relatively few studies applied an external resistance with an insignificant I component. Theoretically, long and extended rubber bands could provide a relatively constant force (that mimics either increase or decrease in W) with negligible I (Galantis and Woledge, 2003, Gosseye et al., 2010, Griffin et al., 1999). However, in most of the studies the bands were either not long and/or stretched enough to provide a relatively constant force over the full movement range (e.g., Israetel et al., 2010, Jakubiak and Saunders, 2008, Wallace et al., 2006). Nevertheless, it has been found that the training with elastic resistance could be more effective than the free-weight resistance alone for developing the lower and upper body strength (Anderson et al., 2008), particularly during transition from eccentric to concentric phase of vertical jumps (Israetel et al., 2010, Wallace et al., 2006). Conversely, an action against purely I is possible when W of the added external weight is compensated, such as in movement performed in horizontal plane. However, those movements have been frequently applied in motor control research (typically single-joint movement; Corcos et al., 1993, Jaric, 2000) suggesting particularly prolonged concentric phase of agonist action, but virtually never applied in routine exercise and rehabilitation procedures. Hence, discerning the effects of weight-type and inertia-type of load on complex movements could give us a beneficial guidance regarding their potential use in training and rehabilitation (Frost et al., 2010).

Vertical jumps appear to be a well-suited model for studying the maximal dynamic output of the lower-limb muscles (Baker et al., 2001b, Cormie et al., 2007c, Driss et al., 2001, Harris et al., 2007, Markovic and Jaric, 2007, McBride et al., 1999, Wilson et al., 1993). In addition, the same jumps have been regularly used as both a training and testing procedure in various physical conditioning programs (Jaric and Markovic, 2009, Markovic et al., 2011). The implicit justification has been that the performance of maximal vertical jumps highly correlate with the maximum performance of other rapid and explosive movements tasks (e.g. running, changing of direction, kicking, throwing; Kukolj et al., 1999). Several loading methods have been applied in both training and testing procedures based on vertical jumps, as well as when studying the adaptation of the jumping kinematic and kinetic pattern (Argus et al., 2011, Cavagna et al., 1972, Markovic and Jaric, 2007, Nuzzo et al., 2010). Some of the methods differed regarding the type of load including the application of stretched rubber providing a constant pulling force that solely mimics the effect of W (Cavagna et al., 1972, Markovic and Jaric, 2007), while the most frequent method of loading has been addition of external weights that increase both W and I (Cormie et al., 2007a, Cormie et al., 2007c, Driss et al., 2001, McBride et al., 1999, Stone et al., 2003). The loading methods also differed regarding the position of external weight, such as positioning a barbell on shoulders (Cormie et al., 2007c, McBride et al., 1999, Nuzzo et al., 2010, Stone et al., 2003) vs. using loaded belt or vest that bring the load closer to the body's center of mass (Argus et al., 2011, Cavagna et al., 1972, Driss et al., 2001, Markovic and Jaric, 2007, Markovic et al., 2011). Therefore, it is not surprising that the effects of external loading regarding the kinematic and kinetic patterns of the tested jumps reported in the literature have been partly inconsistent (see Jaric and Markovic, 2007, Nuzzo et al., 2010 for review). However, none of the studies have explored the selective effects of W and I on the kinematic and kinetic pattern of maximum vertical jumps, as well as on the associated muscular dynamic output.

To address the above discussed unresolved issues, we developed a novel methodology for a selective manipulation of different loading components during vertical jumping. Specifically, the application of the stretched rubber bands, loaded west, and their co-variation on maximum counter-movement jumps (CMJ) allowed for mimicking the addition of W, W+I, and I, respectively. Independently of the type of the load applied, we expected that the loading associated effects would be in line with both the empirical data (e.g., an increase in jumping duration and decrease in jumping performance; c.f., Cormie et al., 2007b, Markovic and Jaric, 2007) and the maximum dynamic output hypothesis (i.e., a decrease in power output). However, the main aim of the study was to explore the selective effects of the W and I on the maximum vertical jump. The findings were expected not only to reveal some fundamental properties of the neuromuscular system and its adaptation, but also to provide potentially valuable information regarding the load optimization in various training and rehabilitation interventions.

METHODS

Participants

Fifteen male college students of sport and physical education program (age 23.5 ± 2.4 years; mean ± standard deviation) participated in this study. Their body mass (78.1±7.5 kg) and body height (180.8 ± 7.4 cm) were assessed by a digital scale and kinanthropometer by Martin, respectively. Percent body fat (13.8 ± 4.7%) was assessed using a bioelectric impedance method (In Body 720; USA). The participants were physically active through their standard academic curriculum that included 6–8 activity classes per week that involved both low and high intensity exercises. However, none of them was an active athlete neither have had experience with regular resistance training. The participants did not report chronic diseases, heart problems, or recent injuries to the musculoskeletal apparatus. They were informed regarding the potential risks associated with the applied testing protocol and asked to sign an informed consent document prior to the testing protocol. The study was approved by the Institutional Review Board, and carried out according to the Declaration of Helsinki.

The pulley device and the applied loads

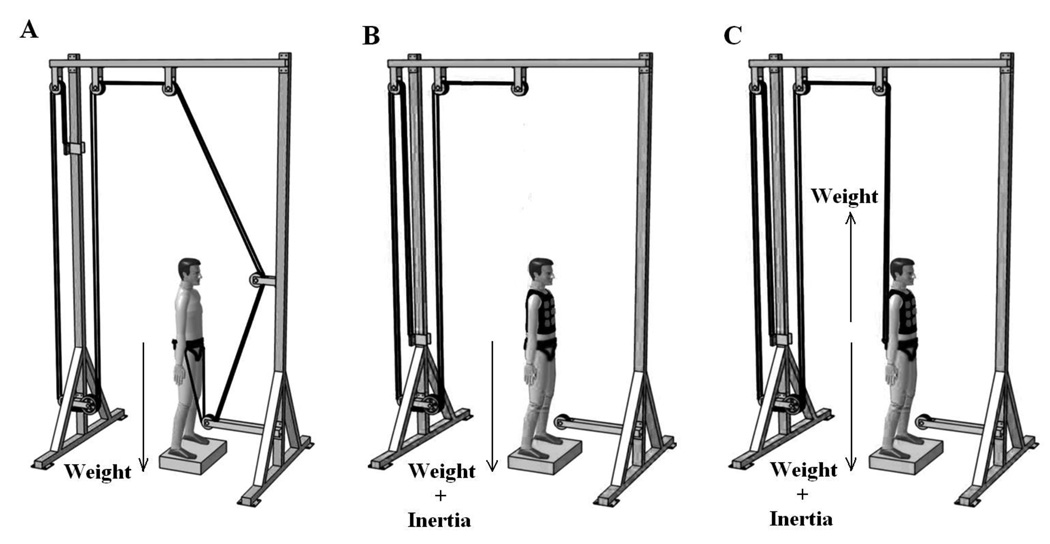
For the purpose of this study, we developed a pulley system to simulate either an increase or decrease in body weight (W; Fig. 1). In particular, rubber bands (resting length 8 m, coefficient of elasticity 42 N/m) were stretched to provide the pulling force that corresponded to 10–40% of individual body W. They were attached to both lateral sides of a belt fixed approximately at the subject's waist and stretched over a system of low friction and low inertia plastic wheels. Note that in the vertical direction the subjects moved their waist during the eccentric and concentric jumps phase approximately within a 0.30 m interval. Therefore, the relative change in their stretched length was approximately between ± 2% and ± 8% of their average length (when exerting force between 40% and 10% of body W, respectively), yielding similar change in the acting force (Fig. 1A). Taking into account also that the rubber bands' mass was negligible, one could assume that the applied pulling forces were nearly constant during the jumping trials and, therefore, mimicked the alterations of W, but not I. The subjects were also wearing a loaded vest (MiR 60Lbs Pro; USA; Fig. 1B) that inevitably added both W and I (Fig. 1B). Finally, note that wearing a loaded vest in combination with the pulling force acting vertically upward allowed for compensation of the vest's W, but not I (Fig.1C). As a result, the following three types of load were applied: (a) the application of solely rubber bands pulling downwards mimicked addition of W, (b) the application of only the loaded vest mimicked the increase in both W and I, while (c) the co-variation of the loaded vest with the rubber bands compensating for the added W by pulling upward, mimicked increase in solely I.

Figure 1.

Figure 1

Open in a new tab

Schematic representation of the applied loads. (A) The elastic bands pulling downward with the approximately constant force simulated increased weight (W), (B) a loaded vest simulated increased both the weight and inertia (W+I), while (C) the combination of the vest and the elastic bands pulling upward simulated increased inertia (I).

Loading conditions

The participants were asked to perform maximum countermovement jumps with arm swing (CMJ) on a force plate (AMTI, BP600400; USA) while the type and magnitude of external load was manipulated. Specifically, they performed CMJ when loaded with 10%, 20%, 30% and 40% of their (a) body weight (W; 110%W, 120%W, 130%W, and 140%W, respectively), (b) weight and inertia (W+I; 110%W+I, 120%W+I, 130%W+I, and 140%W+I), and (c) inertia (I; 110%I, 120%I, 130%I, and 140%I). Therefore, the total number of loading conditions was 13, including the jump performed without either of the external loads (no load). The force platform signal served for fine tuning of either the vest weight, or elastic bands force, or their combination.

Experimental protocol

Each subject completed 3 identical (i.e., two familiarization and one experimental) sessions separated by 3 day of rest. In total, they completed a total of 119 jumps (13 loading conditions × 3 jumps each × 3 sessions). They were also instructed to avoid any strenuous exercise over the course of study. Each session was preceded by a standard warm-up procedure (5 min cycling and 5 min of callisthenic and dynamic stretching). Thereafter, the subjects performed three consecutive CMJ trials under 110%, 120%, 130% and 140 % of the particular load (W, W+I, and I) and three jumps without any external load (no load), in a randomized order. The rest period among jump trials was 15 s and among different loading type conditions was about 2 min. In line with our recent studies (c.f., Markovic et al., 2011) performed according to a similar procedure, as well as according to the participants’ reports, fatigue was never an issue.

Data processing and analysis

The force plate was mounted and calibrated according to the manufacturer’s specifications. Custom-designed Lab VIEW (National Instruments, Version 8.2) programs were used to record and process the recorded vertical component of the ground reaction force (GRF) at the sampling frequency of 1 kHz. The velocity and position of the center of mass were calculated by consecutive integrations of the acceleration signal assessed from GRF. Regarding the kinematic and kinetic pattern of the tested jumps, we calculated the maximum lowering of the center of mass during the eccentric jump phase (Δhecc), duration of the concentric jump phase (Tconc), GRF at the moment of transition from the eccentric to concentric jump phase (Ftrp), and peak GRF during the concentric jump phase (Fpeak). Since the external force applied through the pulley device alters body acceleration during the flight phase, we assessed the jumping performance by the peak velocity of the body during the concentric phase (Vpeak) instead by the jump height (Markovic and Jaric, 2007). Finally, the dynamic output was assessed through the peak power (Ppeak) and mean power output (Pmean) assessed from the concentric jump phase and calculated as a product of velocity and GRF. The reliability of the calculated mechanical variables has been shown to be high across the range of applied loads (Markovic and Jaric, 2007).

Statistical analysis

Since the first jump was always considered as a practice, the jump of the following two with higher Vpeak was taken for further analysis. Descriptive statistics were calculated for all experimental data as mean and standard deviation (SD). The normality of the distribution for all dependent variables was tested by means of the Kolmogorov-Smirnov test. Since no violations of normality were detected (p ≥ 0.16) the effects of 'type' (W, W+I, and I) and 'magnitude' (110%, 120%, 130%, and 140%) of the applied external loads on all dependent variables were tested by means of two-way repeated measures ANOVA. When the main effects were revealed, Bonferroni post-hoc tests were applied. In addition, the partial eta squared (pη2) was calculated for the ANOVAs where the values of the effect sizes 0.01, 0.06 and above 0.14 were considered small, medium and large, respectively (Cohen, 1988). Alpha was set at p = 0.05. All statistical tests were performed using SPSS 16.0 (SPSS Inc, Chicago, IL).

RESULTS

Force profiles

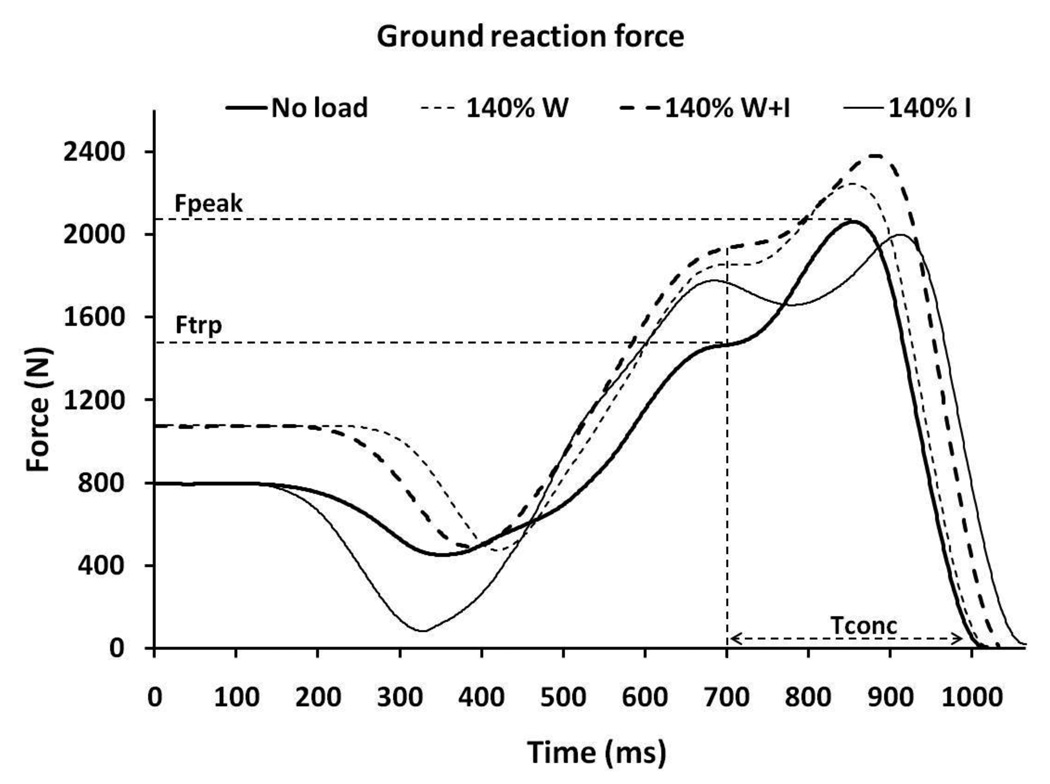
Figure 2 depicts the time series of the vertical component of ground reaction force (GRF) obtained from a representative subject when jumping under no load condition, as well as loaded with additional 40% of weight (140%W), 40% of weight and inertia (140%W+I), and inertia (140%I). The time series are aligned by the instant of transition from eccentric to concentric jump phase. Note that applied jump associated with increased weight (W) also reveal higher peaks of GRF, while the jumps associated with increased inertia (I) depict somewhat prolonged Tconc.

Figure 2.

Figure 2

Open in a new tab

Vertical component of the ground reaction force obtained from a representative subject under no load condition (tick solid line), and when the applied load corresponded to 40% of the body weight (140%W; thin dashed line), weight and inertia (140%W+I; tick dashed line), and inertia (140%I; thin solid line). Note that all 4 force series are aligned with respect to the instant of transition from eccentric to concentric jump phase.

Kinematic and kinetic pattern

The effects of loading on the kinematic and kinetic pattern of the tested jumps is illustrated in Figure 3 and compared with 'no load' conditions. The outcome of the two-way repeated measures ANOVA (main factors being the 'type' and 'magnitude' of the applied load) is shown in Table 1. The results suggest that the subjects lowered their center of mass more when loaded with the W and I then with both weight and inertia (W+I), while there was no effect of the load magnitude. All remaining three variables revealed both the main effects and their interactions. The Δhecc increased with the load magnitude and the effect was more prominent for W and I than for W+I. Tconc also increased with the load magnitude, but only for W+I and I. Finally, both Ftrp and Fpeak increased with the load magnitude, but more for W+I.

Figure 3.

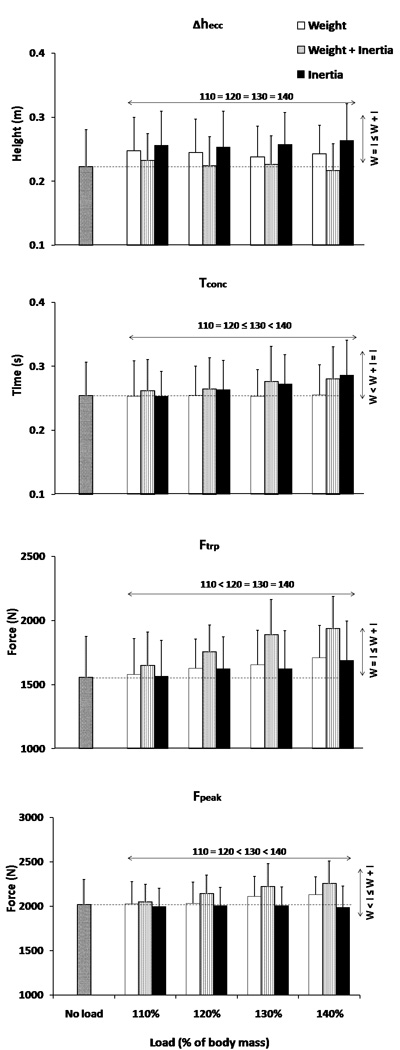
Figure 3

Open in a new tab

Kinematic and kinetic jumping pattern revealed through the maximum lowering of the center of mass during the eccentric jump phase (hecc; A), duration of the concentric phase (Tconc; B), and the ground reaction force (GRF) at the instant of transition (Ftrp; C), and its peak (Fpeak; D) observed under different loading conditions (data averaged across the subjects with standard deviation error bars). The main effects of 'type' and 'magnitude' of the applied load are indicated by vertical and horizontal arrows, respectively, together with the outcomes of the post-hoc tests. Note that < sign shows significant difference from all values on the right, while ≤ indicates that the two adjacent values are not different, while the remote ones are.

Table 1.

Main effects of the load 'type' and 'magnitude' on the dependent variables assessed through their significance and corresponding effect sizes.

Variable ANOVAs F Main Effect
p - level		 Effect size
pη2 		Effect size
descriptor
Δhecc Type 17.99 0.001 0.562 Large
Load 1.04 0.363 0.069 Small
Interaction 1.97 0.136 0.123 Moderate
Tconc Type 11.08 0.000 0.442 Large
Load 14.77 0.000 0.513 Large
Interaction 3.99 0.001 0.222 Large
Ftrp Type 17.82 0.000 0.560 Large
Load 22.15 0.000 0.613 Large
Interaction 3.32 0.006 0.192 Large
Fpeak Type 32.87 0.000 0.701 Large
Load 22.23 0.000 0.614 Large
Interaction 7.64 0.000 0.353 Large
Vpeak Type 84.07 0.000 0.875 Large
Load 658.31 0.000 0.979 Large
Interaction 17.25 0.000 0.522 Large
Ppeak Type 16.41 0.000 0.540 Large
Load 39.14 0.000 0.737 Large
Interaction 8.01 0.000 0.364 Large
Pmean Type 11.40 0.000 0.449 Large
Load 3.16 0.034 0.184 Large
Interaction 6.27 0.000 0.309 Large
Open in a new tab

Jumping performance and dynamic output

The effects of the type and magnitude of the external load on the maximum jumping performance and dynamic output are shown in Figure 4 and Table 1. In general, Vpeak decreased with the load magnitude, but the most and the least prominent decrease was associated with W+I and W, respectively. Both Ppeak and Pmean decreased with the load magnitude. However, it appears that the effect was mainly associated with the increase in I and partly W+I, rather than on solely W.

Figure 4.

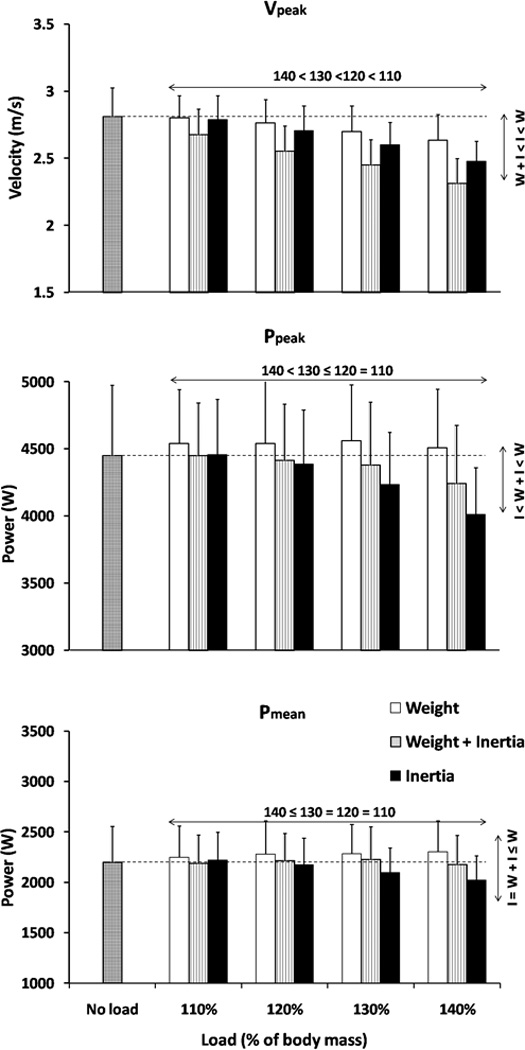
Figure 4

Open in a new tab

Jumping performance and power output revealed through the peak velocity (Vpeak; A), maximum (Ppeak; B), and average power observed during the concentric phase (Pmean; C) observed under different loading conditions (data averaged across the subjects with standard deviation error bars). For other details see legend of Figure 3.

DISCUSSION

We studied the effects of external loading accomplished by selective manipulation of weight (W; a constant downward pulling force exerted by stretched rubber bands), weight and inertia (W+I; a loaded vest added), and inertia (I; W of the vest compensated by rubber bands) on the maximum CMJ performed with arm swing. In general, although the differences among the effects of different types of the applied loads may look subtle, some noteworthy effects emerged. As expected, an increase in all types of the applied loads was associated with a reduced vertical jumping performance, but the most and the least prominent effects were associated with W+I and W, respectively. Both the lowering during the eccentric phase (Δhecc) and the duration of the subsequent concentric jump phase (Tconc) increased when loaded by I. Finally, an increase in loading was associated with moderate decrease in both the peak and average power (i.e., Ppeak and Pmean, respectively), particularly when I was applied. Further discussion will deal with the methodological issues related to the applied loading, as well as with both the overall and selective effects of the particular load types.

From the methodological aspect, it is important to stress that this is the first study that examined the selective effects of W and I on both the mechanical patterns and dynamic output of vertical jumping. Note that using the co-variation of added weight and upward pulley system to isolate the inertial effect of external load has been applied in horizontal gait (De Witt et al., 2008, Teunissen et al., 2007). However, our approach allowed application of both the individual load components and their combination (i.e., W, I, and W+I, respectively) in equal steps. Moreover, we applied the load that acted in the direction of the studied movement (i.e. vertical jumps) instead of orthogonally, such as in walking and running where the manipulation of load cause relatively minor effect of muscle action, as assessed by metabolic cost (Teunissen et al., 2007). Of importance could also be that the loading was applied close to the subjects' center of mass (Chang et al., 2000, De Witt et al., 2008, Teunissen et al., 2007) which is likely to reduce the changes in movement patterns usually associated with loading applied upon the subjects' shoulders (for details see, Cronin and Sleivert, 2005). Taken together with the high reliability of the obtained dependent variables (Markovic and Jaric, 2007), the above discussed issues collectively support our methodological approach to studying the effect of different loading components on maximum vertical jumping. However, the selection of CMJ also reduced the range of the applied loads since the empirical evidence suggests that applying loads higher than 30–40% body W dramatically changes the jumping pattern even in young and physically active individuals (Markovic and Jaric, 2007, Markovic et al., 2011). Since the regular annual testing of the participants reveals the average maximum load lifted during 1-repetition maximum squat of about 120 kg while also acting against their own body weight, it appears that the applied load range (i.e., 10–40% of body W) corresponded to only about 15% of the maximum strength of their leg extensors. This could explain relatively weak loading associated effects obtained in the present study.

The observed findings revealed both the overall loading effects and the partly distinctive effects of particular loading types. Regarding the overall loading effects on the studied jumps, it should be kept in mind that various methodological differences could be responsible for partly inconsistent finding in the literature (see Introduction for details). Nevertheless, an increase in external loading is generally expected to be associated with altered kinematic and kinetic jumping pattern to maximize both the performance (such as movement velocity) and the mechanical output (such as peak power; Baker et al., 2001a, Baker et al., 2001b, Newton and Kraemer, 1994, Wilson et al., 1993). It is generally believed that the power output in complex movement depends on the coordination pattern, rather than on the power output of individual muscles (c.f., Wakeling et al., 2010). The recorded alterations of movement patterns are mainly in line with other studies of external loading applied in vertical jumping (Markovic and Jaric, 2007), bench throws (Newton et al., 1997) and gait (Chang et al., 2000, De Witt et al., 2008). In particular, we observed that an addition of either W, or I, or both (i.e., W+I) were associated with decreased peak velocity (Vpeak) and an increase in the GRF (as seen through Ftrp and Fpeak). Similar effects were also observed in running performed under selective W and I loading (Chang et al., 2000). Note that the jumping height is proportional to Vpeak squared, which explains relatively weak effect of load on jumping performance measured through Vpeak, instead through regularly recorded jumping height. However, Tconc increased with load without an overall increase in the body lowering, while the load associated decrease in Δhecc was observed in recent studies of loaded CMJ (Markovic and Jaric, 2007, Markovic et al., 2011). However, note that these authors manipulated only W by applying similar rubber bands and, probably even more importantly, they tested CMJ performed without arm swing. Finally, the maximum dynamic output as assessed through the Ppeak and Pmean decreased with an increase in load. This finding isin line with maximum dynamic hypothesis (Jaric and Markovic, 2009) suggesting that the muscular system of the lower limbs is designed to produce maximum dynamic output when loaded with the W and I of one's own body (Argus et al., 2011, Markovic and Jaric, 2007, Nuzzo et al., 2010). However, it should be also kept in mind that in the present study we only applied positive loading which could considerably restrict drawing conclusions regarding the optimizing of external loads (Jaric and Markovic, 2009, Nuzzo et al., 2010).Therefore, to generalize the overall effects of external loading on CMJ discussed in the present paragraph, one could apply a full range of external loads (i.e., from positive to negative ones) on both the CMJ performed with and without arm swing.

Due to the novelty of the methods applied, the most important findings of the present study could be those related to the selective effects of different load types. The effects can be assessed both through the type-magnitude interactions and through the effect sizes (see Table 1 for the data). Regarding the jumping kinematic and kinetic patterns, the selective effects of different load types were relatively week. In particular, Δhecc was similar for the three types of load, while the differences among their effects on Tconc and Ftrp were relatively small. Nevertheless, higher Ftrp and Fpeak mainly associated with W+I could be explained by particularly reduced movement velocity (as seen through Vpeak). A similar adaptation of active vertical forces to weight and inertia has been observed in running (Chang et al., 2000, De Witt et al., 2008). Regarding the jumping performance and dynamic output, the smallest negative effect of external load on Vpeak (and, therefore, on the jumping performance) was revealed by W, and the largest by W+I. Therefore, it should not be surprising that W also revealed the smallest effect on both Ppeak and Pmean. Altogether, one could conclude that while applying W+I leads to an increase in ground reaction forces (and, likely, muscle forces), the application of only W mainly preserves the movement pattern and performance and still allows for relatively higher power output. The last finding is also in line with relatively small changes in kinematic patterns of running associated with the unloading method that mimicked W (Gosseye et al., 2010).

Interpretation of the above discussed selective effects of the different load types is severely restricted because of several reasons. First, the type-specific differences among the effects are relatively small and the important reason could be a relatively narrow range of the load magnitudes applied (see above for more details). Second, even relatively small differences in the jumping kinematic pattern can considerably affect the jumping kinetic and dynamic variables (Dugan et al., 2004). Movement coordination may strongly affect the overall mechanical output of the muscular system (Wakeling et al., 2010) and, therefore, the recorded changes in movement performance and power output could be a result of both the external loading and the movement pattern adaptation. Third, a more comprehensive set of kinematic variables and, particularly, EMG data are needed for more elaborate study of the mechanisms (e.g., kinematic, kinetic, neural, etc) that lead to the adjustments to different load types and magnitudes. Of apparent theoretical importance could be to explore whether there are independent adaptation strategies to changes in W and I in vertical jumps, as they could exist in horizontal gait (De Witt et al., 2008). Therefore, further research is needed to reveal the mechanisms involved in the selective effects of W and I on the patterns vertical jumping and other types of explosive movements. Nevertheless, in addition to several general effects discussed above, the present study also reveals some findings of potential importance for load optimization in various rehabilitation and strength training procedures. Specifically, applying a load through a constant force acting only in one direction independently of the movement velocity and acceleration (such as the rubber bands mimicking W in the present study) could be beneficial training strategy when selecting an external load that would minimally violate the technique and affects the performance, while still allowing for a relatively high muscle power. However, the loading of the body segments with external resistance that provides both W and I (such as in routine application of external weights) could lead to the increased muscle forces. In line with the data obtained from the mechanical models of isolated muscle-tendon complex (Galantis and Woledge, 2003), addition of solely I only prolongs movement duration, while being the least beneficial for the power output. These findings suggest that the present line of research should be also extended towards the exploration and optimization of the related training and rehabilitation procedures.

To conclude, an increase in loading magnitude was associated with an expected increase in GRF and decrease in both the jumping performance and muscle power output. However, due to the novelty of the methods applied, of more importance could be that discernible differences among the effects of W, W+I, and I were recorded even within a relatively narrow loading range. In particular, an increase in W was associated with the smallest changes in movement kinematic pattern and smallest reduction of jumping performance, while also allowing for the highest power output. Conversely, W+I loading was associated with the highest GRF and, likely, muscle forces. Finally, the lowest maxima of GRF and power were associated with I. Since the problem studied is not only of potential importance for understanding fundamental properties of the neuromuscular system, but also for optimizing loading in standard athletic training and rehabilitation procedures, further research is apparently needed. Although we selected CMJ performed with arm swing as the most ‘natural’ (and, therefore, ecologically valid) type of vertical jumps, the current research should be extended to other types of jumps (e.g., comparison of CMJ with and without arm swing, squat and other vertical jumps), as well as to other explosive tasks that do not allow for a thorough adjustment of the movement pattern to different loading conditions. Finally, a comprehensive assessment of the kinematic, kinetic, and myoelectric patterns could reveal the neural control mechanisms underlying the observed adjustments to different load types, while the interventional studies could provide the data that could help in load optimization in various rehabilitation and athletic training procedures.

Acknowledgments

This work was supported in part, by NIH grant AR06065, and a grant from Serbian Research Council (#175037).

Biographies

graphic file with name nihms344092b1.gif

Bojan Leontijevic

Bojan Leontijevic received his M.S. degree in kinesiology in 2008 from Belgrade University. He is currently a Ph.D. student, as well as a Teaching Assistant at the School of Sport and Physical Education of the Belgrade University. His main research interest includes the effects of external loading on human movement performance, as well as the training and testing of soccer players.

graphic file with name nihms344092b2.gif

Nemanja Pazin

Nemanja Pazin received his M.S. degree in kinesiology in 2008 from Belgrade University. He is a Ph.D. student at the doctoral program of the School of Sport and Physical Education of the Belgrade University, as well as a research fellow at the Department of Kinesiology of the Pennsylvania State University. His main research interest includes the effects of external loading on rapid movements, as well as the methods for testing muscle function.

graphic file with name nihms344092b3.gif

Predrag R. Bozic

Predrag Bozic received his M.S. in kinesiology in 2008 and Ph.D. in kinesiology in 2011 from Belgrade University. He works as a researcher in the Republic Institute for Sport, Serbia. His main research interest includes early selection in young athletes and training and testing of elite athletes, as well as the methods for testing of muscle function.

graphic file with name nihms344092b4.gif

Milos Kukolj

Milos Kukolj received the MS in kinesiology in 1978 and a Ph.D. in kinesiology in 1982 from Belgrade University. He worked as an Assistant, Associate Professor and Professor at the School of Sport and Physical Education of Belgrade University. His main research interest covers various anthropomotoric aspects of human movements, particularly including the training and testing in both non-athletes and athletes.

graphic file with name nihms344092b5.gif

Dusan Ugarkovic

Dusan Ugarkovic received his MD in 1977, and his MS degree in 1985 and Ph.D. in 1990 in sports medicine from Belgrade University. He worked as a physician at the National Institute for Sport Medicine until 1989, and thereafter as an Assistant Professor, Associate Professor and a Professor at the School of Sport and Physical Education of Belgrade University. His research interest includes various aspects of sport medicine, particularly the training methods and body composition in both children and athletic populations.

graphic file with name nihms344092b6.gif

Slobodan Jaric

Slobodan Jaric received the MS degree in biomedical engineering in 1981 and a Ph.D. in kinesiology in 1986 from Belgrade University. He worked as an Assistant, Associate Professor and a Research Professor at the Belgrade University until 1999, and as an Associate Professor at the National Institute for Working Life and the Umea University in Sweden between 1999 and 2002. Currently he is a Professor of motor control at the University of Delaware and an Adjunct Professor of the Belgrade University. His research interest includes motor control, biomechanics of human movements, and sports biomechanics.

Footnotes

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

Conflict of interest statement:

Authors declare no conflicts of interest.

References

  1. Anderson CE, Sforzo GA, Sigg JA. The effects of combining elastic and free weight resistance on strength and power in athletes. J Strength Cond Res. 2008;22(2):567–574. doi: 10.1519/JSC.0b013e3181634d1e. [DOI] [PubMed] [Google Scholar]
  2. Argus CK, Gill ND, Keogh JW, Hopkins WG. Assessing Lower-Body Peak Power in Elite Rugby-Union Players. J Strength Cond Res. 2011 doi: 10.1519/JSC.0b013e3181ddfabc. [DOI] [PubMed] [Google Scholar]
  3. Baker D, Nance S, Moore M. The load that maximizes the average mechanical power output during explosive bench press throws in highly trained athletes. J Strength Cond Res. 2001a;15(1):20–24. [PubMed] [Google Scholar]
  4. Baker D, Nance S, Moore M. The load that maximizes the average mechanical power output during jump squats in power-trained athletes. J Strength Cond Res. 2001b;15(1):92–97. [PubMed] [Google Scholar]
  5. Bevan HR, Bunce PJ, Owen NJ, Bennett MA, Cook CJ, Cunningham DJ, Newton RU, Kilduff LP. Optimal loading for the development of peak power output in professional rugby players. J Strength Cond Res. 2010;24(1):43–47. doi: 10.1519/JSC.0b013e3181c63c64. [DOI] [PubMed] [Google Scholar]
  6. Cavagna GA, Zamboni A, Faraggiana T, Margaria R. Jumping on the moon: power output at different gravity values. Aerosp Med. 1972;43(4):408–414. [PubMed] [Google Scholar]
  7. Chang YH, Huang HW, Hamerski CM, Kram R. The independent effects of gravity and inertia on running mechanics. J Exp Biol. 2000;203(Pt 2):229–238. doi: 10.1242/jeb.203.2.229. [DOI] [PubMed] [Google Scholar]
  8. Corcos DM, Jaric S, Agarwal GC, Gottlieb GL. Principles for learning single-joint movements. I. Enhanced performance by practice. Exp Brain Res. 1993;94(3):499–513. doi: 10.1007/BF00230208. [DOI] [PubMed] [Google Scholar]
  9. Cormie P, Deane R, McBride JM. Methodological concerns for determining power output in the jump squat. J Strength Cond Res. 2007a;21(2):424–430. doi: 10.1519/R-19605.1. [DOI] [PubMed] [Google Scholar]
  10. Cormie P, McCaulley GO, McBride JM. Power versus strength-power jump squat training: influence on the load-power relationship. Med Sci Sports Exerc. 2007b;39(6):996–1003. doi: 10.1097/mss.0b013e3180408e0c. [DOI] [PubMed] [Google Scholar]
  11. Cormie P, McCaulley GO, Triplett NT, McBride JM. Optimal loading for maximal power output during lower-body resistance exercises. Med Sci Sports Exerc. 2007c;39(2):340–349. doi: 10.1249/01.mss.0000246993.71599.bf. [DOI] [PubMed] [Google Scholar]
  12. Cormie P, McGuigan MR, Newton RU. Developing maximal neuromuscular power: Part 1 - biological basis of maximal power production. Sports Med. 2011a;41(1):17–38. doi: 10.2165/11537690-000000000-00000. [DOI] [PubMed] [Google Scholar]
  13. Cormie P, McGuigan MR, Newton RU. Developing maximal neuromuscular power: Part 2 - training considerations for improving maximal power production. Sports Med. 2011b;41(2):125–146. doi: 10.2165/11538500-000000000-00000. [DOI] [PubMed] [Google Scholar]
  14. Cronin J, Sleivert G. Challenges in understanding the influence of maximal power training on improving athletic performance. Sports Med. 2005;35(3):213–234. doi: 10.2165/00007256-200535030-00003. [DOI] [PubMed] [Google Scholar]
  15. De Witt JK, Hagan RD, Cromwell RL. The effect of increasing inertia upon vertical ground reaction forces and temporal kinematics during locomotion. J Exp Biol. 2008;211((Pt 7)):1087–1092. doi: 10.1242/jeb.012443. [DOI] [PubMed] [Google Scholar]
  16. Driss T, Vandewalle H, Quievre J, Miller C, Monod H. Effects of external loading on power output in a squat jump on a force platform: a comparison between strength and power athletes and sedentary individuals. J Sports Sci. 2001;19(2):99–105. doi: 10.1080/026404101300036271. [DOI] [PubMed] [Google Scholar]
  17. Dugan EL, Doyle TL, Humphries B, Hasson CJ, Newton RU. Determining the optimal load for jump squats: a review of methods and calculations. J Strength Cond Res. 2004;18(3):668–674. doi: 10.1519/1533-4287(2004)18<668:DTOLFJ>2.0.CO;2. [DOI] [PubMed] [Google Scholar]
  18. Frost DM, Cronin J, Newton RU. A biomechanical evaluation of resistance: fundamental concepts for training and sports performance. Sports Med. 2010;40(4):303–326. doi: 10.2165/11319420-000000000-00000. [DOI] [PubMed] [Google Scholar]
  19. Galantis A, Woledge RC. The theoretical limits to the power output of a muscle-tendon complex with inertial and gravitational loads. Proc Biol Sci. 2003;270(1523):1493–1498. doi: 10.1098/rspb.2003.2403. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Gosseye TP, Willems PA, Heglund NC. Biomechanical analysis of running in weightlessness on a treadmill equipped with a subject loading system. Eur J Appl Physiol. 2010;110(4):709–728. doi: 10.1007/s00421-010-1549-9. [DOI] [PubMed] [Google Scholar]
  21. Griffin TM, Tolani NA, Kram R. Walking in simulated reduced gravity: mechanical energy fluctuations and exchange. J Appl Physiol. 1999;86(1):383–390. doi: 10.1152/jappl.1999.86.1.383. [DOI] [PubMed] [Google Scholar]
  22. Harris NK, Cronin JB, Hopkins WG. Power outputs of a machine squat-jump across a spectrum of loads. J Strength Cond Res. 2007;21(4):1260–1264. doi: 10.1519/R-21316.1. [DOI] [PubMed] [Google Scholar]
  23. Israetel MA, McBride JM, Nuzzo JL, Skinner JW, Dayne AM. Kinetic and kinematic differences between squats performed with and without elastic bands. J Strength Cond Res. 2010;24(1):190–194. doi: 10.1519/JSC.0b013e31819b7995. [DOI] [PubMed] [Google Scholar]
  24. Jakubiak N, Saunders DH. The feasibility and efficacy of elastic resistance training for improving the velocity of the Olympic Taekwondo turning kick. J Strength Cond Res. 2008;22(4):1194–1197. doi: 10.1519/JSC.0b013e31816d4f66. [DOI] [PubMed] [Google Scholar]
  25. Jaric S. Changes in movement symmetry associated with strengthening and fatigue of agonist and antagonist muscles. J Mot Behav. 2000;32(1):9–15. doi: 10.1080/00222890009601355. [DOI] [PubMed] [Google Scholar]
  26. Jaric S, Markovic G. Leg muscles design: the maximum dynamic output hypothesis. Med Sci Sports Exerc. 2009;41(4):780–787. doi: 10.1249/MSS.0b013e31818f2bfa. [DOI] [PubMed] [Google Scholar]
  27. Kukolj M, Ropret R, Ugarkovic D, Jaric S. Anthropometric, strength, and power predictors of sprinting performance. J Sports Med Phys Fitness. 1999;39(2):120–122. [PubMed] [Google Scholar]
  28. Lund RJ, Dolny DG, Browder KD. Optimal loading during two different leg-press movements in female rowers. Med Sci Sports Exerc. 2004;36(1):148–154. doi: 10.1249/01.MSS.0000106177.12763.2E. [DOI] [PubMed] [Google Scholar]
  29. Markovic G, Jaric S. Positive and negative loading and mechanical output in maximum vertical jumping. Med Sci Sports Exerc. 2007;39(10):1757–1764. doi: 10.1249/mss.0b013e31811ece35. [DOI] [PubMed] [Google Scholar]
  30. Markovic G, Vuk S, Jaric S. Effects of Jump Training with Negative versus Positive Loading on Jumping Mechanics. Int J Sports Med. 2011;32(5):365–372. doi: 10.1055/s-0031-1271678. [DOI] [PubMed] [Google Scholar]
  31. McBride JM, Triplett-McBride T, Davie A, Newton RU. A comparison of strength and power characteristics between power lifter, olympic lifters, and sprinters. J Strength Cond Res. 1999;13(1):58–66. [Google Scholar]
  32. McMahon TA. Muscles, reflexes, and locomotion. Princeton: Princeton University Press; 1984. [Google Scholar]
  33. Newton RU, Kraemer WJ. Developing explosive muscular power: implications for a mixed methods training strategy. Strength Cond J. 1994;16:20–31. [Google Scholar]
  34. Newton RU, Murphy AJ, Humphries BJ, Wilson GJ, Kraemer WJ, Hakkinen K. Influence of load and stretch shortening cycle on the kinematics, kinetics and muscle activation that occurs during explosive upper-body movements. Eur J Appl Physiol Occup Physiol. 1997;75(4):333–342. doi: 10.1007/s004210050169. [DOI] [PubMed] [Google Scholar]
  35. Nuzzo JL, McBride JM, Dayne AM, Israetel MA, Dumke CL, Triplett NT. Testing of the maximal dynamic output hypothesis in trained and untrained subjects. J Strength Cond Res. 2010;24(5):1269–1276. doi: 10.1519/JSC.0b013e3181d68691. [DOI] [PubMed] [Google Scholar]
  36. Stone MH, O'Bryant HS, McCoy L, Coglianese R, Lehmkuhl M, Schilling B. Power and maximum strength relationships during performance of dynamic and static weighted jumps. J Strength Cond Res. 2003;17(1):140–147. doi: 10.1519/1533-4287(2003)017<0140:pamsrd>2.0.co;2. [DOI] [PubMed] [Google Scholar]
  37. Teunissen LP, Grabowski A, Kram R. Effects of independently altering body weight and body mass on the metabolic cost of running. J Exp Biol. 2007;210(Pt 24):4418–4427. doi: 10.1242/jeb.004481. [DOI] [PubMed] [Google Scholar]
  38. Wakeling JM, Blake OM, Chan HK. Muscle coordination is key to the power output and mechanical efficiency of limb movements. J Exp Biol. 2010;213(3):487–492. doi: 10.1242/jeb.036236. [DOI] [PubMed] [Google Scholar]
  39. Wallace BJ, Winchester JB, McGuigan MR. Effects of elastic bands on force and power characteristics during the back squat exercise. J Strength Cond Res. 2006;20(2):268–272. doi: 10.1519/R-16854.1. [DOI] [PubMed] [Google Scholar]
  40. Wilson GJ, Newton RU, Murphy AJ, Humphries BJ. The optimal training load for the development of dynamic athletic performance. Med Sci Sports Exerc. 1993;25(11):1279–1286. [PubMed] [Google Scholar]

RESOURCES