Does Understanding Relational Terminology Mediate Effects of Intervention on Compare Word Problems?

Abstract

The purpose of this study was to assess whether understanding relational terminology (i.e., more, less, and fewer) mediates the effects of intervention on compare word problems. Second-grade classrooms (n = 31) were randomly assigned to 3 conditions: researcher-designed word-problem intervention, researcher-designed calculation intervention, or business-as-usual (teacher-designed) control. Students in word-problem intervention classrooms received instruction on the compare problem type, which included a focus on understanding relational terminology within compare word problems. Analyses, which accounted for variance associated with classroom clustering, indicated that (a) compared to the calculation intervention and business-as-usual conditions, word-problem intervention significantly increased performance on all three subtypes of compare problems and on understanding relational terminology; and (b) the intervention effect was fully mediated by students’ understanding of relational terminology for 1 subtype of compare problems and partially mediated by students’ understanding of relational terminology for the other 2 subtypes.

Word problems are challenging for children and adults alike (Verschaffel, 1994), and children struggle to solve word problems even when they perform competently on the calculations required to solve those problems. In fact, incorrect answers on word problems are often the result of correct calculations performed on incorrect problem representations (Lewis & Mayer, 1987). This suggests a failure to understand the language of word problems (Briars & Larkin, 1984; Cummins, Kintsch, Reusser, & Weimer, 1988; Hegarty, Mayer, & Green, 1992; Lewis & Mayer; Riley & Greeno 1988). Mathematics word-problem solving is transparently different from calculations because word problems are presented linguistically, challenging students to read and interpret the problem, represent the semantic structure of the problem, and choose a solution strategy. Understanding the language of word problems (the first step in the process) may facilitate primary-grade students’ ability to represent the word-problem structure and therefore choose and complete the solution strategy successfully (Stern, 1993).

The purpose of the present study was to assess whether the effects of intervention designed to enhance second graders’ performance on compare problems are mediated by their understanding of relational terminology (e.g., which in this study refers to the terms more, less, and fewer). In this introduction, we briefly describe three types of simple arithmetic word problems, turning our attention quickly to the defining features of the most difficult of these problem types, compare problems, to clarify how relational terminology makes this problem type most challenging and how linguistic features of compare problems form three subtypes of compare problems. Then, we summarize prior work on the approach to word-problem intervention we adopted in the present study, which incorporates a strong focus on building student capacity to represent the problem situation. The focus of the present study was the instructional unit addressing the compare problem type, which incorporates instruction designed to promote understanding of relational terminology within compare problems. Finally, we explain the purpose of the present study and state our hypotheses.

Compare Problems and Relational Terminology

Simple word problems, which are solved using one-step addition or subtraction, are key components of the primary-grade mathematics curriculum. Based on their semantic structure and the situation described in the story, a variety of researchers classify these problems into three types: combine, change, and compare problems (e.g., Cummins, Kintsch, Reusser, & Weimer, 1988; De Corte, Vershaffel, & De Win, 1985; Morales, Shute, & Pellegrino, 1985; Powell, Fuchs, Fuchs, Cirino, & Fletcher, 2009; Riley, Greeno, & Heller, 1983; Verschaffel, 1994), although sometimes different labels are used. This classification structure distinguishes among problems in which sets are combined (e.g., Rose has 3 dogs. Maury has 2 cats. How many animals do the children have?), in which a change in one set occurs over time (e.g., Rose had 3 dogs. Then she found 2 cats. How many animals does Rose have?), and in which sets are compared (e.g., Rose has 3 dogs. Maury has 2 cats. How many more animals does Rose have than Maury?). Compare problems are more difficult than combine or change problems for primary-grade students, even though the calculations required for all three problem types is similar (e.g., Briars & Larkin, 1984; Carpenter, & Moser, 1984; Cummins et al., 1988; De Corte, Verschaffel, & Verschueren, 1982; Garcia, Jimenez, & Hess, 2006; Morales et al., 1985; Powell et al., 2009; Riley & Greeno, 1988; Verschaffel, 1994). Compare problems are the most difficult problem type for two reasons. First, compare problems describe a static relationship (which can also be true for combine problems, but not for change problems). Second, only compare problems incorporate relational terminology.

In the present study, we focused on compare problems because of the challenge they pose for primary-grade students. In compare problems, two sets or quantities are compared and through this comparison, the difference between them emerges as a third set (i.e., the difference set). In compare problems, any of these three sets can be the unknown quantity students are asked to find. Three subtypes of compare problems are formed based on which quantity is unknown. The most common subtype is the difference set unknown in which both static sets are given, and the difference set is found (see sample problems 1 and 4 in Table 1). When the difference set is given, either the compared set is unknown (see sample problems 2 and 5 in Table 1) or the referent set is unknown (see sample problems 3 and 6 in Table 1). As the unknown quantity changes, the language and story structure change, which impacts the problem difficulty. When the compared set is unknown, that set is the subject of the relational statement (see problem 2 in Table 1: Tom, whose quantity is unknown, has 5 more marbles than Jill); when the referent set is unknown, that set is the object of the relational statement, with a pronoun used in the subject (see problem 3 in Table 1: She, whose quantity is unknown, has 5 more marbles than Tom).

Table 1.

Subtypes of Compare Problems

Unknown (Subtype)	Sample Compare Problems
	Using Additive Relational Terminology
Difference	Jill has 5 marbles. Tom has 8 marbles. How many marbles does Tom have more than Jill?
Compared	Jill has 3 marbles. Tom has 5 more marbles than Jill. How many marbles does Tom have?
Referent	Jill has 8 marbles. She has 5 more marbles than Tom. How many marbles does Tom have?
	Using Subtractive Relational Terminology
Difference	Jill has 5 marbles. Tom has 8 marbles. How many marbles does Jill have less than Tom?
Compared	Tom has 8 marbles. Jill has 3 fewer marbles than Tom. How many marbles does Jill have?
Referent	Tom has 5 marbles. He has 3 less than Jill. How many marbles does Jill have?

Although all three of these subtypes of compare problems describe a comparative relationship, problems with unknown referent sets are the most difficult, followed by problems with unknown compared sets, and problems with unknown difference sets are generally easiest to solve (Riley & Greeno, 1988; Morales et al., 1985). One potential reason for the differential difficulty among the subtypes is the way in which the relational terminology is presented. For problems with the difference set unknown, the relational terminology is presented in the question. For problems with the compared or referent sets unknown, the relational terminology is incorporated in a relational statement, from which students may have greater difficulty determining the comparative relationship.

One way to evaluate the connection between relational terminology and performance on compare problems is to remove these terms and replace them with alternative wording. Two variations of compare problems, using equalize and won’t get statements, are common ways to rephrase compare problems without changing the underlying problem structure. Take the standard form of a compare problem, “Jill has 5 marbles. Tom has 8 marbles. How many marbles does Tom have more than Jill?” The equalize phrasing is, “Jill has 3 marbles. Tom has 8 marbles. How many marbles does Jill need to have as many as Tom?” The won’t get phrasing is, “There are 10 kids at the birthday party. There are 8 cupcakes. How many kids won’t get a cupcake?” Fuson, Carroll, and Landis (1996) assessed first and second graders on the standard form versus equalize phrasing for all three subtypes and found that students consistently scored higher with equalize than standard phrasing. Hudson (1983) found that younger children were more successful with won’t get phrasing than the standard form. Fan, Mueller, and Marini (1994) documented similar results when they assessed performance on compare, equalize, and won’t get problems. These studies, in which eliminating relational terminology from compare problems reduces difficulty, suggest that relational terminology may be central to students’ relatively low performance on the compare problem type.

A related body of work looks at the relational statements specifically within problems with unknown compared or referent sets. These studies test the viability of Lewis and Mayer’s (1987) consistency hypothesis as an explanation for the increased difficulty of unknown referent set problems. In unknown compared set problems, the relational term (more or less/fewer) is consistent with the calculation required for solution: When more is used, addition is required; when less/fewer is used, subtraction is required. This is illustrated in the two problems involving the unknown compared set in Table 1. For problem 2, in which additive relational terminology is used, adding is required to find the unknown compared set; for problem 5, in which subtractive relational terminology is used, subtracting is required to find the unknown compared set. By contrast, in unknown referent set problems, the relational term (more or less/fewer) is inconsistent with the calculation required for solution. This is illustrated for the two problems involving the unknown referent set in Table 1. For problem 3, in which additive relational terminology is used, subtracting is required to find the unknown referent set; for problem 6, in which subtractive relational terminology is used, adding is required to find the unknown referent set. Such inconsistency creates greater cognitive complexity that is the case for a consistent relationship, requiring students to ignore the well-established association between more with increases and addition and less with decreases and subtraction. Also, the relational statement in problems with the compared set unknown defines the relationship in terms of the newly introduced set; by contrast, problems with an unknown referent set define the relationship in relation to the already given set, with a pronoun used to refer to that already given set. For these reasons, Lewis and Mayer proposed that problems with unknown referent sets require problem solvers to rearrange the relational statement. For example, in this problem with an unknown referent set, “Jon has 4 apples. He has 3 fewer apples than Eric. How many apples does Eric have?,” the problem solver rearranges the second sentence to “Eric had 3 more apples than Jon” before determining the solution procedures. Within the consistency hypothesis, a prerequisite for successfully rearranging the relational statement is that problem solvers understand the symmetry of relational terminology (to change fewer to more) and can effectively reverse the position of the object and subject of the sentence to generate a relational statement that describes an equivalent relationship. Verschaffel, De Corte, and Pauwels (1992) documented that students were more successful when solving unknown compared set problems. Yet, even though students spent more time solving problems with unknown referent sets, which suggests rearrangement, this extra time did not lead to greater accuracy, providing only mixed support for Lewis and Mayer’s consistency hypothesis.

To further explore the consistency hypothesis, Stern (1993) conducted two studies assessing students’ understanding of the symmetrical relationship of more to less/fewer in relation to solving compare problems with unknown referent sets. In line with the consistency hypothesis, Stern hypothesized that understanding this symmetrical relationship was most pertinent to solving compare problems with unknown referent sets. First graders were presented with pictures of two quantities and asked to match relational statements with each picture. For example, students had to decide whether one, both, or neither statement (e.g., “There are 2 more cows than pigs” and “There are 2 fewer pigs than cows”) matched a picture. Although students understood the meanings of the sentences, some students failed to understand that more and fewer could be interchanged to describe the same relationship, and low performance on this task was related to students’ ability to solve problems with unknown referent sets. As revealed in these studies, difficulty in interpreting relational terminology is one plausible explanation for poor performance on compare problems. Problems with unknown referent sets stand out as most difficult among the compare word-problem subtypes, potentially requiring an understanding of the symmetrical relationship between more and less/fewer.

Word-Problem Interventions

In most classrooms, word-problem instruction focuses predominantly on the calculation strategies required for solution, with little emphasis on strategies for building student capacity to represent the problem situation (cf. Willis & Fuson, 1988). To address this problem, Willis and Fuson (1988) and Fuson and Willis (1989) taught students to use schematic drawings to represent the structure of compare, combine, and change word-problem types. Using a pre-post design, they showed that this approach promoted “good-to-excellent” (Willis & Fuson, p. 192) posttest performance among high and average second-grade students. This approach to instruction is connected to schema theory (Cooper & Sweller, 1987; Gick & Holyoak, 1983), by which students develop schemas for problem types (e.g., combine, change, and compare) and learn to recognize the defining features of each problem type, categorize a problem as belonging to a problem type, and apply the corresponding solution procedures for that problem type.

Two programs of randomized control studies have extended the Fuson and Willis studies, and efficacy has been demonstrated. Jitendra and colleagues have enjoyed success teaching students to recognize distinctions among combine, change, and compare word problems while representing these problem types with conceptual diagrams (e.g., Jitendra, Griffin, Deatline-Buchman, & Sczesniak, 2007; Jitendra, Griffin, Haria, Leh, Adams & Kaduvettoor, 2007). As with Fuson and Willis, each diagram is unique to the underlying structure of the problem type. Students are encouraged to represent problem structures with the diagrams before solving problems. For compare problems, the conceptual diagram depicts the mathematical structure of the comparison between a bigger and smaller quantity. Students first learn to use the diagram when all numerical information (i.e., compared, referent, and difference sets) is provided; then, problems are presented with unknown quantities, mirroring each of the three compare word-problem subtypes. Students put the two given quantities into the diagram and put a question mark (?) in place of the unknown. In these studies, schema-based instruction has been causally linked to improvement in overall word-problem performance, but effects specifically for compare problems have not been reported.

A second program of research has also assessed the efficacy of an approach to word-problem instruction based on schema theory, in which students are taught the defining features of combine, change, and compare problem types to scaffold problem representation and solution strategies. This second approach to schema theory differs from that of Jitendra and colleagues in two ways. The first distinction between the two lines of randomized control trials, which is not central to the present study, concerns an explicit focus on transfer in the instructional design. This led the researchers to call the instructional approach schema-broadening instruction (SBI). For information on the nature of that transfer instruction and for research showing that SBI promotes transfer to problems with unexpected features within the taught problem types (e.g., irrelevant information, relevant information presented outside the narrative in figures or tables, presentation of problems in real-life contexts), see Fuchs, Fuchs, Prentice, Burch, Hamlett, Owen, et al., 2003.

The second distinction, which is pertinent to the present study, is that students are taught to represent problem structures in terms of mathematical expressions. For example, in the first compare problem-type lesson, two representations of the problem structure are used to introduce the meaning of compare problems: a conceptual diagram, similar to Fuson’s and Jitendra’s diagrams, and a mathematical expression (“B – s = D,” where B is bigger number, s is the smaller number, and D is the difference number). Working with compare stories that first have no missing information but gradually introduce missing information, students fill in quantities in the diagram and in the mathematical expression. The conceptual diagram is gradually faded in favor of the more accessible mathematical expression (which students can more easily generate on their own). Students are taught to identify important information in the problem and build a number sentence, in the form of B – s = D, showing×as the unknown. (For combine problems, the representation is part 1 plus part 2 equals the total or P1 + P2 = T; for change problems, start quantity plus or minus change quantity equals end quantity or S +/− C = E.)

We note that in opting for a single representation for the compare problem type, rather than separate representations for the three subtypes of compare problems, the goal was to (a) facilitate children’s appreciation of the broader problem type, underscoring the semantic structure of the problem situation that remains constant across subtypes (even as the placement of missing information occurs in different sets), and (b) promote correct classification of problems by reducing the working memory burden and the complexity associated with teaching nine problem types (e.g., three subtypes for each problem type: compare, combine, and change problems). We also note that, once students identify the semantic category of a problem (i.e., determine that the problem is a compare problem rather than a combine or change problem), they identify which piece of information is missing, which builds appreciation of the subcategories within the problem type. Also, many students gradually adopt a more direct approach for deriving the solution, even as they continue to appreciate and work within the problem-type framework. In either case, the sequence of steps embedded in students’ solutions appropriately reflect the problem’s additive or subtractive nature and addresses the three subcategories within each of the three superordinate word-problem types (Fuchs, Zumeta, Schumacher, Powell, Seethaler, Hamlet, et al., 2010).

In a series of randomized control trials, SBI increased word-problem performance across combine, change, and compare problems (Fuchs, Powell, Seethaler, Cirino, Fletcher, Fuchs, et al., 2009; Fuchs, Seethaler, Powell, Fuchs, Hamlett, & Fletcher, 2008; Fuchs, Zumeta, et al., 2010). However, only Fuchs, Zumeta, et al. (2010) separated effects by problem type. Performance favored SBI for combine, change, and compare problem types, but learning appeared less robust for compare problems, the most difficult problem type.

In all three lines of studies, an essential feature of intervention for solving compare problems is representing the problem structure as the bigger number minus the smaller number equals the difference number: In Fuson’s and Jitendra’s work, students enter these components of the compare problem into a diagram; in the Fuchs line of work, into B – s = D. In either case, understanding relational terminology is necessary to do this successfully. Yet, explicit instruction on understanding relational terminology was not reported in Fuson’s or Jitendra’s work or incorporated in the Fuchs line of studies. In the Fuchs, Zumeta, et al. (2010) database, in which student performance was evaluated by problem type, students represented the underlying structure of compare problems inaccurately more often than for combine or change problems (e.g., for “Carol has $10. Anne has 5 more than Carol. How much more money does Carol have than Anne?,” the student wrote 10 + 5 = 15). For this reason, in the most recent iteration of word-problem intervention, as described in the present study, we incorporated instruction to promote understanding of relational terminology in the compare unit. The hope was that better understanding of relational terminology would contribute to the efficacy of SBI intervention.

Purpose of the Present Study

The purpose of the present study was to gain insight into whether understanding of relational terminology mediates the effects of intervention on compare problems. The present study occurred within the context of a larger investigation in which classrooms were randomly assigned to word-problem (WP) intervention, calculations (CAL) intervention, or business-as-usual control (see Table 2 for distinctions between the larger study and the present study). In all three conditions, teachers designed and conducted the majority of the mathematics program, but only in WP and CAL was a portion of the students’ instructional time designed and implemented by the researchers. For 17 weeks, WP or CAL students received researcher-designed whole-class instruction (twice weekly for 30–40 minutes per session), while WP and CAL at-risk students also received researcher-designed tutoring (three times weekly for 20–30 minutes per session).

Table 2.

Distinctions between Larger Investigation and the Present Study

Larger investigation	Present study
Time Frame
Weeks 1–17	Weeks 8–13
Content of WP Intervention
Introductory unit (weeks 1–2)
Combine problem unit (weeks 3–7)
Compare problem unit (weeks 8–13)	Compare problem unit (weeks 8–13)
Change problem unit (weeks 14–17)
Measures
Mix of combine, compare, and change problems	Compare problems with greater sampling of subtypes Relational understanding
Data Collection
Pretesting: before week 1	Pretesting: after week 7
Pretesting: before week 1	Posttesting: after week 13

In the larger investigation, WP intervention addressed three problem types (combine, change, and compare problem types), with the compare unit spanning weeks 8 through 13. In the larger investigation, outcome measures were administered before and after the 17-week intervention. These measures mixed the three problem types and did not assess understanding of relational terminology. In the present study, outcome and mediator measures were administered immediately before and after the unit on compare problems (i.e., at end of weeks 7 and 13 of the larger investigation). The present study outcome measure specifically assessed compare problems, with deeper sampling of the three compare problem subtypes, and the mediator, understanding of relational terminology, was also assessed. There was no overlap between the measures used in the present study and those reported in the larger investigation. (See Table 2.)

The hypotheses in the present study were based on (a) previous SBI intervention research showing efficacy without the emphasis on relational terminology (Fuchs et al., 2008; Fuchs et al., 2009), (b) prior investigations of student performance on compare problems (e.g., Cummins et al., 1988; De Corte et al., 1985; Fuchs, Zumeta, et al., 2010; Garcia et al., 2006; Morales et al., 1985; Powell et al., 2009; Riley & Greeno, 1988; Verschaffel, 1994), and (c) earlier work suggesting a connection between understanding relational terminology and solving compare problems (e.g., Lewis & Mayer; 1987; Stern, 1993; Vershaffel, 1994; Vershaffel et al., 1992). First, we posited that students receiving WP intervention would significantly outperform those in CAL and control conditions on compare problems, who would perform comparably to each other. Then, we conducted mediation analyses to address the following hypotheses: (a) WP intervention enhances students’ understanding of relational terminology; (b) students’ understanding of relational terminology in turn improves student performance on each of the compare problem subtypes; and (c) students’ understanding of relational terminology at least partially mediates the effects of WP intervention on the compare problem subtypes. In these ways, we sought to extend knowledge about whether understanding relational terminology is a generative mechanism within WP intervention for enhancing student performance for the three subtypes of compare problems. We propose the following causal mechanism: When students are provided with explicit instruction on the meanings of relational terminology and the symmetrical relationship between more and less/fewer within a word-problem context, they apply this understanding to interpret compare problems, which enhances understanding the relationships in those problems. Understanding these relationships in compare problems increases students’ ability to accurately represent the structure of compare problems and in turn solve them.

Method

Participants

The present study was conducted in the context of a larger investigation (see Table 2). In the larger investigation, 32 second-grade teachers (all female) from a large metropolitan school district volunteered to participate. Blocking within school, we randomly assigned their classrooms to one of three conditions: WP intervention (n = 12 classrooms), CAL intervention (n = 12 classrooms), or control (n = 8 classrooms). Soon after random assignment, one CAL teacher’s classroom was dissolved, leaving 11 classrooms in this condition. Consented students in the 31 classrooms were included in the larger investigation if they had at least one T-score above 35 on the Vocabulary or Matrix Reasoning subtests of the Wechsler Abbreviated Intelligence Scale (WASI; The Psychological Corporation, 1999) and were a native English speaker or had successfully completed and exited an English Language Learner program. As part of the larger investigation, students completed pretests on calculation and word-problem measures to establish equivalency among treatment groups using Vanderbilt Story Problems (Fuchs & Seethaler, 2008), Addition Fact Fluency (Fuchs, Hamlett, & Powell, 2003), and Single-Digit Story Problems (adapted from Carpenter & Moser, 1984; Jordan & Hanich, 2000; Riley et. al., 1983). To identify risk for inadequate learning outcomes, we applied cut scores, empirically derived from a previous database (e.g., Fuchs, Zumeta, et al., 2010), to the latter two measures. Students who scored below specified cut-points on both measures qualified for tutoring in the WP and CAL conditions. At-risk students in WP classrooms received word-problem tutoring; at-risk students in CAL classrooms received calculations tutoring (at-risk students in control classrooms did not receive tutoring from the researchers).

For the present study, we included all students who were not absent for the pretest and posttest sessions on the compare unit testing (respectively conducted at end of week 7 and end of week 13). We thereby included 169 students from 12 classrooms in WP (142 not-at-risk and 27 at-risk students), 155 students from 11 classrooms in CAL (128 not-at-risk and 27 at-risk students), and 118 students from eight classrooms in control (98 not-at-risk and 20 at-risk students). See Table 3 for teacher demographic data, and student demographics, and student performance on the measures administered to assess initial comparability for students among treatment groups. Chi-square analysis and analysis of variance (ANOVA) revealed that teachers did not differ as a function of condition on race or sex but did differ on years teaching. Post-hoc analysis revealed WP teachers had significantly fewer years of teaching experience than CAL teachers (p = .035) or control teachers (p = .044), who were not different from each other (p = .94). We did not consider this problematic because teachers did not deliver whole-class instruction or tutoring and because the role of years teaching in determining student outcomes is not clear (e.g., Wolters & Daugherty, 2007). Students did not differ as a function of condition on sex, race, subsidized lunch, years retained, or the three mathematical measures used to assess initial performance comparability.

Table 3.

Demographic Information

	WP (teachers, n = 12) (students, n = 169)				CAL (teachers, n = 11) students,n = 155				control (teachers, n = 8) (students, n = 118)
Variable	%	(n)	M	(SD)	%	(n)	M	(SD)	%	(n)	M	(SD)	χ2	p	F	p
Teachers
Male	0	(0)			0.0	(0)			0.0	(0)
Race													2.27	0.32
African American	25.5	(3)			18.2	(2)			0.0	(0)
Caucasian	75	(9)			81.8	(9)			100.0	(8)
Years Teaching			11.00	(9.42)			20.27	(10.24)			20.63	(10.54)			3.26	0.05
Students
Male	50.3	(85)			43.2	(67)			47.5	(56)			1.78	0.41
Race													2.61	0.96
African American	33.9	(57)			36.1	(56)			32.2	(38)
Caucasian	37.5	(63)			34.9	(54)			38.1	(45)
Asian	4.8	(8)			3.2	(5)			5.9	(7)
Hispanic	17.9	(30)			19.4	(30)			15.2	(18)
Other	5.9	(10)			6.4	(10)			7.6	(9)
Subsidized Lunch	75.1	(127)			82.6	(128)			76.3	(90)			2.53	0.28
Retained	6.5	(11)			7.1	(11)			10.2	(12)			1.46	0.48
Measures to asses comparability
*Addition Fact Fluency			9.54	(4.91)			9.85	(5.18)			9.31	(4.88)			0.40	0.67
*Single-Digit Story Problems			8.11	(4.11)			8.03	(3.76)			7.52	(3.61)			0.91	0.40
Vanderbilt Story Problems			9.49	(6.03)			9.89	(5.39)			8.66	(5.30)			1.63	0.20
Math Status													1.31	0.97
Low in word problems	20.7	(35)			20.0	(31)			22.0	(26)
Low in calculations	11.8	(20)			10.3	(16)			11.9	(14)
Low in both	18.9	(32)			17.4	(27)			20.3	(24)

Note

^*These measures were also used to screen at-risk status.

Classroom and Tutoring Mathematics Instruction across Conditions

In the present study, researcher-designed intervention supplemented the teachers’ mathematics instructional program. That is, the research-designed intervention constituted only a portion (typically 20%) of the WP and CAL teachers’ mathematics program. In terms of the nature of the classroom teachers’ word-problem instruction in the three study conditions, we asked all 31 classroom teachers to complete a brief questionnaire immediately following the compare unit to describe the word-problem instruction they delivered as part of their mathematics program outside the instruction the researchers had provided.

Across conditions, teachers reported strong reliance on the district’s textbook program, Houghton Mifflin Math (Greenes et al., 2005). As described in the second-grade textbook teacher edition, word-problem instruction guides teachers to help students (a) understand, plan, solve, and reflect on the content of word problems, (b) apply problem-solution rules, and (c) perform calculations. Word problems used in the textbook program require simple arithmetic for solution and are the same problem types included in the larger investigation’s WP intervention (i.e., combine, change, compare). Even so, the textbook rarely presents compare problems for which the unknown is the compared or referent set. Beyond reliance on the textbook program teachers reported similar strategies across conditions: a focus on keywords for deciding whether to add and subtract (which unfortunately encourages students to ignore the semantic structure of problems) and teaching students to write number sentences or draw pictures to show their work.

It is important to note that none of the classroom teachers in the CAL or control conditions reported using instructional methods similar to those used in the WP condition, and we saw no evidence in student work on the compare problems outcome measure that they relied on those methods. It is also important to note that by controlling classroom variance in the analyses (i.e., nesting students within their classroom in the analyses), we accounted for variations in the nature and quality of the 31 teachers’ classroom instruction when estimating the effects of other variables (i.e., pretest performance, study condition, and students’ understanding of relational terminology) on students’ compare-problem learning.

Researcher-Designed WP intervention

See Table 4 for an overview of key components of WP intervention. Asterisked items are specific to the compare problem unit.

Table 4.

Key Components of WP Intervention for Compare Problems

Two-level prevention: Whole class (30–45 min/session twice weekly) + tutoring (20–30 min/session 3 times/week)
Implementers: RA teachers and RA tutors
Content
	Unit 1: Foundational Skills
	Unit 2: Combine problems
	*Unit 3: Compare problems
	Unit 4: Change problems
SBI Methods
	Instruction on RUN strategy (Read the problem, Underline the question, Name the problem type)
	Instruction on meaning of the compare problem type: Role playing situation with manipulatives; representing problem situation with a conceptual diagram and a mathematical expression; fading conceptual diagram to rely routinely on the mathematical expression as the semantic representation of the problem type
	Instruction on strategy for solving problem
		Name problem type: Recognize defining features of each problem type to categorize that target problem
		Match the problem type with representational mathematical expression for the selected problem type
		Use the representation mathematical expression to build a number sentence for the target problem
			Identify unknown and enter it in the number sentence in place letters in equation
			Enter givens and enter them in the number sentence in place of letters in equation
			Enter mathematical signs into the number sentence
			Solve for x
			Label numerical answer
*Relational Terminology Instructional Methods
	Whole-Class Instruction
		*Instruction on meaning of more, less, and fewer
		*Instruction on covering difference number to decide which quantity is more/less (e.g., “Tom has 5 more than Sally” becomes “Tom has more than Sally”)
		*Instruction on and practice writing alternative relational statements that preserve meaning
	Tutoring Activities
		*Review of more, less, and fewer
		*Review of which items are being compared in relational statements
		*Instruction on meaning of greater than (>) and less than (<) symbols
		*Application of < and > to relational terms to assist in determining bigger and smaller entities
		*Practice pulling these lessons together in the Difference Game with relational statements, with
		*Compare problems, using a greater variety of comparative terms
			*Underline two entities being compared (e.g., Tom; Sally)
			*Find relational term; write greater/less than symbol above it to decrease working memory demands
			*Write B over name associated with bigger quantity; s over name associated with smaller quantity to further reduce working memory demands

^*Specific to compare problem type unit, which was the focus of the present study. Otherwise, instructional strategies were analogous across combine, compare, and change problem types.

Organization and overview

As part of a two-level prevention system, classrooms were randomly assigned to control or researcher-designed intervention (WP or CAL), which involved implementation of a two-level prevention system. The first level of the prevention system was whole-class instruction, which occurred twice weekly for 30–45 min per session, which was incorporated into the teachers’ standard mathematics instructional block but, as noted, represented only a part of the classroom teachers’ program. The second level was individual tutoring for at-risk students, which occurred three times weekly for 20–30 min per session and aligned with the instructional sequence of whole-class instruction. Students were introduced to new skills during whole-class instruction and tutoring augmented whole-class instruction rather than replicating it; that is, tutoring provided additional strategies and provided further explanation for the hardest concepts addressed in whole-class instruction. Such a two-level prevention system is an education reform that has gained popularity for decreasing students’ risk for long-term academic difficulty (see Vaughn & Fuchs, in press). Whole-class instruction was provided by research assistant teachers (RA teachers); tutoring was provided by research assistant tutors (RA tutors). In this paper, we refer to WP intervention as SBI; however, RA teachers, RA tutors, and students referred to the WP intervention as Pirate Math. In addition, in WP intervention, RA teachers, RA tutors, and students referred to combine, compare, and change problems as total, difference, and change problems, respectively. The names of the problem types were chosen to enhance comprehensibility for the second graders participating in the study (see Willis & Fuson [1988] who also adapted problem type names for second graders).

SBI began with Unit 1 (weeks 1–2), which addressed foundational problem-solving skills important to the subsequent three units. Each of the subsequent units focused on one of the three problem types, with cumulative review. Combine problems were the focus of Unit 2 (weeks 3–7); compare problems were the focus of Unit 3, with cumulative review on combine problems (weeks 8–13); change problems were the focus of Unit 4, with cumulative review on combine and compare problems (weeks 14–17). So, the compare unit, which is the focus of the present study, ran six weeks (from weeks 8 through 13 of the larger investigation’s intervention; see Tables 2 and 4).

Nature of WP intervention

SBI taught students to conceptualize word problems in terms of problem types, to recognize defining features of each problem type, and to represent the structure of each problem type with an overarching equation (i.e., a + b = c; d − e = f). For each problem type, the unit began by introducing students to the structure for that problem type. In the first compare lesson, the RA teacher called two students of different heights to the front of the classroom and led a discussion of the comparison in heights, introducing students to a conceptual diagram that mirrored the physical comparison. This was repeated with other concrete objects. Two representations of the problem structure were used to build meaning of compare problems, the conceptual diagram (just mentioned) as well as a mathematical expression (“B – s = D,” where B is the bigger number, s is the smaller number, and D is the difference number). Working with compare stories that first had no missing information but gradually introduced missing information, students filled quantities into the diagram and into the mathematical expression. The conceptual diagram was gradually faded in favor of the mathematical expression (which students can more easily use on their own). Students were taught to identify important information in the problem and build a number sentence, in the form of B – s = D, showing×as the unknown.¹

In a previous unit, which focused on the combine problem type, students had been taught to RUN through a problem before solving it (i.e., Read the problem, Underline the question, and Name the problem type). This RUN strategy was also used for compare problems. Students named the problem type by thinking of defining features of each problem type taught. To help identify compare problems, students were taught to ask themselves whether two things are being compared. Students were also taught to use the following procedure to solve compare problems. First, they identified the representation of the underlying structure for compare problems: B – s = D. Second, they identified the unknown in the compare problem they were solving and placed×under that position of the equation. Third, students identified, checked off, and wrote important given numbers under the compare equation, B – s = D. Fourth, students wrote the mathematical signs (- and =). Finally, students solved the problem by finding x, using a number-list strategy they had been taught in the introductory unit, and they labeled the numerical answer. We note that many students gradually adopted a more direct approach for deriving solutions, even as they continued to appreciate and work within the problem-type framework. In either case, the sequence of steps within students’ solutions appropriately reflected the problem’s additive or subtractive nature and addressed the three subcategories within each of the compare problem subtypes. As hypothesized in the literature, children are expected to rely on a part-part-whole schema to solve addition and subtraction word problems (e.g., Kintsch & Greeno, 1985; Resnick, 1983). Yet, as shown by Fuson and Willis (1989) and Willis and Fuson (1988), although second-grade children improve word-problem performance when taught distinctive schema for change, compare, and combine problem types, they show no evidence of relying on a single part-part-whole schema for representing those problem types. Therefore, we did not emphasize part-part-whole relations in the transition from problem representation to solution.

Missing information (x) can occur in any of the three positions: B, s, or D. Using the strategies we taught, when the compared or referent set is unknown,×is positioned underneath B or s in the compare equation. Students were first taught to solve problems with the difference set unknown (as in “Jill has 8 marbles. Tom has 5 marbles. How many more marbles does Jill have than Tom?”), because these problems are the easiest subtype of compare problems. In difference set unknown compare problems, determining which numbers represent the bigger and smaller quantities requires an understanding of whether 8 is bigger or smaller than 5, thus representing B – s = D as 8 – 5 = X. When the difference set is given and either the compared set (e.g., Jill has 8 marbles. Tom has 5 fewer marbles than Jill. How many marbles does Tom have?) or the referent set (e.g., Jill has 8 marbles. She has 5 more marbles than Tom. How many marbles does Tom have?) is unknown, problems are more difficult to represent because determining whether the unknown is the bigger or smaller amount requires understanding of the relational statement in the problem. To represent the problem structure when the difference set is given (as in the two examples just provided), students must translate the relational statement to understand that 5 is the difference, Tom has the smaller amount, and Jill has the bigger amount. This leads them to represent B – s = D as 8 – X = 5. These harder compare problem subtypes were introduced once students practiced representing and solving the easiest compare problem subtype.

Relational terminology instruction

During whole-class instruction on the compare unit, RA teachers introduced the instructional component focused on helping students interpret relational statements. First, the meanings of more, less, and fewer were defined and reviewed. Second, students were taught to cover the difference number to decide what is the bigger or smaller amount using the relational term (e.g., in “Tom has 5 fewer marbles than Jill,” the student covers 5 and re-reads; if Tom has less than Jill, he has the smaller amount and Jill therefore must have the bigger amount). Third, students practiced writing an alternative relational statement that preserves the structure of the original sentence by switching the subject and object of the sentence and switching the relational term to its opposite (e.g., more instead of less/fewer). In the case of “Tom has 5 less marbles than Jill,” the new sentence would read, “Jill has 5 more marbles than Tom.” In the new sentence, Jill still has the bigger amount and Tom the smaller amount and the difference amount is 5. These activities had two purposes: (a) to teach the meaning of the relational terms for determining the bigger and smaller amounts in problems with unknown compared or referent sets and (b) to teach the symmetrical relationship of more to less/fewer. This activity occurs in 9 of the 11 compare unit lessons.

In tutoring on the compare unit, the following activities addressed relational meaning, centered on the Compare Game. In the first tutoring lesson of the compare unit, students learned the foundational elements for the game including (a) a review of the meanings of more, less, and fewer (as taught in whole-class instruction); (b) a review of which items are being compared in the relational sentence (as taught in whole-class instruction); (c) instruction on the meanings of the greater than (>) and less than (<) symbols (not addressed in whole-class instruction); and (d) application of the (>) and (<) to the relational term (i.e., more, less, or fewer) to assist in determining which amount is bigger or smaller (not addressed in whole-class instruction). After this initial instruction, students played the Compare Game, as follows. The RA tutor provided a relational sentence. Students underlined the two things being compared, writing the (>) or (<) symbols over the relational term in the sentence, and write B and S on the two things being compared. For example, consider this relational statement, “Jess has $5 more than Kesha.” First, students underlined Jess and Kesha; second, they found the relational term, more, and wrote a greater than symbol (>) above; and finally, students wrote B over Jess’s name and s over Kesha’s name. This shows Jess has the bigger amount and Kesha has the smaller amount.

In the second through fifth tutoring lessons on compare problems, students played the Compare Game using three relational statements in each session. In the sixth lesson, relational statements were replaced with entire compare word problems, as students applied the same steps just described. After completing those steps, students identified whether the unknown was the bigger or smaller amount. In subsequent lessons, students played the Compare Game with a mix of relational statements and compare word problems. In lesson 11, students learned to determine the bigger and smaller quantities when presented with new relational terminology (e.g., older-younger and taller-shorter). For the remainder of the compare unit, the stimuli in the Compare Game mixed relational statements and compare word problems with all the relational terms. When solving compare problems throughout tutoring, RA tutors reminded students to use methods from the Compare Game to interpret the relationship and accurately represent the problem structure in their number sentences represent compare problems. When students struggled in solving compare problems, RA tutors encouraged them to use the (<) and (>) symbols and write “B” or “S” above items to facilitate correct problem representations.

Lesson activities

Each whole-class lesson incorporated five activities: (a) a review of previously taught concepts and solution strategies; (b) the daily lesson, in which the RA teachers introduced new material; (c) teacher-led seatwork, which involved students working along with the RA teacher on one word problem pertinent to the days’ lesson; (d) partner work, in which students solved two to three word problems in dyads; and (e) individual work, in which students were accountable for completing one word problem independently for which they earn points. During the review, the daily lesson, and teacher-led seatwork, the RA teacher asked lots of questions to encourage active student participation and called different students up to the board to assist in segments of the lesson. In these segments, the RA teacher gradually shifted responsibility from teacher to the student. During partner work and individual work, the RA teacher circulated throughout the room engaging with dyads to scaffold and support understandings. Students were encouraged to use their daily scores to monitor their progress.

Each tutoring lesson comprised four activities: (a) a two-minute review activity for practicing previously taught foundational skills from the introductory unit; (b) the lesson, which introduced new strategies and provided guidance to students through two to three word problems while the RA tutor gradually decreased support; (c) a two-minute sorting game in which students received practice in recognizing the defining features of and naming problem types; and (d) completion of an independent word problem for which students earned points. The individual format provided ample opportunity for the RA tutor to scaffold instruction for student understanding and performance. As with whole-class instruction, students were encouraged to use their performance/score on the independent word problem to monitor their own progress.

Researcher-Designed CAL intervention

CAL intervention, which RA teachers, RA tutors, and students referred to as Math Wise, was structured with whole-class and tutoring components, in parallel fashion to WP. CAL intervention focused on addition and subtraction combinations and procedural calculations (it did not focus on word problems). As with WP intervention, weeks 8 through 13 of the larger investigation was the intervention period for the present study (i.e., we pretested CAL and control students at the end of week 7 and posttested them at the end of week 13). During weeks 8–13, the focus of CAL intervention was subtraction combinations and procedural subtraction calculations with and without regrouping. Addition, which had been taught in the weeks prior to week 8, was included as mixed review. The relationship between whole-class instruction and tutoring, as well as the lesson activities, were structured similarly across WP and CAL intervention.

Fidelity of implementation

Each of six RA teachers delivered whole-class lessons in both conditions (WP and CAL). Each RA teacher was responsible for teaching one to three classrooms. Twelve RA tutors delivered tutoring in both conditions (WP and CAL). Tutoring occurred outside the classroom at times when students did not miss important instruction, as determined by the classroom teacher. Each RA tutor was responsible for tutoring three to six at-risk students, approximately half of whom received WP tutoring; the other half CAL tutoring.

To facilitate the delivery of a standard program that could be used to index efficacy protocol and to promote fidelity of implementation, we used lesson guides to support RAs’ understanding of the instruction. Lesson guides were studied prior to instruction; RAs were not permitted to memorize or read portions of the guides. RA teachers and tutors attended separate one-day introductory trainings on intervention procedures and salient features of the WP and CAL interventions and additional 2-hour trainings prior to each unit. Three RA teachers had prior experience with both intervention programs and modeled their initial lessons for the novice RA teachers so they could observe lessons in action. Six RA tutors were returning from the previous year; seven RA tutors were new. Returning RA tutors were paired with new tutors to practice the tutoring procedures prior to working with students. Subsequent trainings occurred for RA teachers and RA tutors before each unit.

All RA teachers and tutors used audio-digital recording devices to record 100% of lessons. To assess whether additional training was necessary, experienced RAs conducted live observations and listened to audio recordings. To quantify treatment fidelity, we randomly sampled 20% of the audiotapes (RAs were not aware of which lessons would be coded) to represent the WP and CAL conditions, RAs, and lessons comparably. Each classroom was represented 7 to 8 times during whole-class instruction, and each tutored student was represented 9 to 10 times. Prior to the study, we had prepared a checklist for every lesson, which listed the essential components of that lesson. As coders listened to tapes, they checked the essential components to which the RA adhered, with the percentage of essential components then derived. In WP, fidelity for the compare unit was 96.54% for whole-class instruction and 94.23% for tutoring; fidelity for relational instruction (i.e., the Compare Game) within tutoring lessons was 99.26%. In CAL, fidelity for lessons taught during the same timeframe as the WP compare unit was 98.75% for whole-class instruction and 92.03% for tutoring.

Measures

Measures to assess comparability as a function of study condition

As described under Participants, to assess treatment group comparability at the start of the study, we used one calculation measure of (Addition Fact Fluency, Fuchs et al., 2003) and two word-problem measures (Single-Digit Story Problems [Jordan & Hanich, 2000]; Vanderbilt Story Problems [Fuchs & Seethaler, 2008]). Addition Fact Fluency comprises addition number combinations with sums from 0–12; alpha on this sample was .88. Single-Digit Story Problems comprises 14 combine, change, or compare word problems requiring addition or subtraction combinations for solution. The tester reads each item aloud; students have 30 sec to write an answer and can ask for re-reading(s). Alpha on this sample was .80. With Vanderbilt Story Problems, students complete 18 combine, change, or compare problems with missing information in all three positions, with and without irrelevant information and with and without charts/graphs. Alpha on this sample was .85. See Table 4 for means and standard deviations among the three groups.

Major study measures

For the present study, we assessed performance on a measure of compare problems and on students’ understanding of relational terminology. Compare Problems includes 16 compare problems: six with the referent set unknown, six with the compared set unknown, and four with the difference set unknown. The score is the number of correct responses, including labels. For referent set unknown problems, 12 is the maximum score; for compared set unknown problems, 12 is the maximum score; and for difference set unknown problems, 8 is the maximum score. Alpha on this sample was .92 for the entire Compare Problem Measure. Alpha was .80, .82, and .76 for referent, compared, and difference set unknown subtype problems, respectively.

Relational Tasks assesses understanding of relational terminology in the context of word problems with two tasks. The first presents eight compare problems with the compared or referent sets unknown. Rather than solving problems, students determine which quantity is bigger and smaller and which quantity is unknown (i.e., the bigger, smaller, or difference amount). The second task comprises eight relational statements that are similar to those phrased in problems in which the compared set is unknown. For each relational statement, students determine which sentence preserves the described relationship. Students are given three sentences from which to choose along with a “none of the above” option. The first task assesses understanding of relational terminology as it directly relates to representing compare problems via mathematical expressions. The second task assesses understanding of the symmetrical relationship of the terms more to less/fewer. The presentation and response format was not the same as procedures from WP intervention. Alpha on this sample was .91, and the maximum score was 32.

Testing Procedure

At the start and end of the compare unit, each time during one 50-min testing session, we administered Compare Problems and Relational Tasks. Students in all conditions were tested in the same timeframe. RA teachers conducted both testing sessions. Scripted protocols were used to ensure tests were administered consistently. For compare problems, students were asked to solve each word problem. Although students were directed to show their work, they were not prompted to use strategies from the WP intervention. For Relational Tasks, testers first explained and students completed sample items, and students had the opportunity to ask questions before testing began. For both measures, testers read each problem twice and advanced the class to the next item when all but two students were finished.

Data Analysis and Results

Table 4 displays adjusted posttest scores on Compare Problems (i.e., the outcome) and Relational Tasks (i.e., the mediator) for the three conditions and a combined “comparison” condition (across the CAL and business-as-usual control groups; see below). Performance by the three problem subtypes is also provided.

Preliminary Analyses

We used regression analysis to assess the tenability of combining CAL and business-as-usual control conditions to form one comparison group on Compare Problems; we did the same on Relational Tasks. Each time, we controlled for performance at the start of the compare unit and accounted for the hierarchical structure of the data. Each analysis revealed no significant difference between these two groups. We combined these two conditions to serve as one comparison group not only given the lack of significant differences but also (a) because both conditions received word-problem instruction from the basal text, which did not include SBI or a focus on relational terminology, and (b) because including a separate business-as-usual control group with only eight classrooms achieves power to detect a minimum effect size (ES) of only 0.83, whereas combining the two groups to form one comparison group with 19 classrooms boosts power to detect a minimum ES of 0.66. Furthermore, we examined the pattern of the mediation effect when using three separate conditions versus merging the two comparison conditions (CAL and control). The pattern was the same. The reason for merging the two control groups was to gain the statistical power required to also account in the model for the variance associated with classrooms (n = 31).²

To assess pretreatment comparability of WP versus the combined comparison group at the time of random assignment, we conducted regression analysis that accounted for the hierarchical structure of the data using HLM software, which showed that the groups were comparable on Addition Fact Fluency, Single-Digit Story Problems, and Vanderbilt Story Problems (respective p values = .79, .49, and .80; effect sizes = 0.01, 0.03, and 0.01).

Assessing the Proposed Causal Mechanism

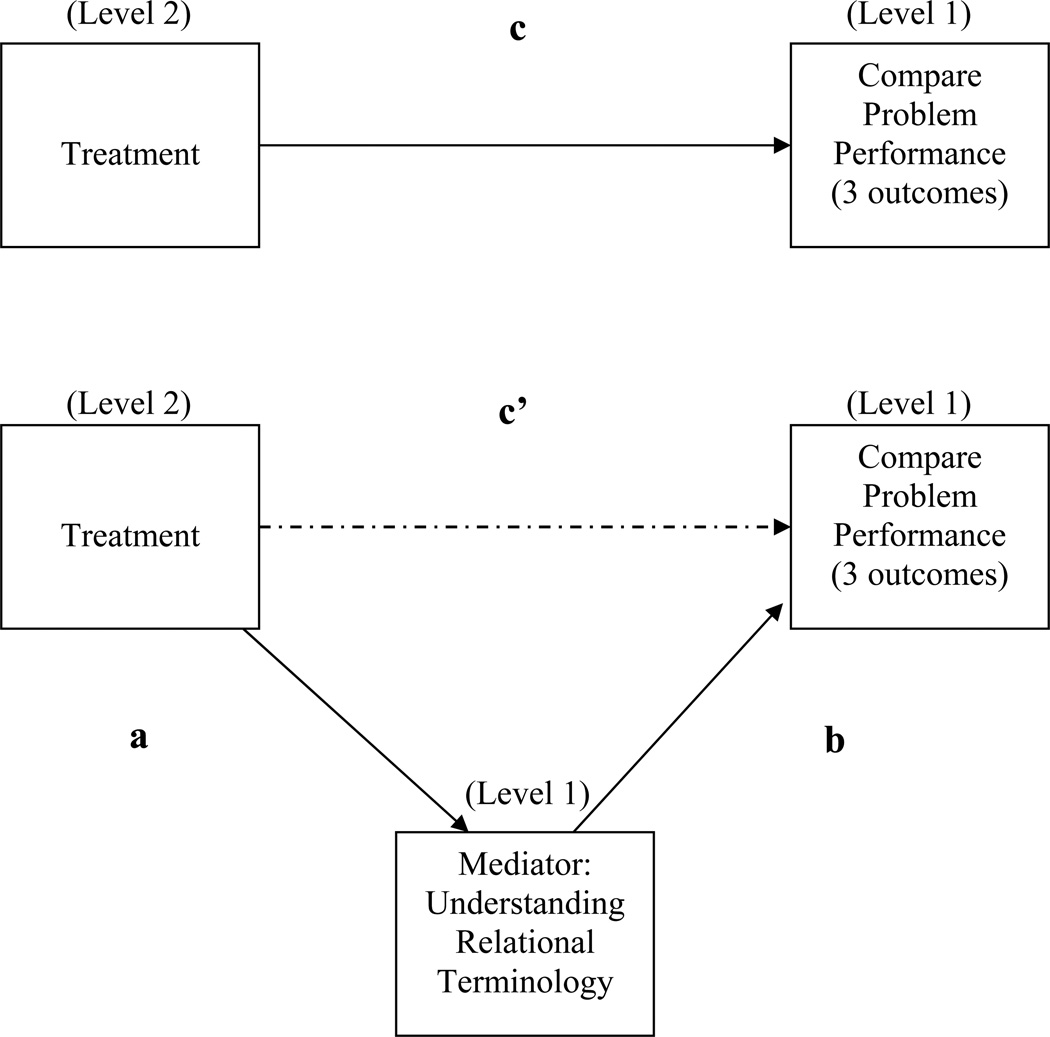
We used student pretest scores on Compare Problems as a covariate in all analyses. To test whether intervention effects were mediated by students’ understanding of relational terminology, we conducted a three-step mediation analysis (MacKinnon, 1994; MacKinnon, 2008; Zhang, Zypher, & Preacher, 2009) using regression while accounting for the hierarchical structure of the data. Treatment was a Level 2 (classroom) variable; the mediator (Relational Tasks) and the outcome (each of the three Compare Problem scores, one for each subtype of compare problems) were Level 1 (student) variables. Figure 1 displays the overarching mediation model we tested along with relevant paths we used to assess the direct and indirect effects for each of these analyses.

Figure 1.

Mediation Model Tested. The first panel shows the direct effect (path c) from the first step in the mediation analysis. The second panel shows the second (path a) and third steps (paths b and c') in the mediation analysis (based on Zhange, Zypher, & Preacher, 2009). Treatment is a Level 2 (classroom) variable and the mediator (Relational Tasks) and the outcome (each of the 3 Compare Problem subtypes) are Level 1 (student) variables. For each path, the coefficient and significance level are included on Table 6.

In the first mediation analyses, we looked at the compare subtype with the difference set unknown. In the first step of the analysis, we assessed the effects of treatment condition on the outcome (performance for unknown difference set problems) controlling for initial unknown difference set performance (path c on Figure 1). The first model in Table 5 shows treatment condition was a significant predictor of performance for problems with unknown difference sets favoring WP over the comparison group (ES = 0.47 where ES = difference in adjusted means divided by the pooled, unadjusted SD.) In the second step, we assessed the effects of treatment on the mediator (Relational Tasks). The second model in Table 6 shows treatment condition was a significant predictor of the mediator (path a on Figure 1) (ES = 0.26 favoring WP over the comparison group). In the third and final step of the mediation analysis, we assessed the effects of treatment condition and the mediator (Relational Tasks) on the outcome (performance for unknown difference set problems), controlling for initial performance on Compare Problems of the unknown difference set subtype (paths b and c'). The third model shows treatment condition and the mediator each remained significant when both were included in the model (paths b and c'). Thus, understanding relational terminology did not fully mediate intervention effects for compare problems with the difference set unknown. To determine whether the indirect effect was however significant, we applied the Sobel test (Baron & Kenny, 1986), which was significant (p = .038; see Table 6 for coefficient values), indicating that understanding relational terminology partially mediates intervention effects on compare word problems with unknown difference sets.

Table 5.

Adjusted Posttest Scores for Major Study Measures

		WP		CAL		control		Comparison CAL+Control
	classrooms students	(n = 12) (n = 169)		(n = 11) (n = 155)		(n = 8) (n = 118)		n = 19) (n = 273)
Measures		M	(SE)	M	(SE)	M	(SE)	M	(SE)
Relational Tasks
Adjusted Posttest		19.33	(0.42)	16.90	(0.43)	17.75	(0.50)	17.26	(0.33)
Difference Problems Overall (16)
Adjusted Posttest		11.51	(0.31)	9.99	(0.32)	9.71	(0.37	9.87	(0.25)
Unknown Difference Set (4)
Adjusted Posttest		3.32	(0.13)	2.50	(0.13)	2.12	(0.15)	2.37	(0.10)
Unknown Compared Set (6)
Adjusted Posttest		4.79	(0.19)	4.12	(0.19)	4.04	(0.22)	4.08	(0.15)
Unknown Referent Set (6)
Adjusted Posttest		4.08	(0.18)	3.01	(0.19)	2.96	(0.22)	2.99	(0.14)

Note. The numeral next to each item for Difference Problems is the number of test items for each problem category.

Table 6.

Mediation Analyses to test the Proposed Causal Mechanism

		Unknown Difference Set				Unknown Compared Set				Unknown Referent Set
Model		B	SE	p	PC	B	SE	p	PC	B	SE	p	PC
Step 1	Treatment on Outcome (Difference Problem Subtest)
	Constant	1.99	0.26	< 0.001		5.00	0.33	< 0.001		4.31	0.25	< 0.001
	Difference Problem covariate	0.54	0.05	< 0.001		0.51	0.04	< 0.001		0.52	0.05	< 0.001
	Treatment	−0.89	0.21	< 0.001	c	−1.06	0.38	0.008	c	−1.47	0.32	< 0.001	c
Step 2	Treatment on Mediator (Relational Tasks)
	Constant	19.39	0.78	< 0.001		19.39	0.78	< 0.001		19.39	0.78	< 0.001
	Treatment	−2.09	0.97	0.041	a	−2.09	0.97	0.041	a	−2.09	0.97	0.041	a
Step 3	Treatment and Mediator (Relational Tasks) on Outcome (Difference Problem Subtest)
	Constant	1.01	0.25	< 0.001		0.99	1.19	0.41		1.65	0.68	0.023
	Difference Problem covariate	0.39	0.04	< 0.001		0.33	0.05	< 0.001		0.39	0.05	< 0.001
	Relational Tasks posttest	0.073	0.01	< 0.001	b	0.113	0.06	< 0.001	b	0.095	0.018	< 0.001	b
	Treatment	−0.85	0.19	< 0.001	c'	−0.62	0.33	0.073	c'	−1.3	0.29	< 0.001	c'

Note. PC = the path coefficient relevant to the mediation analysis in Figure 1. To assess the significance of the indirect effect for unknown difference and referent sets, we looked at paths a*b to assess the interaction.

We repeated this three-step process to determine mediation effects for the two other subtypes of compare problems: unknown compared set problems and unknown referent set problems. Table 6 displays coefficient values for each step of the mediation analysis for the relevant paths. For problems with unknown compared sets, step 1 revealed treatment was a significant predictor of the outcome (ES = .25 favoring WP over the comparison group), step 2 revealed treatment was a significant predictor of the mediator (ES = .26), and in the third step, the mediator remained significant, and the treatment effect was no longer significant when both were included in the model. In this way, for compare problems with unknown compared sets, relational terminology fully mediated intervention effects.

For problems with unknown referent sets, results were similar to problems with unknown difference sets. The first and second steps were both significant, favoring the WP condition. Treatment was a significant predictor of the outcome, ES = .39, and treatment was a significant predictor of the mediator, ES = .26. In the third step, when treatment and the mediator were both included in the model, both remained significant. To assess the indirect effect, we applied the Sobel test (Baron & Kenny, 1986), which was significant (p = .045), indicating that relational terminology partially mediates intervention effects for compare problems with unknown referent sets.

Discussion

The purpose of this study was to assess whether students’ understanding of relational terminology mediates WP intervention effects. We situated instruction on relational terminology within a unit on compare problems because understanding relational terminology is highly relevant for this problem type (Lewis & Mayer, 1987; Stern, 1993). We posited the following causal mechanism: When students receive instruction on relational terminology, their understanding of that terminology improves, and this improved understanding increases their ability to represent the structure of each of the three subtypes of compare problems and solve these problems correctly. Research indicates that students who lack understanding of relational terminology have difficulty solving compare problems (De Corte et al., 1985; Fan et al., 1994; Fuson et al., 1996; Hudson, 1983; Stern, 1993; Verschaffel, 1994). Yet, we identified no prior studies that assessed whether instruction on understanding relational terminology affects performance on compare problems or affects students’ understanding of relational terminology. We also identified no studies that assessed whether understanding of relational terminology mediates the effects of instruction designed to enhance students’ competence in handling compare word problems.

In the first steps of the mediation analyses, we found significant effects for WP intervention on all three compare problem subtype outcomes (unknown difference sets, unknown compared sets, and unknown referent sets). The WP intervention, based on SBI, includes several instructional components that likely contributed to increased performance. For example, students were taught to understand the underlying structure of the problem type, with the goal of fostering students’ comprehension of the story structure, and to identify the problem type before applying solution procedures. In addition, we taught students to represent the problem with mathematical expressions in terms of the bigger, smaller, and difference quantities and to apply solution rules. Recognizing the problem type before solving it is central to applying the successful solution strategies in SBI. As with the present study, prior randomized control studies have found support for the efficacy of SBI when assessing performance on a mix of combine, change, and compare problems (Fuchs, et al., 2008; Fuchs, et al., 2009; Fuchs, Zumeta, et al., 2010; Jitendra, Griffin, Deatline-Buchman, et al., 2007; Jitendra, Griffin, Haria, et al., 2007). In the present study, we isolated effects for compare problems, the most difficult of the three problem types.

In the second step of the mediation analysis, we found significant effects for WP intervention on understanding relational terminology. Within the compare unit, we incorporated instruction to explicitly teach students the meaning of relational terms and the symmetry between more and less/fewer. Within whole-class instruction, students learned to identify relational statements and determine which amount is bigger or smaller. Students also learned to write equivalent relational statements by changing the relational term and switching the subject and object of sentences. In addition, to address the working memory demands associated with word-problem development (e.g., Fuchs, Geary, et al., 2010a, 2010b; Swanson & Beebe-Frankenberger, 2004), we provided at-risk students with strategies for reducing the working memory demands involved in deciphering and operating on relational statements: At-risk students learned to write the greater than (>) or less than (<) symbol over the relational term once they deciphered its meaning, to write “B” and “s” above the bigger and smaller amounts once they identified which entity was larger, and to mark the unknown quantity with×once they determined which quantity was unknown. Prior research assessing students’ understanding of relational terminology (e.g., (De Corte et al., 1985; Fan et al., 1994; Fuson et al., 1996; Hudson, 1983; Stern, 1993; Verschaffel, 1994) suggests that such understanding is most important when solving compare problems with unknown referent sets. Yet, instruction on relational terminology has not been the focus of previous work. Our findings add to the existing literature by suggesting that instruction on relational terminology enhances students’ understanding of these terms within the context of compare problems.

The third step in the mediation analysis provides support, at least in part, for our proposed causal mechanism. In this step, we simultaneously included treatment and the relational understanding mediator variable as predictors of performance on each of the three compare problem subtype outcomes. Results showed that WP intervention and the mediator each remained significant predictors (paths b and c') when included in the same regression equation for two compare problem subtypes: those with unknown difference sets and those with unknown referent sets. To assess the indirect effect for these outcomes, we applied the Sobel test, which showed that intervention effects were partially mediated by understanding of relational terminology for both of these outcomes. For the third compare problem subtype, those with unknown compared sets, results showed that WP intervention (path c') was no longer a significant predictor of the outcome when the mediator (path b) was included in the model. So, for compare problems with unknown compared sets, intervention effects were fully mediated by students’ understanding of relational terminology.

According to MacKinnon (2008), mediation analysis identifies whether specific program components help explain treatment effects. For each of the three compare problem subtypes, the mediator was significant, and partially or fully mediated intervention effects. Thus, indicating that understanding relational terminology is an important mechanism in explaining performance on compare problems and an active instructional ingredient in the context of SBI intervention. Only for the subtype of compare problems with the unknown compared set was the mediation effect complete. For this subtype, which is easier than the unknown referent set subtype but harder than the unknown difference set subtype (e.g., Garcia et al., 2006; Morales et al., 1985; Riley & Greeno, 1988), the instructional focus on relational terminology appeared to provide adequate scaffolding, in and of itself, for promoting student success. Perhaps these problems of moderate difficulty, relative to the other two subtypes, were closer to the students’ zone of proximal development. By contrast, the mediation effect for the easiest and most difficult compare problem subtypes was only partial. For the easiest subtype, the unknown difference set subtype (Morales et al.; Riley & Greeno), the least sophisticated understanding of relational terminology is required (Stern, 1993), suggesting that other SBI components of intervention contributed, on top of the relational understanding component, to help bolster student understanding. Even so, understanding of relational terminology, as reflected in the partial mediation, was still an important mechanism for enhancing performance. Interestingly, for the most difficult subtype, unknown referent set problems (Morales et al.; Riley & Greeno), the mediator effect was also partial. This may seem surprising because this subtype demands the most developed understanding of relational terminology for accurate solution (Stern). Perhaps, the difficulty of the unknown referent set subtype requires the additional support afforded by the other SBI instructional components or that more intensive instruction on understanding relational terminology is required for such understanding to completely mediate the effects of SBI efficacy. Even so, the partial mediation effect again suggests understanding relational terminology is an important contributor to success. Clearly, more research is needed to extend insight into how understanding of relational terminology interacts with instructional intervention on compare problems to determine student success.

The present study’s findings suggest teaching students to understand relational terminology, with the major focus on the meanings of more, less, and fewer and determining bigger and smaller quantities, is an important ingredient for enhancing performance on compare problems. This findings must, however, be understood within the context of five study limitations. First, explicit instruction on other relational terms (e.g., longer, shorter, older, younger) was not included in whole-class instruction and was incorporated only on three days of tutoring. Moreover, our outcome and mediator measures only included items with more, less, and fewer and determining bigger and smaller quantities. Future research should explore whether instruction on the limited set of relational terms addressed in the present study transfers to a broader set of vocabulary.

Second, we remind readers that although mediation analysis is designed to identify whether specific program components help explain intervention effects, a stronger demonstration of the effects of relational terminology instruction would involve a randomized control trial in which participants are randomly assigned to receive high quality word-problem instruction with and without relational terminology instruction. Future randomized control trials should be conducted toward this end.

A third limitation of the present study is that the instructional backdrop for relational understanding instruction was SBI, in which instruction relied on a single mathematical representation for the compare problem type, rather than separate representations for the three compare problem subtypes. In taking this approach, our goal was to (a) facilitate children’s appreciation of the broader compare problem type, underscoring the semantic structure of the problem situation that remains constant across the compare problem subtypes (even as the placement of missing information occurs in different roles of the problem-type situation), and (b) promote correct classification of problems by reducing the working memory load and the complexity associated with teaching nine problem types (across combine, compare, and change problems). Once students identified the semantic category of a problem, they then identified which piece of information was missing; the hope was to encourage appreciation of the subcategories within the problem type. Also, many students in the present study gradually adopted a more direct approach for deriving solutions, even as they continued to appreciate and work within the problem-type framework. In either case, the hope was that the sequence of steps within students’ solutions appropriately reflects the additive or subtractive nature of problems and addresses the three subcategories within each of the three superordinate word-problem types. Even so, it is possible that encouraging children to model word problems in a more informal, flexible way that follows the semantics of the narrative may be superior to the SBI approach we took in the present study and may offer advantages for teaching students relational terminology within a more natural approach. In a similar way, it is also possible that teaching representations for three compare problem types may be superior to teaching one unified compare problem type and enhance the effects of relational terminology instruction. Empirical tests designed to test the effects of relational terminology instruction, when contextualized with SBI versus instruction that encourages more informal strategies and when contextualized in SBI studies with a unified versus multiple representations of compare problems, are fruitful directions for future research. Such studies might also investigate whether the cognitive resources associated with word-problem development, such as working memory, oral language ability, or nonverbal reasoning ability (e.g., Fuchs, Geary, et al., 2010a, 2010b; Swanson & Beebe-Frankenberger, 2004), moderate efficacy of these different instructional approaches.

The fourth limitation is that we did not separate effects for at-risk students who received tutoring. We opted against analyzing data for this subset of students for two reasons. One was that classrooms were randomly assigned to WP and CAL conditions that, by definition, included whole-class instruction as well as tutoring for at-risk students. That is, each of these intervention conditions was conceptualized as a 2-level condition as is the case within responsiveness-to-intervention systems that provide a unified prevention framework. The other reason was sample size for detecting effects: Only 27 (of 169) WP students and 27 (of 155) CAL students received tutoring (with only 20 [of 118] control students who would have received tutoring if their classrooms had been randomly assigned to the WP or CAL condition). Such a mediation analysis would be sorely underpowered. Future studies might systematically investigate the contribution of tutoring to the efficacy of relational understanding instruction, by randomly assigning classrooms to whole-class intervention conditions and then stratifying by classroom to randomly assign students to tutoring. In this way, students would receive tutoring with and without the whole-class instructional component, thereby providing the basis for isolating the contributions of whole-class instruction and tutoring. The final limitation is that we did not assess follow-up, and future work is clearly warranted to examine the durability of the effects demonstrated in the present study.

With these limitations in mind, we tentatively draw some implications for school practice. Our findings suggest that word-problem instruction focused on the language demands in those word problems is important. This makes sense given prior research showing that oral language ability is a unique predictor of word-problem development (e.g., Fuchs, Geary, et al., 2010a, 2010b) and is uniquely associated with word-problem difficulty (Fuchs, Fuchs, Stuebing, et al., 2008). In our WP intervention on compare problems, we relied on SBI, which teaches students to identify the story structure before solving problems, while focusing students’ attention on understanding relational terminology. Results suggest that such SBI promotes learning specifically of compare problems, the most difficult problem type addressed in the primary grades. Moreover, findings suggest that understanding relational terminology at least partially mediates the effects of SBI on compare problem learning; that incorporating instruction focused on relational terminology may afford added value for promoting student success with compare word problems; and, in a more general sense, that language instruction within the context of word-problem instruction may represent a productive avenue for enhancing students’ development of competence in handling word problems.

Highlights.

• When used in word problems, relational terminology is challenging for young students.

• Instruction on relational terminology was tested within a word-problem intervention, using a randomized control trial.

• Students’ problem-solving skills improved more than a comparison group

• Students’ understanding of relational terms also improved.

  Word-problem outcomes were mediated by students’ understanding of relational terms.