Mitral Valve Annuloplasty

Abstract

Mitral valve annuloplasty is a common surgical technique used in the repair of a leaking valve by implanting an annuloplasty device. To enhance repair durability, these devices are designed to increase leaflet coaptation, while preserving the native annular shape and motion; however, the precise impact of device implantation on annular deformation, strain, and curvature is unknown. Here we quantify how three frequently used devices significantly impair native annular dynamics. In controlled in vivo experiments, we surgically implanted eleven flexible-incomplete, eleven semi-rigid-complete, and twelve rigid-complete devices around the mitral annuli of 34 sheep, each tagged with 16 equally-spaced tantalum markers. We recorded four-dimensional marker coordinates using biplane videofluoroscopy, first with device and then without, which were used to create mathematical models using piecewise cubic splines. Clinical metrics (characteristic anatomical distances) revealed significant global reduction in annular dynamics upon device implantation. Mechanical metrics (strain and curvature fields) explained this reduction via a local loss of anterior dilation and posterior contraction. Overall, all three devices unfavorably reduced annular dynamics. The flexible-incomplete device, however, preserved native annular dynamics to a larger extent than the complete devices. Heterogeneous strain and curvature profiles suggest the need for heterogeneous support, which may spawn more rational design of annuloplasty devices using design concepts of functionally graded materials.

1 Introduction

More than half a century ago, the first mitral valve procedure was performed to correct a leaking valve under open heart conditions [32]. While the initial technique was based on leaflet corrections alone, mitral valve repair today calls for a combination of leaflet and annular procedures coupled with implantation of an annuloplasty device [9]. Since it was established more than four decades ago [7], mitral valve annuloplasty has become progressively refined, and is now considered the gold standard for the treatment of mitral regurgitation due to most etiologies [35].

The most common form of clinical mitral valve disease is mitral regurgitation with systolic retrograde flow from the left ventricle to the left atrium. It affects more than 2.5 million Americans today; a number that is expected to double by 2030 as the population ages and grows [15]. Annually, more than 300,000 people world-wide, 44,000 in the United States alone, undergo open heart surgery due to mitral valve disease [1].

The rationale behind mitral annuloplasty is to correct mitral valve insufficiency by restoring the physiological form and function of the healthy mitral valve apparatus [9]. The healthy mitral valve undergoes significant dynamic changes in shape and size during the cardiac cycle [36]. These changes are largely due to the dynamic motion of the mitral annulus [39], a fibrous structure of collagenous connective tissue that attaches the mitral leaflets and the left atrium to the left ventricle and the aortic root [24]. From diastole to systole, the annulus undergoes a sphincteric motion, narrowing the orifice area to enhance coaptation of the two leaflets [46]. The orifice area is further reduced by a pronounced three-dimensional configuration during systole, the characteristic saddle shape [23, 31]. These dynamic changes are believed to be important to satisfactory mitral valve function in terms of optimizing leaflet coaptation [22] and theoretically minimizing leaflet tissue stresses [37, 44].

The challenge today is to improve the diseased, often distorted shape of the mitral valve and restore a more physiological configuration, while preserving normal native annular dynamics [10]. Today, the cardiac surgeon can select from a wide variety of annuloplasty devices [4], flexible, semi-rigid, or rigid, incomplete or complete, planar or saddle-shaped, see Figure 1. While all devices seek to increase leaflet coaptation and support the posterior annulus against dilation, flexible incomplete fabric bands are particularly designed to preserve the three-dimensional contour of the native annulus [10]. The design goal of semi-rigid rings is to maintain coaptation and valve integrity during systole, while permitting good hemo-dynamics during diastole [8]. Rigid, complete rings are designed to induce radical reshaping of very dilated annuli associated with left ventricular dilatation and systolic dysfunction [13]. Despite progress during the past decades, the characterization and selection of different annuloplasty devices remains largely qualitative and subjective.

Fig. 1.

Three common annuloplasty devices compared in the current study: the flexible-incomplete Cosgrove^© band (top), the semi-rigid-complete Physio^© ring (middle), and the rigid-complete Geoform^© ring (bottom). The left column shows photographs of the devices from the atrial view, where the anterior portion is arranged to be at the top, while the posterior portion is at the bottom. The right column shows the mathematical representation of the mitral valve annulus in its native state, black, and upon device implantation, white, both at end diastole. Photographs courtesy of Edwards Lifesciences.

In this study, we sought to quantify to what extent flexible-incomplete, semi-rigid-complete, and rigid-complete devices succeed in meeting their design goals. Although related studies had been conducted in the past [20,46], none of those were based on quantitative side-by-side comparisons of three mechanistically different devices, where each study subject was used as its own control [3]. Here, we used a hybrid experimental-computational approach to quantify device-induced alterations in annular dynamics, both globally in terms of common clinical criteria and locally in terms of mechanical field quantities. The unique combination of in-vivo biplane videofluoroscopy and non-linear field theories of mechanics allowed us to identify local extrema in strain [4,38,42], stress [21,26,27], and curvature [14,29,39] fields in addition to standard global clinically-used parameters [18,24]. With these, we tested the hypothesis that annuloplasty device implantation, irrespective of device design, affects mitral annular dynamics. We also qunatified to which extent flexible bands and semi-rigid rings succeed in preserving native annular dynamics, compared to rigid rings.

2 Methods and Materials

2.1 Animal Experiments

All animals received humane care in compliance with the Principles of Laboratory Animals Care formulated by the National Academy of Sciences and published by the National Institutes of Health. This study was approved by the Stanford Medical Center Laboratory Research Animals Review Committee and conducted according to Stanford University policy.

For this study we used 34 adult, male Dorsett-hybrid sheep (49±5 kg). We first administered ketamine intramuscularly for placement of a single peripheral intravenous line, and then anesthetized the sheep with sodium thiopental. Following intubation, we ventilated the sheep mechanically with inhalational isoflurane. To control secretion and bradycardia, we gave glycopyrrolate as needed. Next, we performed a thoractomy to gain access to the mitral valve via a direct atrial approach, a longitudinal incision through the roof of the left atrium. Subsequently, we surgically implanted 16 radiopaque miniature tantulum markers on the perimeter of the mitral valve annulus under cardiopulmonary bypass and cardioplegic arrest. We sutured six markers onto characteristic annular landmarks, one marker at each trigone, one at the mid anterior portion, one at the mid posterior portion and one at each commissure, see Figure 2. We then subdivided the annulus into segments of equal length using the remaining ten markers. Once all markers were secured at their respective locations, we implanted one of the three frequently used annuloplasty devices (Edwards Lifesciences, Irvine, CA, USA): flexible-incomplete polyester fabric Cosgrove bands in n = 11 animals [10], semi-rigid-complete Elgiloy steel Physio rings in n = 11 animals [8], and rigid-complete titanium Geoform rings in n = 12 animals [13], see Figure 1. We implanted all devices in a releasable fashion [3], and then closed the left atrium. Supplemental videos in [3] illustrate atrial access, marker locations, and ring release.

Fig. 2.

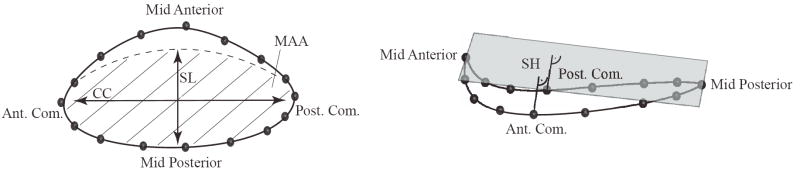
Example of a piecewise cubic, three-dimensional spline, solid line, approximating the 16 marker coordinates in space, top view (left) and lateral view (right). We implant markers, black spheres, at the anterior and posterior trigones, at the mid anterior portion, at the mid posterior portion and at each commissure. Additionally, we place ten markers to subdivide the annulus into 16 segments of approximately equal length. The figure also illustrates mitral annular area (MAA), septal-lateral distance (SL), commissure-commissure distance (CC), and saddle height (SH).

2.2 Data Acquisition

After marker and device implantation, we weaned the animals off cardiopulmonary bypass and transfered them to the catheterization laboratory. Here, under acute, open chest condition, we took biplane videofluoroscopic images of the valves with implanted devices at a sampling frequency of 60Hz. Simultaneously, we recorded blood pressure in the left ventricle, in the aorta, and in left atrium through catheter micromanometer pressure transducers. After recording the first series of images, we released the devices, see Figure 3, and pulled them to the atrial roof. In a second series of images, we collected the control data without the devices in place. Off-line, we utilized a semi-automated image processing and digitization software [33], to obtain four-dimensional coordinates χ_n(t) for all n= 1, …, 16 markers, for three consecutive heart beats, both with annuloplasty devices implanted and without.

Fig. 3.

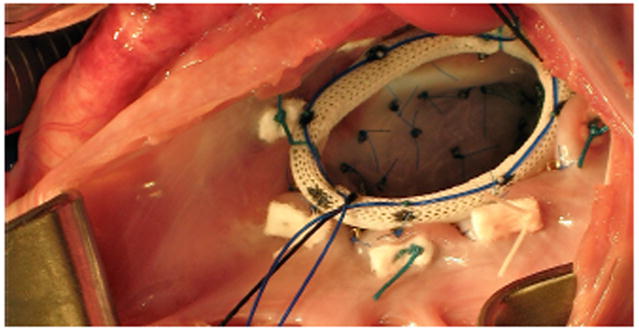
Intraoperative photograph illustrating releasable device implantation. Prior to implantation, the ring is prepared by stitching the middle parts of eight double-armed sutures evenly spaced through the ring fabric. Drawstring sutures through their loops, shown in blue, enable the in vivo release of the implanted device. This technique allows us to use each individual treated animal as its own control [3].

2.3 Mathematical Model

In the subsequent analyses, we utilized mathematical splines to approximate the mitral valve annulus [16]. Splines are smooth, piecewise-polynomial functions of a particular order used to interpolate or approximate a given set of data points. From the 16 four-dimensional marker coordinates χ_n(t), we created 16 piecewise cubic Hermitian splines,

$$\mathit{c}(s,t)={\sum }_{i=0}^3{b}_{i,3}(s){\mathit{\beta }}_i(t)$$ (1)

parameterized in terms of the arc length s, for each discrete time point t throughout the cardiac cycle [39]. Here,

$$\begin{array}{ll}{b}_{0,3}=-s^3+3s^2-3s+1& b_{1,3}=3s^3-6s^2+3s\\ b_{3,3}=s^3& b_{2,3}=-3s^3+3s^2\end{array}$$ (2)

are the Bernstein polynomials of degree three and

$$\begin{array}{ll}{\mathit{\beta }}_0={\mathit{x}}_0(t)& {\mathit{\beta }}_1={\mathit{x}}_0(t)+{\mathit{m}}_0(t)/3\\ {\mathit{\beta }}_3={\mathit{x}}_1(t)& {\mathit{\beta }}_2={\mathit{x}}_1(t)-{\mathit{m}}_1(t)/3\end{array}$$ (3)

are corresponding Bernstein coefficients [16, 40]. The Bernstein coefficients are parameterized in terms of the positions x₀, x₁ and slopes m₀, m₁ at the beginning and end point of each spline segment. For each discrete time point t, we determined these coefficients β_i(t) by solving a least squares problem.

$${\sum }_{\mathrm{n}=1}^{16}\Vert {\chi }_{\mathrm{n}}-{\mathit{c}}_{\mathrm{n}}(s,t)\Vert +\lambda {\mathit{\int }}_s{\Vert {\mathrm{d}}_s^2\mathit{c}(s,t)\Vert }^2\mathrm{d}s\to \min$$ (4)

The first term minimizes the distance from the markers positions χ_n to the spline curve c_n(s, t). The second term minimizes the second derivative ${\mathrm{d}}_s^2\mathit{c}(s,t)$ of the overall spline, enforcing smoothness through the penalty parameter λ. In addition, we applied linear equality constraints to ensure C²-continuity. This allowed us to calculate continuous derivatives up to degree two, required to evaluate mechanical metrics such as strain and curvature along the entire annulus for every point in time [39].

2.4 Characterization Using Clinical Parameters

In the literature, various clinical parameters have been introduced to characterize dynamic changes of the mitral valve annulus throughout the cardiac cycle. The most popular ones are the septal-lateral annular distance that describes the length of the short axis of the almost elliptical orifice area of the mitral valve, the commissure-commissure distance that is equivalent to the long axis, the eccentricity, the mitral annular area, the annular perimeter, and the saddlehorn height that measures non-planarity of the annulus, see Figure 2.

With the mathematical model derived in the previous section, we calculated the septal-lateral and commissure-commissure distances after projecting the spline representation onto a best-fit plane to orthogonalize the planar and non-planar parameters. Using this best-fit-plane projection, we calculated the eccentricity from a fitted ellipse and determined the mitral annular area from its area. Using the line integral along the arc-length parameter s, we calculated the three-dimensional annular perimeter. Last, we calculated the saddle height as the distance of the commissural points to a plane that passes through the mid anterior and mid posterior points and is equidistant to both commissures. To quantify dynamic changes upon device implantation, we determined the percentage change

$$\mathrm{Change}=\left[p_{\mathrm{S}}-p_{\mathrm{D}}\right]/p_{\mathrm{D}}\cdot 100\%$$ (5)

of the peak values p in systole (S) and diastole (D) for each parameter, with and without device.

2.5 Characterization Using Mechanical Fields

The mathematical representation of the annulus derived in Section 2.3 allows us to easily extract mechanically relevant fields such as deformation, strain, and curvature. Strain is a measure of the relative displacement of continuum points along the annular perimeter between time t and the reference time t₀, here selected to coincide with minimum left ventricular pressure (LVP_min) [38]. As a field quantity, strain allows us to evaluate precisely, on a local level, where and to which extent the mitral valve annulus undergoes contraction and dilation, both in its native state and upon device implantation. We calculated the Green-Lagrange strain E(s, t) along the annulus,

$$E(s,t)=\frac{1}{2}\left[{\mathrm{d}}_s\mathit{c}{(s,t)}^2/{\mathrm{d}}_s\mathit{c}{(s,t_0)}^2-1\right]$$ (6)

where the term in the brackets represents the stretch squared minus one. The stretch was calculated as the ratio between the lengths of the local tangent vectors d_sc(s, t) in the current configuration at t and in the reference configuration at t₀. It is defined as

$${\mathrm{d}}_s\mathit{c}(s,t)={\sum }_{i=0}^3{\mathrm{d}}_s{b}_{i,3}(s){\mathit{\beta }}_i(t)$$ (7)

in terms of the first derivatives of the Bernstein polynomials (2)

$$\begin{array}{ll}{\mathrm{d}}_s{b}_{0,3}=-3s^2+6s-3& {\mathrm{d}}_s{b}_{1,3}=9s^2-12s+3\\ {\mathrm{d}}_s{b}_{3,3}=3s^2& {\mathrm{d}}_s{b}_{2,3}=-9s^2+6s\end{array}$$ (8)

and the coefficients β_i(t) from the minimization problem (4). Curvature is a measure of the deviation of a smooth curve from a line. It can be interpreted as the reciprocal of the radius of a circle fit to each point of a curve in the plane spanned by the curve’s tangent and its normal. We calculated the curvature κ(s, t) along the annulus,

$$\kappa (s,t)=\Vert {\mathrm{d}}_s\mathit{c}(s,t)\times {\mathrm{d}}_s^2\mathit{c}(s,t)\Vert /{\Vert {\mathrm{d}}_s\mathit{c}(s,t)\Vert }^3$$ (9)

where the second derivative

$${\mathrm{d}}_s^2\mathit{c}(s,t)={\sum }_{i=0}^3{\mathrm{d}}_s^2{b}_{i,3}(s){\mathit{\beta }}_i(t)$$ (10)

is expressed in terms of the second derivatives of the Bernstein polynomials (2)

$$\begin{array}{ll}{\mathrm{d}}_s^2{b}_{0,3}=-6s+6& {\mathrm{d}}_s^2{b}_{1,3}=18s-12\\ {\mathrm{d}}_s^2{b}_{3,3}=6s& {\mathrm{d}}_s^2{b}_{2,3}=-18s+6\end{array}$$ (11)

and the coefficients β_i(t) from the minimization problem (4). We evaluated strain and curvature fields, averaged over all animals of each group, at four discrete time points, at End Diastole (ED), End IsoVolumic Contraction (EIVC), End Systole (ES), and End IsoVolumicRelaxation (EIVR), see Figure 4.

Fig. 4.

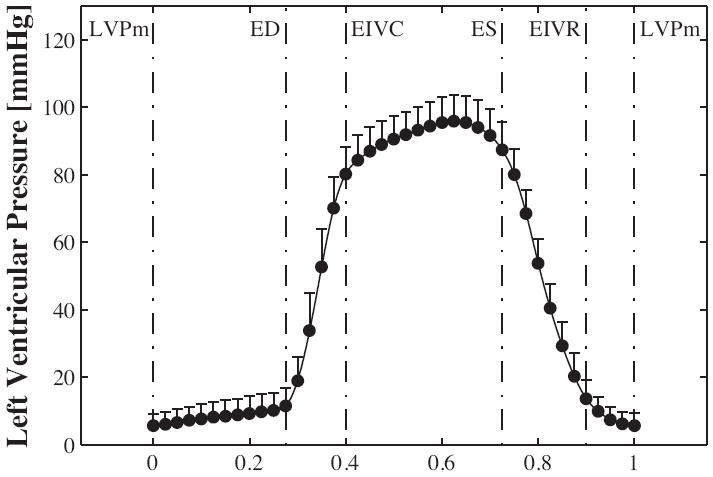
Left ventricular pressure displayed over the normalized cardiac cycle. Mean ± one standard deviation is shown for n = 34 animals without device. The graph shows the four characteristic time points at End Diastole (ED), End IsoVolumic Contraction (EIVC), End Systole (ES), and End IsoVolumic Relaxation (EIVR).

2.6 Statistics

We performed statistical analyses for the six clinical metrics and the hemodynamic data, see Figure 5 and Table 1. All bar graphs depict mean ± one standard deviation. To identify differences between device and control groups, we applied a two-sided, dependent student t-test. We visually checked normality using histograms. We analyzed the difference between control and device groups for all clinical parameters using one-way ANOVA. Last, we performed the post-hoc analysis using the Tukey test. For t-test and ANOVA, we defined the significance level to be 0.05.

Fig. 5.

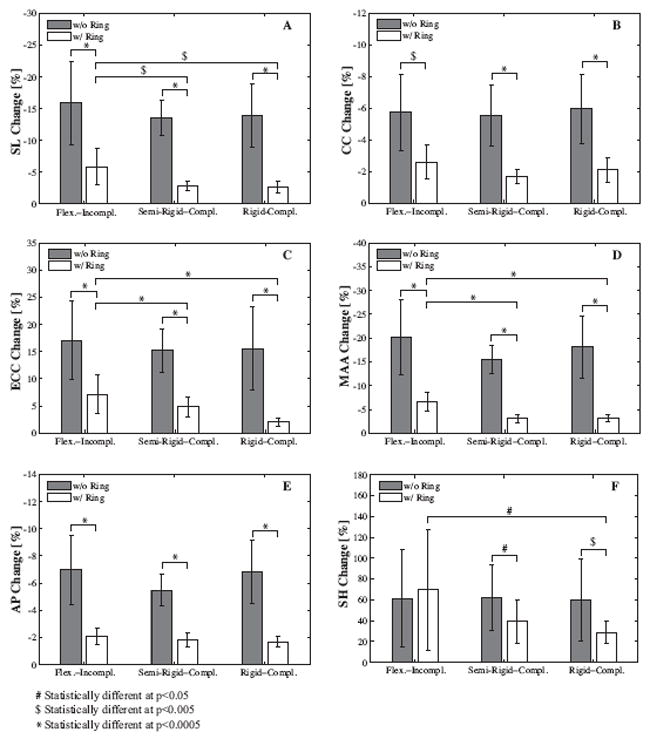
Clinical parameters describing mitral valve annular dynamics without, grey bars, and with device, white bars, for flexible-incomplete, semi-rigid-complete, and rigid-complete devices. Bars show mean ± one standard deviation of changes in peak values during diastole versus systole. SL septal-lateral distance (A), CC commissure-commissure distance (B), ECC eccentricity (C), MAA mitral annular area (D), AP annular perimeter (E), and SH saddlehorn height (F).

Table 1.

Hemodynamic data for three device groups without and with devices implanted. Data include Heart Rate (HR), Maximum Pressure Gradient (dP/dt_max), End Diastolic Volume (EDV), End Systolic Volume (ESV), Stroke Volume (SV), Left Ventricular End Diastolic Pressure (LVEDP), Left Ventricular End Systolic Pressure (LVESP), and Maximum Left Ventricular Pressure (LVP_max); ± One Standard Deviation (STD).

		HR (beats/min)	dP/dt (mmHg/s)	EDV (cc)	ESV (cc)	SV (cc)	EF (-)	LVEDP (mmHg)	LVESP (mmHg)	LVPmax (mmHg)
Flex.-Incompl.	Mean	99.38	1406.53*	117.50	92.12	25.39	0.22	11.42	95.27	96.53
No Device	± STD	14.12	285.58	12.99	12.41	8.44	0.06	4.94	8.86	8.42
Flex.-Incompl.	Mean	99.43	1577.49	118.55	92.53	26.02	0.22	10.86	96.87	97.91
Device	± STD	13.41	360.61	13.39	13.38	10.39	0.07	5.28	6.98	6.20
Semi-Rigid-Compl.	Mean	93.28	1349.73	122.73	92.21	30.52	0.25	10.27*	91.76	95.69
No Device	± STD	11.48	313.30	22.03	15.50	9.88	0.06	4.39	7.96	7.29
Semi-Rigid-Compl.	Mean	92.92	1394.42	122.59	93.27	29.32	0.24	8.80	90.88	95.28
Device	± STD	10.28	310.74	24.47	16.74	10.96	0.05	3.63	5.58	5.81
Rigid-Compl.	Mean	92.08	1313.12	114.04	88.10	25.95*	0.23*	12.05	90.78	96.41
No Device	± STD	10.32	314.94	14.07	14.95	8.73	0.07	6.26	7.16	7.86
Rigid-Compl.	Mean	93.24	1387.54	112.80	89.55	23.25	0.21	11.56	91.43	96.96
Device	± STD	10.12	410.18	12.82	14.94	10.20	0.08	6.14	7.25	7.16

^*indicates statistically significant difference between groups without and with devices.

3 Results

Analysis of the collected marker coordinates and hemodynamic data revealed normal cardiac function in all animals with and without device, see Table 1.

Figure 4 shows the time-aligned averaged left ventricular pressure over the normalized cardiac cycle [38], displayed for all n = 34 animals without device. With the device implanted, as expected, all annuli adapted the shape of the device, see Figure 1, right, white annuli. With the device released, the mathematical annulus models displayed no apparent discontinuities. We compared the geometry for each annulus to data without prior annuloplasty, which had been collected in our laboratory in the past [46]. In this comparison, we observed no significant deviations from normal physiological shape in response to annuloplasty, see Figure 1, right, black annuli. Maximum deviations between the spline representation and the discrete marker positions were found to lie in the sub-millimeter range, and were therefore of the same order of magnitude as the digitization error itself [12].

3.1 Clinical Parameters of Annular Dynamics

Figure 5 summarizes the clinical characteristics of annular dynamics without, grey bars, and with device, white bars, for the flexible-incomplete, semi-rigidcomplete, and rigid-complete devices. For all n = 34 control data sets without device, changes were −14.4 ± 5.0% in septal-lateral distance, − 5.7 ± 2.1% in commissure-commissure distance, +15.9 ± 6.4% in eccentricity, −17.9 ± 6.2% in mitral annular area, − 6.4 ± 2.1% in annular perimeter, and +61.0 ± 38.4% in saddle height. In general, all three devices showed the tendency to freeze annular dynamics and to reduce dynamic changes throughout the cardiac cycle. Specifically, for both semi-rigid and rigid rings, student t-tests showed statistically significant differences for all clinical parameters between groups without and with device, with p<0.0005 for septal-lateral and commissure-commissure distances, eccentricity, mitral annular area, and annular perimeter for both groups, p<0.05 for saddle height for semi-rigid rings and p<0.005 for saddle height for rigid rings. The flexible band showed statistically significant changes in annular dynamics with p<0.0005 for septal-lateral distance, eccentricity, mitral annular area, and annular perimeter and p<0.005 for commissure-commissure distance, but not for saddle height.

As expected, one-way ANOVA revealed no statistically significant differences between the three groups without device, grey bars, for any of the clinical parameters. However, we were able to show statistically significant differences in dynamic changes between the three device groups with device, white bars, with p<0.0005 for eccentricity and mitral annular area, p<0.005 for septal-lateral distance, and p<0.05 for saddle height, while the differences for commissure-commissure distance and annular perimeter remained statistically insignificant. Tukey post-hoc analysis showed that changes in septal-lateral distance, eccentricity, mitral annular area, and saddle height with device were larger in the flexible band group than in the semi-rigid and the rigid ring groups.

3.2 Mechanical Fields of Annular Dynamics

Figures 6 and 7 depict the mechanical characteristics of mitral annular dynamics without, rows 1,3,5, and with device, rows 2,4,6, for flexible-incomplete, semi-rigid-complete, and rigid-complete devices. Figure 6 illustrates regional variations in annular strains at four characteristic time points throughout the cardiac cycle. Red colors indicate annular dilation or tension, while blue colors indicates annular contraction or compression, relative to the reference configuration at LVP_min.

Fig. 6.

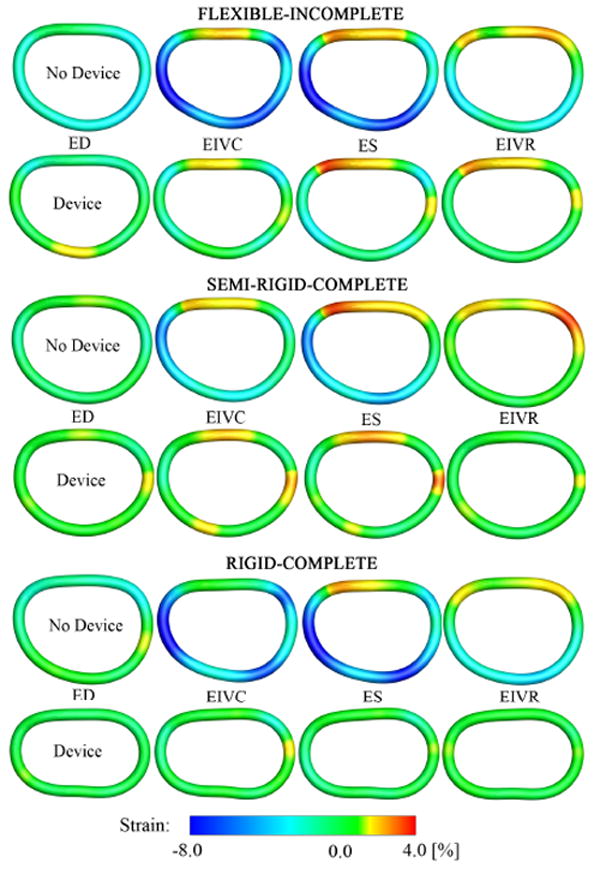
Mechanical strain fields describing mitral annular dynamics without, rows 1,3,5, and with device, rows 2,4,6, for flexible-incomplete, semi-rigid-complete, and rigid-complete devices. Illustrated are the average spline representations of the annuli from an atrial view. The annuli are arranged such that the anterior portions are at the top while the posterior portions are at the bottom. Annular strains are displayed at four characteristic time points: End Diastole (ED), End IsoVolumic Contraction (EIVC), End Systole (ES), and End IsoVolumic Relaxation (EIVR). Red indicates annular dilation/tension, blue indicates annular contraction/compression, relative to the reference configuration at LVP_min.

Fig. 7.

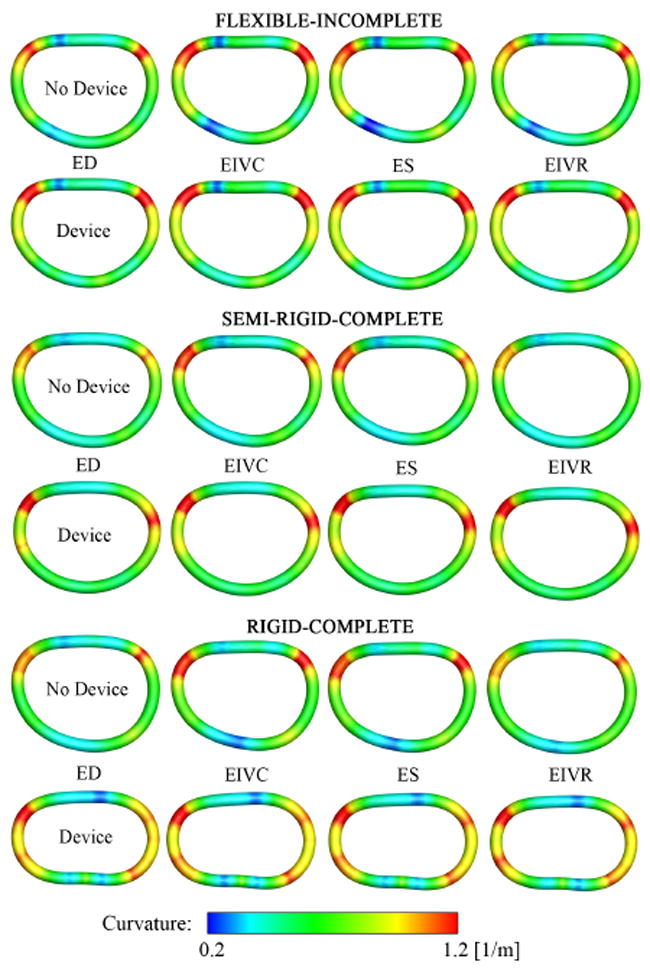
Mechanical curvature fields describing mitral annular dynamics without, rows 1,3,5, and with device, rows 2,4,6, for flexible-incomplete, semi-rigid-complete, and rigid-complete devices. Illustrated are the average spline representations of the annuli from an atrial view. The annuli are arranged such that the anterior portions are at the top while the posterior portions are at the bottom. Annular curvature is displayed at four characteristic time points: End Diastole (ED), End IsoVolumic Contraction (EIVC), End Systole (ES), and End IsoVolumic Relaxation (EIVR).

The control groups without device, rows 1,3,5, displayed the characteristic annular dynamics with approximately 8% contraction in the posterior annulus and approximately 4% dilation in the anterior annulus. All devices, rows 2,4,6 severely affected mitral annular dynamics, and, in average, significantly reduced temporal and regional strain variations.

For the flexible band, Figure 6 top, at all four time points, strains were non-negative throughout the entire posterior annulus, while without device, the posterior annulus displayed maximum contractile strains of −10.0%. However, in the anterior section, strains remained virtually unaffected by the device, in fact, they even increased slightly upon device implantation from +2.7% to +3.5%. For the semi-rigid ring, Figure 6 middle, device implantation eliminated contractile strains in the posterior annulus at all four time points. Furthermore, tensile strains in the anterior annulus appeared generally smaller upon device implantation. For the rigid ring, Figure 6 bottom, at all four time points, the entire annulus showed a significant strain reduction. Both tensile strains in the anterior annulus and contractile strains in the posterior annulus were substantially reduced in the rigid ring group in comparison to its control group without device. Figure 7 illustrates regional variations in annular curvature at four characteristic time points. All devices reduced the temporal variation in curvature throughout the cardiac cycle when compared to their control groups. In the control groups, rows 1,3,5, the curvature increased from diastole to systole, especially in the commissural regions. Upon device implantation, rows 2,4,6, these changes were significantly reduced. For the flexible band group, Figure 6 top, points of maximum curvature were identical with and without device. For the semi-rigid ring group, Figure 6 middle, local extrema were slightly shifted upon device implantation. For the rigid ring group, Figure 6 bottom, the curvature was altered considerably upon device implantation, alternating between several local extrema along the perimeter.

4 Discussion

We characterized the dynamics of the mitral valve annulus in the beating ovine heart, both with and without three commonly used annuloplasty devices. We had previously validated the underlying method using healthy baseline data derived from 55 sheep [39]. Here, we hypothesized that annuloplasty devices reduce annular dynamics, irrespective of their design. Our results confirm our hypothesis, and, in addition, demonstrate that incomplete flexible bands, as intended, [10], preserve annular dynamics more than did complete rings.

4.1 Discussion of Clinical Parameters

Figure 5 summarizes the characteristic dynamic behavior of the native mitral annulus during the cardiac cycle, see grey bars. From diastole to systole, the native mitral annulus displays its characteristic sphincteric motion, resulting in a significant reduction in mitral annular area of −17.9±6.2%. Furthermore, the asymmetric change in septal-lateral and commissure-commissure distances, −14.4 ± 5.0% versus −5.7 ± 2.1%, forces the mitral valve annulus to take a more elliptical shape in systole, resulting in an increase in eccentricity of +15.9 ± 6.4%. Finally, the annulus undergoes a change in its three-dimensional configuration, resulting in a more pronounced saddle shape in systole than in diastole, manifesting itself in a remarkable increase in saddle height of +61.0 ± 38.4%.

Figure 5 demonstrates that annuloplasty device implantation does affect native annular dynamics, irrespective of device type, see white bars. Changes in septallateral and commissure-commissure distances, eccentricity, mitral annular area, and annular perimeter are significantly reduced, causing the annulus to lose a large portion of the sphincteric motion upon device implantation. Changes in saddle height are significantly reduced by semi-rigid and rigid rings, but not by flexible bands. Changes in septal-lateral distance, eccentricity, mitral annular area, and saddle height remain significantly larger in the flexible band group, than in semi-rigid and rigid ring groups, however, this is not true for the commissure-commissure distance and the annular perimeter. We conclude that the flexible band, indeed, preserves annular dynamics to a larger degree than the semi-rigid and rigid rings.

4.2 Discussion of Mechanical Fields

While global clinical metrics are relatively straightforward to calculate and to interpret, they are known to mask local mechanisms and phenomena. To support the conclusions suggested by clinical metrics, to identify local effects and regional variations, and to provide further insight into mitral annular dynamics, the analysis of mechanical field values is of critical importance. To fully appreciate the dynamic motion of the mitral valve annulus, we refer to the supplemental videos in [39].

Figure 6 illustrates the heterogeneity of annular strains throughout the cardiac cycle. The side-by-side comparison of control and device data, rows 1,3,5 versus rows 2,4,6, allows us to identify mechanisms that might be crucial to healthy mitral valve function, but are impaired by device implantation. For example, we observe that for all three devices, the reduced change in annular perimeter can be attributed to a loss of posterior contraction, rows 2,4,6, which is characteristic for the healthy annulus during systole, rows 1,3,5. The side-by-side comparison of the different devices, rows 2,4,6, allows us to quantify repair mechanisms that might help to optimize future device design. For example, it is evident that the incomplete band, row 2, preserves the characteristic dynamics of the anterior segment, while the complete rings, rows 4,6, do not.

Figure 7 illustrates the spatial heterogeneity in annular curvature throughout the cardiac cycle. The side-by-side comparison of control and device data demonstrates that all three devices, rows 2,4,6, alter the native curvature, rows 1,3,5. Both the flexible band and the semi-rigid ring, row 2,4, succeed in maintaining regions of maximum and minimum curvature, rows 1,3, closely mimicking the native curvature profile. The rigid ring, row 6, however, overwrites the natural curvature pattern, row 5, almost throughout the entire perimeter. Curvature changes indicate alterations in bending dynamics, which might disturb the natural force balance of the mitral valve complex and induce locally elevated stresses. Altered stress profiles could potentially trigger tissue remodeling, which, in turn, could further affect normal mitral valve function [45].

4.3 Comparison to Previous Studies

A number of studies have been conducted in animals [18, 41, 47] and in humans [11,17,34], with the common goal to quantify whether flexible and semi-rigid devices can preserve annular dynamics. Interestingly, the results deviate considerably [46]. Some studies have hypothesized that annular dynamics are diminished, independent of the implanted device. This hypothesis has been confirmed in the beating ovine heart, in which flexible bands have shown no significant advantage over semi-rigid rings in terms of preservation of annular dynamics [18]. Other experiments have hypothesized that flexible bands and rings preserve annular dynamics at least to some degree. In-vivo studies in animals [41,47] and sonomicrometry studies in patients [11, 34] have confirmed these assumptions. Discrepancies between these findings have been attributed primarily to differences in device types, animal models, etiologies, measurement techniques, and study duration [46]. Despite all this past effort there is no controlled animal experiment that allows a direct side-by-side comparison between flexible bands, semi-rigid rings, and rigid rings. None of the existing studies have applied a releasable ring technique [3], to use each treated subject as its own control. Furthermore, existing studies base their conclusions solely on clinical metrics [5], without performing mechanical analyses to support their conclusions. We believe that the current study, by overcoming these limitations, will contribute significantly to our understanding of mitral valve annuloplasty.

4.4 Clinical Significance

Dynamic annular changes, from a three-dimensional configuration with reduced saddlehorn height during diastole to a configuration with increased saddlehorn height during systole, might be critical to reduce leaflet stress [23, 37, 44] and to support the sphincteric motion which reduces mitral annular area [24]. During diastole, the sphincteric motion of the mitral valve annulus increases the orifice area and therewith aids left ventricular filling [6]. During systole, a reduction in the orifice area facilitates coaptation between the anterior and posterior leaflets. First, abolishing any of these mechanisms may be detrimental to mitral valve function and yield suboptimal repair results [8, 10, 45]. Second, fixing the anterior annulus and preventing it from buckling into the mitral valve orifice during systole might disturb native dynamic motion of the left ventricular outflow tract [30]. Third, annuloplasty device rigidity could theoretically impair left ventricular function [2, 25].

This suggests that annuloplasty devices, which preserve the native dynamics of the mitral valve complex might be beneficial. Here, we show that flexible bands maintain annular dynamics to a larger extent than do semi-rigid and rigid rings, and may therefore be advantageous. Overall, of course, annuloplasty device selection depends on multiple factors, of which preservation of annular dynamics is only one. Conversely, for example, the Geoform very rigid, complete ring is a diseasespecific ring specifically designed to reduce the septal-lateral distance dimension of the mitral annulus disproportionally more than the commissure-commissure distance dimension in patients with congestive heart failure due to left ventricular dilatation and systolic dysfunction, e.g., functional mitral regurgitation (FMR) and ischemic mitral regurgitation (IMR) [13, 48].

4.5 Mechanical Relevance

Mechanical field quantities such as strain [4, 38, 42], stress [21, 26, 27], curvature [14, 19, 39] and regionally varying stiffness [28], provide valuable insight into the complex dynamics of the mitral valve apparatus. Spatial and temporal variations of these fields might help to identify the mechanistic origin of repair failure, for example elevated stresses on suture lines. Ultimately, mechanical fields may help to improve current standards in valvular repair.

The mechanical design goals of the Cosgrove flexible band are to increase leaflet coaptation and to support the posterior annulus against dilation, while maintaining the native three-dimensional contour of the annulus in patients with degenerative mitral regurgitation, e.g., mitral valve prolapse [10]. Made of barium sulfate impregnated silicone rubber with a polyester velour fabric covering, it is specifically designed to preserve physiological function. Our study shows that the flexible band preserves the native saddle shape with changes in saddle height similar to the native annulus. Of all three devices, it comes closest to mimicking natural annulus sphincteric motion, with largest changes in septal-lateral distance, eccentricity, mitral annular area, and saddle height. Except for reduced posterior contraction, it preserves native strain and curvature profiles throughout the entire cardiac cycle. The mechanical design goal of the semi-rigid Physio ring is to remodel the mitral annulus while maintaining coaptation and valve integrity in systole and permitting good hemodynamics in diastole [8]. Made of layers of Elgiloy steel bands separated by polyester film strips, it is specifically designed to allow for progressive posterior flexibility and for physiologic contractility during systole. Our clinical and mechanical metrics failed, however, to confirm this design goal. Changes in clinically-used parameters are significantly reduced when compared to the control group, and significantly smaller than in the flexible band group. Strain profiles demonstrate a significant loss of posterior contraction. Strains are close to zero almost throughout the entire cardiac cycle. Despite the Physio design criteria, it seems that annular motion is almost entirely frozen.

The mechanical design goals of disease-specific rigid, complete rings such as Geoform include more radical annular reshaping and disproportionate down-sizing of the septal-lateral distance annular dimension than partial rings, to reduce mitral regurgitation caused by enlargement and dysfunction of the left ventricle, while preserving orifice area [48]. Made of a titanium alloy base covered by silicone rubber with a polyester velour fabric covering, Geoform is designed to bring the annulus inward and to raise the posterior mitral valve apparatus and posteromedial papillary muscle in an attempt to counteract the outward and downward leaflet tethering seen in patients with left ventricular dysfunction and congestive heart failure [13]. Our study confirms that the Geoform rigid ring succeeds in significantly reducing annular dynamics throughout the entire cardiac cycle. Its strain profiles are close to zero at all four characteristic time points. Its curvature profiles mimic its non-physiological geometry, specifically designed to reform the shape and function of the left ventricle and reduce chronic disease progression.

4.6 Limitations

General limitations of the experimental method and the mathematical model of the mitral valve annulus are summarized in a previous publication [39]. For this particular study, it is important to keep in mind that our data have been collected acutely, in healthy sheep. Under chronic conditions, scaring of suture and repair sites may unfavorably affect annular dynamics. Accordingly, annular dynamics might not be preserved to such a large degree as demonstrated here, under acute conditions. Under diseased conditions, the dynamics of the mitral valve may be considerably altered before device implantation becomes necessary. Although our data suggest that, under healthy conditions, the flexible band induces the smallest change in mitral annular dynamics, these results may differ in diseased hearts.

5 Conclusion

This study was motivated by the hypothesis that annuloplasty device implantation, irrespective of the device design, reduces mitral annular dynamics. In a comparison of three routinely used repair devices, flexible-incomplete, semi-rigid-complete, and rigid-complete, we observed significant device-induced alterations in common clinically-used parameters in all three groups. While these global clinical parameters are relatively straightforward to calculate and to interpret, they fail to reveal local phenomena and regional variations. We demonstrated that a complementary analysis of mechanical field quantities can provide additional insight into the mechanistic origin of device-induced alterations. In side-by-side comparisons of native and altered strain and curvature profiles, we identified mechanisms that might be crucial to healthy mitral valve function, but are unfavorably impaired by device implantation, e.g., a significant loss of posterior contraction. In side-by-side comparisons of the different devices, we quantified repair mechanisms that might help to optimize future device design, e.g., functionally graded support to preserve native anterior dilation. Overall, our results confirm our initial hypothesis that annuloplasty device implantation reduces mitral annular dynamics. In addition, our study demonstrates that flexible bands, according to their design goals, preserve annular dynamics to a higher degree than semi-rigid and rigid rings.