Abstract
The disposition effect is a phenomenon in which investors hold onto losing assets longer than they hold onto gaining assets. In this study, we used functional magnetic resonance imaging (fMRI) to measure the response of valuation regions in the brain during the decision to keep or to sell an asset that followed a random walk in price. The most common explanation for the disposition effect is preference-based: namely, that people are risk-averse over gains and risk-seeking over losses. This explanation would predict correlations between individuals’ risk-preferences, the magnitude of their disposition effect, and activation in valuation structures of the brain. We did not observe these correlations. Nor did we find evidence for a realization utility explanation, which would predict differential responses in valuation regions during the decision to sell versus keep an asset that correlated with the magnitude of the disposition effect. Instead, we found an attenuated ventral striatum response to upticks in value below the purchase price in some individuals with a large disposition effect. Given the role of the striatum in signaling prediction error, the blunted striatal response is consistent with the expectation that an asset will rise when it is below the purchase price, thus spurring loss-holding behavior. This suggests that for some individuals, the disposition effect is likely driven by a belief that the asset will eventually return to the purchase price, also known as mean reversion.
Keywords: fmri, neuroeconomics, decision making
Introduction
The disposition effect is a behavioral phenomenon in which investors “sell winners too early and ride losers too long” (Shefrin and Statman, 1985). There is robust field evidence that investors sell shares of stock significantly more often after an increase in the value of the shares, than they do after a decrease in value (Choe and Eom, 2009; Ferris et al., 1988; Grinblatt and Keloharju, 2001; Odean, 1998). This occurs despite the behavior being suboptimal in terms of profit earning (Choe and Eom, 2009; Odean, 1998). In experimental settings, where complex market forces are not present and participants are not experienced investors, the disposition effect still exists (Da Costa et al., 2008; Vlcek and Wang, 2008; Weber and Camerer, 1998). Even when decision-makers are aware that losing assets are more likely to continue falling, they hold onto these assets more than they hold onto rising assets (Weber and Camerer, 1998). These observations suggest that the disposition effect is a common property of decision-making and not simply a product of the stock market or limited to investors.
Several explanations for the disposition effect have been suggested. The most common is preference-based: namely, that people are risk-averse over gains and risk-seeking over losses (Kahneman and Tversky, 1979; Lakshminarayanan et al., 2010; Shefrin and Statman, 1985). Assuming that the purchase price of an asset is the reference point upon which investors judge gains or losses, then risk-aversion over gains would lead to the selling of assets when the value of the shares rise (the less risky option), while risk-seeking over losses would lead to holding assets when the value of the shares fall (the more risky option). This explanation is based on prospect theory, which assumes a value function that is concave over gains, but convex over losses (Kahneman and Tversky, 1979). Although risk-preference is often suggested as the driving force behind the disposition effect, several theoretical papers and experimental studies have questioned whether a preference-based explanation can fully explain the disposition effect (Barberis and Xiong, 2009; Kaustia, 2010; Vlcek and Wang, 2008). Alternatively, the realization utility hypothesis suggests that investors receive utility from the act of realizing a gain or loss, driving investors to sell gains to receive positive utility and hold losses to avoid negative utility (Barberis and Xiong, 2008). Another explanation suggests that investors have an irrational belief in mean reversion (Barberis and Thaler, 2002). This explanation predicts that an investor would hold onto a losing asset with the expectation that it would rise and sell a gaining asset with the expectation that it would fall. Despite it being an important phenomenon in finance, there is no consensus in the behavioral economics literature that mean reversion drives the disposition effect, although some experimental studies have found evidence for such a relationship (Andreassen, 1988; Hung and Yu, 2006). Hence, the question remains as to whether the disposition effect is driven by asymmetric risk-preferences over gains and losses, realization utility, or by belief-related mechanisms such as mean reversion.
In this paper, we utilize functional magnetic resonance imaging (fMRI) during an asset-trading task to test these alternative theories of the disposition effect. We measured the blood oxygenation level dependent (BOLD) response in valuation regions of the brain during decisions to keep or to sell an asset that followed a random walk in price. A preference-based explanation for the disposition effect would predict correlations between individuals’ risk-preferences, the magnitude of their disposition effect, and activation in valuation structures of the brain. A realization utility explanation would predict differential responses in valuation regions during the decision to sell versus keep an asset that correlate with the magnitude of the disposition effect. Finally, if participants believe that the asset price will eventually revert to the mean, we would predict an attenuated ventral striatum response to upticks in value below the purchase price and a greater response to upticks in value above the purchase price for individuals with a disposition effect. The ventral striatum has been shown to signal prediction error, and thus an expectation of a rise in asset price followed by an uptick should result in lessened striatal activity. Conversely, if an expectation of a fall in asset price is met by an uptick, striatal activity should increase. Of these three theories, the fMRI data were most consistent with an irrational belief in mean reversion.
Methods
Thirty-eight participants (18 female; 18 – 51 years) were recruited from the Emory University campus and completed the asset-trading task. Of this group, thirty-three participants were scanned using fMRI (17 female; 18 – 51 years). Of the thirty-three scanned participants, we excluded one participant from our imaging model because of excessive motion and five participants because they lacked observations for the regressors of interest. This was due to a high variability in participant behavior that was tied to the number of observations in each of the regressors in our model. All participants were right-handed, reported no psychiatric or neurological disorders, or other characteristics that might preclude them from safely undergoing fMRI. All participants provided informed consent to experimental procedures approved by the Emory University Institutional Review Board. Prior to beginning the experiment, participants were told that they would be paid $20 for showing up, and $30 for completing three questionnaires, including the BIS/BAS, EPQR, and a risk-preference worksheet. The total amount of $50 had to be used in the subsequent asset-trading task, where participants could earn an additional $50, or lose $50. Therefore the total possible compensation ranged from $0 to $100 (actual $30 – $75).
Asset trading task
Participants completed 40 trials of an asset-trading task while undergoing fMRI. The main screen of the asset-trading task consisted of a graph with relative value (in dollars) of an asset on the y-axis, and time (in periods) on the x-axis. For each trial, participants were initially forced to purchase an asset worth $50 using all of the money they earned prior to entering the scanner ($50). A gray circle at relative value zero and period 10 indicated the purchase point. To make sure that the current decision period was always centered on the screen, each asset had a 10-period history prior to purchase that was different for all 40 assets. Each history was generated in the same manner as the forward asset price trajectory – by generating a random walk beginning at the purchase price, but in this case going backwards for ten periods. After a button press, the asset subsequently increased or decreased in value by $5 with equal probability.
Participants were then given the choice of keeping the asset for another period, or selling the asset for its worth in that period. If participants chose to keep the asset, it again increased or decreased by $5 with equal probability after a 3 second delay. A single decision period is shown in figure 1 (panel A). To avoid influencing participant decision-making by having a finite number of periods where participants potentially behave differently towards the end of the trial, we implemented an infinite horizon. This was accomplished by using a ‘soft’ ending, where the trial ended and asset force-sold with a 5% probability each time the participant chose to keep the asset (Camerer and Weigelt, 1993; Noussair and Matheny, 2000). Participants could therefore keep the asset as long as they wanted, keeping in mind that each trial had a 5% probability of ending each time they kept the asset. If participants chose to sell the asset, they earned what the asset was worth in that period. Each sell period was followed by five periods where they saw what trajectory the price would have followed had they of kept the asset. Each time the asset was sold or force-sold, participants saw an outcome screen stating the relative amount that their asset was sold for. The maximum relative value that the asset could reach was +$50, and minimum of −$50. Participants were given full information regarding the determination of asset price and the infinite horizon prior. Participants were verbally tested on the probabilities and independence of the asset pricing, and completed two practice trials prior to the actual asset-trading task.
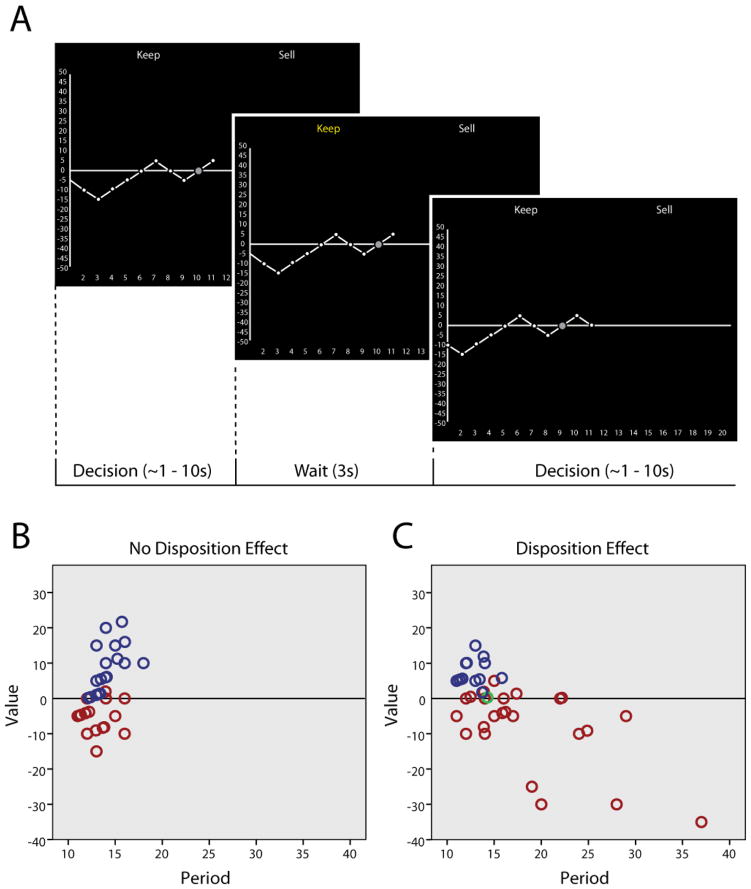
Figure 1.
Asset trading task overview. (A) Participants were forced to purchase an asset for $50 (purchase point marked by a gray circle). The asset price then followed a random walk, always increasing or decreasing in increments of $5 with equal probability. At each period, participants chose to keep or sell the asset (first panel). After the participant made a choice, the choice was highlighted for 3 seconds (second panel). The next period outcome was then shown and the participant could immediately make a decision (third panel). An infinite horizon was implemented, where there was a 5% probability of the trial ending (and asset being force-sold). Therefore, participants were able to keep the asset as many periods as they liked, with the caveat that each time they kept the asset, there was a 5% chance of the trial ending. (B) and (C) show data from subjects without a disposition effect (left; average integral of 10.4 $*periods) and with a disposition effect (right; average integral of −46.8 $*periods). Each data point represents the period in which an asset was sold or force-sold (assets that were held until the trial ended). Trials in which the overall integral of asset price through time was positive are shown in blue, negative in red, and zero in green. Forty trials are shown for each participant.
Note that because the size and probability of an increase or decrease in asset value was always equal and independent across periods, the expected value of keeping the asset was the same as selling the asset at every decision point. Furthermore, because the random-walk nature of the asset price, there is no optimal selling strategy that maximizes earnings in the task. Therefore, no matter what strategy is taken, participants on average earn a relative value of $0 across trials ($50).
Behavioral data analysis
To measure the disposition effect for each individual, we computed the integral of asset value (in dollars) relative to purchase price over time and averaged across all trials. If each asset was held regardless of value and never sold, the average integral would be close to zero because the price of the asset followed a random walk (Figure 1; panel B). If assets below the purchase price were held longer than assets above the purchase price, then the average integral would be negative (Figure 1; panel C).
We estimated risk-preference and loss aversion parameters using a method developed by Tanaka, Camerer, & Nguyen (2010). Participants were given three series of paired lotteries. In each series, participants were asked to choose the point at which they would switch from lottery A to lottery B. The expected value of lottery B increased downward in each series. By solving a system of inequalities in which constant relative risk aversion is assumed (U(x) = xα), a unique set of risk-preference and loss aversion parameters were estimated for each participant.
To understand the factors that were most important in driving participants’ decisions to keep or sell, and thus create an imaging model most relevant to participant behavior, we estimated a mixed-effects logistic regression with “keep” or “sell” for each period as the outcome variable (1 for sell, 0 for keep), five fixed-effects regressors which described local asset price characteristics, and a subject-wise regressor describing the magnitude of a participant’s disposition effect. Subject was included as a random-effects factor. The regression took the following form:
Valuet was the value of the asset at time t (which ranged from −50 to 50 in multiples of 5). Value′t was the difference in value from time t to t-1 (which could carry values −5 or 5). We subsequently refer to value′t as “delta” throughout this paper. Value″t was the change in price direction, calculated the following way: (valuet – valuet-1) – (valuet-1 – valuet-2). Thus, value″t can carry values of 10, 0, or −10. DE was the average integral across trials for each participant, which was a measure of the individual’s disposition effect. We also included interaction terms between DE and the main effects in order to probe where people with a disposition effect behaved differently.
fMRI data acquisition and analysis
Functional imaging was performed with a Siemens 3 T Trio whole-body scanner. T1-weighted images (TR = 2600 ms, TE = 3.02 ms, flip angle = 8°, 240 × 256 matrix, 176 sagittal slices, 1 mm3 voxel size) were acquired for each subject prior to the four experimental runs. For each experimental run, T2*-weighted images using an echo-planar imaging sequence were acquired, which show blood oxygen level-dependent (BOLD) responses (echo-planar imaging, TR = 2000 ms, TE = 30 ms, flip angle = 73°, FOV = 192 mm × 192 mm, 64 × 64 matrix, 33 3.5-mm thick axial slices, and 3 × 3 × 3.5 mm voxels).
fMRI data were analyzed using SPM8 (Wellcome Department of Imaging Neuroscience, University College London) using a standard 2-stage random-effects regression model. Data were subjected to standard preprocessing, including motion correction, slice timing correction, normalization to an MNI template brain and smoothing using an isotropic Gaussian kernel (full-width half-maximum = 8 mm). Task regressors were modeled using a standard canonical hemodynamic response function. Our model focused on the decision period, which encompassed the time at which the outcome of the asset increase or decrease was shown, to the time in which a participant made a response. To attempt to capture the response only to the asset price increase or decrease outcome, we also created an alternative model using an impulse function at the moment the asset increase or decrease was shown, leaving the rest of the decision period in the model baseline. In both models, we separated these periods into five separate regressors: the first period in the trial where participants hit the ‘continue’ button to see whether the asset increased or decreased in value, decisions above the purchase price, decisions below the purchase price, decisions at the purchase price, and the periods after an asset was sold. Decisions above and below the purchase price were modulated by choice (keep vs. sell), valuet, and delta (valuet – valuet-1). We also included a regressor for the outcome screen. The 3-second interval where the participant’s choice was highlighted was randomly assigned to four regressors of no-interest to prevent correlation with the constant. Because individual behavior varied greatly, and was reflected in the number of observations in each regressor, we concatenated all runs in our model together, and included n – 1 dummy variables to account for run differences. This allowed us to avoid complex contrast weights for each participant, given the high likelihood of missing regressors for multiple runs. Six motion parameters and a single constant were also included for each subject.
Statistical thresholds were determined based on the smoothness of the second-level contrasts. We used AlphaSim, a routine in AFNI, to estimate the combination of height and extent thresholds that yielded a whole-brain FDR < 0.05 (10,000) iterations. To do this, we used 3dFWHMx to estimate image smoothness from the square root of the masked SPM-generated residual (ResMS) image. We then used AlphaSim with a voxel-level threshold of p < 0.001 to find the cluster threshold at which the whole-brain FDR would be < 0.05, and which ranged from 42 to 57 voxels, depending on the specific contrast.
Results
We found evidence for a robust disposition effect in our task. As a measure of the disposition effect, we took the integral of asset price averaged across trials. Across all participants (38 including behavioral and scanned), the average integral was −27.7 $*periods (σ = 31.4, range = −113.6 – 18.9), which was significantly different from zero [t(37) = −5.4, p < 0.001]. This indicates that participants spent significantly more time below the purchase price than above the purchase price across trials. The majority of participants displayed the disposition effect (31 of 38 had integrals less than zero). As another measure of the disposition effect, participants sold the asset when it was below the purchase price significantly less often (mean = 6.5 trials, σ = 5.6) than when the asset was above the purchase price (mean = 14.4 trials, σ = 5.5; t(37) = 5.4, p < 0.001]. Furthermore, the average number of periods the asset was kept above the purchase price (mean = 6.3 periods, σ = 3.0) was significantly lower than the average number of periods below the purchase price [mean = 9.3, σ = 5.2; t(37) = −4.9, p < 0.001].
The magnitude of the disposition effect varied widely across participants, ranging from a large disposition effect (integral of −113.6 $*periods) to an anti-disposition effect (integral of 18.9 $*periods). The heterogeneity in the disposition effect could be driven primarily by individual differences in gain-selling behavior, loss-holding behavior, or both. The mean integral was significantly correlated with the average period in which an asset was sold or force-sold below the purchase price (r = −0.73, p < 0.001), but not the average period in which an asset was sold or force-sold above the purchase price (r = −0.13, p = 0.43). This suggests that the heterogeneity in the disposition effect was driven primarily by the length of loss holding. For this reason we focused the imaging analysis on decision-making below the purchase price, i.e. in the loss domain.
A preference-based explanation of the disposition effect would suggest that risk-preference should be correlated with the magnitude of the disposition effect. Overall, our risk-preference questionnaire revealed that participants were slightly risk-averse, with a mean α = 0.91 (σ = 0.34), which was consistent with past studies on risk preference (Tversky and Kahneman, 1992). The mean loss aversion parameter, however, was higher (λ = 3.8, σ = 3.6) than is typically reported in the literature (λ ~ 2). This was driven primarily by several outliers with unusually high estimates for the loss aversion coefficient. The median value of λ = 2.7 was closer to that found in the literature. We found no correlation between the risk-preference parameters, the loss aversion coefficients, and the disposition effect, providing further behavioral evidence against a preference-based explanation of the disposition effect (Vlcek and Wang, 2008).
Participants were not asked in a structured manner about their beliefs in the task, however casual conversation during debriefing revealed that a large portion of participants expressed a ‘hope’ that the asset would return to the purchase price when at a loss, despite being aware of the random-walk nature of the price. It is important to note that self-reporting of the motivation behind investment decisions might not accurately reflect the underlying process driving decisions. More formally, psychological aspects of participant behavior were gathered through BIS/BAS and EPQR questionnaires. We found no significant correlations between these personality measurements and the disposition effect. A negative correlation between BAS reward and the disposition effect approached significance (r = −0.32, p = 0.06), however using Bonferroni correction for multiple comparisons makes the trend much less compelling.
In order to build an imaging model that best reflects participant behavior, we ran a logistic regression with the decision to sell or keep as the outcome variable, and characteristics of the asset price as regressors. We found that for any given period there was a low probability of selling (Table 1). The largely negative constant represents the fact that for each trial, the participant could sell on only one period (what would be the final one). Consequently, the default prediction, with all other values set to zero, was that a participant would keep the asset for any particular period. We found that three regressors significantly (p < 0.05) predicted participant choice behavior: the value of the asset, the change in value of the asset from the previous period, and the change in price direction. These three characteristics of the asset price were subsequently included in our imaging model.
Table 1.
Effect of asset price characteristics on keep/sell behavior.
Results of keep/sell decisions regressed onto local asset price characteristics using a logistic regression. Participants had a greater propensity to sell when the asset price increased in value (valuet), decreased from the previous period (valuet′), and had a positive change in price direction (valuet″). Valuet″ was calculated by taking the difference between (valuet – valuet-1) and (valuet-1 – valuet-2). A larger average integral (more negative for a greater disposition effect; DE) increased the probability of making a sell decision. We found significant interactions between the disposition effect and local asset price characteristics.
| Coefficient | Std. Error | z | P > z | [95% Conf. | Interval] | |
|---|---|---|---|---|---|---|
| Valuet | 0.036 | 0.005 | 6.95 | 0.000 | 0.026 | 0.047 |
| Valuet′ | −0.091 | 0.016 | −5.79 | 0.000 | −0.122 | −0.060 |
| Valuet″ | 0.027 | 0.010 | 2.78 | 0.005 | 0.008 | 0.047 |
| Integral (DE) | 0.021 | 0.005 | 4.68 | 0.000 | 0.0126 | 0.031 |
| Valuet × Integral | −0.001 | 0.000 | −7.78 | 0.000 | −0.001 | −0.001 |
| Valuet′ × Integral | −0.004 | 0.000 | −8.06 | 0.000 | −0.005 | −0.003 |
| Valuet″ × Integral | 0.001 | 0.000 | 3.78 | 0.000 | 0.001 | 0.002 |
| Constant | −1.90 | 0.186 | −10.21 | 0.000 | −2.259 | −1.531 |
Imaging
Our neuroimaging model was based on two behavioral observations: 1) that heterogeneity in the disposition effect was mostly due to decisions below the purchase price; and 2) that the repressors in our behavioral model that described local asset price characteristics (valuet, valuet′, valuet″), predicted participant keep/sell behavior. We therefore created a model focusing on the decision period, which was divided into decisions above the purchase price (gains), and decisions below the purchase price (losses). These decision periods were modulated by participant choice (keep vs. sell), value, and delta. We report coordinates of activation and their corresponding statistics in Table 2. As would be expected, a simple contrast between decisions over gains versus losses revealed robust ventral striatal activation. Ventral striatal activity was not significantly correlated with overall asset price relative to the purchase (neither in the gain nor loss domain). Instead, we found that the ventral striatum responded to upticks in delta both above and below the purchase price, which was the difference between the current asset price, and the price in the previous period (Figure 2). This suggests that a change in asset price from the previous period best explains variation in the BOLD response during the decision-making period within the ventral striatum, as opposed to the total present value of the asset.
Table 2.
Whole-brain analysis results for selected contrasts.
| Structure | L/R | Maximum T | Cluster Size | Z | P (unc) | X | Y | Z |
|---|---|---|---|---|---|---|---|---|
| Decision Gain - Decision Loss | ||||||||
| Middle Occipital | R | 10.97 | 174 | 6.84 | 3.9E-12 | 18 | −94 | 9.5 |
| Ventral Striatum | L | 7.40 | 710 | 5.50 | 1.89E-08 | −18 | 14 | −8 |
| Ventral Striatum | R | 6.88 | 495 | 5.26 | 7.33E-08 | 15 | 14 | −8 |
| Medial Pre Frontal | R | 5.83 | 555 | 4.70 | 1.29E-06 | 24 | 47 | −8 |
| Thalamus | L, R | 5.74 | 78 | 4.65 | 1.64E-06 | 0 | −7 | 6 |
| Superior Parietal Lobule | L | 4.64 | 382 | 3.98 | 3.47E-05 | −33 | −55 | 45 |
| Superior Parietal Lobule | R | 4.61 | 308 | 3.96 | 3.71E-05 | 21 | −61 | 48 |
| Below PP × Delta (Positive) | ||||||||
| Middle Occipital | R | 7.12 | 87 | 5.30 | 5.94E-08 | 24 | −97 | 9.5 |
| Putamen/Ventral Striatum | L | 5.75 | 243 | 4.61 | 2.06E-06 | −30 | −13 | 2.5 |
| Superior Parietal | R | 5.64 | 510 | 4.55 | 2.74E-06 | 21 | −64 | 59 |
| Putamen | R | 5.51 | 135 | 4.47 | 3.89E-06 | 33 | −7 | −1 |
| Dorsolateral PFC | R | 5.28 | 119 | 4.34 | 7.23E-06 | 57 | 2 | 27 |
| Pre-Motor | R | 5.03 | 193 | 4.19 | 1.4E-05 | 27 | 11 | 55 |
| Pre-Motor | L | 4.40 | 57 | 3.78 | 7.72E-05 | −21 | −4 | 59 |
| Superior Parietal | L | 4.36 | 131 | 3.76 | 8.54E-05 | −15 | −70 | 59 |
| Above PP × Delta (Positive) | ||||||||
| Cuneus | L | 5.93 | 466 | 4.73 | 1.1E-06 | −6 | −82 | 17 |
| Ventral Striatum | L, R | 5.48 | 236 | 4.48 | 3.78E-06 | −9 | 5 | −12 |
| Lingual Gyrus | R | 4.23 | 94 | 3.69 | 0.000114 | 12 | −82 | −1 |
| Sell – Keep | ||||||||
| Anterior Cingulate | L, R | 7.52 | 1097 | 5.39 | 3.55E-08 | 9 | 29 | 27 |
| Cuneus | L, R | 6.73 | 1353 | 5.04 | 2.38E-07 | 12 | −85 | 13 |
| Insula | R | 6.18 | 1290 | 4.77 | 9.17E-07 | 42 | 14 | −12 |
| Insula | L | 5.83 | 360 | 4.59 | 2.22E-06 | −36 | 11 | −1 |
| Thalamus | L, R | 5.67 | 354 | 4.51 | 3.31E-06 | 6 | −19 | 2.5 |
| Inferior Parietal | R | 5.34 | 226 | 4.32 | 7.77E-06 | 54 | −40 | 59 |
| Dorsolateral PFC | R | 5.19 | 157 | 4.23 | 1.15E-05 | −45 | 5 | 31 |
| Posterior Cingulate | L, R | 5.08 | 228 | 4.17 | 1.53E-05 | 6 | −22 | 31 |
| Inferior Parietal | L | 4.94 | 301 | 4.09 | 2.19E-05 | −54 | −34 | 55 |
| Cerebellum | R | 4.68 | 150 | 3.93 | 4.30E-05 | 24 | −52 | −26 |
Figure 2.
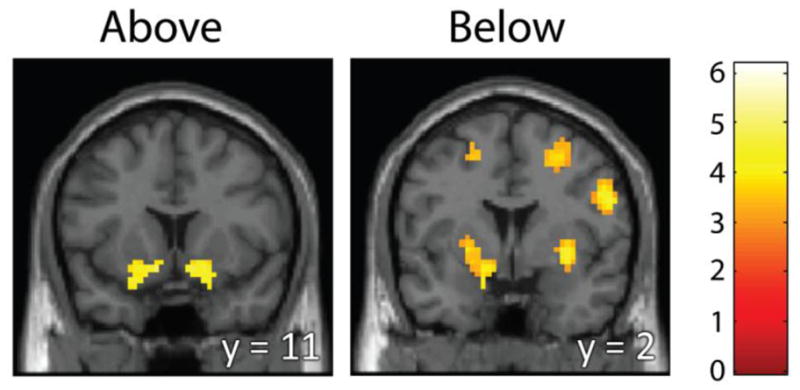
Whole-brain analysis for identifying brain regions responding to positive delta. Regions are shown whose BOLD response increased with an increase in asset price from the previous period, above (left) and below (right) the purchase price. We find ventral striatal activity both above and below the purchase price in response to upticks in value. Below the asset price, we also find DLPFC and motor area activation. Coronal sections are shown here (MNI y = 11 above, and y = 2 below). Statistical thresholding was set at p < 0.001, k ≥ 53 (above), and k ≥ 42 (below), resulting in a whole-brain FDR<0.05 for both contrasts.
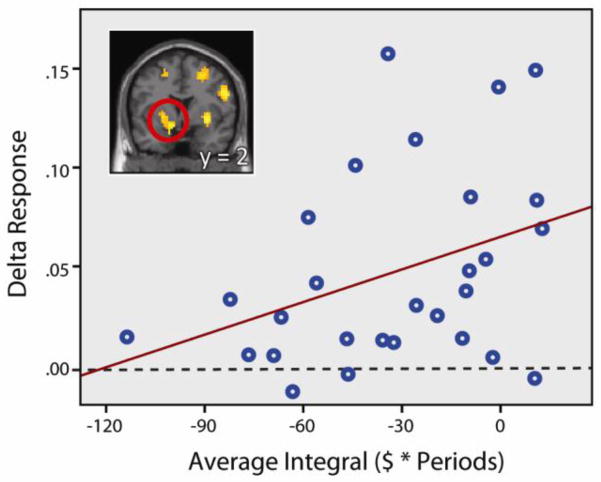
Because of the evidence implicating the striatum in the process of valuation during decision-making, and its role in explaining individual heterogeneity in decision-making strategies (Venkatraman et al., 2009), we extracted beta values from the left and right ventral striatum and putamen clusters from the aforementioned delta contrast for decisions below the purchase price (right panel; Figure 2). These beta values describe the slope of the relationship between the BOLD response and delta and were correlated with the magnitude of the disposition effect; both correlations approached significance (r = .367, p = .055; r = .360, p = .057, left and right respectively). However, in an alternative model where an impulse function was used to model the immediate response to an increase or decrease in asset value (as opposed to the entire decision period), we find significant correlations in the left and right ventral striatum (r = 0.384, p = 0.044 and r = 0.395, p = 0.037 for left and right, respectively). This suggests that our results are likely driven by immediate outcome response as opposed to deliberation over keeping vs. selling the asset. Participants who did not have a disposition effect displayed positive striatal responses to upticks in value, but participants who had large disposition effects showed little striatal response (Figure 3; left ventral striatum/putamen cluster). This relationship was not seen for decisions above the purchase price, where the BOLD response was significantly modulated by delta but not correlated with the magnitude of the disposition effect (r = .252, p = .187). We found no correlation between the measured utility curvature (indicative of risk-preference) of individual participants and overall activity in the left and right ventral striatum/putamen below the purchase price (r = 0.09, p = 0.64 and r = 0.10, p = 0.60 for both, respectively), as well as above the purchase price (r = −0.18, p = 0.36). Whole-brain correlation analysis revealed no brain regions whose response to delta correlated with utility curvature, above or below the purchase price.
Figure 3.
Relationship between striatal response to upticks in value below the purchase price and the magnitude of the disposition effect. Beta values in the left ventral striatum during decisions below the purchase price, modulated by the change in asset price from the previous period (delta), correlated with the magnitude of the disposition effect, as measured by the integral (r = 0.367, p = 0.055). A more negative integral is associated with a larger disposition effect. Participants who showed a larger disposition effect were more likely to show little or no response in the ventral striatum to upticks in value.
To test whether the disposition effect was driven by a differential response to realized (sold) versus paper (kept) gains and losses, we contrasted sell versus keep decisions (averaged across gains and losses). We found a significant difference for this contrast in bilateral insula, DLPFC, thalamus and ACC, among other regions (Figure 4; Table 1), areas consistently activated for risk-averse choices and decisions to quit loss-chasing behavior (Campbell-Meiklejohn et al., 2008; Paulus et al., 2003; Preuschoff et al., 2008). However, none of these regions were significantly correlated with the magnitude of the disposition effect. We found no activation in typical reward-related regions, such as the ventral striatum or medial prefrontal cortex (MPFC) that was greater for sell than keep decisions (even at a liberal threshold of p < 0.05, k ≥ 10). We also found no regions significantly more active for keep than sell decisions at our statistical threshold (p < 0.001, k ≥ 57). However, at a more liberal threshold (p < 0.005, k ≥ 10) we found greater activation in the ventral striatum and MPFC for keep versus sell (Campbell-Meiklejohn et al., 2008; Kuhnen and Knutson, 2005). Neither the ventral striatum nor MPFC activation from the [keep – sell] contrast correlated with the magnitude of the disposition effect (r = −0.23, p = 0.26, and r = 0.24, p = 0.24, for ventral striatum and MPFC, respectively). Even when separated for decisions above and below the purchase price, whole-brain correlation analysis on [keep – sell] and [sell – keep] contrasts revealed no brain regions whose activity significantly correlated with the disposition effect or with participant risk-preference.
Figure 4.

Whole-brain contrast between decisions to sell versus keep. A greater BOLD response was observed in the bilateral insula, DLPFC, and ACC during decisions to sell versus keep an asset (MNI y = 11). This is consistent with past research where participants quit chasing losses, but inconsistent with a realization utility explanation of the disposition effect. Statistical thresholding was set at p < 0.001, k ≥ 57, resulting in a whole-brain FDR< 0.05.
Discussion
The disposition effect is a robust behavioral phenomenon in which individuals hold onto losing assets longer than they hold onto gaining assets. Here, we tested three theories on why people display a disposition effect using an asset-trading task and fMRI: a risk-preference, realized utility, and an irrational belief in mean reversion. We found three pieces of evidence suggesting that a preference-based explanation of the disposition effect does not fully explain the phenomenon. First, we found that a behavioral measure of risk-preference did not correlate with the magnitude of the disposition effect. Second, we found no correlation between measured risk-preference parameters and BOLD response in valuation regions. Third, we found no correlation between the disposition effect and activation in regions previously shown to be correlated with risk attitude, namely the MPFC. Similarly, we did not find a relationship between the disposition effect and differences in keep/sell activations in reward-related brain regions, as would be predicted by differences in realized utility. Instead, our results are more consistent with a mean reversion hypothesis. We show that for decisions below the purchase price, a greater disposition effect is correlated with a blunted ventral striatum response to upticks in value in some individuals. Given the established role of the ventral striatum in signaling reward-prediction errors (RPE) (Pagnoni et al., 2002; Schultz, 2010), this blunted response is consistent with meeting an expectation of an uptick towards the mean.
Behaviorally, our data did not point towards a risk-preference view of the disposition effect. According to this explanation, the disposition effect reflects an asymmetry in risk-preference across gains and losses (Kahneman and Tversky, 1979; Lakshminarayanan et al., 2010). Risk-preference is often measured using choice-based paradigms that estimate utility function curvature (Binswanger, 1980; Holt and Laury, 2002; Tversky and Kahneman, 1992). Often these measurements are tied to individual variation in aspects of financial and non-financial decision-making, suggesting validity in their ability to predict real-world decision-making (Anderson and Mellor, 2008; Barsky et al., 1997). We used a similar choice paradigm that estimated both utility function curvature (risk-preference) and loss aversion (Tanaka et al., 2010). Consistent with past literature, we found that our participants were both risk-averse and loss-averse on average (Tversky and Kahneman, 1992). However, neither curvature of the utility function nor loss aversion correlated with the disposition effect in our task, which builds on evidence that risk attitude is not driving the disposition effect (Vlcek and Wang, 2008).
Our imaging data further suggest that risk-preference does not fully explain the disposition effect. A large body of evidence has demonstrated that a network of brain regions, including the ventral striatum, MPFC, and orbitofrontal cortex (OFC) is closely associated with the economic concept of expected utility and the behavioral concept of reward (Berridge and Robinson, 2003; Delgado, 2007; Knutson et al., 2001; Montague and Berns, 2002; Plassmann et al., 2007). Activity in these regions scale with both the expected and subjective value of stimuli (Kable and Glimcher, 2007; Knutson et al., 2001). Moreover, the ventral striatum and MPFC are not limited to the processing of gains, but they also process expected loss during decision-making (Brooks et al., 2010; Tom et al., 2007). Individual risk-preference is directly related to the subjective valuation (i.e. utility) of potential outcomes during choice. Thus, if risk attitude played a role in our task, we should have found that activity in the aforementioned brain regions was correlated with risk-preference parameters. However, none of the relative activations between keep versus sell decisions were correlated with subject risk-preference in these regions. In addition, there were no brain regions where the BOLD response to delta was correlated with risk-preference. This suggests that subject heterogeneity in risk-preference did not significantly contribute to decisions in our asset-trading task.
In addition to finding no valuation regions that correlated with measures of risk-preference, we found no significant correlation between the magnitude of the disposition effect and activity in these same regions. For example, activity in the ventral MPFC has been found to positively correlate with individual measures of risk seeking when risky decisions are made, while activity in the lateral OFC and dorsal MPFC positively correlates with risk-aversion when less-risky decisions are made (Christopoulos et al., 2009; Tobler et al., 2007; Xue et al., 2009). When we compared risky (keep) versus riskless (sell) decisions below the purchase price, we found no correlation between ventral MPFC, lateral OFC, or dorsal MPFC activity and the disposition effect. We found the same absence of correlation when comparing riskless (sell) versus risky (keep) decisions.
The realization utility theory suggests that investors get a jolt of positive utility when they sell a stock at a gain, and a jolt of negative utility when they sell a stock at a loss (Barberis and Xiong, 2008). In this theory, people want to avoid the pain of negative utility so they hold onto losses, and because they want to receive the pleasure of positive utility they sell gains. This hypothesis would suggest that individual differences in the disposition effect should be correlated with the magnitude of the BOLD response in valuation-related brain regions during the decision to sell versus keep an asset, as others have found (Frydman et al., 2011). In our study, we did not find such correlations. However, if the receipt of realization utility requires the act of completing a successful investing episode (including purchase and sale), it is possible that our experimental design did not capture this because our participants did not have a choice about purchasing the assets (only selling).
Though the aforementioned lack of results supporting alternative hypothesis is not definitive, our results are more consistent with an irrational belief in mean reversion. We found a negative correlation between the magnitude of the disposition effect and the ventral striatum response to upticks in value when the asset price was below the purchase price. This finding is consistent with models of reward prediction error (RPE) in the striatum (Hollerman and Schultz, 1998; O’Doherty et al., 2003; Schultz, 1997) which suggest that the striatum responds only to unexpected upticks in value. In its simplest form, the RPE is computed by taking the difference between the reward received and the reward that was expected. At each period in our task there was a 50/50 probability of an increase or decrease in asset value. Thus, the objective expected value of the asset was always $0. Any uptick in value should therefore result in a positive RPE, and consequently a ventral striatum response, regardless of the total present value of the asset. Although one might predict a decreasing marginal striatal response as the total asset value increases, one would not predict a blunted response to upticks in value when the asset value was negative. Thus, the lack of a striatal response would suggest no RPE, even though the asset had increased in value. Previous neuroimaging studies have shown that the striatal response to reward disappears when the subject can fully predict the reward (Berns et al., 2001; McClure et al., 2003; O’Doherty et al., 2003; Pagnoni et al., 2002). Thus, the lack of striatal response to upticks in value suggests that some subjects with a large disposition effect predicted the uptick when the asset was in the loss domain, implying that they were expecting a return to the mean. Our results build on previous behavioral research that supports an irrational belief in mean reversion (Andreassen, 1988; Vlcek and Wang, 2008; Weber and Camerer, 1998).
Acknowledgments
We thank C. N. Noussair for experimental design input and manuscript feedback and S. E. Moore for help with programming the experiment. Funding was provided by a grant from the National Institute on Drug Abuse (DA024045) through the American Recovery and Reinvestment Act (ARRA).
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Anderson LR, Mellor JM. Predicting health behaviors with an experimental measure of risk preference. Journal of Health Economics. 2008;27:1260–1274. doi: 10.1016/j.jhealeco.2008.05.011. [DOI] [PubMed] [Google Scholar]
- Andreassen PB. Explaining the price-volume relationship: the difference between price changes and changing prices. Organizational Behavior and Human Decision Processes. 1988;41:371–389. [Google Scholar]
- Barberis N, Thaler RH. A Survey of Behavioral Finance. SSRN eLibrary; 2002. [Google Scholar]
- Barberis N, Xiong W. NBER Working Papers. 2008. Realization Utility. [Google Scholar]
- Barberis N, Xiong W. What drives the disposition effect? An analysis of a long-standing preference-based explanation. The Journal of Finance. 2009;64:751–784. [Google Scholar]
- Barsky RB, Juster FT, Kimball MS, Shapiro MD. Preference parameters and behavioral heterogeneity: An experimental approach in the health and retirement study. Quarterly Journal of Economics. 1997;112:537–579. [Google Scholar]
- Berns GS, McClure SM, Pagnoni G, Montague PR. Predictability modulates human brain response to reward. The Journal of Neuroscience. 2001;21:2793–2798. doi: 10.1523/JNEUROSCI.21-08-02793.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berridge KC, Robinson TE. Parsing reward. Trends in neurosciences. 2003;26:507–513. doi: 10.1016/S0166-2236(03)00233-9. [DOI] [PubMed] [Google Scholar]
- Binswanger HP. Attitudes toward risk: experimental measurement in rural India. American Journal of Agricultural Economics. 1980;62:395–407. [Google Scholar]
- Brooks AM, Chandrasekhar PVS, Charles N, Monica CC, BEJ, Berns GS. From bad to worse: striatal coding of the relative value of painful decisions. Frontiers in Neuroscience. 2010 doi: 10.3389/fnins.2010.00176. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Camerer CF, Weigelt K. The Double Auction Market: Institutions, Theories, and Evidence. Addison-Wesley; Reading, MA: 1993. Convergence in experimental double acutions for stochastically lived assets; pp. 355–396. [Google Scholar]
- Campbell-Meiklejohn DK, Woolrich MW, Passingham RE, Rogers RD. Knowing when to stop: the brain mechanisms of chasing losses. Biological psychiatry. 2008;63:293–300. doi: 10.1016/j.biopsych.2007.05.014. [DOI] [PubMed] [Google Scholar]
- Choe H, Eom Y. The disposition effect and investment performance in the futures market. Futures. 2009;29:496–522. [Google Scholar]
- Christopoulos GI, Tobler PN, Bossaerts P, Dolan RJ, Schultz W. Neural correlates of value, risk, and risk aversion contributing to decision making under risk. The Journal of Neuroscience. 2009;29:12574–12583. doi: 10.1523/JNEUROSCI.2614-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Da Costa N, Mineto C, Da Silva S. Disposition effect and gender. Applied Economics Letters. 2008;15:411–416. [Google Scholar]
- Delgado MR. Reward-related responses in the human striatum. Annals Of The New York Academy Of Sciences. 2007;1104:70–88. doi: 10.1196/annals.1390.002. [DOI] [PubMed] [Google Scholar]
- Ferris SP, Haugen RA, Makhija AK. Predicting contemporary volume with historic volume at differential price levels: evidence supporting the disposition effect. The Journal of Finance. 1988;43:677–697. [Google Scholar]
- Frydman C, Barberis N, Camerer CF, Bossaerts PL, Rangel A. Testing Theories of Investor Behavior Using Neural Data. SSRN eLibrary; 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grinblatt M, Keloharju M. What makes investors trade? The Journal of Finance. 2001;56:589–616. [Google Scholar]
- Hollerman JR, Schultz W. Dopamine neurons report an error in the temporal prediction of reward during learning. Nature Neuroscience. 1998;1:304–309. doi: 10.1038/1124. [DOI] [PubMed] [Google Scholar]
- Holt CA, Laury SK. Risk aversion and incentive effects. The American Economic Review. 2002;92:1644–1655. [Google Scholar]
- Hung MW, Yu HY. A heterogeneous model of disposition effect. Applied Economics. 2006;38:2147–2157. [Google Scholar]
- Kable JW, Glimcher PW. The neural correlates of subjective value during intertemporal choice. Nature Neuroscience. 2007;10:1625–1633. doi: 10.1038/nn2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kahneman D, Tversky A. Prospect theory - analysis of decision under risk. Econometrica. 1979;47:263–291. [Google Scholar]
- Kaustia M. Prospect theory and the disposition effect. Journal of Financial and Quantitative Analysis. 2010;45:791–812. [Google Scholar]
- Knutson B, Adams CM, Fong GW, Hommer D. Anticipation of increasing monetary reward selectively recruits nucleus accumbens. The Journal of Neuroscience. 2001;21:RC159. doi: 10.1523/JNEUROSCI.21-16-j0002.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuhnen CM, Knutson B. The neural basis of financial risk taking. Neuron. 2005;47:763–770. doi: 10.1016/j.neuron.2005.08.008. [DOI] [PubMed] [Google Scholar]
- Lakshminarayanan VR, Chen MK, Santos LR. The evolution of decision-making under risk: framing effects in monkey risk preferences. Journal of Experimental Social Psychology. 2010;47:693–689. [Google Scholar]
- McClure SM, Berns GS, Montague PR. Temporal prediction errors in a passive learning task activate human striatum. Neuron. 2003;38:339–346. doi: 10.1016/s0896-6273(03)00154-5. [DOI] [PubMed] [Google Scholar]
- Montague PR, Berns GS. Neural economics and the biological substrates of valuation. Neuron. 2002;36:265–284. doi: 10.1016/s0896-6273(02)00974-1. [DOI] [PubMed] [Google Scholar]
- Noussair C, Matheny K. An experimental study of decisions in dynamic optimization problems. Economic Theory. 2000;15:389–419. [Google Scholar]
- O’Doherty JP, Dayan P, Friston K, Critchley H, Dolan RJ. Temporal difference models and reward-related learning in the human brain. Neuron. 2003;38:329–337. doi: 10.1016/s0896-6273(03)00169-7. [DOI] [PubMed] [Google Scholar]
- Odean T. Are investors reluctant to realize their losses? The Journal of Finance. 1998;53:1775–1798. [Google Scholar]
- Pagnoni G, Zink CF, Montague PR, Berns GS. Activity in human ventral striatum locked to errors of reward prediction. Nature Neuroscience. 2002;5:97–98. doi: 10.1038/nn802. [DOI] [PubMed] [Google Scholar]
- Paulus MP, Rogalsky C, Simmons A, Feinstein JS, Stein MB. Increased activation in the right insula during risk-taking decision making is related to harm avoidance and neuroticism. NeuroImage. 2003;19:1439–1448. doi: 10.1016/s1053-8119(03)00251-9. [DOI] [PubMed] [Google Scholar]
- Plassmann H, O’Doherty J, Rangel A. Orbitofrontal cortex encodes willingness to pay in everyday economic transactions. The Journal of Neuroscience. 2007;27:9984–9988. doi: 10.1523/JNEUROSCI.2131-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Preuschoff K, Quartz SR, Bossaerts P. Human insula activation reflects risk prediction errors as well as risk. The Journal of Neuroscience. 2008;28:2745–2752. doi: 10.1523/JNEUROSCI.4286-07.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schultz W. A Neural Substrate of Prediction and Reward. Science. 1997;275:1593–1599. doi: 10.1126/science.275.5306.1593. [DOI] [PubMed] [Google Scholar]
- Schultz W. Dopamine signals for reward value and risk: basic and recent data. Behavioral and brain functions: BBF. 2010;6:24. doi: 10.1186/1744-9081-6-24. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shefrin H, Statman M. The disposition to sell winners too early and ride losers too long: theory and evidence. The Journal of Finance. 1985;40:777–790. [Google Scholar]
- Tanaka T, Camerer CF, Nguyen Q. Risk and time preferences: linking experimental and household survey data from Vietnam. American Economic Review. 2010;100:557–571. [Google Scholar]
- Tobler PN, O’Doherty JP, Dolan RJ, Schultz W. Reward value coding distinct from risk attitude-related uncertainty coding in human reward systems. Journal of Neurophysiology. 2007;97:1621–1632. doi: 10.1152/jn.00745.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tom SM, Fox CR, Trepel C, Poldrack RA. The neural basis of loss aversion in decision-making under risk. Science. 2007;315:515–518. doi: 10.1126/science.1134239. [DOI] [PubMed] [Google Scholar]
- Tversky A, Kahneman D. Advances in prospect theory: cumulative representation of uncertainty. Journal of Risk and Uncertainty. 1992;5:297–323. [Google Scholar]
- Venkatraman V, Payne JW, Bettman JR, Luce MF, Huettel SA. Separate neural mechanisms underlie choices and strategic preferences in risky decision making. Neuron. 2009;62:593–602. doi: 10.1016/j.neuron.2009.04.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vlcek M, Wang M. Speculating in gains, waiting in losses: an experimental study on the disposition effect. SSRN Working Paper Series 2008 [Google Scholar]
- Weber M, Camerer C. The disposition effect in securities trading: an experimental analysis. Journal of Economic Behavior & Organization. 1998;33:167–184. [Google Scholar]
- Xue G, Lu Z, Levin IP, Weller JA, Li X, Bechara A. Functional dissociations of risk and reward processing in the medial prefrontal cortex. Cerebral Cortex. 2009;19:1019–1027. doi: 10.1093/cercor/bhn147. [DOI] [PMC free article] [PubMed] [Google Scholar]