Condensational Growth of Combination Drug-Excipient Submicrometer Particles for Targeted High Efficiency Pulmonary Delivery: Comparison of CFD Predictions with Experimental Results

Abstract

Purpose

The objective of this study was to investigate the hygroscopic growth of combination drug and excipient submicrometer aerosols for respiratory drug delivery using in vitro experiments and a newly developed computational fluid dynamics (CFD) model.

Methods

Submicrometer combination drug and excipient particles were generated experimentally using both the capillary aerosol generator and the Respimat inhaler. Aerosol hygroscopic growth was evaluated in vitro and with CFD in a coiled tube geometry designed to provide residence times and thermodynamic conditions consistent with the airways.

Results

The in vitro results and CFD predictions both indicated that the initially submicrometer particles increased in mean size to a range of 1.6–2.5 µm for the 50:50 combination of a non-hygroscopic drug (budesonide) and different hygroscopic excipients. CFD results matched the in vitro predictions to within 10% and highlighted gradual and steady size increase of the droplets, which will be effective for minimizing extrathoracic deposition and producing deposition deep within the respiratory tract.

Conclusions

Enhanced excipient growth (EEG) appears to provide an effective technique to increase pharmaceutical aerosol size, and the developed CFD model will provide a powerful design tool for optimizing this technique to produce high efficiency pulmonary delivery.

INTRODUCTION

It is well known that conventional inhalers are inefficient at delivering pharmaceutical aerosols to the lungs. Large depositional losses typically occur in the device and extrathoracic airways. Current in vivo and in vitro studies indicate that characteristic mouth-throat (MT) depositional losses range from approximately 25–60% for HFA pressurized metered dose inhalers (MDIs) (1–5) and from 50– 70% for dry powder inhalers (DPIs) (3,6,7). The deposition of aerosol in the MT region results in wasted medication, increased side effects (8), and high intersubject variability (9).

One promising and cost-effective approach to improve the lung delivery of pharmaceutical aerosols is referred to as controlled aerosol growth. In this method, submicrometer aerosols are delivered at the mouth or nose. The submicrometer size of the aerosol droplets or particles results in substantially less deposition and loss compared with conventional aerosols, which are typically around 2 µm or greater. Increasing the size of the aerosol as it enters and once it is inside the lungs is then used to ensure deposition and full lung retention. In one form, the initially submicrometer aerosol is delivered with a stream of saturated or supersaturated air that is above body temperature. Cooling of the saturated air in the respiratory tract results in water vapor condensation onto the droplets, growth, and enhanced lung deposition. This approach, referred to as enhanced condensational growth (ECG), was first demonstrated by Longest et al. (10) and was shown to be effective for lung delivery in the studies of Hindle and Longest (2) and Tian et al. (11).

A second method to achieve size increase and improved delivery of pharmaceutical aerosols is to formulate combination particles composed of a drug and hygroscopic excipient. This method is suitable for drugs that are inherently hygroscopic or hydrophobic due to the presence of the hygroscopic excipient. High relative humidity naturally occurring in the airways is used to produce hygroscopic growth of the aerosol once it has entered the lungs. Longest and Hindle (12) proposed this approach, referred to as enhanced excipient growth (EEG), and evaluated the size increase of submicrometer aerosols composed of a variety of drug and hygroscopic excipient combinations. Under typical respiratory exposure conditions, large final to initial diameter growth ratios were observed (2.1–4.6) for hygroscopic and non-hygroscopic drugs and a range of excipients.

A number of studies have proposed models of hygroscopic growth for environmental and pharmaceutical aerosols in the airways. Ferron et al. (13) showed that pure sodium chloride particles could increase in size by a factor of approximately 4. Drug aerosols were also shown to increase in size, but growth was variable based on the material considered and occurred to a lesser extent than with conventional salts. Finlay and Stapleton (14) and Finlay (15) showed that two-way coupling significantly limits the size increase of conventional drug aerosols greater than approximately 3 µm. Two-way coupling refers to the effect of the aerosol phase on the surrounding air, as well as the effect of the surrounding air on the aerosol. Considering computational fluid dynamics (CFD) models, Zhang et al. (16) showed that concentrations of sodium chloride greater than 10% by mass were required to influence droplet deposition in the upper airways.

To simulate the ECG approach, Longest et al. (10) considered a 1-D uncoupled model of hygroscopic droplet growth. It was observed that small increases in relative humidity above saturation conditions resulted in large increases in final droplet size. Longest and Hindle (17) then developed a CFD model of ECG in a straight tubular geometry designed to provide a residence time of approximately 0.2 s, which is consistent with the transit time of a droplet from the mouth to the first respiratory bifurcation. Comparisons with concurrent in vitro results indicated that two-way coupling between the aerosol and air phase influenced the final size. Nevertheless, initially submicrometer particles were found to increase in size to above 2 µm. This CFD model was then applied to assess the performance of ECG in an upper tracheobronchial (TB) geometry (2), the entire TB airways (11), and a nasal replica (18).

Relatively few studies have considered the size change of pharmaceutical particles or droplets containing more than one solute. Longest and Kleinstreuer (19) considered the evaporation of 12 component droplets containing volatile and semi-volatile compounds and showed that adequate agreement with experimental results could be achieved using Raoult’s law to define surface vapor pressures. Longest and Hindle (12) considered the growth of combination drug and hygroscopic excipient aerosols using a coupled 1-D model of well mixed droplets. Two-way interactions between the aerosol, air, and wet walls of the respiratory tract were considered. Results of this model matched concurrent in vitro experiments of final aerosol size exiting a tubular geometry with a residence time of 0.2 s. However, this 1-D model cannot be used to predict aerosol deposition in the complex extrathoracic, tracheobronchial, and alveolar airways. In order to predict the effectiveness of EEG delivery and optimize performance, a CFD model of hygroscopic growth for combination-particle aerosols is needed.

The objective of this study was to investigate the growth of combination drug and excipient submicrometer aerosols generated from different sources using both in vitro experiments and a newly developed CFD model. Submicrometer combination drug and excipient particles were generated using both the benchtop capillary aerosol generator (CAG) (17,20) and the commercially available handheld Respimat inhaler (21,22). Growth was evaluated in a coiled tube EEG geometry with wet walls designed to provide a residence time consistent with a typical inhalation cycle (approximately 2 s). Model predictions of size increase after passage through the test geometry were compared with in vitro results. In the model, both one-way and two-way interactions were considered between the discrete and continuous phases. The CFD predictions were then used to characterize the rate of particle size increase that occurs with EEG over a 2 s exposure period. Finally, CFD predictions of size change along with experimental results were compared with the multicomponent aerosol growth correlations previously proposed by Longest and Hindle (12) for conditions in the respiratory airways.

MATERIALS AND METHODS

Experimental Overview

The growth of combination submicrometer aerosols was considered with initial drug to excipient mass ratios of 50:50 in a model EEG geometry. A non-hygroscopic drug was selected, budesonide, in order to ensure that the observed growth arises entirely from the inclusion of the hygroscopic additive. Three hygroscopic excipients were considered, which were a representative salt (sodium chloride; NaCl), a weak acid (citric acid; CA), and a sugar (mannitol, MN). Based on the previous study of Longest and Hindle (12), NaCl should provide the most growth followed by CA and MN. Budesonide was considered in combination with each of the hygroscopic excipients and combination particle aerosols were generated using the benchtop CAG platform. To test the EEG concept applicability using a second aerosol generation method, budesonide and CA combination particle aerosols were generated using the handheld Respimat inhaler. Growth was determined as both the final geometric diameter achieved as well as the growth ratio of geometric particle diameters based on both the in vitro results and numerical predictions. Computational and experimental growth ratios were also compared with the algebraic correlations developed by Longest and Hindle (12).

EEG Test Geometry and Boundary Conditions

To determine the aerosol size of combination drug and excipient particles at the end of an inhalation cycle, an EEG test geometry was developed that provided a mean 2.4 s residence time during which the aerosol was exposed to airway thermodynamic conditions. This time period was considered physiologically representative of the inhalation portion of a breathing cycle for typical pharmaceutical aerosols. Size increase within the EEG geometry was evaluated both experimentally and using CFD simulations. A coiled tube configuration was selected in order to provide the required residence time in a compact design that could be enclosed in an environmental chamber to control the temperature and humidity. A sufficiently large diameter of the tubing was required to prevent deposition of the larger droplets as the aerosol passed through the geometry prior to entering the cascade impactor for sizing. The coiled tube model is displayed in Fig. 1 and is composed of ventilator tubing with an internal diameter of 22 mm wrapped around a 35.6 cm (14 inch) support structure. Separate aerosol and humidity streams entered the growth tube inlet through a dual flow mouthpiece, previously introduced by Hindle and Longest (2). A bend in the tubing with a 20 cm radius of curvature was included at the outlet (Fig. 1), which in the experiments was used to connect the coil to the Andersen cascade impactor (ACI) for aerosol sizing. In practice, the EEG approach relies on the natural humidity in the lungs to foster aerosol size increase. However, a source of external relative humidity was included in this study to maintain constant thermodynamic conditions within the passive EEG geometry over the time course of the experiments. This humidified airstream was supplied from a modified compressed air-driven humidifier system (Vapotherm 2000i, Stevensville, MD) which was able to control temperature within±0.08°C at 37.6°C.

Fig. 1.

Coiled tube geometry for evaluating the growth of combination drug-excipient submicrom-eter particles over a residence time of approximately 2.4 s. The walls of the geometry were wetted before the experiment and supplemental humidified air was supplied to maintain saturation conditions within the model.

Boundary conditions in the CFD model were set to match the experimental setup for the two aerosol generation methods considered. Inlet conditions for the CAG and Respimat inhalers are provided in Table I. For the CAG system, the humidity inlet was characterized by a steady state flow rate of 27 L/min. To produce a submicrometer aerosol, the CAG platform was actuated into a 900 ml drying chamber. Air from this chamber was pulled into the EEG geometry at 1 L/min over a period of approximately 2 min. The Respimat inhaler was also actuated into the 900 ml drying chamber to produce a submicrometer aerosol. To better approximate bolus aerosol delivery with the Respimat inhaler, air from the chamber was pulled into the EEG geometry at a flow rate of 14 L/min over a period of approximately 5 s. To determine aerosol number concentrations, a condensation particle counter (CPC 3022A, TSI Inc, Shoreview, MN) was used at the outlet of the EEG geometry, where the coiled tube connected to the ACI. The CPC was operated in high flow mode (5 L/min) with a sampling frequency of 1 s. The mean aerosol number concentration reported in Table I for the CAG was based on individual aerosol concentration measurements during the first 30 s following actuation, which accounted for 80% of the aerosol mass delivered to the impactor. In contrast, the condensation particle counter had an insufficiently short sampling time (sampling frequency = 1 s) to accurately capture the concentration of the rapid bolus delivery with the Respimat inhaler. Instead, the number concentration of the Respimat aerosol was estimated analytically based on the delivery of a 15 µL liquid solution, an initial mass median aerodynamic diameter of 5.3 µm, and a delivery period of 1.5 s, as reported by Longest and Hindle (22).

Table I.

Inlet Conditions for the Two Submicrometer Particle Generation Methods

Aerosol generation method	CAG	Respimat
Humidity inlet
Flow rate (L/min)	27	14
Temperature (°C)	37.6	37.6
Relative humidity (%)	99.0	99.5
Vapor mass fraction (Yv)	0.0392	0.0394
Concentration (part/cm3)	NA	NA
Aerosol inlet
Flow rate (L/min)	1	14
Temperature (°C)	31.0	23.0
Relative humidity (%)	63.1	45.0
Vapor mass fraction (Yv)	0.0173	0.00769
Concentration (part/cm3)a	1.4 × 107	5.5 × 105

^aEstimated for the aerosol inlet

To model the experimental boundary conditions, a wall temperature of 37.6°C and relative humidity (RH) of 100% were assumed. Some evaporation and condensation in the initial section of the EEG geometry may result in wall temperature fluctuations. However, these differences are expected to be small as temperature gradients are quickly dissipated compared with the total residence time of the aerosol. In the CFD model, a straight section of tubing was included after the final curvature to prevent recirculating flow from crossing the outlet plane. However, the final droplet size was assessed in the model at the position of the ACI inlet just after the final curvature.

Experimental Design

For the CAG, aerosols were generated from a solution vehicle of 50% ^w/_w water and 50% ^w/_w ethanol containing 0.4% ^w/_v budesonide and 0.4% ^w/_v hygroscopic excipient. The excipients employed were NaCl, CA and MN. The capillary aerosol generation system is described and considered in detail by the previous studies of Hindle et al. (20) and Longest et al. (23). Aerosols were generated using a solution mass flow rate of 10 mg/s for 2 s into a 900 ml spacer chamber and sampled into the EEG tubing geometry via the dual flow mouthpiece at 1 L/min as described above. The total flow in the EEG geometry was 28 L/min following the addition of heated humidified air at 27 L/min (Table I).

For Respimat aerosol generation, aerosols were generated from a solution vehicle of 10%^w/_w water and 90% ^w/_w ethanol containing 0.4% ^w/_v budesonide and 0.4% ^w/_v CA. The solution formulation was loaded into an empty formulation canister and the Respimat inhaler was primed to waste. A single actuation from the Respimat inhaler was fired into a 900 ml spacer chamber and sampled into the EEG test geometry via the dual flow mouthpiece at 14 L/ min. The total flow in the EEG geometry was 28 L/min following the additional of heated humidified air at 14 L/ min (Table I).

The EEG test geometry was placed in a controlled temperature environment (Espec, Hudsonville, MI) and supplied with humidified air through the dual flow mouthpiece at nominal conditions of 37°C and 99% RH to maintain simulated respiratory conditions. Walls of the growth section were pre-wetted to simulate the wet walled conditions of the respiratory tract, which stimulates aerosol growth. The outlet of the EEG geometry was connected to the inlet of the Andersen cascade impactor (Graseby-Andersen Inc, Smyrna, GA) operated at a flow rate of 28 L/min to determine the size distribution of the droplets following exposure to humidified conditions.

The initial size distributions of the aerosols as they exited the spacer chamber were also determined using the ACI with airflow conditions identical to those used during the EEG experiment. Aerosols were sampled directly from the dual flow mouthpiece into the ACI operated at 28±2 L/min and maintained at 25°C by placing it in the environmental chamber. For the CAG experiment, the aerosol was sampled at 1 L/min from the spacer chamber via the aerosol inlet of the dual flow mouthpiece. Additional air (45–55% RH and 25°C) at 27 L/min was delivered to the impactor via the humidified air inlet of the dual flow mouthpiece. Similarly for the Respimat experiment, aerosol was sampled at 14 L/min from the spacer chamber via the aerosol inlet of the dual flow mouthpiece. Additional air (>90% RH and 25°C) at 14 L/min was delivered to the impactor via the humidified air inlet of the dual flow mouthpiece

The temperature and humidity of the humidified air and the temperature of the aerosol mixture stream at the inlet to the EEG test geometry were measured in separate experiments. These measurements were performed using the Humicap Handheld Meter (HMP75B, Vaisala, Helsinki, Finland) positioned at the mid-plane of the tubing and a sheathed Type K thermocouple (Omega Engineering Corp., Stamford, CT) positioned at the mid-plane of the tubing. The Humicap Handheld Meter has a stated temperature accuracy of ±0.2°C (at 20°C) and ±0.25°C (at 40°C). It has a RH accuracy of ±1.7% (at 20°C) and ±1.8% (at 40°C) between 90% and 100% RH. The probe was factory calibrated using traceable standards and supplied with a NIST calibration certificate. The probe was housed in a plastic filter and incorporated a sensor pre-heater which was employed to prevent condensation during equilibration prior to measurement. Due to the equilibrium time required for the humidity probe, the RH of the aerosol stream entering the geometry was established analytically based on the mass of injected liquid, temperature, and air flow rate (Table I).

For both the initial and final particle size distributions, following aerosol generation, washings using appropriate volumes (5–25 ml) were collected from the impaction plates to determine the drug deposition. A 1:1 admixture of methanol and deionized water was used, and the solutions were then assayed using validated HPLC-UV methods for budesonide. The mass of budesonide on each impaction plate was determined and used to calculate both the initial and final aerodynamic particle size distributions of the drug and combination aerosols. Aerosol particle size distributions were reported as mass distribution recovered from the impactor. The mass median aerodynamic diameter (MMAD) was defined as the particle size at the 50th percentile on a cumulative percent mass undersize distribution (D50) using linear interpolation. At least four replicates of each experiment were performed.

Continuous Phase Simulations

For the coiled tube geometry of interest, the Reynolds number ranges from 60 at the CAG aerosol inlet to 1,700 once the flow streams are combined. Considering the presence of coaxial jet flow, the combination of two flow streams, and curvilinear streamlines, laminar through turbulent conditions are expected for this range of Reynolds numbers. To resolve these multiple flow regimes, the low Reynolds number (LRN) k–ω model was selected based on its ability to accurately predict pressure drop, velocity profiles, and shear stress for transitional and turbulent flows (24,25). The conservation of mass and momentum equations used with the LRN k–ω model are available from Wilcox (25) and were previously reported by Longest and Xi (26). Similarly, the equations governing turbulent kinetic energy (k) and specific dissipation rate (ω) were also reported by Longest and Xi (26).

Considering heat and mass transfer, the governing convective-diffusive equations were previously reported by Longest and Hindle (17). These expressions include turbulent dispersion terms, with the turbulent Schmidt and Prandtl numbers equal to 0.9 (27). A water vapor source term was included in the mass transfer relation to account for the increase (or decrease) of water vapor during evaporation (or condensation) when simulating two-way coupling. Similarly, a continuous phase energy source (or sink) term was included in the energy equation to account for the presence of the disperse phase.

To evaluate droplet condensation and evaporation, cases with one-way or two-way interactions with the continuous phase were considered. In one-way coupling, condensation and evaporation at the droplet surface do not affect the continuous phase. This assumption is valid if the droplet concentration is sufficiently dilute such that water gain or loss from the continuous phase can be neglected. In addition to the effect of the surrounding conditions on the droplets, two-way coupling considers the effect of the droplets on the continuous phase. Evaporation or condensation at the droplet surface results in mass and energy sources or sinks in the continuous phase. Further details on the simulation of two-way coupled flow fields during droplet evaporation and condensation are provided in Longest and Hindle (17).

Discrete Phase Simulations

Based on previous experiments, mean aerosol sizes from 500 nm to greater than 3 µm are expected in the current EEG system (12). The associated polydisperse aerosol distributions can range from 200 nm through approximately 6 µm. To address this broad range of aerosol sizes and to accommodate the calculation of aerosol evaporation and condensation, a Lagrangian particle tracking method was employed (28,29). The Lagrangian transport equations can be expressed

$$\frac{d{\upsilon }_i}{dt}=\frac{f}{{\tau }_p}(u_i-{\upsilon }_i)+g_i(1-\alpha )+f_{i,\mathit{\text{Brownian}}}$$ (1)

and

$$\frac{d{x}_i}{dt}={\upsilon }_i(t)$$ (2)

Here υ_i and u_i are the components of the particle and local fluid velocity, g_i denotes gravity, and α is the ratio of mixture to droplet density ρ/ρ_d. The characteristic time required for a particle to respond to changes in fluid motion, or the particle relaxation time, is expressed as ${\tau }_p={\mathrm{C}}_{\mathrm{c}}{\rho }_d{d}_d^2/18\mu$, where C_c is the Cunningham correction factor for submicrometer aerosols based on the expression of Allen and Raabe (30), d_d is the variable droplet diameter, and µ is the absolute viscosity. The pressure gradient or acceleration term for aerosols was neglected due to small values of the density ratio (28). The drag factor f, which represents the ratio of the drag coefficient to Stokes drag, is based on the expression of Morsi and Alexander (31). The effect of Brownian motion on the trajectories of submicrometer particles has been included as a separate force per unit mass term at each time-step (29).

To model the effects of turbulent fluctuations on droplet trajectories, a random walk method was employed (32–34). While deposition is not the focus of this study, a near-wall anisotropic correction to turbulent particle dispersion was also included (23,35).

The droplet evaporation and condensation model employed in this study is similar to previous approximations for salts (36–38) and multicomponent aerosols (17,19,39,40). The heat and mass transfer relations for multicomponent hygroscopic droplets in the respiratory airways were previously reported by Longest and Xi (26). This model employs a rapid mixing approach, which assumes conditions inside the droplet are constant and gradients are negligible compared with gradients in the air phase. The droplet model accounts for interdependent heat and mass transfer, which results in droplet heating during condensation and cooling during evaporation as a function of the surrounding temperature. Mass and heat fluxes at the droplet surface are modified for non-continuum effects using the Knudsen correlation (41,42). Blowing velocity effects were also considered (26).

Considering particle and droplet properties, the densities of the multicomponent droplets are calculated as

$${\rho }_d=(m_w+m_{\mathit{\text{drug}}}+m_{ex})\left(\frac{{\rho }_w}{m_w+\frac{m_{\mathit{\text{drug}}}{\rho }_w}{{\rho }_{\mathit{\text{drug}}}}+\frac{m_{ex}{\rho }_w}{{\rho }_{ex}}}\right)$$ (3)

In this expression, m and ρ are the masses and densities of water (w), drug, and hygroscopic excipient (ex). The mass fraction of water vapor on the droplet surface is a critical variable, which is significantly influenced by both temperature and drug concentration. For a combination particle of soluble drug and excipient, γ_υ,surf is calculated as

$${\gamma }_{\upsilon ,surf}=\frac{SK{P}_{\upsilon ,sat}(T_d)}{{\rho }_{air}{R}_{\upsilon }{T}_d}$$ (4)

where P_υ,sat (T_d) is the temperature dependent saturation pressure of water vapor, calculated from the Antoine equation (43), and R_v is the gas constant of water vapor. The influence of the Kelvin effect on the droplet surface concentration of water vapor is expressed as

$$K=\text{exp}\left[\frac{4\sigma (T_d)}{d_d{\rho }_d{R}_{\upsilon }{T}_d}\right]$$ (5)

where σ(T_d) is the temperature dependent surface tension of the droplet. In Eq. 4, the water activity coefficient, S, describes how dissolved molecules affect the surface concentration of water vapor, i.e., the hygroscopic effect, and can be expressed as

$$S={\left(1+\frac{i_{drug}{\chi }_{drug}+i_{ex}{\chi }_{ex}}{{\chi }_w}\right)}^{-1}$$ (6)

for a drug and hygroscopic excipient combination particle where χ represents the mole fraction of each component. The i coefficients account for the effect of molecular dissociation during dissolution and are sometimes referred to as van’t Hoff factors. The i values of the solutes were previously determined by Longest and Hindle (12) for use in Eq. 6. At high concentrations of drug and excipient, the available water may not be sufficient to dissolve all of the material. In these cases, χ_drug and χ_ex are replaced by the mole fraction solubility limits of each compound in water. This approach assumes an initial droplet model of a solid core of un-dissolved material surrounded by a layer of liquid with a saturated concentration of each solute. This representation persists until there is enough water to fully dissolve the drug and excipient. In either case, the mole fraction of water in the droplet is calculated as

$${\chi }_w=1-{\chi }_{drug}-{\chi }_{ex}$$ (7)

Numerical Solution

To solve the governing mass and momentum conservation equations in each of the cases considered, the CFD package Fluent 12 (ANSYS, Inc.) was employed. User-supplied Fortran and C programs were used for the calculation of initial flow and droplet profiles, hygroscopic droplet evaporation and condensation, near-wall anisotropic turbulence approximations, near-wall particle interpolation (29), Brownian motion (29), as well as heat and mass sources and sinks during two-way coupling. All transport equations were discretized to be at least second order accurate in space. For the convective terms, a second order upwind scheme was used to interpolate values from cell centers to nodes. The diffusion terms were discretized using central differences. To improve numerical accuracy, hexahedral grids were employed (44,45). Grid converged results based on negligible change in the velocity and temperature fields (< 1%) as well as negligible differences in the outlet droplet size (< 5%) were established for a mesh consisting of 460,000 control volumes. It is estimated that a similar resolution of the flow field would require approximately one order of magnitude more tetrahedral control volumes (44,45).

For the one-way coupled solution, particle trajectories were calculated within the steady flow fields of interest as a post-processing step. The integration scheme employed to solve Eq. 1 and Eq. 2 was based on the Runge–Kutta or implicit method (depending on particle size) with a minimum of 20 integration steps in each control volume. An error control routine was also employed to actively adapt the particle time-step and maintain sufficient accuracy bounds (28). Doubling the number of integration steps within each control volume had a negligible (less than 1%) effect on cumulative particle deposition and growth values.

For the two-way coupled solutions, steady state flow fields were again assumed. Inlet droplet concentrations as described previously of 1.4 × 10⁷ and 5.5 × 10⁵ part/cm³ for the CAG and Respimat inhaler, respectively, were considered to enter the geometry at the aerosol inlet (Table I). The number of continuous phase iterations to discrete phase updates was set at 100. Doubling and halving this value had a negligible impact on the final aerosol size predicted. The coupled simulation was continued through 2,000 continuous phase iterations resulting in a minimum of 20 discrete phase updates. Convergence was determined based on mass, momentum and energy residuals below 1×10⁻⁵. Decreasing this convergence criterion by an order of magnitude and increasing the number of continuous phase iterations by a factor of two had a negligible impact on the results. In each size bin, 1,000 computational droplets were simulated resulting in 9,000 total trajectories for each combination particle considered. Increasing the number of droplets simulated in each bin by a factor of 10 had a negligible impact on the predicted final particle sizes (< 3%).

RESULTS

Initial budesonide particle size distributions based on measurements with the ACI are presented in Fig. 2 for both the CAG and Respimat aerosols. The measured mass median aerodynamic diameters (MMADs) and standard deviations (SDs) for budesonide in combination particles generated with NaCl, CA and MN using the CAG were 750 (SD=33) nm, 590 (97) nm, and 900 (84) nm, respectively. The MMAD of budesonide in combination particles generated with CA using the Respimat was 850 (88) nm. Based on analytical estimates, there was sufficient mass transfer potential in the spacer to allow for complete drying of the droplets. As a result, the initial aerosols were assumed to consist of dry particles for each case. Inaccuracies created by this assumption will be evaluated by comparisons of growth predictions with experimental measurements. That is, some water remaining in the initial particles will result in a reduced hygroscopic potential such that experimental growth values will be less than predicted with the CFD model for dry particles. Assuming dry particles consisting of 50:50 drug:excipient mass ratios, the densities of the combination budesonide particles with NaCl, CA, and MN excipients are 1,367, 1,249, and 1,196 kg/m³, respectively. The resulting initial mean geometric diameters (d_o) for the CAG and Respimat combination particle aerosols are provided in Table II. It is noted that the CFD results of this study are reported in terms of geometric diameters.

Fig. 2.

Aerodynamic size distribution of the initial aerosols from the CAG and Respimat inhalers based on measurements in the ACI. Midpoint diameters are based on the 9 stages of the ACI operated at approximately 30 L/min.

Table II.

Comparison of Experimental and CFD-predicted Growth Characteristics of Combination Particles

Method	Excipienta	Intial diameter do (µm)b	Experimental final diameter (µm)b	CFD final diameter one-way coupled (µm)c	CFD final diameter two-way coupled (µm)c
CAG	NaCl	0.641 (0.03)d	2.51 (0.22)d	3.02	2.31e
CAG	CA	0.527 (0.1)	1.6 (0.23)	1.70e	1.45e
CAG	MN	0.823 (0.08)	2.1 (0.1)	2.18e	2.09e
Respimat	CA	0.760 (0.08)	2.1 (0.32)	2.15e	2.08e

^aA drug (budesonide) to excipient mass ratio of 50:50 was used in all cases

^bExperimentally measured MMADs were converted to mean geometric diameters using particle density

^cGeometric diameters

^dValues representing experimental standard deviations (SD) are reported in parentheses

^eCFD predictions within +/− one SD of the experimental value

Relative humidity values in the EEG geometry following aerosol generation with the CAG are displayed in Fig. 3 for both one and two-way coupled simulations. In both cases, RH rapidly increases to approximately 98% and then gradually increases to within the range of 99–100%. As a result, the coiled tube configuration provides stable near-saturated conditions for aerosol growth. Furthermore, the occurrence of near-saturated conditions through a majority of the tube coupled with a residence time of approximately 2.4 s provides a reasonable estimate of physiological conditions within the respiratory tract. Figure 3b illustrates the effects of two-way coupling for the case of the budesonide:NaCl aerosol from the CAG. For this case, a small reduction in RH values is observed due to the accumulation of water vapor on the discrete phase. However, RH values remain within the range of 99– 100% for a majority of the geometry. The effect of this reduction in available water vapor on the final aerosol size will be evaluated by considering droplet trajectories. Little visible difference was observed between the one and two-way coupled solutions for the budesonide:CA and budesonide:MN aerosols. As a result, contour plots for these cases are not shown but are consistent with Fig. 2a. These small differences are likely because the CA and MN combination particles are less hygroscopic than the NaCl combination particles (12) and, therefore, reduce the available water vapor by only a small amount. Similarly, negligible visible differences were observed between the one and two-way coupled RH fields for the Respimat budesonide:CA combination particle aerosol.

Fig. 3.

Relative humidity conditions for the CAG system based on (a) one-way coupled and (b) two-way coupled approximations. The two-way coupled approximation displayed in panel (b) is for the case of budesonide with NaCl. All other fully coupled results produced negligible RH differences compared with the one-way coupled case.

Initial and final geometric diameters based on the in vitro experiments and CFD simulations are compared in Table II. Considering the one-way coupled model, all predictions are within one standard deviation of the experimental results except for the CAG aerosol with budesonide:NaCl particles. Including two-way coupling in the model results in all predictions falling within one standard deviation of the experimental data. Moreover, all CFD predictions of final size are within a 10% relative error of the experimental values. As a result, the CFD model appears to provide excellent agreement to the experimental predictions of final aerosol size in this test system.

To visualize the particle characteristics during transit through the EEG geometry, particle trajectories colored according to geometric diameter during hygroscopic growth are illustrated in Fig. 4 for the CAG delivery system and all drug:excipient combinations considered. Panels in the left and right columns represent one and two-way coupled simulations, respectively. In all cases, gradual growth of the droplets is observed to occur starting with the initial submicrometer sizes and continuing through final sizes greater than a minimum of approximately 1.5 µm. As expected, the budesonide:NaCl combination particles are the most hygroscopic resulting in a final size of 3.0 µm for the one-way coupled model. From the study of Longest and Hindle (12), CA combination particles should achieve more growth than the MN combination particle aerosol based on the hygroscopic potentials of these excipients. However, the budesonide:CA combination particles had a smaller initial mean size (d_geo=527 nm) compared with the budesonide: MN combination particles (d_geo=823 nm). As a result, the one-way coupled final diameter predictions for the CA and MN excipients were 1.70 and 2.18 µm, respectively. Considering two-way coupling, a large effect on final size is observed for the budesonide:NaCl aerosol with the final geometric diameter reduced from 3.02 to 2.31 µm (Fig. 4a vs. b). In contrast, much smaller reductions are observed for the CA (1.7 vs. 1.45) and MN (2.18 vs. 2.09) cases.

Fig. 4.

Particle trajectories colored according to diameter for (a and b) budesonide:NaCl, (c and d) budesonide:CA, and (e and f) budesonide:MN. Left and right panel columns represent one-way and two-way coupled calculations, respectively. For all cases considered, growth appears to occur through a majority of the flow domain with diminishing size increase near the outlet. Coupling effects are greatest for the case of the budesonide:NaCl aerosol and negligible for the budesonide:MN combination.

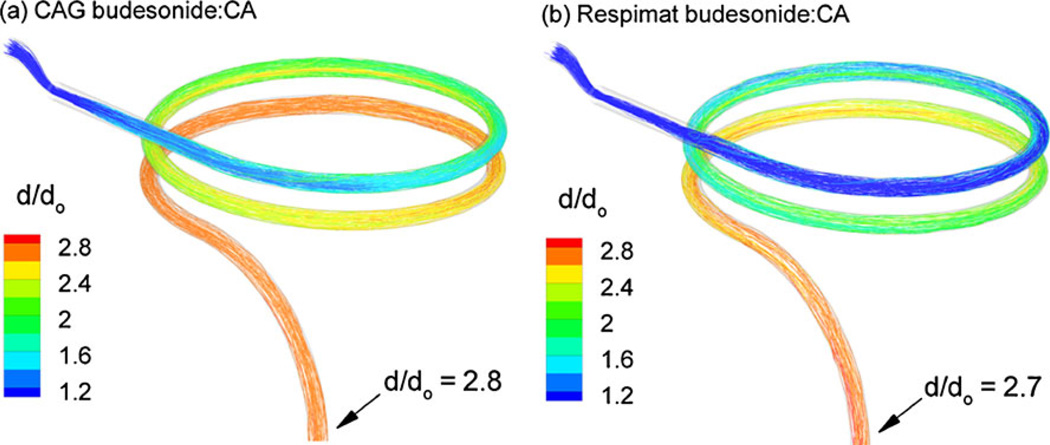
A comparison of trajectories for the CAG and Respimat systems is presented in Fig. 5 in terms of final to initial geometric diameter ratios. For both aerosol generation methods, the budesonide:CA combination particles were compared using the two-way coupled results. The initial geometric diameters for the CAG and Respimat systems were 527 nm and 760 nm, respectively. Adjusting the aerosol inlet number concentrations of both cases to conditions in the combined flow stream results in n_CAG=5.0×10⁵ part/cm³ and n_Respimat=2.75×10⁵ part/cm³. Based on the trajectories, growth occurs somewhat slower for the Respimat aerosol, likely due to the larger amount of ambient air pulled into this system. Based on the finding that two-way coupling does not appreciably affect growth for the budesonide:CA combination particle aerosol produced by the CAG, differences in number concentration are likely a small factor. Despite slower growth for the Respimat system, the outlet growth ratio is nearly equivalent to that observed for the CAG inhaler (2.7 vs. 2.8). As a result, it appears that very similar growth performance can be achieved with the Respimat inhaler, which delivered the dose as a short 1.5 s bolus, compared with the continuous extended delivery mode employed with the CAG aerosol.

Fig. 5.

Particle trajectories contoured based on diameter growth ratio for the budesonide:CA aerosol generated using the (a) CAG and (b) Respimat inhaler. The bolus delivery of the Respimat inhaler appears to reduce the growth ratio by a negligible amount.

Final to initial diameter growth ratios are presented in Fig. 6 for all aerosols considered based on the experiments and CFD models. As observed with outlet diameters, the diameter growth ratios for one-way coupled models agree very well compared with the experimental results with the exception of the budesonide:NaCl combination particle aerosol. For this case, accounting for two-way coupling improves agreement between the model and experiment. In general, growth ratios of approximately 3 and greater were achieved for budesonide:NaCl and budesonide:CA combination particle aerosols generated using the CAG. Growth ratios just below three are observed for the budesonide:MN combination particles generated using the CAG and for the budesonide:CA combination particles generated by the Respimat. These growth ratios are expected to be sufficient to increase the diameter of initially submicrometer particles to values that will ensure full lung retention of the aerosol.

Fig. 6.

Diameter growth ratios based on experimental results compared with CFD predictions using the one-way and two-way coupled modeling approaches for both CAG and Respimat aerosols. Agreement with the experiments is only improved using the fully coupled model for the budeso-nide:NaCl aerosol. In all other cases, the one-way coupled model provides a good estimate of the experimental result that is inside the range of one experimental standard deviation.

Longest and Hindle (12) proposed correlations for the growth of drug:excipient aerosols in a model of the respiratory airways. Results of the current study are compared with the algebraic correlations of Longest and Hindle (12) in Fig. 7. These correlations predict final to initial diameter growth ratios as a function of growth coefficients (GCs), which account for the hygroscopic growth potential of the drug and excipient as well as the initial makeup of the particle or droplet. Results of the current study are compared with growth correlation Eq. 23 from Longest and Hindle (12) in Fig. 7a, which neglects two-way coupling. As expected, Eq. 23 provides a good estimate of the experimental and coupled CFD results for MN and CA (first and second data points), but over predicts growth of NaCl. In contrast, Eq. 27 from Longest and Hindle (12), which includes the effects of two-way coupling, provides excellent agreement with the experiments and all coupled CFD predictions (Fig. 7b). These comparisons indicate that the correlations proposed by Longest and Hindle (12) can accurately predict growth in the EEG coiled tube system used in the current study. Conversely, the growth tube configuration provides an approximate representation of aerosol size increase in the respiratory airways, as modeled in the previous study of Longest and Hindle (12).

Fig. 7.

Comparison of growth ratios determined using the experiments and CFD models with algebraic correlations (a) Eq. 23 and (b) Eq. 27 from Longest and Hindle (12). Relatively good agreement is observed in comparison with Eq. 23, which neglects two-way coupling. Improved agreement is observed for the fully coupled CFD and experimental results with Eq. 27, which does account for two-way coupled growth. It is concluded that the previously developed algebraic correlations can adequately predict aerosol size change for combination drug:excipient submicrometer particles over standard inhalation periods.

DISCUSSION

In summary, the condensational growth of initially submicrometer particles composed of a drug and a hygroscopic excipient in a saturated environment that was thermodynamically consistent with the respiratory airways was explored using in vitro experiments and a newly developed CFD model. Two methods of generating submicrometer aerosols were tested. With the first method, the aerosol was produced using the CAG and the dose was delivered over a period of approximately 2 min from a spacer chamber, which is consistent in delivery time with standard nebulizer operation. The second method of aerosol generation was a commercially available handheld softmist inhaler, the Respimat. In this example, a spacer chamber was employed to ensure that the particles were dry following aerosol generation from a formulation that consisted of drug and excipient dissolved in an 90/10 (%^w/_w) ethanol/water solution. The aerosol was delivered to the EEG test geometry over the time period of approximately one inhalation cycle. In both cases, size increase was evaluated in a heated and humidified coiled tube geometry that provided a transit (or humidity exposure) time consistent with approximately one inhalation cycle (~ 2.4 s). In vitro experimental results indicated that the budesonide:NaCl, budesonide:CA, and budesonide:MN combination particles all increased from submicrometer size to final mean diameters ranging from 1.6 to 2.5 µm. The CFD predictions of final aerosol size matched the in vitro results to within a 10% relative error for all drug:excipient combinations. The simulation of two-way coupling was only required to accurately match the budesonide:NaCl combination, which displayed the largest growth ratio (i.e., d/d_o=3.9). Otherwise, the much simpler one-way coupled approximation was sufficient. Both the CFD model and in vitro results indicated final to initial diameter growth ratios of around 3 and above for the combination particles from both generation platforms. Finally, the growth results of this study closely matched predictions from the correlations proposed by Longest and Hindle (12), which included a similar transit time through the model but were based on a more exact representation of the respiratory airways.

One finding of this study is that a combined user-developed and commercial CFD code implementing a number of simplifying assumptions can accurately predict the growth of combination drug and excipient aerosols from initially dry particles to dilute droplets over an extended exposure period. This growth process is physically complex involving a hydrophobic drug and hygroscopic excipient, initially saturated multicomponent solutions, coupled droplet heat and mass transfer, and coupled heat, mass, and momentum transfer with the surrounding three-dimensional continuous phase and wall boundaries. Furthermore, small changes in the continuous phase temperature and RH fields are known to produce large changes in the final droplet sizes (26). Despite these complexities, the CFD model accurately (within 10%) predicted the final size of the polydisperse aerosol obtained in the concurrent experiments.

In developing the CFD model, one critical question is whether two-way coupling affects the final aerosol size obtained. Finlay (15) developed a set of non-dimensional parameters that can be used to predict when two-way coupling should be considered and when it can be neglected depending on a number of factors including aerosol number concentration and thermodynamic conditions. These expressions were previously shown to be predictive of coupling effects, specifically for ECG delivery with variable degrees of supersaturation in the airways (10, 17). As an alternative to these expressions, it is observed that with EEG delivery the RH and temperature are consistent with airway conditions (99.5% RH and 37°C). Under these conditions, results indicate that two-way coupling becomes important as size increases to near 3 µm and above for the aerosol concentrations considered in this study (~ 5×10⁵ part/cm³). Therefore, as a general observation, one-way coupling can be assumed for final sizes less than or equal to approximately 2.5 µm and two-way coupling is needed for larger diameters with particle concentrations of approximately 5×10⁵ part/cm³ and EEG delivery. More refined estimates of coupling can be assessed using the non-dimensional analysis of Finlay (15), the growth correlations of Longest and Hindle (12), or comparisons of CFD predictions.

Figure 7 demonstrates that the results of both the experiment and two-way coupled simulations match the growth correlations predicted by Longest and Hindle (12) very well. The previous study by Longest and Hindle (12) validated the numerical model results using a short duration of particle exposure to humidity (~ 0.2 s). The validated numerical model was then applied to conditions consistent with airway exposure including appropriate airway diameters and inhalation times. The experimental results of the current study help to validate the numerical model and resulting growth correlation of Longest and Hindle (12) by considering an extended exposure time (Fig. 7). In contrast, the coiled tube conditions used in the setup are not geometrically similar to the respiratory airways. With EEG, a majority of size increase is experienced in the lower airways where diameters are much smaller compared to the coiled tube configuration. As a result, more growth will occur in the actual respiratory tract and the coiled tube represents a conservative model of size increase. Nevertheless, comparisons between this study and the correlations of Longest and Hindle (12) indicate a very good match of predicted diameter growth ratios. This finding indicates that the EEG test geometry is sufficient to capture the thermodynamic growth conditions of the airways. However, more realistic computational and experimental models are needed to accurately capture deposition as growth occurs within the respiratory tract.

The CFD simulations and resulting particle trajectory pathlines reveal interesting characteristics about growth during EEG delivery. Size increase is observed to occur gradually from the initial submicrometer diameters and continue through most of the geometry (Fig. 4). This is expected as the RH field increases from initially subsaturated to saturated conditions (Fig. 3). Comparisons of size at the ACI inlet with positions further downstream indicate that growth of the aerosol is nearly complete at the model outlet. Still, some additional size increase (< 20%) may be expected over the course of an entire respiratory cycle (i.e., ~5 s). Considering respiratory drug delivery, the observed steady rate of size increase may be very beneficial. The aerosol will likely remain in the submicrometer size regime through the delivery device and extrathoracic airways. Significant growth will likely not occur until RH values reach approximately 100% and the aerosol velocity begins to slow due to airway bifurcations in the tracheobronchial region. This relatively slow rate of growth may make EEG delivery ideal for targeting medications to the lower portion of the tracheobronchial airways and the alveolar region. In contrast, aerosol size increase during ECG appears to occur more rapidly (2,11,17), which points toward the use of this approach for targeting deposition throughout the airways, including the upper tracheobronchial region. Still, further testing is needed for both condensational growth approaches to optimize deposition within the lungs and to target deposition within specific regions of the respiratory tract.

Based on results of this study, EEG appears to be a very effective and practical method to induce pharmaceutical aerosol growth from initially submicrometer to conventional sizes. As with ECG, it is expected that the initially submicrometer aerosol will minimize deposition in the extrathoracic airways while the final conventional size will ensure full lung retention. As reported by Longest et al. (18), the initially small aerosol size can also be used to improve transport through the delivery lines in non-invasive and invasive mechanical ventilation delivery. In the current study, formation and delivery of the submicrometer combination particles was demonstrated for two generation methods at clinically relevant doses of drug. Using both of these platforms, the desired size increase to approximately 2 µm was observed. Use of a non-hygroscopic drug in this study provides a conservative estimate of the final size that can be achieved with most combination drug:excipient particles. Some hygroscopicity of the drug leads to substantially larger final sizes (12). The final aerosol size may also be increased by increasing the initial aerosol size (i.e., ~ 900 nm) and by increasing the amount of excipient in the particle. Predictions of the resulting particle sizes can be easily assessed using the correlations proposed in the study of Longest and Hindle (12).

Limitations of the current study include the assumption of initially dry particles, the use of simple relations for the calculation of hygroscopic effects, and the inclusion of external humidity in the model setup. Based on analytical calculations, there is sufficient potential for full evaporation of the initial aerosol in the spacer resulting in dry initial particles. Attempts to verify this assumption experimentally were complicated by the relatively long sampling times required to determine RH values in the spacer coupled with the transient nature of the system. At the calculated initial RH conditions reported in Table I, some water may remain in the particles. Furthermore, the deliquescence point of a combination particle composed of a non-hygroscopic drug and hygroscopic excipient is not known. However, the high degree of agreement between the model predictions and experimental results provides evidence that the dry particle assumption is reasonable and the model is sufficiently accurate in terms of growth predictions. Considering hygroscopic effects, Eq. 6 represents a form of Raoult’s law for calculating the water activity coefficients. In general, Raoult’s law is considered accurate for dilute solutions. However, the i coefficients implemented in this study were previously measured for the drug and excipients of interest through the saturation limits (12). Again, agreement with the experimental results indicates that the hygroscopic nature of the particles is adequately modeled. Finally, the EEG approach is intended to implement the thermodynamic conditions naturally found in the respiratory airways to foster particle growth. In the experiments, continuous steady state delivery of the CAG aerosol over 2 min was found to produce drying of the pre-wetted walls without supplemental humidity. The addition of supplemental humidity was used to produce saturated conditions more consistent with the respiratory tract in vivo.

CONCLUSIONS

In conclusion, results of this study indicate that the developed CFD model can accurately simulate the transport and hygroscopic size increase of combination drug: excipient submicrometer droplets in comparison with experiments. The in vitro results and CFD predictions both indicate that the initially submicrometer particles increase in size to a range of 1.6 to 2.5 µm for a non-hygroscopic drug with a 50:50 drug:excipient ratio. The associated diameter growth ratios ranged from 2.6 to 3.9, which should be sufficient to foster near full lung retention of the aerosol. CFD results highlighted gradual and steady size increase of the aerosol, which should be effective for minimizing extrathoracic deposition and producing deposition deep within the respiratory tract. Based on the results of this study, EEG appears to provide an effective and practical technique to increase pharmaceutical aerosol sizes from the submicrometer range to values that will ensure full lung retention. The developed CFD model will be implemented to optimize both submicrometer aerosol generation devices and delivery to the airways. Future work is needed in order to predict deposition within more realistic models the airways, develop improved aerosol generation techniques, and optimize this approach for maximum lung delivery as well as targeting the site of deposition within the airways.

ABBREVIATIONS

ACI

Andersen cascade impactor

CA

citric acid

CAG

capillary aerosol generator

CFD

computational fluid dynamics

DPI

dry powder inhaler

ECG

enhanced condensational growth

EEG

enhanced excipient growth

GC

growth coefficient

HFA

hydrofluoroalkane

HPLC

high-performance liquid chromatography

LRN

low Reynolds number

MDI

metered dose inhaler

MMAD

mass median aerodynamic diameter

MN

mannitol

MT

mouth-throat

NaCl

sodium chloride

RH

relative humidity

SD

standard deviation

TB

tracheobronchial