A Time-Varying Effect Model for Intensive Longitudinal Data

Abstract

Understanding temporal change in human behavior and psychological processes is a central issue in the behavioral sciences. With technological advances, intensive longitudinal data (ILD) are increasingly generated by studies of human behavior that repeatedly administer assessments over time. ILD offer unique opportunities to describe temporal behavioral changes in detail and identify related environmental and psychosocial antecedents and consequences. Traditional analytical approaches impose strong parametric assumptions about the nature of change in the relationship between time-varying covariates and outcomes of interest. This paper introduces time-varying effect models (TVEM) that explicitly model changes in the association between ILD covariates and ILD outcomes over time in a flexible manner. In this article, we describes unique research questions that the TVEM addresses, outline the model-estimation procedure, share a SAS macro for implementing the model, demonstrate model utility with a simulated example, and illustrate model applications in ILD collected as part of a smoking-cessation study to explore the relationship between smoking urges and self-efficacy during the course of the pre- and post- cessation period.

Introduction

Understanding temporal change is a central concern in the behavioral sciences. For example, developmental psychologists are concerned with examining systematic psychological changes (e.g., cognitive, social, personality, and emotional development) that occur during different stages and transitions (e.g., childhood, adulthood) in human beings. Understanding these critical behavior changes includes (1) describing behavior change, (2) predicting behavior change, and (3) identifying cause and effect explanations of behavior change. Accurately describing behavior change is the foundation for both predicting change and identifying causal mechanisms of change (Wohlwill, 1970, 1973). A careful description of behavior change should cover, at minimum, how a specific behavior evolves over time (i.e., the shape of change) and how it is systematically related to environmental, biological, and psychological factors.

To accurately characterize behavior change, three elements need to be ideally integrated: (a) a well-articulated theoretical model of change, (b) a longitudinal study with suitable temporal design that affords a clear and detailed view of the process, and (c) a statistical model that operationalizes the theoretical model (Collins, 2006). Longitudinal panel data and widely used statistical methods (e.g., hierarchical linear modeling; Raudenbush & Bryk, 2002) have been useful for answering many important research questions, such as estimating the effect of a treatment on a behavioral outcome and depicting the shape of a growth trend with familiar forms. Understanding behavior change often goes beyond estimating treatment effects or fitting a simple (e.g., linear, quadratic, or cubic) growth pattern; rather it requires “solid empirical foundations built upon accurate depictions of change” (Adolph, Robinson, Young, & Gill-Alvarez, 2008, p. 541). Panel data with a small number of waves coupled with commonly used statistical methods are currently incapable of describing detailed features of behavior change (e.g., irregular ups and downs and time-varying effects). Instead, more intensive longitudinal data and advanced statistical models are needed for describing detailed behavior patterns and changing relationships between a behavior and relevant factors.

The goal of this article is three-fold: (1) to introduce a new statistical model, emphasizing new types of research questions that can be addressed, (2) to demonstrate applications of the model to an intensive longitudinal study of positive affect and self-efficacy among participants in a smoking cessations trial, and (3) to make this model readily available for applications by presenting SAS code and SAS macro. Specifically, the current paper demonstrates that time-varying effect modeling (TVEM; Hastie & Tibshirani, 1993; Hoover, Rice, Wu, & Young, 1998) is suited for studying the temporal change of behavioral or psychological outcomes and their relationship to relevant covariates, using intensively sampled longitudinal data (ILD). More importantly, this approach allows for assessing both temporal changes and their relationship to covariates directly from observations, without posing any assumptions regarding the shape (i.e., linear, quadratic, or cubic) of the trajectories.

This paper is organized as follows. In the first section, we provide an overview of the features of behavior change, and argue why more flexible statistical models and more intensive observation of behavior are needed in order to more accurately describe behavior. In the second section, we detail the distinct features of ILD. In the third section, we provide a conceptual and technical overview of TVEM. In the fourth section, we describe technical details for fitting TVEM, implementation of this approach using SAS, and comparison of this approach with other popular methods. In the fifth section, we apply TVEM to simulated and real examples. A brief description of the syntax of a SAS macro for fitting TVEM is provided in the appendix.

A Review of Behavior Change

Change Score or Course of Change

The way that researchers have conceptualized change has evolved significantly. It was once popular in many fields to describe change as the difference in a behavior at two time points (e.g., before and after treatment; or ages 4 and 8). Measuring change with two observations is sufficient for some purposes (e.g., estimating treatment effects) and remains useful. However, it ignores the course of change between the two points in time. That is, different courses of change, which may represent different mechanisms of change, often give rise to the same increment across only two waves of measurement. Hence, the course of change provides more detailed information than change scores regarding the mechanism of change. Specifically, an accurate portrayal of the course of change provides information about (1) the overall shape of change (e.g., increasing, decreasing, U-shape, or sigmoidal?), and (2) when the greatest amount of change takes place, or whether the rate of change is constant over the study period. Such information may better shed light on what causes a specific change (i.e., mechanism of change), offer a better prediction of behavior change, and/or provide information leading to new theories of development (Gottlieb, 1976; Siegler, 2006; Wohlwill, 1973).

Change in Associations

Many factors may contribute to the temporal change of a specific behavioral or psychological outcome. For example, stress may be affected by multiple environmental (e.g., retirement, exam-taking) and social factors (e.g., marital satisfaction). Similarly, the urge to smoke can be triggered by environmental cues (e.g., presence of other smokers) as well as psychological factors (e.g., negative affect). In the current behavioral literature, it is a convention to assume the association between an outcome of interest and covariate (environmental, social, or psychological) is constant over time. This assumption implies that the outcome is associated with covariates similarly (in both magnitude and direction) at any two points in time. Although this assumption provides a parsimonious model, it may not capture the richness of the underlying process of change. On the contrary, “no man ever steps in the same river twice, for it's not the same river and he is not the same man” (Heraclitus). Naturally, the interaction between a psychological outcome (the “man”) and relevant covariates (the “river”) might also evolve over time. That is, timing may play a critical role in the magnitude and direction of the association between particular explanatory variables and the behavior of interest. For example, negative affect may play an important role in triggering smoking urges in early stages of smoking cessation, but a much weaker role following the acquisition of coping strategies. To contrast, the relation between time spent with family and mood might be positive during childhood, but negative during adolescence (an example offered by a reviewer).

In recent years, a few articles have mentioned the phenomenon of time-varying associations (e.g., Collins, 2006; Walls & Schafer 2006; Fok & Ramsay, 2006). In a smoking cessation study, Li, Root, & Shiffman (2006) found that negative affect towards urge to smoke changed during various stages of the smoking cessation process, illustrating that behavior change is a complex, dynamic phenomenon. For a comprehensive understanding of complex behavior changes, it is essential to consider the temporal changes in the associations between the behavior and other covariates, in addition to change in the behavior itself.

Shape of Change

Change has long been an active topic in behavior science, as reflected in many books such as Harris (1963), Nesselroade & Baltes (1979), Gottman (1995), Collins & Sayer (2001), Singer & Willett (2003), Nagin (2005), as well as in an overwhelming number of journal articles. It is a convention in behavioral research to assume a shape of change as a pre-specified form: linear, quadratic, or exponential. Although for some situations such a specification can be convincingly justified by a well-established theory, for most other situations, the actual course of change may be quite complicated (Adolph et al., 2008) and may not be adequately captured by any familiar or convenient parametric form. Often, a pre-specified or simple form for change is the result of a lack of informative theoretical models, rich observations, or suitable statistical methods. Although often necessary, reliance on pre-specified forms may cause mis-specification of the functional form of change. This, in turn, could lead to inaccurate or even misleading conclusions (e.g., imagine what conclusion would be reached if a linear curve were fit to human growth data, while the true growth curve is largely stable but with periods, like infancy and puberty, of rapid change). Understanding the process of change is, in general, an iterative learning process: one relies on prior knowledge (or theory) regarding the shape of the underlying trajectory to inform a statistical function, while reliable prior knowledge should be drawn from suitable analysis of observations from pilot studies. It is a process of trial-and-error and “is difficult and fraught with uncertainty” (Collins & Graham, 2002, p. S94).

New Strategy

One strategy to speed up this iterative learning process and decrease uncertainty in the exploratory trial-and-error process is to learn the shapes (of trajectory and of the change of associations) directly from observations, instead of relying on prior knowledge of the form for the shape, which is generally not available or reliable.

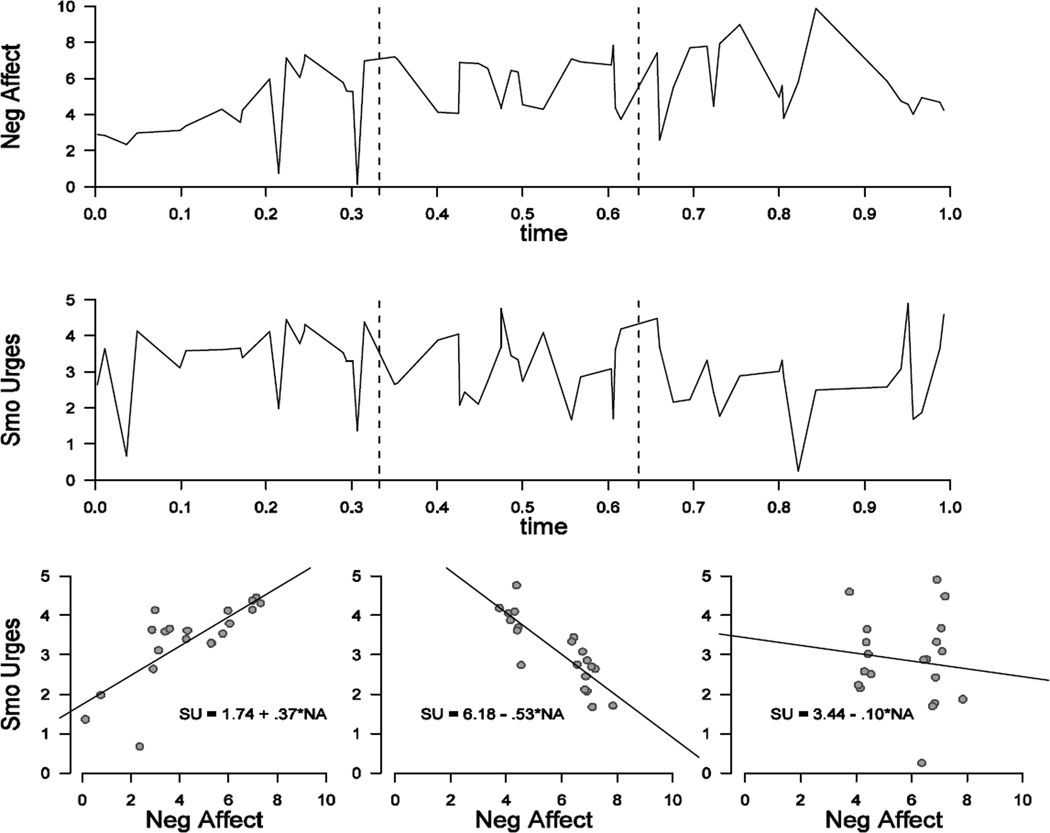
Figure 1 provides a hypothetical example illustrating the existence of temporal change in urge to smoke, and in the effect of negative affect on urge to smoke. Instead of correlating smoking urges and negative affect across the entire time interval, we broke down time into three periods (i.e., [0,0.33), [0.33,0.67), and [0.67,10]) in order to explore whether direction and strength of the relationship changes with time. From the three scatter plots at the bottom of Figure 1, it is clear that the relationship between negative affect and smoking urge in the first time interval (between 0 and .33) is positive, changing to negative in the middle, and zero during the last time interval. Breaking the time period into 3 intervals was only an illustration. By breaking the study period into much finer intervals, one might reveal how the relationship between negative affect and smoking urge changes gradually as time progresses.

Figure 1.

A Hypothetical example of the time-varying relationship between negative affect and urge to smoke. The solid line in the upper plot represents the negative affect scores from a single individual plotted over the time interval [0, 1]. Smoking urges for the same individual are plotted in the middle graph. Vertical dashed lines partition the study period into three equally spaced intervals: [0, .33), [.33, .67), [.67, 1.0]. Corresponding scatter plots of negative affect and smoking urges from the three periods are plotted at the bottom. Fitted linear regression lines demonstrate the directionality and the extent of the association between negative affect and smoking urges.

This hypothetical example also hints at what is needed to implement this strategy of learning the shapes of change directly from data. First, we need dense observations so that the data contain fine-grained information regarding the change of interest. Fortunately, as discussed in the next section, ILD are available to serve this purpose. Second, statistical models and estimation techniques are also essential. We will show in the following sections that TVEM and relevant nonparametric techniques are suitable for this objective.

Intensive Longitudinal Data

Recent technological innovations such as web-based assessments, hand-held computers, GPS systems, and automatic portable devices (e.g., pedometers, heart rate monitors, time-recording pill and cigarette dispensers) allow for frequent and comprehensive sampling of human behaviors and accompanying environmental, psychological, and physiological states. In addition, many longitudinal studies of developmental trends across the life span have lasted decades, resulting in more than ten repeated measurements for participants. The resulting data are referred to as ILD (Walls & Schafer, 2006), to distinguish them from traditional longitudinal data with, typically, only a few repeated observations. Although there is no agreed-upon threshold for what constitutes ILD, ILD are generally collected at more than “a handful of time points,” (Walls & Schafer, 2006, p. xiii) yielding tens or even hundreds of observations for each study participant.

ILD share a similar form with traditional longitudinal data, as denoted by

$$\left\{t_{\mathit{\text{ij}}},y_{\mathit{\text{ij}}},x_{\mathit{\text{ij}}1},\dots ,x_{\mathit{\text{ijp}}}\right\},i=1,\dots ,n;j=1,\dots ,m_i,$$

where n represents the total number of subjects, and m_i the total number of measurements for subject i. In addition, t_ij is the measurement time of the j -th observation for the i -th subject; y_ij is the outcome and (x_ij1, …, x_ijp) are the p covariates of subject i measured at time t_ij.

Like traditional longitudinal data, ILD have a nesting structure, with repeated observations within an individual likely to be correlated. In addition, such data are often unbalanced, with different assessment times within and across individuals, leading to a preponderance of missing values and unevenly spaced observations over time.

A distinct feature of ILD is that the number of measurements for each participant is substantially larger, implying much denser or longer observation of phenomenons, compared to a traditional longitudinal study. This dense observation is primarily motivated by new types of research questions, focusing on fine-grained temporal changes in human behavior or psychosocial processes, as well as related co-variation and causation (Collins, 2006). Due to the dense and comprehensive observations ILD is expected to contain detailed information regarding temporal changes of behaviors. Therefore, the development of appropriate statistical methods to extract the information and capture the temporal changes of interest from ILD is needed.

Approaches to Answering Questions of Temporal Change

Multilevel or hierarchical modeling has been widely applied (Raudenbush & Bryk, 2002, Singer & Willet, 2003), and has been successfully extended to handle ILD (Walls, Jung & Schwartz, 2006; Schwartz & Stone, 1998). To capture the temporal changes in the outcome and the association between the outcome and time-varying covariates, one general form of the multilevel model (MLM) is conceptualized in the following manner:

$$y_{\mathit{\text{ij}}}={\beta }_{00}+{\beta }_{01}·t_{\mathit{\text{ij}}}+({\beta }_{10}+{\beta }_{11}·t_{\mathit{\text{ij}}})·x_{\mathit{\text{ij}}}+r_{00i}+r_{01i}·t_{\mathit{\text{ij}}}+(r_{10i}+r_{11i}·t_{\mathit{\text{ij}}})·x_{\mathit{\text{ij}}}+{\epsilon }_{\mathit{\text{ij}}},$$ (1)

when there is only one time-varying covariate x_ij. In this model, we call β₀₀, β₀₁, β₁₀, β₁₁ the fixed effects, and r_00i, r_01i, r_10i and r_11i the random effects. When random effects are omitted, this model reduces to the simple linear regression model for repeated assessments:

$$y_{\mathit{\text{ij}}}={\beta }_{00}+{\beta }_{01}·t_{\mathit{\text{ij}}}+({\beta }_{10}+{\beta }_{11}·t_{\mathit{\text{ij}}})·x_{\mathit{\text{ij}}}+{\epsilon }_{\mathit{\text{ij}}}.$$ (2)

In the above MLM, the mean trajectory of the outcome is assumed to change linearly over time, as is the association between the outcome and covariate. This MLM can be further extended to consider more complex developmental forms (e.g., quadratic, cubic). However, such a model quickly becomes complex, while not allowing much flexibility in terms of shape (i.e., when the shape of change does not follow quadratic or cubic patterns or are unknown a priori).

Time-Varying Effect Model

An extension of MLM is thus greatly needed to model the time-varying relationship between the covariates and outcome with ILD. In this paper, we propose the use of a TVEM, which is a special case of varying-coefficient model (Hastie & Tibshirani, 1993). For simplicity, we start with the situation with a continuous outcome y_ij and a single time-varying covariate x_ij. In this such situation, TVEM takes the following form:

$$y_{\mathit{\text{ij}}}={\beta }_0(t_{\mathit{\text{ij}}})+{\beta }_1(t_{\mathit{\text{ij}}})·x_{\mathit{\text{ij}}}+{\epsilon }_{\mathit{\text{ij}}}.$$ (3)

The random errors ε_ij¹ in Equation 3 are assumed to be normally and independently distributed. This equation implies that, at time t_ij, the mean of y (when x = 0) is β₀(t_ij). In a similar fashion, the slope β₁(t_ij) represents the strength and direction of the relationship between the covariate and the outcome at a particular time point t_ij. It is important to notice that both the intercept β₀ and the slope β₁ are time-specific and change their values at different points in time. That is, at two different time points, for example, $t_{\mathit{\text{ij}}}^{\prime }\text{ and }{t}_{\mathit{\text{ij}}}(t_{\mathit{\text{ij}}}^{\prime }\ne t_{\mathit{\text{ij}}})$, the intercept ${\beta }_0(t_{\mathit{\text{ij}}}^{\prime })$ and the slope ${\beta }_1(t_{\mathit{\text{ij}}}^{\prime })$ may be different from β₀(t_ij) and β₁(t_ij), respectively. Thus, not only x_ij but also its regression coefficient for predicting y_ij depends on t_ij.

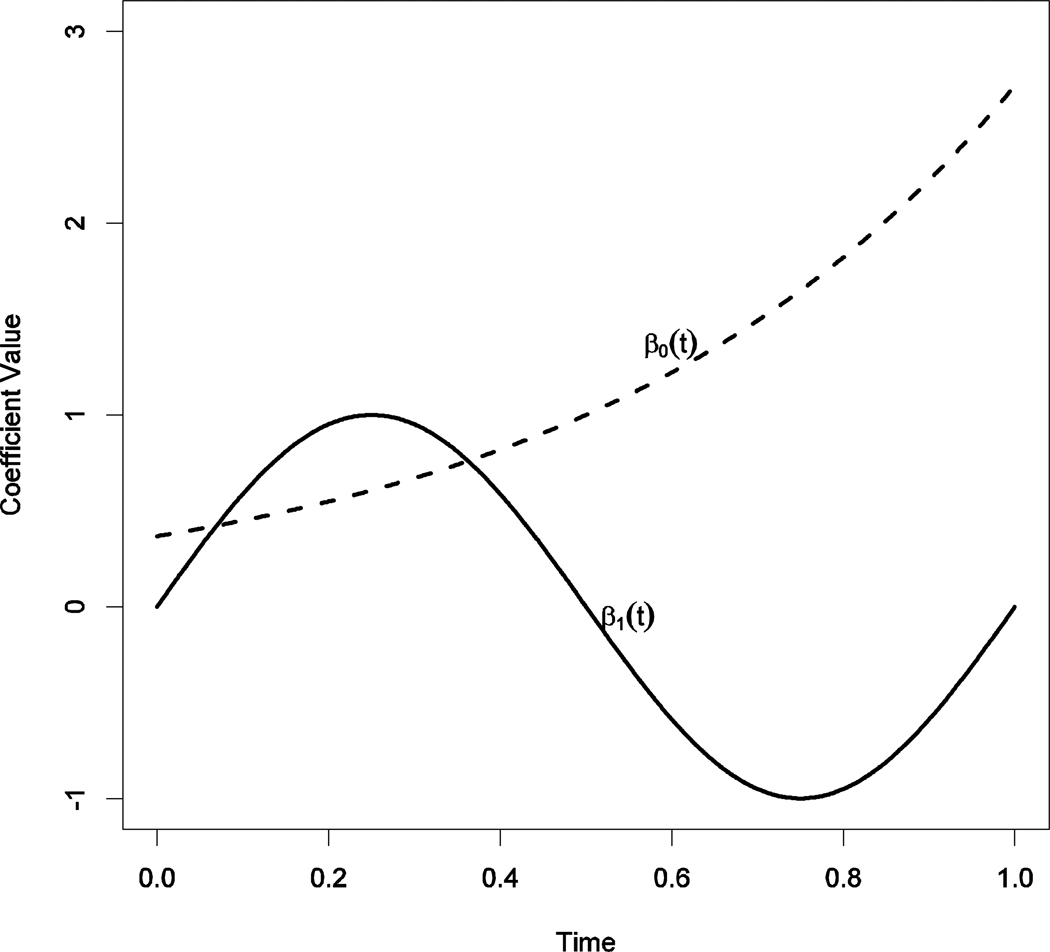
The intercept β₀(·) and slope β₁(·) are assumed to be continuous functions of time and are called coefficient functions. These functions can be summarized numerically for each separate time point, but it is more common to depict them graphically as a function of time. Figure 2 presents an example of such hypothetical intercept and slope functions. The dotted line in Figure 2 summarizes an intercept function (i.e., an outcome trajectory for individuals with a zero level on the time-varying covariate), while the solid line corresponds to the impact of a time-varying covariate (X) on outcome (Y) over time. Specifically, at the beginning of the study (time = 0.0), the mean of Y is about 0.4 (i.e., β₀(0.0)=0.4), and the slope is about 0 (β₁(0.0)=0; i.e., change in X is not associated with change in Y). When time equals .25, the mean of Y is about 0.5 (i.e., β₀(0.25)=0.5) and the slope is about 1 (β₁(0.25)=1.0; i.e., a change of 1 unit in X would correspond to an increase of 1 unit in Y). Suppose we have collected measurements of X and Y generated by a model with intercept function and slope function as shown in Figure 2. Then, for observations measured around time 0, we may expect a scatter plot similar (qualitatively) to the third plot at the bottom of Figure 1, and for observations around time 0.25, we may expect a scatter plot similar (qualitatively) to the first plot at the bottom of Figure 1. The gradual and smooth change in both the intercept and the slope reveals that we can expect a gradual transition in the outcome and the relationship between the outcome and the covariate from one point to the next. Overall, there is a progressive increase in Y, and the association between X and Y follows a periodic trend. In the real world, such a periodic trend in association may suggest that certain biological process (e.g., cyclic hormone fluctuation) may be involved in the temporal change of outcome and association. In addition, using Equation 3 to describe such a phenomenon, one would end with a linear trajectory and a constant slope function (since there is no obvious increasing or decreasing trend in β₁(t) in Figure 2), and miss the richness in the change phenomenon.

Figure 2.

Hypothetical intercept (β₀(t), dashed line) and slope (β₁(t), solid line) functions that change values over the course of the time period [0, 1].

Thus, one of the goals of TVEM is to reveal the shape of the coefficient functions over time. Conveniently, this model does not pose any parametric assumptions on these functions, since their shapes are largely unknown in advance. Rather, TVEM assumes only that the relationship changes over time in a smooth fashion. Specifically, the coefficient functions can take any form, given that they are smooth (i.e., with no sudden jumps or break points). We call a function smooth if its first-order derivative function is continuous. Visually, a smooth function should change its value gradually over time. More details about how a TVEM can be fit will be presented in the next section.

While TVEM closely resembles Equation 2, the difference between them is fundamental. Equation 2 pre-specifies polynomial or other parametric forms to the coefficient functions, but TVEM allows these functions to take nearly any form, and the form is revealed directly from data. In other words, while Equation 2 tries to force the data into a prespecified shape, TVEM tries to find a shape that follows the change in the data. Consequently, Equation 2 is vulnerable to model misspecification when there is a lack of reliable prior information to assure a correct model specification, but TVEM is free of such model misspecification and is expected to objectively reveal the shapes of these coefficient functions. This freedom comes with a price: more data are needed to fit a TVEM than to fit a similar parametric model. This is due to the need to estimate functions in TVEM, in contrast to a few unknown parameters in a parametric model. Fortunately, ILD provide suitable resource to encourage applications of TVEM.

Finally, Equation 3 can be readily extended to include multiple covariates. Some of which can be time-invariant, and others time-varying. In case of time-invariant covariates (e.g., treatment), it is possible to explore how their effect changes with time, instead of assuming a constant overall effect. Furthermore, one can specify some of these coefficient functions to follow certain parametric forms in situations where there is sufficient evidence for such specification, while others are allowed to change freely. Random effects to capture between-individual differences in the effects of time-varying covariates can also be added, as demonstrated in the implementation part in the next section.

Estimation of the Time-Varying Effect Model

This section focuses on the estimation procedure of TVEM and contains some technical details. Estimation of unknown functions (e.g., intercept β₀(·) and slope β₁(·) functions in Equation 3) has been studied extensively in the statistical literature (e.g., Wu & Zhang, 2006; Fitzmaurice, Davidian, Verbeke, & Molenberghs, 2007). Current popular methods can be broadly classified into spline-based methods such as smoothing spline (Wahba, 1990), P-spline (Eilers & Marx, 1996; Ruppert & Carroll, 2000; Ruppert, Wand, & Carroll, 2003), and regression splines (Stone, Hansen, Kooperberg, & Truong, 1997), and kernel-based methods like LOESS (Cleveland, 1979) and local polynomial kernels (Fan & Gijbels, 1996; Wu & Zhang, 2002). While there are proponents and critics of each of these approaches, we selected the P-spline method as the estimation procedure for TVEM due to its flexibility and computational efficiency. At the end of this section, we briefly describe alternative methods including smoothing spline, regression spline, and kernel-based methods.

P-Spline-Based Methods

Parameter-function estimation based on P-spline contains two major steps.

Step 1: approximation using truncated power basis. We noted that one of the assumptions of TVEM is that parameter functions follow a smooth changing pattern. Mathematically, any smooth function defined over an interval [a, b], e.g., f(t) t,∈[a, b], can be approximated with a polynomial function. However, very high-order polynomials may be needed to approximate such a function satisfactorily; therefore, this is not recommended due to the so called, “Runge Phenomenon” (i.e., oscillation at the boundaries of an interval that occurs when using high-order polynomials for polynomial interpolation or approximation) (Dahlquist & Björk, 1974). Instead, a simpler approach is to locally approximate the function over a small sub-interval of [a, b] with lower-order polynomials, because a lower-order polynomial can provide a good approximation to a function over a small interval (i.e., consider the idea of Taylor expansion) even though it does not fit the function well over the whole range. On this basis, we could partition the interval [a, b] into K + 1 smaller intervals, which are determined by K dividing points, or knots, with {τ₁, τ₂, …, τ_K} with a = τ₀ < τ₁ < τ₂ < ⋯ < τ_K < τ_K+1 = b. Then, within each small interval [τ_r, τ_r+1), 0 ≤ r ≤ K, we consider approximating f(t) accurately with lower-order polynomial functions.

One approach to implementing this idea is to use the following truncated power basis:

$$1,t,t^2,\cdots ,t^q,{(t-{\tau }_1)}_{+}^q,{(t-{\tau }_2)}_{+}^q,\cdots ,{(t-{\tau }_K)}_{+}^q,$$ (4)

where

$${(t-\tau )}_{+}^q=\{\begin{array}{cc}\hfill 0\hfill & \text{if }t\le \tau ,\hfill \\ \hfill {(t-\tau )}^q\hfill & \text{if }t>\tau ,\hfill \end{array}$$

and is called truncated power function of order q with knot τ. The first q + 1 functions in Equation 4 are the q + 1 power functions of t of order 0,1,2, …, q, and the remaining K functions are truncated q order power functions determined by the K knots τ₁, …,, τ_K, respectively. The specification of q is, in general, less crucial, and we set q = 2 hereafter. It can be shown that a linear combination of these truncated power basis functions is a quadratic polynomial within each interval [τ_r, τ_r+1) for r = 0,1, …, K, and, hence, is a piecewise quadratic function over [a, b]. Such piecewise polynomials have continuous first-order derivatives. Approximating f(t) t,∈[a, b] with a linear combination of the basis functions in Equation 4, say,

$$\tilde{f}(t)=a_0+a_1·t+a_2·t^2+{\displaystyle \sum _{k=1}^K}{a}_{q+k}·{(t-{\tau }_k)}_{+}^q,$$ (5)

is essentially equivalent to approximating f(t) interval by interval with quadratic polynomials (since q = 2). Piecewise polynomials are also called spline functions, which explains the word spline in the term P-spline. In practice, the number K is specified by the researchers and its selection will be discussed at the end of this section. Given K, the K knots are either equally spaced over [a, b] such that

$${\tau }_r=a+r(b-a)/(K+1),r=1,2,\dots ,K,$$

where a and b are the smallest and largest observation times, respectively; or they are equally spaced over sample quantiles of all observation times:

$${\tau }_r=t_{(1+[\mathit{\text{rN}}/(K+1)])},r=1,2,\dots ,K,$$

where N = ∑_im_i is the total number of observations, t_(k) denotes the k th observation time after sorting all N observation times from small to large, and [rN / (K + 1)] denotes the integer part of [rN / (K + 1)]. The latter method results in a nearly equal number of observations in each of the K + 1 intervals.

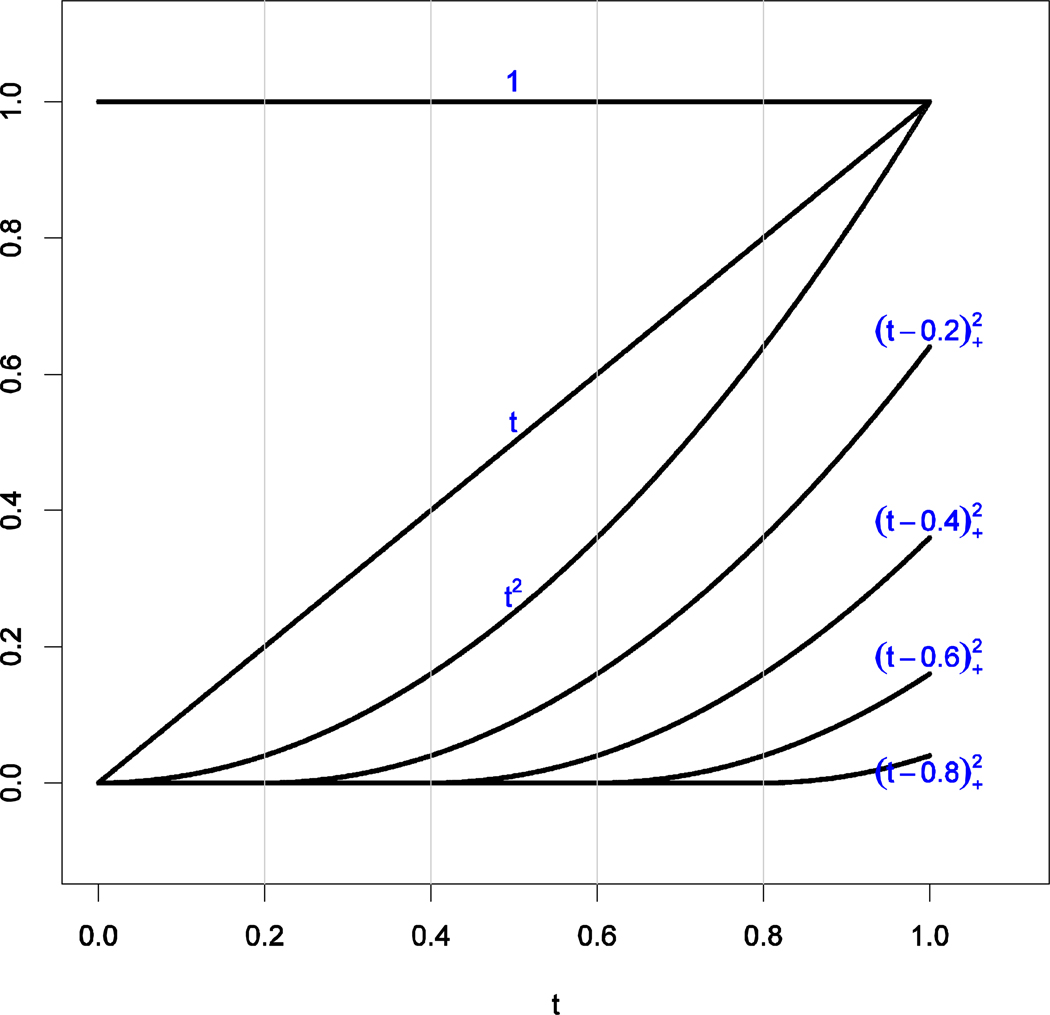
Figure 3 presents a truncated power basis with q = 2 and knots .2, .4, .6, and .8 over the range [0,1]. It includes the first three polynomials 1, t, t², and the four truncated power functions with nonzero values starting at knots .2,.4,.6 and .8, respectively.

Figure 3.

Plots of seven truncated power basis functions with knots at 0.2, 0.4 ,0.6, and 0.8. These seven basis functions (of time) are: $b_1(t)\equiv 1,b_2(t)=t,b_3(t)=t^2,b_4(t)={(t-0.2)}_{+}^2,b_5(t)={(t-0.4)}_{+}^2,b_6(t)={(t-0.6)}_{+}^2,b_7(t)={(t-0.8)}_{+}^2$. Appropriate linear combinations of these functions are used to approximate coefficient functions in fitting a TVEM.

The key to the effectiveness of this approach is that we can approximate any smooth function f(·) over a specified interval by a spline as defined in Equation 5 as accurately as possible, given large enough K. To demonstrate this, we consider approximating and assessing the accuracy of the approximation for the following three functions over the interval [0,1]:

$$f_1(t)=\text{exp}(2t-1),f_2(t)=8t(1-t),f_3(t)={\text{sin}}^2(2\pi t).$$

We define the accuracy of approximation as the maximum absolute difference between a function f(t) and its approximation function f̃(t):

$$d=\underset{t\in [0,1]}{{\displaystyle \text{max}}}|f(t)-\tilde{f}(t)|.$$

For a given K and for each of the three functions, we can find the optimal linear combination of the basis functions. Here we define “optimal” as being closest to the original function in term of the absolute difference. Table 1 lists the maximum absolute differences between these three functions and their corresponding optimal approximations for different numbers of knots that are equally spaced. When K = 0, quadratic polynomials are used to approximate these three functions over the whole interval [0,1]. As shown in Table 1, the overall trend is such that as K increases, the distance between the original and optimal approximating function decreases, indicating a progressive increase in approximation accuracy. Because the function 8t(1 − t) is actually a quadratic function, it is expected that we can find its perfect approximation. For the most complicated sinusoid function, sin²(2πt), we can still obtain a quite accurate approximation, in that the maximum absolute difference d is less than 0.1, when K ≥ 6. It should be noted that using quadratic function (K = 0) to fit this sinusoid function leads to significant bias (i.e., d >1.0).

Table 1.

Accuracy of Using Truncated Power Splines to Approximate Three Functions

	Functions being approximated
K	exp(2t − 1)	8t(1 − t)	sin2(2πt)
0	0.0450	0.0000	1.0003
1	0.0121	0.0000	1.0057
2	0.0038	0.0000	0.4993
3	0.0018	0.0000	0.6125
4	0.0010	0.0000	0.1828
5	0.0006	0.0000	0.1438
6	0.0004	0.0000	0.0735
7	0.0002	0.0000	0.0413
8	0.0002	0.0000	0.0281
9	0.0001	0.0000	0.0204
10	0.0001	0.0000	0.0146

Note. K is the number of knots of the truncated power splines used to approximate the three functions. K = 0 implies that quadratic functions are used to approximate these functions. Numbers under each function are the “minimal” maximum absolute difference between this function and any truncated power splines with given number of knots (0–10).

From the above example, it is reasonable to assume that the two unknown functions β₀(·) and β₁(·) in Equation 3 can be well-approximated by certain linear combinations of basis functions in Equation 4:

$${\beta }_0(t)\approx a_0+a_{1}t+a_2{t}^2+{\displaystyle \sum _{k=1}^K}{a}_{2+k}{(t-{\tau }_k)}_{+}^2,$$

and

$${\beta }_1(t)\approx b_0+b_{1}t+b_2{t}^2+{\displaystyle \sum _{k=1}^K}{b}_{2+k}{(t-{\tau }_k)}_{+}^2,$$

given an appropriate number of knots K. Thus, to estimate the unknown coefficient functions β₀(·) and β₁(·), it suffices to estimate the unknown coefficients of the linear combinations, a₀, a₁, …, a_2+K and b₀, b₁, …, b_2+K.

Replacing the unknown functions β₀(·) and β₁(·) in Equation 3 with the above linear combinations, we obtain

$$y_{\mathit{\text{ij}}}\approx a_0+a_1{t}_{\mathit{\text{ij}}}+a_2{t}_{\mathit{\text{ij}}}^2+{\displaystyle \sum _{k=1}^K}{a}_{2+k}{(t_{\mathit{\text{ij}}}-{\tau }_k)}_{+}^2+b_0{x}_{\mathit{\text{ij}}}+b_1{t}_{\mathit{\text{ij}}}{x}_{\mathit{\text{ij}}}+b_2{t}_{\mathit{\text{ij}}}^2{x}_{\mathit{\text{ij}}}+{\displaystyle \sum _{k=1}^K}{b}_{2+k}{(t_{\mathit{\text{ij}}}-{\tau }_k)}_{+}^2{x}_{\mathit{\text{ij}}}+{\epsilon }_{\mathit{\text{ij}}}.$$ (6)

This turns out to be a linear regression model with $\{1,t_{\mathit{\text{ij}}},t_{\mathit{\text{ij}}}^2,{(t_{\mathit{\text{ij}}}-{\tau }_1)}_{+}^2,\dots ,{(t_{\mathit{\text{ij}}}-{\tau }_K)}_{+}^2\}\text{ and }\{x_{\mathit{\text{ij}}},t_{\mathit{\text{ij}}},x_{\mathit{\text{ij}}},t_{\mathit{\text{ij}}}^2,x_{\mathit{\text{ij}}},{(t_{\mathit{\text{ij}}}-{\tau }_1)}_{+}^2{x}_{\mathit{\text{ij}}},\dots ,{(t_{\mathit{\text{ij}}}-{\tau }_K)}_{+}^2{x}_{\mathit{\text{ij}}}\}$ as covariates, and a₀, a₁, …, a_2+K and b₀, b₁, …, b_2+K as coefficients, which can be easily estimated with ordinary least squares (OLS). Denoting â₀, â₁, …, â_2+K and b̂₀, b̂₁, …, b̂_2+K as estimates for a₀, a₁, …, a_2+K and b₀, b₁, …, b_2+K, the functions β₀(·) and β₁(·) can be estimated by

$${\widehat{\beta }}_0(t)={\widehat{a}}_0+{\widehat{a}}_{1}t+{\widehat{a}}_2{t}^2+{\displaystyle \sum _{j=1}^K}{\widehat{a}}_{2+j}{(t-{\tau }_j)}_{+}^2,$$ (7)

$${\widehat{\beta }}_1(t)={\widehat{b}}_0+{\widehat{b}}_{1}t+{\widehat{b}}_2{t}^2+{\displaystyle \sum _{j=1}^K}{\widehat{b}}_{2+j}{(t-{\tau }_j)}_{+}^2.$$ (8)

Step 2: smoothing using penalty. The estimates of coefficient functions based on OLS (i.e., Equations 7 and 8) might be quite rough and contain unnecessary fluctuations, especially when K is large but the underlying coefficient functions are relatively simple. This is because the resulting model (Equation 6) corresponding to large K is more complicated than needed for fitting the underlying pattern in data, and hence exaggerates minor fluctuations (due to randomness) in the data. This phenomenon is also called overfitting. To avoid overfitting, the P-spline based method goes one step further and smooths the estimated functions, instead of stopping at Equations 7 and 8. Because the second derivative of the function ${(t-\tau )}_{+}^2$ is 0 when t ≤ τ, and 1 when t > τ, the coefficients {a_2+j, j = 1,2, … K} and {b_2+j, j = 1,2, … K} of the truncated power functions represent “amounts of jump” in the second order derivatives of the estimated functions at knots τ₁, …, τ_K, and are directly related to smoothness of the estimated functions. Thus, one approach to obtain smoother estimates, suggested by Ruppert (2002) and Wand (2003), is to shrink the coefficients, {a_2+j, j = 1,2, …, K} and {b_2+j, j = 1,2, …, K}, toward zero by minimizing

$$\mathit{\text{SSE}}+{\lambda }_1{\displaystyle \sum _{j=1}^K}{a}_{2+j}^2+{\lambda }_2{\displaystyle \sum _{j=1}^K}{b}_{2+j}^2$$ (9)

with respect to the coefficients {a_j, b_j, j = 0, 1, 2, …, K + 2}, where SSE stands for sum of squared errors such that

$$\mathit{\text{SSE}}={\displaystyle \sum _{i=1}^n}{\displaystyle \sum _{j=1}^{m_i}}[y_{\mathit{\text{ij}}}.-\left(a_0+a_1{t}_{\mathit{\text{ij}}}+a_2{t}_{\mathit{\text{ij}}}^2+{\displaystyle \sum _{k=1}^K}{a}_{2+k}{(t_{\mathit{\text{ij}}}-{\tau }_k)}_{+}^2\right){-\left(b_0{x}_{\mathit{\text{ij}}}+b_1{t}_{\mathit{\text{ij}}}{x}_{\mathit{\text{ij}}}+b_2{t}_{\mathit{\text{ij}}}^2{x}_{\mathit{\text{ij}}}+{\displaystyle \sum _{k=1}^K}{b}_{2+k}{(t_{\mathit{\text{ij}}}-{\tau }_k)}_{+}^2{x}_{\mathit{\text{ij}}}\right)]}^2.$$

This method reduces to OLS when λ₁ = λ₂ = 0, however, if λ₁ or λ₂ are very large, this approach will shrink the estimated β₀(·) or β₁(·) towards a global quadratic polynomial by forcing {a_2+j, j = 1,2, … K} or {b_2+j, j = 1,2, … K} to 0. Thus, λ₁ and λ₂ control the trade-off between the goodness of fit and the smoothness of the estimated functions and are called smoothing parameters or tuning parameters. The term ${\lambda }_1{\displaystyle {\sum }_{j=1}^K}{a}_{2+j}^2+{\lambda }_2{\displaystyle {\sum }_{j=1}^K}{b}_{2+j}^2$ in Equation 9 can be viewed as a penalty term, which prevents {a_2+j, j = 1,2, … K} and {b_2+j, j = 1,2, … K} from being too large in absolute value. This explains the P in the P-spline method, which stands for penalized.

Using suitable smoothing parameters is crucial to obtaining satisfactory estimates of coefficient functions. In the literature, the generalized cross-validation (GCV; Wahba, 1990) score, can be used to select optimal smoothing parameters. However, optimizing GCV score with respect to multiple smoothing parameters effectively relies on carefully designed algorithms (Gu & Wahba, 1991; Wood, 2008) which are available only in several specific R packages (e.g., Wood, 2011; Gu, 2004). Alternatively, Wand (2003) suggested a different approach by exploring the connection between P-spline and mixed effect models. Instead of optimizing Equation 9 with certain tuning parameters λ₁ and λ₂, this approach treats {a_2+k, b_2+k, k = 1, 2, …, K} in Equation 6 as random variables with normal distributions:

$$a_{2+k},~N(0,{\eta }_1),b_{2+k}~N(0,{\eta }_2),k=1,2,\dots ,K,$$

and expands Equation 6 into a linear mixed effect model in which a₀, a₁, a₂ and b₀, b₁, b₂ are fixed effects, and a₂₊₁, …, a_2+K and b₂₊₁, …, b_2+K are random effects, with variance parameters η₁ and η₂, respectively. Intuitively, the variance parameters have similar effect as the tuning parameters on shrinking the coefficients (i.e., a₂₊₁, …, a_2+K and b₂₊₁, …, b_2+K). For example, small variance parameters imply that the coefficients should not bound away from 0 too much. These small variance parameters have the same effect as large tuning parameters (i.e., λ₁, λ₂). On the contrary, large variance parameters imply that the coefficients can deviate from 0 more freely, and have the same effect as small tuning parameters,. More formally, we notice that the logarithm of the joint density of response y_ij and random effects of the resulting linear mixed effect model is

$$-\frac{N}{2}\text{log}(2\pi {\sigma }^2)-\frac{K}{2}\text{log}(2\pi {\eta }_1)-\frac{K}{2}\text{log}(2\pi {\eta }_1)-\frac{\mathit{\text{SSE}}}{2{\sigma }^2}-\frac{1}{2{\eta }_1}{\displaystyle \sum _{k=1}^K}{a}_{2+k}^2-\frac{1}{2{\eta }_2}{\displaystyle \sum _{k=1}^K}{b}_{2+k}^2.$$ (10)

The last three terms in Equation 10 equal to Equation 9 multiplied by −1/2σ², if we denote ${\lambda }_1=\frac{{\sigma }^2}{{\eta }_1},\text{ and }{\lambda }_2=\frac{{\sigma }^2}{{\eta }_2}$. This suggests an intrinsic connection between the variance parameters η₁ and η₂ and the tuning parameters λ₁ and λ₂: by choosing suitable variance parameters, we can also reach “optimal” balance between fitness and smoothness. Naturally, one would choose the restricted maximum likelihood (REML) estimate of η₁ and η₂. Denote σ̂², η̂₁, η̂₁ as the REML estimate of variance components. It has been shown that $(\frac{{\widehat{\sigma }}^2}{{\widehat{\eta }}_1},\frac{{\widehat{\sigma }}^2}{{\widehat{\eta }}_2})$ are comparable (though different because they are derived from different criteria) to the “optimal” tuning parameter (λ₁, λ₂) selected by GCV score (Krivobokova & Kauermann, 2007). Consequently, the MLE of {a_l, b_l : l = 0,1,2} and the best linear unbiased predictor (BLUP) of {a_2+k, b_2+k, k = 1,2, …, K} for the reduced linear mixed model are comparable to the {a_l, b_l : l = 0,1,2, …, 2 + K} under the optimal choice of (λ₁, λ₂) based on GCV. In addition, the mixed-effects model approach is shown to be less sensitive to mis-specification of error dependence structure, compared to GCV-based approach (Krivobokova & Kauermann, 2007). Furthermore, the existence of robust mixed model software on several platforms (e.g., SAS PROC MIXED, R package nlme) make this approach an excellent choice in practice, without having to use specialized algorithms.

Implementation Using SAS

The implementation of the P-spline approach to estimating TVEM using SAS is quite straightforward. Here we demonstrate the procedure using a real example, which we describe in more detail in the next section. The real data set contains four variables: ID (subject id), T (measurement time in days, which range from −3 to 13 with day 0 being the quit day), SE (self efficacy), and PA (positive affect). In order to study positive affect and how the relationship between positive affect and self-efficacy change over time, we fit the following TVEM

$$\mathit{\text{SE}}={\beta }_0(T)+{\beta }_1(T)\mathit{\text{PA}}+\epsilon .$$

For illustration purposes only, suppose we use 4 knots at (τ₁, …, τ₄) = (0,3,6,9), though we have tried different number of knots (i.e., K = 1 to 5) in empirical analysis. Replacing the coefficient functions with splines, and treating the coefficients of truncated power functions as random effects, the above TVEM becomes a linear mixed effect model:

$$\mathit{\text{SE}}=\left\{a_0+a_{1}T+a_2{T}^2+{\displaystyle \sum _{k=1}^4}{a}_{2+k}{(T-{\tau }_k)}_{+}^2\right\}+\left\{b_0+b_{1}T+b_2{T}^2+{\displaystyle \sum _{k=1}^4}{b}_{2+k}{(T-{\tau }_k)}_{+}^2\right\}\mathit{\text{PA}}+\epsilon ,$$

with

$$(a_3,\dots ,a_6)\prime ~N(0,{\eta }_1{\mathrm{I}}_4),(b_3,\dots ,b_6)\prime ~N(0,{\eta }_2{\mathrm{I}}_4).$$

Thus, to implement the above steps in SAS, we first need to generate new covariates representing $T^2,{(T-0)}_{+}^2,{(T-3)}_{+}^2,{(T-6)}_{+}^2,{(T-9)}_{+}^2,\text{ and }T\times \mathit{\text{PA}},T^2\times \mathit{\text{PA}},{(T-0)}_{+}^2\times \mathit{\text{PA}},{(T-3)}_{+}^2\times \mathit{\text{PA}},{(T-6)}_{+}^2\times \mathit{\text{PA}},{(T-9)}_{+}^2\times \mathit{\text{PA}}$. The following SAS code is used for this.

DATA SEPA;
 SET SEPA;
 T2 = T**2;
 PT1 = ((T−0)**2)*(T>0);
 PT2 = ((T−3)**2)*(T>3);
 PT3 = ((T−6)**2)*(T>6);
 PT4 = ((T−9)**2)*(T>9);
 XT = T*PA; XT2 = (T**2)*PA;
 XPT1 = ((T−0)**2)*(T>0)*PA;
 XPT2 = ((T−3)**2)*(T>3)*PA;
 XPT3 = ((T−6)**2)*(T>6)*PA;
 XPT4 = ((T−9)**2)*(T>9)*PA;
RUN;

With the new covariates added to the data set, we now fit the above mixed effect model using SAS PROC MIXED.

PROC MIXED DATA = SEPA METHOD=reml;
 Class ID;
 Model SE = T T2 PA XT XT2 /solution;
 Random PT1–PT4 /S TYPE=TOEP(1);
 Random XPT1–XPT4 /S TYPE=TOEP(1);
RUN;

Notice that in the SAS code we put “PT1–PT4” and “XPT1–XPT4” into two groups of random effects to reflect the fact that the variance components η₁ and η₂ could be different. This step will produce estimates of fixed effects “T”, “T2”, “PA”, “XT”, and “XT2” (â₁, â₂, b̂₀, b̂₁, b̂₂) plus the intercept (â₀) and BLUP of random effects “PT1–PT4” (â₃ through â₆) and “XPT1–XPT4” (â₃ through b̂₆). We can then estimate the coefficient functions:

$${\widehat{\beta }}_0(t)={\widehat{a}}_0+{\widehat{a}}_{1}t+{\widehat{a}}_2{t}^2+{\displaystyle \sum _{k=1}^4}{\widehat{a}}_{2+k}{(t-{\tau }_k)}_{+}^2,{\widehat{\beta }}_1(t)={\widehat{b}}_0+{\widehat{b}}_{1}t+{\widehat{b}}_2{t}^2+{\displaystyle \sum _{k=1}^4}{\widehat{b}}_{2+k}{(t-{\tau }_k)}_{+}^2.$$

One may repeat the above steps using different K, to obtain satisfactory fit. Thus, it would be convenient to have a SAS macro which treats K as a parameter and automatically generates required covariates, invokes PROC MIXED, and outputs the estimates needed. To this end and also to make TVEM conveniently accessible to applied researchers, we developed a user-friendly SAS macro that is available for download from http://methodology.psu.edu. Some details of the syntax of this SAS macro as well as the sample code are provided in the Appendix. The application section illustrates the use of the macro with simulated and empirical examples.

Before we move to the more technical issue of knots selection and model selection, we comment here that the P-spline-based approach can be extended to estimate a more complicated TVEM which includes random effects and certain error dependence structure. To illustrate this, we consider a TVEM with random intercepts (i.e., different subjects may have different initial values of SE)

$${\mathit{\text{SE}}}_{\mathit{\text{ij}}}={\alpha }_i+{\beta }_0(T_{\mathit{\text{ij}}})+{\beta }_1(T_{\mathit{\text{ij}}}){\mathit{\text{PA}}}_{\mathit{\text{ij}}}+{\epsilon }_{\mathit{\text{ij}}},{\alpha }_i~N(0,{\tau }^2),$$

and assume, for illustration, that {ε_ij, j = 1,2, …, m_i} follows AR(1) model. To fit this model, we only need to change the SAS code for fitting mixed effect models:

PROC MIXED DATA = SEPA METHOD=reml;
 Class ID;
 Model SE = T T2 PA XT XT2 /solution;
 Random PT1–PT4 /S TYPE=TOEP(1);
 Random XPT1–XPT4 /S TYPE=TOEP(1);
 Random Int /S TYPE=TOEP(1) Subject = ID;
 Repeated / type=AR(1) Subject=ID;
RUN;

That is, we added a “Random” statement for random intercepts, and a “Repeated” statement for the error dependence structure (AR(1) here). Clearly, through careful specification of the corresponding statements in PROC MIXED, one can fit a very specific TVEM by using the P-spline-based approach.

Selection of the Number of Knots

Theoretically, we only need to choose a large enough K in the P-spline based approach, and then optimally estimate the coefficients using the linear mixed-effects model. However, there is no common knowledge of how large K should be. For example, Wand (2003) suggested K = min(N/4,35) with N being the number of distinctive measurement times, while Ruppert (2002) suggested that K around 10 is enough for estimating monotone or single mode functions, but K around 20 is needed for estimating more complicated functions with multiple modes.

In practice, one often needs to try different number of knots and compare their model fittings. We suggest to start with a moderate number of knots, like K = 10. Such a number of knots is sufficient for capturing overall features of rather complicated shapes and providing useful information about the complexity of the time-varying phenomena for further adjustment of K. In addition, in practice, we may expect that the shapes of change may range in complexities: some may follow familiar parametric forms, but others may be too complicated to be described by any familiar forms. A moderate number of knots is in the mid-range of enabling moving up to fit more complicated models and moving down to simpler (or even parametric) models. Taking this into account, we propose the following procedure for choosing K in psychology research:

1. Start from a reasonable number of K (e.g., 10), and record the Akaike's information criterion (AIC; Akaike 1974) or Bayesian information criterion (BIC; Schwarz 1978) values of the fitted model;

2. Inspect the shapes of the estimated coefficient functions;

3. Decrease K gradually if the estimated coefficient functions are mostly stable (constant, or linear in time). Increase K gradually if the functions change substantially over time. Record the values of AIC and BIC for models with different numbers of knots.

4. Choose the optimal K based on the smallest values of AIC or BIC indices.

In the calculation of AIC or BIC for model comparison, we let the degrees of freedom be the “effective degrees of freedom,” as defined in Ruppert (2002), to take into account the effect of the penalty terms in Equation 9. AIC and BIC may choose different final models because the penalty for additional parameters in BIC is stronger than that of the AIC. Consequently, BIC prefers a simpler model than AIC does. We leave the choice between AIC and BIC up to researchers, since different researchers may have different preferences regarding the two model-selection criteria. A systematic comparison of AIC, BIC, and other criteria for the selection of K is an important direction for further research. In general, when K is large enough, further increasing K will not cause significant change in AIC/BIC and in the estimated coefficient functions (since appropriate penalty will counter the effect of overfitting).

In exploratory research, one does not have to stop at the estimated coefficient functions under the selected optimal K. Rather, further model selection, leading to a more parsimonious model, is often possible. When some estimated coefficient functions under the optimal K have familiar shapes (i.e., linear, quadratic), it is reasonable to hypothesize that these coefficient functions may indeed have parametric forms. One could then fit a semi-parametric TVEM in which some coefficient functions follow a parametric form, and use AIC or BIC to compare the fit of the simplified model to that of the full TVEM. In this way, TVEM enables researchers to follow an objective evidence-based modeling procedure: (a) starting from the most flexible model, and (b) gradually reducing to a parsimonious model based on knowledge revealed by more general models.

Alternative Methods

The P-spline-based approach described in the last section is just one of several popular approaches to estimating coefficient functions of TVEM. In this section, we first briefly describe other popular approaches which have also been well-established in the statistical literature, and then compare these approaches, and explain why we choose to introduce the P-spline based approach in this article.

Smoothing splines

Considering estimating Equation 3 again, the smoothing splines approach (Wahba, 1990; Green and Silverman, 1994) minimizes the following penalized log-likelihood function:

$${\displaystyle \sum _{i=1}^n}{\displaystyle \sum _{j=1}^{m_i}}{\{y_{\mathit{\text{ij}}}-{\beta }_0(t_{\mathit{\text{ij}}})-{\beta }_1(t_{\mathit{\text{ij}}})\}}^2+{\lambda }_1{\displaystyle \int }{\{{\beta }_0^{″}(t)\}}^2\mathit{\text{dt}}+{\lambda }_2{\displaystyle \int }{\{{\beta }_1^{″}(t)\}}^2\mathit{\text{dt}},$$

with respect to function β₀(t) and β₁(t), where the first term represents the fidelity of the model to the data, and ∫{β″(t)}²dt is a roughness measurement of the function β(t), and ∫{β″(t)}²dt = 0 if β(t) is a linear function. Solving the above optimization problem is equivalent to estimating the coefficient functions using piecewise polynomials (i.e., natural cubic splines, Wahba, 1990) using all the distinct measurement times as knots. Again, in this approach, the smoothing parameters λ₁ and λ₂ control the trade-off between goodness of fit and smoothness of the fitted coefficient functions, and one can use GCV (Wahba, 1990) or generalized maximum likelihood (GML; Wahba, 1985) to choose appropriate smoothing parameters.

Regression splines

Like the P-spline-based approach and smoothing splines, the regression spline approach (Stone et al, 1997) also uses splines to approximate coefficient functions. In contrast to P-spline-based approach or smoothing splines, regression splines uses a small number of knots (e.g., 3–5). In order to obtain satisfactory fit, this approach relies on careful choice of the number of knots and the locations of knots, which could be achieved by the adaptive knot allocation strategies recommended in Stone et al. (1997). Fok & Ramsay (2006) employs regression splines, using different number of knots without adjusting the locations of the knots, in the analysis of the personality study of Brown & Moskowitz (1998).

Kernel-based methods

Unlike spline-based approaches which approximate unknown coefficient functions with splines over a given study period, the kernel-based methods, also called locally weighted polynomial regression methods, estimate the unknown intercept function β₀(t) and coefficient function β₁(t) pointwise. More specifically, to estimate β₀(t₀) and β₀(t₀) for a given time point t₀, kernel based methods approximate the coefficient functions with linear functions (i.e., β₀(t) ≈ a₀ + a₁ · (t − t₀) and β₁(t) ≈ b₀ + b₁ · (t − t₀)) in a time window [t₀ − h, t₀ + h], and transform the nonparametric model into a (locally) linear regression model. The choice of bandwidth (h) balances the smoothness and fitness of the estimated coefficient functions: the larger the bandwidth, the smoother the estimated functions but at the cost of larger bias. The discussion of the specification of weights and the choice of bandwidth are beyond the scope of this article. Interested readers are referred to Fan & Gijbels (1996), and Wu & Zhang (2002). In addition, Li et al (2006) contains an application of using local polynomial method to fitting a smoking cessation data set.

Summary

Although these approaches look quite different, they actually share similar ideas: they all approximate unknown functions with simpler functions, globally or locally, and they all consider balancing the trade-off of fitness (good approximation) and smoothness (less fluctuation) by adjusting certain tuning parameters (i.e., bandwith h for kernel-based approach, smoothing parameters for smoothing splines and P-spline-based approach, and knots positions for regression splines). These approaches will obtain similar results. However, these approaches do differ with respect to implementation: the regression splines and smoothing splines require specific algorithms and software, which is not widely used among behavioral scientists, while the kernel-based approach may require an advanced bandwidth selection procedure (Fan & Gijbels, 1996), which is beyond the reach of practical users. Thus, we suggest the use of P-spline based approach because it very easy to implement using popular software like SAS PROC MIXED, and also flexible enough to consider more complicated TVEM with random effects and certain error dependence.

Applications

This section provides two examples of implementing TVEM in ILD research. Our first example is simulated, where we evaluate performance of the model. The second example presents empirical data from a smoking cessation study, testing the time-varying effect of positive affect on self-efficacy towards smoking cessation.

A Simulated Example

Our first demonstration uses a simulated data set. The advantage of using simulated data for illustration purposes is that the true model is known and, thus, the method's performance can be evaluated by comparing the estimated results to the true model.

Data generation

Two ILD sets were generated for samples of 50 and 100 individuals, respectively, with 30 repeated assessments per person. Measurement times for each individual were set to be uniformly distributed over the interval of [0,1]. To mimic a real situation, each individual was designed to have approximately responses missing completely at random. This yields, on average,30 × 0.8 = 24 observations per person. For an individual i, two covariates, x_ij1 and x_ij2, and the outcome variable, y_ij, were generated at measurement times t_ij. To create x_ij1 and x_ij2, we first generated two independent standard normal random numbers, z_ij1 and z_ij2. Then, we let x_ij1 equal if z_ij1 > 0 and equal otherwise, and specified x_ij2 as $(z_{\mathit{\text{ij}}1}+z_{\mathit{\text{ij}}2})/\sqrt{2}$. In this way, x_ij1 was created as a binary variable and x_ij2 followed a standard normal distribution. Furthermore, the covariates were correlated (Pearson r ≈ 0.56) as in many practical situations.

Model specification

For both data sets, the following TVEM specifies the relationship between the covariates and the outcome:

$$y_{\mathit{\text{ij}}}=a(t_{\mathit{\text{ij}}})+b(t_{\mathit{\text{ij}}})·x_{\mathit{\text{ij}}1}+c(t_{\mathit{\text{ij}}})·x_{\mathit{\text{ij}}2}+e_{\mathit{\text{ij}}},$$ (11)

where

$$a(t)=\text{exp}\left(2t-1\right),b(t)=8t(1-t),c(t)=2{\text{sin}}^2(2\pi t),$$

and the error term follows the AR(1) structure:

$$e_{\mathit{\text{ij}}}=\rho ·e_{i(j-1)}+{\epsilon }_{\mathit{\text{ij}}},$$

with ε_ij being independent and identically distributed Gaussian random variables with variance σ². Specifically, in our simulations, we set ρ = 1 and σ² = 1.

Estimation procedure

To estimate the coefficient functions in Equation 11, we started by specifying the number of knots at 5, and progressively increasing them up to 9, recording the AIC and BIC model fit statistics. To mimic a real situation, we pretended that we did not know the true covariance structure, but assumed a working independence structure for the error terms in the estimation.

Results

The values of AIC and BIC for different numbers of knots in the estimation are listed in Table 2. For both data sets, the BIC suggests a model with 6 knots, while the AIC suggests one with 6 knots (n=50) and one with 7 knots (n=100). Figure 4 presents the estimated coefficient functions using 6 knots, which are nearly indistinguishable from those using 7 knots.

Table 2.

Fit Statistics for the TVEM Fitted to Simulated Data

	n = 50		n = 100
K	AIC	BIC	AIC	BIC
5	3500.3	3528.5	6928.5	6966.5
6	3491.8	3514.0	6919.2	6958.9
7	3498.2	3528.6	6917.4	6959.2
8	3498.2	3529.2	6920.2	6963.1
9	3498.2	3529.1	6919.1	6963.1

Note. K is the number of knots for the truncated power splines. Numbers in bold are the minimal AIC/BIC values in each column.

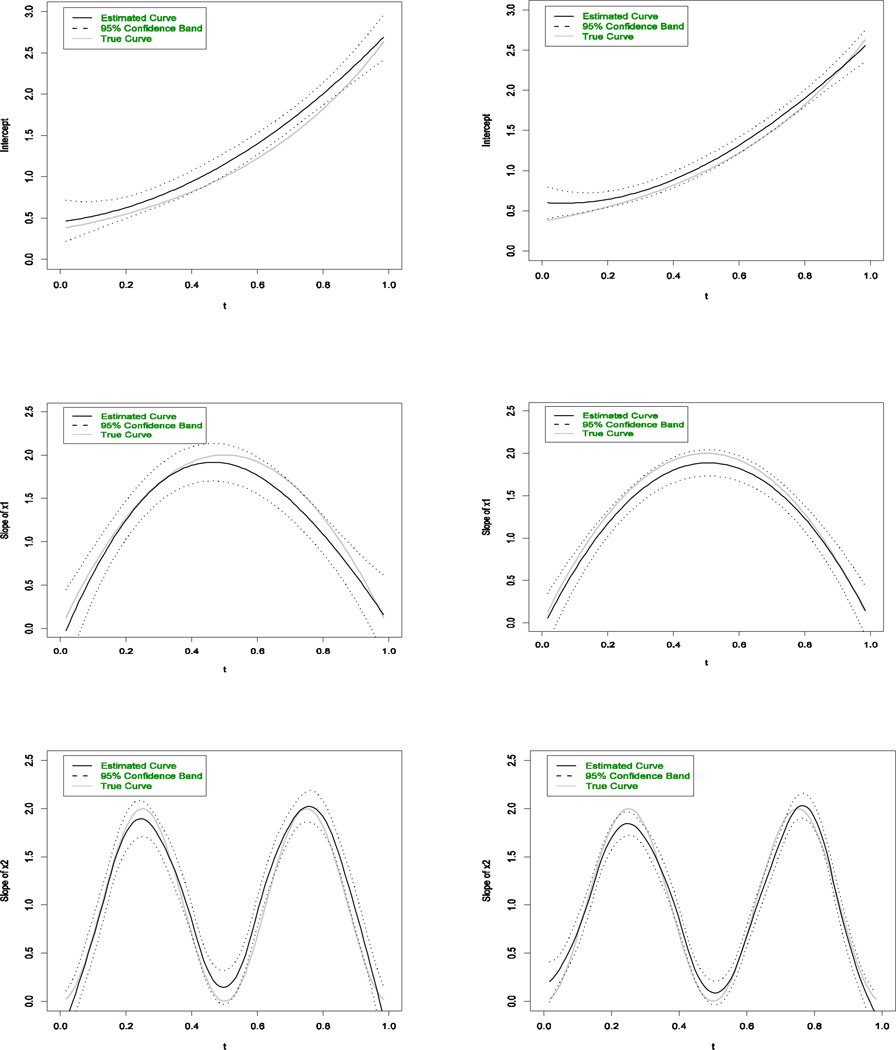
Figure 4.

Estimated coefficient functions for simulated data with 6 knots. Left column: sample size =50; right column: sample size =100. Top row: intercept function; middle row: coefficient function for X₁; bottom Upper row: coefficient function for X₂.

Overall, the performance of the P-spline based method is satisfactory in that it revealed the underlying shapes of all three coefficient functions: the true coefficient functions are largely within the 95% confidence band of the estimated coefficients and quite close to the estimated coefficients. The confidence bands for the estimated coefficient functions in the right column are narrower than their counterparts in the left column in Figure 4. This indicates that the increased sample size could lead to more accurate estimates of these coefficient functions, as expected. Another important finding from the simulation study is that the number of knots in the final model is not essential for recovering the true underlying function, as long as it is large enough. The estimated functions with larger than 6 knots look very similar; the AICs are similar as well.

Note that we assumed an independent error process in estimation, while our data were generated from a model with an AR(1) covariance structure. This model mis-specification did not compromise the results. According to Liang & Zeger (1986), mis-specification of the covariance structure does not affect the consistency of the estimated coefficient functions, although it does result in wider confidence bands due to decreased estimation efficiency.

An Empirical Example: Smoking Cessation Study

The ILD for our empirical example come from a randomized controlled clinical trial designed to evaluate the efficacy of the scheduled reduced smoking (SRS) cessation intervention (Cinciripini, Wetter & McClure, 1997) in a sample of newly diagnosed cancer patients awaiting a cancer-related surgery (Shiyko, Li, & Rindskopf, in press). SRS is a behavioral intervention, entailing a gradual reduction of smoking on a pre-determined schedule delivered by a personal digital assistant (PDA). By asking people to smoke on PDA prompts, SRS attempts to eliminate the “free will” component of the smoking behavior and increase self-efficacy (SE) for quitting smoking (Cinciripini, Lapitsky, Seay, Wallfisch, Kitchens, & Van Vunakis, 1995; Cinciripini et al., 1997). In addition, PDAs were used to assess the momentary affective state and self-efficacy at random points throughout a day. The effect of momentary positive affect on smoking abstinence self-efficacy over the course of behavior monitoring period is the focus of the current analysis.

Data description

Sixty-six individuals in the SRS condition yielded 1665 momentary assessments of positive affect (PA) and self-efficacy, averaging 24.5 assessments per person (SD = 25.2, median = 17.5, min = 1, max = 117). Analytically, we were interested in the relationship between positive affect and self-efficacy for smoking abstinence immediately prior to and following a quit attempt (QA). The QA was defined as the originally scheduled quit date or a person-initiated quit date, depending on which occurred earlier. Time of QA served as an origin of the time scale, taking negative values for days preceding a QA (for the minimum of −3) and positive values for days following a QA (for the maximum of 13). In addition, time (days before or after QA), could take fractional value, to accommodate multiple-times-per-day assessment schedule.

Self-efficacy of the ability to abstain from smoking was assessed by two 5-point Likert-type questions, targeting confidence in one's ability to refrain from smoking after surgery and in the following 6 months, ranging from 0 (not at all confident) to 4 (completely confident). Responses to these two items (Pearson r = .90, SE = .004) were averaged to comprise an overall post-surgery abstinence self-efficacy. The measure of positive affect was an average of responses to four PANAS scale items (Cronbach's alpha = .93; Watson, Clark, & Tellegen, 1988), assessing the degree of feeling strong, proud, inspired, and determined on a 4-point scale, ranging from 0 (very slightly or not at all) to 4 (extremely). Average level of positive affect across all time points and all individuals was 1.77 points (SD = 1.24). Average level of self-efficacy was 2.52 (SD = .87).

Drop-out occurred when a smoker stopped using PDA before his/her scheduled stopping time (i.e., having surgery). Relapse did not necessarily lead to drop-out, because some smokers still responded to PDA prompts even after after they relapsed. In total, 28 of 60 smokers stopped using PDA. We divided the 60 subjects into drop-out (stopped using PDA) and non-drop-out subgroups, and compared the spaghetti plots (not shown here) of self-efficacy post-QA of these two sub-groups. The two spaghetti plots look quite similar, which indicates that the drop-outs did not depend on self-efficacy level. Hence, in our analysis, we assumed the drop-outs were non-informative, and analyzed them the same way as complete data.

Model specification and model fitting

To examine temporal changes in the relationship between positive affect (PA) and smoking abstinence self-efficacy (SE), the following TVEM was fitted:

$${\mathit{\text{SE}}}_{\mathit{\text{ij}}}={\beta }_0(t_{\mathit{\text{ij}}})+{\beta }_1(t_{\mathit{\text{ij}}})·{\mathit{\text{PA}}}_{\mathit{\text{ij}}}+e_{\mathit{\text{ij}}}.$$ (12)

In Equation 12, β₀(·) is the intercept function, representing the self-efficacy trajectory over the course of about 2 weeks for patients who reported very low positive affect (PA = 0). Of note, 13.3% of affect assessments were at that level. The slope function β₁(·) characterizes the progressive pattern of the relationship between the intensity of positive affect and abstinence self-efficacy over the same time interval. Changes in the magnitude and direction of the relationship between positive affect and self-efficacy pre- and post- QA are of particular interest to us. Practically speaking, the slope function tells us by how much the outcome, SE, is expected to change with a unit change in PA, across the study time continuum. Thus, instead of a single slope parameter, commonly estimated in MLM, we obtain a magnitude of parameters, the values of which change with time. In cases in which an estimated function is not constant, the effect of a covariate should be interpreted with reference to a specific time interval.

The P-spline-based method was employed to progressively fit the specified model. The number of knots for intercept and slope functions were varied, and changes in BIC and AIC fit indices were compared to determine the best fitting model.

Results

Table 3 presents values of BIC and AIC indices for models with zero through five knots. Based on the smallest BIC and AIC criteria, the model with a single knot for the intercept and slope function parameters was identified as the best fitting model. More complicated models (knots > 5) were not considered due to progressive worsening of the fit indices (i.e. increasing AIC and BIC). Since both intercept and slope functions were estimated with a single-knot TVEM, Equations (7) and (8) which define shapes of the functions, would simplify to contain only one additional term a₃(t − τ₄)², where a single knot K = 1 is placed at 4 days, a point that is splitting the study time into two equal intervals (a default option in the TVEM macro).

Table 3.

Fit Statistics for the TVEM Fitted to Self-Efficacy and Positive Affect Empirical Data

K	BIC	AIC
0	3996.3	3963.8
1	3994.6	3957.2
2	4000.9	3960.8
3	4002.6	3960.3
4	4002.1	3960.4
5	4002.2	3960.5

Note. K is the number of knots for the truncated power splines. Numbers in bold are the minimal AIC/BIC values in each column.

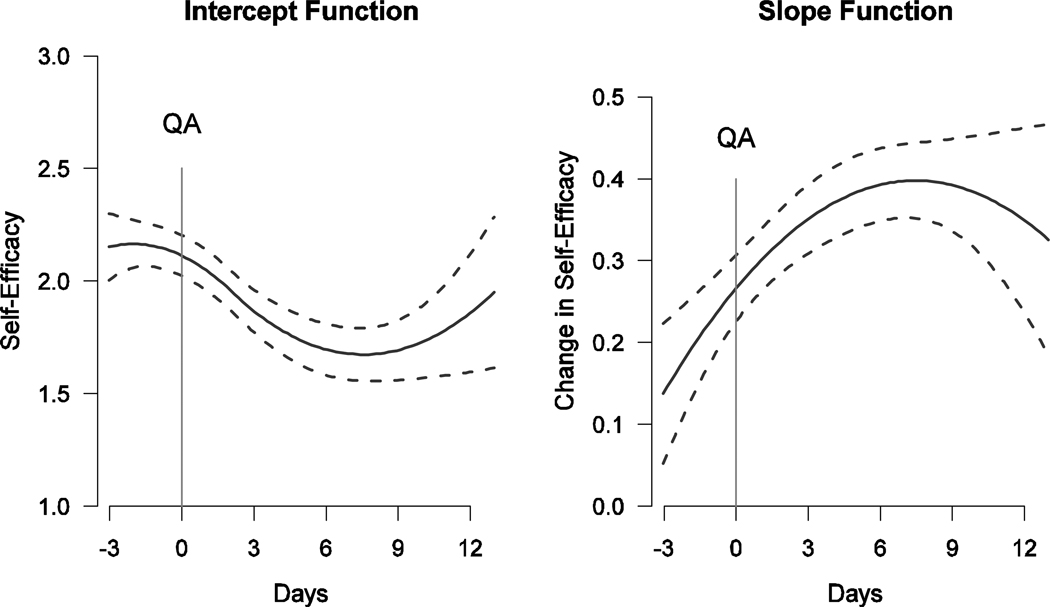
Parameter estimates of the final model are summarized graphically in Figure 5. Because of the fluctuating magnitude and direction of intercept and slope parameters, it appears that time serves an important role in defining the model. In the graphical summary of the intercept function, we can see that individuals who reported zero positive affect experienced a decrease in self-efficacy following their QA. Initially, they were more than moderately (Self-Efficacy ≈ 2) confident in their ability to refrain from smoking in the post-surgical period, but they gradually transitioned to being less than moderately (SE < 2) confident. There was a slight increase in intercept function towards the study end with a widening confidence interval, which is attributable to more sparse observations. Thus, the interpretation of this change should be cautious. Likely, SE is leveling off towards the end.

Figure 5.

Intercept (left plot) and slope (right plot) function estimates for the empirical data. In each plot, the solid line represents the estimated intercept or slope function, and the dotted lines represent the 95% confidence interval of the estimated function.

The slope function shows that the effect of positive affect on quitting self-efficacy increased with time. Prior to QA, the effect of positive affect ranged somewhere from .14 to .26; following the QA, it ranged from .26 to .39, signifying an increased association between positive affect and one's self-efficacy to abstain from smoking. Similarly to the intercept function, temporal changes towards the end of study are likely to be an artifact of data sparseness.

Implications from Empirical Data

Self-efficacy towards smoking cessation has been long considered one of the defining factors of success in quitting smoking (e.g., Dornelas, Sampson, Gray, Waters, & Thompson, 2000; Gritz, Carmack, de Moor, Coscarelli, Schacherer, Meyers, & Abemayor, 1999; Houston & Miller, 1997; Ockene, Emmons, Mermelstein, Perkins, Bonollo, Voorhees, & Hollis, 2000; Smith, Kraemer, Miller, DeBusk, & Taylor, 1999; Taylor, Houston-Miller, Killen, & DeBusk, 1990; Taylor, Miller, Herman, Smith, Sobel, Fisher, & DeBusk, 1996). Some cross-sectional studies explored correlates of SE, with positive affect being one of them (e.g., Martinez, Tatum, Glass, Bernath, Ferris, Reynolds, & Schnoll, 2010). Negative affect has been previously linked with an increase in smoking urges post quit (e.g., Li et al., 2006; Shiffman, Paty, Gnys, Kassel, & Hickcox, 1996), but no studies explored possible time-varying associations between NA and SE.

Based on the results of TVEM, time was shown to play an important role in defining the strength of the association between PA and SE. Overall, individuals with higher levels of PA reported higher SE. This relationship was magnified, however, following the quit attempt. This finding may suggest that future smoking cessation intervention strategies could target a patient's positive affect around the quit attempt. Traditional approaches like multilevel modeling would estimate the average effect of PA on SE. However, the flexibility of TVEM allowed for a full exploration of the relationship without setting a priori constraints on the shape of intercept and association functions.

In this example, a model with one knot was sufficient to describe the relationship. In other word, these estimated coefficient functions were piecewise (two pieces to be exact) quadratic functions which can be represented as

$${\beta }_0(t)=a_0+a_{1}t+a_2{t}^2+a_3{(t-4)}_{+}^2,{\beta }_1(t)=b_0+b_{1}t+b_2{t}^2+b_3{(t-4)}_{+}^2;$$

since the single knot was placed at τ = 4in this example when K = 1. It might be reasonable to hypothesize that these coefficient functions can be represented by cubic or quartic functions. This implies that TVEM can be used as an exploratory tool to hint at whether the course of changes follow certain familiar parametric form. In this study, however, we are reluctant to try higher order polynomials due to the Runge phenomenon.

Discussion

In this paper, we introduced TVEM as a novel approach for analyzing ILD to study the course of change. With technological innovations, collection of ILD in the behavioral sciences is increasing, which opens new opportunities to address empirically important questions about the relationship between time-varying covariates and outcomes of interest. TVEM provides a flexible medium for exploring this relationship and incorporating time as a third dimension. In the model, the influence of a covariate is reduced to a momentary period, such that the strength and magnitude of the association vary as time changes.

While TVEM has not been previously used in psychological research, its potential is evident. ILD are frequently being collected for quickly changing phenomena, such as positive or negative affect, self-efficacy, urges, and blood pressure. Not only do these factors change on a momentary basis, but their influence on each other may also be subject to fluctuations. TVEM allows studying this change as a function of time. Importantly, the model does not assume any specific pattern of the relationship, and the underlying non-parametric nature allows any longitudinal shapes to be accommodated.

The non-parametric nature of the model can be used in several ways. First, it can account for inherently non-linear longitudinal relationships, resulting in a model with temporal ups and downs. The simulated data is an example of such applications. Alternatively, TVEM can be used as a diagnostic tool to help simplify the shape of a certain varying relationship to a known parametric function, based on graphical summaries and fit statistics.

While the focus of this article was on time-varying covariates, TVEM can be expanded to incorporate invariant covariates as well to study how their impact changes with time. For instance, the effect of a treatment (e.g., for smoking cessation, for regulation of blood-sugar in diabetics, or for improving exercise habits) may change over time. In those cases, researchers may be interested in observing the trajectories of behavior change in response to an intervention. For example, by including gender in the model, we can obtain separate estimates of coefficient functions for males and females.

We introduced a very basic TVEM in this paper, and this model can be extended to more complicated TVEMs to describe individual differences (i.e., by including random effects), and inter-correlation of repeated observations. However, it is worth noting that ILD may contain complicated (unique) error structures, since observations may be nested within the same days, month, and so forth. Such error structures are not standard options in popular software like SAS PROC MIXED, and extensive research on how to incorporate specific error structure of ILD is needed.

As TVEM has not yet been extensively studied, little is known about the required sample size, the required number of repeated assessments,² the impact of missing data, and inter-variability across individuals on the robustness of model estimation. The answers to these questions await future research. Our simulated example with 100 individuals and about 25 measurements per individual, however, demonstrates satisfactory model performance.

Future extensions of TVEM might allow the modeling of non-normally distributed outcomes employing generalized linear models, and modeling inter-individual variability in coefficient functions through incorporating random coefficient functions. Such extensions could make TVEM more appealing in applications, and this motivates our continued work in this area.

Appendix

To facilitate the implementation of the spline-based method for the estimation of the time-varying effect model, we have developed a SAS Macro, %TVEM, to estimate the time-varying effect model. The source code for this macro is available on the APA website (http://apa.apa.org) and the website of the Methodology Center of the Pennsylvania State University (http://methodology.psu.edu). In this section, we will briefly describe the syntax of this macro using an artificial example.

Suppose the SAS data set new_data contains the following variables:

• subjects' identification, character variable;

• measurement time for each observation, different subjects may have different times of measurement;

• a dependent variable;

• an intercept, the value of which equals 1 for all observations;

• a binary covariate;

• a continuous covariate.

The data set new_data has a longitudinal structure (Table 4).

Table 4.

Data Structure of the Dataset new_data

	Variable names
Observation	subj	y	t	x0	x1	x2
1	1	0.74397	0.00591	1	0	−1.71718
2	1	−0.68537	0.01378	1	0	−1.99814
3	1	0.20471	0.01772	1	1	0.59689
4	1	−0.63517	0.02559	1	1	−0.21331
5	1	2.08357	0.02953	1	1	1.10735
6	2	1.70600	0.00197	1	1	1.28186
7	2	0.49824	0.00591	1	1	1.55535
8	2	0.52604	0.00984	1	0	−0.84808
9	2	0.20461	0.01378	1	1	0.80863
10	2	−1.05567	0.02165	1	0	0.60380
∶	∶	∶	∶	∶	∶	∶

Note. This table illustrates the layout of the dataset new_data by listing the values of 6 variables for 10 hypothetical observations.

The model with varying effect to be estimated is as follows:

$$y(t)=a(t)·x_0(t)+b(t)·x_1(t)+c(t)·x_2(t)+e(t).$$

Below is the SAS code to fit this model:

%TVEM(
    mydata = new_data, /* dataset, longitudinal data structure */
    id = subj,   /* subject ID indicator */
    time = t,    /* time indicator */
    dep = y,     /*the outcome */
    class_var = ,  /* classification variables */
    tcov = x0 x1 x2,  /* variables with time-varying coefficients */
    cov_knots = 5 5 5, /*the number of knots for each time-varying covariate 

*/
    cov = ,       /* covariates with time-constant coefficients */
    evenly = 0,     /*knots evenly in space (0) or on quantiles (1) */
    scale = 100,    /* the number of time points to be plotted */
    outfilename =    /* name of a file to save plot data */
    );

The meanings of the first four parameters: mydata, id, time, dep, in the above macro code are self-explanatory. The meaning of the other 6 parameters are explained as follows.

The Meaning of the Last 6 Parameters in SAS Macro %TVEM

Parameter	Description
class_var	Names the classification variables in the analysis. Classification variables can be either character or numeric (e.g., day of week, race).
tcov	The names of all covariates with time-varying effect in the time-varying effect model. Notice that an all 1 variable, like x0 in this example, should be included in this parameter if the time-varying effect includes an intercept function.
cov_knots	The number of inner knots are specified for all time-varying parameters (e.g., intercept and slopes).
cov	The names of all covariates assumed to have non-varying coefficients are listed in this parameter. These covariates (value) can be time-varying. In our example, we don't have such covariates and simply leave the statement blank.
evenly	This parameter determines the positions of inner knots. We provide two methods: one (evenly=1) is to place inner knots evenly in space over the range of measurement times of all observations, zero (evenly=0) is to place them on evenly distributed quantiles of the pooled observation times.
scale	This parameter determines the number of grid points to be plotted in the graphs. By default, the number of grid points for parameter coefficient functions and their confidence bands are set to 100.
outfilename	Output file name. The macro generates a csv file with path and name specified by this parameter. This csv file contains the data for plotting the coefficient curves and their confidence bands in a spreadsheet software package if needed. By default, the csv file is saved in the temporary SAS working directory with the name plot_data.csv.