Fibrillization Propensity for Short Designed Hexapeptides Predicted by Computer Simulation

Abstract

Assembly of normally soluble proteins into ordered aggregates, known as amyloid fibrils, is a cause or associated symptom of numerous human disorders, including Alzheimer’s and the prion diseases. Here we test the ability of discontinuous molecular dynamics (DMD) simulations based on PRIME20, a new intermediate-resolution protein force field, to predict which designed hexapeptide sequences will form fibrils, which will not, and how this depends on temperature and concentration. Simulations were performed on 48 peptide systems containing STVIIE, STVIFE, STVIVE, STAIIE, STVIAE, STVIGE, and STVIEE starting from random coil configurations. By the end of the simulations STVIIE and STVIFE (which form fibrils in vitro) form fibrils over a range of temperatures, STVIEE (which doesn’t form fibrils in vitro) doesn’t form fibrils, and STVIVE, STAIIE, STVIAE, and STVIGE (which don’t form fibrils in vitro) form fibrils at lower temperatures but stop forming fibrils at higher temperatures. At the highest temperatures simulated, the results on the fibrillization propensity of the seven short de novo designed peptides all agree with the experiments of López de la Paz and Serrano. Our results suggests that the fibrillization temperature (temperature above which fibrils cease to form) is a measure of fibril stability and that by rank ordering the fibrillization temperatures of various sequences PRIME20/DMD simulations could be used to ascertain their relative fibrillization propensities. A phase diagram showing regions in the temperature-concentration plane where fibrils are formed in our simulations is presented.

Introduction

Fibril or amyloid formation is a symptom in nearly 40 diseases^1–7. Although a different protein and a different organ system are involved in each of these diseases, the fibrils associated with all of them exhibit “cross-β structure”, which consists of layers of β-sheets running parallel to the fibril axis containing strands that run perpendicular to the fibril axis⁸. Views on fibril formation have changed over the years. Fibril formation was originally thought to be an aberration specific to disease-related proteins like Aβ, α-synuclein and the prion proteins. The discovery in the late 90s⁹ that non-disease related proteins could also form amyloid prompted the view that fibrillization is driven by generic features common to most proteins, e.g., hydrophobicity and the tendency to hydrogen bond¹⁰, under slightly- denatured concentrated conditions. In recent years the emphasis has shifted again to the role played by sequence in determining whether or not a protein will form fibrils. Evidence suggests that the sequence of a protein, particularly the hydrophobicity, size and charge of the side-chains, impacts its ability to adopt cross-β structure and to form steric-zipper spines and salt bridges, as well as the number of β-sheet layers, the location of disordered loops protruding from the structure, and the speed of fibrillization and/or oligomerization ^11–14. This paper is concerned with how variations in peptide sequence and system temperature affect the likelihood that a particular sequence will form a fibril and the kinetic events that occur along the fibrillization pathway.

Many of the fibril-forming proteins contain short, truncated sequences of largely hydrophobic amino acids that act as the Velcro that drives the peptides together. These protein fragments form fibrils themselves and help determine whether or not the parent peptide will form fibrils¹⁵. Examples of short fragments of amyloidogenic proteins that themselves fibrillize, include KLVFFAE (β-amyloid), NFGAIL (islet amyloid polypeptide), DFNKF (human calcitonin), and VGGAVVTGV (α-synuclein), all of which contain at least one aromatic side chain or strong hydrophobic residue. The identities and positions of the side chains along these short fragments are key, with certain amino acids enhancing and other amino acids hindering assembly into ordered structures¹⁶. The identities and positions of the side chains also determine the kinetics of the aggregation process which in turn influences the likelihood that a particular sequence will adopt a fibrillar structure or form oligomeric intermediates.

We test the ability of molecular dynamics simulations based on our new intermediate-resolution protein force field, PRIME20, to predict which short sequences will form fibrils, which will not, and how this depends on temperature. Computer simulations provide a tool complementary to experimental research that gives us a molecular-level picture of the kinetics of protein aggregation. The value of this approach lies in the insights provided about the molecular mechanisms that drive these processes, information that cannot be obtained directly from experiment. PRIME20 is a new implicit-solvent intermediate-resolution model of protein geometry and energetics that is applicable to all twenty amino acids¹⁷. It was designed to be used with discontinuous molecular dynamics (DMD), a fast alternative to traditional molecular dynamics applicable to systems interacting via discontinuous potentials, such as the square–well potential^18–26. PRIME20’s ability to distinguish the different roles played by each amino acid in protein aggregation processes is being validated here by comparing its fibrillization propensity predictions to experimental data existing in the literature.

An alternative way to predict the fibrillization propensities of specific peptide sequences or regions on a protein is to develop phenomenological equations that correlate fibrillization rates to intrinsic sequence-dependent factors and to extrinsic factors. Regression of experimental data on a variety of sequences taken from the literature²⁷, and on Aβ42, α-synuclein and tau¹⁶ to a simple linear equation revealed that the most important sequence-dependent factors were the characteristics of the individual amino acids including hydrophobicity, patterns of hydrophobic and polar residues, charge, and α-helical and β-sheet propensities. Extrinsic factors that proved to be important were concentration, pH, and ionic strength; temperature was not considered due to insufficient experimental data. The location of a sequence within a folded protein was found to affect its fibrillization propensity since buried amino acids are protected from interaction with other proteins²⁸. A variety of empirical algorithms, some available on web servers, have been developed for predicting aggregation propensity²⁹: these are summarized in a recent review. Most are aimed at predicting aggregation-prone regions within larger proteins. Computer simulation provides a complimentary approach to these prediction algorithms. Its advantage is that the molecular properties of each amino acid are based on first principles calculations; its disadvantage is that a simulation has to be conducted for each sequence, making this an inefficient approach for gauging fibrillization propensity. All-atom folding simulations on single hexapeptides and decapeptides have been used to regress the factors which are most important in aggregation; hydrophobic interactions were found to play a dominate role³⁰. To our knowledge there have been no simulation studies of specific multi-peptide systems starting from random initial configurations aimed at determining the relative aggregation propensities of different specific sequences. Although a number of coarse-grained models have been developed which contribute substantially to our understanding of the mechanisms that underlie protein aggregation, most lack the ability to directly account for sequence specificity³¹.

In this work, simulations are used to examine the kinetics along the entire pathway towards fibril formation as well as the final fibrillar structure. We simulate the spontaneous assembly of large systems containing the de novo designed peptide of López de la Paz and Serrano, STVIIE¹⁴ and six variations STVIFE, STVIVE, STAIIE, STVIAE, STVIGE, and STVIEE. The peptides were chosen to include those that formed fibrils and those that did not to give us both positive and negative controls. Forty-eight peptide systems are simulated using PRIME20/DMD starting from random configurations of random coils at high temperatures. Our purpose is to test the ability of PRIME20 to distinguish the role played by each of the twenty different amino acids in fibril formation, to validate PRIME20’s ability to predict each sequence’s propensity to form fibrils, and to contribute to the fundamental understanding of the fibril formation pathway. The systems are cooled slowly to the desired simulation temperature. We explore how changing sequence and temperature affect the aggregation pathway by monitoring the formation of different structures such as non-fibrillar β-sheets, disordered aggregates and fibrils.

This paper is organized as follows. In the next section, we describe the peptide model and simulation method. In the following section, we present the results obtained from simulation of multi-peptide systems at various conditions. The last section is a discussion of our results.

Results

The database that serves as our test bed is the large-scale scanning mutagenesis experiment by López de la Paz and Serrano on the small designed amyloid peptide STVIIE. STVIIE was designed using the PERLA algorithm to generate self-associating hexapeptide sequences. STVIIE was shown to form “very regular and homogeneous” fibrils in vitro making it an ideal candidate for further scanning mutagenesis experiments³². Fibrils were grown for 20 days at an initial concentration of 1mM at pH 7.4 and at room temperature (25°C), and then concentrated to 10mM. Fibrils were observed by circular dichroism(CD) and electron microscopy (EM) 10 days later. In the mutagenesis experiments each residue on STVIIE was replaced by nineteen of the twenty naturally occurring amino acids^14,32 to determine which of the 114 combinations were still able to form fibrils. They found that the identity and position of the substituted amino acid determined the peptide’s ability to form β-sheets, and the likelihood and rate of β-sheet association into fibrils. Mutations at positions 3, 4 and 5 were the most sensitive, especially at position 5 where only aromatic substitutions I5F and I5Y were still able to form fibrils, although the substitution of tyrosine formed less fibrils than those of phenylalanine.

In an attempt to better understand their experimental results¹⁴, López de la Paz and Serrano performed MD simulations on six different sequences (STVIIE, STVIFE, STVIGE, STVIAE, SAVIIE and SGVIIE) arranged in six-stranded β-sheets to determine which side chain mutations would destabilize the β-sheet³³. They found that sequence mutations at position five of STVIIE were most likely responsible for disruption of fibril formation.

Here we present our simulation results on 48-peptide- systems containing the de novo designed peptides : STVIIE, STVIFE, STVIVE, STAIIE, STVIAE, STVIGE, and STVIEE. The results are compared to the in vitro results of López de la Paz and Serrano^14,32 that STVIIE and STVIFE form fibrils but STVIVE, STAIIE, STVIAE, STVIGE, and STVIEE do not.

Table 1 presents results at four selected temperatures: low T*=0.13, intermediate T*=0.17, 0.175, and high T*=0.18. The table and later figures list the percentage of peptides at the end of the simulation runs that are monomers, in non-fibrillar β-sheets (meaning distorted, bent, largely out-of-register, or single β-sheets as opposed to well ordered cross-β structures), in disordered aggregates (disordered small oligomers, disordered chains attached to ordered structures), or in fibrils. In our simulations at low temperature, T*=0.13, STVIIE readily forms fibrils (well ordered cross-β structures) and so do STVIFE, STVIVE, STAIIE, and STVIAE. The latter three sequences (STVIVE, STAIIE, STVIAE) also form non-fibrillar β-sheets. STVIGE and STVIEE do not form many fibrils. Instead, a high percentage of the β-sheets observed for STVIGE are non-fibrillar (bent or largely out-of register) and for STVIEE are single β-sheets. These are labeled as being “slightly ordered” in Table 1. As we increase T* to intermediate temperatures T*=0.17, the top five peptides on the list continue to have high fibrillar content, the number of non-fibrillar β-sheets decreases (except for STVIIE) and the number of monomers increases, especially for STVIGE which no longer forms fibrils. As we increase T* still further to intermediate temperature T*=0.175, the number of sequences having high fibrillar content has dropped from five to three ; the two sequences, STAIIE and STVIAE, that cease to form fibrils at this temperature have large numbers of peptides in the monomers and non-fibrillar categories. Finally as we increaseT* to high temperatures, T*=0.18, the only peptide systems to show a high percentage of fibril structures are STVIIE and STVIFE.

Table 1.

Percentage of peptides in each sequence that are in monomer, non-fibrillar β-sheet, disordered aggregates and fibril conformations at the end of low temperature (T*=0.13), intermediate temperatures (T*=0.17, 0.175), and high temperature (T*=0.18) simulations at 10mM concentration. Values in parenthesis indicate error bars. We compared final structures at high temperature (T*=0.18) with the experimental results (Growth in vitro).

De Novo Designed Sequence	T*	% of monomers	% of non-fibril β-sheets	% of disordered aggregates	% of fibrils	Structure	Growth in vitro
STVIIE	0.13	0.0(0.0)	8.5(8.4)	1.0(0.8)	90.5(7.8)	Ordered
STVIFE	0.13	0.0(0.0)	10.6(7.1)	0.9(0.7)	88.5(6.6)	Ordered
STVIVE	0.13	0.0(0.0)	27.0(17.7)	0.0(0.0)	73.0(17.7)	Ordered
STAIIE	0.13	0.0(0.0)	29.4(18.8)	0.0(0.0)	70.6(18.7)	Ordered
STVIAE	0.13	0.0(0.0)	33.4(25.0)	0.0(0.0)	66.6(25.1)	Ordered
STVIGE	0.13	0.0(0.0)	60.2(9.8)	0.0(0.0)	39.8(9.8)	Slightly Ordered
STVIEE	0.13	0.0(0.0)	94.7(10.5)	0.0(0.0)	5.3(10.5)	Slightly Ordered
STVIIE	0.17	2.2(1.4)	11.3(6.2)	0.5(0.3)	86.0(7.4)	Ordered
STVIFE	0.17	0.2(0.2)	1.0(0.2)	0.2(0.0)	98.6(0.4)	Ordered
STVIVE	0.17	5.8(2.5)	12.1(4.3)	0.9(0.2)	81.2(6.6)	Ordered
STAIIE	0.17	15.8(4.6)	8.2(4.6)	2.9(1.5)	73.2(9.1)	Ordered
STVIAE	0.17	10.8(3.0)	13.5(8.6)	1.7(0.7)	74.0(9.3)	Ordered
STVIGE	0.17	56.1(1.2)	24.0(1.8)	20.0(0.6)	0.0(0.0)	Disordered
STVIEE	0.17	26.1(1.4)	69.8(2.0)	4.0(0.7)	0.0(0.0)	Slightly Ordered
STVIIE	0.175	8.7(3.3)	8.0(4.7)	1.6(0.6)	81.8(7.5)	Ordered
STVIFE	0.175	3.3(1.6)	2.9(1.4)	0.6(0.3)	93.2(1.9)	Ordered
STVIVE	0.175	15.4(3.8)	10.5(3.9)	3.3(1.3)	70.9(8.0)	Ordered
STAIIE	0.175	41.4(2.7)	35.6(5.3)	16.5(2.6)	6.5(10.2)	Disordered
STVIAE	0.175	41.0(1.5)	41.3(2.5)	15.2(1.0)	2.5(1.6)	Disordered
STVIGE	0.175	66.2(1.2)	12.1(1.1)	21.7(0.4)	0(0.0)	Disordered
STVIEE	0.175	55.4(3.7)	29.1(6.0)	15.5(2.3)	0(0.0)	Disordered
STVIIE	0.18	21.6(4.0)	9.3(3.4)	5.2(1.9)	64.0(8.2)	Ordered	Yes
STVIFE	0.18	9.4(3.8)	2.9(1.7)	1.4(0.6)	86.2(5.2)	Ordered	Yes
STVIVE	0.18	40.7(6.1)	20.9(7.5)	15.0(4.7)	23.4(18.2)	Disordered	No
STAIIE	0.18	58.7(1.0)	18.2(1.1)	23.0(0.2)	0.1(0.1)	Disordered	No
STVIAE	0.18	58.8(0.5)	16.6(0.6)	24.4(0.3)	0.2(0.1)	Disordered	No
STVIGE	0.18	72.0(0.3)	6.5(0.1)	21.5(0.4)	0.0(0.0)	Disordered	No
STVIEE	0.18	68.9(0.9)	10.8(1.2)	20.2(0.6)	0.0(0.0)	Disordered	No

The comparison with experiments can be seen in Table 1. In discussing this table our criterion for labeling a simulation as having formed a fibril is that 40% or more of the peptides are in fibrillar structures by the end of the simulation. Using this definition we observed that at low temperatures, STVIIE, STVIFE, STVIVE, STAIIE and STVIAE form highly ordered fibril structures in contradiction to the experimental results for latter three sequences. At intermediate temperature T*=0.175, STVIVE still forms fibrils in contradiction to the experimental results. At high temperatures, however, we observe fibrils only for STVIIE and STVIFE (in agreement with experiment); STVIVE, STAIIE, STVIAE, STVIGE and STVIEE do not form fibrils (also in agreement with experiment). Although STVIVE does form a fair number of fibril structures (23.4%) at high T*, this number is below our cutoff; also most (55.7%) of the peptides are in monomer and disordered structures. It might at first seem puzzling that different aggregation behaviors are observed for STVIVE and STVIIE since we used the same pair interaction potential and hydrogen bond criteria for V and I (see Material and Methods). The reason for this is that we used different distances between the side-chain centroids and Cα (2.400Å for I), (2.002Å for V) and different square well ranges ( 6.831Å for I-I, 6.556Å for I-V and 6.488Å for V-V) .

In comparing our simulation results to experiments, it is appropriate to ask which of the four ranges of reduced temperatures that we considered are most likely to correspond to the experimental conditions of López de la Paz and Serrano. (Recall that their experiments were performed at a single temperature, 25°C.) The agreement between simulation and experiment on whether or not a particular sequence forms fibrils is best at high temperature T*=0.18. There our predictions as to which of the seven sequences form fibrils are all correct. This was not unexpected based on our previous investigations. In other simulation work performed in our group on polyalanine²⁴ and on Aβ(16–22)³⁴, we have found that there is a range of temperatures over which fibrils form for a given concentration and that fibrils are most likely to form at a “marginal” temperature above which the system forms random coils.

Here we formally define the fibrillization temperature T_f to be the temperature above which fibrils will not form spontaneously at a given concentration. Based on our own simulations at T > T_f we believe that this is same as the temperature above which well-ordered fibrils dissociate; we have not, however, done extensive checks to determine if there is any hysteresis. The fibrillization temperature is a measure of the stability of a fibril just as the folding temperature is a measure of the stability of a folded protein. These transitions from a fibril state to no-fibril state are fairly sharp functions of temperature and can be understood by analogy with protein folding transitions as stemming from a two-state model. In protein folding the two states are the folded state and the random coil state whereas here the two states are the fibrillization template and other non-stacked configurations. The conclusion that we draw from these results is that to use simulations to predict whether or not fibrils will appear in real experiments, one should perform simulations at a variety of temperatures. The higher T_f for forming fibrils in simulations is, the higher the propensity to form fibrils in vitro is. Another way of thinking of this is that T_f is a measure of the stability of the fibril just as the protein folding temperature is a measure of the stability of a folded structure. Thus the higher the value of T_f is, the more likely that a fibril structure will form and be stable.

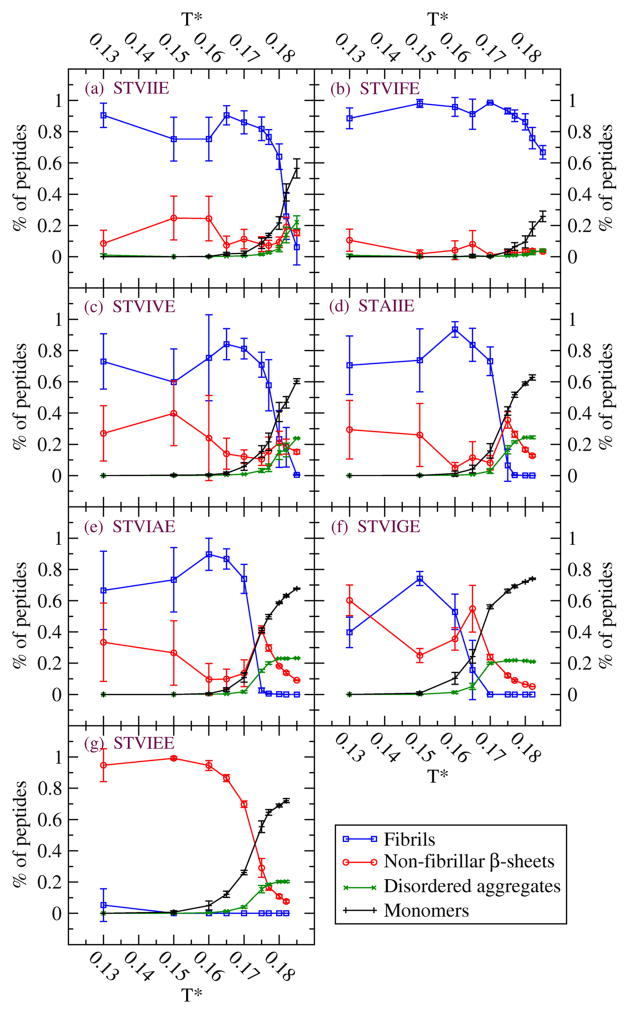
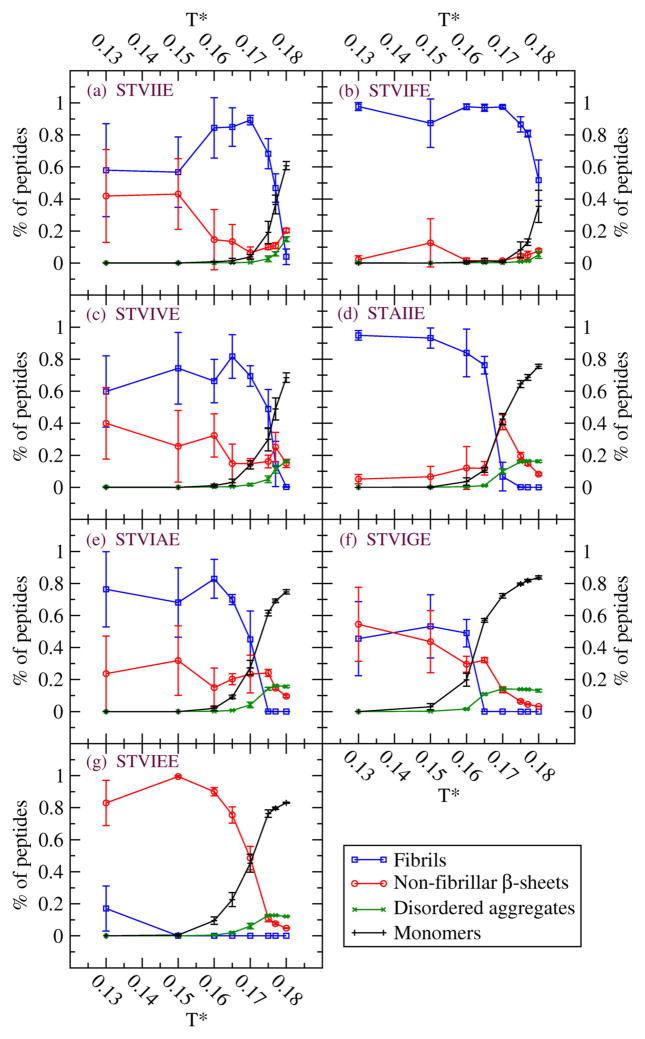
Figures 1 and 2 summarize our simulation results on the de novo designed sequences at the end of the simulations at ten temperatures and c=10mM (Fig.1) and at eight temperatures and c=5mM (Fig.2). The values for T_f depend on the sequence. From Fig 1, the values of T_f at c = 10mM for the seven sequences are STVIFE(T_f=0.185), STVIIE(0.18), STVIVE(0.177), STVIAE(0.17), STAIIE(0.17), STVIGE(0.16), and STVIEE(0.0); these are consistent with the results and discussion from Table 1. At low temperatures, T*=0.13, 0.15 and 0.16 there are large fluctuations in the percentages of peptides in fibrils and in non-fibrillar β-sheets. At these conditions the β-sheets are highly distorted and out-of-register; it seems that well ordered cross-β structures tend to be prohibited kinetically so that different independent runs evolve very different structures. At lower concentration, c= 5mM, the T_f values for the seven sequences follow the same order but with slightly lower T_f values than at c= 10 mM.

Figure 1.

Four observables at c=10mM for seven sequences (a) STVIIE (b) STVIFE (c) STVIVE (d) STAIIE (e) STVIAE (f) STVIGE (g) STVIEE. Percentage of peptides in fibrils (blue circle), non-fibrillar β-sheets (red circle), disordered aggregates (green X) and monomers (black cross). Non-fibrillar β-sheets refer to distorted β-sheets or single β-sheets without stacking. Disordered aggregates can be small disordered oligomers at high temperatures or disordered peptides attached to β-sheets or fibrils at low temperatures.

Figure 2.

Four observables at c=5mM for seven sequences (a) STVIIE (b) STVIFE (c) STVIVE (d) STAIIE (e) STVIAE (f) STVIGE (g) STVIEE.

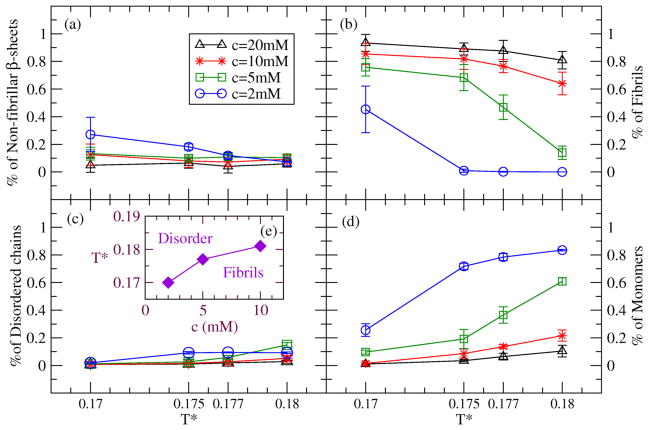
Figure 3 presents the values of our four observables for STVIIE at four temperatures (T*=0.17, 0.175, 0.177, 0.18) and four concentrations (c=20mM, 10mM, 5mM, 2mM). The dominant observables are the percentages of peptides in fibrils (Fig.3(b)) and in monomers (Fig.3(d)). At T*=0.175, the percentage of peptides forming fibrils is above 40% (our threshold for deciding if fibrils have formed) at three concentrations (c=20, 10, and 5mM). At higher temperature T*=0.18, the percentage of peptides forming fibrils is above 40% at two concentrations c=20 and 10mM. A phase diagram showing regions in the temperature-concentration plane where fibrils are formed in our simulations is presented in Fig.3(e).

Figure 3.

Concentration titration of four observables at four temperatures (T*=0.17, 0.175, 0.177 and 0.18) for STVIIE. Concentrations are 20mM (black triangle), 10mM (red star), 5mM (green square), and 2mM (blue circle). Percentage of peptides in (a) non-fibrillar β-sheets, (b) fibrils, (c) disordered aggregates and (d) monomers. (e) Phase diagram for three concentrations based on our simulations.

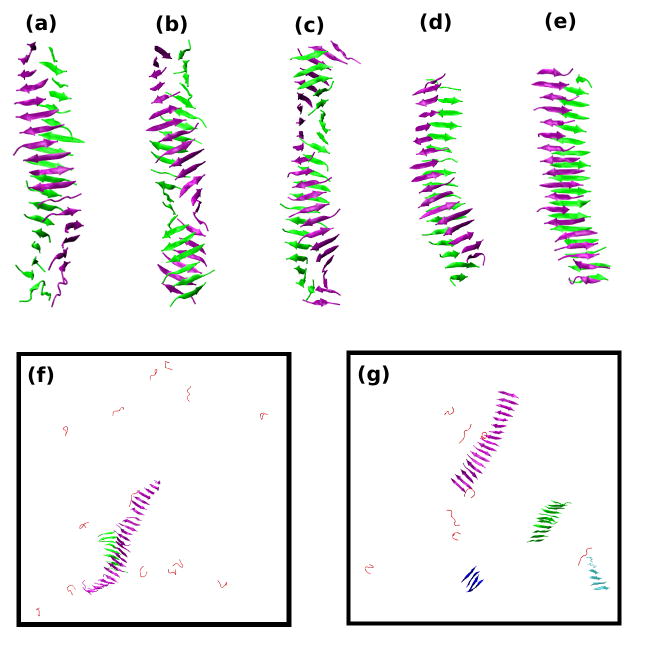
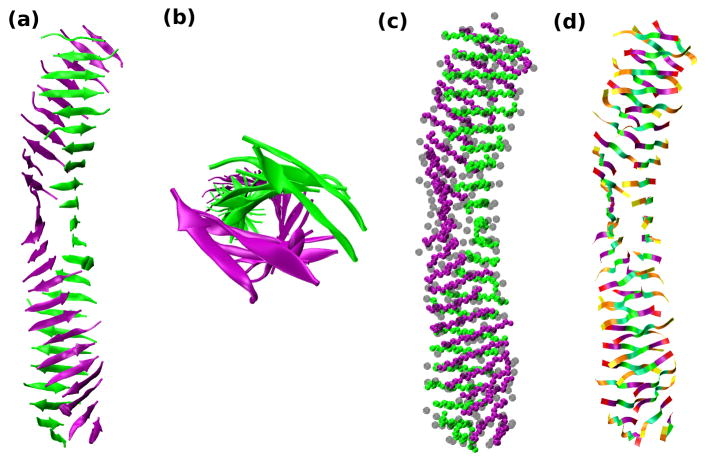
Figure 4 shows snapshots of the aggregate structures observed at the end of simulations for seven sequences. Figure 4(a) shows a well-ordered bi-layer fibril (proto-filament) formed by STVIIE peptides, a robust fibril former^14,32, at near fibrillization temperature T*=0.18 and c=10mM during a single run. Mixed β-sheets having parallel (roughly 40%) and anti-parallel (60%) pairs of strands are observed at all temperatures below T_f. The β-sheets in this simulation form fairly easily; little to no disordered aggregate is seen (data not shown) at any point along the aggregation pathway. Unlike the perfectly planar fibrils formed by polyalanine that we saw in earlier simulations²⁵; the two β-sheets appear to twist around each other along the fibril axis. The fibril structures shown in Fig 4(b) for STVIFE at T*=0.18 and in Fig 4(c) for STVIVE at T*=0.175 are similar to that in Fig. 4(a) for STVIIE. However the fibril structures for STAIIE at T*=0.17 (Fig. 4(d)) and for STVIAE at T*=0.17 (Fig.4(e)) look like somewhat planar; they are less twisted and have many out-of-register β-strands compared to those in Figs 4(a) to (c) . The final structures for STVIGE at T*=0.165 in different independent runs are either bi-layer β-sheets similar to Fig. 4(e) or single β-sheets. Figure 4(f) for STVIGE shows a large single β-sheet with an attached small β-sheet. Figure 4(g) shows snapshots at the end of the simulation on STVIEE, a peptide that does not form fibrils in vitro, at T*=0.165 and c=10mM. At this temperature, the STVIEE peptides form β-sheets, but the β-sheets never come together to associate into fibrils.

Figure 4.

Final structures near T_f and at c=10mM for seven sequences. (a) STVIIE at T*=0.18. (b) STVIFE at T*=0.18. (c) STVIVE at T*=0.175. (d) STAIIE at T*=0.17. (e) STVIAE at T*=0.17. (f) STVIGE at T*=0.165. (g) STVIEE at T*=0.165. The only structures shown for the first five sequences are the dominant fibril structures; monomers and small oligomers are not shown. All structures are shown for the last two sequences. The β-sheets are depicted with different colors for easy viewing.

Our results on which sequences form fibrils and which do not make good physical sense if we think about the types of residues that were substituted at position 5 on STVIIE. All of the de novo designed peptides considered tend to favor β-sheets so the key to forming fibrils seems to be the strategic placement of residues that have the ability to bring two sheets together in a stack. For example, substituting a highly hydrophobic aromatic group like F in STVIFE induces fibril formation but substituting a charged residue like E in STVIEE hinders it. Figure 5 depicts simulation snapshots of STVIFE at T*=0.17 and c=10mM shown as cartoon, sphere, and ribbon diagrams for clarity. The details of the structures are evident from the side view in Fig.5(a), the view down the fibril axis in (Fig.5(b) which shows the twist of the β-sheets, the sphere diagram in Fig.5(c), which shows the side-chain placements and the ribbon diagram in Fig.5(d) which distinguishes the different residues . It is apparent that STVIFE forms an extremely well-ordered bi-layer fibril with all 48 peptides involved. However placing a single glycine at the highly exposed position 5 as in STVIGE dramatically reduces fibril formation as we saw in the tables and Fig.4(f).

Figure 5.

Simulation snapshot for STVIFE at T*=0.17 and c=10mM. All 48 peptides are shown in (a) a cartoon diagram, (b) a cartoon diagram showing a view down the fibril axis , (c) a sphere diagram with side-chain spheres in transparent gray, and (d) a ribbon diagram with the identities of the side chain residues indicated by the color block on the ribbon. Serine (S) --yellow, Threonine (T)-- orange, Valine (V) -- mint green, Isoleucine (I) --light green, Phenylalanine (F) -- purple and Glutamate (E) – red

Discussion

In this paper we have used discontinuous molecular dynamics, a fast alternative to traditional molecular dynamics, in combination with PRIME20, a new intermediate resolution protein model applicable to all 20 amino acids, to simulate the spontaneous aggregation of 48-peptide systems containing the hexapeptide sequences STVIIE, STVIFE, STVIVE, STAIIE, STVIAE, STVIGE, and STVIEE. Experiments performed by López de la Paz and Serrano showed that the first two of these sequences fibrillized while the remaining five did not, providing us with a nice test bed to evaluate the ability of DMD/ PRIME20 simulations to predict which peptides will form fibrils and which will not. Simulations were performed over a range of reduced temperatures to assess the extent to which amorphous aggregates, beta sheets and fibrillar structures formed.

Starting from a random configuration of random coil conformations, fibrillar structures formed spontaneously, depending upon the sequence and the temperature. Those sequences that formed fibrils did so over a range of temperatures above which the system remains a collection of random coils and below which the system becomes frozen in disordered aggregates. STVIIE and STVIFE (which form fibrils in vitro) readily formed fibrils in our simulations over a range of temperatures; STVIEE (which does not form fibrils in vitro) did not form fibrils in our simulations. STVIVE, STAIIE, STVIAE, and STVIGE (which do not form fibrils in vitro) formed fibrils in our simulations at lower temperatures but stop forming fibrils at higher temperatures. None of the designed peptides show a preference for parallel or antiparallel strand within their β-sheets or for amorphous intermediates along their fibrillization pathway.

The best results are found at the highest temperatures that we simulated where our results on the fibrillization propensity of the seven short de novo designed peptides all agree with the experiments of López de la Paz and Serrano^14,32. This is consistent with other simulation work in our group³¹ which shows that the best fibrils form at a marginal temperature, the fibrillization temperature (T_f). Our results suggests that T_f is a measure of fibril stability (just as the protein folding temperature is a measure of a protein’s stability) and that by rank ordering T_fs of various sequences, PRIME20/DMD simulations could be used to ascertain their relative fibrillization propensities.

The good comparison between our simulation results on fibrillization propensities at high temperature and the experiments of López de la Paz and Serrano^14,32 serves to validate the PRIME20 force-field and geometric representation, although more work along these lines needs to be done. PRIME20 seems to be capturing the unique features of the various amino acids that contribute to the propensity of a peptide to form fibrillar structures.

A major weakness of our approach is that we have not yet been able to make a satisfying connection between our reduced temperature and real temperature. The results that we present here however suggest a good way around this problem. We are now collaborating with experimentalists who plan to measure T_fs of a variety of short peptides. (This has not been done to our knowledge since most fibrillization experiments are typically performed at a single temperature). By comparing the experimental and simulation results on T_fs we should be able to relate our reduced temperature to absolute temperature.

The DMD/PRIME20 approach that we have presented here could in future be used to discriminate between the various mechanistic models of protein aggregation kinetics that have appeared in the literature. This would necessitate performing more systematic concentration and temperature titrations recording the populations of all different types of oligomers and β-sheets, and fitting the rate constants associated with the master equations from the various kinetic models. Examples of models that could be considered include Finke-Watzky’s two step minimalistic model, Ferrone’s nucleation analysis, Powers-Powers’ three kinetic pathways depending on concentration, Xue-Radford’s systematic analysis and Knowles-Dobson’s kinetics dominated by secondary nucleation events^35–40. Work along these lines is currently underway in our laboratory with particular focus on polyalanine and Aβ(16–22).

Even though PRIME20 has been successful in simulating the STVIIE–type sequences and KLVFFAE³⁴ (the latter showing good agreement with atomistic simulations and experiment), there is room for improvement. Our use of a single sphere side chain means that we are limited in terms of the extent to which we can incorporate atomistic details. For example a single sphere makes it harder to well describe the two polar atoms on N and Q or the π-π interactions between large aromatic side-chains by a single sphere. Charged interactions among K, R, and E might be underestimated in the pair-interaction parameters since a single sphere includes carbons as well as charged atoms (charged nitrogen and oxygen). Hence more spheres might be necessary for some amino acids. Our choice of a single sphere was motivated by our experiences simulating polyglutamine using a 4-sphere side chain model; those simulations took many months. We will keep developing PRIME20 and studying other proteins or peptides with larger or longer residues with a view towards developing a more advanced model with more spheres for some of the side-chains.

Materials and Methods

Model Peptide and Forces

In this work we apply a new implicit solvent force field PRIME20 to describe the geometry and energetics of the short segments of heteropeptides sequences considered here. PRIME20 was recently introduced by Cheon et al.¹⁷ as an extension of PRIME, an implicit solvent intermediate-resolution protein model previously used in simulations of the aggregation of polyalanine and polyglutamine. PRIME was originally developed by Smith and Hall^16–17 and later improved by Nguyen et al.²³ More recently the PRIME model was extended to the study of polyglutamine peptides²² illustrating its versatility. In PRIME, the protein backbone is represented by three united atom spheres, one for the amide group (NH), one for the carbonyl group (CO), and one for the alpha-carbon and its hydrogen (C_αH). In the original version of PRIME, each side chain was represented by a single sphere for polyalanine and by a chain of four spheres for polyglutamine. In PRIME 20, the twenty possible side chains are each modeled as single spheres of unique size, atomic mass and C_α—R bond length. All backbone bond lengths and angles are set to realistic values. In order to maintain the trans-configuration we fix the consecutive C_α—C_α distance. The side chains are positioned relative to the protein backbone so that all residues are L-isomers. The solvent molecules in our system are modeled implicitly.

All forces between the united atom spheres are modeled with discontinuous potentials, e.g. hard sphere and square-well interactions. The excluded volume of each of the peptide’s four united atoms is modeled using a hard sphere interaction. The covalent bond lengths are maintained using a hard sphere interaction that prevents them from moving outside of the range (1+δ)l to (1−δ)l, where l is the ideal bond length and δ is the tolerance, which is set at 2.375% ⁴¹. Ideal backbone bond angles, C_α—C_α distance, and the residue L-isomerization are maintained by imposing a series of pseudobonds whose lengths are also allowed to fluctuate by 2.375%.

Hydrogen bonding is represented in PRIME 20 as a square well attraction of depth ε_HB and width 4.5Å between the backbone amide and carbonyl groups. Hydrogen bonds are anisotropic in nature so we constrain their formation to occur only when the NH united atom vector and the CO united atom vector point towards each other and the angle between those vectors is restricted between 120° and 180°. Further details on the hydrogen bonding model can be found in our earlier work^21,23,25. The system temperature is scaled by the hydrogen bonding energy between the backbone NH and CO, ε_HB, so that the reduced temperature is T* = k_BT/ε_HB.

The non-hydrogen-bonding interactions in PRIME20 are all modeled as square well interactions between the spherical units on each amino acid with strength (well depth) and range determined individually for each pair. Since solvent is modeled implicitly these are all effective interactions or potentials of mean force. In PRIME20, the energy parameters that describe the side chain / side chain interactions and the hydrogen bonding interactions between backbone NH and CO, and between side chain and side chain were derived in the following way. Briefly, the twenty possible amino acids were classified into 14 groups: [LVI] [F] [Y] [W] [M] [A] [C] [ED] [KR] [P] [ST] [NQ] [H] [G], according to their side chain size, hydrophobicity, and possibility of side-chain hydrogen bonding. The energy parameters were determined by Cheon et al.¹⁷ using a perceptron-learning algorithm and a modified stochastic learning algorithm to optimize the energy gap between 711 known native states from the PDB and decoy structures generated by gapless threading. The number of independent pair-interaction parameters was chosen to be small enough to be physically meaningful yet large enough to give reasonably accurate results in discriminating decoys from native structures. A total of nineteen interaction parameters with a 5.75Å heavy atom criterion were used to describe the side chain energetics. Further details about PRIME20 can be found in reference¹⁷.

Discontinuous Molecular Dynamics

Discontinuous molecular dynamics (DMD) is a variant on standard molecular dynamics that is applicable to systems of molecules interacting via discontinuous potentials (e.g., hard sphere and square-well potentials). Unlike soft potentials such as the Lennard-Jones potential, discontinuous potentials exert forces only when particles collide, enabling the exact (as opposed to numerical) solution of the collision dynamics. This imparts great speed to the algorithm, allowing sampling of longer time scales and larger systems than traditional molecular dynamics. The particle trajectories are followed by locating the time between collisions and then advancing the simulation to the next collision (event)^42–43. DMD on chain-like molecules is generally implemented using the “bead string” algorithm introduced by Rapaport^44–45 and later modified by Bellemans et al.⁴¹ Chains of square-well spheres can be accommodated in this algorithm by introducing well-capture, well-bounce, and well-dissociation “collisions” when a sphere enters, attempts to leave, or leaves the square well of the adjacent sphere. In this paper, DMD simulations are performed in the canonical ensemble (NVT) with the initial velocities chosen randomly from a Maxwell-Boltzmann distribution about the desired system temperature. The initial positions of the particles or spheres are chosen randomly while still ensuring that no geometrical constraints are violated.

In DMD simulations of protein aggregation, the number of particles in the system is chosen by specifying the concentration, c = N/L³, where N is the number of molecules in the box and the simulation box length. We set L = 159Å(20mM), 200Å(10mM), 252Å(5mM), 342Å(2mM), a value large enough to prevent the molecules from interacting with themselves but small enough to allow them to interact with their periodic image. The simulation proceeds according to the following schedule: identify the first event (e.g., a collision), move forward in time until that event occurs, calculate new velocities for the pair of spheres involved in the event and calculate any changes in system energy resulting from hydrogen bond events or side chain interactions, find the second event, and so on. Types of events include excluded volume events, bond events, and square-well hydrogen bond and side chain interaction events. For more details on DMD simulations with square-well potentials, see articles by Alder and Wainwright⁴² and Smith et al.⁴³

A total of seven model systems are studied in this work; all contain 48 peptides at concentrations c = 10mM, 5mM (seven sequences) and 20mM, 2mM (one sequence). The peptides considered are STVIIE, STVIFE, STVIVE, STAIIE, STVIAE, STVIGE, and STVIEE. As was the case in the experiments of Lopez de la Paz and Serrano, our peptides are effectively capped in terms of net charge because we have a neutral NH sphere at the N-terminal and a neutral CO sphere at the C-terminal. Each simulation is started at high temperature to ensure a random initial configuration and then slow-cooled to the temperature of interest to minimize kinetic trapping. Slow-cooling is achieved by decreasing the temperature in discrete steps starting from a high temperature until we reach the desired simulation temperature. The simulation temperature is maintained using the Andersen thermostat⁴⁶; in this method all the particles undergo random infrequent “events” or “collisions” with a ghost particle that reassigns the particle’s velocity randomly from a Maxwell-Boltzmann distribution centered at the simulation temperature. Five simulations are run for each sequence at the given temperature and concentration (state). Error bars are taken to be the standard deviation at each state. All simulations are run for approximately 100–300 billion collisions depending on simulation conditions, sequence, temperature and concentration. The length of the run was determined by checking to see how long it took to reach the state where the observables ceased to change with time.

The formation of β-strands, β-sheets, amorphous aggregates and fibrils are monitored and analyzed. We also check to see if the β-strands in a β-sheet are arranged in a parallel or anti-parallel configuration. The criteria for assigning the types of structures formed are the following. If each peptide in a group of peptides has at least two inter-peptide hydrogen bonds or side chain interactions with a neighboring peptide in the same group, then that group is classified as an aggregate. Aggregates can be either ordered or amorphous. If an aggregate contains β-sheets or fibrils, we classify it as an ordered aggregate. If each peptide in a group of peptides has at least 3 inter-peptide β-hydrogen bonds to a particular neighboring peptide in the group, we classify this group as a β-sheet. (A β-hydrogen bond is a hydrogen bond between two residues whose backbone angles are in the β-region of the Ramachandran plot.) If at least two β-sheet structures form inter-sheet side chain interactions (at least four side chain interactions per peptide per β-sheet), we classify this as a fibril; otherwise, we classify this and isolated β-sheets as non-fibrillar β-sheet structures. If an aggregate does not contain β-sheets but the peptides in the aggregate have any side chain contacts, then the aggregate is considered amorphous. If an aggregate contains peptides with less than 3 inter-peptide β-hydrogen bonds between neighboring chains then this is also considered to be an amorphous aggregate.

• We examine aggregation propensities of 7 hexapeptide sequences based on STVIEE.

• Discontinuous molecular dynamics simulations & PRIME 20 are performed on 48 peptides.

• Fibrillar structures form spontaneously, depending on sequence and temperature.

• At highest temperatures, predicted aggregation propensities agree with experiments.

• Results suggest fibrillization propensity is related to fibrillization temperature.