Using Brain Imaging to Track Problem Solving in a Complex State Space

Abstract

This paper describes how behavioral and imaging data can be combined with a Hidden Markov Model (HMM) to track participants’ trajectories through a complex state space. Participants completed a problem-solving variant of a memory game that involved 625 distinct states, 24 operators, and an astronomical number of paths through the state space. Three sources of information were used for classification purposes. First, an Imperfect Memory Model was used to estimate transition probabilities for the HMM. Second, behavioral data provided information about the timing of different events. Third, multivoxel pattern analysis of the imaging data was used to identify features of the operators. By combining the three sources of information, an HMM algorithm was able to efficiently identify the most probable path that participants took through the state space, achieving over 80% accuracy. These results support the approach as a general methodology for tracking mental states that occur during individual problem-solving episodes.

A characteristic of many complex problem-solving tasks is that no two episodes are the same. In solving problems, each individual will take a different path to solution, with each path reflecting a complex and unobservable train of thought. Newell and Simon (1972), when faced with the challenge of understanding such problem solving, tackled it in the most direct way possible by simply asking participants to tell them what they were thinking. While verbal protocols have been subject to criticism (Nisbett & Wilson, 1977), this methodology has borne considerable fruit (for a review, see Ericsson & Simon, 1993). Another method for addressing the challenge is to monitor eye movements, which offers a less intrusive way of tracking thought that has also had some success (e.g., Salvucci & Anderson, 2001). However, verbal protocols and eye movements have their limits and the goal of this paper is to explore a new methodology for tracking the sequential structure of thought in a complex state space.

This new methodology uses Hidden Markov Models (HMMs; e.g., Rabiner, 1989) to impose a sequential structure on the results of multi-voxel pattern analysis (MVPA) of fMRI data (e.g., Abdelnour & Huppert, 2009; Davatzikos et al., 2005; Haxby et al., 2001; Haynes et al., 2005; Haynes & Rees, 2005; Hutchinson et al., 2009; Mitchell et al., 2008; Norman et al., 2006). We have already reported some success in using these techniques to track the sequence of steps taken by participants solving algebra problems (Anderson et al., 2010, in press). However, these problems had a linear structure without much branching, whereas a hallmark of many complex problem-solving tasks is that their state space can branch widely and no two participants may follow the same path to solution. In this paper we show how these previously used techniques can be scaled up to problems that involve extensive branching.

To test our methodology we chose to study a variation of a children’s memory game most commonly known as Concentration. In a typical version of the game there is a deck of cards consisting of pairs of matching items (e.g., two cards depicting the same animal). The game begins with all cards placed face down and arranged randomly. On each turn, a player flips over two cards in sequence in an attempt to find a matching pair. If the selected cards match, then they are removed; if they mismatch, then they are flipped back over. The player must remember the locations and identities of previously selected cards to find matches as the game progresses. In the single-player version of the game, the goal is to match all pairs of cards in the fewest number of turns. The memory game has been studied in previous research for a variety of purposes. Several researchers have used it to explore individual differences (e.g., children versus adults, Gellatly, Jones, & Best, 1988; women versus men, McBurney, Gaulin, Devineni, & Adams, 1997; deaf versus hearing signers, Arnold & Murray, 1998). The memory game has also been used to investigate issues such as the difference between egocentric and allocentric spatial representations in memory (Lavenex et al., 2011) and the memory advantage of fitness-relevant stimuli (Wilson, Darling, & Sykes, 2011). Much of this work has used single-player versions of the game, as we will.

Our variation of the memory game is illustrated in Figure 1. Each game involves an array of 16 memory cards, eight of which contain algebra equations (math cards) and the other eight of which contain anagrams (verbal cards). The cards are arranged randomly and the algebra equations and anagrams are not visible until their cards are selected during a turn. Each turn of the game involves selecting a pair of cards by clicking on each card using a mouse, with the goal of finding a pair of matching cards. Math cards are considered to match if their algebra equations have the same solution for X (see Figure 1) and verbal cards are considered to match if their anagrams can be unscrambled to form words that are semantically related (Figure 1b shows the matching pairs: CUTE–UGLY, ARMY–NAVY, FLUFF–FUZZ, and NOISE–SOUND). Thus, participants must solve the algebra equations and unscramble the anagrams to determine which cards match. When participants select a pair of matching cards, the algebra equations or anagrams are replaced by the value of X or the unscrambled words, respectively (see the blue cards in Figure 1c). When participants select a pair of nonmatching cards, the selected cards return to their initial blank displays with no markings indicating that they had been visited (see the red cards in Figure 1c). Consequently, participants must remember the locations of previously visited, nonmatched cards for subsequent turns when they eventually discover their matching counterparts. Participants can select cards in any order and the goal is to end up with all the cards matched in the fewest number of turns.

Figure 1.

Sample illustrations of the memory game. The locations and identities of the algebra equations and anagrams are shown in A and the corresponding solutions are shown in B. During game play, a problem was not shown until its card was selected and a solution was not shown until its card was matched. Unselected and unmatched cards appeared in red with no text. An example of what the game display might look like for a participant about halfway through a game is shown in C. For a full video reproduction of a game played by an actual participant, see http://act-r.psy.cmu.edu/publications/pubinfo.php?id=993.

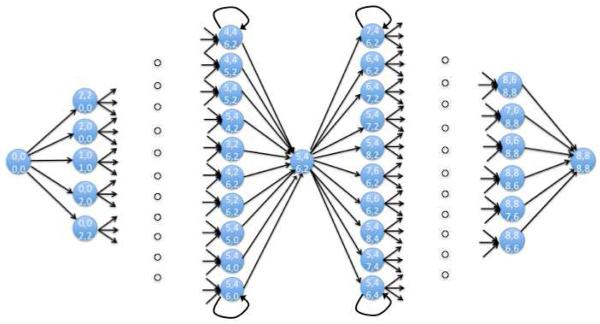
There are many possible ways to characterize the state space of this game but we started with a 625-state characterization where each state characterizes a possible game situation. At any point in time the state of the game can be characterized by how many math cards have been visited, how many of the visited math cards have been matched, how many verbal cards have been visited, and how many of the visited verbal cards have been matched. Just looking at the 8 math cards or the 8 verbal cards there are 25 possible states as given in Table 1. Combining both math and verbal cards, we get 25 × 25 = 625 states. Figure 2 illustrates a subset (34 states) of that space. The arrows in that graph connect states to possible successor states if the player chooses the appropriate cards. These transitions between states are called operators and there are 24 operators characterized by whether the first and the second cards of a pair involved first or return visits to math or verbal cards and whether they resulted in another pair of cards being matched. These 24 operators are given in Table 2. They can result in staying in the state or changing the state to one with more cards visited or matched. An average of 14.9 operators are legal in the 625 states. There are loops in the state space where two visited nonmatching cards are revisited without a resulting change in the state (while such operators apply to many of the states in Figure 2, only four loops are illustrated). Ignoring these loops, there are approximately 1.5 × 10¹⁸ possible sequences of operators that traverse the state space from no cards visited to all cards matched. If one includes such loops, which occur with some frequency in practice, there would be an infinite number of possible operator sequences. Thus, this state space provides a good test of our ability to identify the unique mental sequences of participants performing a problem-solving task. Indeed, we observed 246 games played by 18 participants and there was no repetition of a complete solution path.

Table 1.

The 25 states of the math cards or the verbal cards

Number of Cards
Visited	Matched
0	0
1	0
2	0
2	2
3	0
3	2
4	0
4	2
4	4
5	0
5	2
5	4
6	0
6	2
6	4
6	6
7	0
7	2
7	4
7	6
8	0
8	2
8	4
8	6
8	8

Figure 2.

An illustration of a fragment of the state space for the memory game. Each circle represents one of the states – 34 of the 625 states are represented. The four digits in each state reflect the number of visited math cards, the number of matched math cards, the number of visited verbal cards, and the number of matched verbal cards. The state space is shown as beginning with the state of no cards matched, passing through some of the states with cards matched, and ending in a state with all cards matched.

Table 2.

The 24 operators for the memory game

Card 1	Card 2	Match
Math First	Math First	no
Math First	Math Return	no
Math First	Verbal First	no
Math First	Verbal Return	no
Math Return	Math First	no
Math Return	Math Return	no
Math Return	Verbal First	no
Math Return	Verbal Return	no
Verbal First	Math First	no
Verbal First	Math Return	no
Verbal First	Verbal First	no
Verbal First	Verbal Return	no
Verbal Return	Math First	no
Verbal Return	Math Return	no
Verbal Return	Verbal First	no
Verbal Return	Verbal Return	no
Math First	Math First	yes
Math First	Math Return	yes
Math Return	Math First	yes
Math Return	Math Return	yes
Verbal First	Verbal First	yes
Verbal First	Verbal Return	yes
Verbal Return	Verbal First	yes
Verbal Return	Verbal Return	yes

Given that we know the actual cards participants selected, we have a firm definition of ground truth for this task, thereby allowing us to accurately evaluate our modeling results. We informed our algorithm of when participants clicked cards in the display but not which cards were clicked. Thus, the interpretation task in this application is to determine the identities of these clicks (i.e., whether a math card or a verbal card was selected, whether it was a first visit or a return visit, and whether the turn resulted in a match or a nonmatch). This approach allows us to investigate merging multiple data sources – in this case, latency data and imaging data. We chose to have math cards and verbal cards because we wanted to investigate the ability of this methodology to distinguish periods of mathematical engagement from periods of engagement in non-mathematical activities. Making this discrimination is critical in the context of mathematical tutors (Anderson et al., 2010, in press) where one wants to identify when students are on task and when they are not.

While we reserve a detailed description of our approach to tracking states in this task until after we describe the experiment and its results, we outline briefly the approach taken here. For modeling a participant’s trajectory through the state space in a given game, we use the behavioral data from that participant’s other games and from the games of other participants to parameterize a behavioral model that characterizes the probability of various operators in various states and the timing of various events. While no game was the same, there were definite statistical regularities that the model captures. The regularities in this behavioral model are used to parameterize an HMM algorithm to identify the clicks. However, the classification performance achieved using just the behavioral data is poor. We use MVPA of the imaging data to help identify the operators and, in so doing, substantially improve classification accuracy. We show that using either the imaging data without the benefit of the behavioral data or the behavioral data without the imaging data results in much worse performance than the combination, thereby illustrating the benefit of combining the multiple sources of information.

Methods

Participants

Eighteen individuals from the Carnegie Mellon University community (6 females, 12 males; ages 18–29 with a mean of 23 years) participated in a single fMRI session lasting approximately 70 minutes for monetary compensation.

Memory Game

Design

The game was played using a mouse-based interface programmed in Tscope (Stevens, Lammertyn, Verbruggen, & Vandierendonck, 2006). During a turn, the first card was selected by clicking the left mouse button when the mouse cursor (a white arrow) was on the red back of the card. The card was immediately “flipped over” to reveal a problem (an anagram or an algebra equation) printed in white 16-point Arial font on a black background. Participants viewed the problem on the first card for as long as they desired, then selected a second card in the same manner. Participants viewed the problem on the second card for as long as they desired (the problem on the first card remained visible; see Figure 1c), then clicked the right mouse button to end the turn. Thus, each turn consisted of three mouse clicks: a left click to select the first card, a left click to select the second card, and a right click to end the turn.

After the click to end the turn, one of two things would happen. If the participant had selected a pair of matching cards, the algebra equations or anagrams were replaced by the value of X or the unscrambled words, respectively, and the backgrounds of the matched cards turned blue (see Figure 1b). If the participant had selected a pair of nonmatching cards, the selected cards were immediately “flipped back over” to show their red backs. There were no markings to indicate that nonmatched cards had been visited (see Figure 1c). Consequently, participants had to remember the locations of previously visited, nonmatched cards for subsequent turns when they eventually discovered their matching counterparts. Participants were allowed to select cards in any order, subject to the constraints that they could not select the same card twice during the same turn and they could not select cards that had already been matched. Mouse clicks that either violated these constraints or were otherwise inappropriate (e.g., making a right click when a left click was required, clicking on the empty space between cards, etc.) were relatively rare and had no effect on the game display.

Materials

We chose anagrams and algebra equations as problems because solving both of them requires high-level cognitive operations involving symbol manipulation. However, the symbols to be manipulated differ between problem types (viz., letters versus numbers). Thus, anagrams and algebra equations likely involve similar (but not identical) cognitive operations that are carried out by partially overlapping brain regions.

Each matching pair of anagrams involved a pair of unscrambled words that we judged to be related based on semantics, being either synonyms (e.g., CASH and MONEY), antonyms (e.g., DARK and LIGHT), or related in some other relatively transparent way (e.g., JUDGE and COURT). Words were selected such that each word was four or five letters in length and its letters could not be rearranged to form any other English word (verified using the Internet Anagram Server at http://wordsmith.org/anagram). An anagram of each word was constructed by doing two random transpositions of letters that did not result in a mirror image of the word. For example, GJDUE was the anagram for JUDGE based on J–G and G–U transpositions. We restricted the words to four or five letters and the anagrams of them to two transpositions on the basis of pilot studies in which separate groups of participants solved various anagrams outside the context of the memory game. These studies revealed that fewer than 50% of anagrams involving more than five letters or more than two transpositions could be solved within a 30-second time limit. In contrast, participants were able to correctly solve more than 85% of anagrams involving four or five letters and only two transpositions, often in less than 10 seconds. Thus, the anagrams used in the memory game were solvable by most participants.

Each matching pair of algebra equations involved two equations of the generic form AX + B = C that had the same solution for X. Equations were constructed such that A and B were both single-digit numbers greater than 1, C was less than 100, X values from 2–9 occurred equally often across all equations, and every equation was unique. We restricted the algebra equations to the form AX + B = C on the basis of pilot studies in which separate groups of participants solved algebra equations outside the context of the memory game. These studies revealed that participants were able to correctly solve more than 90% of algebra equations of that form, often in less than 10 seconds and with a latency distribution that was similar to the distribution for anagram solutions. Thus, the algebra equations used in the memory game were solvable by most participants and similar in difficulty (in terms of latency and accuracy) to the anagrams.

There were a total of 56 anagram pairs and 56 algebra pairs. The pairs for each problem type were divided into 14 sets of four pairs for use in 14 separate games (no problems were repeated). For anagram sets, the four pairs were chosen to be unrelated to each other to limit confusion about which unscrambled words constituted a matching pair (e.g., anagrams for the word pairs CASH–MONEY and PENNY–CENT were in different sets). For algebra sets, the four pairs were chosen to have different values of X as their solutions. Anagram and algebra sets were randomly assigned to the 14 games.

Procedure

Participants received instructions about how to play the memory game prior to scanning. These instructions included an overview of the game interface and an explanation of what constituted anagram and algebra matches. Participants were told that the goal of the game was to match all the cards in the fewest number of turns. Two “strategy tips” were given to help them achieve this goal. First, they were instructed to solve each anagram or algebra equation when it was first encountered, then to remember the solution for subsequent matching. Second, they were instructed not to use a strategy of selecting cards randomly without solving the problems because it would lead to more turns than necessary. Participants were also informed that they could take as much time as needed on each turn because their performance goal concerned the number of turns, not the time per turn.

Following the instructions, participants were placed in the scanner, where they played two demo games during structural image acquisition to become familiar with the game interface. The demo games involved different sets of problems (with simpler three- or four-letter anagrams involving one or two transpositions) than those used in the experimental games, but the games were identical in all other respects. Participants played a total of 14 experimental games during functional image acquisition. The games were divided into seven pairs, with one pair for each scanning block. Each block started with a prompt indicating the game numbers (e.g., “Games 7 and 8”) and scanning was synchronized with the offset of the prompt. The two games were then played, with each game preceded and followed by a 16-second fixation period consisting of a white cross presented in the center of a black background. The duration of each block varied with how long it took participants to finish the games.

The 18 participants each played 14 games, blocked into 7 pairs of games. Six games are not in the analysis because of failures in recording scanner data. Thus, a total of 246 games were used for classification purposes.

FMRI Data Acquisition and Initial Analysis

Functional images were acquired using gradient echo-planar imaging (EPI) on a Siemens 3T Allegra Scanner using a standard RF head coil (quadrature birdcage), with 1.5-s repetition time (TR), 30-ms echo time (TE), 73° flip angle, and 20-cm field of view (FOV). The EPI sequence was single-shot, and no navigator echo correction was used. We acquired 26 oblique-axial slices on each full-volume scan using a 3.2-mm-thick, 64×64 matrix. The anterior commissure – posterior commissure (AC-PC) line was on the 8th slice from the bottom. EPI scanning blocks ranged in length from a minimum of 127 scans to a maximum of 441 scans. The mean number of scans per imaging block was 246 with a standard deviation of 66 scans. Each participant’s EPI images were motion-corrected using their first EPI image as the reference image (AIR; Woods et al., 1998). Head-movement was negligible among participants. Maximum correction for any translation was 1.7mm and maximum correction for any rotation was 2.8 degrees. Neither slice-timing correction nor temporal filtering was applied to these data.

Structural images were acquired immediately prior to functional images and were obtained using a T2 structural imaging sequence with 5610-ms TR, 73-ms TE, flip angle of 150 degrees and FOV of 20 cm. We acquired 34 oblique-axial slices using a 3.2-mm slice thickness and 256×256 matrix yielding 0.78125-mm × 0.78125-mm voxels in the x-y plane. The AC-PC line was on the 12th slice from the bottom.

Acquired images were processed using the NIS system. Motion-corrected EPI images were coregistered to our local common reference structural MRI (a participant in multiple prior experiments) by means of a 12-parameter 3-D registration (AIR; Woods et al., 1998) and smoothed with a 6-mm full-width-half-max 3-D Gaussian filter to accommodate individual differences in anatomy.

Past research (see discussion in Anderson, in press) has found that we achieve best MVPA classification in these complex tasks using activity over the whole brain. To avoid overfitting the data it is necessary to use relatively large regions of activity. Therefore, we continued our practice of using large regions created by evenly distributing 4×4×4 voxel cubes over the 26 slices of the 64×64 acquisition matrix. To minimize correlation because of smoothing, a between-region spacing of 1 voxel was used in the x- and y- directions in the axial plane and one slice in the z-direction. The final set of regions was acquired by applying a mask of the structural reference brain and excluding regions where less than 70% of the region’s original 64 voxels survived. This resulted in 345 regions.¹

Results

Our general approach to interpreting a given game from a participant is to combine three sources of information from that participant’s other games and from the games of other participants. The first two sources are behavioral: information about what actions a participant is likely to take at different states in the game and the time they spend taking these actions. The third source is the brain imaging patterns associated with these actions. We discuss each of these sources separately, then how they are combined, and finally the performance of the algorithm that uses these three sources of information.

Information Source 1: Transition Probabilities

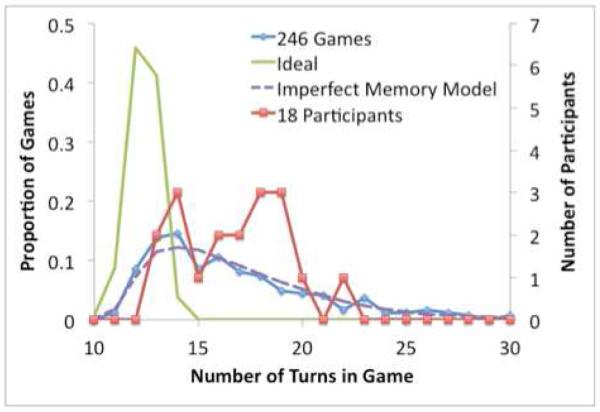
While the number of turns it takes to finish a game depends in part on exactly where the cards are (e.g., there are lucky sequences that get all 8 matches right away), it depends more on the choice of the right operators in a state. The “246 Games” line in Figure 3 shows the distribution of the number of turns taken by participants to finish the individual games. The mean number of turns is 16.9 and the standard deviation is 4.8, comparable to past results involving a 16-card version of the memory game (e.g., Lavenex et al., 2011). The “Ideal” line in Figure 3 shows the ideal distribution of number of turns (based on one million simulated games), assuming perfect memory, which has a mean of 12.24. Depending on the random placement of cards, the minimum number of turns could vary from 8 to 15, although 8 was never observed in the million simulations and 9 and 15 only had a frequencies of about 1 in 10,000. The “18 Participants” line in Figure 3 shows the distribution of mean turns per game for participants, rounded to the nearest integer. Individual participants ranged from a mean of 12.7 turns to 22.6 turns. It appears that at least a couple of participants approached ideal behavior but many of them took many more turns than the minimum. These results suggest that most participants were not always able to remember the locations of past cards, thereby leading to more return visits and, by extension, more turns, than necessary.

Figure 3.

Distributions of the number of turns. See discussion in text.

We developed a simple Imperfect Memory Model that reflects these memory failures. The model forgets the location of a matching card with probability p_f. However, even if the card is forgotten the model remembers that there was a matching card. If the model forgets the location of a card it tries one guess among the visited cards². We determined the value of p_f that matched the performance of individual participants in terms of mean number of turns. Individuals had estimated probabilities of forgetting the location that varied from .07 to .92 (reflecting the wide range of mean number of games for participants in Figure 3). The “Imperfect Memory Model” line in Figure 3 shows the expected distribution of turns taken in individual games for the 18 participants with their estimated probabilities of forgetting.

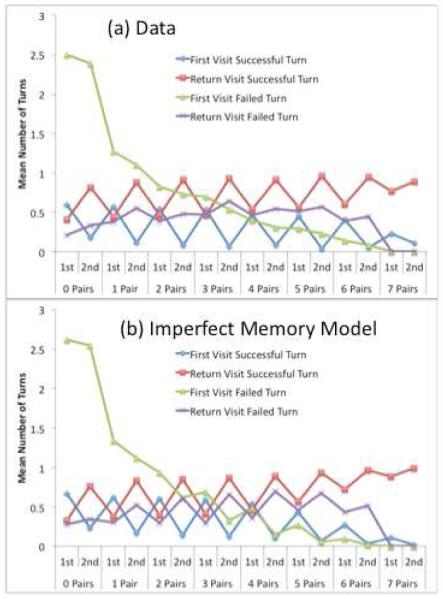
Figure 4 provides a revealing analysis of what is happening during the course of the game and indicates that the simple Imperfect Memory Model is capturing some significant features. The figure organizes the game along the x-axis according to how many pairs of cards have been matched. Within each number of pairs matched, the x-axis distinguishes between the first and second cards in a pair. Minimally, one pair of cards has to be turned over before another match is achieved (and that is the only option for the 8^th match) but on average more cards are turned over for earlier matches. The figure plots the number of cards turned over in four categories determined by whether it is the first visit or a return visit to the card and whether the card results in a match or not. We plotted the observed data in part (a) of the figure and the performance of the Imperfect Memory Model in part (b). The two patterns show a striking correspondence both in absolute values and pattern (r = .986):

1. Of logical necessity there is one successful visit per card per match count. The two cards in a match were either visited for the first time or on a return visit. Number of first-visit successes and return-visit successes display a sawtooth pattern such that the first card in a match is more likely to be a first visit. This reflects the common pattern of visiting a new first card and then recalling and choosing a matching card as the second card.

2. Ideally, there should be no return visits that do not result in matches, but in fact participants and the model averaged more than 6.4 such visits over a game. These reflect memory failures in the model, where it is making a wrong guess about the location of a matching card.

3. As the game progresses, there is a decline in the number of failed first visits. This reflects both exhausting the unvisited cards on the board and the increased chances that a newly visited card will match a visited card. The total number of visits in this category (11.5 for participants and 11.3 for model) is more than ideal behavior (8.8). This reflects failures to remember the location of a visited card that matches a first visit to a new card.

Figure 4.

(a) Number of times different types of cards are viewed as a function of how many cards have been matched and whether it is the first or second card. (b) Predictions of the Imperfect Memory Model.

We conclude this analysis of choice behavior by noting two other factors, one of which turns out not to be important and one of which is important. First, one might have expected there to be a different pattern of choices for math versus verbal cards. For instance, a participant might have tried to match all the verbal cards before turning to the math cards (contrary to instructions). This would show up in return visits because a participant has no control over the cards they turn over for first visits. However, the patterns in Figure 4a are basically identical if plotted separately for verbal and math cards.

On the other hand, there is a consideration that expands the state space in our HMM beyond the 625 states laid out in the introduction: The outcome of the previous turn has an impact on the outcome of the current turn. Specifically, if the second card turned over on the previous turn did not match the first card, participants have a strong tendency to make a return visit to a card of the same type (math or verbal) on the current turn. For instance, when the last card turned over was a nonmatching math card, 39% of the time the next card visited was a return visit to a math card but only 14% of the time it was a return visit to a verbal card. Conversely, if the last card turned over was a nonmatching verbal card, 41% of the time the next card turned over was a return visit to a verbal card and only 12% of the time it was a return visit to a math card. The model also shows this trend because it is trying to find the matching card: 34% of the time it returns to a card of the same kind and 17% to a different card. Also, participants tend to visit a new card after a successful turn that resulted in a match: 53% of the time they visit a new card after successful turns and 28% of the time after unsuccessful turns. The model shows this same tendency: the corresponding numbers are 51% and 26%.

The consequence of this dependency on past action is that if we work with only a 625-state model, we violate the Markov property that future behavior only depends on the current state. To capture this dependency, we had to complicate the state space in the HMM to reflect whether the last card on the previous turn was a matching card on that turn, a nonmatching math card, or a nonmatching verbal card. This increases the size of the HMM’s state space to 625*3 = 1875 states. We could not find any violations of the Markov property using this larger state space, but given the complexity of that space we cannot be sure that there is not some hidden violation.

The Imperfect Memory Model plays a critical role in predicting participant behavior and serves as our first source of information. It generates predictions about the probabilities for each operator in each of the 1875 states for each participant for each game, given an estimate of p_f for that participant based on his or her performance on other games.

Information Source 2: Click Timing

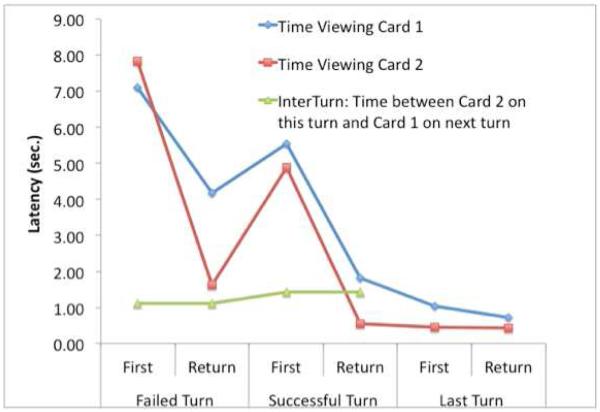
Every turn involves 3 clicks: a click to turn over the first card, a click to turn over the second card, and a click to move on to the next turn. The duration between the first and the second clicks reflects the time spent viewing the first card and we will refer to this as Card 1 Time (t₁). The duration between the second and the third clicks will be referred to as Card 2 Time (t₂). The time between the third click and the first click of the next turn will be referred to as the InterTurn Time (t₃). Figure 5 shows the mean times as a function of whether the turn was a failure, a success, or the last turn (logically, the last turn is a success and it is not followed by an InterTurn Time). Within these categories, the figure indicates whether the card was inspected for the first time or whether it was a return visit (a distinction only meaningful for Card 1 and 2 Times). The InterTurn times and the times for the last card are particularly short. Excluding these times, we performed an analysis of variance on the times for the two cards, varying four within-participant factors: All 4 main effects were significant:

1. Match: Failures (5.18 sec) were slower than successes (3.20 sec), F(1,17) = 62.59, p < .0001. This probably reflects the fact that processing a matching card is primed by having seen its matching counterpart earlier.

2. Position: Card 1 Time (4.66 sec) was longer than Card 2 Time (3.72 sec), F(1,17) = 4.91, p < .05, reflecting some acceleration during a turn.

3. Visit: First visits (6.33 sec) took longer than return visits (2.05 sec), F(1,17) = 107.79, p < .0001. This reflects the fact that on return visits subjects have already solved the problem. There is an interaction between card position and visit (F(1,17) = 7.03, p < .05) such that the advantage for a return visit is particularly strong for the second card.

4. Type: Math cards (4.85 sec) were viewed for a longer time than verbal cards (3.53 sec), F(1,17) = 17.51, p < .001.

Figure 5.

Mean times for various events, classified by whether they involve viewing Card 1, viewing Card 2, or are the subsequent InterTurn. Data are also divided according to whether it was a failed turn versus a successful turn and whether it was a first visit or a return visit. Data for the last turn of the game are plotted separately.

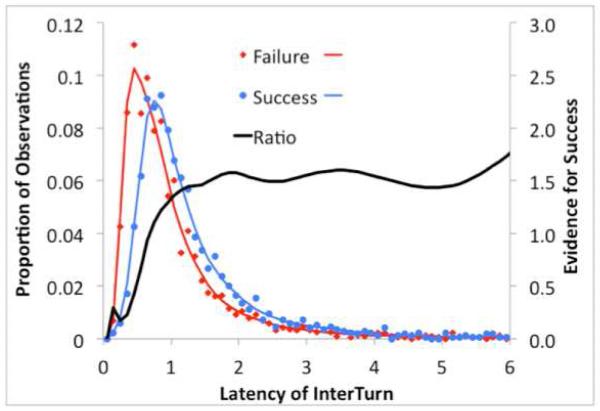
While there are large differences among the conditions in Figure 5 it is also the case that the distribution of latencies is quite variable within each condition. The standard deviation of individual latencies in each condition is approximately equal to the mean. To illustrate, Figure 6 shows a pair of such latency distributions, for InterTurns that followed failed turns and for those that followed successful turns. Even though the means are close (1.12 sec versus 1.42 sec), as are the standard deviations (1.30 sec versus 1.31 sec), the distributions are distinguishable. The figure displays fitted empirical densities (using the MATLAB function ksdensity). The line labeled “Ratio” is the ratio of the two densities and shows the amount of the evidence for a successful turn. As can be seen, long InterTurns provide almost 2:1 evidence for success, whereas very short InterTurns provide even stronger evidence for failure. Relative ratios like these enable us to use the times to predict what is happening on a turn.

Figure 6.

An illustration of how the exact latencies provide evidence about an event, even in a case like this where the mean failure and success times for InterTurns are similar (see Figure 5). The ”Ratio” line is the ratio between the empirical densities for failures and successes.

Information Source 3: Imaging Data

The other source of information is the imaging data. As we have shown elsewhere (Anderson et al., 2010), the best identification comes from using a scan that comes after the event of interest at a delay that corresponds to the lag of the hemodynamic function. In the case of this experiment, with a TR of 1.5 seconds, that is 3 scans later. Our fMRI measure was the percent difference between the activity in a voxel for that scan and the average activity of that voxel for that game.

We trained a linear discriminant classifier (McLachlan, 2004) to categorize the scans as coming from one of six categories: (1) first visit to a math card, (2) return visit to a math card, (3) first visit to a verbal card, (4) return visit to a verbal card, (5) InterTurn after a failed match, and (6) InterTurn after a successful match. We excluded the data from 9 of the 345 regions (leaving 336) because they had more than 1% outliers, defined as percent changes of 10% or more of baseline. As noted above, we used the response that occurred 3 scans (4.5 seconds) later to classify the scan. Sometimes multiple events (first card, second card, InterTurn) occurred within a scan and in these situations we created separate cases, one for each event with the same set of 336 BOLD values. There were 29,892 scans from the cases from the 246 games across the 18 participants. To classify scans from a game we used the data from all other participants and from all other games for that participant. We duplicated the participant’s data from the other games 17 times so that it would count as much as the data from the other participants. This meant that there were nearly 60,000 training cases for each game. On average, a game consisted of 122 scans (which were not included with the training cases for that game).

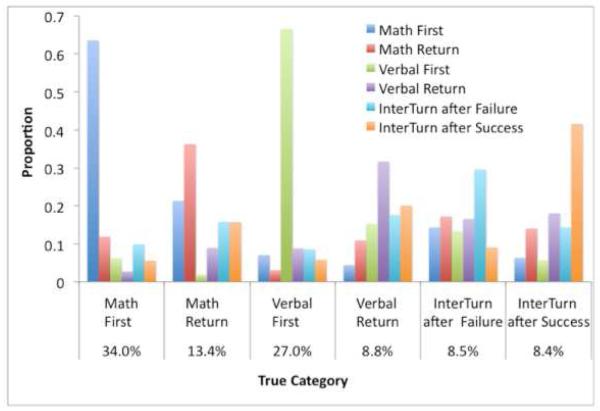
The linear discriminant analysis (LDA) provided estimates of the conditional probabilities that the fMRI pattern in a scan came from each of the 6 categories. Classifying each scan as coming from the category with the highest conditional probability, Figure 7 shows the proportion of scans from each category assigned to the various categories. The overall accuracy is 53.2% of scans correctly classified while chance would be 20.7%³. In every case, scans are assigned to the correct category more often than to any incorrect category. Thus, the classifier is able to predict the data with much better than chance accuracy even though its ability to discriminate among categories is somewhat short of what one might like. In the next section we achieve better performance by combining the output of the classifier with the behavioral data.

Figure 7.

Ability of the linear discriminant function to distinguish among categories. The x-axis gives the various categories and proportion of scans from that category. The bars for each category show the proportion of scans in each category assigned to each of the six possible categories. Information sufficient to recreate this analysis is available in the files available at http://act-r.psy.cmu.edu/publications/pubinfo.php?id=993.

The above 53.2% accuracy reflects what can be obtained by combining data from other participants and other games from the current participant. Using only data from other participants we achieve 46.3% accuracy. This reflects the degree to which activation patterns generalize across participants. Using only other games of the current participant we do somewhat better, achieving 49.1% accuracy. The additional benefit of the other participants (raising accuracy to 53.2%) reflects the benefit of more training data.

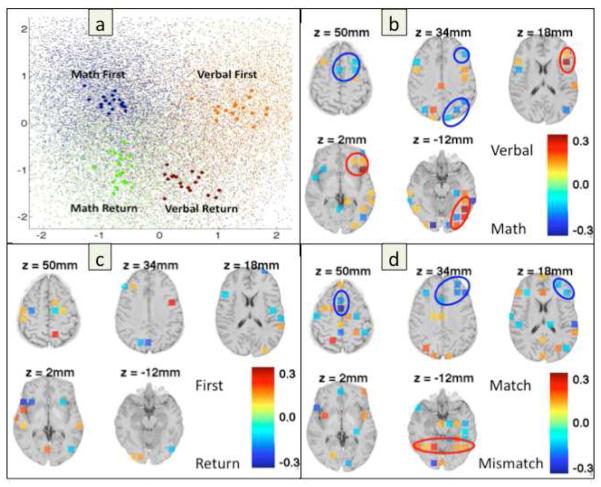
We followed this classification with further analyses⁴ to identify the regions that were predicting specific types of activity. In these analyses we did not use the hold-one-out methodology, which is critical for our prediction purposes in Figure 7 and in later sections, but rather used all the relevant scans. First, we focused on the scans where the participant was viewing a card and we did a LDA of these into four categories: (1) first visit to a math card, (2) return visit to a math card, (3) first visit to a verbal card, and (4) return visit to a verbal card. Figure 8a shows the projection of the LDA onto two dimensions that account for 98.9% of the variance in the LDA (66.9% for the first dimension and 32.0% for the second). The x and y coordinates for points in Figure 8a are linear combinations of the normalized activations for each of the regions (z-scores, z_i):

$$x_i=\sum _{j=1}{a}_j{z}_i{y}_i=\sum _{j=1}{b}_j{z}_i$$

Figure 8a shows both the average values for the 18 subjects plus the placement of most of the scans (86.2% of scans have values in the space shown). The mean values for the subjects are linearly separable with the first dimension (x-axis) going from math to verbal card while the second dimension (y-axis) goes from return to first visit. Given that there is no logical requirement that the two dimensions be so interpretable, it seems clear that these dimensions are accounting for systematic trends in the brain-wide activation.

Figure 8.

(a) Representation of the two dimensions in the projection of the LDA for the four categories: first visit to a math card (blue), return visit to a math card (green), first visit to a verbal card (orange), and return visit to a verbal card (brown). Large dots represent mean participant values and small dots individual scans. (b) Regions with strong weightings on the first dimension that reflects the math versus verbal dimension. (c) Regions with strong weightings on the second dimension that reflects the first versus return visit dimension. (d) Regions with strong weightings in the LDA for discriminating between InterTurns after matching a pair and InterTurns after mismatching. See text for further discussion.

Figure 8b shows the mapping of the first dimension back onto the brain regions, representing regions with weightings (a_j in the equation for x_i) having absolute values greater than .1 (range is from −.42 to .33 for the weights for this dimension). Among the regions that indicate a math card are left parietal, premotor, and prefrontal regions that have been implicated in other studies of arithmetic and routine algebraic problem solving (e.g., Anderson, 2005; Anderson et al., 2011; Dehaene et al., 2003; Fehr et al., 2007; Kesler et al., 2006). Among the regions that indicate a verbal card are left prefrontal regions close to Broca’s area and left visual/temporal regions close to the “word form area” (Cohen & Dehaene, 2004). We would expect to see these areas active as participants unscramble an anagram. Figure 8c shows the mapping of the second dimension back onto the brain regions, representing regions with weightings (b_j in the equation for y_i) having absolute values greater than .1 (range is from −.23 to .23 for this dimension). Unlike Figure 8b, the interpretation of regions in Figure 8c is not clear.

Figure 8d reports the results of a separate LDA of the InterTurns scans, looking at regions that separated scans following a match versus a mismatch. It displays regions with weightings having absolute values greater than .1 (range is from −.29 to .22). Many of the regions identified can be interpreted. With respect to mismatch, the figure highlights regions of the anterior cingulate, which have been associated with error and conflict (e.g., Botvinick et al., 2001; Falkenstein et al., 1995) and anterior prefrontal regions, which have been associated with post-task processing (e.g., Reynolds, 2006). With respect to match, there is a range of areas highlighted in the vicinity of the left and right fusiform. This probably reflects participants inspecting the solutions that have been revealed.

Figure 8d shows regions where the InterTurn activation predicts success of the just completed turn. InterTurn activity also predicts properties of the next turn but it does not do so as strongly as it predicts success of the previous turn. For instance, in a binary discrimination one can achieve 66% accuracy in using InterTurn activity to predict whether the next turn will be a match, but 75% accuracy in predicting whether the just completed turn was a match.

Combining the Three Sources with a Hidden Markov Model

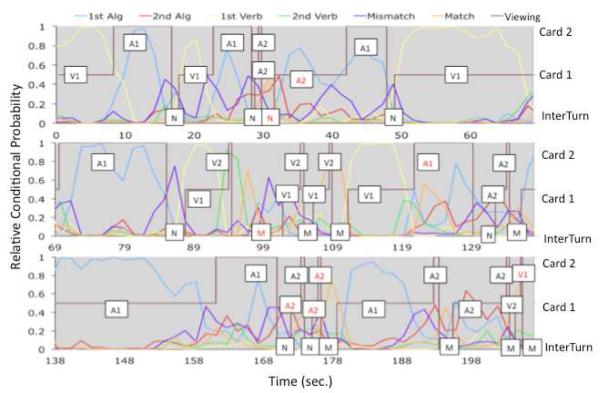
Figure 7 shows success at classifying a single scan in isolation. The challenge is to sew these single-scan classifications into a coherent interpretation of an entire game. Figure 9 shows a typical case of the data we have to work with⁵. This is a record of a 16-turn game that spanned 138 scans or 207 seconds. The brown line tracks whether the participant is viewing Card 1, Card 2, or is in an InterTurn. The other lines in the figure give the conditional probabilities of the various interpretations, normed to sum to 1. The goal is to label the various turns as to whether they involved verbal or math cards, first or return visits, and matches or nonmatches. Some turns can be classified relatively easily. For example, the first turn appears to involve selection of a verbal card for Card 1 and then a math card for Card 2, resulting in a mismatch. This classification would be correct. However, the brief third turn is quite hard to decipher and the fourth turn seems to involve two first visits to math cards, but Card 1 was actually a return visit to a math card (perhaps the participant was solving it again).

Figure 9.

An example of classification performance for a single game. The brown line indicates whether the participant was viewing Card 1, Card 2, or InterTurn (value 0). The other lines show the relative evidence from the classifier for the 6 interpretations of a turn. The symbols in the boxes indicate the true identity of the event: V1 = first visit to a verbal card, V2 = return visit to a verbal card, A1 = first visit to a math (algebra) card, A2 = return visit to a math card, N = nonmatch, and M = Match. Symbols in red are cases that the algorithm failed to classify correctly.

Our classification algorithm assigns an interpretation to a game, where an interpretation implies one of the 24 possible operators (see Table 2) for each turn, where an operator implies a category for each card and the InterTurn. For the example, there would be 24¹⁶ possible interpretations for the 16 turn game in Figure 9. There are various sorts of constraints we can bring to bear in finding the interpretation. First, there is the logical constraint that by the end of the game, the participant must have matched all the cards; thus, there must be exactly 8 first visits to math cards, 8 first visits to verbal cards, and 8 matches in the sequence. Such constraints rule out many interpretations but still leave a very large number of possible legal interpretations (we estimate more than 10¹⁷ interpretations). The probability of any interpretation is determined by the probability of the transitions between states, the card and InterTurn times, and the fMRI data. If we designate an interpretation as a sequence of r operators o_k that generate a path through the state space, then the probability of any legal interpretation can be given as:

$$p(o_1{o}_2\cdots o_r\mid \mathit{times},\mathit{fMRI})\infty \prod _{k=1}^{r}p{(o_k\mid s_{k-1})}^{\ast }p(t_{k1},t_{k2},t_{k3}\mid o_k)p({\mathit{fMRI}}_k\mid o_k)$$ Equation 1

The terms p(o_k|s_k−1) are the probabilities of particular operators, given the various states. The terms p(t_k1,t_k2,t_k3| o_k) are the probabilities of the times associated with the two cards and the subsequent InterTurn, given the operator. The final term p(fMRI_k|o_k) denotes the probability of the fMRI patterns obtained for the scans associated with the kth operator. We discussed the basis for each of the terms in this expression in the earlier sections describing the three sources of information used for classification. Below we explain in more detail how they were calculated for use in the HMM.

1. Operator probabilities, p(o|s): As we discussed under transition probabilities, there are 1875 states when we take into account the prior action. Not all of the 24 operators are possible in particular states. For instance, if there is only one verbal card that has been visited, it is not possible to revisit two verbal cards. Nonetheless, there are over 25,000 legal state–operator combinations and we used the Imperfect Memory Model to estimate their probabilities⁶. The behavior of the model is determined by a probability p_f of forgetting the location of a visited card. For a given game, we estimated a value of p_f to match the number of turns taken by that participant on other games. We then simulated 100,000 games to get estimated predictions for that game for that participant. To counter effects of overfitting, these predictions were combined (weighted .75) with an equal representation of all legal moves (weighted .25).

2. Operator times, p(t₁,t₂,t₃|o): As we discussed under click timing, the time spent viewing a card varied with whether it was the first or the second card, a first visit or a return visit to that card, a math or a verbal card, and whether the turn was a failure or a success. The combination of these four variables yields 16 conditions for the two card times, t₁ and t₂. The InterTurn time, t₃, varied with whether the turn was a failure or a success, adding two more conditions. We estimated the empirical distributions for these 18 conditions from the other games for a participant using the MATLAB ksdensity function (Figure 6 shows the estimated empirical distributions for the InterTurn times, although for illustration purposes it has all the data from all participants). We made our estimates participant-specific because of large individual differences. For instance, participants varied by a factor of more than 3:1 in the length of time they spent on first visits (the range is from 3.2 to 10.4 sec) and in the relative ratio of time on math and verbal cards (the math/verbal ratio varies from 0.8 to 2.3). The probability densities from these empirical distributions were combined to get the probability of the 3 times associated with an operator:

   $$p(t_1,t_2,t_3\mid o)=p{(t_1\mid o)}^{\ast }p{(t_2\mid o)}^{\ast }p(t_3\mid o)$$ Equation 2
3. Image Probabilities, p(fMRI|o): The final term involves the conditional probability of the fMRI images for that turn, given an interpretation of the turn as an operator o. An interpretation involves assigning the first and the second cards to one of four categories (math first visit, math return visit, verbal first visit, and verbal return visit) and the InterTurn to one of two categories (match or nonmatch). Figure 7 illustrated the calculation of the probabilities that various scans came from these categories. This was based on the conditional probabilities p(fMRI_j| category) of the 336 region values associated with a particular scan j if the scan came from a specific category. Denoting the interpretation of three steps (Card 1, Card 2, and InterTurn) as s₁, s₂, and s₃, and the number of scans in each step as n₁, n₂, and n₃, the probability of the image data for an operator is:

   $$p(\mathit{fMRI}\mid s_1,s_2,s_3)=\prod _{i=1}^3\prod _{j=1}^{n_i}p({\mathit{fMRI}}_{ij}\mid s_i)$$ Equation 3

   Note this probability is calculated as a product of a large number of conditional probabilities. This reflects the naïve Bayes assumption that the probability of each image depends only on the category and is independent of the other images. While this assumption is probably inaccurate, it results in a reduction of parameters and so minimizes the problems of overfitting.

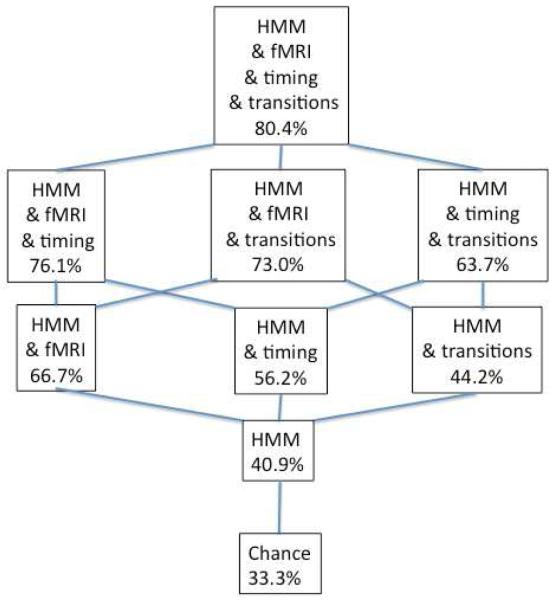
We used the standard Viterbi algorithm for hidden Markov models to efficiently identify the most probable interpretation (Rabiner, 1989). We were able to correctly classify 80.4% of the 12,495 steps, which is far above chance. Chance is 25% for each of the cards and 50% for the InterTurn, for an overall value of 33.3%. This classification accuracy reflects the combined contributions of the three sources of information. We can explore the relative contributions of these sources by eliminating their informativeness: making all legal transformations equally probable, making all times equally probable for a operator, or making the imaging data equally probable for all categories. Figure 10 shows the results for all possible combinations, including “HMM,” which is simply letting an uninformed HMM find a path in the state space from start to end in the observed number of turns. Its performance is 40.9%, still better than chance. In terms of the contribution of different information sources, fMRI provides the most, latency data next, and transition probabilities the least. The combination of the two behavioral sources (latency data and transition probabilities) is approximately equal to the imaging data.

Figure 10.

An illustration of the contributions of different sources of information to the success of classification. Information sufficient to recreate this analysis is available in the files available at http://act-r.psy.cmu.edu/publications/pubinfo.php?id=993.

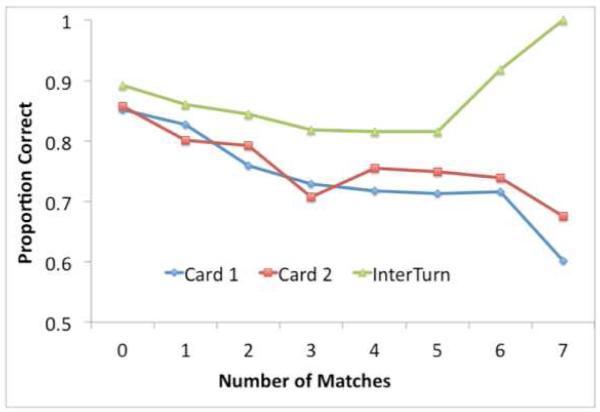
Figure 11 shows how accuracy of classification for the full model (involving all three sources of information) varies as a function of the interval type (Card 1, Card 2, or InterTurn) and the number of pairs of cards matched. Accuracy is generally higher for the InterTurn because there are only two possibilities (match or nonmatch). Accuracy at classifying the InterTurn rises sharply at the end when few cards are left and most turns are matches. In contrast, the classification of the cards tends to drop off with number of matches. This reflects the fact that later turns tend to be return visits which offer fewer scans for classification and for which accuracy of scan classification is lower (see Figure 7).

Figure 11.

Accuracy in classification as a function of number of matches.

Discussion

This research establishes that the earlier HMM methodology (Anderson, 2010; Anderson, Betts, Ferris, & Fincham, in press) can be scaled up to track thought in a complex state space with a high branching factor. In part, this success reflects a general approach of combining a number of weak classifiers to obtain better classification (e.g., Polkar, 2007). Figure 10 shows that combining three sources of information (fMRI data, timing data, and transition probabilities) with an HMM yields better than 80% accuracy, whereas using less information produces lower accuracy. The fMRI data and the timing data could have been combined without the use of an HMM: One could simply identify the most probable operator for each turn given these two sources of information without reference to position in the state space. In this case the accuracy is 74.2%, while adding the HMM and its transition probabilities increases accuracy to 80.4%. Moreover, use of an HMM does more than just boost performance on individual turns—it provides a coherent interpretation of the game. If we look at the classifications produced by combining the fMRI and the timing data without an HMM, none of the 246 games was classified in a logically consistent sequence. Some games had too many or too few math cards or verbal cards visited, or too many or too few matches; others had cards revisited before they could have been visited, etc.

There are some features of our approach that warrant discussion. The decision to use LDA might not seem obvious given the many other classification approaches available (Pereira et al., 2009). Examination of our imaging data suggests that voxel activity is distributed as a multivariate normal. If it were a perfect multivariate normal, LDA would deliver the optimal classification. It also delivers the conditional probabilities required by the logic of an HMM approach. We have examined a number of alternative methods sometimes associated with improved performance in the literature, such as support vector machines (SVMs) with radial basis functions and other kernels. However, we get the best results with LDA. Hsu et al. (2009) noted that LDA is much more efficient and does not have accuracy disadvantages relative to SVMs when the numbers of features and instances are large.

A critical decision in our approach was to find some abstraction of the state space that resulted in a small number of categories for classification. It would not be possible to train classifiers for all the states in that space. Rather than trying to recognize the 625 (or 1875) states we focused on classifying the 24 operators. We decomposed these operators into 3 steps (Card 1, Card 2, InterTurn) and used 6 categories of steps (see Figure 7) to characterize these operators. Note that we used the same categories for the first and second cards. We explored using more categories (such as different categories for each card) but this resulted in overfitting and worse performance.

Another distinctive feature of our approach was the use of large, coarse-grained regions. We have looked at using finer-grained regions but this results in overfitting. While it is possible that a judicious selection of a subset of smaller regions might result in better performance, this does not seem to be what is limiting performance. Consider the six misclassifications of cards in Figure 9:

• Four of these misclassifications (in the last row of Figure 9) are for brief visits that take less than a scan. Thus, there is little imaging data to guide their classification. Given just imaging data, only 72% of cards are correctly identified as to whether they are math or verbal when they are visited for less than 2 seconds. In contrast, accuracy is 90% for longer visits.

• The card misclassification in the first row of Figure 9 involves misclassifying a return visit to a math card as a first visit. This illustrates another problem. Both the imaging and timing data in this case are much more like what is observed on a first visit to a math card than on a return visit. We suspect that this is an instance of the participant actually solving the equation again, effectively treating it as a first visit to a math card. If so, this is really not a misclassification but a problem with our definition of ground truth.

• The card misclassification in the second row of Figure 9 involves the converse error of classifying a first visit to a math card as a return visit. This reflects an interesting consequence of the logic of the Viterbi algorithm. The combined imaging and timing data are actually consistent with the correct classification of this card. However, the system is looking for an overall coherent interpretation and there can only be 8 first visits to math cards. It has stronger evidence for classifying the card in the first row as a first visit than for the card in the second row.

In none of these cases does the misclassification problem reflect the absence of finer spatial information.

The focus of this paper has been on the classification of events in a complex state space and the memory game has been chosen as a paradigm for creating a challenging space with a strong definition of ground truth. However, as reviewed in the introduction, the primary interest in this task in past research has been as a tool to study memory. The Imperfect Memory Model described in this paper, which involved estimating each participant’s probability of forgetting, was used simply to obtain transition probabilities for the HMM. The only other effort we know of to model individual memory performance in this task is by Lavenex et al. (2011), who proposed a buffer model to estimate participants’ working memory capacities. Their model assumes that participants have perfect memory for the last n locations that they have visited and not matched, where n is an estimate of working memory capacity. According to this model, if a participant fails to revisit a card that would yield a match, it is because that card is no longer in the working memory buffer. If so, the participant should move on to visit a new card. In contrast, our Imperfect Memory Model predicts that memory failures would involve revisits but to the wrong card. This is because our model has perfect memory for which cards it has visited, but it sometimes forgets which visited locations go with which visited cards. This aspect of our model is consistent with past work on the memory game showing that participants are very good at recognizing the identities of the cards they have seen, but less accurate at remembering the locations of the cards (Eskritt, Lee, & Donald, 2001). In our experiment, when participants failed to revisit a matching card, they revisited some other card 72% of the time⁷. On average, at these points of memory failures, 71% of all unmatched cards have been visited. Thus, participants are not returning to visited locations any more that one would predict if one assumed they were just randomly choosing among the unmatched cards. Thus, it seems that they are neither under-sampling visited locations in this circumstance, as the Lavenex model would imply, nor over-sampling them, as our model would predict. This suggests that actual memory is a more complex mixture of memory for the identities and the locations of items than what is represented in either model. Perhaps a more accurate memory model would provide a basis for better identification of participants’ trajectories in the state space.

By focusing on classification in a complex state space, this paper provides a stronger foundation for subsequent applications of the methodology we have described. For example, as discussed in Anderson et al. (2010, 2011), one application is to improve the design of tutoring systems. Indeed, one of the original motivations of the present task was to establish that this methodology could distinguish between different kinds of problem solving—in this case, solving anagrams versus algebra problems—to identify when participants were engaged in mathematical thinking and when they were not. Another application would be to collect data on trial-by-trial measures of internal states. For example, we hope to use such data to identify when participants use retrieval versus computation during the course of skill acquisition (e.g., Delaney et al., 1998). In addition, as discussed in Anderson (in press), we can use model evaluation methods associated with HMMs to evaluate alternative models or discover new models. All these examples highlight the potential of using the extremely rich data that come from fMRI in conjunction with behavioral data and modeling techniques to reach a new level of discrimination in tracking problem solving.