Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2013 Mar 10.
Published in final edited form as: Exp Cell Res. 2011 Dec 29;318(5):521–526. doi: 10.1016/j.yexcr.2011.12.003

Characterization of mechanical behavior of an epithelial monolayer in response to epidermal growth factor stimulation

Ruiguo Yang , Jennifer Y Chen §, Ning Xi , King Wai Chiu Lai , Chengeng Qu , Carmen Kar Man Fung , Lynn S Penn §, Jun Xi §,*
PMCID: PMC3288599  NIHMSID: NIHMS347093  PMID: 22227009

Abstract

Cell signaling often causes changes in cellular mechanical properties. Knowledge of such changes can ultimately lead to insight into the complex network of cell signaling. In the current study, we employed a combination of atomic force microscopy (AFM) and quartz crystal microbalance with dissipation monitoring (QCM-D) to characterize the mechanical behavior of A431 cells in response to epidermal growth factor receptor (EGFR) signaling. From AFM, which probes the upper portion of an individual cell in a monolayer of cells, we observed increases in energy dissipation, Young’s modulus, and hysteresivity. Increases in hysteresivity imply a shift toward a more fluid-like mechanical ordering state in the bodies of the cells. From QCM-D, which probes the basal area of the monolayer of cells collectively, we observed decreases in energy dissipation factor. This result suggests a shift toward a more solid-like state in the basal areas of the cells. The comparative analysis of these results indicates a regionally specific mechanical behavior of the cell in response to EGFR signaling and suggests a correlation between the time-dependent mechanical responses and the dynamic process of EGFR signaling. This study also demonstrates that a combination of AFM and QCM-D is able to provide a more complete and refined mechanical profile of the cells during cell signaling.

Keywords: AFM, QCM-D, cell mechanics, EGFR signaling, cytoskeleton, cell adhesion

Introduction

Mechanical properties of cells have attracted considerable interest because of their importance to the understanding of biological processes, such as mitosis, apoptosis, adhesion, and migration [1]. Among the techniques that are capable of measuring mechanical properties of cells [2], atomic force microscopy (AFM) is one of the most popular choices because of its ability to probe individual cells with low force and high precision [3]. To do this, the top surface of a live cell is indented with the tip of an AFM probe to generate a force-displacement curve [4], which can provide the mechanical properties of the upper portion of the cell, such as elasticity, energy dissipation, and hysteresivity. Cell elasticity is characterized by Young’s modulus, E. Energy dissipation is the amount of mechanical energy lost as heat during each cycle of indentation by the AFM tip, and corresponds to the area enclosed by the approach and retraction curves (i.e., the areas within the hysteresis loop, Ha and Hb in Figures 1A and 1B, respectively) [5]. This loss of energy is believed to be caused primarily by frictional and viscous damping within the cell [5, 6]. Hysteresivity, η, is defined as the ratio of the area within the hysteresis loop to the area under the approach curve. This term is analogous to hysteresivity or hysteresis used by others [6–9] to quantify the contribution of dissipated mechanical energy relative to energy input during the approach portion of the indentation.

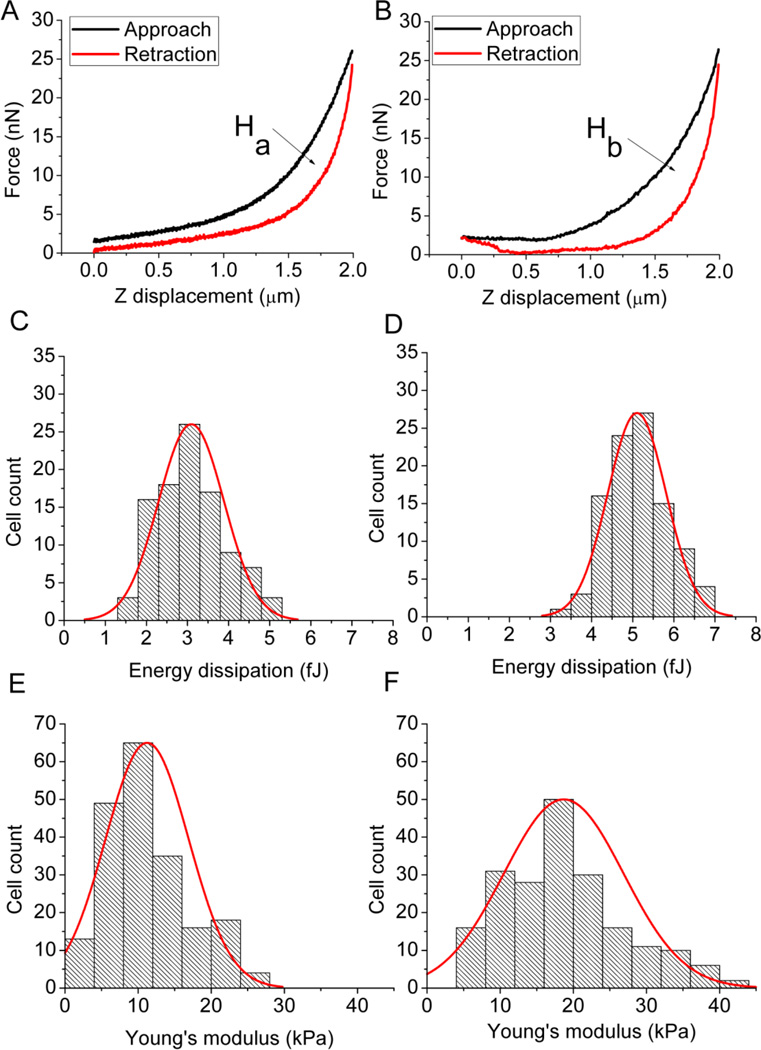
Figure 1.

Figure 1

Open in a new tab

Typical force displacement curves from AFM force curve measurement of the A431 cell in the absence of EGF (A), and in the presence of 40 nM of EGF (B). The area of the hysteresis loop (Ha and Hb), enclosed between the approach and retraction curves, corresponds to the energy dissipation, which increased from 2.9 fJ of Ha (A) to 5.2 fJ of Hb (B). Histograms of the distributions of the energy dissipation of one hundred randomly selected cells with (C) and without the EGF stimulation (D). The energy dissipation increased from 3.09 ± 0.79 fJ in the absence of EGF (C) to 5.10 ± 0.71 fJ (mean ± SD, p < 0.05) in the presence of 40 nM of EGF (D). Histograms of the distributions of the Young’s modulus of two hundred randomly selected cells with (E) and without the EGF stimulation (F). The Young’s modulus increased from 11.2 ± 2.8 kPa in the absence of EGF (E) to 18.7 ± 2.0 kPa (mean ± SD, p < 0.05) in the presence of 40 nM of EGF (D).

In contrast to AFM, the quartz crystal microbalance with dissipation monitoring (QCM-D) has not been widely used in characterization of cell mechanics, even though its applications in other biological analyses have been well documented [10–12]. As a highly sensitive acoustic sensor, QCM-D provides label-free, non-invasive, and real-time measurement of the change in energy dissipation factor, ΔD, of a cell monolayer attached to the surface of an oscillating sensor crystal [13]. ΔD is defined as the ratio of the loss of mechanical energy per oscillation period of the sensor crystal to the total mechanical energy stored in the system. Because the acoustic signal diminishes exponentially with distance above the surface of the quartz crystal oscillator on which the cells are deposited, it probes primarily the basal area of the cell monolayer [12, 14], and ΔD for adherent cells can be expected to be related to changes in contact area of the cells, strength or quality of adhesion between the cell and matrix [15, 16].

We are interested in tracking mechanical changes in A431 cells (human epidermoid carcinoma) in response to epidermal growth factor (EGF), which is the cognate ligand to the transmembrane receptor, epidermal growth factor receptor (EGFR). EFGR regulates cell growth, proliferation, motility, and differentiation through its downstream signaling pathways [17, 18]. In a previous study, we used the QCM-D technique to monitor the cellular response due to high-affinity EGFR signaling [19]. In the present study, we sought to further characterize the mechanical behavior of A431 cells in response to EGF by using a combination of AFM and QCM-D, in which AFM probes the top surface of the cell monolayer and QCM-D probes the bottom surface. While it might be deemed desirable to test both top and bottom surfaces of cells by means of a single mechanical test method, no single test method has access to both top and bottom surfaces of cells in a monolayer. We expected that these combined techniques would offer greater insight into the EGFR-mediated cellular response than either technique alone.

Material and Methods

Reagents and material

Dulbecco’s modified Eagle’s medium (DMEM), fetal bovine serum (FBS), antibiotics, trypsin–EDTA, HEPES buffer, and HBSS buffer were purchased from Invitrogen (Carlsbad, CA). A431 cells were obtained from American Type Tissue Collection (Manassas, VA). Human epidermal growth factor (EGF) was purchased from Peprotech (Fisher Scientific, Pittsburg, PA). All other chemicals were obtained from Sigma-Aldrich (St. Louis, MO).

Cell culture

A431 cells were cultured in T75 Corning culture flasks and were maintained under a humidified atmosphere at 37°C and 5% CO2 in DMEM medium containing 10% FBS, 100 IU/ml penicillin, and 100 µg/ml streptomycin. The cells were usually harvested at 90% confluency.

AFM measurement and data processing

The cultured cells were seeded onto glass coverslips and then allowed to grow in a Petri dish at normal cell culture condition. Once they reached 90% confluency, the attached cells were washed with phosphate-buffered saline (PBS) and starved in serum-free medium for 18 hrs. On the day of AFM measurement, the attached cells were washed and then incubated with the assay buffer (20 mM HEPES in HBSS buffer, pH 7.2) in the Petri dish at 37°C for 2 hours, followed by the addition of EGF at desired concentrations. AFM force curve measurements were made on single cells from 40 minutes prior until 60 minutes after the addition of EGF to the cell layer. To determine statistical distributions of energy dissipation and Young’s modulus, measurements were performed on 100 to 200 randomly selected cells before and after EGF stimulation [20].

All AFM measurements were performed in an aqueous environment at 37°C on Bioscope (Bruker AXS, Inc., Santa Barbara, CA) with a Nanoscope IV controller. The temperature was maintained by a polyimide film heater underneath the cell culture dish during the AFM measurement. The AFM probe consists of a conically shaped tip on a silicon nitride cantilever (Bruker AXS, Santa Barbara, CA) with a spring constant of 0.06 N/m. The force applied to indent the cell was kept below 30 nN, with a resulting deformation of less than 500 nm (<10% of cell height). This probing depth was deep enough to ensure that the cytoskeleton remodeling was registered [21] but was shallow enough to eliminate any influence from the solid substrate underlying the cells [22]. The force curves were generated at a probe-tip loading rate of 1 Hz, which corresponded to a vertical velocity of 5.8 µm/s. At this low velocity, the hysteresis can be attributed to energy dissipation within the cell, and not to transient interaction between the probe tip and the cell surface [5].

The elastic modulus was determined from the Hertzian model for a conically shaped tip indenting an elastic body [23]:

F=kd=2π·E1−ν2δ2tanα

where F is the applied force, d is the deflection of the cantilever, and k is the spring constant of the cantilever. Also, α is the half angle of the cone-shaped tip, ν is the Poisson's ratio, δ is the indentation depth, and E is Young’s modulus. The half open angle of the tip is 17.5°, and Poisson's ratio is taken to be 0.5, the value for an incompressible material. Energy dissipation and hysteresivity, η, were defined above.

QCM-D measurement

QCM-D experiments were conducted according to the protocol described previously [19], except that all assays in this report were carried out on glass-deposited, polished, circular (14 mm, QSX 303), AT-cut quartz sensor crystals. In brief, the A431 cells were allowed to attach and grow on the top side of glass sensor crystal in humid atmosphere at 37°C and 5% CO2. On the day of the QCM-D measurement, each sensor with cells attached was mounted in an open module (Q-sense) and incubated in 400 µL of the assay buffer (20 mM HEPES in HBSS buffer, pH 7.2) at 37°C. After stable baselines were achieved for all four sensors, the assay buffer was removed from each module and replaced with 400 µL of assay buffer (at 37°C) containing a measured amount of EGF. The changes in dissipation factor (ΔD) for the third overtone were recorded at 37°C for a period of 3 hours. The sensing depth of this overtone is approximately 100 nm from the surface of the oscillating sensor crystal [14]. Because of the variations that are often associated with cell assays, each experiment described here was conducted on three replicate cell samples to ensure the reliability and reproducibility of the results.

Fluorescence imaging

Cells grown on glass coverslips were allowed to pre-incubate in 1 mL of the assay buffer (20 mM HEPES in HBSS buffer, pH 7.2) at 37°C for 1 hour. After pre-incubation, the assay buffer was removed and replaced with 10 nM of EGF in 1 mL of the assay buffer pre-warmed to 37°C. After various reaction times (0 minute, 30 minutes, or 60 minutes) at 37°C, cells on glass coverslips were fixed/permeabilized in a solution containing 0.1% Triton X-100 and 3% paraformaldehyde in PHEM buffer (60 mM PIPES, 25mM HEPES, 10mM EGTA, 2mM MgCl2 and pH 6.9) for 20 minutes. The resulting cells were stained with CF488A phalloidin conjugate (Biotium, Inc., Hayward, CA) in PBS with 2% BSA at room temperature for 20 minutes. Then the excess phalliodin solution was removed by rinsing with 2% BSA in PBS. Coverslips with stained cells were mounted with DAPI (Vector Laboratories, Inc., Burlingame, CA) and the cells were imaged with an inverted fluorescence microscope (Zeiss Axioplan 2). Images were processed with the use of Slidebook 5.0 software (Intelligent Imaging Innovations).

Results and Discussion

Mechanical responses probed by AFM

Figure 1 shows the results of the AFM measurements, with the controls (no EGF) in the left panel and the experimentals (40 nM EGF) in the right panel. Figures 1A and 1B show typical force curves for one indentation cycle. A hysteresis loop is visible in both figures, but the larger enclosed area (Hb) in Figure 1B indicates that treatment with EGF induced an increase in energy dissipation of the cell. The energy dissipation values for one hundred randomly selected cells with and without the EGF stimulation were pooled and analyzed. The results of the statistical analysis of these energy dissipation values are summarized in Figures 1C and 1D, showing that the average energy dissipation of the cell increased from 3.09 ± 0.79 fJ to 5.10 ± 0.71 fJ (mean ± SD, p < 0.05) as a result of the treatment with 40 nM EGF.

The force curves can also provide a quantitative assessment of the effect of EGF on cell elasticity. Young’s moduli (E) of individual cells were determined with the aid of the Hertzian model, the results of the statistical analysis of two hundred randomly selected cells, summarized in Figures 1E and 1F, show that 40 nM EGF induced a statistically significant increase in E, from 11.2 ± 2.8 kPa to 18.7 ± 2.0 kPa (mean ± SD, p < 0.05).

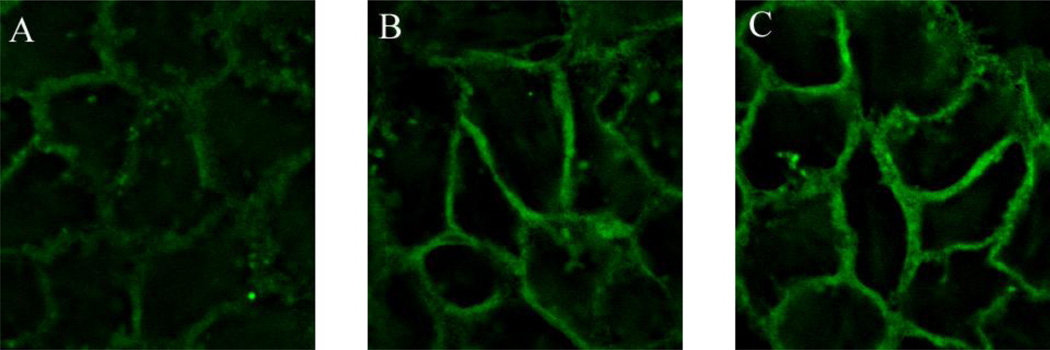
The change in Young’s modulus in cells has often been attributed to remodeling of the cytoskeleton [24], which can be induced by EGF treatment [25, 26]. Under our assay condition, EGF-induced remodeling of the cytoskeleton was vividly shown (Figure 2) when a monolayer of A431 cells treated with 10 nM of EGF exhibited an increase in brightness of the fluorescently labeled actin in the membrane skeleton over the time (30 and 60 min). Thus the increase in Young’s modulus observed in our AFM study is most likely due to remodeling of the cytoskeletal structures of A431 cells in response to EGF treatment.

Figure 2.

Figure 2

Open in a new tab

Reorganization of actin filament in a monolayer of A431 cells induced by the treatment of 10 nM of EGF at 37°C for (A) 0 min (no treatment), (B) 30 min, and (C) 60 min. F-actin was labeled with CF488A-conjugated phalloidin. The EGF treatment induced time-dependent increase in assembly of actin filament as shown by the increase in brightness in the membrane skeleton of A431 cells.

Cells mediate their functions through signaling pathways in a temporally complex manner [27]. Thus, we sought to characterize the time-dependent mechanical response of cells in order to evaluate the connection between EGF exposure, cell signaling, and the mechanical response.

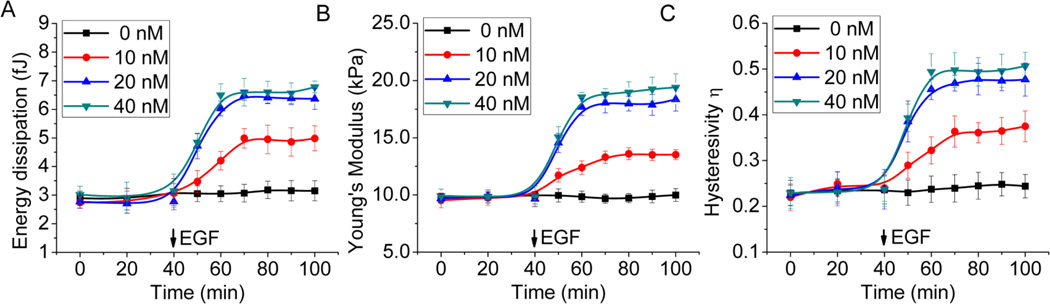
Figure 3 shows the time-dependent mechanical responses of A431 cells under various concentrations of EGF (0, 10 nM, 20 nM and 40 nM). To obtain a time-response curve, AFM force curves were first obtained at each time point at a frequency of 1Hz. Then energy dissipation, Young’s modulus (E), and hysteresivity (η), were extracted from the force-displacement curves and replotted versus the time. The EGF was not added to the cells until a stable baseline had been exhibited for 30 min. Upon the addition of EGF, the cells exhibited progressive increases in energy dissipation, Young’s modulus, and hysteresivity, a clear indication of time dependence. These increases correlate well with the observed time-dependent increase in assembly of actin filaments (Figure 2). At the highest concentration of EGF (40 nM), all three responses had nearly doubled by the end of the 60-min treatment. Dose dependence was in evidence also; all three responses increased monotonically as dose of EGF was increased from zero to 40 nM. Additionally, the values of all three responses at 20 nM of EGF shown in Figure 3 were very close to those at 40 nM of EGF, which indicates that the responses tend to saturate at higher concentrations of EGF. Such saturable responses are characteristic of a receptor-mediated cellular response. Also noteworthy from Figure 3 is that all mechanical responses began to level off between 20 to 30 minutes after EGF stimulation. This suggests that the majority of cellular processes responsible for the increases of these mechanical responses occurred during the first 30 min upon the EGF stimulation. This agrees well with the reported time required for EGFR signaling and trafficking in A431 cells [28, 29], which suggests a correlation between the time-dependent mechanical responses of the cells and the dynamic process of EGFR signaling.

Figure 3.

Figure 3

Open in a new tab

Dynamic mechanical responses of A431 cells to stimulation with four different doses of EGF: 0, 10 nM, 20 nM, and 40 nM. A 30-min baseline was established for each measurement prior to the addition of EGF. Each data point of the plots was determined from an average of 10 force displacement curves recorded at the time for a period of 10 min. Trend lines were used to connect each data point to illustrate the trend for each response curve. All mechanical responses in (A) energy dissipation, (B) Young’s modulus, (C) hysteresivity show a dose-dependence of EGF. The responses in the presence of 10 nM, 20 nM, and 40nM of EGF show a progressive increase over the time of the EGF stimulation.

Based on the depth of the indentation (~500 nm) of the AFM tip, the cytoskeleton was the main structural component of the cell probed. This means that the observed increases in energy dissipation and hysteresivity (Figure 3) can be attributed to processes associated with the cytoskeleton, such as internal friction and actin depolymerization [6]. The time dependence of the hysteresivity, η (Figure 3C), provides additional insight into the mechanical ordering state of the cells. According to structural damping model [7], the ratio η of energy dissipation to energy input should remain constant, unless the mechanical ordering state of the cell is changed [6]. Therefore, the increases in η may be interpreted as an indication of a more disordered mechanical ordering state, i.e., a more fluid-like state of the cell [6, 30]. A fluid-like state is more favorable for morphological changes, such as cell rounding, membrane ruffling, and filopodia extension, all of which have been observed in A431 cells responding to EGF stimulation [28, 31].

Mechanical response probed by QCM-D

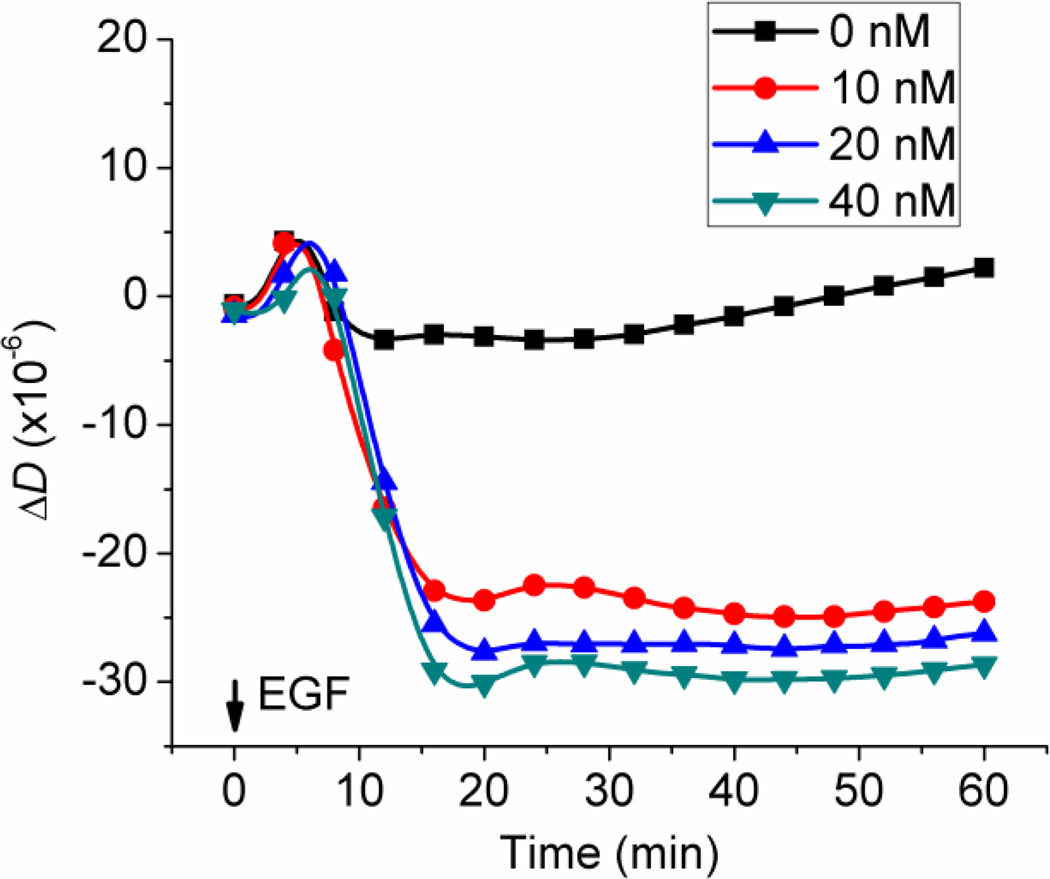
Figure 4 shows representative dose-dependent and time-dependent changes in ΔD, of the monolayer of A431 cells in response to EGF. As a mechanical property, the change in energy dissipation factor, ΔD reveals the mechanical energy loss relative to the energy input per measurement cycle of the QCM-D, which is analogous to hysteresivity, η, computed from the AFM measurements. However, unlike the AFM results shown in Figure 3C, where η increased with time and with dose, the QCM-D detected a decrease in ΔD with time and with dose. The completely opposite trends being shown by ΔD and η clearly indicate that the cytoskeleton-associated processes within the cell body that are responsible for the increases in η are not likely to be predominantly responsible for the decreases in ΔD. This is not unexpected considering ΔD and η are determined by the two techniques that probe different regions of the deposited cells. As the increases in η suggest a shift of the mechanical ordering state of the cell bodies toward a more fluid-like state, the decreases in energy dissipation factor (ΔD) imply a shift of the mechanical ordering state of the basal area of the cells toward a more solid-like state [6]. Such contrast in alteration of mechanical ordering states signifies that the mechanical responses to EGFR signaling are regionally specific. This is right in line with the basic principle of mechanics that the mechanical response of a constrained portion of a body (the basal surface of adhered monolayer of cells) is different from that of the non-constrained portion (the top, free surface of the cell monolayer). Since the QCM-D senses approximately 100 nm into the basal area of the cell, the causes of the decreases in ΔD can be reasonably explained by diminished cell adhesion leading to rupture of the integrin-matrix bonds, reduction of the adhered area, release of trapped liquid medium, etc. [15, 16, 32].

Figure 4.

Figure 4

Open in a new tab

Real-time QCM-D measurement of energy dissipation of A431 cells in response of four different doses of EGF: 0, 10, 20 nM, and 40 nM, The initial increase of the ΔD signal during the first 5 min of each plot was an artifact caused by the solution transfer.

Interestingly, both ΔD and η required about the similar amount of time (20 to 30 min depending on the dose) to reach their plateaus after the addition of EGF. Both quantities showed signs of saturation at the two highest levels of doses (20 nM and 40 nM). These similarities suggest that both of these regional mechanical responses (ΔD and η) were mediated by closely coupled cell signaling pathway(s) of EGFR.

Conclusions

The results of this study indicate a regionally specific mechanical behavior of the cell in response to EGFR signaling. This conclusion was based on the opposite trends being shown by ΔD, in the basal area of cells, and by η, in the upper portion of cells. Additionally, the results suggest a correlation between the time-dependent mechanical responses and the dynamic process of EGFR signaling. This study demonstrates that a combination of AFM and QCM-D is able to provide a more complete and refined mechanical profile of the cells during cell signaling than either technique alone. The combined use of these two techniques to examine different parts of cells can ultimately provide further insight into the process of cell signaling itself.

Highlights.

  1. EGF induces time- and dose-dependent increases in energy dissipation, Young’s modulus, and hysteresivity for the bodies of cells.

  2. EGF induces time- and dose-dependent decreases in energy dissipation factor for the basal areas of cells.

  3. The EGF-induced changes in mechanical properties of the cells are regionally specific.

  4. The time-dependent mechanical responses can be correlated with the dynamic process of EGFR signaling.

  5. A combination of AFM and QCM-D is able to provide a more complete and refined mechanical profile of the cells.

Acknowledgement

This work was supported by NSF Grants IIS-0713346 and DMI-0500372, ONR Grants N00014-04-1-0799 and N00014-07-1-0935, and NIH Grant R43 GM084520.

Abbreviations

AFM

atomic force microscopy

QCM-D

quartz crystal microbalance with dissipation monitoring

EGFR

epidermal growth factor receptor

EGF

epidermal growth factor

Footnotes

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

References

  • 1.Janmey PA, McCulloch CA. Cell Mechanics: Integrating Cell Responses to Mechanical Stimuli. Annual Review of Biomedical Engineering. 2007;9:1–34. doi: 10.1146/annurev.bioeng.9.060906.151927. [DOI] [PubMed] [Google Scholar]
  • 2.Addae-Mensah KA, Wikswo JP. Measurement Techniques for Cellular Biomechanics In Vitro. Exp. Biol. Med. 2008;233:792–809. doi: 10.3181/0710-MR-278. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 3.Radmacher M. Studying the Mechanics of Cellular Processes by Atomic Force Microscopy. In: YuLi W, Dennis ED, editors. Methods in Cell Biology. Vol. Volume 83. Academic Press; 2007. pp. 347–372. [DOI] [PubMed] [Google Scholar]
  • 4.Radmacher M. Measuring the elastic properties of biological samples with the AFM. IEEE Engineering in Medicine and Biology Magazine. 1997;16:47. doi: 10.1109/51.582176. [DOI] [PubMed] [Google Scholar]
  • 5.Alcaraz J, Buscemi L, Grabulosa M, Trepat X, Fabry B, Farr R, Navajas D. Microrheology of Human Lung Epithelial Cells Measured by Atomic Force Microscopy. Biophysical Journal. 2003;84:2071–2079. doi: 10.1016/S0006-3495(03)75014-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 6.Smith BA, Tolloczko B, Martin JG, Grutter P. Probing the Viscoelastic Behavior of Cultured Airway Smooth Muscle Cells with Atomic Force Microscopy: Stiffening Induced by Contractile Agonist. Biophysical Journal. 2005;88:2994–3007. doi: 10.1529/biophysj.104.046649. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 7.Fredberg JJ, Stamenovic D. On the imperfect elasticity of lung tissue. Journal of Applied Physiology. 1989;67:2408–2419. doi: 10.1152/jappl.1989.67.6.2408. [DOI] [PubMed] [Google Scholar]
  • 8.Collinsworth AM, Zhang S, Kraus WE, Truskey GA. Apparent elastic modulus and hysteresis of skeletal muscle cells throughout differentiation. American Journal of Physiology - Cell Physiology. 2002;283:C1219–C1227. doi: 10.1152/ajpcell.00502.2001. [DOI] [PubMed] [Google Scholar]
  • 9.Fung YC. Structure and Stress-Strain Relationship of Soft Tissues. American Zoologist. 1984;24:13–22. [Google Scholar]
  • 10.Dixon MC. Quartz crystal microbalance with dissipation monitoring: Enabling real-time characterization of biological materials and their interactions. J. Biomol. Tech. 2008;19:151–158. [PMC free article] [PubMed] [Google Scholar]
  • 11.Marx KA. The quartz crystal microbalance and the electrochemical QCM: Applications to studies of thin polymer films, electron transfer systems, biological macromolecules, biosensors, and cells. Springer Series on Chemical Sensors and Biosensors. 2007;5:371–424. [Google Scholar]
  • 12.Heitmann V, Reiss B, Wegener J. The quartz crystal microbalance in cell biology: Basics and applications. Springer Series on Chemical Sensors and Biosensors. 2007;5:303–338. [Google Scholar]
  • 13.Hook F, Rodahl M, Brzezinski P, Kasemo B. Energy dissipation kinetics for protein and antibody-antigen adsorption under shear oscillation on a quartz crystal microbalance. Langmuir. 1998;14:729–734. [Google Scholar]
  • 14.Le Guillou-Buffello D, Gindre M, Johnson P, Laugier P, Migonney V. An alternative quantitative acoustical and electrical method for detection of cell adhesion process in real-time. Biotechnology and Bioengineering. 2011;108:947–962. doi: 10.1002/bit.23005. [DOI] [PubMed] [Google Scholar]
  • 15.Fredriksson C, Kihlman S, Rodahl M, Kasemo B. The Piezoelectric Quartz Crystal Mass and Dissipation Sensor: A Means of Studying Cell Adhesion. Langmuir. 1998;14:248–251. [Google Scholar]
  • 16.Rodahl M, Hook F, Fredriksson C, Keller CA, Krozer A, Brzezinski P, Voinova M, Kasemo B. Simultaneous frequency and dissipation factor QCM measurements of biomolecular adsorption and cell adhesion. Faraday Discuss. 1997:229–246. doi: 10.1039/a703137h. [DOI] [PubMed] [Google Scholar]
  • 17.Lemmon MA, Schlessinger J. Cell signaling by receptor tyrosine kinases. Cell. 2010;141:1117–1134. doi: 10.1016/j.cell.2010.06.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 18.Carpenter G. Receptors for epidermal growth factor and other polypeptide mitogens. Annu. Rev. Biochem. 1987;56:881–914. doi: 10.1146/annurev.bi.56.070187.004313. [DOI] [PubMed] [Google Scholar]
  • 19.Chen JY, Li M, Penn LS, Xi J. Real-Time and Label-Free Detection of Cellular Response to Signaling Mediated by Distinct Subclasses of Epidermal Growth Factor Receptors. Analytical Chemistry. 2011;83:3141–3146. doi: 10.1021/ac200160u. [DOI] [PubMed] [Google Scholar]
  • 20.Fung CKM, Xi N, Yang R, Seiffert-Sinha K, Lai KWC, Sinha AA. Quantitative Analysis of Human Keratinocyte Cell Elasticity Using Atomic Force Microscopy (AFM) NanoBioscience, IEEE Transactions on. 2011;10:9–15. doi: 10.1109/TNB.2011.2113397. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 21.Schillers H, Wälte M, Urbanova K, Oberleithner H. Real-Time Monitoring of Cell Elasticity Reveals Oscillating Myosin Activity. Biophysical Journal. 2010;99:3639–3646. doi: 10.1016/j.bpj.2010.09.048. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 22.Melzak KA, Moreno-Flores S, Lopez AE, Toca-Herrera JL. Why size and speed matter: frequency dependence and the mechanical properties of biomolecules. Soft Matter. 2011;7:332–342. [Google Scholar]
  • 23.Touhami A, Nysten B, Dufrene YF. Nanoscale Mapping of the Elasticity of Microbial Cells by Atomic Force Microscopy. Langmuir. 2003;19:4539–4543. [Google Scholar]
  • 24.Kuznetsova TG, Starodubtseva MN, Yegorenkov NI, Chizhik SA, Zhdanov RI. Atomic force microscopy probing of cell elasticity. Micron. 2007;38:824–833. doi: 10.1016/j.micron.2007.06.011. [DOI] [PubMed] [Google Scholar]
  • 25.Rijken PJ, van Hal GJ, van der Heyden MAG, Verkleij AJ, Boonstra J. Actin Polymerization Is Required for Negative Feedback Regulation of Epidermal Growth Factor-Induced Signal Transduction. Experimental Cell Research. 1998;243:254–262. doi: 10.1006/excr.1998.4142. [DOI] [PubMed] [Google Scholar]
  • 26.Rijken PJ, Post SM, Hage WJ, van Bergen en Henegouwen PMP, Verkleij AJ, Boonstra J. Actin Polymerization Localizes to the Activated Epidermal Growth Factor Receptor in the Plasma Membrane, Independent of the Cytosolic Free Calcium Transient. Experimental Cell Research. 1995;218:223–232. doi: 10.1006/excr.1995.1150. [DOI] [PubMed] [Google Scholar]
  • 27.Kholodenko BN, Hancock JF, Kolch W. Signalling ballet in space and time. Nat Rev Mol Cell Biol. 2010;11:414–426. doi: 10.1038/nrm2901. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 28.Chinkers M, McKanna JA, Cohen S. Rapid rounding of human epidermoid carcinoma cells A-431 induced by epidermal growth factor. J. Cell Biol. 1981;88:422–429. doi: 10.1083/jcb.88.2.422. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 29.Wiley HS. Trafficking of the ErbB receptors and its influence on signaling. Experimental Cell Research. 2003;284:78–88. doi: 10.1016/s0014-4827(03)00002-8. [DOI] [PubMed] [Google Scholar]
  • 30.Fabry B, Maksym GN, Butler JP, Glogauer M, Navajas D, Fredberg JJ. Scaling the Microrheology of Living Cells. Physical Review Letters. 2001;87 doi: 10.1103/PhysRevLett.87.148102. 148102. [DOI] [PubMed] [Google Scholar]
  • 31.Chinkers M, McKanna JA, Cohen S. Rapid induction of morphological changes in human carcinoma cells A-431 by epidermal growth factors. J. Cell Biol. 1979;83:260–265. doi: 10.1083/jcb.83.1.260. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 32.Lichtner RB, Wiedemuth M, Noeske-Jungblut C, Schirrmacher V. Rapid effects of EGF on cytoskeletal structures and adhesive properties of highly metastatic rat mammary adenocarcinoma cells. Clinical and Experimental Metastasis. 1993;11:113–125. doi: 10.1007/BF00880072. [DOI] [PubMed] [Google Scholar]

RESOURCES