Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2013 Feb 15.
Published in final edited form as: Neuroimage. 2011 Nov 12;59(4):3166–3172. doi: 10.1016/j.neuroimage.2011.11.008

Striatal Topography of Probability and Magnitude Information for Decisions Under Uncertainty

Gregory S Berns 1, Emily Bell 1
PMCID: PMC3288668  NIHMSID: NIHMS338648  PMID: 22100418

Abstract

Most decisions involve some element of uncertainty. When the outcomes of these decisions have different likelihoods of occurrence, the decision-maker must consider both the magnitude of each outcome and the probability of its occurrence, but how do individual decision makers combine the two dimensions of magnitude and probability? Here, we approach the problem by separating in time the presentation of magnitude and probability information, and focus the analysis of fMRI activations on the first piece of information only. Thus, we are able to identify distinct neural circuits for the two dimensions without the confounding effect of divided attention or the cognitive operation of combining them. We find that magnitude information correlates with the size of the response of the ventral striatum while probability information correlates with the response in the dorsal striatum. The relative responsiveness of these two striatal regions correlates with the behavioral tendency to weight one more than the other. The results are consistent with a second-order process of information aggregation in which individuals make separate judgments for magnitude and probability and then integrate those judgments.

Introduction

Most decisions involve some element of uncertainty. When the outcomes of these decisions have different likelihoods of occurrence, the decision-maker must consider both the magnitude of each outcome and the probability of its occurrence. In traditional economic analysis, individuals are assumed to make decisions to maximize their expected utility, where the expected utility is the benefit of each possible outcome multiplied by the probability of its occurrence (von Neumann and Morgenstern, 1944). Variations of expected utility theory (EUT) allow for distortions of the utility and probability functions (Allais, 1953; Kahneman and Tverksy, 1979; Starmer, 2000). For outcomes with positive utility, all current models of rational choice require the monotonic combination of probability with expected utility. In other words, larger magnitudes of outcomes are better than smaller ones, and higher probabilities are better than lower ones.

How do individual decision makers combine the two dimensions of magnitude and probability? The single system hypothesis suggests that a combined metric of expected utility, including both probability and magnitude, exists throughout brain systems that play a role in decision making but particularly in reward-related regions like striatum and perceptual decision regions like parietal cortex (Fiorillo et al., 2003; Glimcher et al., 2005; Kable and Glimcher, 2007). In contrast, the dual system hypothesis suggests that there are largely distinct neural systems for the processing of magnitude and probability. While reward-related brain regions, particularly the ventral striatum, are consistently found to have increased activity in response to higher magnitudes of expected reward (Knutson et al., 2001; Tobler et al., 2005; Tom et al., 2007; Yacubian et al., 2006), a variety of different regions have been observed to encode variables related to probability of reward, including insula, ventromedial prefrontal cortex (VMPFC), dorsolateral prefrontal cortex (DLPFC), anterior cingulate cortex (ACC), and parietal cortex (Berns et al., 2008; Hsu et al., 2005; Huettel et al., 2006; Knutson et al., 2005; Paulus et al., 2001; Platt and Glimcher, 1999; Shadlen and Newsome, 2001; Venkatraman et al., 2009).

It has been surprisingly difficult to reach consensus about the separability of probability weighting, utility, and expected utility in the brain. Many of the human studies suggest that these elements are separable, but many of the non-human primate studies suggest that they are not. Undoubtedly, much of the disagreement arises from differences in the way in which experiments are operationalized, differences in how monkeys and humans learn, and differences between experiential learning (e.g. reinforcement learning) versus cognitive learning (e.g. learning to multiply two numbers together). Part of the problem is that when making risky decisions, agents are presented with two dimensions of information. It has been demonstrated that when individuals are faced with multiple dimensions of information, they tend to make judgments on each dimension and then integrate the judgments, as opposed to integrating the information and then making a judgment (Shaw, 1982). Here, we approach the problem by separating in time the presentation of magnitude and probability information, and focus the analysis of fMRI activations on the first piece of information only. This approach isolates the processing of magnitude and probability without the confounding effect of divided attention or the cognitive operation of combining them.

Methods & Materials

Participants

Thirty participants (21 female, 9 male; 18-45 years) were recruited from the Emory University campus area. All participants were right-handed, reported no psychiatric or neurological disorders, or other characteristics that might preclude them from safely undergoing MRI. All participants provided informed consent to experimental procedures approved by the Emory University Institutional Review Board. Participants received a base pay of $40 with the opportunity to win an additional $80 depending on decisions made during the experiment.

Task Design

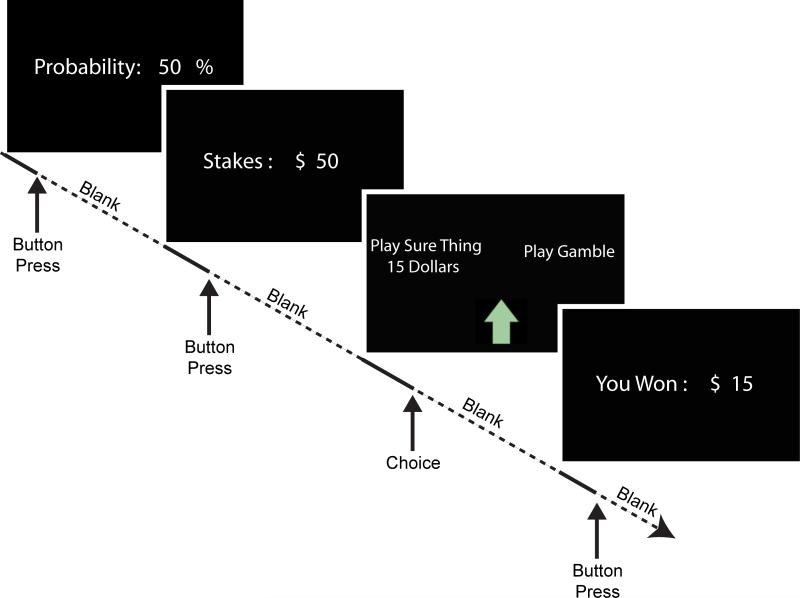
The experimental task was designed to measure independently the neural responses to two dimensions of a simple lottery decision: the probability of an outcome and the magnitude of the outcome. While previous studies have presented both pieces of information simultaneously, it is generally impossible to know how an individual allocates their attention to probability and magnitude. Here, we measured responses to probability and magnitude by separating the delivery of the two pieces of information by presenting only one piece at a time (Fig. 1).

Figure 1.

Figure 1

Open in a new tab

Timeline of a trial in which probability and magnitude information are separated in time. This is an example of a “Probability First” trial. The probability of winning is shown first (minimum of 2 s up to a button press), which is followed by a variable length blank screen. The magnitude of the stakes is then shown similarly, which is followed by the choice screen, and then the results of the choice. All blank screen durations were variable from 2 – 6 s. “Magnitude first” trials reversed the order of stakes magnitude and probability information. “Simultaneous” trials presented both probability and magnitude on one screen.

We used five different values for both the magnitudes and probabilities: 20, 30, 50, 70, and 80. Magnitude was denoted by $ (e.g. $ 20), and probability was denoted by % (e.g. 20 %). A trial consisted of the display of both magnitude and probability information, but three different order conditions were used: 1) probability then magnitude (each presented alone), 2) magnitude then probability (each presented alone), and 3) probability and magnitude simultaneously. The third condition was divided so that half of these trials presented the probability on top and the other half presented the magnitude on top. With five values for both probability and magnitude, there were 25 combinations, and each was presented in each of the three order conditions, for a total of 75 trials. These trials were divided into 4 runs of approximately 19 trials each, which lasted approximately 10 minutes, depending on individuals’ decision times. On each trial, the participant had to choose either the lottery or the default “sure thing” option of $15, which was equivalent to the average expected value of all of the lotteries. Participants indicated their decision between “The Sure Thing of $15” and “Play Gamble” by moving an arrow to point at their choice. After their choice, the outcome was displayed. To calculate the outcome for each accepted gamble, an integer between 1 and 100 was randomly chosen. If the random number was less than the trial probability, then the participant won the stakes from the trial. The outcome was always presented even when the participant chose the sure thing. After completion of all four runs and all scans, the participant rolled a dice to randomly choose one trial to realize their winnings.

The order of the trials was predetermined by a random number generator and was identical for every participant. Each of the 75 trials had the same layout, differing only by the order of the information presented in each trial. All of the inter-stimulus intervals (ISI) and inter-trial intervals (ITI) were jittered and optimized prior to the start of the experiment and were predetermined and identical for all participants.

MRI Scanning

Neuroimaging data were collected using a 3 Tesla Siemens Magnetron Trio whole body scanner (Siemens Medical Systems, Erlangen, Germany). Functional data consisted of thirty-three axial slices that were sampled with a thickness of 3.5 mm and encompassing a field of view of 192 mm with an inplane resolution of 64 × 64 (T2* weighted, TR = 2000ms, TE = 30ms). FMRI data were analyzed using SPM5 (Wellcome Department of Imaging Neuroscience, University College London) using a standard 2-stage random-effects regression model. Data were subjected to standard preprocessing, including motion correction, slice timing correction, normalization to an MNI template brain and smoothing using an isotropic Gaussian kernel (full-width half-maximum = 8mm).

Behavioral Model

We formulated a behavioral model to see how the different conditions influenced the participants’ decisions. By design, the experiment separately presented probability and magnitude, so the initial behavioral models included independent and additive terms for probability and magnitude. For each individual subject, we used logistic regression to determine the weight of the following factors on the likelihood of accepting the gamble: probability, stakes, and order:

log[PGi(1−PGi)]=β0+βprobProbabilityi+βmagMagnitudei+βP1stProbFirsti+βM1stMagFirsti (1)

where, on trial i, PG is the likelihood of accepting the gamble, Probability is the probability (20%, 30%, 50%, 70%, 80%), Magnitude is the outcome ($20, $30, $50, $70, $80), and ProbFirst and MagFirst are dummy variables for the condition order (0 & 0 is the simultaneous condition).

The results of this analysis showed that the coefficients for order were not significant in any subject. Subsequently, we used a reduced model with only probability and magnitude:

log[PGi(1−PGi)]=β0+βprobProbabilityi+βmagMagnitudei (2)

In this model, all coefficients were significant for all participants except three people, who were excluded from subsequent analyses. From this model, we calculated a subjectwise parameter that gauged the relative sensitivity to probability and magnitude: PMdiff = βprob – βmag.

Although this additive model was well-suited for the serial design of the experiment, it makes stronger assumptions than a standard expected utility (EU) model (in particular, linearity and additivity). For comparison to forms that assume maximization EU, we also fit the following two behavioral models:

log[PGi(1−PGi)]=β0+βprobProbabilityi+βmagMagnitudei+βEVProbiMagi (3)

which allowed for the multiplicative interaction of probability and magnitude, and more conventionally an EU-type model:

log[PGi(1−PGi)]=β0+βEVProbiMagiα (4)

where α was varied from 0.2 to 1.5 with the best fit for each subject determined by Akaike's information criterion (AIC).

fMRI Analysis

To minimize the effects of automatization (making the same responses to probability and magnitude combinations without thinking about it), we focused our analysis on the initial presentations of each combination and thus restricted the fMRI analysis to the first two runs (Phelps et al., 2001). At the first level, the model contained seven conditions. The first five conditions indicated the type of information and the order in which it was presented: probability first, magnitude first, probability second, magnitude second, and both simultaneously. Each of these conditions was modeled as a variable duration event for the time that the information was presented. Probability and magnitude were included as parametric modulators for their corresponding conditions. The sixth and seventh conditions segregated the choice period into “sure thing” and “gamble” trials (also variable duration events up to, and including, the choice). Subject motion parameters were included as nuisance regressors. All regressors were convolved with a standard HRF function. Contrasts from the first-level model were entered into a second-level model using a one-sample t-test. Using the AlphaSim routine in AFNI, we estimated the combination of height and extent thresholds that yielded a whole-brain FDR < 0.05 (10,000 iterations). We used 3dFWHMx to estimate the image smoothness from the square root of the SPM-generated ResMS image and input into AlphaSim. Finally, using a voxel level threshold of P<0.001, the extent threshold that yielded a cluster level alpha of 0.05 was determined to be k≥49 (Logan and Rowe, 2004; Zhang et al., 2009).

To identify probability-responsive regions and magnitude-responsive regions, we examined the contrasts formed from the parametric modulators for probability and magnitude on the probability-first and magnitude-first conditions respectively. Because only one piece of information had been presented at that point in the trial, this approach eliminates the possibility of divided attention between two pieces of information. Beta values from these contrasts were then extracted from regions of interest (primarily the striatum) and checked for correlation with the PMdiff metric for each subject.

Results

The behavioral model indicated that probability and magnitude were both positively correlated with the likelihood of accepting the gamble over the sure thing. Except for three subjects, the coefficients for probability and magnitude (Eqn. 2) were significant for all participants (see supplement). Consequently, the form with an interaction term in Eqn. 3 was overspecified and resulted in almost no significant coefficients. The form based on an EU-type function (Eqn. 4) yielded significant coefficients for all subjects. However, when we compared the fit of Eqn. 2 and 4, the models were not significantly different based on the AIC [paired T(29)=1.41, p=0.170]. The average r2 for both models was essentially the same (0.66 for EU and 0.64 for additive) and not significantly different [paired T(29)=1.77, p=0.09]. Thus, we conclude that the additive model is as good (or no worse) than an EU-type model, but the additive model has the advantage of separating the weighting of probability and magnitude. There was substantial variation in the size of the coefficients and the difference between βprob and βmag. The mean PMdiff was 5.835 (7.09 s.d.). Thus, for most subjects βprob was greater than βmag, indicating that probability had a greater effect on their decision than magnitude. The consistency of subjects’ choices was measured by the percentage of times a given combination of probability and magnitude resulted in the same choice (gamble or sure thing). On average, subjects made the same choice 78% of the time (range: 60-100%).

Analysis of decision times indicated that subjects got steadily faster in each run, from an average of 724 ms in run 1 to 610 ms in run 4 [F(3,87)=6.25, P<0.001]. The decision times in run 1 and 2 were not significantly different from each other [F(1,29)=1.29, P=0.266], the difference between run 1 and 3 trended toward significance [F(1,29)=3.43, P=0.074], and the difference between run 1 and 4 were significantly different [F(1,29)=16.1, P<0.001], thus supporting the combination of fMRI runs 1 and 2 in the analysis, and separating out runs 3 and 4.

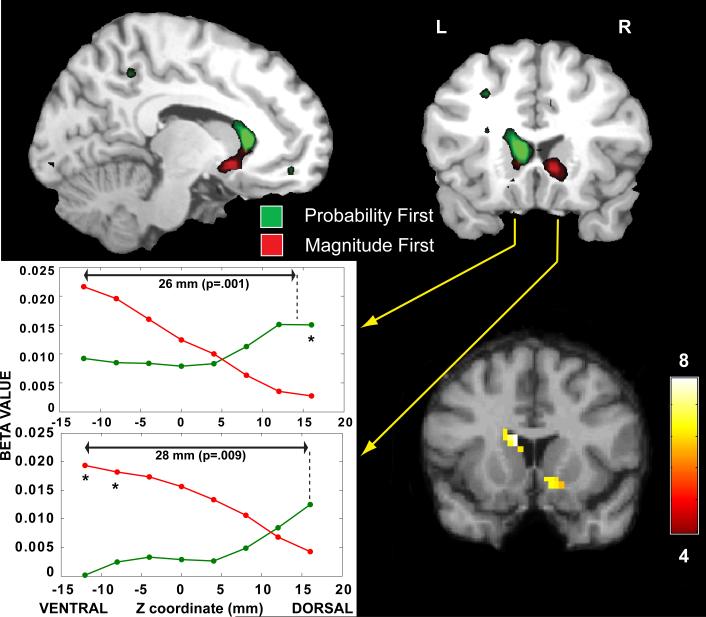
Several brain regions showed correlations with probability or magnitude when those pieces of information were presented first (Table 1). The striatum, however, was of particular interest. We found that both probability and magnitude were correlated with striatal activity, but there was a clear topography with the dorsal striatum correlated with probability and the ventral striatum correlated with magnitude (Fig. 2). To determine whether these apparent differences in topography were statistically different, we took two approaches. First, we examined the contrast between prob1st (modulated by probability) and mag1st (modulated by magnitude). We restricted this analysis to the striatal regions identified in the corresponding individual contrasts by using them as a masking. Within these regions, the dorsal and ventral extremes were significantly different on a voxelwise basis (P<0.05, implementing a two-sided t-test via an F-contrast in SPM). Second, because the two regions of the striatum are in close proximity, the spatial smooting performed in the preprocessing would be expected to result in the overlap of two gaussians. This was confirmed by examing a cross-section of beta values as a function of the Z-coordinate through the head of the caudate (Fig. 2). Here, we find evidence of opposing gradients along the ventral-dorsal axis for probability and magnitude information, which was significantly different on a voxelwise basis at the extremes. Moreover, from these cross-sections, we can estimate a distance of approximately 26-28 mm between the spatial peaks of the probability and magnitude information. Given the spatial width of these profiles, we determined whether the distance between the peaks was significantly different. A Z-statistic was calculated by: Z=d/sqrt(σ12/2 + σ12/2) where d is the distance between the peaks and σ1 and σ2 are the standard deviations of the two spatial profiles. With this method, the centroids of probability and magnitude information were statistically different in both the left (Z=3.30, P=0.001) and right striatum (Z=2.62, P=0.009).

Table 1.

Brain regions correlated with parametric modulators for probability and magnitude. Regions were thesholded at voxel level P<0.001 and cluster size ≥ 49. The subjectwise correlation (R) with measures of probability-magnitude weighting (PMdiff) are shown (and significance, P).

Region MNI coordinates Voxels Z R with PMdiff P
PROBABILITY FIRST
Dorsal striatum -9, 21, 7 85 4.97 0.02 0.93
Visual cortex 30, -78, 14 284 4.45 -0.09 0.65
Parahippocampal gyrus 24, -27, -7 110 4.04 -0.135 0.5
MAGNITUDE FIRST
Ventral striatum 6, 3, -11 229 4.37 -0 .5 0.008
Posterior cingulate cortex 18, -36, 35 60 4.24 -0.32 0.11
L DLPFC -24, 30, 11 71 3.73 -0.26 0.19
Thalamus -3, -15, 11 50 3.65 -0.34 0.08
Open in a new tab

Figure 2.

Figure 2

Open in a new tab

Brain regions in which the BOLD activation was correlated with the probability (green) or magnitude (red) of the outcome when presented as the first piece of information (P<0.001). The level of striatal response was correlated with both probability and magnitude but was topographically distinct with probability located dorsally and magnitude ventrally. The spatial profile of activation (lower left) for the left (upper panel) and right (lower panel) striatum indicated opposing gradients along the ventral-dorsal axis (X coordinate = ±12, Y coordinate = 16). From these cross-sections, we estimate a distance of approximately 26-28 mm between the spatial peaks of the probability and magnitude information. Given the spatial width of these profiles, the distance between the peaks was significantly different in both the left (Z=3.30, P=0.001) and right striatum (Z=2.62, P=0.009). This was confirmed on a voxelwise basis (*P<0.05) within the striatal clusters by an F-test on the contrast of parametric modulators: [prob1st × prob – mag1st × mag] (lower right), which was masked by the union of the probability and magnitude contrasts above [F(1,28)>4, P<0.05].

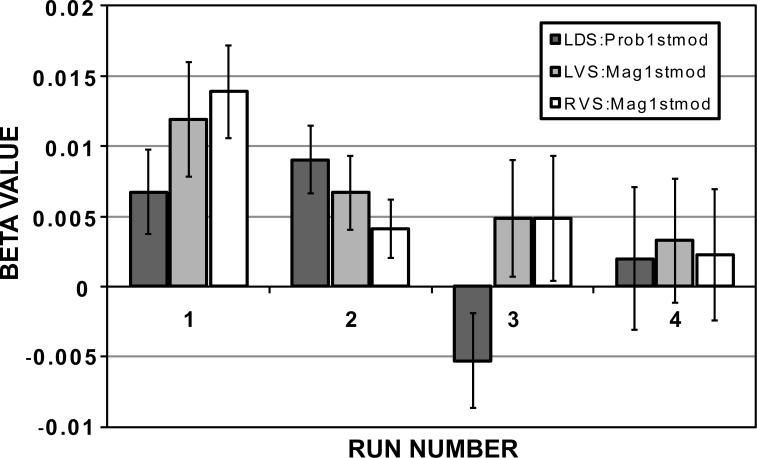
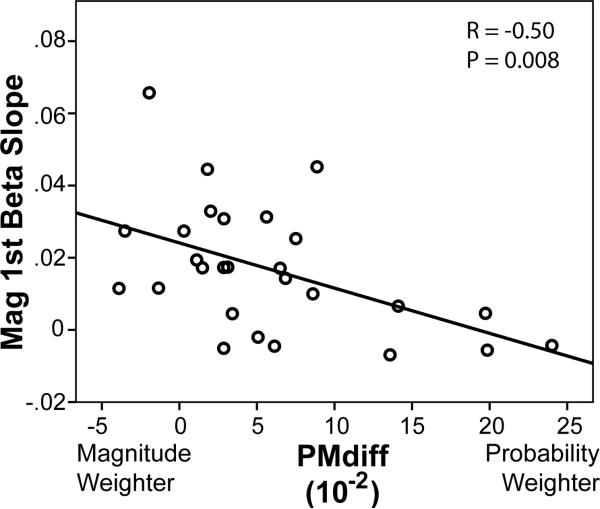
When the beta values for the parametric modulators of probability and magnitude were extracted from these ROIs for each run separately, we found a declining trend such that all were essentially zero by the fourth run (Fig. 3). Given that the behavioral choices were not significantly different across runs, this suggests some form of neural habituation and the rationale for using the initial presentations in the first 2 runs as the best estimate of neural responsiveness to probability and magnitude information. Extracting the beta values for the parametric modulators of probability1st × probability and magnitude1st × magnitude for the magnitude-first and probability-first regions in Figure 2, and averaging over the voxels within each region, we found a significant negative correlation of PMdiff with the betas for magnitude in the ventral striatum (Fig. 4) but no correlation with of PMdiff with the betas for probability in the dorsal striatum (R=0.02, p=0.93). Importantly, since the regions were defined by the parametric modulators for probability and magnitude across all subjects (without regard to the PMdiff metric), the correlation to PMdiff is independent of the identification of the ROIs (Vul et al., 2009).

Figure 3.

Figure 3

Open in a new tab

Beta values within the left (LVS) and right (RVS) ventral striatum and left dorsal striatum (LDS) ROIs as a function of run number. The beta values for the parametric modulators of probability 1st × probability and magnitude 1st × magnitude were averaged within the ROIs shown in Figure 2 separately for each run. All regions showed a declining trend in the size of the beta values as run number increased, such that they were all essentially zero by run 4. Given that behavioral choices were unchanged with run number, this suggests a neural habituation with repetition.

Figure 4.

Figure 4

Open in a new tab

Relationship between the relative degree that individuals weighted probability and magnitude information in their decisions (PMdiff) to the degree of activation in the ventral striatum to magnitude information (Mag 1st Beta Slope). The slope of the activation is a measure of how much the BOLD signal increases per dollar of the outcome. Subjects who were strong magnitude weighters (left) had significantly more responsiveness to magnitude information in the ventral striatum than probability weighters (right).

Discussion

It has long been known that individuals do not combine probability information in a linear manner with magnitude information. Prospect theory, and subsequent variants, have proposed a nonlinear weighting function in which low probabilities are overestimated and high probabilities underestimated (Kahneman and Tverksy, 1979; Prelec, 1998; Tversky and Kahneman, 1992; Wu and Gonzalez, 1996). Although these S-shaped forms fit aggregate data, there is a high degree of subject heterogeneity (Abdellaoui, 2000). Moreover, few mechanistic explanations exist for the underlying cause of these distortions.

Previous neuroeconomic experiments of decision making under uncertainty have typically presented both elements simultaneously (Berns et al., 2008; Christopoulos et al., 2009; Hsu et al., 2009; Huettel et al., 2006; Smith et al., 2009). The implicit assumption has been that people do, in fact, consistently combine probability and magnitude information. However, a large body of research has shown that when multiple pieces of information are presented simultaneously, individuals naturally focus their attention on some elements more than others. Thus, the problem with presenting probability and magnitude simultaneously is that in most neuroimaging experiments we don't know how an individual is dividing their attention. Consequently, a failure to observe responses in a particular brain region may not mean that the region doesn't process a type of information; it could also be the case that nobody paid attention to it. Here, we address this limitation by presenting probability and magnitude information separately. Although one might argue that this is an artificial separation, even when the two pieces of information are presented simultaneously, the subject still must read them sequentially. Our design simply controls this process and extends it in time.

The finding that the ventral striatum processes expected magnitude is consistent with a large body of research that has demonstrated this structure's role in processing the expectation of reward. In this context, it is not surprising that the ventral striatum activity correlated with the magnitude of the expected payoff. Signals in the ventral striatum have been variously interpreted as reward expectation (Knutson et al., 2001; Knutson et al., 2005), reward prediction error (Montague and Berns, 2002; O'Doherty et al., 2004; Samejima et al., 2005; Schultz et al., 1997; Schultz and Dickinson, 2000), incentive salience (Robinson and Berridge, 1993; Zink et al., 2004), and expected utility (Glimcher et al., 2005; Rangel et al., 2008). What is common across all of these interpretations, however, is the monotonic relationship between the magnitude of the reward and the magnitude of the response in the ventral striatum. The larger the expected reward (or RPE), the larger the striatal response. Our findings are consistent with this monotonicity.

While the ventral striatum was linked to magnitude information, we found that the dorsal striatum was correlated with probability information. Although several studies have demonstrated probability-related signals in the striatum for passive tasks (Delgado et al., 2005; Knutson et al., 2005; Preuschoff et al., 2006; Tobler et al., 2007; Yacubian et al., 2006), relatively few have directly varied probability with the goal of identifying probability-specific signals in the brain during choice. Three previous studies of choice examined brain regions correlated with the probability of monetary outcome, with one identifying the striatum (Hsu et al., 2009) and two not (Paulus and Frank, 2006; Smith et al., 2009). Interestingly, Hsu et al. identified a region of the striatum intermediate between the ventral and dorsal zones that we found associated with magnitude and probability respectively. Similarly, in a previous study of choice for probabilistic electric shocks, we also found evidence for the encoding of probability in the dorsal striatum (Berns et al., 2008). However, all of these experiments presented probability and magnitude information simultaneously.

Although we found differences in the striatal location between magnitude and probability processing, these differences were subtle. When considered in isolation, the individual contrasts of magnitude and probability information were indicative of ventral and dorsal locations. The arbitrary nature of thresholding, however, might give the appearance of two regions being distinct. As an alternative test, we considered the voxelwise difference between magnitude and probability contrasts. This revealed two clusters within the union of the two contrasts, but at modest significance levels (ranging from P=0.05 to 0.01). These two clusters were located at the dorsal and ventral extremes of the striatum (Figure 2). However, a voxelwise comparison has limited power when two regions of activation lie in such close proximity to each other. Because the striatum is a small structure, and the activation data were smoothed with a gaussian kernel, it is possible that even if magnitude and probability information were processed in distinct striatal regions, we might not detect them due to smoothing. A more appropriate test of separation should consider the spatial profile of activation. In fact, when plotted in cross-section along the ventral-dorsal axis, we found a gaussian profile of activation for both magnitude and probability information on both the left and right (Figure 2). When the distance between the peaks of these profiles was compared to their widths with a Z-test, we found that the locations of magnitude and probability information were significantly different (P=0.001 and .009 for left and right sides). Although the Z-test in space is strongly indicative of separate striatal locations for magnitude and probability, we note that there is still a large degree of overlap in the middle striatum, suggesting a possible location in which the two dimensions are combined during decision making.

Several previous studies have implicated the dorsal striatum in aspects of decision making, particularly reinforcement learning (Jessup and O'Doherty, 2011; Li and Daw, 2011; O'Doherty et al., 2004; Samejima et al., 2005). While the role of the striatum, particularly the ventral striatum, is well established in classical conditioning and signaling reward-prediction errors, there is less agreement when it comes to decision-making tasks and instrumental learning. With more sophisticated models that include choice policies, the specific role of the dorsal striatum has been suggested to function as the “actor” in actor-critic models (Li and Daw, 2011; O'Doherty et al., 2004). In these models, the actor uses a prediction-error signal to modify the associations between stimuli and responses. However, as Li and Daw noted, the dissociation of value and policy signals has been difficult in choice tasks due to the conflation of value and choice in most experimental designs (Li and Daw, 2011). Thus, the issue of whether the dorsal striatum is primarily involved in mapping stimulus-response relationships or signaling reward prediction errors of outcomes is still debated (Balleine et al., 2007).

Although there are commonalities of our experiment with the RL-literature, an important difference is in the role of learning. By design, RL-tasks emphasize the learning of an association of reward with a neutral stimulus. In economic experiments, because the reward parameters are presented directly – i.e. the magnitude and probability of outcomes – it is assumed that participants have already learned what this information means before entering the experiment. Given this assumption, our results suggest two different striatal signals. In most prediction-error models of learning, a prediction error can occur for two different reasons: 1) a reward was expected, but the magnitude was greater than expected; or 2) a reward occurred unexpectedly (i.e. the prior probability was low). Normally the weights in such models are adjusted by the prediction errors and will come to represent the expected value of the stimuli. Thus, a large weight might reflect a high value reward or one that is received frequently. For humans, it is likely that these two dimensions are processed, at least initially, as distinct entities. And so the existence of multiple prediction error signals seems plausible, similar to that found in primate striatum for separate classes of neurons that encode action-value and goal-value (Lau and Glimcher, 2008) or the dual-system model proposed by Daw et al. (Daw et al., 2005). The existence of a separate prediction error for frequency of outcomes, without regard to magnitude, would also explain previous neuroimaging findings that implicate the striatum in signaling saliency (Cooper and Knutson, 2008; den Ouden et al., 2010; Horvitz, 2000; Schiffer and Schubotz, 2011; Wittman et al., 2008; Zink et al., 2006; Zink et al., 2004; Zink et al., 2003).

The existence of two prediction signals creates an obvious problem for the decision maker. Either the decision maker integrates them into an approximation of expected value, or they use one or the other. We found behavioral evidence for all three strategies. Some participants relied predominately on probability information to make their choices, some relied on magnitude information, and some used both (Figure 4). Interestingly, the responsiveness of the ventral striatum to magnitude information was positively correlated with the behavioral propensity to rely on magnitude information (a negative correlation with PMdiff). Thus, the striatal responses had behavioral manifestations, even before the second piece of information was presented. The dorsal striatum did not show this relationship, which suggests that all subjects processed probability information similarly, and that the behavioral differences were primarily a result of how much weight they gave the magnitude information. There are, of course, many different forms for modeling how probability and magnitude information are integrated (Kahneman and Tverksy, 1979; Prelec, 1998; Tversky and Kahneman, 1992; Wu and Gonzalez, 1996), but all make assumptions about the shape of these functions. We chose to model the behavioral effects of probability and magnitude with by using an additive logistic model. Interestingly, we found that this additive form was as good as an EU-type form in modeling individuals’ choices , but the additive form had the advantage that the coefficients obtained gave a direct readout of the relative weighting of probability and magnitude information. The PMdiff metric, however, may be interpreted in the context of EU; namely, a large positive PMdiff is behaviorally equivalent to a large concave curvature of the utility function (e.g. someone who is risk-averse), while a negative PMdiff is behaviorally equivalent to a convex utility function (someone who is risk-seeking). Thus, the correlation of the ventral striatal responsiveness with PMdiff could also reflect the individual risk preference, with greater responsiveness linked to risk-seeking. Finally, it has been suggested that the striatum encodes the variance of financial rewards (Christopoulos et al., 2009; Preuschoff et al., 2006). Although we did not specifically design our experiment to test this hypothesis, we note that the conditions of our experiment with larger magnitudes also had larger variances relative to the sure thing.

Decision under uncertainty is fundamentally a problem of divided attention. Two pieces of information – probability and magnitude – must be integrated to form an objective expectation of reward. Assuming that individuals can accurately process each dimension alone (a dubious assumption for probability), integrating the two is a complex cognitive operation. To perform this integration, the individual must attend to both elements, hold them in working memory, combine them, and compare the result to another option, also held in working memory. The observation of distinct signals for probability and magnitude is consistent with a second-order model of information integration (Shaw, 1982). In a second-order model, decision criteria are formed for each dimension of information and then the two criteria are integrated to form a response. For example, the agent would form a tentative response (gamble or sure-thing) based on probability and another tentative response based on magnitude. If the two responses are in agreement, then the choice process is complete. If the two types of responses differ, then the agent must choose one or the other to arrive at their actual choice. In contrast, a first-order model, which is implicit to expected utility theory, the decision maker integrates the two pieces of information and then applies a decision criterion to the result. For example, the agent would first multiply probability and magnitude (or some transformation of them), and if the result exceeded a threshold criterion, then they would choose the gamble. However, the non-overlapping representations of probability and magnitude information in the striatum is more consistent with the second-order model. Previous studies of basal ganglia connectivity have shown that the ventral striatum receives the majority of its inputs from the medial PFC and OFC, while the dorsal striatum receives inputs from the DLPFC (Draganski et al., 2008). In fact, the ventral striatal region we identified as being modulated by magnitude information spreads into the MPFC/OFC. At slightly lower thresholds of significance (P<0.005), we also observe L DLPFC (-27, 24, 38) activity significantly modulated by probability information. Thus, the likely inputs for the two streams of information follow known frontostriatal connectivity patterns.

Our results have implications for understanding the cognitive distortions that occur when individuals make decisions under uncertainty. Economic models, such as prospect theory, postulate a distortion of probability and/or magnitude information. Although the source of these distortions is not known exactly, perceptual processes are frequently implicated. In addition to perceptual distortions, our results suggest that the sequential processing of two dimensions of information, occurring in distinct regions of the striatum, may result in a second-order decision process in which judgments are aggregated instead of information.

Supplementary Material

01

Highlights.

  • We used sequential presentation of probability and magnitude information

  • Ventral striatum was associated with processing magnitude information

  • Dorsal striatum was associated with processing probability information

  • Behavioral preference for magnitude associated with ventral striatum responsiveness

Acknowledgements

We are grateful to C. Monica Capra, Michael J. Prietula, Andrew Brooks, W. Gavin Ekins, Brittany Anderson, and Sara E. Moore for helpful discussions and comments on this paper. This work was funded by a grant from the National Institute on Drug Abuse (DA024045) through the American Recovery and Reinvestment Act (ARRA).

Footnotes

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

References

  1. Abdellaoui M. Parameter-free elicitation of utility and probability weighting functions. Management Science. 2000;46:1497–1512. [Google Scholar]
  2. Allais M. Le comportement de l'homme rationnel devant le risque: critique des postulats et axiomes de l'ecole Americaine. Econometrica. 1953;21:503–546. [Google Scholar]
  3. Balleine BW, Delgado MR, Hikosaka O. The role of the dorsal striatum in reward and decision-making. Journal of Neuroscience. 2007;27:8161–8165. doi: 10.1523/JNEUROSCI.1554-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Berns GS, Capra CM, Chappelow J, Moore S, Noussair C. Nonlinear neurobiological probability weighting functions for aversive outcomes. NeuroImage. 2008;39:2047–2057. doi: 10.1016/j.neuroimage.2007.10.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Christopoulos GI, Tobler PN, Bossaerts P, Dolan RJ, Schultz W. Neural correlates of value, risk, and risk aversion contributing to decision making under risk. Journal of Neuroscience. 2009;29:12574–12583. doi: 10.1523/JNEUROSCI.2614-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Cooper JC, Knutson B. Valence and salience contribute to nucleus accumbens activation. NeuroImage. 2008;39:538–547. doi: 10.1016/j.neuroimage.2007.08.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Daw ND, Niv Y, Dayan P. Uncertainty-based competition between prefrontal and dorsolateral striatal systems for behavioral control. Nature Neuroscience. 2005;8:1704–1711. doi: 10.1038/nn1560. [DOI] [PubMed] [Google Scholar]
  8. Delgado MR, Miller MM, Inati S, Phelps EA. An fMRI study of reward-related probability learning. NeuroImage. 2005;24:862–873. doi: 10.1016/j.neuroimage.2004.10.002. [DOI] [PubMed] [Google Scholar]
  9. den Ouden HEM, Daunizeau J, Roiser J, Friston KJ, Stephan KE. Striatal prediction error modulates cortical coupling. Journal of Neuroscience. 2010;30:3210–3219. doi: 10.1523/JNEUROSCI.4458-09.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Draganski B, Kherif F, Kloppel S, Cook PA, Alexander DC, Parker GJM, Deichmann R, Ashburner J, Frackowiak RSJ. Evidence for segregated and integrative connectivity patterns in the human basal ganglia. Journal of Neuroscience. 2008;28:7143–7152. doi: 10.1523/JNEUROSCI.1486-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Fiorillo CD, Tobler PN, Schultz W. Discrete coding of reward probability and uncertainty by dopamine neurons. Science. 2003;299:1898–1902. doi: 10.1126/science.1077349. [DOI] [PubMed] [Google Scholar]
  12. Glimcher PW, Dorris MC, Bayer HM. Physiological utility theory and the neuroeconomics of choice. Games and Economic Behavior. 2005;52:213–256. doi: 10.1016/j.geb.2004.06.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Horvitz JC. Mesolimbocortical and nigrostriatal dopamine responses to salient non-reward events. Neuroscience. 2000;96:651–656. doi: 10.1016/s0306-4522(00)00019-1. [DOI] [PubMed] [Google Scholar]
  14. Hsu M, Bhatt M, Adolphs R, Tranel D, Camerer CF. Neural systems responding to degrees of uncertainty in human decision-making. Science. 2005;310:1680–1683. doi: 10.1126/science.1115327. [DOI] [PubMed] [Google Scholar]
  15. Hsu M, Krajbich I, Zhao C, Camerer CF. Neural response to reward anticipation under risk is nonlinear in probabilities. Journal of Neuroscience. 2009;29:2231–2237. doi: 10.1523/JNEUROSCI.5296-08.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Huettel SA, Stowe CJ, Gordon EM, Warner BT, Platt ML. Neural signatures of economic preferences for risk and ambiguity. Neuron. 2006;49:765–775. doi: 10.1016/j.neuron.2006.01.024. [DOI] [PubMed] [Google Scholar]
  17. Jessup RK, O'Doherty JP. Human dorsal striatal activity during choice discriminates reinforcement learning behavior from the gambler's fallacy. Journal of Neuroscience. 2011;31:6296–6304. doi: 10.1523/JNEUROSCI.6421-10.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Kable JW, Glimcher PW. The neural correlates of subjective value during intertemporal choice. Nature Neuroscience. 2007;10:1625–1633. doi: 10.1038/nn2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Kahneman D, Tverksy A. Prospect theory: An analysis of decision under risk. Econometrica. 1979;47:263–291. [Google Scholar]
  20. Knutson B, Adams CM, Fong GW, Hommer D. Anticipation of increasing monetary reward selectively recruits nucleus accumbens. Journal of Neuroscience. 2001;21:RC159. doi: 10.1523/JNEUROSCI.21-16-j0002.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Knutson B, Taylor J, Kaufman M, Peterson R, Glover G. Distributed neural representation of expected value. Journal of Neuroscience. 2005;25:4806–4812. doi: 10.1523/JNEUROSCI.0642-05.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Lau B, Glimcher PW. Value representation in the primate striatum during matching behavior. Neuron. 2008;58:451–463. doi: 10.1016/j.neuron.2008.02.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Li J, Daw N. Signals in human striatum are appropriate for policy update rather than value prediction. Journal of Neuroscience. 2011;31:5504–5511. doi: 10.1523/JNEUROSCI.6316-10.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Logan BR, Rowe DB. An evaluation of thresholding techniques in fMRI analysis. NeuroImage. 2004;22:95–108. doi: 10.1016/j.neuroimage.2003.12.047. [DOI] [PubMed] [Google Scholar]
  25. Montague PR, Berns GS. Neural economics and the biological substrates of valuation. Neuron. 2002;36:265–284. doi: 10.1016/s0896-6273(02)00974-1. [DOI] [PubMed] [Google Scholar]
  26. O'Doherty J, Dayan P, Schultz J, Deichmann R, Friston K, Dolan RJ. Dissociable roles of ventral and dorsal striatum in instrumental conditioning. Science. 2004;304:452–454. doi: 10.1126/science.1094285. [DOI] [PubMed] [Google Scholar]
  27. Paulus MP, Frank LR. Anterior cingulate activity modulates nonlinear decision weight function of uncertain prospects. NeuroImage. 2006;30:668–677. doi: 10.1016/j.neuroimage.2005.09.061. [DOI] [PubMed] [Google Scholar]
  28. Paulus MP, Hozack N, Zauscher B, McDowell JE, Frank L, Brown GG, Braff DL. Prefrontal, parietal, and temporal cortex networks underlie decision-making in the presence of uncertainty. NeuroImage. 2001;13:91–100. doi: 10.1006/nimg.2000.0667. [DOI] [PubMed] [Google Scholar]
  29. Phelps EA, O'Connor KJ, Gatenby JC, Gore JC, Grillon C, Davis M. Activation of the left amygdala to a cognitive representation of fear. Nature Neuroscience. 2001;4:437–441. doi: 10.1038/86110. [DOI] [PubMed] [Google Scholar]
  30. Platt ML, Glimcher PW. Neural correlates of decision variables in parietal cortex. Nature. 1999;400:233–238. doi: 10.1038/22268. [DOI] [PubMed] [Google Scholar]
  31. Prelec D. The probability weighting function. Econometrica. 1998;66:497–527. [Google Scholar]
  32. Preuschoff K, Bossaerts P, Quartz SR. Neural differentiation of expected reward and risk in human subcortical structures. Neuron. 2006;51:381–390. doi: 10.1016/j.neuron.2006.06.024. [DOI] [PubMed] [Google Scholar]
  33. Rangel A, Camerer C, Montague PR. A framework for studying the neurobiology of value-based decision making. Nature Reviews Neuroscience. 2008;9:545–556. doi: 10.1038/nrn2357. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Robinson TE, Berridge KC. The neural basis of drug craving: an incentive-sensitization theory of addiction. Brain Research Reviews. 1993;18:247–291. doi: 10.1016/0165-0173(93)90013-p. [DOI] [PubMed] [Google Scholar]
  35. Samejima K, Ueda Y, Doya K, Kimura M. Representation of action-specific reward values in the striatum. Science. 2005;310:1337–1340. doi: 10.1126/science.1115270. [DOI] [PubMed] [Google Scholar]
  36. Schiffer A-M, Schubotz RI. Caudate nucleus signals for breaches of expectation in a movement observation paradigm. Frontiers in Human Neuroscience. 2011;5 doi: 10.3389/fnhum.2011.00038. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Schultz W, Dayan P, Montague PR. A neural substrate of prediction and reward. Science. 1997;275:1593–1599. doi: 10.1126/science.275.5306.1593. [DOI] [PubMed] [Google Scholar]
  38. Schultz W, Dickinson A. Neuronal coding of prediction errors. Annual Review of Neuroscience. 2000;23:473–500. doi: 10.1146/annurev.neuro.23.1.473. [DOI] [PubMed] [Google Scholar]
  39. Shadlen MN, Newsome WT. Neural basis of perceptual decision in the parietal cortex (area LIP) of the rhesus monkey. Journal of Neurophysiology. 2001;86:1916–1936. doi: 10.1152/jn.2001.86.4.1916. [DOI] [PubMed] [Google Scholar]
  40. Shaw ML. Attending to multiple sources of information: I. the integration of information in decision making. Cognitive Psychology. 1982;14:353–409. [Google Scholar]
  41. Smith BW, Mitchell DGV, Hardin MG, Jazbec S, Fridberg D, Blair RJ, Ernst M. Neural substrates of reward magnitude, probability, and risk during a wheel of fortune decision-making task. NeuroImage. 2009;44:600–609. doi: 10.1016/j.neuroimage.2008.08.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Starmer C. Developments in non-expected utility theory: the hunt for a descriptive theory of choice under risk. Journal of Economic Literature. 2000;XXXVIII:332–382. [Google Scholar]
  43. Tobler PN, Fiorillo CD, Schultz W. Adaptive coding of reward value by dopamine neurons. Science. 2005;307:1642–1645. doi: 10.1126/science.1105370. [DOI] [PubMed] [Google Scholar]
  44. Tobler PN, O'Doherty JP, Dolan RJ, Schultz W. Reward value coding distinct from risk attitude-related uncertainty coding in human reward systems. J Neurophysiol. 2007;97:1621–1632. doi: 10.1152/jn.00745.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Tom SM, Fox CR, Trepel C, Poldrack RA. The neural basis of loss aversion in decision-making under risk. Science. 2007;315:515–518. doi: 10.1126/science.1134239. [DOI] [PubMed] [Google Scholar]
  46. Tversky A, Kahneman D. Advances in prospect theory. Cumulative representation of uncertainty. Journal of Risk and Uncertainty. 1992;5:297–323. [Google Scholar]
  47. Venkatraman V, Payne JW, Bettman JR, Luce MF, Huettel SA. Separate neural mechanisms underlie choices and strategic preferences in risky decision making. Neuron. 2009;62:593–602. doi: 10.1016/j.neuron.2009.04.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. von Neumann J, Morgenstern O. Theory of Games and Economic Behavior. Princeton University Press; Princeton: 1944. [Google Scholar]
  49. Vul E, Harris C, Winkielman P, Pashler H. Puzllingly high correlations in fMRI studies of emotion, personality, and social cognition. Perspectives on Psychological Science. 2009;4:274–290. doi: 10.1111/j.1745-6924.2009.01125.x. [DOI] [PubMed] [Google Scholar]
  50. Wittman BC, Daw ND, Seymour B, Dolan RJ. Striatal activity underlies novelty-based choice in humans. Neuron. 2008;58:967–973. doi: 10.1016/j.neuron.2008.04.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Wu G, Gonzalez R. Curvature of the probability weighting function. Management Science. 1996;42:1676–1690. [Google Scholar]
  52. Yacubian J, Glasher J, Schroeder K, Sommer T, Braus DF, Buchel C. Dissociable systems for gain- and loss-related value predictions and errors of prediction in the human brain. J Neurosci. 2006;26:9530–9537. doi: 10.1523/JNEUROSCI.2915-06.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Zhang H, Nichols TE, Johnson TD. Cluster mass inference via random field theory. NeuroImage. 2009;44:51–61. doi: 10.1016/j.neuroimage.2008.08.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
  54. Zink CF, Pagnoni G, Chappelow J, Martin-Skurski M, Berns GS. Human striatal activation reflects degree of stimulus saliency. NeuroImage. 2006;29:977–983. doi: 10.1016/j.neuroimage.2005.08.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
  55. Zink CF, Pagnoni G, Martin-Skurski ME, Chappelow JC, Berns GS. Human striatal responses to monetary reward depend on saliency. Neuron. 2004;42:509–517. doi: 10.1016/s0896-6273(04)00183-7. [DOI] [PubMed] [Google Scholar]
  56. Zink CF, Pagnoni G, Martin ME, Dhamala M, Berns GS. Human striatal response to salient nonrewarding stimuli. Journal of Neuroscience. 2003;23:8092–8097. doi: 10.1523/JNEUROSCI.23-22-08092.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

01
NIHMS338648-supplement-01.zip (18.5KB, zip)

RESOURCES