Mechanical analysis of Drosophila indirect flight and jump muscles

Abstract

The genetic advantages of Drosophila make it a very appealing choice for investigating muscle development, muscle physiology and muscle protein structure and function. To take full advantage of this model organism, it has been vital to develop isolated Drosophila muscle preparations that can be mechanically evaluated. We describe techniques to isolate, prepare and mechanically analyze skinned muscle fibers from two Drosophila muscle types, the indirect flight muscle and the jump muscle. The function of the indirect flight muscle is similar to vertebrate cardiac muscle, to generate power in an oscillatory manner. The indirect flight muscle is ideal for evaluating the influence of protein mutations on muscle and cross-bridge stiffness, oscillatory power, and deriving cross-bridge rate constants. Jump muscle physiology and structure are more similar to skeletal vertebrate muscle than indirect flight muscle, and it is ideal for measuring maximum shortening velocity, force-velocity characteristics and steady-state power generation.

1. INTRODUCTION

The use of Drosophila as a model organism has had a major impact on many fields of biology. Over the past couple of decades, progress has been made to expand its utility in muscle physiology by developing preparations from two Drosophila thoracic muscles, the indirect flight muscle (IFM) and jump muscle for mechanical evaluation. These two muscles are very interesting as they possess informative and adaptive physiological characteristics [1-3], but combined with the power of Drosophila genetics, their use to answer many interesting and relevant muscle biology questions is greatly enhanced. These muscles have been used to investigate the structure-function characteristics of muscle proteins [4-6], determine mechanisms behind muscle and cardiac diseases [7] and study the molecular basis of muscle fiber type diversity [1, 8]. In this review we focus on the preparations, equipment, and mechanical analysis techniques that have been developed to analyze the functional properties of IFM and jump muscles. Investigate

2. Drosophila Indirect Flight Muscle

The IFM is composed of 12 dorsal longitudinal muscle (DLM) fibers and 14 dorsal ventral muscle (DVM) fibers inside the thorax. The fibers are about a millimeter in length and have an oval shape when viewed in cross-section. The fibers range between 100 to 200 micrometers in diameter. The IFM fibers do not directly attach to the wings, but instead attach to the cuticle. The deformation of the cuticle acts on a specialized hinge that causes the wings to move [9]. The two sets of IFM contract out of phase with each other to set up a resonance vibration in the thorax, similar to that of a tuning fork [10]. The stiffness of the IFM, plus the stiffness of the cuticle and inertia of the wings are the major influences on wing beat frequency and wing stroke amplitude with further adjustments possible from some of the small direct flight muscles [11-12] and perhaps by modulating the stiffness of the IFM through calcium concentration [13]. This is in contrast to most other animal muscle types where the firing rate of the motor nerve sets the muscle contraction frequency. Instead, the IFM fibers of Drosophila are asynchronous, meaning they do not contract synchronously with each nerve action potential from the flight muscle motor nerve [14]. The IFM has a very prominent stretch activation response which, along with shortening deactivation, allows for net work and power generation at relatively high calcium concentrations [14]. These adaptations enable the very high contraction frequencies required for flight without incurring the high cost of calcium pumping with each contraction cycle. These high speed adaptations also influence the types of muscle mechanical measurements that can be made with Drosophila IFM.

2.1 IFM dissection and skinned fiber preparation

We prepare IFM fibers for mechanical evaluation from female Drosophila that have been raised at 18°C as the females are larger than the males and flies raised at colder temperatures are slightly larger than flies raised at higher temperatures. The larger size makes fiber dissection easier, but is not essential for a good skinned fiber preparation. Fibers are normally dissected from the thoraces of 2 to 3-day-old Drosophila. The IFMs of younger flies are still growing, adding thick and thin filaments [15], thus fibers from younger flies generate less force and power [16]. However, we are sometimes forced to use younger flies as some muscle protein mutations cause myofibril ultrastructure deterioration once the flies start using their IFMs. For example, we use fibers from newly eclosed to 2-hour-old flies for our embryonic myosin based chimeric mutants [16].

2.1.1 Dissection of IFM

The first step in IFM dissection is removal of the head, abdomen and wings using fine spring scissors (Vannas 4 mm spring scissors, Fine Science Tools) and forceps (Dumont #5, Fine Science Tools) (Figure 1A). The thorax, with the legs still attached, is placed in a Plexiglas chamber. This chamber is made by drilling a 2 cm diameter hole through a 0.5 cm high, 2.5 cm by 7.5 cm Plexiglas rectangle and gluing it to a standard glass microscope slide of the same length and width. The chamber contains dissection solution (pCa 8.0, 5 mM MgATP, 1 mM free Mg²⁺, 0.25 mM phosphate, 5 mM EGTA, 20 mM N,N-bis(2-hydroxyethyl)-2-aminoethanesulfonic acid (BES, pH 7.0), 175 mM ionic strength, adjusted with Na methane sulfonate, 1 mM DTT, 50% glycerol and 0.5% Triton X-100). The dissection chamber is kept cold by using it on a custom designed aluminum stage cooled by a cold water/radiator fluid mixture at 4°C from a chiller (ThermoFlex900, Thermo Electron Corporation, Waltham MA) flowing through milled out channels in the stage. The stage has a 2 cm diameter hole in the center to allow light in from the bottom if desired. Two cuts, using very fine spring scissors (Mini-vannas, 2 mm, Fine Science Tools), are made to split the thorax open (Figure 1B), one through the ventral cuticle between the two sets of legs and the other through the dorsal cuticle. The dorsal cut can be made off to one side to ensure that the opposite side’s set of DLM fibers are not damaged. At this step, the dissection solution can access the fibers and skinning begins. The fibers should remain in this solution for 1 hour.

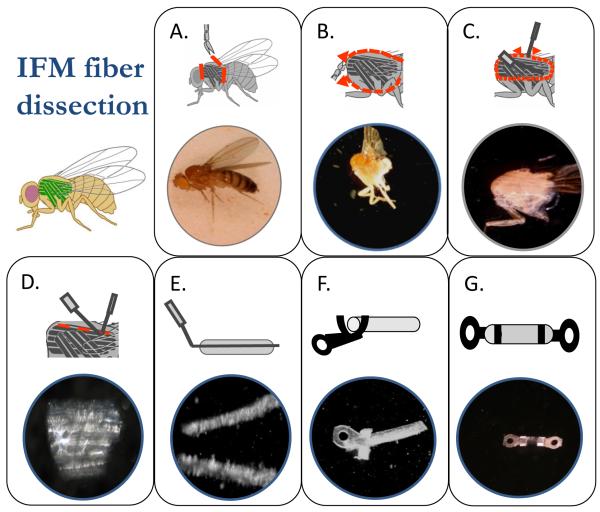
Figure 1.

Dissection and T-clipping of an IFM fiber. The steps of preparing an IFM fiber for mechanical measurements are A) isolation of the thorax by removing the head, abdomen and wings, B) splitting the thorax in half and immersing it in skinning solution, C) removing the bundle of DLM fibers, D) separating the 6 fibers in the bundle from each other, E) splitting one of the fibers in half, F) clamping the tabs of the T-clips around the ends of the fiber to produce G) a clipped IFM fiber preparation.

The next and subsequent steps in the dissection require custom designed probes. Tungsten wire probes are made by electrochemical etching in a saturated solution of NaNO₃. A direct current power supply is connected to a carbon rod, the negative terminal, that is immersed in the nitrate solution and the other end of the circuit, the positive terminal, is connected to a banana clip. We connect the clip to the shaft of a hypodermic needle into which 0.005 inch diameter tungsten wire (Small Parts, Inc.) has been inserted and crimped into place. The wire is bent appropriately for the specific probe and shaped by repeated immersions into the etching solution.

One key to successful IFM fiber preparation is careful extraction of the fibers from the half thorax (Figure 1C). There are no tendons to cut as the fibers attach directly to the cuticle, so the fibers must be carefully detached at their insertion points. Detachment is performed using a tungsten wire probe that has a 45 degree bend prior to an approximately 200 μm long and 50 μm tip that rapidly narrows to a sharp point. A combination up and down sewing machine-like motion and a slight side to side motion works best to detach a bundle of DVM fibers (Figure 1D bottom). The fibers can be transferred to 0.5 ml of storage solution (dissection solution minus Triton X-100) in another dissection dish once the fibers have soaked for 1 hour in dissection solution (or alternatively moved after one of the next two dissection steps). A wire loop small enough to support a drop of solution such that the fiber bundle is supported by surface tension makes a good transfer device. The fibers are held together by tracheal tubes that must be severed, using a straight pair of tungsten wire probes that have a fine but not sharp point to separate the fibers (Figure 1D). The IFMs are directly oxygenated through these tubes. A scissors-like motion and side to side motion are used to separate the fibers, taking care not to stretch or stab the fibers with the probes. The individual fibers have an oval shape when viewed in cross-section with a definite long and short axis. The best fibers are split longitudinally down their middle, as parallel to the myofibrils as possible, to produce fibers with a diameter of approximately 125 μm. The probe for splitting the fiber in half is bent at about a 45 degree angle. The portion after the bend is slightly longer than the length of the fiber. This probe should have a very thin, non-tapered tip, ~20 μm in diameter. This probe is easily damaged, so new ones need to be made frequently. A half-fiber enables better diffusion of MgATP and other solution components into and out of the fiber.

Fibers left in the dissection solution longer than one hour gradually become softer and more compliant. If left overnight in dissection solution, they produce less force and power than fibers used immediately or stored in storage solution (dissection solution without Triton-X 100). Fibers transferred to storage solution can be stored for at least a week at −20°C without any performance degradation.

2.1.2 T-clipping

The IFM fibers are attached to the force transducer and length change motor using aluminum foil T-clips (Figure 1F & 1G). The T-clips are laser cut from food grade aluminum foil (MicroConnex, Snoqualmie, WA). Due to their small size, the clips are not completely cut free from the foil, but are left attached to rectangular strips so we end up with the clips arranged in rows of about 50 per strip. The clips can be scaled and cut at various sizes to match different fiber diameters. The size of the hole is important to enable the T-clip to fit snugly on the force and length hooks so it does not move during some of the more abrupt mechanical perturbations. The tabs of the T-clips are pre-bent into a U-shape while still attached to strips of aluminum foil. This makes wrapping them around the fiber ends easier (Figure 1F). The clips are cut off the strips and stored in a large drop of glycerol in a Petri dish until needed.

Proper attachment of the clips to the fibers is a balance between clamping the ends of the fiber tightly enough so the fiber does not slide around in the clip, but not so tight that the ends of the fiber are crushed (Figure 1G). A good guide is that the fiber should bulge slightly where it emerges from the clip. Poor clipping is the most common cause of a fiber generating less than normal force and power. A clipped fiber that is not gripped tight enough by the T-clips is sometimes obvious as the fiber will slide inside the tabs of the T-clip when manually lengthened and shortened on the muscle mechanics apparatus. Different sized and shaped stainless steel probes help provide the correct amount of force in the correct direction onto the tabs of the clip to securely wrap them around the fiber. All of the myofibrils that make up the fiber must be captured between the clips. An end-tuft of the fiber emerging from the back side of the tabs and slightly over the hole helps prevent slippage. The distance between the two clips is typically 150-250 μm. The length of IFM fibers is too short for glutaraldehyde fixation of the ends. However, end-compliance has not been a problem given the very high sarcomeric stiffness of IFM muscle fibers. The fiber is transferred into the muscle mechanics chamber on a flat spatula (Double-ended micro spatula, Fine Science Tools) that is slightly wider than the length of the clipped fiber preparation to minimize the amount of storage solution transferred with the fiber.

2.2 Muscle mechanics apparatus

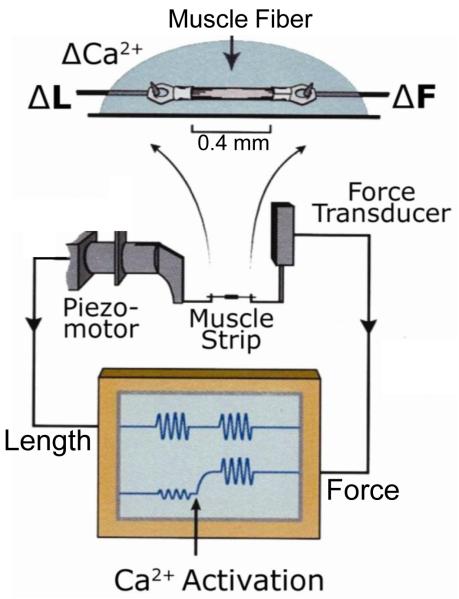
Most of the components of the IFM mechanics apparatus are similar to other skinned fiber apparatuses (see Aurora Scientific or World Precision Instruments web sites for commercially available apparatuses). The basic set-up is illustrated in Figure 2. The apparatus is built on an inverted compound microscope to enable accurate measurements of fiber dimensions. A rectangular prism (Edmund Optics, Barrington, NJ) is adhered to the glass bottom of the chamber so that the height of the muscle fiber, in addition to its length and width, can be measured using a compound microscope and video analysis software (Ion Optix, Milton, MA). A stereo-zoom microscope (SZ40, Olympus) is mounted on a boom stand above the mechanics apparatus for visualization when mounting clipped fibers onto the hooks. The fiber is strung between tungsten wire hooks, created as described for the tungsten probes, attached at one end to a piezo actuator linear motor (P-840.10, PI, Auburn, MA) with a high voltage driver (E505.00 LVPZT Amplifier) and position sensor (E509.x.1 PZT Servo Controller). A 15 micron throw motor works best for IFM fibers as it has the fastest excursion speed of the motors made by PI. Motors with longer throws cannot move fast enough in a sine wave pattern at high oscillation frequencies ( > 400 Hz) without a significant decrease in their amplitude of oscillation. The other hook is attached to a force transducer, Akers gauge (AE-801, SensorOne, Sausalito, CA). The Akers gauge is held in a custom made aluminum block. The hook is epoxied (EP30HT Masterbond, Hackensack, NJ) onto the gauge. The gauge is coated with black caulk (832, Dow Corning, Midland, MI) to eliminate its light sensitivity. After coating with epoxy, each gauge is calibrated by hanging weights from its hook and determining the voltage output from a custom built amplifier. The most important components of the amplifier besides voltage amplification are offset and gain adjustments.

Figure 2.

Muscle mechanics apparatus. After the fiber is T-clipped and skinned, it is mounted on length hooks from the peizo length driver and Aker’s gauge force transducer. The display screen indicates passive and active sinusoidal analysis.

A custom built voltage amplifier is connected in series with the position sensor and contains an adjustable gain and offset. The voltage signals enter the computer via a break-out board (BNC-2110, National Instruments) and A/D computer card and software (NI-DAQ 7, National Instruments). The timing of the arrival of the signals to the computer from the force and position sensors must be assessed to determine if the two are synchronous. If there is a delay in one relative to the other, a correction must be made. This is critical for measurements such as work loops where very accurate timing between length and force changes is essential, especially at the high length change frequencies required for Drosophila fibers. Our control and analysis software was written by Dr. Bradley Palmer (U. of Vermont) using Igor Pro (Wavemetrics, Lake Oswego, OR). The software controls the muscle mechanics apparatus, data sampling, and has some on-line data analysis capabilities.

Most IFM experiments are performed at 15°C. To maintain the fiber bathing solution chamber at this temperature the chamber is cooled using a recirculating ambient water bath to remove the heat generated by the thermoelectric cooling module (Marlow Industries, Dallas, TX). Temperature feedback is through a temperature probe attached to the side of the muscle bathing chamber. The solution temperature immediately adjacent to the fiber is monitored by a separate temperature probe and the temperature setting adjusted to correct for the influence of room temperature.

2.3 Solutions

IFM fibers do not hold up well when transferred between bathing chambers, the typical method used to change bathing solutions for most muscle mechanics apparatuses. Active IFM fibers often rip, pull out of the t-clip or are damaged when pulled through air-water interfaces. IFM fibers perform better if solutions are exchanged (remove and then replace a portion of the bathing solution) in a single chamber, using a 10 or 20 μl pipette. We fill a single, 0.6 ml circular chamber with mineral oil to prevent solution evaporation and then inject a 30 μl bubble of relaxation solution (pCa 8.0, 12 mM MgATP, 30 mM creatine phosphate, 600 U/ml creatine phosphokinase, 1 mM free Mg²⁺, 5 mM EGTA, 20 mM BES (pH 7.0), 200 mM ionic strength, adjusted with Na methane sulfonate, 1 mM DTT) into the center of the chamber.

We determine the correct chemical composition of bathing solutions from a program written by Bob Godt [17] that uses dissociation constants to calculate the free ion concentrations in solution. This is especially important for accurate free calcium concentration determination. In 2006, we determined that high [MgATP] is needed because of IFM myosin’s low affinity for MgATP [1]. All our standard solutions now use greater than 10 mM ATP with a regenerations system of 30 mM creatine phosphate and 600 U/ml creatine phosphokinase.

2.4 Mounting the fiber onto the apparatus

Once the fiber is securely clipped, it’s transferred from storage solution using a spatula shaped tool and floated on the surface of the relaxing solution bubble under the oil. The hooks are raised up into the holes of each T-clip or the clips are very carefully placed over the wire tungsten hooks using a fine tipped tungsten wire probe. If the fiber sinks to the bottom of the solution bubble, then carefully pick it up by one of the clips and place it on the hooks.

2.5 Determining the correct starting length for IFM experiments

Unfortunately, it is very difficult to view Drosophila IFM sarcomeres using light microscopy or laser diffraction due to the IFM fibers thickness and, more significantly, tracheal tubes that permeate the fiber. During Drosophila flight, gas exchange occurs directly from the environment into the fiber through spiracles in the cuticle that are connected to tracheal tubes that enter the fibers (Figure 1D, white strands). Instead of using a specific sarcomere length to set the starting muscle length for experiments, optimal muscle length is determined empirically by increasing fiber length until the fiber produces its maximum amount of power in activating solution (same as relaxation solution, but pCa adjusted to 5.0) as measured using sinusoidal analysis (see section 2.6.3) [16]. A typical increase is 10-20% from slack length. This is generally about 2 mN/mm² resting tension. IFM fibers need this high resting tension to perform optimally. Lower resting tension results in lower power production.

2.6 Mechanical measurements

2.6.1. Isometric tension

Isometric tension measurements are the most basic that can be made with Drosophila indirect flight muscle. The amount of calcium activated isometric tension produced is very low compared to other muscle types. For example, the jump muscle (see below) produces about 30-fold more active isometric tension [2]. The net active tension (total tension minus passive tension) produced by IFM fibers is about 1-2 mN/mm² [18]. A low duty ratio [19] and perhaps the stretch activation mechanism [20] decreases isometric tension compared to other muscle types. Duty ratio is the amount of time the cross-bridge spends bound to actin divided by the total time a cross-bridge takes to go through the entire cross-bridge cycle [19]. Faster myosins must spend less time bound so they do not impede other myosins pulling on actin. However, less time bound also means fewer cross-bridges at any given time binding to actin which decreases active isometric force. It has also been proposed that low isometric tension is necessary for stretch activation and shortening deactivation mechanisms that enable IFM to produce work and power at saturating calcium concentrations [20].

In contrast, the amount of passive tension produced by Drosophila IFM is high relative to other muscle types. Typical resting tension at optimal power producing length is about 2 mN/mm² [18]. This is 2-3 times higher than the jump muscle [2]. The higher passive tension in IFM is due to shorter isoforms of the titin-like filaments from the sallimus gene, namely kettin and sls(700), and projectin [21]. High resting stiffness and low isometric tension are characteristic of many asynchronous muscles [22-24], though not of all asynchronous muscles or for all solution conditions for a given muscle [25].

2.6.2. Tension transient analysis

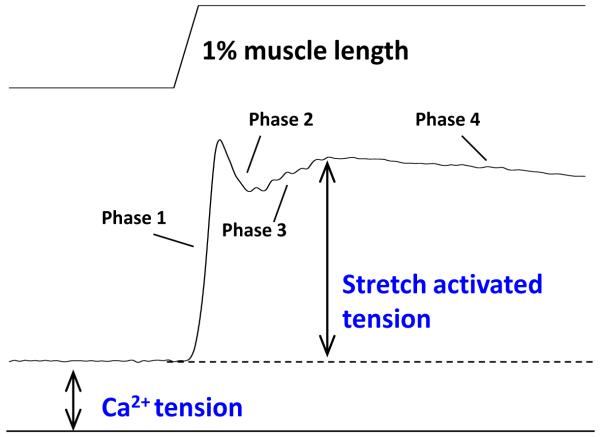
Analysis of the tension response to a step change in muscle length (ML) was most notably used by Ford, Huxely and Simmons as a method to gain insight into the cross-bridge contraction mechanism [26]. They divided the tension response into four components or phases. These phases can be seen in Drosophila IFM at ~pCa 4.5 (Figure 3). For lengthening steps, phase 1 is an immediate tension rise concomitant with stretch. Phase 2 is a very quick tension decay. Phase 3 is a slower, delayed increase in tension, and phase 4 is a very slow decay in tension. The IFM is an excellent preparation for performing step analysis as long as high time resolution is possible as phases 2 and 3 are extremely rapid [27]. Stretch activated muscle, including IFM, possesses a very prominent phase 3 amplitude. The term stretch activation is used to describe this delayed increased in force following a rapid length increase (Figure 3). To determine the rates of three of the phases, we typically fit phases 2-4 [26] with the sum of three exponential curves: a₁[1−exp(−k₁t)]+a₂exp(−k₂t)+a₃exp(−k₃t)+offset, where k₁, k₂ and k₃ are the rate constants. The offset adjusts for non-zero starting values.

Figure 3.

Transient step analysis. A length (top) and tension (bottom) trace from an IFM fiber undergoing a 1% muscle length increase in 0.5 ms. The four phases of the tension response are indicated along with calcium and stretch activated tensions. Stretch tension is typically 2-3 fold higher than calcium activated tension.

2.6.3 Sinusoidal analysis

Sinusoidal analysis is a method adapted from viscoelastic material property measurements. This technique is also one of the best ways to characterize the mechanical properties of IFM fibers due to their high passive stiffness and short I - bands. Muscle fiber length is oscillated through a small amplitude sine wave while recording the tension response (Figure 4A). A set of frequencies to oscillate the muscle through is chosen proportional to the speed of the muscle type. For wild type IFM, we typically test 50 frequencies from 0.5 to 650 Hz [16]. The amplitude is kept small to maintain linearity of the tension response with the length change (i.e. the tension response must also be sinusoidal). The amplitude and phase of the tension response are used to calculate the complex stiffness (also called complex modulus) of the muscle. More information can be gained by separating the complex modulus into its viscous and elastic modulus components. The elastic modulus, or in phase stiffness, is influenced by molecular components of the muscle that behave as springs (the elastic modulus is the normalized spring constant). The elastic modulus provides information about cross-bridge stiffness if the measurement is made while the fiber is in rigor [28]. The viscous modulus is the normalized damping coefficient (a dashpot). The viscous modulus is proportional to work produced by an active muscle. Thus a positive viscous modulus value is work absorbed, while a negative viscous modulus value means the muscle is producing work at that frequency. Power production can be calculated from work and the frequency of muscle oscillation. Information about muscle kinetics can be gleaned by determining the frequency at which the greatest amount of work or power is produced, or by examining other frequency points such as the lowest complex modulus frequency point (the dip frequency). Subtle changes due to protein mutations can often be revealed by examining changes to these maximum or minimum frequencies.

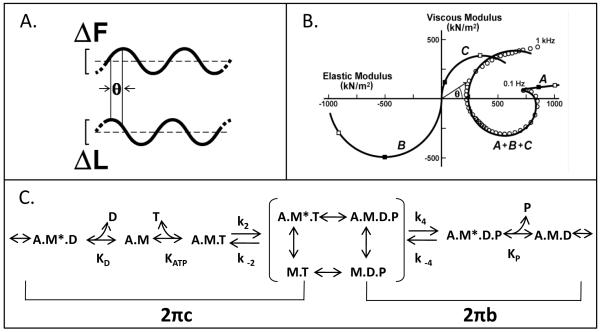
Figure 4.

Sinusoidal analysis. A) Small amplitude sinusoidal length changes (0.25% ML peak to peak) are applied to the muscle fiber. The phase and amplitude relation between the applied length change (ΔL) and resulting force change (ΔF) are measured over a range of frequencies (f = 0.5-1000 Hz). The complex modulus is calculated as the ratio of tension change (ΔF divided by fiber cross-sectional area) and the fractional change in muscle length. B) In the Nyquist plot, the viscous modulus (the 90° out-of-phase component of the complex modulus) is plotted versus elastic modulus (the in-phase component of the complex modulus). Circles are data points from a wild-type IFM fiber. We fit the data in the Nyquist plot with the equation y(f) = A (2π if /α)^k − B if /(b+if) + C if /(c+if), where $\mathrm{i}=\sqrt{-1}$, α = 1 Hz, and k is a unitless exponent, to yield components A, B and C, where coefficients A, B and C are the magnitudes expressed as mN per mm² fiber cross-sectional area. The characteristic frequencies of B and C are b and c, expressed in Hz. Plotted individually, the three terms deconvolve into the three solid line plots. The viscous modulus of B is negative, which denotes work-producing cross-bridge processes, whereas the viscous modulus of C is positive, which denotes work-absorbing cross-bridge processes. Work (J m⁻³) is equal to π E_v (ΔL/L)², where E_v is the viscous modulus, and ΔL/L is the amplitude of the sinusoidal length change divided by the length of the fiber between the two T-clips. Power (W m⁻³) is equal to frequency (f) times π E_v (ΔL/L)². C) The mechanical rate constants b and c, after converting to their time domain equivalents, 2πb and 2πc, can be used to calculate cross-bridge association and rate constants when combined with this six-state cross-bridge model [1, 30]. M is myosin, A is actin, T is MgATP, D is MgADP, and P is phosphate. The asterisk signifies a second conformational state. For conceptual purposes, the primary transitions that influence 2πb and 2πc when a myosin isomerization between Pi and ADP release is rate limiting are bracketed. See Swank et al. [1] for a full mathematical description. Modified from Swank et al. [1].

Sinusoidal analysis can be taken one or two steps further to gain more detailed information about fiber kinetics. One can fit the complex modulus to obtain the mechanical rate constants 2πb and 2πc which can be generally related to steps of the cross-bridge cycle (Figure 4B and 4C) [29-30]. The mechanical rate constants are derived by fitting the complex modulus from every fiber to a 3-term equation. This is based on the equation originally developed by Kawai and Brandt [30] for muscle sinusoidal analysis and has been slightly modified to be more suitable for IFM [1] : Y(f) = A (2π if/α)^k − B if /(b +if) + C if/ (c +if), where f is the applied frequency of oscillation (0.5-650 Hz), i is the square root of −1, α is defined as 1 Hz, and k is a unit-less exponent [1]. The first term (A) reflects the viscoelastic properties of passive structures within the fiber, while the second and third term (B and C) reflect an outcome of transitions between cross-bridge states (changes in complex moduli due to the strain-sensitivity of cross-bridge rate constants) that are exponential in the time domain. Process B is primarily influenced by work-producing steps of the cross-bridge cycle while process C is influenced by work-absorbing steps prior to and including myosin detachment from actin. Processes B and C appear as hemispheres in the Nyquist plot with characteristic frequencies b and c (Figure 4B) [1]. In the time domain, these frequencies correspond to mechanical rate constants 2πb and 2πc. According to Kawai and Brandt, 2πb and 2πc are equivalent to the tension transient rates for Phase 3 and Phase 2, respectively [29].

2.6.4. Cross-bridge rate constants from sinusoidal analysis

By combining sinusoidal analysis with variation in [Pi], [MgATP] or [MgADP], elementary rate constants of a six-state cross-bridge model can be derived. Varying [Pi], [MgATP] or [MgADP] alters the steady-state distribution of cross-bridges states, a shift observed by changes to 2πb and 2πc values [29-30]. Thus, to determine elementary cross-bridge rate constants from sinusoidal analysis, we use algebraic derivations that relate muscle mechanical rate constants 2πb and 2πc to affinity and rate constants of a six-state cross-bridge scheme [1]. We typically fit the sum and product of 2πb and 2πc versus [MgATP]. Alternatively, we can separately fit 2πb versus [Pi] and 2πc versus [MgATP]. However, the second method requires a simplifying assumption, that 2πc >> than 2πb [30]. If this is not the case, then the first method of fitting sum and product to substrate or hydrolysis product, is a more accurate method of deriving rate constants [1].

2.6.5. Work loops

While sinusoidal analysis can be used to measure the work and power generation capabilities of a muscle, the work loop technique [31] is a better method for measuring the amount of work and power produced by a muscle under conditions it experiences during locomotion [32]. Figure 5 shows a typical work loop from Drosophila IFM. The fiber is driven through a muscle length change and waveform pattern that mimics the in vivo length change pattern. We typically apply ten identical consecutive sinusoidal cycles to the muscle and record both tension and muscle length change traces. Positive work (work produced by the muscle during shortening) and negative work (work absorbed by the muscle during lengthening) are determined by calculating the area under the tension curve during shortening and lengthening, respectively, for each cycle using the equation work = ∫Fdl, where F is tension and dl is fiber length change. Negative work is subtracted from positive to calculate net work, and net work multiplied by oscillation frequency to determine power. For these calculations, we use the work and power values from the 8^th cycle as by the 6^th or 7^th cycle, power settles down to a constant value.

Figure 5.

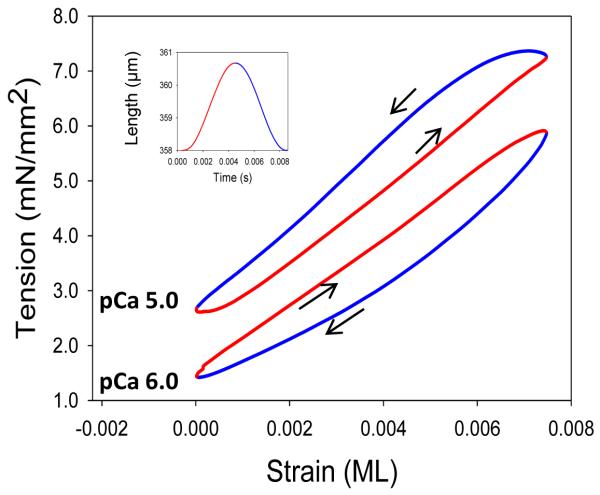
Work loop analysis. Two IFM fiber work loop traces are shown, one that produces positive work, the counterclockwise loop at pCa 5.0, and one that shows only work absorption, clockwise at pCa 6.0. Arrows indicate clockwise and counterclockwise loops. The inset shows one muscle length change cycle and the color coding of red for muscle lengthening and blue for muscle shortening. The IFM fiber was oscillated at 125 Hz at 0.75% ML.

IFM is unique in that high amounts of positive work and power can be generated at saturating calcium levels. With most other muscle types, only work absorption would occur, as the tension during lengthening would be higher than during shortening [14]. The ability to generate positive work and power is due to highly developed stretch activation and shortening deactivation. All striated muscle types display these two properties to some extent: skeletal has very little, cardiac a moderate amount and insect IFM the most stretch activation [33]. Perhaps a better way to define if a muscle is “stretch activated” would be if it has enough stretch activation and shortening deactivation to generate work or power at a high, constant calcium level. In other words, work can be produced without calcium cycling during each length change cycle.

The conditions that generate the most work and power for Drosophila are 0.75% to 1% ML amplitude at 125 Hz oscillation frequency at pCa 4.5 [20, 34]. This is using a perfectly sinusoidal ML change. It is likely that the in vivo ML change is not exactly sinusoidal and that other waveform shapes could enable more power production from IFM.

2.7 Limitations on the use of IFM

The IFM is highly evolved for its very specialized task of producing power at very high frequencies [1]. However, this high degree of specialization has produced adaptations that limit its use to perform some of the more typical muscle mechanical measurements. The IFM has a short and relatively inextensible I band due to the presence of relatively short isoforms of projectin and sallimus gene products, members of the titin family of elastic connecting filaments [35-38], which limit its length excursion. Mechanical measurements requiring a long length change, such as slack tests to measure unloaded shortening velocity and force-clamps to generate force-velocity curves, are difficult, if not impossible to perform. However, Drosophila has another muscle type that has a much more extensible I-band that undergoes longer length changes in vivo – its jump muscle.

3. The jump muscle

The other Drosophila thorax muscle that is amenable to muscle mechanical measurements is the tergal depressor of the trochanter (TDT), more commonly referred to as the jump muscle. The jump muscle is used to power jumping, which for Drosophila is usually a prelude to flight [39]. The structure of the jump muscle is much different than IFM. The jump muscle has much smaller diameter fibers that are roughly rectangular in shape when viewed in cross-section and are arranged in two layers [40]. The myofibrils are rectangular with one side about 3 times as long as the other. The fibers are aligned in parallel in the dorsal 2/3 of the muscle, while the ventral 1/3 is pinnate. The top inserts into the dorsal cuticle, the bottom into the middle leg. Unlike the IFM, the leg muscles are probably synchronous, one nerve impulse per muscle contraction. The muscle is fully activated by calcium and does not show prominent stretch activation when the muscle is rapidly lengthened [40].

3.1 Jump muscle preparation

The first reported measurements of Drosophila jump muscle mechanics [40] and, to our knowledge, the only other group to measure Drosophila jump muscle mechanics used the entire muscle. They t-clipped the tendon that inserts into the middle leg and the dorsal end of the muscle that was left attached to its insertion with the thoracic cuticle. Using a whole muscle probably limited the effectiveness and types of experiments that could be performed. Attempts by our lab resulted in slow or no activation when using an entire jump muscle. When the whole jump muscle did activate, the fibers often ripped out of the T-clip. These problems were likely due to difficulties with uniform calcium diffusion into the whole muscle and securely attaching and aligning all the fibers in parallel between the T-clips.

To avoid these problems, we developed a jump muscle preparation that consisted of only eight to ten fibers [2]. We dissect jump muscle fibers from the thoraces of 2 to 3-day-old female Drosophila. The jump muscle ultrastructure does not seem to be as easily damaged by myosin mutants as the IFM, thus we can use fibers from 2-3 day old flies even when analyzing mutants that cause ultrastructure deterioration in the IFM. The start of the jump muscle dissection is the same as for the IFM. The head, abdomen and wings are removed. Each thorax is split in half and the jump muscle is freed from the cuticle by cutting off the dorsal quarter of the half thorax and severing the middle leg at the coxa and pleura junction (Figure 6A). The jump muscle is trimmed to remove any of the remaining coxa tendon since the fibers become pinnate as they insert along the length of the tendon. The extracted jump muscle is chemically demembranated (skinned) in the same dissection solution as IFM fibers.

Figure 6.

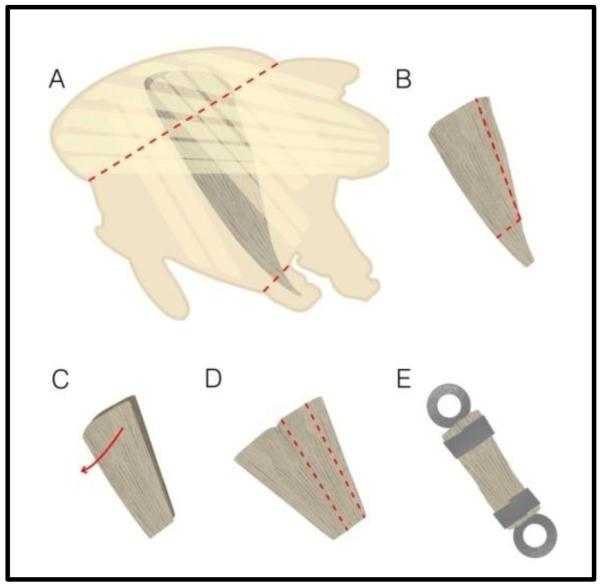
Jump muscle preparation. After isolating the thorax, the jump muscle is A) removed from the half thorax by cutting as shown by the red dotted lines. B) The jump muscle is pared down in size and C) the two-layered muscle is split open to become one single layer of fibers. D) A strip of 8-10 fibers is cut from the muscle and E) fastened between two T-clips. Modified from Eldred et al. [2].

After one hour at 4°C, the demembranated jump muscles are transferred to storage solution and split vertically in an asymmetric manner such that the four to six smaller diameter fibers, that may express a different myosin isoform from the larger diameter fibers [41], are cut off and discarded (Figure 6B). The posterior section is split open to separate the two layers of fibers that make up the depth of the jump muscle (Figure 6C). The single layer of fibers is then pared down to a preparation consisting of 8 to 10 large jump muscle fibers (Figure 6D) and T-clipped similar to IFM fibers except the preparation is wider and not as deep (Figure 6E). This preparation results in faster activation and less damage to the muscle compared to the full muscle as it is more securely and uniformly held in the T-clips. Aligning the fibers as parallel as possible between the T-clips produces better quality mechanics data. The jump muscle preparation is mounted on the fiber mechanics rig using T-clips that are altered to fit the jump muscle preparation dimensions. The resulting dimensions of the preparation, between the proximal ends of the clips, average about 140 μm in length, 110 μm in width and 45 μm in depth [2].

3.2 Jump muscle mechanical apparatus

The muscle mechanics apparatus for jump muscle experiments is similar to the one described above (section 2.2) for IFM with the following differences. Unlike IFM, jump muscle sarcomere length can be measured. A compound light microscope and software analysis package (Ion Optix, Milton, MA) is used to obtain jump muscle sarcomere length. A video image of the jump muscle is captured from an inverted compound microscope using a 40x objective. Measurements from three locations on the muscle are averaged to determine sarcomere length as sarcomere length varies slightly due to minor length differences between the fibers that make up the preparation. It is nearly impossible to clamp all the fibers between the clips at precisely the same length. The servo motor of the jump muscle apparatus has a longer throw, 30 μm (P-841.20 Physik Instrumente, Karlsruhe, Germany), to accommodate the greater muscle length change required for slack test and force – velocity curves, and less than 0.5 millisecond response time when used with position feedback. Changes in the composition of the muscle bathing solution are accomplished by moving the fiber into a new chamber with an automated chamber switching device from Aurora Scientific (Ontario, Canada). The mechanics apparatus is controlled by the same custom written software as the IFM apparatus.

The same solutions are used for the jump muscle mechanics experiments as for IFM experiments except for one additional solution. A pre-activating solution (same as relaxation solution (pCa 8.0)), but with only 0.5 mM EGTA) is interposed between relaxing and activating solutions rather than transferring the muscle directly from relaxing solution at pCa 8.0 (5 mM EGTA) to activating solution at pCa 5.0. The jump muscle activates faster and is less likely to rip when preactivating solution is used. This is likely due to faster and more uniform calcium entry and binding to troponin C in each sarcomere [42].

3.3 Mechanical measurements with Jump muscle

3.3.1 Unloaded shortening velocity

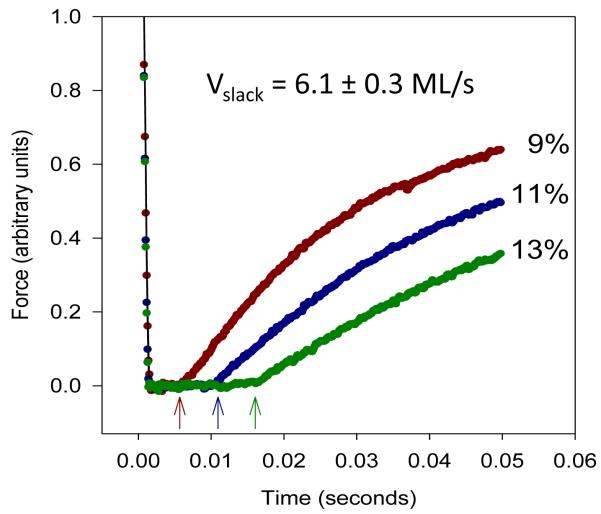
The longer I-band of the jump muscle allows us to perform more types of mechanical measurements with the jump muscle than the IFM. The slack test is used to measure unloaded shortening velocity (V_slack) [43-44]. The jump muscle is first set at a sarcomere length of 3.6 micrometers in relaxing solution, activated by moving into preactivating solution for two minutes and then into activating solution. For jump muscle, the shortening required is a minimum of 9% ML in less than 5 milliseconds [2]. This reduces force levels to zero; the muscle is “slack”. The time taken for the force level to rise above zero, when slack is eliminated from the muscle, is measured (Figure 7). The maximum unloaded muscle shortening speed is determined by plotting multiple muscle length changes versus time required to take up the slack. The shortening velocity of wild-type jump muscle is about 6 μm/s which is similar to that of mouse fast skeletal muscle fiber types [45].

Figure 7.

Examples of slack tests using the jump muscle. The activated jump muscle is shortened at the maximum speed of the motor to introduce slack into the muscle. The amount of shortening (% ML) is shown to the right of the traces. Arrows indicate the time points at which force redevelopment has started for each shortening length. Modified from Eldred et al. [2].

3.3.2 Force-velocity curves

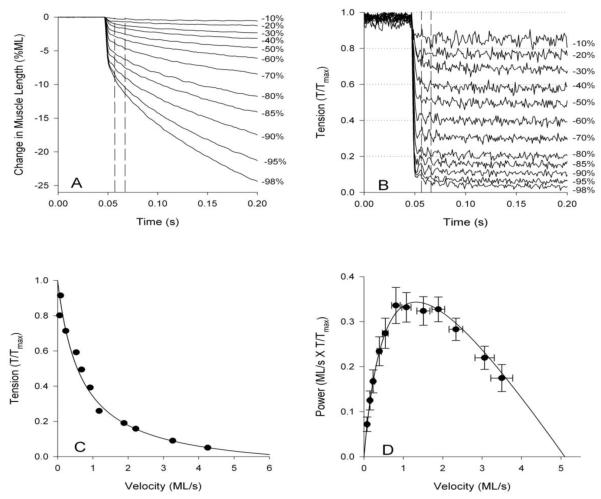
To determine force-velocity relationships and steady-state power generation, the force-clamp technique can be used [44, 46]. Fibers are rapidly shortened when fully activated until the tension level drops to a predetermined set level by feeding back the tension signal to the servo system. The percent maximum tension is plotted versus velocity at the set tension level resulting in the characteristic hyperbolic force-velocity curve (Figure 8). Power is calculated by multiplying tension and velocity. We call this steady-state power as power is calculated from force and velocity at constant shortening velocities rather than conditions where the fiber is cyclically shortening or lengthening such as sinusoidal analysis or work loops.

Figure 8.

Tension-velocity curves and steady-state power curves using the jump muscle. A) The muscle is shortened at a speed that will maintain B) a constant set tension level. Numbers to the right indicated the percent decrease in tension from maximum isometric tension. Vertical dotted lines indicate the time period over which shortening velocity was calculated. C) Tension and velocity are plotted to reveal the characteristic hyperbolic shape of the tension-velocity curve. D) Power is calculated by multiplying tension and velocity and, in this case, plotted against velocity rather than tension. Modified from Eldred et al. [2].

3.3.3 Common mechanical measurements

Almost all of the measurements described for the IFM can be made on the jump muscle, but with some interesting caveats. Sinusoidal analysis can be applied to jump muscle to obtain complex, elastic and viscous modulus. However, preliminary results suggest that no positive work or power generation is possible with the wild type skinned jump muscle as the viscous modulus is positive at all ML oscillation frequencies. This is likely due to much less prominent stretch activation and shortening deactivation in jump muscle. One should still be able to fit the resultant Nyquist plot with the complex modulus equation to obtain muscle mechanical rate constants and, in theory, calculate rate constants of the cross-bridge cycle if [Pi], [MgATP] and/or [ADP] are varied as described for IFM. We have not yet tried this with the jump muscle.

Work loops on skinned jump muscle can be performed, but this is a less informative technique to use as the wild-type jump muscle just absorbs work. For the jump muscle to generate positive work and power, one would need to use a live preparation that can be electrically stimulated at the appropriate time to turn on and off the muscle. However, a cyclical length change manner is not likely how the muscle is used in vivo, thus it makes more sense to calculate work and power from force-clamp experiments as the muscle is likely rapidly shortened at a fairly constant velocity to power jumping.

Isometric tension measurements are easier to perform with the jump muscle as it generates about 30 – fold higher active tension than the IFM [2]. The increased resolution for tension measurements was apparent when we expressed an embryonic (EMB) muscle myosin in the jump muscle and observed tension increase from 37 to 53 mN/mm² [2]. Using the jump muscle, we observed a subtle leftward shift in the Force-pCa curve when expressing EMB that was not obvious when expressed in IFM. The higher duty ratio of the EMB myosin increases co-operative thin filament activation at lower calcium levels. Passive tension of the jump muscle is similar to a typical vertebrate muscle. At the same length that generated 37 mN/mm² active tension, passive tension was only 1 mN/mm² [2]. In contrast, IFM passive tension is slightly higher than calcium activated tension [16].

Jump muscle tension length curves are not as clean as those from single fiber preparations due to the necessity of using 8-12 fibers in our preparation that are not all necessarily at exactly the same sarcomere length. However, an advantage of the jump muscle is that sarcomere length is possible to measure as there are no tracheal tubes permeating the muscle as is the case for IFM. We empirically determined that a sarcomere length of 3.6 μm is a good starting length for experimental protocols that involve shortening as there was no significant decrease in tension between 3.6 and 3.0 μm [2]. This suggests most of the shortening is occurring on the plateau of the tension sarcomere length curve. However, to our knowledge, there have not been any measurements of thin and thick filament lengths for Drosophila jump muscle which would be very helpful to confirm the optimal sarcomere length for mechanics experiments.

4. Concluding remarks

To our knowledge, the IFM and the jump are the only muscles that have been isolated from the adult Drosophila body for mechanical measurements. Mechanical measures of the larval musculature have been made, but these have used preparations made of the entire larva, multiple larval muscles or have been restricted to isometric force measurements [47]. There are also visual methods for measuring some in vivo Drosophila heart muscle mechanical parameters [48]. Thus, combined with the power of Drosophila genetics, the IFM and jump are the two muscles poised to reveal many more interesting features of dynamic muscle physiology, muscle protein isoforms, and mechanisms behind mutations that cause muscle and heart diseases.