Abstract
The visual system can automatically interpolate or “fill-in” the boundaries of objects when inputs are fragmented or incomplete. A canonical class of visual stimuli known as illusory-contour (IC) stimuli have been extensively used to study this contour interpolation process. Visual evoked potential (VEP) studies have identified a neural signature of these boundary completion processes, the so-called IC-effect, which typically onsets at 90–110ms and is generated within the lateral occipital complex (LOC). Here we set out to determine the delimiting factors of automatic boundary completion with the use of illusory contour stimuli and high-density scalp recordings of brain activity. Retinal eccentricity, ratio of real to illusory contours (i.e. support ratio), and inducer diameter were each varied parametrically, and any resulting effects on the amplitude and latency of the IC-effect were examined. Somewhat surprisingly, the amplitude of the IC-effect was found to be impervious to all changes in these stimulus parameters, manipulations that are known to impact perceived illusion strength. Thus, this automatic stage of object processing appears to be a binary process in which, so-long as minimal conditions are met, contours are automatically completed. At the same time, the latency of the IC-effect was found to vary inversely with support ratio, likely reflecting the additional time necessary to interpolate across the relatively longer induced boundaries of the implied object. These data are interpreted in the context of a two stage object-recognition model that parses processing into an early automatic perceptual stage that is followed by a more effortful conceptual processing stage.
Keywords: visual processing, electrophysiology, visual evoked potentials, object processing, illusory-contours
INTRODUCTION
The visual system can readily interpolate object identity under less than optimal viewing conditions, permitting us to bridge gaps in the contours of incomplete or obstructed objects, a process termed “perceptual completion” in the cognitive neurosciences. Using illusory contour (IC) stimuli, first described by Schumann (1900) and subsequently by Kanizsa (1976), a well-studied stimulus class whose processing time-course in humans has been carefully detailed using visually-evoked potentials (VEPs) (e.g., Murray, et al., 2002; Foxe, et al., 2005), we sought to better understand the limits of perceptual completion by explicitly taxing IC processing. In a series of three experiments manipulating key features of this canonical stimulus class – spatial extent, support ratio, and inducer size – we aimed to systematically vary the strength of the illusion while concurrently measuring cortical processing using high-density VEP recordings.
ICs can be induced using Pac-man-shaped disks (Figure 1a), oriented so that the contours of their “mouths” are relatively closely aligned. When aligned and placed not too far from one another, typical viewers perceive a two-dimensional object of homogeneous and somewhat increased luminance superimposed upon the background (though no luminance difference physically exists). This illusory object’s contours give the impression that they continue the real contours of the mouths of the inducers, despite a physical gap between them (Peterhans & von der Heydt, 1989; Ringach & Shapley, 1996; Murray, et al., 2002; Halko, et al., 2008). In other words, we perceive a square (or another shape, depending on the configuration of the inducers) even though only four Pac-men exist. The perception of such a shape could be considered an error of processing as it is essentially an inaccurate representation of the existing physical stimulus. However, this error provides an excellent window onto fundamental operations of the visual system as it works to analyze the confusion of inputs impinging on the retina, producing both different perceptions and different VEPS. This affords researchers the opportunity to parse object processing into its constituent parts.
Figure 1.
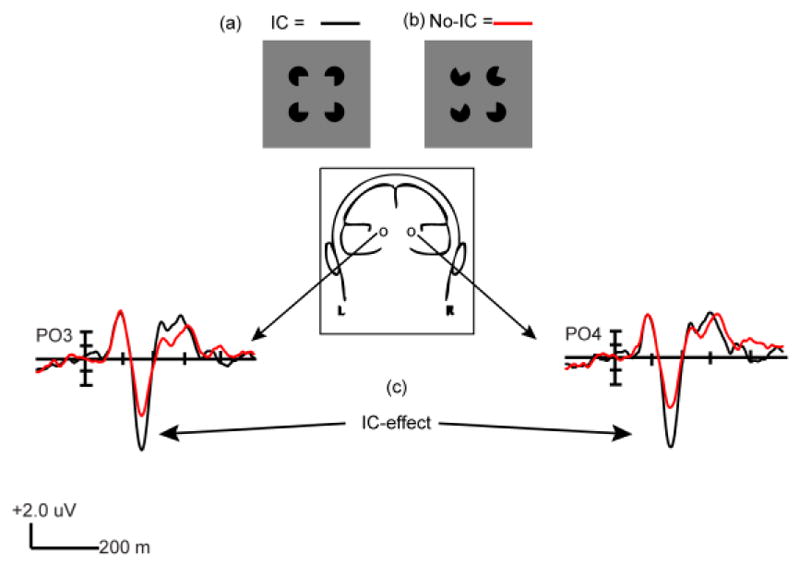
(a) Kanizsa type Illusory-contour square in contour-forming configuration (IC). (b) Non-contour forming configuration (No-IC). (c) Example of IC-effect from Experiment 1 Level 2.
VEPs, with their exquisitely fine temporal resolution, have been extensively used to study IC processing on a millisecond timescale (Sugawara & Morotomi, 1991; Herrmann, et al., 1999; Murray, et al., 2002; Murray, et al., 2004; Foxe, et al., 2005; Murray, et al., 2006; Shpaner, et al., 2009; Fiebelkorn, et al., 2010). They have revealed two dissociable phases of object processing, comprising what are thought to reflect temporally dissociable perceptual and conceptual modes (Tulving & Schacter, 1990; Doniger, et al., 2001). Sensitivity to ICs is first measurable as a difference between visually evoked potentials (VEPs) during the onset phase of the N1 component, beginning at ~ 90ms and peaking at ~ 150 ms, during which contour-forming configurations (Figure 1a) evoke a substantially more negative amplitude over lateral occipital scalp sites than non-contour forming configurations (Figure 1b). Hereafter, we will refer to this first phase of IC processing as the “IC-effect” (Figure 1c) (Murray, et al., 2002). This effect has been localized to a cluster of ventral stream regions known as the lateral occipital complex (LOC) (Murray, et al., 2002; Sehatpour, et al., 2006; Fiebelkorn, et al., 2010), a system of areas associated with object processing (Malach, et al., 1995; Grill-Spector, et al., 1998; Sehatpour, et al., 2008; Lucan, et al., 2010). It has been associated with automatic completion of object boundaries, accomplished without reference to stored representations (Murray, et al., 2002; Foxe, et al., 2005; Shpaner, et al., 2009).
The second temporally dissociable processing phase associated with completion of IC images and fragmented objects is observed from ~230 extending to 400 ms. This phase is evoked when initial input is insufficient for object recognition, as with objects degraded by obstruction or novel orientation (Doniger, et al., 2000; Doniger, et al., 2001; Doniger, et al., 2002; Foxe, et al., 2005; Murray, et al., 2006; Sehatpour, et al., 2006). During this process, sensory information is believed to be actively compared with existing representations of objects, filling-in the missing information, a completion process historically referred to as “perceptual closure” (Bartlett, 1916; Snodgrass & Feenan, 1990). This second VEP component has been termed the Ncl (negativity for closure) (Doniger, et al., 2000). Both the IC-effect and Ncl have been source-localized to the LOC (Sehatpour, et al., 2006; Sehatpour, et al., 2008) pointing to the fact that these two separable phases of object processing are achieved within the same cortical structures.
Recent work supports a model of IC processing whereby early object segmentation is accomplished automatically during the perceptual stage, via the completion of contours (Shpaner, et al., 2009). What is less clear, since no complete contours exist in ICs, is upon what parameters boundary completion is dependent. Retinal extent has been measured as influencing the perceived strength of ICs in behavioral studies in adults (Dumais & Bradley, 1976; Banton & Levi, 1992). Inducer size has also been seen to influence illusion strength (Banton & Levi, 1992). Although Shipley and Kellman (1992) observed no relationship dependent upon extent, they and Hadad et al (2010) found that “support ratio”, the proportion of real contour of one side of the induced shape (equal to the diameter of the inducer) to the entire side of that shape (see Figure 2), influences illusion strength measured either by subjective estimate of magnitude (Shipley & Kellman, 1992) or a shape discrimination task (Murray, et al., 2006; Hadad, et al., 2010) requiring clearly perceived contours. As judgment of illusion strength depends upon contour-based information, using electrophysiological measures one might have expected to see an analogous effect during the N1 window when that contour is said to be established. Yet, Murray et al (2006) observed that, when asked to distinguish whether the contours of an IC square were concave or convex, subjects’ accuracy was uncorrelated with magnitude or topography of the first phase of the electrophysiological signature of IC processing. Instead, the observed effects of support ratio were seen in the later conceptual phase indexed by the Ncl, and then only for IC and not control stimuli. In other words, perceptual judgment was temporally dissociable from the laying down of boundaries, a process which appears largely indifferent to any manipulation carried out thus far.
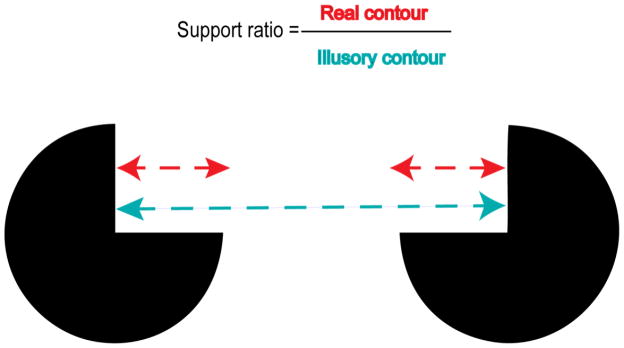
Figure 2.
Support ratio definition
Behavioral studies have manipulated the perception of ICs via masking and varying the spatial extent (Ringach & Shapley, 1996), support ratio (Shipley & Kellman, 1992), occlusion of contours, and whether inducers are moving or static (Halko, et al., 2008). We wished to understand how vulnerable the early phase of object processing is to manipulation of basic contour parameters independent of task obligations. We hypothesized that the limits of the automatic boundary completion phase of object recognition are a function of contour-related parameters and are likely to be revealed as a variation in IC-effect amplitude or latency. VEP paradigms have varied shape, contrast, support ratio, and laterality of presentation (Murray, et al., 2002), but they have not specifically or systematically investigated the impact of these parameters. The following series of three experiments was designed to examine the effect of retinal eccentricity, ratio of real to illusory contours, and inducer diameter while measuring the amplitude and latency of the IC-effect. Shape, luminance, and location of the IC within the visual field were unvarying.
METHODS & MATERIALS
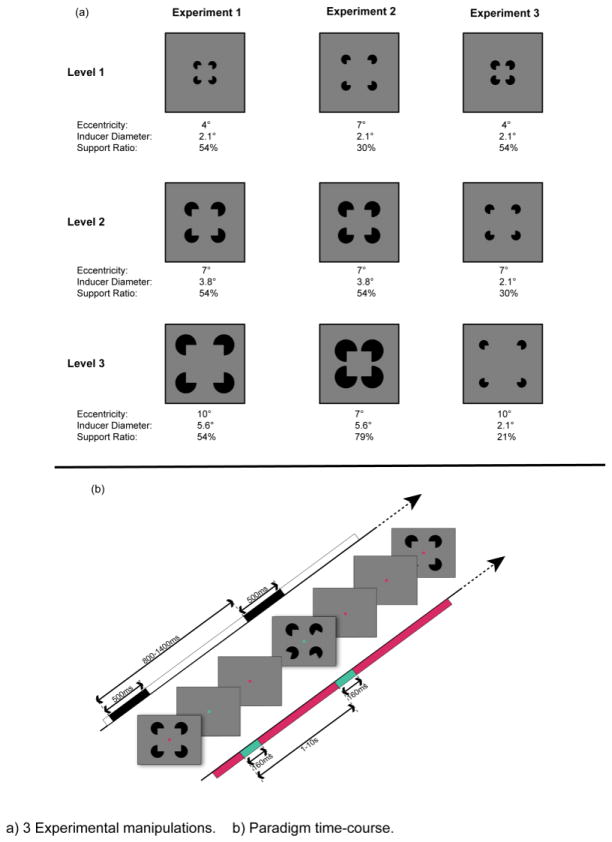
This study comprises three experimental manipulations of spatial extent, support ratio, and inducer diameter of Kanizsa-type illusory squares. Details for stimulus manipulations are described in succession (Figure 3a). The parameters are inescapably intertwined, e.g., if eccentricity is parametrically increased, as is true in Experiments 1 and 3, to hold support ratio constant, the third parameter must also vary. Each of the three experiments thus varies two of three variables, holding the third constant. The paradigm time course is depicted in Figure 3b.
Figure 3.
a) Three Experimental manipulations. b) Paradigm time-course.
Experiment 1: Manipulation of eccentricity and inducer diameter with constant support ratio
Participants
Twelve neurotypical adults (9 female), compensated with course credit or a modest stipend, aged 19 – 31 years (mean (SD) = 23.3 (3.4)) participated. All were recruited from the City College of New York (CCNY) community, reported normal or corrected-to-normal vision, and had normal color vision (Ishihara, 2008). All but one were right-handed (Oldfield, 1971) and all provided written valid consent. The study conformed to the principles outlined in the Declaration of Helsinki and the CCNY Institutional Review Board approved all procedures.
Stimuli & Task
Subjects were comfortably seated in a dimly-lit, sound-attenuated booth 60 cm from a computer monitor. They viewed four black Pac-man-shaped disks, presented against a gray background, arrayed like the number four on a die centered on the screen. These randomly took one of two orientations - either with the 90° angle that comprises their “mouths” pointed toward the center point of the array, equidistant from their vertices, such that they induce in a typical viewer the perception of a Kanizsa-type (Kanizsa, 1976) illusory contour square (IC); or with three of the four inducer mouths rotated away from the center (No-IC). The location of the fourth, non-rotated inducer in the No-IC condition varied randomly. This was done to prevent subjects adopting a spatial strategy to perceive the difference between conditions. The amount of rotation for the other 3 inducers was generated randomly across a range from 20° – 180° for each of the three inducers. These orientations were held consistent thereafter for all presentations of the No-IC condition. Stimuli were generated in MATLAB 7.4.0. Three parametric levels of retinal eccentricity subtended approximately 4°, 7°, and 10° of visual angle. The inducers were 2.1°, 3.8 °, and 5.6 ° in diameter respectively (approximated as though the inducers were viewed foveally). The resulting support ratio (Ringach & Shapley, 1996) – i.e., the proportion of real contour of one side of the square (equal to the diameter of one inducer) to entire side of that square (the portion between the center of the inducers, see Figure 2) – was held constant for the three eccentricity levels at 54%.
Stimuli were presented for 500 ms with a stimulus-onset asynchrony (SOA) varying from 800 – 1400 ms with a square distribution. Subjects were not required to explicitly attend to stimuli as Murray et al (2002) previously showed that explicit attention to IC stimuli is unnecessary to elicit the IC-effect. Ten 3-minute blocks were administered with short breaks, as necessary, to recover from fatigue.
A simultaneously-presented task ensured that participants attended to the center of the screen. This required fixation on a centrally presented red dot, 4 pixels in width and height. The dot changed to green for 160 ms every 1–10 seconds with inter-stimulus-interval (ISI) varied pseudo-randomly on a time-scale uncorrelated with the presentation of the IC stimuli. Random co-occurrence of the color change and IC presentation was < 1%. The 2 colors were selected from a single isoluminant plane of DKL color-space (Derrington, et al., 1984), in which color isoluminance can be approximated via chromatic response of macaque lateral geniculate nuclei neurons. The color shift employed was, for all practical purposes, imperceptible without foveating, due to multiple mechanisms including the relative paucity of cone receptors in peripheral retina (Moreland & Cruz, 1959). Subjects clicked the mouse button with their right index finger for each perceived color change. Average performance for the fixation task ranged from 94 – 100% (Mean (SD): 98 (2)). Instructions focused exclusively upon the fixation task, making no mention of inducers or the illusion they might produce. No formal measure of participants’ awareness of the IC stimuli was taken, but this was added in Experiments 2 and 3. 25% of the subjects in Experiment 1 participated in Experiments 2 and 3. 100% of the participants in Experiments 2 and 3 demonstrated during debriefing that they could perceive illusory contours without any reference having been made that such an illusion might be induced.
Data acquisition and analysis
Continuous EEG was acquired through a Biosemi Active Two system from 64 scalp electrodes, digitized at 512 Hz and referenced to the Common Mode Sense (CMS) which is actively recorded, and the Driven Right Leg (DRL), a passive electrode, that form a feedback loop that acts as a reference. Epochs of continuous EEG (−150 msec before stimulus onset to 1000 ms after) were averaged from each subject in response to each of the two conditions and three levels of stimulus using BESA 5.1.8 EEG software. An artifact rejection criterion of ± 100 μV was applied to reject trials with eye blinks and movement, electrical signals produced by muscle movement or electromyography (EMG), or other sources of noise. An average of 175 ± 50 trials per condition was accepted per subject. Each of the six conditions was averaged, baseline-corrected across an epoch of −80 to +20 ms, and low-pass filtered at 45 Hz with a 24 db/octave roll-off.
Two analyses were planned at the pair of parieto-occipital electrodes of maximal response (PO3 and PO4, based on previously well-characterized topographies for the IC-effect (Murray, et al., 2002; Foxe, et al., 2005)). The first examined the impact of the parameter manipulation on the amplitude of the IC-effect and the other on the peak latency. As this is a well-described effect which this study explicitly tried to modulate, a 20 ms time window surrounding the effect peak was derived from the grand average waveform of each level of retinal eccentricity using MATLAB 7.4.0. These data were referenced to electrode AFz to maximize visualization of a parietal-occipital effect. The latency analysis compared IC-effect peaks, identified as the negative most point derived from individual subject difference waves in a time window of 120 – 220ms. In response to reviewers’ comments, an additional analysis of peak latency was conducted on separate IC and No-IC conditions in order to distinguish effects specific to ICs from effects on the overall N1. Both were analyzed with a repeated-measures ANOVA in SPSS 15.0 with within-subjects factors of IC condition (IC vs. No-IC), parametric level (eccentricity of 4 °, 7°, and 10°), and hemiscalp (PO3, PO4). Significance criteria was α < 0.05.
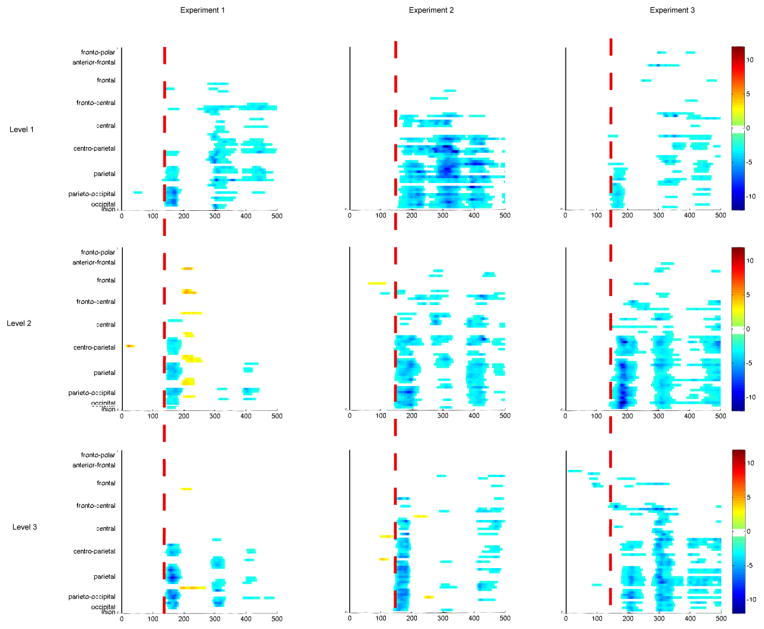
An estimate of onset latency of the IC-effect was also made using point-wise paired t-tests, calculating the first time point where the t-test exceeded the 0.05 alpha criterion and remained so for 15 consecutive time points. The requirement of 15 consecutive time points controls for inflation of type I error due to multiple comparisons (Guthrie & Buchwald, 1991). Because adjacent time points in EEG do not change arbitrarily fast, they are not independent. Consequently, we computed the temporal autocorrelation of the noise in the baseline at a representative electrode for all subjects to determine the lag at which such dependence does not differ from zero (with 95% confidence). This was 15 time points. Of the three experiments, these data were the noisiest, requiring the highest number of consecutive time points. As this was the most conservative requirement, it was applied across all three experiments. The results are displayed as a statistical cluster-plot, plotting estimated latency and scalp region on the x and y axes respectively; t-test results are color-coded, as indicated in Figure 6a. These average onset latencies are more susceptible to the vagaries of signal-to-noise ratio than are the peak onsets and are most usefully interpreted as estimated pictures of onset across scalp regions.
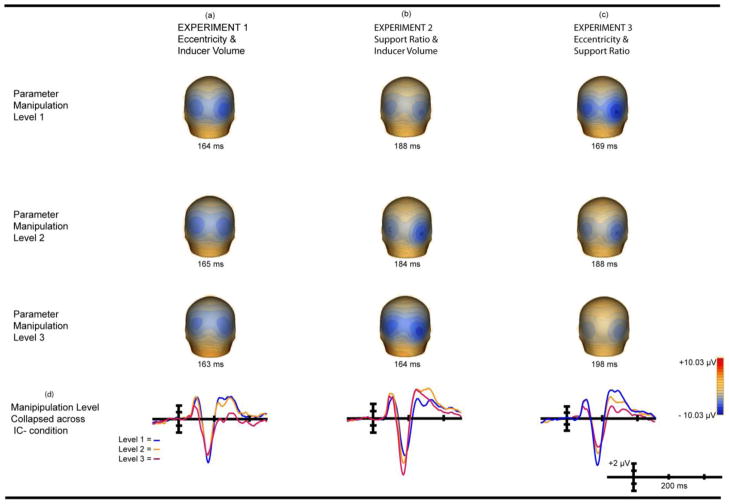
Figure 6. Main Effect Of Manipulation Collapsed Across IC Condition.
Main effect manipulation collapsed across IC Condition from −150 to +500 ms. Electrode PO4 is shown in all cases as it is maximal and representative; there is no statistical difference between hemispheres. Waves are referenced to electrode AFz. (a) Experiment 1 manipulation main effect topography. (b) Experiment 2 manipulation main effect topography. (c) Experiment 3 manipulation main effect topography. (d) Three levels collapsed across IC condition.
Experiment 2: Manipulation of inducer diameter and support ratio with constant eccentricity
Participants
Eleven (5 female) neurotypical adults, compensated with course credit or a modest stipend, aged 20–34 participated, one of whose data was excluded due to excessive noise. Ten subjects (4 female) aged 20 – 34 (mean (SD) = 26.8 (5.5)) data were ultimately analyzed, 25% of whom also participated in Experiment 1. They were recruited from the CCNY community, reported normal or corrected-to-normal vision, and normal color vision (Ishihara, 2008). All but one were right-handed (Oldfield, 1971) and all provided written informed consent. The study conformed to the principles outlined in the Declaration of Helsinki and the CCNY Institutional Review Board approved all procedures.
Stimuli & Task
Black Pac-man-shaped inducers oriented in either the IC or No-IC condition, as described for Experiment 1. Three parametric levels of illusory squares, and a non-shape-inducing counterpart, were used. Inducers subtended 2.1°, 3.8°, and 5.6° of visual angle in diameter (approximated as though centered), producing support ratios of 31, 55, and 79%. Eccentricity was held constant at 7° of visual angle.
Stimulus duration, SOA, number and length of blocks were identical to Experiment 1, as was the central fixation task. Experiments 2 and 3 were administered together, their order counterbalanced across subjects. Average performance for the fixation task ranged from 93 – 100% (Mean (SD): 98 (2)). Subjects were not required to explicitly attend to Kanizsa stimuli. At debriefing, participants received a verbally administered questionnaire probing their awareness of any stimulus besides the color dot of the fixation task. All but one of the participants claimed awareness of other visual information besides the colored dot. When specifically prompted for other “shapes” all but one described something that approximated the inducers or illusory squares. When shown printed images of IC and No-IC conditions of induced triangles and asked what they saw, 100% indicated that they perceived triangles regardless of the order of administration of the conditions. When shown printed IC and No-IC conditions in the square configuration and asked to identify the “square,” 100% of participants pointed to the IC stimulus that resembled the one seen in the experiment.
Data acquisition and analysis
Continuous EEG was acquired in an identical manner to Experiment 1. An artifact rejection criterion of ± 100 μV was applied to all but one subject to reject trials with eye blinks and movement, excessive EMG, or other sources of noise. For one subject with particularly noisy data, the threshold was set at ±120 μV. An average of 220 ± 44 trials per condition was accepted per subject. Each of the conditions was separately averaged, baseline-corrected across an epoch of −80 to +20 ms, and low-pass filtered at 45 Hz with a 24 db/octave roll-off.
Data analysis was carried out at the identical electrodes (PO3 and PO4) for identical effects of the new parameter manipulation on the amplitude and latency of the IC-effect, in an identical manner to Experiment 1 for amplitude and peak latency. Both were analyzed with a repeated measures ANOVA in SPSS 15.0 with within-subjects factors of IC condition (IC vs. No-IC), parametric level (support ratios of 31, 55, and 79%), and hemiscalp (PO3, PO4). Onset latency was estimated via point-wise paired t-tests, and depicted as a statistical cluster plot, as described for Experiment 1.
Experiment 3: Manipulation of eccentricity and support ratio with constant inducer diameter
Participants
The eleven participants in Experiments 2 and 3 were identical. Data from ten were ultimately submitted to analysis.
Stimuli & Task
Black Pac-man-shaped inducers, oriented in either the IC or No-IC condition were presented as described earlier. The manipulation of shape parameters changed again. As in Experiment 1 the retinal eccentricity of the three parametric levels of illusory squares subtended approximately 4°, 7°, and 10° of visual angle. The corresponding support ratios were 54, 30, and 21%. This time the inducer diameter was constant at 2.1° of visual angle.
Stimulus duration, SOA, number and length of blocks were all identical to Experiments 1 and 2, as was the fixation task. Average performance for the fixation task ranged from 95 – 100% (Mean (SD): 98 (.02)) and study instructions confined their focus to this task, making no mention of the IC stimuli or inducers. As this experiment was administered along with Experiment 2, subjects received the debriefing questionnaire described above.
Data acquisition and analysis
Continuous EEG was acquired in an identical manner to Experiments 1 and 2. An artifact rejection criterion of ± 100 μV was applied to all subjects to reject trials with eye blinks and movement, excessive EMG, or other sources of noise. An average of 226 ± 26 trials per condition was accepted. Each of the conditions was separately averaged, baseline-corrected and low-pass filtered as above.
Data analysis was carried out at the identical electrodes (PO3 and PO4) for the effects of the third parameter manipulation on the amplitude and latency of the IC-effect as before. Amplitude as well as peak and onset latency analyses were conducted as above. Data was submitted to repeated measures ANOVA using SPSS 15.0, with within-subjects factors of IC condition (IC vs. No-IC), parametric level (4°, 7°, and 10° of visual angle and respective support ratios of 54, 30, and 21%), and hemiscalp (PO3, PO4).
Dipole Source Modeling
We modeled current sources of the IC-effect using the same 20 ms time window used in the original analyses. BESA uses a least squares algorithm which fits signal to dipoles that explain a maximal amount of variance. We constrained the solution to two symmetrical dipoles. Whether they fit LOC location or not, the stability of the best fit model supplied by BESA was challenged by changing locations. Miltner (1994) reports an average 1–2 cm error rate using this method. The average source is reported in Talairach coordinates at the end of the Results section.
RESULTS
Note: significant two-way interactions are only reported if germane to the question of interest. Greenhouse Geiser corrections were applied, as noted, for violations of sphericity.
Experiment 1: Manipulation of eccentricity and inducer diameter with constant support ratio
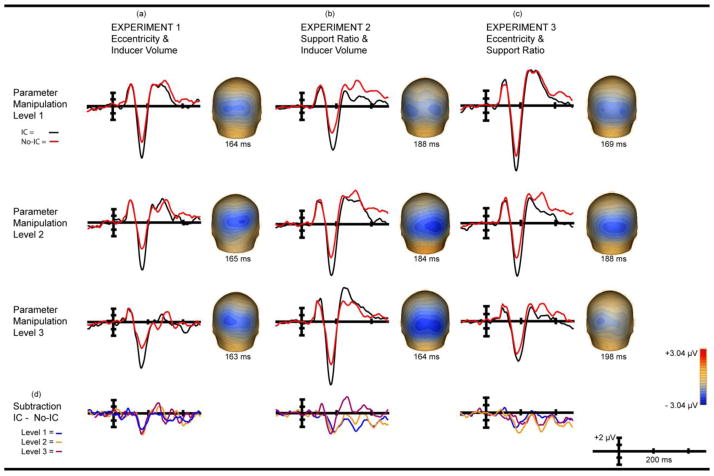
The effect of eccentricity on the amplitude of the IC-effect was calculated using the area beneath the curve for the 20 ms window centered on the effect and derived from the grand average of each eccentricity level. The IC-effect of level 1 of the parameter manipulation (4° retinal eccentricity/2.1° inducer diameter/54% support ratio) peaked at 164 ms; a window of 154 – 174 ms was used. For level 2 (7° retinal eccentricity/3.8° inducer diameter/54% support ratio) the window was 155–175 ms, and for level 3 (10° retinal eccentricity/5.6° inducer diameter/54% support ratio) 153 – 173 ms. These data were submitted to a 2 × 3 × 2 repeated-measures ANOVA with within-subjects factors of IC condition (IC vs. No-IC), parametric level ( 4°, 7°, and 10° of retinal eccentricity), and hemiscalp (PO3, PO4). A main effect of IC condition was observed (F( 1, 11) = 82.35; p < 0.0000019; η2partial = 0.88) (Figure 4a) confirming the presence of the IC-effect (Murray, et al., 2002). There were no main effects of hemiscalp or retinal eccentricity (Figure 6d). Of most relevance to the experimental question, the IC condition x eccentricity interaction was not significant (F(2,22) = 1.46; p = 0.25; η2partial = 0.12) (Figure 4d) indicating no measurable effect of eccentricity on the amplitude of the IC-effect.
Figure 4. Main Effect of IC-Condition (IC-effect) & Interaction of IC-Condition x Manipulation.
Main effect wave forms show IC condition (black) & No-IC condition (red) from −150 to +500 ms. Electrode PO4 is shown in all cases as it is maximal and representative and there is no statistical difference between hemispheres. Waves are referenced to electrode AFz (a) Experiment 1 IC condition main effect. (b) Experiment 2 IC condition Main effect. (c) Experiment 3 IC condition main effect. (d) IC condition x manipulation interaction for three experiments.
Peak latency comparisons were calculated on the basis of the peak amplitudes of individual subject difference waves between the IC conditions. These were submitted to a 2 × 3 repeated-measures ANOVA with factors of hemiscalp and eccentricity level. No main effects or interactions were observed. Specific to the question of interest, there was no main effect of eccentricity (F (2, 22) = 2.22; p = 0.13; η2partial = 0.17) suggesting no effect of eccentricity on peak latency of the IC-effect. In addition, estimation of onset latency of IC conditions was conducted using point-wise paired t-tests (see Methods). The near equivalence of the three onset latencies of the IC-effect is evident in the statistical cluster-plots (Figure 5a) (~ 135 – 140 ms across the 3 manipulations) and mirrors the stability of the peak latency. A comparison of peak latency effects for IC and No-IC conditions yielded no interaction of IC condition x eccentricity (F(2,22) = 0.08; p = 0.92), suggesting that absence of peak latency differences is equivalent in the overall N1 versus the IC-effect.
Figure 5. Statistical Cluster Plots Comparing IC Conditions.
Color values indicate the result of point-wise paired t-tests for 15 consecutive points (see Methods), comparing IC Conditions over a −15 to +500 ms time period (x-axis) and scalp region (y-axis). α = 0.05. baselined from −80 to +40 ms, referenced to AFz. The red line aids in comparing onset latencies. Statistically significant peak latency comparisons were observed in Experiment 2 between levels 2 & 3 and 1& 3 and in Experiment 3 between levels 1 & 2 and 1 & 3. There were no significant peak latency differences in Experiment 1.
Experiment 2: Manipulation of support ratio and inducer diameter with constant eccentricity
The effect of support ratio on amplitude used the area beneath the curve for the 20 ms window centered on the peak amplitude of the IC-effect, calculated from the grand average of each manipulation level. The peak amplitude of level 1 (30% support ratio/2.1° inducer diameter/7° retinal eccentricity) differed by hemisphere, peaking at 191 ms in the left and 186 ms in the right. The amplitude for a 20 ms window centered on the average peak amplitude of the two hemispheres - 178 – 198 ms - was submitted to analysis. For level 2 (54% support ratio/3.8° inducer diameter/7° retinal eccentricity) the peak amplitudes were 180 ms and 188 ms for the left and right hemispheres respectively. The window applied was 174–194 ms. For level 3 (80% support ratio/5.6° inducer diameter/7° retinal eccentricity), the peak amplitude was 164 ms at both electrodes and a window of 154 – 174 ms was used. These data were submitted to a 2 × 3 × 2 repeated-measures ANOVA with within-subjects factors of IC condition (IC vs. No-IC), parametric level ( 30%, 54%, and 80% support ratio and 2.1°, 3.8°, and 5.6° diameter inducers), and hemiscalp (PO3, PO4). A main effect of IC condition was observed (F( 1, 9) = 45.08; p < 0.000087; η2 partial = 0.83), again confirming the presence of the IC-effect (Figure 4b) (Murray, et al., 2002). A main effect of parametric level was also observed (Figure 6d) (F(2, 18) = 18.82; p < 0.000039; η2 partial = .68), reflecting an overall increase in VEP amplitude relative to support ratio and inducer diameter. No main effect of hemiscalp was observed. Of primary interest, the IC condition x level interaction was not statistically significant (Figure 4d) (F(2,18) = 1.04; p = 0.37; η2 partial = .10).
Post-hoc pairwise comparisons with a Bonferroni correction to adjust for Type I error inflation were conducted to unpack the main effect of parametric level (Figure 6d). As it is collapsed across IC conditions, this likely reflects ongoing extrastriate processing of basic sensory characteristics typically visible at N1 latency rather than object identification per se (Murray, et al., 2001; Foxe & Simpson, 2002). It is the presence of a main effect in the absence of an interaction with the IC-effect that makes more distinct the mechanism that may underlie the IC-effect, and is the subject of more thorough treatment in our discussion. The comparisons of level 1 vs. level 3 (t9 = 4.78; p < 0.003) and level 2 vs. level 3 (t9 = 4.68; p < 0.003) were significant. Increasing support ratio and inducer volume increases the amplitude of the N1 but has no impact upon the IC-effect.
Peak latency comparisons were calculated on the basis of individual subject peaks from IC minus No-IC differences waves submitted to a 2 × 3 repeated-measures ANOVA with the factors of hemiscalp and eccentricity level. The effect of interest – a main effect of parameter - was significant (Figure 4d) (F(2,18) = 9.74; p < 0.003; η2partial = 0.52). No interactions were observed. Post-hoc pairwise comparisons with a Bonferroni correction applied to adjust for Type I error inflation revealed significance for the comparison of level 2 vs. level 3 (t9 = 3.10; p = 0.038) and level 1 vs. level 3 (t9 = 4.24; p = 0.007). The latency of the IC-effect, collapsed across hemiscalp, decreased as support ratio and inducer volume increased. The more divergent 3rd condition, with a support ratio of 79% in the IC condition, was mainly responsible for driving this effect. Onset latency of IC conditions, as represented in the statistical cluster-plots (Figure 5b), covers only an 11 ms range: ~ 152 ms for level 1, ~144 ms for level 2, and ~141 ms for level 3. The difference is small, but mirrors the direction seen in peak latency. A 2 × 3 × 2 repeated-measures ANOVA with within-subjects factors of IC-Condition, parametric level, and hemiscalp was conducted to disambiguate the origin of peak latency effects. The interaction of IC-condition x level proved nearly significant: F(2,18) = 3.25; p = 0.06. While it would be inappropriate to run apply post-hoc analyses to the individual conditions, it is evident from a glance at the mean differences between parameter levels that the IC-forming condition drives this effect (IC1: 1 vs 2 = 8.4; 2 vs 3 = 5.3; 1 vs 3 = 13.7; No-IC: 1 vs 2 = 7.8; 2 vs 3 = 0.7; 1 vs 3 = 8.5). The overall N1 varies only 8.5 ms between parameter levels at its maximum, however the IC-forming condition varies nearly 14 ms.
Experiment 3: Manipulation of eccentricity and support ratio with constant inducer diameter
The effect of eccentricity and support ratio on amplitude used the area beneath the curve for the 20 ms window centered on the peak amplitude of the IC-effect, derived from the grand average of each level of the manipulation. Level 1 peak amplitude (54% support ratio/4° retinal eccentricity/2.1° inducer diameter) differed slightly between hemispheres, peaking at 168 ms in the left and 170 in the right. The amplitude for the 20 ms window centered on the average peak of the two hemispheres - 159 – 179 ms - was submitted to analysis. For level 2 (30% support ratio/7° eccentricity/2.1° inducer diameter) the peak amplitudes were 186 ms and 189 ms for left and right hemispheres respectively. The window applied was 178–198 ms. For level 3 (21% support ratio/10° eccentricity/2.1° inducer diameter), the peak amplitude was 199 ms and 197 ms for left and right hemispheres respectively; a window of 188 – 208 ms used. These data were submitted to a 2 × 3 × 2 repeated-measures ANOVA with within-subjects factors of IC condition (IC vs. No-IC), parametric level (54%, 30%, and 21% support ratio and 4°, 7°, and 10° retinal eccentricity), and hemiscalp (PO3, PO4). As expected, a robust main effect of IC condition was observed (Figure 4c) (F (1, 9) = 64.88; p < 0.000021; η2partial = 0.88). A main effect of parametric level was also observed (Figure 6c) (F (2, 18) = 24.61; p < 0.00020 (Greenhouse Geisser corrected); η2partial = 0.73). There was no main effect of hemiscalp and no interactions were significant. Of the greatest interest to us, the IC condition x level interaction was not significant (Figure 4d) (F(2,18) = 2.15; p = 0.15; η2partial = 0.19).
Post-hoc pairwise comparisons with a Bonferroni correction were conducted to unpack the main effect of the parametric manipulation collapsed across IC-condition and hemiscalp. As described in Experiment 2, this likely reflects ongoing extrastriate processing of basic sensory characteristics visible at N1 latency independent of IC condition, not object identification per se. It is relevant to our question in that a main effect of these parameters on N1 amplitude in the absence of a modulation of the IC-effect helps clarify the significance of the lack of interaction we originally explored. Statistical significance was revealed for every contrast. Level 1 vs. level 2 (t9 = −4.87; p < 0.003), level 2 vs. level 3 (t9 = −3.09; p < 0.039), and level 1 vs. level 3 (t9 = −5.31; p < 0.001). Thus, increasing eccentricity while decreasing support ratio decreases N1 magnitude but has no detectable impact upon the IC-effect.
Peak latency comparisons were calculated on the basis on individual subject peak amplitudes. No main effect of hemiscalp was observed, but a main effect of parameter was (Figure 6d) (F(2,18) = 16.78; p < 0.000077; η2partial = 0.65). There were no significant interactions. Post-hoc pairwise comparisons with a Bonferroni correction were conducted to unpack the main effect of parametric level collapsed across hemiscalp. This revealed significance when comparing level 1 with level 2 (t9 = − 3.42; p < 0.023) and level 1 with level 3 (t9 = − 5.40; p < 0.001), with peak IC-effect latency increasing as support ratio decreased and retinal eccentricity increased. A 2 × 3 × 2 repeated-measures ANOVA with within-subjects factors of IC-Condition, parametric level, and hemiscalp was again conducted to disambiguate the origin of peak latency effects. The interaction of IC-condition x level proved significant: F (2,18) = 4.30; p = 0.03. An analysis of the individual mean differences, Bonferroni adjusted, showed that, the manipulation was significant between two of the three comparisons in the IC-condition, but was not significant for any comparison in the No-IC condition. IC-condition: 1 vs 2 (t9 = 4.4; p = 0.20); 2 vs 3 (t9 = 9.3; p = 0.02); 1 vs 3 (t9 = 13.7; p = 0.01). No-IC condition: 1 vs 2 (t9 = 3.4; p = 0.30); 2 vs 3 (t9 = 2.7; p = 0.93); 1 vs 3 (t9 = 6.1; p = 0.27. ). We find no evidence for significant changes in overall N1 latency, but IC-effect latency clearly does change as a function of the manipulation.
Onset latency is represented in statistical cluster-plots (Figure 5c). In this case, the largest support ratio (level 1) onset at ~137 ms, level 2 at ~ 145 – 150 ms, although some fronto-central activity is evident as early as 140 ms. For the smallest support ratio - level 3, parietal and occipital-parietal IC-sensitive activity is not seen until ~ 175 – 180 ms, however, frontal and fronto-central activity is evident to the greatest degree in this condition, and onsets at ~ 140 ms. Onset latency thus increased as support ratio decreased and eccentricity increased, mirroring the pattern of peak latency, in all but frontal scalp regions.
Signal-to-Noise Ratio Analysis
In response to a reviewer’s comments, we measured SNR as a means of comparing sensitivity of our measures across experiments. We used the pre-stimulus period as an estimate of background noise, and a window encompassing the N1 and the range of the IC-effect (90– 200 ms) as an estimate of signal. Amplitudes were averaged across the conditions and levels of each experiment and squared to yield a rectified value for each subject. These were averaged across time points and electrodes of interest. Signal was divided by noise and converted to decibels in order to be scale-invariant. The resulting SNRs were compared using a two-sample Kolmogorov-Smirnov test. The mean (SD) of SNRs across the subjects of each experiment were: Experiment 1 = 19.03 (3.75); Experiment 2 = 23.60 (4.01); Experiment 3 = 21.83 (3.30). All three SNRs are extremely robust, pointing to the high sensitivity of our measures. The comparison of SNRs for Experiments 1 and 2 did reach significance (p = 0.05), however, the comparison of Experiment 1 and 3 (p = 0.49) and Experiments 2 and 3 (p = 0.68) did not. In latency comparisons for all experiments, our effect size (η2) exceeded Cohen’s threshold for a large effect (0.1379) (Cohen, 1988) in every case.
Dipole Source Model
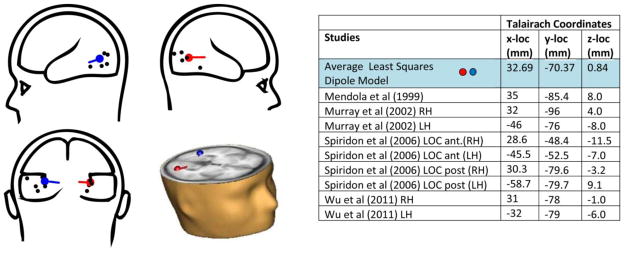
The average of the modeled dipoles of the IC-effect (averaging the solutions across conditions and experiments) are depicted in transparent cartoon brains as well as superimposed on an MRI representation of an axial slice within Talairach space (Figure 7). The colored dots correspond to modeled locations. For reference, Mendola et al (1999), Murray et al (2002), and Wu et al’s (2011) coordinates from their fMRI experiments of LOC response to Kanizsa-type ICs across multiple configurations, and Spiridon et al’s (2006) study of object vs. scrambled object stimuli, which differentiates anterior and posterior portions of the LOC, are depicted in black. The LOC is generally described as composed of both dorsal-caudal (lateral occipital) and ventral-anterior (posterior fusiform with possible overlap of ventral occipital areas) regions. It is situated in the lateral occipital sulcus extending into the posterior inferior temporal sulcus (Grill-Spector, et al., 2001; Grill-Spector & Malach, 2004). As can be seen in the composite diagram, our averaged coordinates fall well within the bounds described in the fMRI literature. The average distance (SD) between each condition’s coordinates and the average is 1.54 (0.57) cm. Taking into account the spatial resolution of ERP and the error rate of such estimates, these data support our interpretation of the modeled locations as within lateral occipital complex.
Figure 7. Dipole Source Analysis.
“Glass brain” dipole model depictions (modeled dipoles represented in red and blue; reference studies in black); dipoles modeled in MRI axial slice (bottom right quadrant); Table with Talairach coordinates, this study’s model is highlighted in blue.
DISCUSSION
We set out here to investigate the extent to which early electrophysiological signatures of illusory contour processing in humans were modulated or delayed as a function of parametric manipulations associated in numerous studies with perception of illusion strength. The stimulus class we employed is a much-used proxy of basic object processing because, while providing two equivalent conditions at the physical stimulus level which differ only in their configuration, one induces perception of an object and the second does not. This perceptual contrast is indexed by a highly robust electrophysiological difference between signals that peaks at ~150 ms - the IC-effect. It is associated with the automatic establishment of object boundaries, and has been definitively localized to visual object processing regions of the human lateral occipital complex. What precisely does this processing stage represent? Recent VEP work specifies the mechanism behind this earliest object processing stage as specifically reflecting contour integration processes (Shpaner, et al., 2009). We therefore hypothesized that manipulation of the basic contour parameters of retinal extent and support ratio would be reflected in a variation of the amplitude and/or latency of the IC-effect. With this information we hoped to better understand the processes underlying the effect and what they explain about the limits of the visual system’s ability to interpolate object contours from incomplete information at this automatic stage of processing. We remind the reader that the participants in Experiment 1 overlapped 25% with the identical samples of Experiments 2 and 3. Our comparisons of results are interpretive; explicit statistical comparisons among the three experiments were not conducted.
Parametric variations of illusion strength and the amplitude of early IC processing effects
Much to our surprise, no matter which manipulation was applied, the IC-effect was observed under all studied conditions. This was so despite subjects’ attention to an orthogonal task, and the fact that no explicit mention of the illusion was ever made. Still, decreasing support ratio (i.e. increasing the relative extent of illusory contour to be interpolated) delayed the latency of the IC-effect but not the overall N1, whereas its amplitude was invariant to manipulation of absolute or relative spatial extent of contours. This was so notwithstanding concurrent large-scale changes in the overall VEP amplitude during the same processing time frame, independent of IC condition, which rules out potential explanations of the current findings based on a lack of sensitivity of the measures used.
Two retinal eccentricity variations were explored. In one, inducer volume changed to hold support ratio constant and in the other support ratio varied, leaving inducer volume constant. As the extent of a perceived contour increases, one might expect a greater number of cells to be activated and a concomitantly larger VEP to result. Yet despite increasing across a wide range of visual angles - from 4° to 10° – there was no measured change in IC-effect amplitude. These electrophysiological findings are in accord with the behavioral finding that length of contours does not affect judgment of illusion clarity (Shipley & Kellman, 1992).
However, illusion strength has been observed to change relative to support ratio (Shipley & Kellman, 1992; Hadad, et al., 2010). We manipulated support ratio in two ways. In one case, the inducer volume changed, holding retinal eccentricity constant. Support ratio varied greatly from 30% to nearly 80%. In the second, with inducer volume held constant, the eccentricity varied inversely with support ratio that spanned 21% to 54%. The range encompassed in six manipulations in two experiments with identical samples varied from nearly complete squares, requiring only 20% of contour length to be filled-in, to a condition in which 80% of the contour was missing. Remarkably, in no case was a significant modulation of the magnitude of the IC-effect measured.
What can explain the invariance of amplitude of the IC-effect to contour manipulation, and how should these results be interpreted in light of previous assertions that the strength of edge interpolation of ICs is determined by support ratio? Whether varying literal contour length or length of real to illusory contour, these quantitative differences are not matched by differences in the amplitude of the IC-effect. It is worth restating that no square actually exists until its contours are induced, and even then its perception is illusory. These results offer a different interpretation from Shipley and Kellman’s because, at the onset of the IC-effect, no object yet exists. Doniger et al’s (2001) temporally distinct perceptual and conceptual modes of object processing offer a reasonable explanation of the present results. They reflect the pre-semantic contribution of sufficient sensory information to suggest that an object exists, but prior to the time when that sensory information is actively compared with semantic memory representations, accomplishing the conceptual identification of the object. The IC-effect appears to capture the binding of the inducers as a single object. Only following the establishment of boundaries relative to the statistical properties of the inducers is the enclosed region segmented from background (Shpaner, et al., 2009). Murray et al (2006) further suggested that the contribution of conscious judgments made about object parameters, such as judgment of illusion strength, occur subsequent to that object’s segmentation from the rest of space. The present study supports this contention. The IC-effect seems to reflect a binary process – contours are completed or they are not. The amplitude of the effect appears to contain no quantitative information about how much contour is completed, and the perception of a square where only Pac-men exist results because a statistical estimate determines the outcome of this binary process.
But the IC-effect reflects more than an estimate which sometimes produces an “error” in representing nature. Vision permits recognition of a single object from multiple perspectives. This quality of invariant object processing is remarkable given that the sensory imprint of the multiple perspectives on our retina can be vastly different. Previous fMRI and electrophysiological work has linked the LOC to such invariant recognition (Malach, et al., 1995; Grill-Spector, et al., 1998), the same complex of structures to which the IC-effect and the Ncl have been localized (Foxe, et al., 2005; Sehatpour, et al., 2006). The binding of objects from discrete components as reflected by the IC-effect does not vary parametrically as contour parameters are varied, at least not within the ranges explored in these experiments. We see this invariant neural response as a prerequisite for the invariant object processing that is subserved by the LOC.
Changes in the timing of contour processing as a function of the distances to be interpolated
Support ratio did modulate the latency of the IC-effect, perhaps because the amount of missing contour relative to real contour determines how much closure must occur. This is reflected in the amount of time that binding takes. As Experiment 1 held support ratio constant, no significant modulation was observed in peak (Figure 4d) or onset (Figure 5a) latency. However differences were observed in Experiments 2 and 3, 75% of whose participants differed from Experiment 1. Increasing support ratio and inducer diameter was met with a speeding up of the IC-effect peak latency but the overall N1 was not impacted to the same degree (Figure 4d). In this case, the extent of the illusory square did not change but the amount of real contour did. Thus, the smaller the gap to be bridged relative to real contour, the less processing is required to bind the inducers, and the sooner initial establishment of the boundaries is completed. T-tests reveal that the latency difference between a support ratio of 30% and 55% was just 2 ms, however, level 3 – with a support ratio of 80%, nearly a complete square – was 20 ms faster, driving this effect. The same was true for varying support ratio inversely with eccentricity: the larger the gap to bridge, the later the peak latency. The alternative explanation that we are witnessing a change in the overall N1 is not supported by our comparison of peak latency for IC and non-IC-forming conditions, which show latency differences to be driven by the IC-condition. Inspection of the waveforms further clarifies this (Figure 4d).
Analysis of onset latencies in Experiments 2 and 3 indicated that the initiation of IC-sensitivity over lateral occipital scalp regions varied with support ratio: the smaller the ratio the later the onset. One can also observe that relatively large support ratios (> 50%) induce more punctate IC-effects with less subsequent processing, whereas smaller support ratios (< 31%) tend to result in increased object processing in the 300 – 400 ms time window, associated with later conceptual closure processes (Doniger, et al., 2001; Foxe, et al., 2005). This suggests that, with larger relative gaps, more object processing is required following contour completion. It is worth noting that, as support ratios decline, more frontal and fronto-central activity is apparent, onsetting at ~140 ms, suggesting that, as the statistical cues for object presence are less robust, frontal processing is recruited to mediate binding. This finding is highly consistent with previous work suggesting frontal cortex facilitation of object recognition on the basis of context (Bar, et al., 2006; Oliva & Torralba, 2007), as well as work by our own group using intracranial recordings in human epilepsy patients, where a clear role for frontal regions in conceptual-level object recognition processes was established (Sehatpour, et al., 2008). In this latter study, we found robust beta-band coherence across a network of regions that comprised lateral prefrontal cortex, the hippocampus, and the LOC when participants were processing fragmented but recognizable images.
Statistical cluster plots for three pairs of identical stimuli across experiments evidence nearly equivalent onset latencies, but peak latencies for Experiment 1 level 2 and Experiment 2 level 2 vary by 20 ms. In addition, the amount of processing associated with the later conceptual time frame varies in all three pairs. This could be the result of different samples in Experiment 1 versus 2 and 3, however, it could also be the result of the contextual effects, i.e., the same parameters will not necessarily be identically processed if they are experienced in different contexts – a subject for future studies.
Modulation of ongoing visual processing independent of contour induction
Despite the invariance of IC-effect amplitude as a function of the parametric manipulations employed across the three reported experiments, clear effects were apparent during the N1 processing timeframe when responses were collapsed across IC condition for the second and third experiments. The presence of these modulations makes clear that the parametric variation in inducer size and spatial extent did result in systematic modulations of the VEP during the N1 processing timeframe, attesting to the sensitivity of our measures to the stimulus manipulations. We begin with Experiment 1 in which retinal eccentricity and inducer diameter were varied but no modulation of the VEP was observed. It is apparent to the eye (Figure 3a) that in this case, larger inducers create more contrast relative to the background than smaller ones, and on the face of it one might expect this to result in activation of more sensory neurons and a concomitant increase in cortical neural activity. However, since the inducers move outward from central space as they grow in this experiment, the so-called cortical magnification factor comes into play (Tootell, et al., 1988). That is, as the neural representation of foveal visual space is considerably magnified in the cortex relative to the periphery (Rovamo & Virsu, 1979; Qiu, et al., 2006), as the inducers occupy increasingly peripheral space, relatively fewer neurons are likely to fire. Hence, a plausible explanation for the lack of modulation of the VEP during the N1 processing timeframe in Experiment 1 (Figure 6d) is that the increased neural activation to be expected from larger inducers was counteracted by their decreased representation as they moved outward from central space. This was likely further impacted by the fact that the regions of early visual cortices that process peripheral locations are located deeper and deeper along the calcarine sulcus, and therefore further and further from the sensors at the scalp surface. In Experiment 2, varying support ratio and inducer diameter, the inducers’ position in space does not vary between conditions. Without offsetting the decrease in activation due to cortical representation, increased activity due to increased inducer size would be expected (whereas support ratio, which only exists in one IC condition and not the other, is irrelevant here). The modulation of the VEP as a result of the experimental manipulation in Experiment 2 bore this out (Figure 6d). As inducer size increased, so did VEP amplitude. In Experiment 3 in which there was manipulation of eccentricity and support ratio, progressively decreasing neural representation resulted from increasingly peripherally located inducers that was not counteracted by a change in inducer size as in Experiment 1. A decrease in VEP amplitude as inducers moved outward from central space was indeed what was observed (Figure 6d).
In contrast to these inducer related modulations of the amplitude of the N1 as a function of inducer size or spatial extent, none of the manipulations altered the amplitude of the IC-effect. This lends support to the speculation that the mechanism underlying the IC-effect reflects the binding of the inducers as objects (in this case, squares), and is blind to any variations in contour related parameters.
Conclusion
In summary, the present results offer further support for dissociable perceptual and conceptual phases of early object processing. During the first of these, indexed by the IC-effect, it appears that components determining object contours may be bound as long as minimal statistical characteristics of contour extent relative to object size are satisfied. It is apparent that these processes take longer when a gap of greater relative extent must be bridged. Possible contextual effects are suggested and remain to be examined in future studies.
Acknowledgments
This study was supported by a grant from the U.S. National Institute of Mental Health (NIMH) to JJF and SM (RO1 - MH085322). Mr. Altschuler is supported by a Robert Gilleece Fellowship through the Program in Cognitive Neuroscience at City College of New York. Mr. Snyder is supported by a Ruth L. Kirschstein National Research Service Award (NRSA) pre-doctoral fellowship from the NIMH (F31 – MH087077). The authors would like to express their gratitude to Dr. Hilary Gomes, Ms. Snigdha Banerjee, Drs. Manuel Gomez-Ramirez, Hans-Peter Frey and John Butler for their valuable support and input during this study. Dr. Russo’s new address is School Psychology & Cognition, Brain & Behavior Areas, Syracuse University Department of Psychology, 430 Huntington Hall, Syracuse, NY 13244, United States.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Banton T, Levi DM. The perceived strength of illusory contours. Perception & Psychophysics. 1992;52(6):676–684. doi: 10.3758/bf03211704. [DOI] [PubMed] [Google Scholar]
- Bar M, Kassam KS, Ghuman AS, Boshyan J, Schmid AM, et al. Top-down facilitation of visual recognition. Proc Natl Acad Sci. 2006;103(2):449–454. doi: 10.1073/pnas.0507062103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bartlett FC. An experimental study of some problems of perceiving and imagining. British Journal of Psychology. 1916;8:222–266. [Google Scholar]
- Cohen J. Statistical Power Analysis for the Behavioral Sciences. 2. Hillsdale, New Jersey: Lawrence Erlbaum Associates; 1988. [Google Scholar]
- Derrington AM, Krauskopf J, Lennie P. Chromatic Mechanisms in Lateral Geniculate Nucleus of Macaque. Journal of Physiology. 1984;357:241–265. doi: 10.1113/jphysiol.1984.sp015499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Doniger GM, Foxe JJ, Murray MM, Higgins BA, Javitt DC. Impaired visual object recognition and dorsal/ventral stream interaction in schizophrenia. Arch Gen Psychiatry. 2002;59(11):1011–1020. doi: 10.1001/archpsyc.59.11.1011. [DOI] [PubMed] [Google Scholar]
- Doniger GM, Foxe JJ, Murray MM, Higgins BA, Snodgrass JG, et al. Activation tiecourse of ventral visual stream object-recognition areas: High density electrical mapping of perceptual closure processes. Journal of Cognitive Neuroscience. 2000;12(4):615–621. doi: 10.1162/089892900562372. [DOI] [PubMed] [Google Scholar]
- Doniger GM, Foxe JJ, Schroeder CE, Murray MM, Higgins BA, Javitt DC. Visual perceptual learning in human object recognition areas: A repetition priming study using high-density electrical mapping. NeuroImage. 2001;13:305–313. doi: 10.1006/nimg.2000.0684. [DOI] [PubMed] [Google Scholar]
- Dumais ST, Bradley DR. The effects of illumination level and retinal size on the apparent strength of subjective contours. Perception & Psychophysics. 1976;19(4):339–345. doi: 10.1068/p130155. [DOI] [PubMed] [Google Scholar]
- Fiebelkorn IC, Foxe JJ, Schwartz TH, Molholm S. Staying within the lines: the formation of visuospatial boundaries influences multisensory feature integration. Eur J Neurosci. 2010;31(10):1737–1743. doi: 10.1111/j.1460-9568.2010.07196.x. [DOI] [PubMed] [Google Scholar]
- Foxe JJ, Murray MM, Javitt DC. Filling-in in schizophrenia: a high-density electrical mapping and source-analysis investigation of illusory contour processing. Cerebral Cortex. 2005;15(12):1914–1927. doi: 10.1093/cercor/bhi069. [DOI] [PubMed] [Google Scholar]
- Foxe JJ, Simpson GV. Flow of activation from V1 to frontal cortex in humans: A framework for defining “early” visual processing. Experimental Brain Research. 2002;142:139–150. doi: 10.1007/s00221-001-0906-7. [DOI] [PubMed] [Google Scholar]
- Grill-Spector K, Kourtzi Z, Kanwisher N. The lateral occipital complex and its role in object recognition. Vision Res. 2001;41(10–11):1409–1422. doi: 10.1016/s0042-6989(01)00073-6. [DOI] [PubMed] [Google Scholar]
- Grill-Spector K, Kushnir T, Edelman S, Itzchak Y, Malach R. Cue-invariant activation in object-related areas of the human occipital lobe. Neuron. 1998;21:191–202. doi: 10.1016/s0896-6273(00)80526-7. [DOI] [PubMed] [Google Scholar]
- Grill-Spector K, Malach R. The human visual cortex. Annu Rev Neurosci. 2004;27:649–677. doi: 10.1146/annurev.neuro.27.070203.144220. [DOI] [PubMed] [Google Scholar]
- Guthrie D, Buchwald JS. Significance testing of difference potentials. Pschophysiology. 1991;28:240–244. doi: 10.1111/j.1469-8986.1991.tb00417.x. [DOI] [PubMed] [Google Scholar]
- Hadad B, Maurer D, Lewis TL. The development of contour interpolation: Evidence from subjective contours. J Exp Child Psychol. 2010;106(2–3):163–176. doi: 10.1016/j.jecp.2010.02.003. [DOI] [PubMed] [Google Scholar]
- Halko MA, Mingolla E, Somers DC. Multiple mechanisms of illusory contour perception. Journal of Vision. 2008;8(11):1–17. doi: 10.1167/8.11.17. [DOI] [PubMed] [Google Scholar]
- Herrmann CS, Mecklinger A, Pfeifer E. Gamma Responses and ERPs in a visual classification task. Clinical Neurophysiology. 1999;110:636–642. doi: 10.1016/s1388-2457(99)00002-4. [DOI] [PubMed] [Google Scholar]
- Ishihara S. Ishihara’s Tests for Colour Deficiency. Tokyo: Kanehara Trading Inc; 2008. Concise Edition ed. [Google Scholar]
- Kanizsa G. Subjective Contours. Scientific American. 1976;234:48–52. doi: 10.1038/scientificamerican0476-48. [DOI] [PubMed] [Google Scholar]
- Lucan JN, Foxe JJ, Gomez-Ramirez M, Sathian K, Molholm S. Tactile shape discrimination recruits human lateral occipital complex during early perceptual processing. Hum Brain Mapp. 2010;31(11):1813–1821. doi: 10.1002/hbm.20983. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Malach R, Reppas JB, Benson R, Kwong KK, Jiang H, et al. Object-related activity revealed by functional magnetic resonance imaging in human occipital cortex. Proc Natl Acad Sci. 1995;92(18):8135–8139. doi: 10.1073/pnas.92.18.8135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mendola JD, Dale AM, BF, Liu AK, Tootell RBH. The representation of illusory and real contours in human cortical visual areas revealed by functional magnetic resonance imaging. J Neurosci. 1999;19(19):8560–8572. doi: 10.1523/JNEUROSCI.19-19-08560.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miltner W, Braun C, Johnson RJ, Simpson GV, Ruchkin DS. A test of brain electrical source analysis (BESA): a simuluation study. Electroencephalogr Clin Neurophysiol. 1994;91(4):295–310. doi: 10.1016/0013-4694(94)90193-7. [DOI] [PubMed] [Google Scholar]
- Moreland JD, Cruz A. Colour Perception with the Peripheral Retina. Journal of Modern Optics. 1959;6(2):117–151. [Google Scholar]
- Murray MM, Foxe DM, Javitt DC, Foxe JJ. Setting boundaries: brain dynamics of modal and amodal illusory shape completion in humans. The Journal of Neuroscience. 2004;24(31):6898 – 6903. doi: 10.1523/JNEUROSCI.1996-04.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murray MM, Foxe JJ, Higgins BA, Javitt DC, Schroeder CE. Visuo-spatial neural response interactions in early cortical processing during a simple reaction time task: a high-density electrical mapping study. Neuropsychologia. 2001;39:828–844. doi: 10.1016/s0028-3932(01)00004-5. [DOI] [PubMed] [Google Scholar]
- Murray MM, Imber ML, Javitt DC, Foxe JJ. Boundary completion is automatic and dissociable from shape discrimination. The Journal of Neuroscience. 2006;26(46):12043 – 12054. doi: 10.1523/JNEUROSCI.3225-06.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murray MM, Wylie GR, Higgins BA, Javitt DC, Schroeder CE, Foxe JJ. The spatiotemporal dynamics of illusory contour processing: Combined high-density electrical mapping, source analysis, and functional magnetic resonance imaging. The Journal of Neuroscience. 2002;22(12):5055–5073. doi: 10.1523/JNEUROSCI.22-12-05055.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oldfield RC. The assessment and analysis of handedness: the Edinburgh inventory. Neuropsychologia. 1971;9:97–113. doi: 10.1016/0028-3932(71)90067-4. [DOI] [PubMed] [Google Scholar]
- Oliva A, Torralba A. The role of context in object recognition. Trends Cogn Sci. 2007;11(12):520–527. doi: 10.1016/j.tics.2007.09.009. [DOI] [PubMed] [Google Scholar]
- Peterhans E, von der Heydt T. Mechanisms of contour perception in monkey visual cortex. II Contours bridging gaps. Journal of Neuroscience. 1989;9:1749–1763. doi: 10.1523/JNEUROSCI.09-05-01749.1989. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qiu A, Rosenau B, Greenberg AS, Hurdal MK, Barta P, et al. Estimating linear cortical magnification in human primary visual cortex via dynamic programming. NeuroImage. 2006;31:125–138. doi: 10.1016/j.neuroimage.2005.11.049. [DOI] [PubMed] [Google Scholar]
- Ringach D, Shapley R. Spatial and temporal properties of illusory contours and amodal boundary completion. Vision Research. 1996;36:3037 – 3050. doi: 10.1016/0042-6989(96)00062-4. [DOI] [PubMed] [Google Scholar]
- Rovamo J, Virsu V. An estimation and application of the human cortical magnifcation factor. Experimental Brain Research. 1979;37(3):495–510. doi: 10.1007/BF00236819. [DOI] [PubMed] [Google Scholar]
- Schumann F. Betrage zur analyse der Gesichtswahrnehmungen. Erse Abhandlung einige beobachtung uber die Zusammenfassung von Gesichtseindrucken zu einheiten. Z Psychol. 1900;23:1–32. [Google Scholar]
- Sehatpour P, Molholm S, Javitt DC, Foxe JJ. Spatiotemporal dynamics of human object recognition processing: An integrated high-density electrical mapping and functional imaging study of “closure” processes. NeuroImage. 2006;29(2):605–618. doi: 10.1016/j.neuroimage.2005.07.049. [DOI] [PubMed] [Google Scholar]
- Sehatpour P, Molholm S, Schwartz TH, Mahoney JR, Mehta AD, et al. A human intracranial study of long-range oscillatory coherence across a frontal-occipital-hippocampal brain network during visual object processing. Proc Natl Acad Sci USA. 2008;105:4399–4404. doi: 10.1073/pnas.0708418105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shipley TF, Kellman PJ. Strength of visual interpolation depends on the ratio of physically specified to total edge length. Perception and Psychophysics. 1992;52(1):97–106. doi: 10.3758/bf03206762. [DOI] [PubMed] [Google Scholar]
- Shpaner M, Murray MM, Foxe JJ. Early processing in the human lateral occipital complex is highly responsive to illusory contours but not to salient regions. Eur J Neurosci. 2009;10:2018–1028. doi: 10.1111/j.1460-9568.2009.06981.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Snodgrass JG, Feenan K. Priming effects in picture fragment completion: support for the perceptual closure hypothesis. J Exp Pschol Gen. 1990;119(3):276–296. doi: 10.1037//0096-3445.119.3.276. [DOI] [PubMed] [Google Scholar]
- Spiridon M, Fischl B, Kanwisher N. Location and spatial profile of category-specific regions in human extrastriate cortex. Hum Brain Mapp. 2006;27(1):77–89. doi: 10.1002/hbm.20169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sugawara M, Morotomi T. Visual Evoked Poetentials Elicited by Subjective Contour Figures. Scandanavian Journal of Psychology. 1991;32(4):352–357. doi: 10.1111/j.1467-9450.1991.tb00886.x. [DOI] [PubMed] [Google Scholar]
- Tootell RBH, Switkes E, Silverman MS, Hamilton SL. Functional anatomy of macaque Striate cortex. II Retinotopic organization. J Neurosci. 1988;8(5):1531–1568. doi: 10.1523/JNEUROSCI.08-05-01531.1988. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tulving E, Schacter DL. Priming and Human Memory Systems. Science. 1990;247:301 – 306. doi: 10.1126/science.2296719. [DOI] [PubMed] [Google Scholar]
- Wu X, He S, Bushara K, Zeng F, Liu Y, Zhang D. Dissociable neural correlates of contour completion and contour representation in illusory contour perception. Hum Brain Mapp. 2011 doi: 10.1002/hbm.21371. [E pub ahead of print] [DOI] [PMC free article] [PubMed] [Google Scholar]