Abstract
The amplitude of the BOLD response to a stimulus is not only determined by changes in cerebral blood flow (CBF) and oxygen metabolism (CMRO2), but also by baseline physiological parameters such as haematocrit, oxygen extraction fraction (OEF) and blood volume. The calibrated BOLD approach aims to account for this physiological variation by performing an additional calibration scan. This calibration typically consists of a hypercapnia or hyperoxia respiratory challenge, although we propose that a measurement of the reversible transverse relaxation rate, R2′, might also be used. A detailed model of the BOLD effect was used to simulate each of the calibration experiments, as well as the activation experiment, whilst varying a number of physiological parameters associated with the baseline state and response to activation. The effectiveness of the different calibration methods was considered by testing whether the BOLD response to activation scaled by the calibration parameter combined with the measured CBF provides sufficient information to reliably distinguish different levels of CMRO2 response despite underlying physiological variability. In addition the effect of inaccuracies in the underlying assumptions of each technique were tested, e.g. isometabolism during hypercapnia.
The three primary findings of the study were: 1) The new calibration method based on R2′ worked reasonably well, although not as well as the ideal hypercapnia method; 2) The hyperoxia calibration method was significantly worse because baseline haematocrit and OEF must be assumed, and these physiological parameters have a significant effect on the measurements; and 3) the venous blood volume change with activation is an important confounding variable for all of the methods, with the hypercapnia method being the most robust when this is uncertain.
Keywords: Calibrated BOLD, Cerebral metabolic rate of oxygen, Functional MRI, Hypercapnia, Hyperoxia
Introduction
The BOLD signal is dependent on changes in cerebral blood flow (CBF) and oxidative metabolism (CMRO2). However, changes in CBF and CMRO2 alone do not determine the amplitude of the BOLD response to neural activity. It is therefore possible to measure BOLD responses with different amplitudes that result from the same underlying changes in CBF and CMRO2. The scale of the BOLD response is determined by the baseline physiological state of the tissue contained within the imaging voxel. This baseline is characterised by the total amount of deoxyhaemoglobin present, which is dependent on the haematocrit, baseline oxygen extraction fraction (OEF), and baseline blood volume. The calibrated BOLD approach (Davis et al., 1998) was proposed to measure changes in CMRO2 using measurements of CBF and BOLD. This is achieved by characterising differences in baseline physiology using a calibration experiment. Traditionally this experiment consists of simultaneous measurements of CBF and BOLD acquired during interleaved periods of normocapnia and hypercapnia (Davis et al., 1998; Hoge et al., 1999). Hypercapnia is induced by presenting the participant with carbon dioxide rich gas mixture (typically 5% CO2, 21% O2, 74% N2) and results in an increase in CBF and the BOLD signal. A model of the BOLD signal is then used to convert these changes into a measure of the baseline physiological state (Davis et al., 1998), under the assumption that baseline CMRO2 is not altered by hypercapnia (Sicard and Duong, 2005; Jain et al., 2011).
More recently an alternative respiratory challenge was presented whereby hypercapnia was replaced with hyperoxia (Chiarelli et al., 2007). Experiments have been performed with oxygen content ranging from 25% (Mark et al., 2011) to 100% (Chiarelli et al., 2007; Goodwin et al., 2009). Hyperoxia does not substantially increase arterial blood oxygen saturation, but does increase the oxygen carried by arterial blood through an increased plasma oxygen concentration. This results in an increase in venous blood oxygen saturation and hence an increase in BOLD signal. A modification of the BOLD signal model used for hypercapnia calibration can then be used to characterise the baseline state (Chiarelli et al., 2007).
However, respiratory challenges are time consuming to set up, uncomfortable and may be contraindicated for some subjects, for example in Chronic Obstructive Pulmonary Disease (COPD) (Moore et al., 2009). Therefore, it would be useful to be able to calibrate without administering gases. It has long been known that the reversible transverse relaxation rate, R2′, is sensitive to venous cerebral blood volume (CBVv) and the concentration of deoxyhaemoglobin ([dHb]) (Yablonskiy and Haacke, 1994). This sensitivity is exploited by the qBOLD approach to make absolute measurements of resting CBVv and OEF (He and Yablonskiy, 2006). However, this method has poor temporal resolution and is not suitable for measuring CMRO2 changes on short timescales. Nevertheless, R2′ is dependent on haematocrit, OEF and blood volume and as such captures most of the characteristics of the baseline physiological state that are important for determining the scaling of the BOLD response, particularly total deoxyhaemoglobin content. Can we therefore use this information to calibrate the BOLD response? In this study we investigate whether R2′ can be used to calibrate the BOLD response through detailed simulation. In addition, we compare this new calibration method with the existing respiratory challenge calibrations, hypercapnia and hyperoxia. The simplifying assumptions of each of these methods are investigated and the uncertainty they introduce into the calibration process assessed.
Theory
A General Model for Calibrated BOLD
The aim of calibrated BOLD is to take measurements of BOLD signal and CBF and combine them with information about the baseline state to estimate CMRO2 changes. This baseline information is gathered from a calibration experiment. In the classic approach introduced by Davis and colleagues, the BOLD response is modeled as:
| (1) |
where δs is the percentage BOLD signal change, f is the CBF ratio and r is the CMRO2 ratio (activation/baseline), and α and β are model parameters. The calibration parameter M that scales the BOLD signal is calculated from the measured BOLD and CBF responses to hypercapnia, with the assumption of no change in CMRO2 (r=1). Physically, the calibration parameter M depends on a number of physiological variables that affect the local deoxyhemoglobin concentration in the baseline state, and so represents an important source of variation across subjects and across brain regions. It also depends on image acquisition parameters, so that M is not simply a property of the brain, and comparing M values across different studies requires some care.
In the current study our goal is take a more general approach to the process of calibration, as a way of accounting for variations in the baseline state, without assuming the simple form of the Davis model. More generally the calibrated BOLD experiment can be stated in the following way,
| (2) |
where B is the calibration parameter and h(f,r) is a function that describes the effect of normalised changes in CBF and CMRO2, on the change in BOLD signal. To model h we use a recently described detailed model for the BOLD response that includes a number of physiological variables that were not included in the original Davis model (Griffeth and Buxton, 2011). The model includes three blood compartments (arterial, capillary and venous) as well as the extravascular compartment, and models BOLD signal contributions from all compartments as well as effects of volume exchange as a blood compartment expands. The model also allows the baseline blood volume fractions to be varied, as well as the volume changes of these vascular compartments with activation. Baseline oxygen extraction fraction and blood haematocrit also can be varied. Although this model does not provide a simple closed form for h(f,r) like Eq. (1), it provides a flexible way to simulate the BOLD response for a wide range of physiological baseline states. The model is described in more detail in the Appendix.
The detailed model allows us to test any proposed method for calibration in the following way. The calibration experiment itself is simulated with the detailed BOLD model for a given set of baseline physiological parameters, and the value of B is calculated for the prescribed calibration method from the simulated BOLD and CBF responses. The activation experiment is then simulated for particular values of f and r with the same baseline physiological parameters, and the BOLD response normalized to the calibration parameter (δs/B) is then plotted as a function of f. This plot represents a simulation of the measured results of a calibrated BOLD study. This procedure is then repeated for many variations of the baseline physiological parameters and the CBF change f, but for the same CMRO2 change r, with each simulation plotted as one point in the δs/B vs. f plot. If the calibration is perfect, these points for a constant r should fall on a single curve, and when the simulations are repeated for a different value of r the points should fall on a distinctly different curve. In this way the calibration completely captures the variability due to the baseline state and the measurements of δs/B and f uniquely define r. Note that the shape of the curve for a particular value of r, which effectively is determined by h, is not what we are after here. Instead, the central question is whether a calibration method produces a clean separation of the points for different values of r.
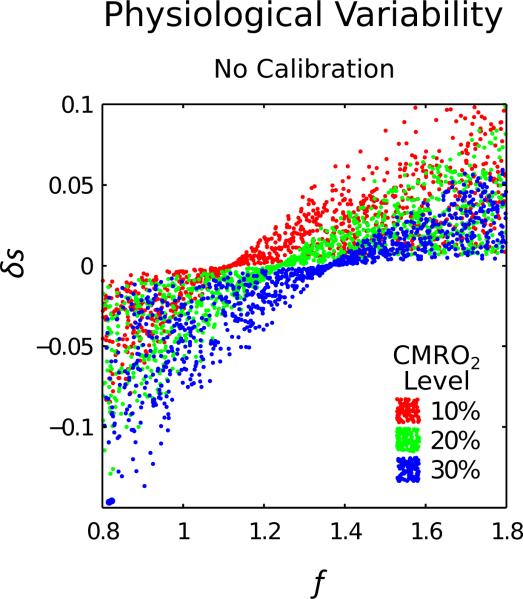
As an initial demonstration of the importance of calibration, Fig. 1 omits calibration and plots δs versus f. Three different levels of CMRO2 change are displayed; 10%, 20% and 30% increases. When baseline haematocrit, Hct, oxygen extraction fraction, E0, and blood volume, V, are randomly varied across the physiological range, all three CMRO2 levels overlap and cannot be clearly separated. A calibration experiment is therefore required to determine B and to reduce the uncertainty in r. This commonly takes the form of a hypercapnia or hyperoxia respiratory challenge, although here we also consider an alternative technique based on measurements of R2′.
Figure 1.
The effect of physiological variability in haematocrit, baseline oxygen extraction fraction and baseline blood volume on the relationship between the BOLD response (δs) and CBF (f). These simulations show that the effect of physiological variability on δs does not allow 10% step changes in CMRO2 to clearly separated, confirming that this information is insufficient to accurately measure CMRO2.
Hypercapnia Calibration
Hypercapnia calibration is performed by presenting a hypercapnic gas mixture to the participant whilst measurements of BOLD signal and CBF are made (Davis et al., 1998). These measurements are combined with the Davis model to estimate the calibration parameter B with Eq (3). Typically this is known as M, with subscript hc added here to distinguish hypercapnia from hyperoxia.
| (3) |
Here, the constants α and β represent flow-volume coupling (Grubb et al., 1974) and the relationship between blood oxygenation and the BOLD signal (Ogawa et al., 1993), respectively. Current practice sets the value of α as 0.2 based on measurements of CBVv, the vascular compartment that underlies the BOLD response (Chen and Pike, 2009). Similarly β is chosen to be 1.3 for experiments performed at 3.0 T (Mark et al., 2011). In the ideal calibration experiment it is assumed that CMRO2 is not altered by hypercapnia (r=1) and this was initially assumed in these simulations.
Hyperoxia Calibration
Hyperoxia calibration is performed in a similar manner to hypercapnia calibration, by presenting a hyperoxic gas mixture to the participant whilst recording measurements of BOLD and CBF (Chiarelli et al., 2007). The BOLD scaling parameter is termed Mho and is equivalent to B in Eq. (2). In the ideal experiment it is assumed that CBF does not change during hyperoxia, in which case measurements of CBF are not necessary during calibration. Hence,
| (4) |
where β takes the same definition as for hypercapnia calibration and [dHb]/[dHb]0 is the change in deoxyhaemoglobin concentration due to breathing the hyperoxic gas mixture, relative to normoxia (Chiarelli et al., 2007). To calculate Mho using Eq. (4) [dHb]/[dHb]0 must be estimated. This is achieved using a model of the oxygen carrying capacity of the blood that is a function of the arterial partial pressure of oxygen (PaO2). In practice this is inferred from the end-tidal pressure of oxygen (PETO2) expired by the participant, taking into account alveolar-arterial oxygen gradient and assuming that the arterial blood is well equilibrated with the gas in the alveoli. This latter assumption relies upon healthy lung function for validity. Oxygen is mostly carried bound to haemoglobin within the blood, however a small amount is carried by the plasma. The PaO2 of the blood determines how much is carried by both of these compartments. The oxygen carried by the plasma is a linear function of PaO2 (ε PaO2) and for bound oxygen the haemoglobin saturation of arterial blood (SaO2) can be calculated from an approximation for the oxygen dissociation curve (Severinghaus, 1979):
| (5) |
During hyperoxia the amount of oxygen carried bound to haemoglobin in the arteries increases slightly, alongside a larger increase in the amount carried as dissolved gas in plasma. Therefore, under hyperoxia the amount of oxygen carried by plasma contributes to a greater degree to the overall delivery of oxygen than during normoxia due to the asymptotic nature of Eq. (5). During passage through the capillary bed the extraction of the excess oxygen in plasma offsets the extraction of oxygen bound to haemoglobin, so that venous haemoglobin saturation increases. However, in the venous blood the partial pressure of oxygen (PvO2) remains low and represents less than 1% of total amount of oxygen carried by venous blood. Therefore, assuming that PvO2 is negligible should not result in a large error and allows [dHb]/[dHb]0 to be estimated as:
| (6) |
where ϕ is the oxygen carrying capacity of haemoglobin (1.34 mlO2 gHb-1), ε is the solubility coefficient of oxygen in blood (0.0031 mlO2 dl-1 mmHg-1), and ΔSaO2 and ΔPaO2 are the change in these parameters due to hyperoxia relative to the normoxic state. Haemoglobin concentration, [Hb], is assumed to be 15 gHb dl-1 (Chiarelli et al., 2007; Mark et al., 2011) and the oxygen extraction fraction, E0, is assumed to be 0.3 (Mark et al., 2011). This value of E0 is lower than the generally reported values of approximately 0.4 (Perlmutter et al., 1987), however we retain this value to reflect current practice in the papers describing the hyperoxia calibration method. Haemoglobin concentration can be converted to haematocrit using a simple approximation, Hct ≈ 0.03 × [Hb]. In summary, the hyperoxia calibration method requires assumed values for several variables. Oxygen carrying capacity and solubility are standard physical parameters that should not vary across subjects. However, haematocrit may well vary across subjects, and baseline O2 extraction fraction could also vary across brain regions within the same subject.
R2′ Calibration
Analytical results (Yablonskiy and Haacke, 1994) and Monte Carlo (Ogawa et al., 1993) simulations have shown that R2′ is a function of blood volume, haematocrit and OEF.
| (7) |
The constant κ subsumes various properties of brain tissue including vessel geometry, magnetic field strength and the susceptibility difference between blood and tissue, and β follows the same definition as in hypercapnia and hyperoxia calibration. If we consider the BOLD signal to be a largely extravascular effect then changes in R2′ determine changes in the BOLD signal. Hence the maximum BOLD signal change during activation is determined by R2′ in the baseline state. Assuming monoexponential decay, the gradient echo (GE) and spin echo (SE) signal at the BOLD echo time, TE, can be described by the following equations, where R2*=R2+R2′.
| (8a) |
| (8b) |
We propose to use the ratio of these signals to define the calibration parameter B.
| (9) |
The echo time, TE, is included to account for the echo time dependence of the magnitude of the BOLD response. This approach assumes that intravascular signal contributions are negligible and that diffusional narrowing does not dominate. These assumptions were tested using an extension of the detailed BOLD signal model (Griffeth and Buxton, 2011). This was achieved by considering the signal contributions from each of the compartments of the detailed signal model under GE and SE pulse sequences during a resting baseline and is described in detail in the Appendix. It must be noted that the measured value of R2′ is dependent on the way in which it is measured. It is generally assumed that the transverse signal decay of a homogenous voxel is monoexponential. However, for time points close to the excitation pulse in a GE sequence, and close to the refocusing pulse for a SE sequence, this decay has been shown to be quadratically exponential in nature (Yablonskiy and Haacke, 1994). In the case of Eq. (9) the SE signal will be acquired in this short echo time regime while the GE signal will be acquired in the long echo time regime. Models for the SE signal compartments were chosen to be consistent with the short echo time regime (Zhao et al., 2007; Uludağ et al., 2009).
Methods
Simulations
The detailed signal model was used to simulate calibration using hypercapnia, hyperoxia and R2′ using Eqs (3), (4) and (9), respectively, as prescriptions for taking specific measured signals and calculating B. Note that the first two methods explicitly depend on the parameter β, which functions as a way to approximate multiple factors affecting the BOLD response. This parameter does not appear in the detailed BOLD model because these different mechanisms are individually modeled. Similarly, the parameter α is related to CBVv change, and in the detailed model the changes in different vascular compartments are simulated.
All simulations were performed in MATLAB (Mathworks, Natick, MA). The main aim of these simulations was to determine how variability in physiology affects the uncertainty in a measurement of CMRO2. For variations in a single parameter simulations are performed by propagating linearly spaced values of this parameter through the detailed signal model. However, for variations in baseline physiology we expect multiple parameters to vary simultaneously and the compound effect of these variations isn't clear. Simple linear ranges for multiple parameters would be slow and produce multidimensional data that is difficult to visualise. Here we take an alternative approach by drawing random combinations of these parameters from predefined ranges. Multiple repeats of this process enable a ‘cloud’ of data to be generated that can be visualised in two dimensions, as shown in Fig. 1.
In order to investigate the sensitivity of each of the calibration methods to baseline physiological variability and the assumptions of each method, the change in BOLD signal was divided by the calibration scaling factor. In the following figures this quantity, δs/B, is plotted against f. These simulations are performed for two different scenarios; fixed CMRO2 level or fixed CBF-CMRO2 coupling value, n, defined as,
| (10) |
Fixed CMRO2 changes enables us to visualise how well different CMRO2 levels can be separated, whilst fixed CBF-CMRO2 coupling shows the uncertainty in these measurements for more physiologically plausible combinations of CBF and CMRO2. Fixed CMRO2 levels of 10%, 20% and 30% increases and CBF-CMRO2 coupling values of n = 1.3, 2 and 3 were simulated. An n value of 1.3 represents a special case where the increase in blood oxygenation due to increased CBF is approximately balanced by increased oxygen extraction due to metabolism, resulting in a net zero BOLD signal change. The exact value of n required to achieve this condition is CBF dependent and can be estimated from the Davis model (Eq. (1)) for specific values of α and β. Therefore, n=1.3 is an approximate BOLD-nulling value for the CBF values simulated.
Each of the calibration parameter values was calculated as described in the Theory section. In summary, the hypercapnia calibration scaling factor, Mhc, is calculated using Eq. (3) under the assumption that CMRO2 does not change (r=1) and a 47% increase in CBF due to hypercapnia (f=1.47). In all simulations α in Eq. (3) was chosen to be 0.2. The hyperoxia calibration, Mho, is calculated using Eq. (4), relying on Eq. (6) to determine [dHb]/[dHb]0, following the method of Mark et al., and [Hb] and E0 in this equation have fixed values of 15 gHb dl-1 and 0.3, respectively (Mark et al., 2011). Hyperoxia calibration was simulated as an ideal experiment where CBF is not altered by hyperoxia. In both traditional methods β was chosen to be 1.3. In R2′ calibration the scaling factor is the product of TE and R2′, and is calculated using Eq. (9). No assumptions about isometabolism or the value of α and β are required.
Baseline Physiological Variation
The parameters that determine the baseline state are haematocrit, baseline OEF and baseline blood volume. Haematocrit is known to vary between males and females with typical ranges of 0.42 – 0.50 and 0.37 – 0.47, respectively (McPhee and Hammer, 2009). However, there is a great deal of overlap and typically calibration methods do not take account of sex during data processing, therefore a range of 0.37 – 0.50 was tested. Ranges for baseline OEF are similarly wide at 0.35 – 0.55 (Marchal et al., 1992). This range was extended at the low end to encompass the assumed OEF value of 0.3 used in the hyperoxia calibration method. The baseline total blood volume fraction is typically measured to be 0.05 in grey matter (Roland et al., 1987). However, to account for the partial volume effect at the low end of the range and for incorporation of large vessels at the high end of the range a total blood volume fraction between 0.01 and 0.1 was tested. Relative volume fractions for arteries, capillaries and veins were fixed at 0.2, 0.4 and 0.4, respectively. This resulted in simulated venous volume fractions in the range 0.004 to 0.04. Finally, the activation induced change in CBF was simulated across a large range (0.8 to 1.8) to encompass all physiologically plausible eventualities. Values for the remaining model parameters are listed in Table 1.
Table 1.
Constants required for the detailed signal model (Griffeth and Buxton, 2011) and extension to simulate R2′.
| Constant | Value | Description |
|---|---|---|
| TE | 32 ms | Imaging echo time. |
| ε A | 1.30 | Ratio of baseline intravascular arterial to extravascular signal (Griffeth and Buxton, 2011). |
| ε C | 1.02 | Ratio of baseline intravascular capillary to extravascular signal (Griffeth and Buxton, 2011). |
| ε V | 0.50 | Ratio of baseline intravascular venous to extravascular signal (Griffeth and Buxton, 2011). |
| 4.3 | Coefficient describing extravascular signal resulting from vessels in the range 16 – 200 μm diameter under a gradient echo (Ogawa et al., 1993). | |
| 0.04 s | Coefficient describing extravascular signal resulting from 5 μm diameter vessels under a gradient echo (Ogawa et al., 1993). | |
| a L,5 | -1.92×10-11 s4 | Coefficients describing extravascular signal resulting from 16 μm diameter vessels under a spin echo (Uludağ et al., 2009). |
| a L,4 | -1.26×10-8 s3 | |
| a L,3 | -2.89×10-6 s2 | |
| a L,2 | 2.51×10-4 s | |
| a L,1 | 0.0067 | |
| a L,0 | -0.0382 s-1 | |
| a S,5 | -1.13×10-11 s4 | Coefficients describing extravascular signal resulting from 5 μm diameter vessels under a spin echo (Uludağ et al., 2009). |
| a S,4 | 0.96×10-8 s3 | |
| a S,3 | -3.22×10-6 s2 | |
| a S,2 | 4.90×10-4 s | |
| a S,1 | -3.58×10-6 | |
| a S,0 | 0.0175 s-1 | |
| Δ | 2.64×10-7 | Susceptibility of fully deoxygenated blood (Spees et al., 2001). |
| Yoff | 0.95 | Blood saturation for equal tissue-blood susceptibility (Spees et al., 2001). |
| R 2,0 | 25.1 s-1 | Intrinsic transverse relaxation rate for extravascular tissue (Perthen et al., 2008). |
Randomly generated combinations of these parameters were selected from their respective ranges, including activation induced CBF change, using a uniform random number generator. A uniform random distribution was chosen as the mean and standard deviation of each of the physiological parameters is not generally known. For each simulation 1,000 repeats of the random parameter generation process were completed. These values were propagated through the detailed signal model to generate a stimulus induced BOLD signal change, δs, and a calibration parameter, B, for each calibration method. To simplify the simulation process CBF was included as an additional randomly generated value providing the third experimental variable of the calibrated BOLD approach.
Flow-Volume Coupling Assumption
A general assumption of all calibrated BOLD methods is that changes in CBVv can be inferred from measurements of CBF through a power law relationship defined by α. An inaccurate value of α would be a source of systematic error. Here we aim to determine the sensitivity of each of the calibration methods to the value of α. Traditionally α was defined as 0.4 based on measurements of total CBV (Grubb et al., 1974), but has more recently been superseded by a value of 0.2 using measurements of venous CBV change (Chen and Pike, 2009). These values were used to test the extremes of the range for flow-volume coupling given our current knowledge. When calculating Mhc, α in Eq. (3) was fixed at 0.2 regardless of the value of the underlying flow-volume coupling. This reflects the way that hypercapnia calibration is performed, whereby a value of α must be assumed that may not reflect the true underlying changes in volume.
Effect of Errors in Assumptions
Assumptions that would lead to the largest sources of error in each method were identified and the effect of systematic error in these assumptions was tested. Baseline physiological variability was not included in these simulations, unless otherwise stated, and standard values for these parameters were assumed (Hct=0.45, E0=0.4, VI,0=0.05).
It has been shown by a number of experiments that hypercapnia may cause a reduction in baseline CMRO2 (Xu et al., 2010). It is normally assumed that there is no change in CMRO2 due to hypercapnia, (r=1). In order to consider the effect of reduced CMRO2 the value of r=0.85 was also simulated to reflect a 15% reduction in CMRO2 during the hypercapnia challenge.
For hyperoxia the estimation of Mho is dependent on the calculation of [dHb]/[dHb]0 from the change in PETO2 measured during hyperoxia. To simplify this calculation values for [Hb] and E0 are assumed (Mark et al., 2011). Simulations were performed to determine whether more accurate values of one or both parameters would enable variations in baseline physiology to be better accounted for. Since the accuracy of these assumptions is dependent on physiological variability, the same approach of generating random combinations of baseline parameters as used for baseline physiological variation alone was used.
Measurements of R2′ are not only sensitive to mesoscopic sources of magnetic field inhomogeneity around blood vessels but also to large scale magnetic field inhomogeneity that are not removed during shimming. The sensitivity of R2′ calibration to large scale magnetic field inhomogeneity was tested by simulating (Eq. (A8)) a frequency difference across the voxel, Δω, of 20 Hz (An and Lin, 2003).
Results
Baseline Physiological Variability
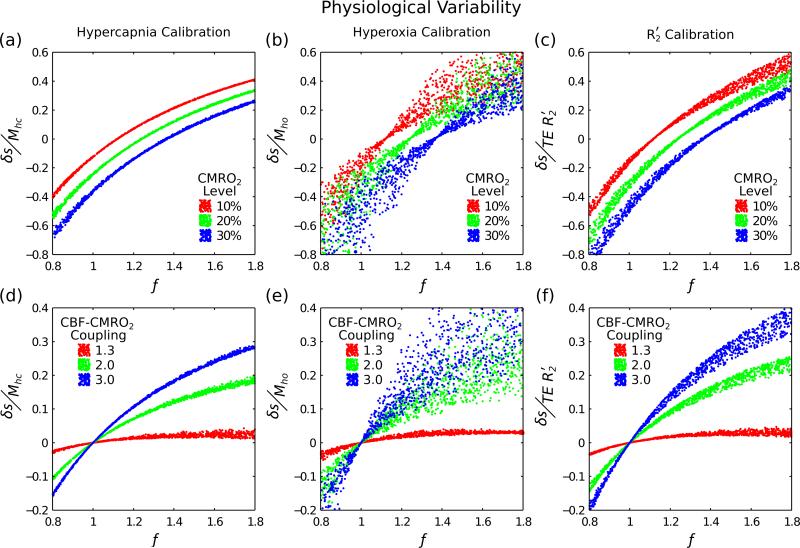
Figure 2 displays the effect of normalising the BOLD signal change using a calibration measurement. All three calibration methods drastically reduce the variability in the relationship between BOLD and CBF (cf. Fig. 1). The width of the lines for each CMRO2 level (Fig. 2a-c), or CBF-CMRO2 coupling value (Fig. 2d-e), are proportional to the error in the final measurement of CMRO2. In an ideal calibration experiment there would be no deviation from the mean and the width of the line would be zero.
Figure 2.
Three different calibration techniques were investigated to account for physiological variability; hypercapnia, hyperoxia, and R2′ calibration (columns left-right). By simultaneously varying haematocrit (0.37-0.50), oxygen extraction fraction (0.30-0.55) and blood volume (0.01-0.10) we are able to assess how well each method copes with this physiological variability. Simulations were performed for both fixed increases in CMRO2 (top row) and for fixed coupling of CBF and CMRO2 (Eq. (10)) (bottom row). For a perfect calibration each of simulated points should fall on a single curve, which should be distinctly different for each CMRO2 level or CBF-CMRO2 coupling value.
For hypercapnia calibration the line width appears to be constant with increasing CBF and independent of the CMRO2 level (Fig. 2a) or CBF-CMRO2 coupling value (Fig. 2d). Hyperoxia calibration shows an increase in the line width with increasing CBF (Fig. 2b,e). The line width is minimised when CBF and CMRO2 balance to give a zero BOLD signal change equivalent to n=1.3 in the plot of CBF-CMRO2 coupling (Fig. 2e). R2′ calibration shows a similar trend to hyperoxia calibration, but with a reduced line width (Fig. 2c,f).
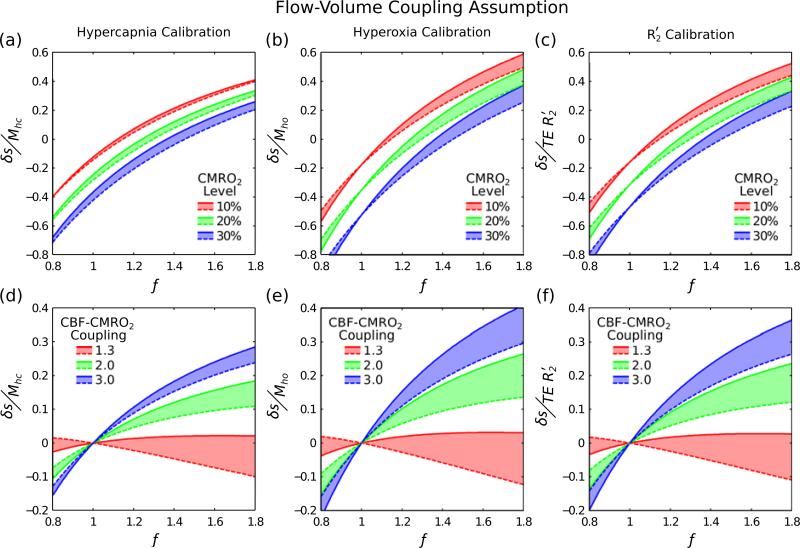
Flow-Volume Coupling Assumption
The effect of assuming that the coupling between CBF and CBVv is accurately known is displayed in Fig. 3. Solid lines are used to represent the case where α=0.2 and dashed lines for when α=0.4. Here we are examining the effect of assuming an incorrect value for α. Therefore, a calibration method with low sensitivity to this parameter should show only a minor shift between these lines, ultimately minimising the error in the measurement of CMRO2.
Figure 3.
An inaccurate assumption of the flow-volume coupling constant α would result in a systematic error. Here the effect of different underlying physiological values of this coupling were investigated where a solid line represents α=0.2 and the dashed line α=0.4. A minimal shift in the dashed line with respect to the solid line would reflect lower sensitivity to the assumed value of α. Physiological variability is not included in these simulations and haematocrit, oxygen extraction fraction and blood volume were assumed to be 0.45, 0.4, 0.05, respectively.
Hypercapnia shows the smallest shift, representing the lowest sensitivity to an inaccurately assumed value of α (Fig. 3a,d). The magnitude of this shift appears to increase with increasing change in the CMRO2 level (Fig. 3a). Hyperoxia and R2′ calibration both show a larger shift than hypercapnia calibration (Fig. 3b,e; Fig. 3c,f). In all cases the effect of assuming an inaccurate value of α causes the greatest effect for n=1.3 in plots of CBF-CMRO2 coupling.
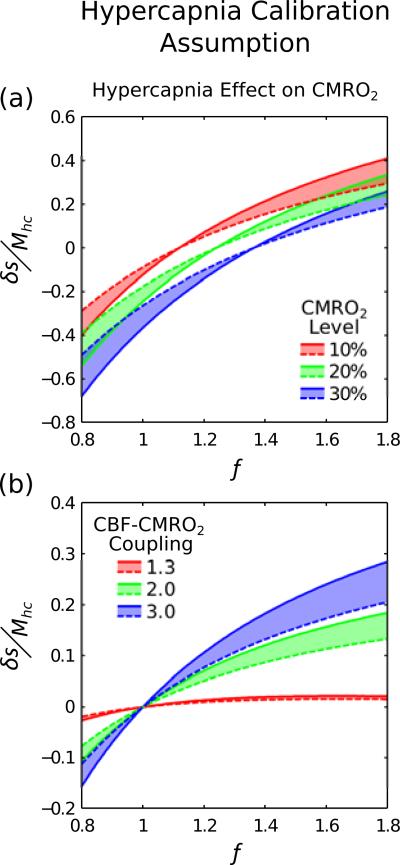
Hypercapnia Calibration Assumption
Figure 4 considers the effect of a change in baseline CMRO2 during hypercapnia. Solid lines represent r=1 during hypercapnia and dashed lines r=0.85. The shift between these lines appears to increase with CMRO2 level (Fig. 4a) and CBF-CMRO2 coupling (Fig. 4b). Unlike flow-volume coupling, changes in CMRO2 during hypercapnia have little to no effect when n=1.3.
Figure 4.
It has been observed that hypercapnia may cause a reduction in baseline CMRO2. Here we consider what effect this would have on hypercapnia calibration when CMRO2 is reduced by 15% (r=0.85 in Eq. (3)). Physiological variability was not included for clarity. Isometabolism (r=1) is plotted as a solid line whilst reduced CMRO2 is plotted as a dashed line. Shifting of the dashed line with respect to the solid line suggests that reduced baseline CMRO2 would have a marked effect on the accuracy of hypercapnia calibration.
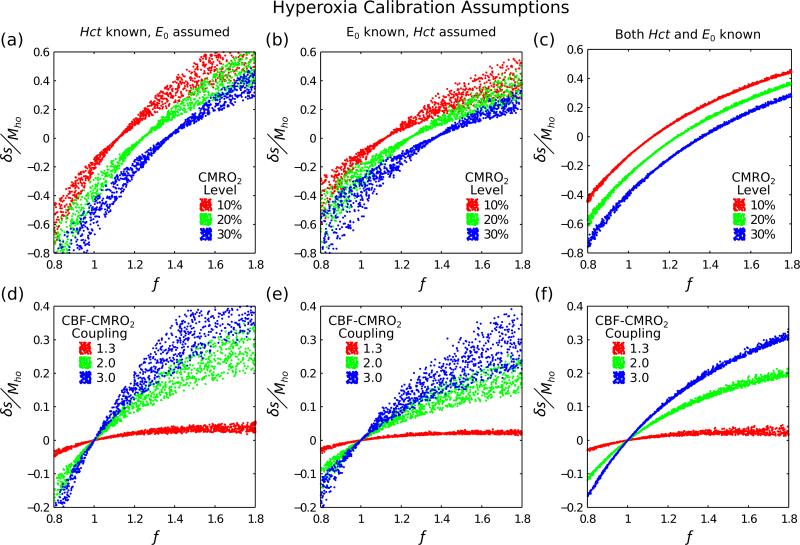
Hyperoxia Calibration Assumptions
Investigation of the origin of the increased variability in hyperoxia calibration is displayed in Fig. 5. Including more accurate information about either haematocrit (Fig. 5a,d) or baseline oxygenation (Fig. 5b,e) reduces this variability. Information about both of these parameters (Fig. 5c,f) reduces variability to similar levels as hypercapnia calibration (Fig. 2a,d).
Figure 5.
Further investigation of hyperoxia calibration was undertaken to better understand the large observed variability. This was achieved by increasing the amount of information used to estimate the calibration scaling factor Mho; haematocrit known, oxygen extraction fraction known and both known (columns left-right). Physiological variability was included as it is the origin of the observed variability in Fig. 2b,e. More information about the baseline physiology reduces the variability in hyperoxia calibration.
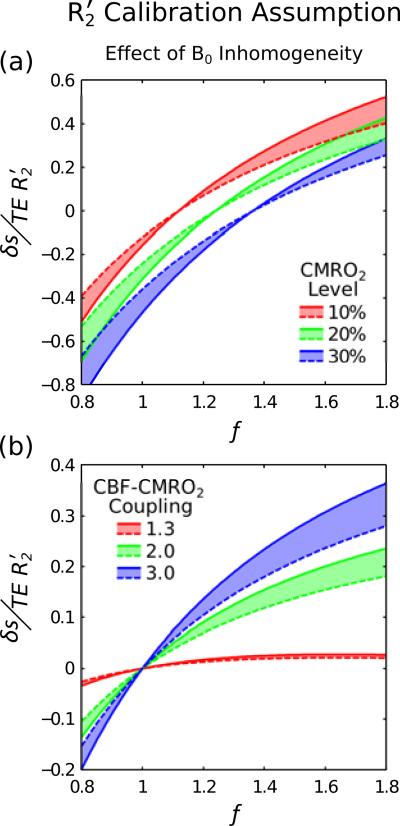
R2′ Calibration Assumption
Figure 6 considers the effect of large scale magnetic field inhomogeneity on R2′ calibration. Solid lines represent a perfectly homogenous field (Δω=0) and dashed lines represent Δω=20 Hz. The shift between these lines is of a similar order to that seen for CMRO2 change during hypercapnia (Fig. 4).
Figure 6.
It is well known that R2′ is sensitive to both mesoscopic and macroscopic sources of magnetic field inhomogeneity. The former represents the effect of blood vessels, which underlies the BOLD response, and the latter is caused by disturbance of the magnetic field by the head. Here we compare perfect field homogeneity (Δω=0), plotted as a solid line, with a through slice gradient Δω=20 Hz, plotted as a dashed line. Shifting of the dashed line with respect to the solid line emphasises that macroscopic field inhomogeneity effects must be minimised.
Discussion
Use of the calibrated BOLD approach has improved the interpretation of fMRI by accounting for physiological variability. Without this calibration procedure measurements of BOLD signal and CBF cannot be used to determine the change in CMRO2 (Fig. 1). However, the extent to which this physiological variability can be characterised by existing methods is not easily accessible in an experimental setting. The simulations performed in this study enable us to investigate these methods and the assumptions that underpin them. Key to this approach was the use of a detailed model of the BOLD effect that allowed us to vary a number of physiological parameters associated with the baseline state and the response to activation. This allowed us to model effects that were not included in the simpler Davis model standardly used for calibrated BOLD experiments. The effectiveness of the different calibration methods was tested by simulating the calibration experiment as well as the activation experiment, and testing whether the measured BOLD response to activation scaled by the calibration parameter combined with the measured CBF response provides sufficient information to reliably distinguish different levels of CMRO2 response despite underlying physiological variability. We evaluated the original hypercapnia method (Davis et al., 1998), the more recently proposed hyperoxia method (Chiarelli et al., 2007) and a novel method based on R2′. The simulation methodology used here has previously been used to optimise hypercapnia calibrated BOLD (Griffeth and Buxton, 2011), the results of which have been applied experimentally (Griffeth et al., 2011). Extensions to the detailed signal model allowed us to simulate R2′ in the baseline state, in order to assess its use as an alternative calibration method.
There were three primary findings of this study: 1) The new calibration method based on R2′ worked reasonably well, although not as well as the ideal hypercapnia method; 2) The hyperoxia calibration method was significantly worse because baseline haematocrit and OEF must be assumed, and variability of these physiological parameters has a significant effect on the measurements; and 3) the venous blood volume change with activation is an important confounding variable for all of the methods, with the hypercapnia method being the most robust when this is uncertain. The results for each of the calibration methods tested are discussed in more detail below.
Hypercapnia Calibration
Simulation of hypercapnia calibration revealed that this method provides an accurate calibration for baseline physiological variability (Fig. 2a,d). The broadening of the line due to physiological variability shows only very weak dependence on the change in CBF. Uncertainty in the value of α causes additional deviation of the lines of CMRO2 that appears to increase with increasing CMRO2 change (Fig. 3a,d). We also tested the resulting errors if the assumption of no CMRO2 change with hypercapnia is wrong. When a reduction in CMRO2 during hypercapnia a shift in the lines of CMRO2 was observed (Fig. 4). This could result in an inaccurate measurement of CMRO2, for example when f=1.6 a 10% CMRO2 change when r=0.85 would appear similar to a 20% change when r=1.
Hyperoxia Calibration
Simulations of hyperoxia calibration, when values for baseline [Hb] and E0 are assumed, predict poor performance of this method for normalising the BOLD signal change (Fig. 2b,e). Further investigation revealed that when more information is known, such as [Hb] (Fig. 5a,d) or E0 (Fig. 5b,e), then uncertainty is reduced. When both variables are known then uncertainty is reduced to the same level as hypercapnia calibration (Fig. 5c,f). This uncertainty is minimised when the combination of CBF and CMRO2 changes result in a net zero BOLD signal (as is also the case for R2′ calibration). This effectively means that the venous oxygen saturation is unchanged between the rest and activated states and hence the physiological variability does not have any effect.
The origin of the observed poor performance of hyperoxia calibrated BOLD can be determined by considering Eq. (6). The change in deoxyhaemoglobin concentration due to hyperoxia ([dHb]/[dHb]0) is determined by the decrease in concentration Δ[dHb] and the baseline concentration [dHb]0. The former is determined by [Hb], as this adjusts the balance of oxygen carried by haemoglobin and plasma, and is independent of E0, whereas the latter is determined by E0 at normoxia and is independent of [Hb]. Accurate values of [Hb] and E0 are therefore required as [dHb]/[dHb]0 is used to convert measurements of the BOLD signal change during hyperoxia to Mho (Eq. (4)). This conversion is provided by the denominator of Eq. (4) producing a scaling of the BOLD signal change equivalent to one over the denominator. For the extremes of the [Hb] and E0 ranges tested here, and a fixed ΔPaO2 of 310 mmHg, this scaling value is in the range 5.9 to 15.6 (assuming β=1.3). In contrast, the approach taken by Mark et al. (Mark et al., 2011) will always scale the hyperoxic BOLD signal change by 7.9 for the same fixed ΔPaO2. Whilst the extremes of the [Hb] and E0 ranges are unlikely to simultaneously exist this analysis illustrates the sensitivity of hyperoxia calibration to assumed values for these parameters, and explains the reduced variability encountered when both are known (Fig. 5c,f). Therefore, hyperoxia calibration may be improved by acquiring more accurate information about baseline physiology. This could be achieved by making direct MR measurements of deoxyhaemoglobin concentration in the sagittal sinus as an approximation for E0 (Jain et al., 2011; Lu et al., 2011) or by measuring the haematocrit from a venous blood sample.
It is unclear whether this expected variability has been observed in the literature, largely due to the limited number of studies having undertaken this calibration. A large spread in the calibration parameter Mho has been observed (Goodwin et al., 2009), which would result from the variability we see, but it is unclear whether the uncontrolled manual hyperoxia challenge employed in this study may have contributed to this effect. Studies using controlled hyperoxic challenges have suggested that the variability in measurements of CMRO2 is lower for hyperoxia calibration when compared with hypercapnia calibration (Mark et al., 2011). The results of our simulations conflict with this observation.
Hyperoxia calibration also shows greater sensitivity to flow-volume coupling than hypercapnia calibration (Fig. 3b,e). The resulting shift in the lines of CMRO2 could result in a large error in the magnitude of the CMRO2 change if the assumed flow-volume coupling does not match the physiological relationship.
R2′ Calibration
The concept of using R2′ to calibrate the BOLD response is based on this parameter's well known dependence on haematocrit, OEF and blood volume (Yablonskiy and Haacke, 1994). Currently this effect is exploited by the qBOLD method to measure baseline blood oxygenation and volume (He and Yablonskiy, 2006). However, to date it has not been used within a calibrated BOLD framework to measure changes in CMRO2 during activation. At first glance it appears that R2′ would be a poor choice for calibration because the BOLD response depends in part on signal changes that would not be captured by R2′. In a gradient-echo based BOLD experiment the signal change is due largely to changes in the transverse relaxation rate R2*, which is taken to be a sum of processes that cannot be reversed by a spin-echo (R2) and processes that can be reversed (R2′). Motional narrowing due to diffusion of spins around sources of magnetic field heterogeneity means that a good part of the intravascular signal changes and part of the extravascular signal change around the smallest vessels cannot be fully refocused by a spin-echo, and so should not contribute to R2′. In addition, volume exchange effects as blood vessels expand also contribute to the BOLD effect, but are not directly related to R2′. Nevertheless, our simulations indicate that R2′ in the baseline state captures much of the physiological variability of the baseline state that does affect the BOLD response. The reason it works as well as it does is probably that R2′ essentially reflects the amount of deoxyhemoglobin in the baseline state, and the other factors affecting the BOLD response for the most part tend to scale with total deoxyhemoglobin.
The main weakness of this calibration method is its sensitivity to magnetic field inhomogeneity. Investigation of a 20 Hz frequency difference across a voxel in one dimension showed that this causes a shift in the lines of CMRO2 that increases with changes in CBF (Fig. 6). The magnitude of this shift is very similar to that caused by CMRO2 changes during hypercapnia calibration. For example, a 10% CMRO2 change when Δω=20 Hz leads to the same R2′ as a 20% change when Δω=0 (f=1.6).
This magnitude of magnetic field inhomogeneity is likely for regions of the brain that are not close to air-tissue interfaces. For regions of the brain closer to the surface, where Δω is larger, measurements of R2′ will need to be corrected for residual field gradients (Yablonskiy, 1998) or their effect minimised by the acquisition technique (Christen et al., 2010). Experiments using the qBOLD technique have shown that this effect can be corrected enabling R2′ calibrated BOLD to become a practical alternative to hypercapna or hyperoxia (He and Yablonskiy, 2006). The major benefit of this alternative method is a reduction in the complexity of the experimental protocol. Equipment to perform a respiratory challenge is not required, saving time and permitting the calibration scan to be based purely on endogenous contrast.
For this approach to yield an accurate calibration factor it is assumed that deoxyhaemoglobin is the dominant source of paramagnetism in the brain. Other possible sources of iron in the brain include ferritin, transferrin, neuromelanin and haemosiderin (Stankiewicz et al., 2007). However, the sensitivity of R2′ to these sources is also dependent on the geometry of the iron deposition. This effect is maximised in the static dephasing regime where the diffusion length of protons around the susceptibility inclusion is much shorter than the dimension of the inclusion itself. This dimension is approximately equivalent to a cylinder with a radius of 7 μm, but this R2′ contrast falls away rapidly with radius. (Boxerman et al., 1995). Very small scale inclusions, such as ferritin and transferrin, do not produce R2′ contrast and appear as a pure R2 effect. There are two main conditions in which elevated values of R2′ are measured in the brain; Parkinson's disease and brain haemorrhage. In Parkinson's disease deposits of iron in the substantia nigra, consisting of neuromelanin granules and iron filled Lewy bodies (Castellani et al., 2000), have been shown to result in elevated R2′ measurements (Ordidge et al., 1994). Lewy bodies have a diameter of approximately 8 μm and are likely to exhibit an R2′ effect. Brain haemorrhage causes bleeding into the tissues of the brain and production of haemosiderin, and has also been shown to increase R2′ (Wismer et al., 1988). If R2′ calibration is to be performed in patients with either of these conditions then care must be taken to avoid affected areas of the brain.
Estimating CMRO2 changes
A measurement of CMRO2 change is the ultimate aim of calibrated BOLD, converting information contained in δs, B and f into a measure of r. In the traditional approach the Davis model plays a dual role, first as a way to convert measured hypercapnia responses into a calibration factor, and second as a way to use that factor in combination with measured responses to activation to estimate the CMRO2 change. In the current analysis we have essentially broken the link between the two steps. With this approach we can consider any potential method for calibrating the BOLD signal, and determine an appropriate form of h(f,r) in Eq. (2) through simulations of both the calibration experiment and the activation experiment with the detailed BOLD model. That is, h(f,r) is given implicitly through the detailed model by the curves in the δs/B versus f plane (e.g., Fig. 2a and 2c for the hypercapnia and R2′ methods, respectively). An appropriate lookup table, or parameterization of the curves in the Figures, would allow calculation of r for a given set of measurements, effectively defining h(f,r). That is, although the Davis model was used to define the calibration experiment for hypercapnia, this was simply used as a particular recipe for calculating a value of B, and the detailed model was used to simulate that recipe and provide curves of how the measured signals vary with different CMRO2 changes. In this way the detailed model provides a form for h(f,r) that is appropriate for the defined method of calculating B. If that method changed (e.g., if the hypercapnia responses were used to calculate M with different values of α and β), then the detailed simulations would provide a shifted set of curves defining a new form of h(f,r) appropriate for the new definition of the method for calculating B.
Conclusion
The simulations performed in this study enable the potential strengths and weaknesses of BOLD calibration methods to be investigated. In addition, a new calibration method is proposed that does not require a respiratory challenge. Hypercapnia calibration is shown to be robust even when isometabolism during hypercapnia is not assumed and the flow-volume coupling is altered. Simulations of hyperoxia calibration reveal hitherto unexplored weaknesses due to the assumptions that must be made in the model of oxygen transport used to estimate the change in venous blood oxygenation due to hyperoxia. This suggests further experimental validation of this method is required before it may be used routinely. Examination of R2′ as a new calibration method show that such a technique is promising. Whilst the uncertainty in the measurement of CMRO2 may be increased when compared with hypercapnia, this method is more generally applicable to the population at large as it does not require gases to be administered. However, further work is needed to develop robust acquisition methods that allow correction for large scale field inhomogeneity effects.
Additionally, in the absence of measurements of CBF, a measurement of R2′ may also be useful as a normalisation procedure to reduce intersubject variability in the BOLD response. These approaches compare the stimulus evoked BOLD response with measurements of the BOLD response to a hypercapnia challenge (Biswal et al., 2007), or with a single aspect of baseline physiology such as CBF (Liau and Liu, 2009) or baseline blood oxygenation (Lu et al., 2008). A measurement of R2′, however, is sensitive to multiple sources of physiological variability through its sensitivity to blood volume, blood oxygenation and haematocrit and may account for a greater degree of intersubject variability than traditional methods.
Acknowledgements
We would like to thank Aaron Simon, Farshad Moradi and David Dubowitz for helpful discussions regarding this work. This work was supported by funding from NIH/NINDS grant NS-036722.
Appendix
Simulations of the effect of changes in CBF, CMRO2 and baseline physiology were performed using a previously reported detailed BOLD signal model (Griffeth and Buxton, 2011). Constants required for this model are detailed in Table 1. This model was further extended to enable R2′ in the baseline resting state to be simulated. Taking Eq. (8) as a starting point, we can expand these relations to include multiple signal compartments for both gradient echo (GE) and spin echo (SE) pulse sequences.
| (A1a) |
| (A1b) |
Here V, S(0), R2* and R2 are the volume fraction, proton density and transverse relaxation rates for their respective compartments indicated by subscripts; intravascular (I), extravascular (E), arterial (A), capillary (C) and venous (V). Parameters with subscript 0 reflect the baseline resting value. Monoexponential decay of each compartment is assumed with echo time TE. The extravascular transverse relaxation rate for both GE and SE signals is modelled as a baseline rate (R2,0) plus an additive term ( or R2E). This term reflects dephasing of the signal due to mesoscopic magnetic field inhomogeneity for GE and incomplete refocussing of this dephasing due to diffusional narrowing in the case of the SE. To complete the model, expressions for intra- and extravascular R2 and R2* are required along with the definition of F(TE), the signal attenuation due to magnetic field inhomogeneity. Intravascular signal was modelled using measurements of the dependency of R2* on haematocrit and blood oxygenation saturation (Y) (Zhao et al., 2007).
| (A2) |
In order to further generalise the detailed signal model, the dependency of A* and C* on haematocrit (Hct) was approximated by linearly fitting to data acquired at 3.0 T (Zhao et al., 2007; Griffeth and Buxton, 2011).
| (A3a) |
| (A3b) |
Similarly R2 was modelled based on measurements of the dependency of blood R2 on oxygenation and haematocrit (Zhao et al., 2007).
| (A4) |
| (A5a) |
| (A5b) |
These measurements were acquired using a single spin echo pulse sequence, stepped through a range of echo time values, and hence are consistent with the short time regime of transverse signal decay (Yablonskiy and Haacke, 1994). Extravascular R2* was modelled using the results of Monte Carlo simulations (Ogawa et al., 1993),
| (A6a) |
| (A6b) |
where the constants and scale for large and small vessels, respectively, and ω0 is the proton Larmor frequency. Vessels are categorised as being large with diameters in the range 16 – 200 μm (arterioles and venules) or small (capillaries) with a diameter of 5 μm (Ogawa et al., 1993). Fully oxygenated blood and tissue do not have the same susceptibility and this is reflected by the blood oxygen saturation offset Yoff, i.e. the point at which fully oxygenated blood and tissue have the same susceptibility (Spees et al., 2001). The results of Monte Carlo simulations for a single spin echo pulse sequence were used to simulate the extravascular R2 (Uludağ et al., 2009). These simulations are consistent with the blood R2 measurements of Zhao et al. and with acquisition in the short echo time regime (Yablonskiy and Haacke, 1994). The large vessel relation was derived from simulations of 16 μm diameter vessels (arterioles and venules) and the small vessel relation from vessels (capillaries) of 5 μm diameter.
| (A7a) |
| (A7b) |
Finally, the signal attenuation of the gradient echo data due to large scale magnetic field inhomogeneity can also be modeled (Yablonskiy, 1998),
| (A8) |
where Δω is the frequency difference across the voxel. The constants detailed in these equations are listed in Table 1.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- An H, Lin W. Impact of intravascular signal on quantitative measures of cerebral oxygen extraction and blood volume under normo- and hypercapnic conditions using an asymmetric spin echo approach. Magn. Reson. Med. 2003;50:708–716. doi: 10.1002/mrm.10576. [DOI] [PubMed] [Google Scholar]
- Biswal BB, Kannurpatti SS, Rypma B. Hemodynamic scaling of fMRI-BOLD signal: validation of low-frequency spectral amplitude as a scalability factor. Magn Reson Imaging. 2007;25:1358–1369. doi: 10.1016/j.mri.2007.03.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boxerman JL, Hamberg LM, Rosen BR, Weisskoff RM. MR contrast due to intravascular magnetic susceptibility perturbations. Magn. Reson. Med. 1995;34:555–566. doi: 10.1002/mrm.1910340412. [DOI] [PubMed] [Google Scholar]
- Castellani RJ, Siedlak SL, Perry G, Smith MA. Sequestration of iron by Lewy bodies in Parkinson's disease. Acta Neuropathol. 2000;100:111–114. doi: 10.1007/s004010050001. [DOI] [PubMed] [Google Scholar]
- Chen JJ, Pike GB. BOLD-specific cerebral blood volume and blood flow changes during neuronal activation in humans. NMR Biomed. 2009;22:1054–1062. doi: 10.1002/nbm.1411. [DOI] [PubMed] [Google Scholar]
- Chiarelli PA, Bulte DP, Wise R, Gallichan D, Jezzard P. A calibration method for quantitative BOLD fMRI based on hyperoxia. Neuroimage. 2007;37:808–820. doi: 10.1016/j.neuroimage.2007.05.033. [DOI] [PubMed] [Google Scholar]
- Christen T, Lemasson B, Pannetier N, Farion R, Segebarth C, Rémy C, Barbier EL. Evaluation of a quantitative blood oxygenation level-dependent (qBOLD) approach to map local blood oxygen saturation. NMR Biomed. 2010;24:393–403. doi: 10.1002/nbm.1603. [DOI] [PubMed] [Google Scholar]
- Davis TL, Kwong KK, Weisskoff RM, Rosen BR. Calibrated functional MRI: mapping the dynamics of oxidative metabolism. Proc. Natl. Acad. Sci. U.S.A. 1998;95:1834–1839. doi: 10.1073/pnas.95.4.1834. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goodwin JA, Vidyasagar R, Balanos GM, Bulte D, Parkes LM. Quantitative fMRI using hyperoxia calibration: Reproducibility during a cognitive Stroop task. Neuroimage. 2009;47:573–580. doi: 10.1016/j.neuroimage.2009.04.064. [DOI] [PubMed] [Google Scholar]
- Griffeth VEM, Perthen JE, Buxton RB. Prospects for quantitative fMRI: investigating the effects of caffeine on baseline oxygen metabolism and the response to a visual stimulus in humans. Neuroimage. 2011;57:809–816. doi: 10.1016/j.neuroimage.2011.04.064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Griffeth VEM, Buxton RB. A theoretical framework for estimating cerebral oxygen metabolism changes using the calibrated-BOLD method: Modeling the effects of blood volume distribution, hematocrit, oxygen extraction fraction, and tissue signal properties on the BOLD signal. Neuroimage. 2011;58:198–212. doi: 10.1016/j.neuroimage.2011.05.077. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grubb RL, Raichle ME, Eichling JO, Ter-Pogossian MM. The effects of changes in PaCO2 on cerebral blood volume, blood flow, and vascular mean transit time. Stroke. 1974;5:630–639. doi: 10.1161/01.str.5.5.630. [DOI] [PubMed] [Google Scholar]
- He X, Yablonskiy DA. Quantitative BOLD: Mapping of human cerebral deoxygenated blood volume and oxygen extraction fraction: Default state. Magn. Reson. Med. 2006;57:115–126. doi: 10.1002/mrm.21108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoge RD, Atkinson J, Gill B, Crelier GR, Marrett S, Pike GB. Investigation of BOLD signal dependence on cerebral blood flow and oxygen consumption: the deoxyhemoglobin dilution model. Magn. Reson. Med. 1999;42:849–863. doi: 10.1002/(sici)1522-2594(199911)42:5<849::aid-mrm4>3.0.co;2-z. [DOI] [PubMed] [Google Scholar]
- Jain V, Langham MC, Floyd TF, Jain G, Magland JF, Wehrli FW. Rapid magnetic resonance measurement of global cerebral metabolic rate of oxygen consumption in humans during rest and hypercapnia. J. Cereb. Blood Flow Metab. 2011;31:1504–1512. doi: 10.1038/jcbfm.2011.34. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liau J, Liu TT. Inter-subject variability in hypercapnic normalization of the BOLD fMRI response. Neuroimage. 2009;45:420–430. doi: 10.1016/j.neuroimage.2008.11.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lu H, Zhao C, Ge Y, Lewis-Amezcua K. Baseline blood oxygenation modulates response amplitude: Physiologic basis for intersubject variations in functional MRI signals. Magn. Reson. Med. 2008;60:364–372. doi: 10.1002/mrm.21686. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lu H, Xu F, Grgac K, Liu P, Qin Q, van Zijl P. Calibration and validation of TRUST MRI for the estimation of cerebral blood oxygenation. Magn. Reson. Med. 2011 doi: 10.1002/mrm.22970. In Press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marchal G, Rioux P, Petit-Taboué MC, Sette G, Travère JM, Le Poec C, Courtheoux P, Derlon JM, Baron JC. Regional cerebral oxygen consumption, blood flow, and blood volume in healthy human aging. Arch. Neurol. 1992;49:1013–1020. doi: 10.1001/archneur.1992.00530340029014. [DOI] [PubMed] [Google Scholar]
- Mark CI, Fisher JA, Pike GB. Improved fMRI calibration: precisely controlled hyperoxic versus hypercapnic stimuli. Neuroimage. 2011;54:1102–1111. doi: 10.1016/j.neuroimage.2010.08.070. [DOI] [PubMed] [Google Scholar]
- McPhee SJ, Hammer GD. Pathophysiology of Disease An Introduction to Clinical Medicine. Sixth Edition Lange Medical Books; 2009. [Google Scholar]
- Moore R, Berlowitz D, Pretto J, Brazzale D, Denehy L, Jackson B, McDonald C. Acute effects of hyperoxia on resting pattern of ventilation and dyspnoea in COPD. Respirology. 2009;14:545–550. doi: 10.1111/j.1440-1843.2009.01509.x. [DOI] [PubMed] [Google Scholar]
- Ogawa S, Menon RS, Tank DW, Kim S-G, Merkle H, Ellermann JM, Ugurbil K. Functional brain mapping by blood oxygenation level-dependent contrast magnetic resonance imaging. A comparison of signal characteristics with a biophysical model. Biophys. J. 1993;64:803–812. doi: 10.1016/S0006-3495(93)81441-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ordidge RJ, Gorell JM, Deniau JC, Knight RA, Helpern JA. Assessment of relative brain iron concentrations using T2-weighted and T2*-weighted MRI at 3 Tesla. Magn. Reson. Med. 1994;32:335–341. doi: 10.1002/mrm.1910320309. [DOI] [PubMed] [Google Scholar]
- Perlmutter JS, Powers WJ, Herscovitch P, Fox PT, Raichle ME. Regional asymmetries of cerebral blood flow, blood volume, and oxygen utilization and extraction in normal subjects. J. Cereb. Blood Flow Metab. 1987;7:64–67. doi: 10.1038/jcbfm.1987.9. [DOI] [PubMed] [Google Scholar]
- Perthen JE, Lansing AE, Liau J, Liu TT, Buxton RB. Caffeine-induced uncoupling of cerebral blood flow and oxygen metabolism: a calibrated BOLD fMRI study. Neuroimage. 2008;40:237–247. doi: 10.1016/j.neuroimage.2007.10.049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roland PE, Eriksson L, Stone-Elander S, Widen L. Does mental activity change the oxidative metabolism of the brain? J. Neurosci. 1987;7:2373–2389. [PMC free article] [PubMed] [Google Scholar]
- Severinghaus JW. Simple, accurate equations for human blood O2 dissociation computations. J Appl Physiol. 1979;46:599–602. doi: 10.1152/jappl.1979.46.3.599. [DOI] [PubMed] [Google Scholar]
- Sicard KM, Duong TQ. Effects of hypoxia, hyperoxia, and hypercapnia on baseline and stimulus-evoked BOLD, CBF, and CMRO2 in spontaneously breathing animals. Neuroimage. 2005;25:850–858. doi: 10.1016/j.neuroimage.2004.12.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spees WM, Yablonskiy DA, Oswood MC, Ackerman JJ. Water proton MR properties of human blood at 1.5 Tesla: magnetic susceptibility, T1, T2, T2*, and non-Lorentzian signal behavior. Magn. Reson. Med. 2001;45:533–542. doi: 10.1002/mrm.1072. [DOI] [PubMed] [Google Scholar]
- Stankiewicz J, Panter SS, Neema M, Arora A, Batt CE, Bakshi R. Iron in chronic brain disorders: Imaging and neurotherapeutic implications. Neurotherapeutics. 2007;4:371–386. doi: 10.1016/j.nurt.2007.05.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Uludağ K, Müller-Bierl B, Uğurbil K. An integrative model for neuronal activity-induced signal changes for gradient and spin echo functional imaging. Neuroimage. 2009;48:150–165. doi: 10.1016/j.neuroimage.2009.05.051. [DOI] [PubMed] [Google Scholar]
- Wismer GL, Buxton RB, Rosen BR, Fisel CR, Oot RF, Brady TJ, Davis KR. Susceptibility induced MR line broadening: applications to brain iron mapping. J Comput Assist Tomogr. 1988;12:259–265. doi: 10.1097/00004728-198803000-00014. [DOI] [PubMed] [Google Scholar]
- Xu F, Uh J, Brier MR, Hart J, Yezhuvath US, Gu H, Yang Y, Lu H. The influence of carbon dioxide on brain activity and metabolism in conscious humans. J. Cereb. Blood Flow Metab. 2010;31:58–67. doi: 10.1038/jcbfm.2010.153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yablonskiy DA. Quantitation of intrinsic magnetic susceptibility-related effects in a tissue matrix. Phantom study. Magn. Reson. Med. 1998;39:417–428. doi: 10.1002/mrm.1910390312. [DOI] [PubMed] [Google Scholar]
- Yablonskiy DA, Haacke EM. Theory of NMR signal behavior in magnetically inhomogeneous tissues: the static dephasing regime. Magn. Reson. Med. 1994;32:749–763. doi: 10.1002/mrm.1910320610. [DOI] [PubMed] [Google Scholar]
- Zhao JM, Clingman CS, Närväinen MJ, Kauppinen RA, van Zijl PCM. Oxygenation and hematocrit dependence of transverse relaxation rates of blood at 3T. Magn. Reson. Med. 2007;58:592–597. doi: 10.1002/mrm.21342. [DOI] [PubMed] [Google Scholar]