Biomedical Tissue Phantoms with Controlled Geometric and Optical Properties for Raman Spectroscopy and Tomography

Abstract

To support the translation of Raman spectroscopy into clinical applications, synthetic models are needed to accurately test, optimize and validate prototype fiber optic instrumentation. Synthetic models (also called tissue phantoms) are widely used for developing and testing optical instrumentation for diffuse reflectance, fluorescence, and Raman spectroscopies. While existing tissue phantoms accurately model tissue optical scattering and absorption, they do not typically model the anatomic shapes and chemical composition of tissue. Because Raman spectroscopy is sensitive to molecular composition, Raman tissue phantoms should also approximate the bulk tissue composition. We describe the fabrication and characterization of tissue phantoms for Raman tomography and spectroscopy. These phantoms have controlled chemical and optical properties, and also multilayer morphologies which approximate the appropriate anatomic shapes. Tissue phantoms were fabricated to support on-going Raman studies by simulating human wrist and rat leg. Surface meshes (triangle patch models) were generated from computed tomography (CT) images of a human arm and rat leg. Rapid prototyping was used to print mold templates with complex geometric patterns. Plastic casting techniques used for movie special effects were adapted to fabricate molds from the rapid prototypes, and finally to cast multilayer gelatin tissue phantoms. The gelatin base was enriched with additives to model the approximate chemistry and optical properties of individual tissue layers. Additional studies were performed to determine optimal casting conditions, phantom stability, layer delamination and chemical diffusion between layers. Recovery of diffuse reflectance and Raman spectra in tissue phantoms varied with probe placement. These phantoms enable optimization of probe placement for human or rat studies. These multilayer tissue phantoms with complex geometries are shown to be stable, with minimal layer delamination and chemical diffusion.

Introduction

Spatially-offset Raman spectroscopy (SORS) adapts the principles of diffuse optical spectroscopy for Raman measurements of tissues and other highly turbid materials.^{1, 2} In SORS, the excitation source and light collection optical fibers are separated. This separation distance enhances the collection of subsurface Raman features relative to fluorescence arising at the surface.^{3, 4} Biomedical applications of SORS include transcutaneous Raman spectroscopy for non-invasive bone chemistry measurements.^5–8 Further development of optical probes for in vivo biomedical applications requires improved analytical standards. Standards are needed to distinguish between the performance of different probe designs, to determine which probe designs are most robust with respect to the varied tissue shapes of different specimens, and to measure the reproducibility and accuracy of deep spectroscopic measurements.

Tissue phantoms are synthetic models of tissue which can serve as analytical standards to link experimental results and theoretical models. Tissue phantoms have been used to calibrate and validate prototype clinical instruments and to optimize the sampling volume of novel probes.^9–16 Commercially available tissue phantoms are commonly made of hard plastics, and are used to calibrate and validate readings from clinical instruments for dual energy x-ray absorptiometry (DEXA), magnetic resonance imaging (MRI), computed tomography (CT) and ultrasound imaging. Tissue phantoms for biomedical optical spectroscopy are used to optimize probes. In addition to phantoms for Raman spectroscopy, phantoms have been used extensively for diffuse reflectance, photoacoustic imaging, optical coherence tomography (OCT), and near-infrared fluorescence.^{1, 2, 5, 7, 9–11, 17–21}

Techniques used to create tissue phantoms are as varied as their applications. A comprehensive review by Patterson and Pogue highlights current technology and challenges in the fabrication and use of tissue phantoms.¹⁷ Tissue phantoms for optical spectroscopy are typically either made with representative materials and optical properties, or controlled geometries. Most semi-solid or solid phantoms are made with simple geometries (rectangular or cylindrical) and include one or more planar layers.^{10, 18–24} The chemical and optical properties of phantoms with simple geometries can be controlled tightly. Multilayer phantoms with controlled complex geometries have previously required that some layers include plastics to hold their shape or isolate layers, however plastics have strong Raman features that are not present in tissues.^{22, 25–27}

A commonly reported system for phantoms is a hydrogel/lipid emulsion combination, which is used to make homogeneous phantoms with reproducible scattering and absorption coefficients.^{25, 27–29} Hydrogels such as gelatin or agarose can add rigidity, lipid emulsions add scattering, and other molecular species add absorption, fluorescence, and Raman scattering features. One commonly reported brand of lipid emulsion is Intralipid, though several other brands have also been used to simulate the optical scattering properties of tissue.^30–34 The absorption coefficient, scattering coefficient and anisotropy values of Intralipid have been reported.^{30, 31, 34} Intralipid has recently been shown to be stable for long periods of time and to have little batch to batch variability in optical scattering properties.³³ The primary factor limiting the lifetime of hydrogel phantoms is bacterial growth. Preservative agents such as sodium azide and penicillin, storage in an inert atmosphere, or storage at 4–5° C in an airtight container can extend the longevity of the phantom. If properly stored and preserved, phantoms can be used for days to weeks.¹⁷

Our first transcutaneous Raman studies underscored the need to develop experimental models that would not only account for tissue optical properties, but also the chemistry and complex geometry of a human or rat limb. Because Raman spectroscopy is sensitive to a material’s chemical composition, Raman tissue phantoms must also approximate the tissue chemistry. Earlier Raman tissue phantoms consisted of a single Teflon sphere suspended in an agar gel. Intralipid, a lipid emulsion normally used for parental nutrition, was added into the agar gel in varying amounts to simulate the optical scattering of tissue.^{9, 35, 36} While these tissue phantoms accounted for optical scattering, they did not model the chemistry of bone tissue, and thus the Raman spectral features. Bone consists primarily of a carbonated apatite mineral and collagen protein.³⁷ The most widely used Raman features of bone mineral appear at 960 cm⁻¹ and 1070 cm⁻¹ corresponding to the phosphate ν₁ symmetric stretch and carbonate ν₁ symmetric stretch, respectively.

Another important factor in deep-tissue Raman spectroscopy is the presence of multiple tissue layers with different anatomical shapes and optical properties.¹² Simple phantom geometries such as spheres or cubes do not adequately model tissue shape and do not accurately model the collection efficiency of subsurface Raman spectra or images. Bones and other tissues do not have simple geometries. The asymmetric shape of the distal radius bone is a clear example of anatomic complexity, but even the long bones of the body are not cylindrical. The complicated mesoscale geometry of tissues should be reproduced by phantoms in addition to the optical properties.

Thus, Raman tissue phantoms should approximate the optical scattering and absorption properties, geometry, and chemical composition. Multilayer tissue phantoms that control these properties have not previously been reported. The goal of this study was to fabricate Raman tissue phantoms with three key features: controlled anatomically realistic geometry, controlled optical properties, and spectral features approximating the tissues under study. These phantoms enable investigation of the effects of mesoscale tissue morphology, light scattering and chemical composition on recovering subsurface Raman spectra or tomographic images.

Previous studies have demonstrated the stability of gelatin phantoms and control over the optical properties. In particular, De Grand et al. described the optical properties of gelatin phantoms to be stable from 600 to 1000 nm for at least 2 weeks.¹⁸ They also noted that diffusion of hemoglobin should be considered for phantoms used over more than 2 weeks. However, multilayer gelatin phantoms have typically used thin layers of plastic to isolate the planar gelatin layers and prevent chemical diffusion. This approach of isolating layers is not feasible for our studies because we are using complicated geometric shapes. Some other studies with multilayer gelatin phantoms have not used isolating plastic layers, but chemical diffusion across connected gelatin layers has not yet been well characterized. We studied diffusion of small organic dyes across planar phantom layers to determine the diffusion properties. White-light diffuse reflectance imaging measured the diffusion of food coloring through the layers to estimate the degradation of geometric features with time and the maximum achievable resolution inherent in the casting process. To better understand the long-term stability of these phantoms, we also examined the effects of casting conditions and storage temperature on dehydration and integrity (delamination). Finally, we present preliminary examples using phantoms with anatomic morphology and controlled optical properties for both laser reflectance imaging and Raman spectroscopy. Although this study focused on using these tissue phantoms for Raman spectroscopy, we expect that the phantoms will also be useful as synthetic models for diffuse reflectance, fluorescence, and tomography.

Methods

Computed tomography (CT) scans of the rat leg

An adult rat was scanned using a micro-computed tomography (µCT) instrument, and the images were reconstructed at a 45 micron voxel resolution. The rat was previously sacrificed as part of other experiments that were performed with approval of the University Committee on the Use and Care of Animals (UCUCA) at the University of Michigan. A commercially available µCT system was used (eXplore Locus SP, GE Healthcare Pre-Clinical Imaging, London, ON, Canada).

Computed tomography (CT) scans of the human arm

Molds for creating Raman tissue phantoms were generated from high resolution CT scans of cadaveric human limbs. Cadaveric human limbs were obtained from the Anatomical Donations program at the University of Michigan Medical School and imaged by clinical CT as part of another ongoing study. Cadavers were imaged instead of living patients to avoid exposing living patients to unnecessary doses of ionizing radiation. Prior to CT imaging, frozen limbs were thawed in a 4°C refrigerator overnight. Limbs were kept in a plastic bag during CT imaging to prevent contamination of the clinical high-resolution computed tomography instrument. CT images were collected in the sagittal, coronal and transverse planes using a high-resolution 64 slice clinical CT instrument (Siemens Somatom Sensation Cardiac 64, Siemens Healthcare, Germany). The imaging parameters were: 250 mm field of view, 0.6 mm slice thickness, 0.55 mm pitch, 64×0.6mm acq., 512×512 matrix.

Generation of 3D renderings in silico and recovery of tissue surface meshes

Surfaces defining the boundaries between the different tissue types were derived from the volumetric CT images (Mimics, Materialise, Leuven, Belgium). CT images were imported into Mimics and a region of interest within the image was selected to encompass the entire limb. Figure 1 shows the in silico rendering of a human arm, as seen in Mimics software. Thresholding, morphological image analysis techniques (erosion, dilation, opening, and closing) and Boolean logic tools (intersection and union) were used to define subvolumes of tissue components including cancellous bone, cortical bone, skin, fat and muscle. Segmentation operations are commonly used for isolating tissues in volumetric medical data.³⁸ Segmentation is also described in more detail in the tutorials included with the Mimics software.

Fig. 1.

Cross-sectional view of CT data of a human distal radius with 3D rendering of surface boundaries in the Mimics software.

Individual surface meshes were generated for each tissue component. Surface meshes were exported, using the .STL file format, to create virtual molds appropriate for multilayer casting of the tissue phantoms (3Matic and Magics, Materialise, Leuven, Belgium). Surface mesh models were also used to render photorealistic 3D images and videos (3D Studio Max, Autodesk Inc., San Rafael, CA USA). Tetrahedral finite element volume meshes were generated from the tissue components, and used as input meshes in NIRFAST software package for Raman tomographic reconstruction and finite element modeling of light propagation.^{39, 40}

Additional 3D figures have been included as supplemental material, available from the journal web site. Supplemental Figures 1 and 3 show the two-layer human and rat models, while Figures 2 and 4 show the models of the corresponding phantom molds, and Figure 5 shows detailed color photographs of the phantoms. These 3D PDF figures can be directly manipulated (rotated, scaled, and cutplanes can be applied), and both the sizes of features and the distances between them can be measured. The 3D figures can be viewed using Adobe Acrobat Reader.

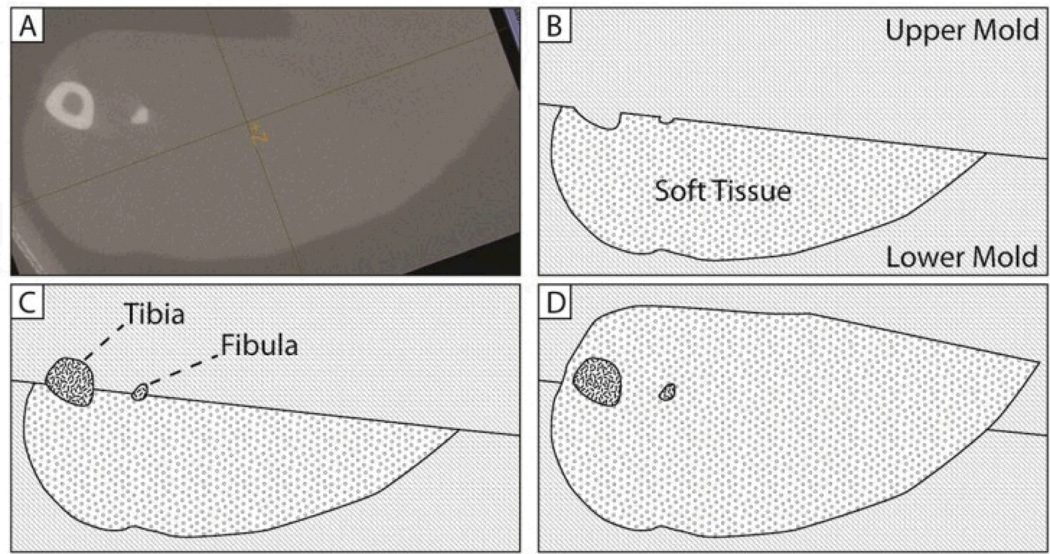
Fig. 2.

Tissue phantom molding process. Phantoms are cast in four steps, shown here as a cross-sectional view through a point near the mid-diaphysis. From an x-ray microCT scan (shown in A) three-dimensional surface meshes corresponding to bone and soft tissue are generated. Molds are rapid-prototyped and then replicated into silicone rubber. Tissue phantoms are cast in several stages using the silicone rubber molds. In B, the lower margin of soft tissue is cast. As shown in C, the upper mold is then exchanged to cast a second layer simulating bone. Finally, as shown in D, a third upper mold is used to fill in the remaining soft tissue.

Fig. 4.

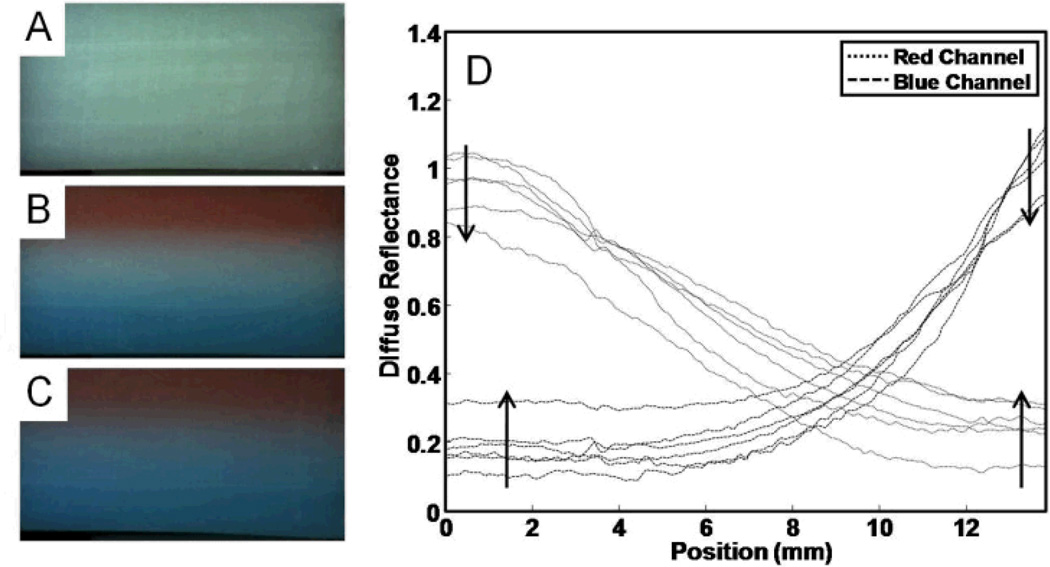
Diffusion of red and blue food dyes through layered planar phantoms. In A, the reference phantom is shown with no added dye. In B, the dye-containing phantom is shown on day 2. In C, the dye-containing phantom is shown on day 7. These images show the red dye layer at the top, the middle has no added coloring, and the bottom layer has blue dye added. In D the diffuse reflectance is shown for the 6 measurement points (at days 1, 2, 3, 4, 6, and 7). The independent axis (position) is shown corresponding to a vertical cross section through the images. Arrows show the trends with time for the series of traces.

Fig. 5.

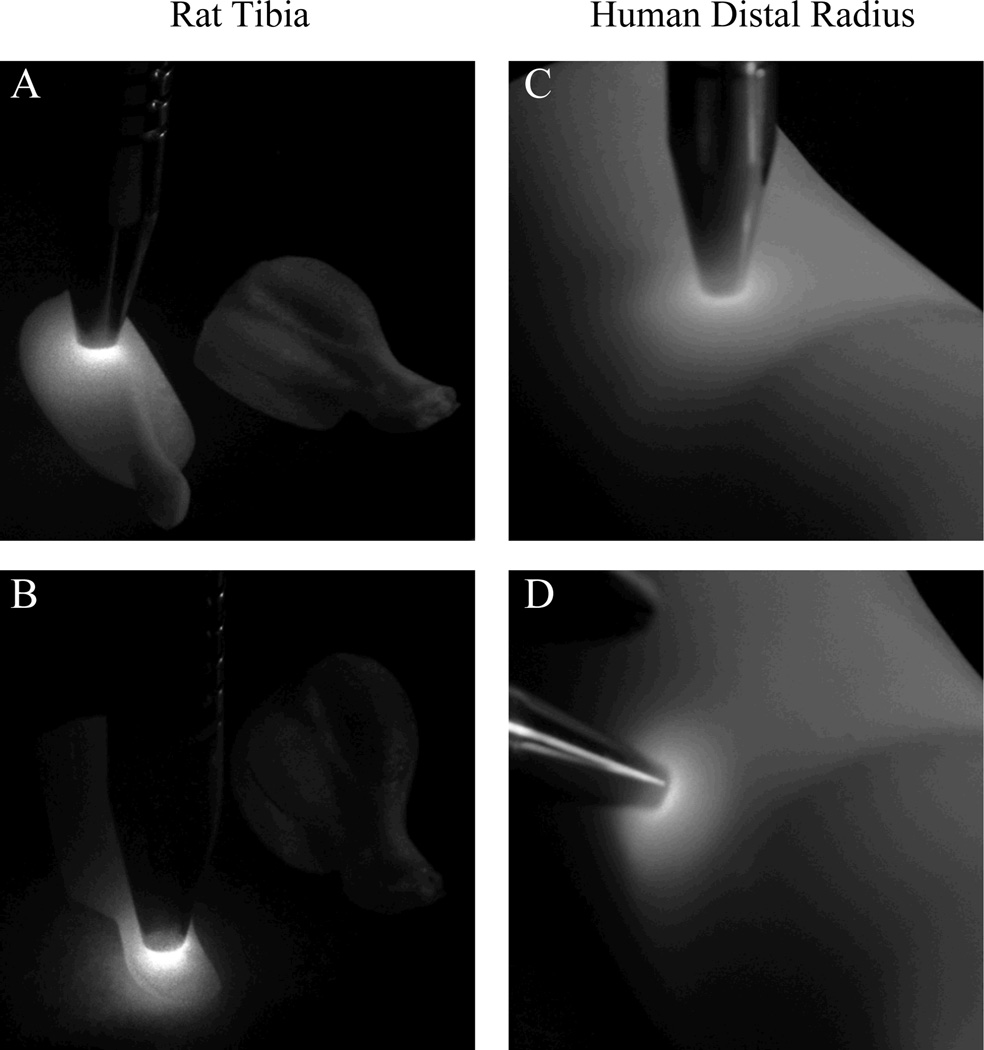
Diffusion of 830 nm laser light through rat tibia and human distal radius tissue phantoms with different illumination positions.

Multi-step molding process

High resolution CT images of rat leg and human wrist were used to create triangular surface meshes and volumetric tetrahedral mesh models of soft tissues and bone. A multistep molding process was used to fabricate gelatin tissue phantoms of a rat leg and human wrist. Techniques used in casting molds for prototyping, for making movie special effects and for sculpting were adapted for casting tissue phantom molds. A three-step molding process was used to create silicone molds from which the gelatin phantoms were cast.

The first step was to create plaster mold templates from the virtual surface mesh molds (the virtual molds are shown in the supplemental figures). A Spectrum Z510 rapid prototype instrument was used to fabricate porous plaster mold templates (Z Corporation, Burlington, MA USA). The second step was to create a negative mold from the plaster molds with polyurethane. The plaster molds were pre-treated with a sealing agent and a mold release agent prior to casting the polyurethane negative molds to avoid permeation of urethane into the porous plaster molds (SuperSeal and Universal Mold Release, Smooth-On, Inc., Easton, PA USA). The polyurethane negative mold (VytaFlex 30, Smooth-On, Inc., Easton, PA USA) was prepared from a 1:1 (w/w) mixture of parts A (prepolymer) and B (developer). Part B was premixed for 10 minutes using a squirrel mixer. The thoroughly mixed polymer was degassed in a vacuum chamber for 2 minutes to remove air bubbles. A thin layer of the polymer mixture was first brushed onto the plaster molds, and then poured into the mold starting at the lowest point to prevent encapsulation of air bubbles. The urethane polymer was allowed to cure overnight at room temperature. Urethane negative molds were used to fabricate several identical silicone molds.

The third step was to create silicone molds from the polyurethane negative molds. The silicone molds were exact replicas of the original plaster molds. Silicone was used because the resulting molds were easy to handle and did not require the use of mold release agents when casting gelatin phantoms. A 1:10 (w/w) mixture of parts A (silicone prepolymer) and B (catalyst) (Mold Max 40, Smooth-On, Inc., Easton, PA USA) was prepared and degassed by vacuum for 2 minutes. Silicone mixture was poured into the polyurethane molds and allowed to cure overnight at room temperature. The silicone did not adhere to the urethane, although rough surface textures added substantial difficulty to separating the final silicone mold from the urethane negative mold. To facilitate removal of silicone from urethane a release agent can be used (Universal Mold Release).

Gelatin tissue phantoms were cast from the silicone molds, based on the method described by De Grand et al.¹⁸ Mold release agents were not used for casting the gelatin phantoms to avoid poor layer adhesion in multilayer phantoms or potential surface degradation. Gelatin was used as the base for the tissue phantoms because it provided an approximation to the optical properties of soft tissue with a Raman spectrum that is similar to collagen. The gelatin base was prepared by adding gelatin (10% w/v) to pH 7.4 phosphate buffered saline (Sigma, St. Louis, MO, USA) at 40–55°C with rapid stirring. If phantoms were to be used for more than two weeks, 0.1 % (w/w) sodium azide was added to the gelatin base as a preservative. No other antibiotic or antifungal agents were incorporated into the gelatin base. Chemical components approximating the chemical components of bone, soft tissue or skin were added into the gelatin base to simulate the major scattering, absorption, fluorescence and Raman signals arising in each tissue layer. Table 1 summarizes the chemical components in each tissue layer and the expected optical contributions. Each tissue layer consisted of a 10% w/v gelatin base, with various additives. Additives were incorporated to mimic the optical and chemical properties of each tissue layer. Liposyn II (Hospira, Lake Forest, IL, USA), gelatin (Accumedia, Lansing, MI, USA), hemoglobin, sodium azide, and hydroxyapatite (Sigma, St. Louis, MO, USA) were used as received. Depending on the layer, 20% Liposyn II (10% v/v) or hydroxyapatite (20% wt/wt) was added for the soft tissue and bone respectively. Phantoms were prepared so that the optical properties (absorption and scattering) approximated those described by Alexandrakis et al.⁴¹ The bone simulating layer was made with 200 mg/ml hydroxyapatite, which is within the clinically relevant range used in the European spine phantom for x-ray and CT calibrations (between 0 and 1.5 g/cm³).⁴²

Table 1.

Chemical composition of layers in the multilayer phantoms.

Tissue Layer	Chemical Composition	Optical Contributions
Bone	20% Liposyn II (10% v/v)	Optical scattering
	Hydroxyapatite (20% w/w)	Raman scattering of bone mineral
	Gelatin	Raman scattering of bone matrix
Soft Tissue	20 % Liposyn II (10% v/v)	Optical scattering
	Gelatin	Raman scattering of soft tissue

The multi-step process of creating multilayer phantoms is shown in Figure 2. Each layer of a tissue phantom was cast into a cavity formed between upper and lower boundaries of silicone rubber molds. The three-dimensional tissue phantom was formed by sequentially casting layers one atop the next, by exchanging the upper layer of the mold to exclude less material for each subsequent casting step. For each layer, chemical components were added into an aliquot of the warmed gelatin base and stirred for 15 minutes to ensure a homogenous mixture before pouring into molds. While warm, the mixtures were degassed using a vacuum chamber until bubbles were no longer observed (typically about 3 minutes). The casting procedure differed for molds with small and large volumes. Prior to casting, large molds were prechilled at 4°C and the gelatin mixture was precooled to 35°C to minimize the time required for the gelatin to set and to minimize settling of components within the gelatin base. Molds with small volumes were kept at room temperature, and the gelatin was cast at 40–55°C to avoid gelling before all the small cavities in the mold (small features) had been filled by the mixture.

Several methods were evaluated for casting gelatin into mold cavities including injecting the hot gelatin mixture into the closed mold through syringes, and pouring the hot gelatin mixture into the open mold prior to assembling the upper and lower molds. For small models, large-bore syringes were used to inject the mixture into the mold. For large models, the mixture was poured into the open mold, and the mold was quickly assembled. The mold was slowly rotated to free any lingering pockets of air, and the mold was then oriented so that any air would rise to an unused portion of the model. After casting, phantoms were stored at 4°C in an air-tight container.

Physical Integrity of Multilayer Planar Phantoms

Two-layered planar gelatin phantoms were constructed to test the physical stability, measured by layer adhesion and mass lost by dehydration, of the phantoms under accelerated stability conditions. The planar phantoms were composed of 10% gelatin with 10% Liposyn II added. Large batches of phantoms were cast into Petri dishes (9cm diameter, 1 cm thick), and small 1cm² rectangles were cut from the batch. Multiple phantom rectangles (N=3–8) were tested under several combinations of casting and storage conditions. The first layer was poured at 40–45 °C and let to set for all experiments. Four different conditions were used to cast the second layer, as shown in Table 2. The first layer was stored at the ‘initial temperature’ for approximately 1 hour before adding the second layer. The phantoms were subjected to accelerated degradation conditions using repeated temperature cycles, either freeze-thaw or cold-thaw, over the course of 7 days. Phantom integrity was measured by mass loss (%) and visual inspection of layers for delamination. Phantoms were stored overnight in either 4°C (refrigerator) or −23°C (freezer), and allowed to equilibrate at room temperature for one hour the following morning. A total of five temperature cycles were performed: a temperature cycle was performed daily for 3 days, a fourth cycle performed at day 6, and a fifth cycle at day 7. There were a total of eight experiments, corresponding to four casting conditions and two types of temperature cycles.

Table 2.

Bilayer planar phantom casting temperatures

Casting Experiment #	1	2	3	4
Initial Temperature (°C)	−23	RTa	RTa	5
Pouring Temperature (°C)	50	50	30	50

^aRT is room temperature.

Mass loss and delamination results are shown in Figure 3. Layer adhesion was measured by visual inspection of the corners and edges of the phantoms. Layer delamination was tested qualitatively by lightly pulling at the corners and edges of the planar tissue phantoms after each storage cycle.

Fig. 3.

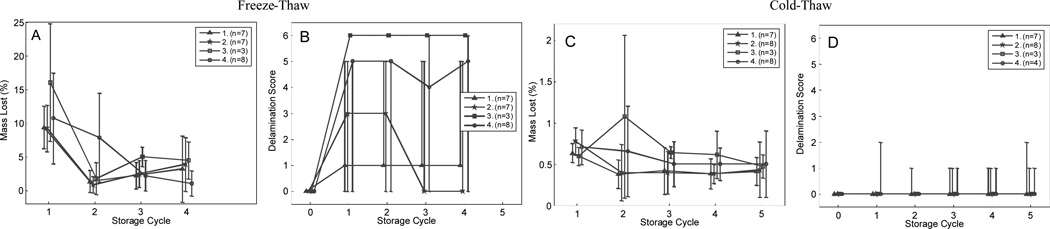
Delamination and dehydration results for phantoms stored at −20 and 4°C. As shown in A, all phantoms lost approximately 10% mass on the first freeze-thaw storage cycle, and 3% with each subsequent storage cycle. As shown in B, Phantoms delaminated appreciably when stored at −20°C. Phantoms stored in a fridge at 4°C lost approximately 0.5% mass with each storage cycle, as shown in C, and remained intact, as shown in D. Data is shown for the four different casting conditions, shown in Table 2. The extent of delamination was scored with ordinal values, based on the following scale: 0 for no observed damage, 1 for a single corner coming apart, 2 for two corners coming apart, 3 for approximately 25 % of the surface area no longer well adhered, 4 for 25 – 50 % of the surface area no longer well adhered, 5 for more than 50 % of the surfaces no longer adhered, and 6 for complete delamination (the layers were no longer joined).

Chemical Diffusion Across Multilayer Planar Phantoms

Three-layer planar phantoms were cast with the inclusion of red and blue food dyes into the top and bottom layers, respectively. Photographs and representative cross-sectional profiles of the diffuse reflectance are shown in Figure 4. Dye-free reference and colored sample phantoms were cast with measured volumes in each layer to ensure equal dimensions. Phantoms were imaged with a RGB digital camera (DCC1645C, Thorlabs, Newton, New Jersey) equipped with a C-mount video lens (D.O. Industries Navitron TV Lens 16mm F1.4, Japan) under illumination by a white LED illumination source (LIU004, Thorlabs, Newton, New Jersey). The camera was positioned perpendicular to the edge of the layered phantom so that all three layers were visible, and the light source was placed at an angle of approximately 22.5° to the camera axis. The camera and light source were approximately 12 inches from the phantom. The phantoms were imaged immediately after casting and daily for 7 days. When not used, phantoms were stored at 4 °C. Diffuse reflectance was calculated by taking −log₁₀(I_sample/I_reference) for each point in the image.⁴³ Diffuse reflectance along the line perpendicular to the layer interface boundaries was calculated for each day. The diffusion pattern was fit (using the Matlab optimization function ‘fminsearch’) using the diffusion model of extended initial distributions, and diffusion coefficients were found for the red and blue channels. The diffusion coefficient was calculated for the two dyes by fitting the reflectance profiles with the diffusion equation for extended initial distributions.⁴⁴

$$C(x,t)=\frac{1}{2}{C}_0\mathit{\text{erfc}}\left(\frac{x}{2\sqrt{\mathit{\text{Dt}}}}\right)$$ (1)

Where erfc is the error-function complement, C is concentration, D is the diffusion constant (in mm²·hours⁻¹), x is position (in mm) and t is time (in hours). A sum-of-square errors minimization was used to fit all measurements using the diffusion equation (Equation 1), and the known x positions (in mm) and known measurement times (in hours), using 4 variables: a diffusion coefficient, temporal offset, reflectance offset, and reflectance intensity. For each set of diffusion data (corresponding to red and blue dye), 100 models were fit using random starting values to initialize the search for optimal fitting coefficients. Some initial inputs returned invalid solutions, the remaining valid solutions were used to estimate the diffusion coefficient and temporal offset required to best fit the reflectance imaging data. From the diffusion coefficient the mean diffusion length for the dye diffusing in one dimension was calculated using Equation 2:

$$\langle x\rangle =\sqrt{2\mathit{\text{Dt}}}$$ (2)

Laser fluence in tissue phantoms

Elastic scattering of 830 nm (600 mW) laser light into tissue phantoms was measured by placing a custom-built fiber optic probe (300 micrometer core diameter fiber in a hypodermic steel ferrule) onto surface of the tissue phantom. After the laser was turned on, a digital camera (PowerShot SD850IS, Canon, Tokyo, Japan) was used to collect photographs of the tissue phantom with the room lights switched off. Representative digital images are shown in Figure 5. Images of elastically (830 nm) and inelastically scattered light (from fluorescence and Raman scattering within the 900–1000 nm interval) within the complex tissue phantoms were also collected for optimization of source and collection fiber optic positions for transcutaneous Raman spectroscopy. Inelastically scattered light was imaged by placing an 834 nm long-pass filter (FF01-834/LP-25, Semrock, Rochester, NY) in front of the camera to block the 830 nm elastically scattered laser light while allowing Raman and fluorescence signal to be imaged (inelastic imaging data not shown).

Raman spectroscopy of tissue phantoms

Raman spectra were collected within two weeks of phantom preparation to ensure the chemical and mechanical integrity of the phantoms. A Raman imaging spectrograph operating at 830 nm with ~100 mW of excitation power was used for all of the Raman measurements (RamanRxn1, Kaiser Optical Systems, Inc., Ann Arbor, MI USA). A hand-held probe was designed in-house and used throughout the experiments (FiberTech Optica Inc., Kitchener, ON Canada). Briefly, as described elsewhere, the hand-held probe consisted of 47 collection (100 µm core diameter) and 19 illumination (200 µm core diameter) fiber-optics.⁴⁵ The illumination fibers were positioned around a 3mm diameter ring, and collection fibers both spaced interspersed in the ring and at the center of the ring in a disc. This collected light at offset positions of 0–3 mm. Raman spectra were collected at multiple sites on the surface of the rat and human arm phantoms. Ten spectra were collected at each measurement site, and each spectrum was collected for 60s.

Preprocessing and analysis of Raman spectra

Raman spectra collected from tissue phantoms were preprocessed using Matlab routines written in-house, including cosmic ray (spike) correction and correction for image distortion.^45–47 Variations in CCD response and the wavelength axis were calibrated using a white light source and neon atomic emission source respectively (HCA, Kaiser Optical Systems, Inc., Ann Arbor, MI, USA). The laser wavelength was determined from a measured Raman spectrum of a Teflon standard. From each measurement, a single summed Raman spectrum was calculated from the 10 spectral images.

Results and Discussion

Multilayer phantoms with accurate geometry, optical and chemical properties were created from high resolution CT images of rat and human limbs. In silico 2D and 3D renderings of skin, bone and soft tissues were created and used to produce physical molds for sequentially casting the tissue phantom layers. Figure 1 shows cross section CT images in the transverse (Figure 1a), coronal (Figure 1b) and sagittal (Figure 1c) planes, with a 3D rendering of surface boundaries corresponding to soft tissue and bone (Figure 1d). As expected, bone tissue was easily distinguished from soft tissue (using CT density) and surface meshes corresponding to cortical and cancellous bone were generated. The surfaces meshes are shown in supplemental figures 1 and 3. Further discrimination of surface boundaries corresponding to tendon, ligament, muscle and fat tissues was more challenging because of the subtle contrast present in CT images. An MRI image should provide improved contrast of different soft tissues and resolve multiple soft tissues or joint spaces. Even if fine features can be resolved in an MRI or CT image, the present casting method has limitations on the complexity and minimum feature size that can be practically created. We found that small intertwined features such as strands of muscle or trabecular bone struts within the marrow space were impractical to cast in a single step. Instead, complex interior components (such as bones with an enclosed marrow region) can be pre-cast in separate molding steps and inset into the outer layers.

An example of the multi-step casting technique for a rat phantom is shown in Figure 2. The initial micro-CT image is shown in Figure 2A. Based on the geometry of the desired tissue features, a 3-layer model was selected for casting first a lower soft tissue layer, then the bone layer, and finally an enclosing upper soft tissue layer. A diagram of the molding steps is shown in Figures 2B–2D. A 2-piece mold is used to sequentially cast these layers. The lower mold is kept constant in all casting steps, while the upper mold is sequentially replaced in each step to cast the successive phantom layers. The final tissue phantom is then removed from the mold.

We tested the integrity of bilayer thin planar phantoms under varying casting and storage conditions. The thickness of the planar phantoms was selected based on the smallest feature cast in our study, the diameter of the rat tibia bone. Layers adhere because the heat from newly-poured layer will melt the surface of the existing layer slightly and allow a small degree of mixing. Small features or thin layers have very little thermal mass and melt the interface to a lesser extent. Bilayer planar phantoms represented the “worst-case” because the edges are exposed to environmental conditions and very little mixing occurs at the interfaces between such thin layers (~ 7–10 mm).

Repeated cycles of freeze-thaw (−23°C to room temperature) or cold-thaw (4°C to room temperature) were used to simulate common storage conditions. Phantom integrity was measured in bilayer phantoms by visual inspection of the layers for delamination and mass loss by dehydration. Mass loss (Figures 3a and 3c) and delamination score (Figures 3b and 3d) of bilayer phantoms after freeze-thaw or cold-thaw cycles are shown in Figure 3. Trends are shown with a line joining the modal score for each storage cycle, and upper and lower error bars denoting the minimum and maximum delamination score or mass loss for each storage cycle. The plotted data show the differences between day 0–1 (storage cycle 1), day 1–2 (storage cycle 2), day 2–3 (storage cycle 3), day 3–6 (storage cycle 4), and day 6–7 (storage cycle 5). Dehydration data for the final storage cycle is shown for the cold-thaw samples only, because most of the freeze-thaw specimens had delaminated after the 4^th freeze-thaw cycle and were discarded.

As expected, bilayer planar phantoms that underwent cycles of freeze-thaw demonstrated significant mass loss. Shown in Figure 3a, the mass loss in phantoms was 10–15% after the first freeze-thaw cycle, regardless of the casting conditions. We hypothesize that primarily water was lost because no salt or lipid residues were observed in the sealed storage containers. Water was lost as a thin crust of ice, which was readily observed on the surface of the gelatin. Water loss was localized to the superficial portion of the gelatin, with only a ~3% mass loss observed in the subsequent freeze-thaw cycles. By contrast, phantoms that underwent cycles of cold-thaw demonstrated only a slight loss of approximately 0.5% mass with each storage cycle, shown in Figure 3c. These results indicate that when stored at 4°C the phantoms could be repeatedly used for spectroscopic analysis without significant loss of phantom integrity or water content.

The trend in delamination score correlates with mass loss, as shown in Figure 3b and 3d. The casting conditions did have an effect on delamination when phantoms were subjected to freeze-thaw cycles. No substantial delamination was observed in phantoms that underwent cycles of cold-thaw. Specimens stored in the freezer delaminated substantially, as indicated by more than 2 delaminated corners. Delamination was most pronounced in the group of phantoms in group 3, where the new layer cast at 30°C. No clear trends were observed between groups 1, 2, and 4, which were cast at 50°C, and we observed a variety of scores for all casting groups. One source of variability in the scores may be from difficulty in assigning an ordinal classification value to delamination, which is essentially a continuous process. The temperature at which the new layer was cast appeared to play a more substantial role in layer adhesion than the temperature of the existing layer. Many of the frozen samples delaminated substantially by the 5^th freeze-thaw cycle. As a result, data for the frozen samples was recorded only until the 5^th freeze-thaw cycle. Delamination appeared to originate at the corners and edges of layer interfaces. Results from the stability experiments indicate that storage at cold (but not freezing) temperatures (4°C) and casting at warmer temperatures (50°C) maximizes phantom durability.

We have not observed delamination in the multilayer anatomically realistic phantoms. We hypothesize that the extra surface area and added geometric complexity in limb-shaped tissue phantoms provided additional stability that contributed to layer adhesion (the layers are interlocked). Limb-shaped tissue phantoms were also mechanically stable, with no visible evidence that phantoms lost their shape after normal use or slight dehydration. Similar to edible molded gelatin, the tissue phantoms retained its original geometry after they were removed from the silicone casting molds. Even though the phantoms are flexible, they returned to their original shape after gentle compression or torque and maintained their shape when left free-standing. The high concentration of gelatin used in the phantoms provides a much more robust material than in the foods most are familiar with. We observed minimal dehydration in the human or rat tissue phantoms after storage in 4°C for one week. However, this small amount of dehydration did not affect the size or shape of the phantom.

Chemical diffusion across phantom layers may affect the sampling volume and accuracy of quantitative measurements. The diffusion rate is one of the principal limiting factors (along with growth of biological agents and decomposition of layer additives) in determining the useful period of the phantoms for quantitative experiments. The diffusion rate will vary with gelatin concentration and composition, storage temperature, and molecular weight of the additive. The chemical diffusion rate should be determined for each set of additives. We measured diffusion of red and blue food dyes in a three layer planar phantom by color imaging of the phantom cross section. Figures 4A–4C show three layer planar phantoms with no dye (Figure 4A), with added dye after 2 days (Figure 4B), and with added dye after 7days (Figure 4C). The phantom with no dye served as a reference. The dyed phantom contained red food dye in the gelatin of the top layer, no dye in the middle layer, and blue food dye in the gelatin of the bottom layer. Diffuse reflectance profiles are shown in Figure 4D, and were calculated by normalizing each measurement image to an image of a reference phantom collected the same diffusion time. The diffusion coefficient of red food dye was estimated as 0.0915 ± 0.0057 (mm²·hour⁻¹) from 71 fitting models. The diffusion coefficient of blue food dye was estimated as 0.0232 ± 0.0011 (mm²·hour⁻¹) from 68 fitting models. Over the seven days of measurements, the red food dye diffused several mm into the middle layer of the phantoms, while the blue food dye diffused much less. These results indicate that small organic dyes (food dyes) diffuse several millimeters per day. Larger molecular components such as hemoglobin should diffuse more slowly, and thus have less inter-layer mixing. Based on these preliminary results, we expect that features smaller than 1 mm will be affected by diffusion within one day.

There was a small amount of initial surface mixing of the layers when the three layer phantoms were cast. The temporal offset parameter was introduced into the diffusion equation to account for the initial inter-layer mixing which occurred during the casting process (and hence already existed at time 0). The temporal offset estimated by the fitting models varied widely, with a median value near 2 hours, and a mean value near 3 hours for both layers (and a large standard deviation of 3 hours). The temporal offset indicates that, the initial inter-layer mixing was equivalent to allowing the layers to diffuse for an additional few hours. This should have only minor consequences on the imaging process, but may limit the maximum achievable resolution. A conservative estimate of the achievable resolution for casting the planar phantom is approximately 740 micrometers (assuming 3 hours of diffusion occurs in the casting process along with the diffusion coefficient from the red food dye). The casting conditions were not optimized to minimize the initial diffusion, we expect that mixing can be reduced with further development. These limitations indicate that this method is not useful for very thin layered phantoms (such as for modeling skin) or for microscopy use. For modeling larger tissue volumes, such as a whole wrist, this resolution limit should not be problematic.

In addition to acting as spectroscopic standards with appropriate geometries, tissue phantoms with anatomic shapes can also be used to measure diffuse reflectance for evaluating spectroscopic probes and for comparison with models of light scattering. The relative intensity of elastic (unfiltered), fluorescent and Raman (using long-pass filters) scattered light can be imaged over the surface of the phantoms using optical filters and digital cameras. Propagation of 830 nm laser light through several phantom geometries was monitored using digital cameras. Figure 5 shows rat leg and human wrist phantoms illuminated by elastically-scattered laser light measured without an optical filter. The contribution from Raman scatter or fluorescence is negligible in comparison with the magnitude of the elastically scattered light so no filter was needed. The photographs show that both the outer and inner layer geometry affected the laser light scattering patterns. This effect is more pronounced in the rat leg phantom, seen in Figures 5a and 5b, which has a small radius of curvature. In Figure 5b, more laser light exited the phantom towards the bottom-left of the image because of the surface curvature, while in 5a, the laser light is blocked from diffusing to the far side of the phantom by the tibia. In Figure 5d, the styloid process of the distal ulna caused a slight distortion of the otherwise circular pattern. In Figure 5d, the excitation light is shown reaching to the bone layer with little laser light passing through the bone. These results support the idea that complex geometries affect the flow of light, and that phantoms for probe design and validation should mimic the anatomical geometries of the target tissues.

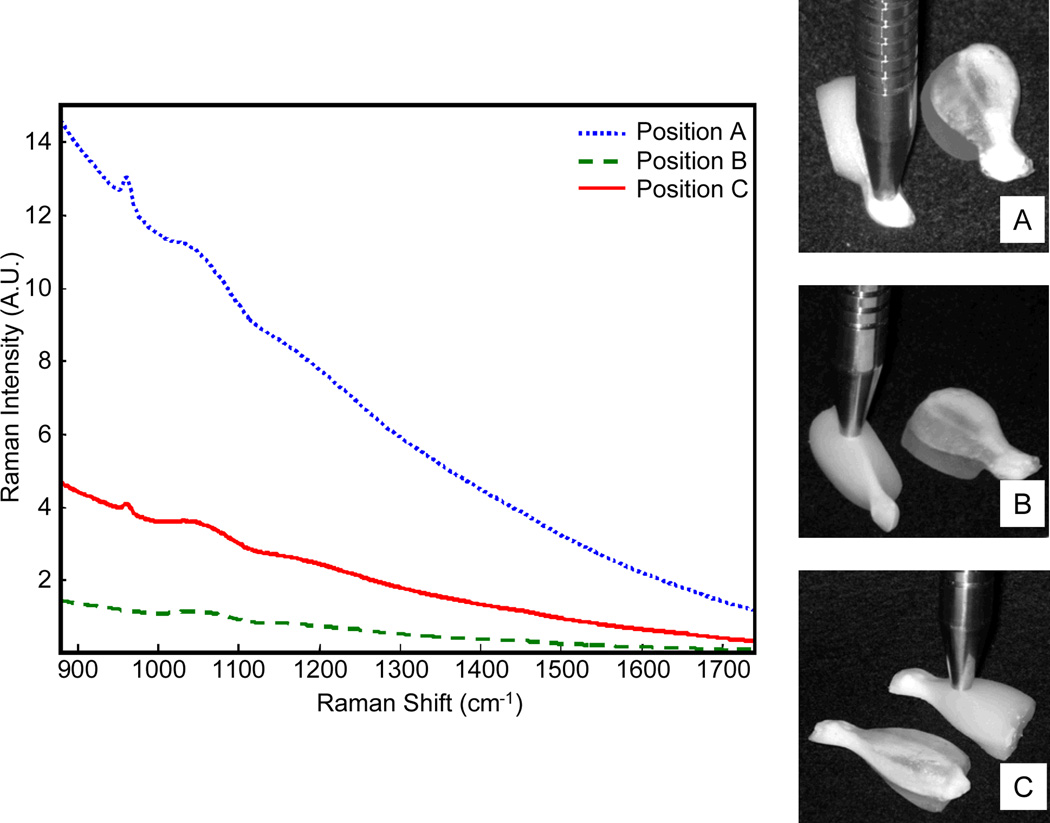
Raman spectra and photography of the rat tissue phantoms are shown in Figure 6. Photographs in Figures 6a–6c show two tissue phantoms of the same anatomic geometry. All measurements were taken on the phantom with added Liposyn (to model optical scattering), and the photographs indicate where the Raman probe was placed for collecting the Raman scattering. The second tissue phantom was included for visual reference only. It contained no Liposyn in the soft tissue layer so that the bone geometry is visible. The first measurement (Figure 6a), was taken at the distal end of the tibia where the bone is relatively thick and is covered by only a thin layer of soft tissue (A, ~0 mm probe-bone separation). In the second measurement (Figure 6b), the probe was positioned near the proximal tibia with little overlaying soft tissue (B, ~1.25 mm probe-bone separation). In the third measurement (Figure 6c), the probe was positioned over the fibula (about half the diameter of the tibia) and there was more overlaying soft tissue (C, ~5 mm probe-bone separation). The Raman spectra showed variability in the recovered spectra, which arose because of the geometry of the layers. The thickness of the overlaying soft tissue was comparable in positions a and b of Figure 6, however the intensity of the phosphate ν₁ peak at ~960 cm⁻¹ varied because there were differences in the width and depth of the subsurface bone layer. At point A, the bone is a nearly spherical knob, while at point B it has a triangular cross-section with a thin point near the surface. Spectra were not corrected for silica signal arising from the unfiltered collection fiber optics, and a broad silica band centered at 1050 cm⁻¹ shows the magnitude of elastically scattered 830 nm excitation light reflected back into the probe. In all spectra shown in Figure 6, a background arises from silicon in the fiber optics, as well as fluorescence background from the gelatin and small amounts of metal ion impurities in hydroxyapatite.

Fig. 6.

Raman spectra collected from the rat tibia phantoms for three probe positions (probe positions are shown at right).

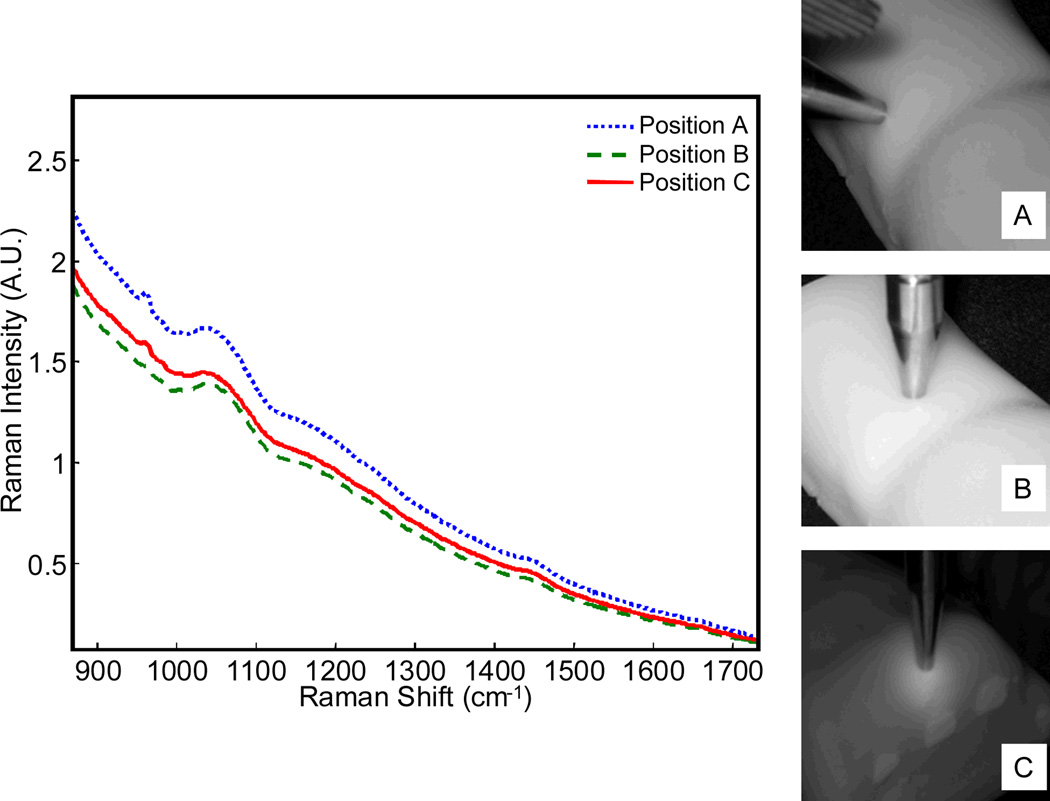
Raman spectra and photographs of human wrist phantoms are shown in Figure 7. Note that the primary Raman feature is the 960 cm⁻¹ phosphate ν₁ band from the uncarbonated synthetic hydroxyapatite mineral in the bone layer. In all of the sites measured, the bone layer was covered by a layer of soft tissue of comparable thickness. While the thickness of the bone layer was comparable at all three sites, the geometries varied. Elastically-scattered laser light was diffusely reflected by the soft tissue layer, and the magnitude of the broad silica band at 1050 cm⁻¹ was similar for all three measurements. The 960 cm⁻¹ Raman band was more intense when the probe was positioned over the distal ulna (A, ~5.5 mm probe-bone separation) as compared to over the third proximal metatarsal (C, ~7 mm probe-bone separation) or between the distal ulna and distal radius (B, ~10 mm probe-bone separation). In particular, the phosphate signal at point B was much lower intensity because it was taken where there is a gap between the ulna and radius.

Fig. 7.

Raman spectra collected from the human distal radius phantoms for three probe positions (probe positions are shown at right).

Conclusions

We report a technique to fabricate multilayer gelatin tissue phantoms with complex geometries, and with optical and chemical properties suitable for deep tissue spectroscopy. These phantoms can serve as analytical standards for tissue spectroscopy, for optical probe development and optimization, and for instrument validation. CT imaging data were used to generate molds for lost-core type casting of layers with complex geometries.¹² The method described can be applied to any anatomic shape (to include detailed interior features), as long as the tissue has a different contrast from surrounding tissues and can be imaged using MRI or CT. Any feature that can be measured can also be reproduced, though the exact molding methodology must be adapted to suit the particular type of desired features and to maintain the appropriate geometric alignment between model layers.

The molding process described here is only one possible way of generating tissue phantoms with complex multilayer geometries. Other potential methods include direct printing of complex geometries using an inkjet-type print head. Advantages of the current casting method include the ability to rapidly produce phantoms of substantial volume and to cast multiple phantoms simultaneously. In this process the molds are simple to fabricate and duplicate, and molds can be reused for casting many phantoms of a given geometry. Disadvantages of this casting method include a limited ability to reproduce small and interwoven features and the difficulty of creating initial molds. Tissue engineering methods might be applicable for creating fine structural detail to improve the accuracy of these phantoms.^{37, 48, 49} Furthermore, the fabrication becomes more complicated with increasing numbers of layers and the probability of casting defects also increases.

Tissue phantoms with anatomically realistic geometries have limitations because they simulate the tissue on a large spatial scale, but do not adequately capture the complicated optical absorption and scattering properties arising from cellular, subcellular and tissue structures that span a range of sizes. Also, polarization and anisotropic effects are not simulated with the cast gelatin phantoms. Even with these limitations, the multilayer geometrically accurate phantoms are an advance over current phantoms which consist of simple geometric shapes or complex geometries with a single layer. Unfortunately, anatomical geometries consist of complicated geometric shapes and cannot be easily described through mathematical formulas or size measurements. For reference, 3D figures of the models used here were included as supplemental materials. The wrist tissue phantom described here is the size and shape of an adult wrist, and the bones of the forearm, wrist and hand are reproduced within the phantom. Due to the widespread availability of CT and MRI imaging equipment, and accessibility of human imaging datasets,^‡ this method allows fabrication of tissue phantoms to mimic almost any human or animal tissue of interest. Finally, because the molded gelatin phantoms do not use plastics, they can be used for composition-sensitive modalities such as fluorescence and Raman spectroscopy.