Assembly of reconfigurable one-dimensional colloidal superlattices due to a synergy of fundamental nanoscale forces

Abstract

We report that triangular gold nanoprisms in the presence of attractive depletion forces and repulsive electrostatic forces assemble into equilibrium one-dimensional lamellar crystals in solution with interparticle spacings greater than four times the thickness of the nanoprisms. Experimental and theoretical studies reveal that the anomalously large d spacings of the lamellar superlattices are due to a balance between depletion and electrostatic interactions, both of which arise from the surfactant cetyltrimethylammonium bromide. The effects of surfactant concentration, temperature, ionic strength of the solution, and prism edge length on the lattice parameters have been investigated and provide a variety of tools for in situ modulation of these colloidal superstructures. Additionally, we demonstrate a purification procedure based on our observations that can be used to efficiently separate triangular nanoprisms from spherical nanoparticles formed concomitantly during their synthesis.

The ability to form ensembles of inorganic nanoparticles with a high degree of control has become one of the main areas of focus in nanoscience research (1). This interest stems from the fact that nanocrystal superlattices often exhibit electronic (2), optical (3), and magnetic (4) properties that are distinct from both the corresponding individual particles and the bulk solid as a result of the interactions between the excitons, surface plasmons, or magnetic moments of the assembled particles (5). Superlattices composed of spherical building blocks have been extensively studied, and researchers now have the ability to synthesize a wide variety of structures (6). However, as new techniques are developed to synthesize high-quality anisotropic nanoparticles with new physical properties that cannot be obtained with spheres alone, researchers are increasingly interested in the rich assembly behavior of particles with reduced symmetry (7–9). Indeed, periodic arrays of these anisotropic building blocks have been shown to possess unique collective properties with applications in various fields including plasmonics (10) and photonics (11). However, to take full advantage of these collective properties, it is necessary to understand the relationship between the architectural parameters of the ensemble and the emergent physical properties. For this purpose, it is crucial to be able to “engineer” the various interactions that exist between nanoparticle building blocks to produce a desired structure (12, 13). The assembly of nanocrystals into ordered arrays can be induced via the manipulation of interparticle interactions including van der Waals (14), electrostatic (15), entropic (16–21), and through highly specific biological interactions (22–24). Herein, we report the assembly of colloidal triangular gold nanoprisms protected by a cetyltrimethylammonium bromide (CTAB) bilayer in a solution of CTAB micelles into highly ordered 1D crystals with unexpected structural features that emerge from a synergy of attractive depletion and repulsive electrostatic interactions. This system is unique in that it allows access to a regime wherein several interparticle forces are of comparable strength, leading to an unusual example of a one-dimensional superlattice of inorganic disc-like nanostructures that is stable in solution. Furthermore, these columnar assemblies are highly reconfigurable through modification of several intensive and extensive variables, providing a means to create tunable stimuli-responsive materials (18, 25).

Depletion forces are purely entropic in nature and arise when small, nonadsorbing molecules, such as surfactants, are added to a colloidal solution of particles (26). Two large particles of radius R immersed in a dispersion of small particles (depletants) with radius r possess an exclusion layer whose thickness is equal to r. As the surfaces of the large particles reach a separation smaller than the diameter of the depletant (2r), their exclusion layers begin to overlap and the total volume available to the depletants is increased, thereby decreasing the free energy of the system by

[1]

where n is the number density of the depletant, k_B is the Boltzmann’s constant, T is the temperature, and ΔV is the volume gained by the overlap of exclusion layers (13). The depletion force can also be thought of in terms of osmotic pressure: The exclusion of the depletant from the space between the particles results in a local concentration gradient that produces a net osmotic pressure acting to push the particles together. The strength of the interaction energy is proportional to the magnitude of the volume gained by bringing two particles together, and therefore depletion forces are particularly attractive for assembling anisotropic building blocks because they can potentially have a more efficient overlap of their exclusion layers compared to spherical building blocks due to directionally dependent interactions (27). Additionally, depletion forces are maximized for smooth surfaces because very little free volume is gained when two rough surfaces approach each other (28). This fact makes plate-like triangular gold nanoprisms an ideal structure to probe depletion force-based assembly because they are extremely anisotropic (aspect ratio of ca. 19) and have atomically flat triangular faces on the top and bottom (29), allowing the strength of the depletion force to be maximized. Colloidal nanoprisms are highly tunable anisotropic structures that exhibit size- and shape-dependent plasmon resonances (30) and are predicted to exhibit unique collective optical properties (5, 9).

In our system, the synergy of depletion and electrostatic forces causes triangular nanoprisms to naturally assemble into one-dimensional lamellar colloidal crystals with interparticle spacings greater than four times the thickness of the nanoprism building blocks. Forces that inherently have no directionality are made to prefer specific interaction modes via particle anisotropy, consistent with previous reports of directional entropic interactions (31). Both types of interactions arise from the presence of the surfactant CTAB: In solution, the CTAB molecules form micelles that act as depletants, driving the entropic association of prisms, whereas the presence of the CTAB bilayer leads to a positive charge on the surface of the prisms (32, 33), causing an electrostatic repulsion between them. The combination of extremely anisotropic particles and charged depletant molecules leads to the formation of robust crystals with interparticle spacings that are significantly larger than the particle size, which, to the best of our knowledge, is an unprecedented example of achieving such large spacings between particles using interparticle forces alone (13). We demonstrate that the lattice parameters are reversibly tunable in situ by manipulating the balance of the forces via a change in surfactant concentration, temperature, or ionic strength. Additionally, we propose a simplified model that explains the large lamellar d spacings observed experimentally by minimizing the free energy of the system, taking into account the relevant interactions. Finally, we utilize the fundamental knowledge gained in this study to develop a procedure to purify the anisotropic triangular gold nanoprisms from the spherical gold nanoparticles formed concomitantly during their synthesis, which has proven to be a challenge to date (29).

Results and Discussion

Gold nanoprisms (henceforth also referred to as prisms) were synthesized according to literature methods with minor modifications (29) (SI Appendix). A typical synthesis produces a mixture of triangular gold nanoprisms (thickness of 7.5 ± 1 nm and three congruent edges) and spherical gold particles (SI Appendix, Fig. S1). Nanoprism edge length was varied from 40–210 nm by changing the ratio of the gold seeds to the gold salt precursor (34). The cationic surfactant CTAB serves as the stabilizing agent in our system. CTAB forms a bilayer structure around the gold nanoprisms, with the inner layer binding to the gold surface via its charged headgroups (32). The adsorbed bilayer has an approximate thickness of 3.2 nm (35, 36) and leads to a net positive charge on the surface of the prisms (32, 33). Because the synthesis of the prisms is carried out at a CTAB concentration of 50 mM, which is 50 times the critical micelle concentration (1 mM) (36), charged CTAB micelles are also present in solution. At a CTAB concentration of 50 mM, the fractional charge of the micelles is approximately 0.26 (37).

Immediately after their synthesis and without further modification, the 7.5-nm-thick prisms (145-nm edge length) naturally assemble into 1D lamellar superlattices in solution with the prisms aligned face-to-face with a center-to-center spacing (d spacing) of 29.9 nm (Fig. 1 A and B). These lamellar nanoprism crystals were characterized by small angle X-ray scattering (SAXS) using the Advanced Photon Source at Argonne National Laboratory. The two-dimensional scattering images were radially averaged over all orientations to produce plots of scattered intensity I(q) versus scattering vector q, where q = 4π sin θ/λ. The SAXS profile for 145-nm edge length prisms (Fig. 1D) features four resolvable diffraction peaks at integer spacings with respect to the first-order peak (q = 0.021, 0.042, 0.063, 0.084 Å^-1), consistent with a highly ordered lamellar structure (38, 39). Although the scattering from the spherical gold particles (form factor) can be seen in the SAXS patterns (39), they were not found to have an effect on the formation of the lamellar nanoprism crystals and, as a result, were disregarded for the remainder of this study (SI Appendix, Fig. S2). Using the Scherrer equation (40), the crystallites were determined to contain a total of 10–15 prisms. Cryoelectron microscopy images of the nanoprism superlattices provide further evidence of the lamellar structure (Fig. 1C). However, it is important to note that the appearance of hexagonal ordering between 1D nanoprism columns and the reduced interparticle spacings observed in the image are likely consequences of the microscopy preparation procedure, as these features are not supported by the SAXS data.

Fig. 1.

Columnar superlattices of anisotropic gold nanoprisms. (A) Nanoprisms form 1D lamellar crystals in solution with an average of 10–15 prisms per crystal. (B) A zoomed in edge-on view of two nanoprisms within a lamellar superlattice where d is the d spacing, d_w is the water region, t_prism is the thickness of the nanoprism, t_bCTAB is the thickness of the CTAB bilayer, and d_CTAB is the diameter of the CTAB micelles. (C) Cryoscanning transmission electron microscopy image of the lamellar crystals. The outlined region highlights an edge-on view of the nanoprism crystals. (Scale bar: 200 nm.) (D) One-dimensional SAXS profile of the as-synthesized Au nanoprisms (145-nm edge length) in solution. The sharp diffraction peaks at q = 0.021, 0.042, 0.063, and 0.084 1/Å indicate a periodic lamellar structure.

A d spacing of approximately 30 nm between 7.5-nm-thick prisms corresponds to a solvent layer (d_w) of approximately 16 nm when the CTAB bilayer on the prisms is taken into account (Fig. 1B). A 1D electron density profile ρ(z) was derived from the SAXS data using a Fourier synthesis method to confirm the large interparticle spacing (39) (SI Appendix, Fig. S3). Anomalous SAXS studies at the X-ray absorption edges of Au and Br revealed that the majority of the Br^- species are located outside of the lamellar superstructures, as opposed to between the nanoprisms that make up the superlattices, suggesting that the majority of the micelles are located outside of the lamellar crystals (SI Appendix, Fig. S4).

According to Eq. 1, bringing the nanoprisms into close proximity increases the total volume available to the CTAB micelles, the depletants in this system, thereby increasing the entropy of the micelles and decreasing the free energy of the overall system. The length scale of traditional depletion forces that take only hard sphere interactions into account is determined by the size of the depletant (13). The CTAB micelles were determined to be approximately 5.8 nm in diameter by small angle neutron scattering (SANS) at the High Flux Isotope Reactor at Oak Ridge National Laboratory (SI Appendix, Table S1), consistent with the literature (41). According to depletion theory, interactions resulting from such small particles at a relatively low volume fraction are weak compared to the repulsive electrostatic interactions and cannot induce assembly. However, in our system, the CTAB micelles are also charged, similar to the CTAB bilayer on the nanoprisms (32). Previous theoretical studies by Walz and Sharma confirm that the presence of a long-range electrostatic repulsion greatly increases both the magnitude and range of the depletion effect (42). We thus inferred that, in addition to the depletion attraction, and possibly a minor contribution from attractive van der Waals interactions, a repulsive force must also be present, originating from electrostatic interactions between the CTAB-coated nanoprisms.

We have developed a simplified model that captures the fundamental physics required to explain the large d spacings of the nanoprism superlattices observed with SAXS based on the hypothesis that the combination of charged prisms and charged CTAB micelles leads to the anomalously large interparticle spacings. The model takes into account the competition between the attractive depletion and van der Waals interactions that favor the formation of lamellar stacks of nanoprisms and the repulsive electrostatic interactions that favor the dispersion of the nanoprisms in solution.

The depletion interaction energy is based on Eq. 1. However, Eq. 1 is only valid for a very dilute system where the depletant behaves as an ideal gas and therefore Eq. 1 must be modified when the depletants are charged and highly concentrated (43, 44). For a system with charged particles and depletants, the volume gain, ΔV in Eq. 1, is larger than it would be for a neutral system. The volume gain is larger because the effective size of the CTAB-coated nanoprisms and the CTAB micelles is increased by some factor δ multiplied by the Debye length κ^-1 (42, 45, 46). To capture this effect, the effective sizes of the prisms (t_prism,eff) and the micelles (d_CTAB,eff) are denoted as t_prism + 2t_bCTAB + 2δ_prismκ^-1 and d_CTAB + 2δ_CTABκ^-1, respectively, where t_prism is the thickness of the prism (7.5 nm), t_bCTAB is the thickness of the CTAB bilayer on the surface of the prism (3.2 nm) (35, 36), and d_CTAB is the diameter of the CTAB micelles (ca. 5.8 nm). For a neutral system, both δ_prism and δ_CTAB would be zero. For our system, δ_prism and δ_CTAB were used as fitting parameters to most accurately capture the variation of the d spacing as a function of the CTAB concentration (45).

Additionally, the effects of the high concentration of depletants must be taken into account. As the concentration of the charged CTAB micelles increases, the osmotic pressure difference within the superlattices compared to the surrounding solution, ΔΠ, does not increase linearly with CTAB concentration as it would for a dilute system. As a result, the higher order coefficients in the virial expansion of the particle distribution function are nonzero and need to be considered (42). To include for this effect, we modeled ΔΠ using the Carnahan–Starling equation of state (45, 47, 48) for a charged micelle system in which

[2]

where n = (N_A/N_agg)(c_CTAB-c_cmc), Φ_eff = n(4/3)π(d_CTAB,eff/2)³, N_A is Avogadro’s number, N_agg is the aggregation number of the micelle (145 for 0.05 M CTAB) (37), c_CTAB is the CTAB concentration, and c_cmc is the critical micelle concentration (1 mM) (36, 45, 47). The values of d_CTAB, N_agg, κ^-1, and the effective charge of the CTAB micelles vary with CTAB concentration, temperature, and ionic strength. The values used in this work are obtained from literature (36, 37, 45, 47) and are summarized in the SI Appendix. For simplicity, we assumed that the CTAB micelles are spherical with an aggregation number that varies predictably with CTAB concentration (37). The depletion interaction energy is therefore given by the following expression:

[3]

where ΔΠ is the osmotic pressure difference, A is the area of a nanoprism triangular face (9,104 nm² for 145-nm edge length prisms), and d is the center-to-center interparticle spacing between prisms. This equation helps explain why depletion interactions favor assembly of anisotropic particles: The reduction in free energy of the system is proportional to the area of the particle A. The prisms have large smooth faces with a large value of A and thus feel depletion attractions at greater distances with low depletant concentrations compared to isotropic spherical particles (27, 28). Additionally, the gain in free energy by aligning the prisms parallel, or face-to-face, is much larger than by aligning side-to-side or side-to-face (27), which is the reason the nanoprisms do not form random aggregates, but instead form periodic lamellar structures. The SAXS patterns did not reveal any ordering of the lamellar superlattices relative to each other in solution (SI Appendix, Fig. S5). It is important to point out that the use of excluded volume and short-range depletion forces to assemble micron-sized platelets is well established in the literature (27). The novelty of the current system lies in the ability to assemble nanoscale particles with interesting optical properties into columnar assemblies with lattice parameters significantly larger than the dimensions of the building blocks by taking advantage of a synergy of fundamental forces.

To calculate the electrostatic interaction energy, the solution of the linearized Poisson–Boltzmann equation is used assuming no charge regulation (47). The expression can be written as

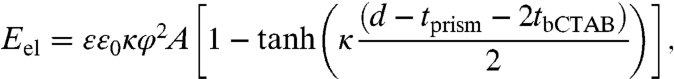[4]

where ε is the relative permittivity of the solvent (in this case, water), ε₀ is the permittivity of free space, φ is the constant potential at the nanoprism surface (0.035 V) (33), and κ is the inverse Debye length, defined as 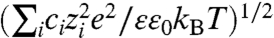(0.372 nm^-1 for 0.05 M CTAB), where c_i and z_i are the concentration and valency of electrolyte i, and e is the elementary charge (49). It should be noted that our calculation of the Debye length takes into account the dissociated micelle counterions as well as any salts added to change the ionic strength of the solution (e.g., NaCl).

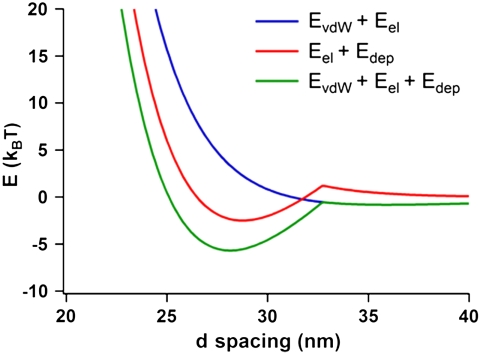
When only electrostatic and depletion interactions are considered, the free energy is minimized at d = 28.8 nm (Fig. 2), which is in good agreement with the d spacing of 29.9 nm observed with SAXS. When van der Waals interactions are included in the energy minimization calculations (see SI Appendix), the free energy minimum shifts slightly to d = 28.1 nm (Fig. 2). However, the minimum in the net interaction energy becomes deeper by approximately 3.2 k_BT. Thus, although van der Waals interactions have a negligible effect on the d spacing of the crystal at a CTAB volume fraction of 0.05, they do make the lamellar crystals more stable. If only van der Waals and electrostatic interactions are considered, the free energy curve does not possess a minimum (Fig. 2), reinforcing the importance of the depletion force in this system.

Fig. 2.

The interaction free energy (in units of k_BT) between two nanoprisms within a lamellar superlattice in a solution of 0.05 M CTAB taking into account the various interparticle interactions. E_vdW, E_el, and E_dep are van der Waals, electrostatic, and depletion interaction energies, respectively. Whereas E_el + E_dep (red) and E_vdW + E_el + E_dep (green) possess a minimum, E_vdW + E_el (blue) does not.

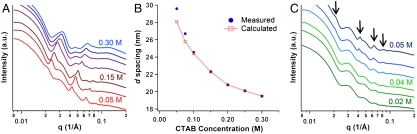
In order to experimentally probe that the lamellar prism assembly is the result of a balance between depletion and electrostatic interactions, four parameters were investigated—CTAB concentration, temperature, ionic strength, and prism edge length—to manipulate the balance of the interactions. According to Eq. 1, the strength of the depletion interaction can be increased via an increase in the number density of CTAB micelles. Consequently, CTAB was incrementally added to increase the overall CTAB concentration from the starting 0.05 to 0.30 M. As is shown in Fig. 3A, with each addition of CTAB, the diffraction peaks shifted to higher q values, indicative of a smaller d spacing between nanoprisms in the lamellar crystals. A sixfold increase in the CTAB concentration led to a 10-nm decrease in the d spacing (Fig. 3B), which agrees with the values calculated using the effective size of the CTAB micelles. The addition of CTAB leads to an increase in the number of CTAB micelles, and although the micelles are slightly larger at higher CTAB concentrations (37), they are also much closer together in the solvent (SI Appendix, Table S1), increasing the net osmotic pressure that acts to bring the prisms together. Conversely, a dilution of the CTAB concentration led to an increase in d spacing and an eventual dissociation of the lamellar crystals at CTAB concentrations of 0.04 M and below (Fig. 3C). This effect was found to be entirely reversible: By cycling between 0.025 and 0.05 M CTAB, the diffraction peaks in the SAXS pattern disappeared and reappeared almost instantaneously, indicating the immediate dissociation and formation of the lamellar crystals, respectively.

Fig. 3.

The effect of CTAB concentration on the d spacing of the lamellar superlattices. (A) One-dimensional SAXS profiles of the 145-nm edge length nanoprism samples as the CTAB concentration is increased from 0.05 M (Bottom) to 0.30 M (Top). The diffraction peaks shift to larger q values, indicating that the interparticle spacing decreases with increasing CTAB concentration. (B) Plot showing the measured (blue circles) and calculated (red squares) d spacing as a function of CTAB concentration. (C) One-dimensional SAXS profiles of the 145-nm edge length nanoprism samples as the CTAB concentration is diluted from 0.05 M (Top) to 0.02 M (Bottom). The diffraction peaks disappear at CTAB concentrations of 0.04 M and below, indicating that the nanoprisms no longer form lamellar superlattices. The arrows indicate the positions of the diffraction peaks.

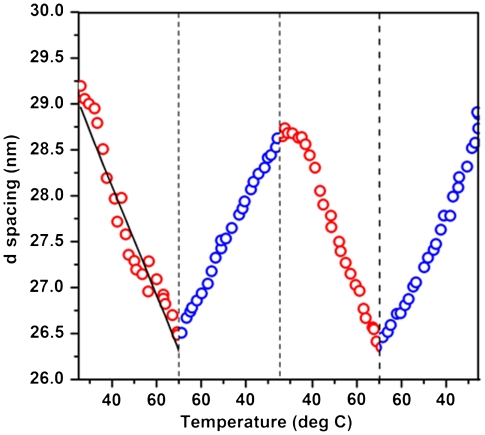
The effect of temperature was studied by increasing the temperature of the colloidal nanoprisms at a constant heating rate of 0.5°/ min using a Peltier device and monitoring the position of the first-order diffraction peak in the SAXS pattern. As the temperature of the system was increased from 25 to 70 °C, the d spacing decreased by 2.8 nm (Fig. 4). This trend is explained by considering the size of the CTAB micelles at various temperatures. An increase in the temperature causes a decrease in the diameter of the CTAB micelles (50), as confirmed by the SANS studies (SI Appendix, Table S1). Because the overall CTAB concentration does not change, the reduction in micelle size leads to an increase in the number of CTAB micelles, which increases the osmotic pressure and acts to bring the nanoprisms closer together. When the temperature-dependent size of the micelles is taken into account, the calculated d spacings are in close agreement with the measured values (Fig. 4). The temperature-dependent interparticle spacing was found to be reversible without hysteresis when the samples were heated and cooled between 25 and 70 °C for two consecutive cycles (Fig. 4).

Fig. 4.

Plot of d spacing as a function of temperature for two consecutive heating (red circles) and cooling (blue circles) cycles showing the reversibility of the temperature-dependent d spacing of the lamellar superlattices. The temperature was cycled between 25 and 70 °C at a constant heating/cooling rate of 0.5 °C/ min. The black line in the first heating cycle represents the calculated d spacings as a function of temperature (see SI Appendix for details).

To manipulate the repulsive electrostatic interactions that exist between the positively charged gold nanoprisms, the ionic strength of the solution was increased via the addition of NaCl, which decreased the Debye length. As NaCl was incrementally brought to a final concentration of 0.1 M, the SAXS patterns maintained their sharp diffraction peaks consistent with lamellar ordering, but the d spacing decreased by 12.2 nm, from 29.1 to 16.9 nm (Fig. 5A). By decreasing the strength of the repulsive electrostatic interaction, the attractive interactions become relatively stronger and decrease the prism-to-prism distance within the 1D crystals, although the depletion interaction also decreases due to the reduction of the effective size of the prisms and micelles. The addition of salt may slightly increase the physical size of the CTAB micelles, but the effect is known to be minimal when chloride-based salts are used compared to bromide-based salts (50). Although the calculated values deviate slightly at higher salt concentrations, they do capture the general trend of the experimental data (Fig. 5A). As with CTAB concentration and temperature, the effect of increased ionic strength on the d spacing is reversible. By centrifuging the prisms at 2,100 × g for 15 s and redispersing the pellet in 0.05 M CTAB, the original d spacing is restored and is reversible over several cycles (Fig. 5B).

Fig. 5.

The effect of ionic strength on the d spacing of the nanoprism superlattices. (A) Plot showing the measured (blue circles) and calculated (red squares) d spacing as a function of NaCl concentration. (B) Plot showing the reversibility of the effect of adding NaCl to the 145-nm edge length nanoprism samples. As the NaCl concentration is cycled three times between 0 and 0.05 M, the d spacing changes from approximately 30 nm to about 20 nm.

Interestingly, manipulation of the ionic strength of the solution allows nanoprisms of varied edge lengths to be assembled into lamellar superlattices. As synthesized, prisms with small edge lengths do not naturally assemble into 1D lamellar crystals in solution. Whereas the SAXS patterns of prisms with edge lengths greater than 145 nm possess four evenly spaced diffraction peaks, those with edge lengths smaller than 120 nm do not (SI Appendix, Fig. S6). The reason for this discrepancy is that, for smaller prisms, the free energy at the minimum is not deep enough to overcome thermal energy (SI Appendix, Fig. S7). Our model suggests that a reduction of the electrostatic interaction will lower the net potential energy at the minimum, thereby leading to favorable formation of lamellar superlattices. To reduce the electrostatic interaction, we decreased the Debye length by adding NaCl to the nanoprism solutions. Triangular nanoprisms with edge lengths of 120, 98, and 80 nm assembled into ordered lamellar superstructures when NaCl was added and brought to concentrations of 0.05, 0.10, and 0.15 M, respectively (SI Appendix, Fig. S8). The smaller the edge length of the prism, the more salt that was needed to overcome the electrostatic interaction and induce assembly, confirming that the depletion interaction is relatively weaker for smaller prisms.

Once a fundamental understanding of the role of the depletion interactions and electrostatic interactions in the assembly of nanoprisms was achieved, the knowledge was applied to develop a purification procedure for the triangular gold nanoprism synthesis. The synthesis developed by Millstone et al. (29) produces both triangular nanoprisms and spherical particles that are difficult to separate, particularly for prisms with small edge lengths. However, by selectively inducing the prisms to assemble into 1D lamellar superlattices through the addition of NaCl, they can be removed from solution using centrifugation and resuspended in 0.05 M CTAB to create highly pure colloidal solutions of nanoprisms. As mentioned above, smaller edge length nanoprisms require a greater amount of NaCl to induce their ordering into lamellar crystals for purification. To purify nanoprisms in 0.05 M CTAB solutions with edge lengths of 120, 100, 80, 60, and 40 nm, NaCl was added to concentrations of 0.2, 0.2, 0.4, 0.4, and 0.8 M, respectively. After 1 h, the samples were centrifuged at 2,100 × g for 15 s. The supernatant was removed and the pellet containing the assembled prisms was resuspended in a solution of 0.05 M CTAB. In the absence of NaCl, the nanoprisms no longer form lamellar crystals and instead redisperse in solution.

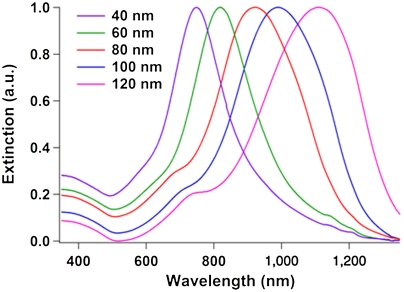
UV-visible near-infrared (UV-vis-NIR) spectroscopy was used to confirm that the triangular nanoprisms were purified from the spherical nanoparticles. The UV-vis-NIR spectrum of an as-synthesized solution of gold nanoprisms contains two primary plasmon resonances: one at approximately 530 nm due to the spherical nanoparticles and another between 700 and 1,300 nm (exact position depends on edge length) due to the nanoprisms (29) (SI Appendix, Fig. S9). The dipole plasmon resonance peak blue-shifts for smaller edge length prisms (51). After purification, the UV-vis-NIR spectra of the samples no longer contain a peak around 530 nm from the dipole resonance of spherical gold particles, indicating spectroscopically pure samples of gold nanoprisms (Fig. 6). Although NaCl has been used to separate gold nanoplates in previous works, the separation effect was attributed to differences in the electrostatic-based aggregation of nanoplates and nanospheres (34). Additionally, the separation procedure took 6 h and resulted in severe etching of the nanoplates. Other methods using short-range depletion forces, coupled with gravitational creaming, have been shown to separate microdisks from microspheres in the past, but generally require several separation steps to achieve significant purity and can take several days (27). In our case, purification can be achieved in as little as 1 h and does not disrupt the original geometry of the triangular prisms, which is particularly important when studying their optical properties, as they are very sensitive to shape and tip sharpness (52).

Fig. 6.

Normalized UV-vis-NIR spectra of purified nanoprisms with edge lengths of 40, 60, 80, 100, and 120 nm. The absence of a peak around 530 nm, indicative of the presence of spherical gold nanoparticles, shows that the nanoprisms are spectroscopically pure.

Conclusions

Understanding the interparticle interactions that control the assembly of anisotropic nanostructures is essential for the design of superlattices of these structures with unique collective properties. In this work, we have shown that depletion forces acting in synergy with electrostatic forces are a powerful tool for assembling nanoscale anisotropic particles with interparticle spacings on the order of or larger than the dimensions of the nanoparticle building blocks. Using highly anisotropic nanoprisms in a solution of CTAB micelles, we were able to access a regime wherein two fundamental forces are of comparable strength, leading to unique one-dimensional superlattice structures which are, themselves, stable colloids. We have shown, both experimentally and theoretically, that the anomalously large d spacings of the lamellar superlattices are the result of an equilibrium between attractive depletion and van der Waals forces and repulsive electrostatic forces. We have also shown that the lattice parameters of the lamellar crystals are reversibly tunable between 17 and 30 nm, almost a factor of two, simply by changing the concentration of the CTAB surfactant, the temperature, and/or the ionic strength of the solution. Finally, by inducing the lamellar ordering of gold nanoprisms in solution, we have developed a methodology to efficiently separate nanoprisms from spherical nanoparticles formed concomitantly during synthesis. The stimuli-responsive behavior of the nanoprism superlattices suggests that this method of assembling nanoscale colloids could potentially be useful for reconfigurable materials that are capable of changing their properties in response to several intensive and extensive variables. Furthermore, because depletion-force-based assembly of anisotropic particles requires only charged particles and a nonadsorbing charged depletant molecule, this method should be applicable to a wide range of particles with extended flat faces, independent of particle composition.