Enabling high-temperature nanophotonics for energy applications

Abstract

The nascent field of high-temperature nanophotonics could potentially enable many important solid-state energy conversion applications, such as thermophotovoltaic energy generation, selective solar absorption, and selective emission of light. However, special challenges arise when trying to design nanophotonic materials with precisely tailored optical properties that can operate at high-temperatures (> 1,100 K). These include proper material selection and purity to prevent melting, evaporation, or chemical reactions; severe minimization of any material interfaces to prevent thermomechanical problems such as delamination; robust performance in the presence of surface diffusion; and long-range geometric precision over large areas with severe minimization of very small feature sizes to maintain structural stability. Here we report an approach for high-temperature nanophotonics that surmounts all of these difficulties. It consists of an analytical and computationally guided design involving high-purity tungsten in a precisely fabricated photonic crystal slab geometry (specifically chosen to eliminate interfaces arising from layer-by-layer fabrication) optimized for high performance and robustness in the presence of roughness, fabrication errors, and surface diffusion. It offers near-ultimate short-wavelength emittance and low, ultra-broadband long-wavelength emittance, along with a sharp cutoff offering 4∶1 emittance contrast over 10% wavelength separation. This is achieved via Q-matching, whereby the absorptive and radiative rates of the photonic crystal’s cavity resonances are matched. Strong angular emission selectivity is also observed, with short-wavelength emission suppressed by 50% at 75° compared to normal incidence. Finally, a precise high-temperature measurement technique is developed to confirm that emission at 1,225 K can be primarily confined to wavelengths shorter than the cutoff wavelength.

Ever since photonic bandgaps were predicted to exist in appropriately designed periodic subwavelength structures (1–3)—i.e., photonic crystals (PhCs), significant interest has garnered in recent years to exploit this property. Coupled with the recent advancements in nanofabrication techniques, many applications have been made possible, ranging from room- and cryogenic-temperature optoelectronic devices for development of all-optical integrated circuits (4), to highly sensitive sensors (5), low-threshold lasers (6), and highly efficient light emitting diodes (7). PhCs also enable us to accurately control spontaneous emission by virtue of controlling the photonic bandgap (1, 8). In particular, metallic PhCs have been shown to possess a large bandgap (9–12) and consequently superior modification of the intrinsic thermal emission spectra is readily achievable. This is extremely promising for many unique applications, especially high-efficiency energy conversion systems encompassing hydrocarbon and radioisotope fueled thermophotovoltaic (TPV) energy conversion (13, 14) as well as solar selective absorbers and emitters for the emerging field of solar thermal, including solar TPV (15–18) and solar thermochemical production of fuels (19). The selective emitters can also be used as highly efficient infrared radiation sources for infrared spectroscopy and sensing applications including highly selective gas and chemical sensing (20, 21).

To date, PhCs have been designed to achieve both highly selective narrow-band thermal emission exhibiting wavelength, directional, and polarization selectivity (21–23) as well as wide-band thermal emission spectra close to blackbody within the design range but suppressed emission otherwise (12, 17, 24–27). In this report, we focus on the design, optimization, fabrication, and characterization of the high performance broadband selective emitter with critical emphasis on obtaining optimized optical response providing the necessary bandwidth that translates into higher power density imperative for large scale solid-state energy conversion, high-temperature performance, and long-range fabrication precision over large areas. In this respect, notable experimental efforts include two-dimensional (2D) square cavities fabricated on tungsten (W) using e-beam lithography and fast atom beam etching (26) and the three-dimensional woodpile stacked W PhC fabricated using a layer-by-layer modified silicon process (12, 25, 28).

However, in order to effectively apply nanophotonic materials in emerging high-temperature large scale energy conversion systems, it is imperative to simultaneously achieve high-temperature stability, uniquely sharp contrast between regions of enhanced and suppressed emission, and precise fabrication of periodic nanostructures over large areas while maintaining macroscopic correlation lengths and ensuring a contamination free surface. Our proposed design overcomes these challenges, thus paving the way to what is an emerging new field of high-temperature nanophotonics for energy conversion applications. Specifically, we demonstrate how thermal emission of our PhC design can easily be optimized for a particular system via Q-matching, whereby the absorptive and radiative rates of the PhC’s cavity resonances are matched, resulting in near-ultimate short-wavelength emittance. We further show how the bandgap edge of our PhC can be tailored to theoretically any wavelength of interest, limited only by intrinsic material properties and fabrication limits, by virtue of controlling the cavity’s resonant frequency. Using this, we present PhC designs capable of an emission contrast of about 4∶1 over 10% wavelength separation, a marked improvement to previously reported work with an approximate emission contrast of 2∶1 (12, 24–28). We further show how we are able to achieve designs with maximum emission at larger wavelengths previously unattainable with this material platform. Next, we present representative designs fabricated using standard nanofabrication techniques amenable to wafer scale batch processing. Results of optical characterization using a precise high-temperature thermal emission measurement technique are then shown. Instead of using physical methods for surface temperature measurement, which is extremely challenging at such high temperatures (29), resulting in erroneous estimations, we developed an estimate of the surface temperature accurate to within ≃3% relative uncertainty. Finally, we confirm that emission at 1,225 K can be primarily confined to wavelengths shorter than the cutoff wavelength.

Design

The majority of the reported selective emitter/absorber designs have focused extensively on multilayer and multimaterial structures (30) as well as metal-dielectric composite coatings (cermets) (31). However, these designs cannot operate at high temperatures (> 1,000 K) due to thermomechanical stresses between layers and interfaces, and chemical reactions between the constituent elements that are initiated at elevated temperatures. Even 3D layer-by-layer structures, such as W woodpile PhC (12, 25, 28), contain multiple interfaces, thus making them fragile. To overcome the aforementioned shortcomings while still maintaining large index contrast, we select a material platform consisting of robust, single-element, broadband tunable spectrally selective infrared emitters composed of a 2D square array of cylindrical holes with period a, radius r, and depth d etched through a large area metallic surface. This relatively simple design allows one to simultaneously achieve near-blackbody emittance at short wavelengths as well as emittance almost as low as a polished metal at long wavelengths, with a sharp cutoff separating the two regimes. This is especially critical for high-efficiency energy conversion.

In general, the enhancement in emission is achieved by coupling into resonant electromagnetic modes. In such systems, the cutoff wavelength is approximately given by the fundamental mode of the cylindrical metallic cavity (26, 27, 32). For radiation with frequencies larger than the fundamental cavity resonant frequency, enhanced absorption occurs due to the increased interaction time with the absorptive metal. On the other hand, radiation with frequencies lower than the fundamental cavity resonant frequency is forbidden from entering the cavities, thus maintaining the desired wavelength selectivity. In this regime, the effective medium theory holds; the increased surface area fraction of air-to-metal decreases the index contrast, resulting in a slightly lower reflectivity. Using these guidelines, we can easily shift the cutoff wavelength by selecting the appropriate r and d. Nevertheless, reliance on these design guidelines alone is not sufficient in maximizing the emittance peaks below the designated cutoff. To further enhance the selective emitter’s performance, we have developed an analytical approach based on coupled-mode theory (33) to select the appropriate r, d, and a. Following this approach, it is found that complete absorption of incident radiation occurs when the radiative (Q_rad) and absorptive quality factors (Q_abs) of the photonic crystal cavity resonances are matched—i.e., satisfying the Q-matching condition (34). If free space radiation is undercoupled to the PhC cavity resonances (Q_rad > Q_abs), insufficient radiation enters the cavity, resulting in suboptimal absorption. On the other hand, if free space radiation is overcoupled to the PhC cavity resonances (Q_abs > Q_rad), the radiation escapes before it is completely absorbed.

In order to obtain maximum peak emittance that approaches the theoretical blackbody in the vicinity of the designated cutoff wavelength, the Q-matching condition for the fundamental mode has to be satisfied. Following the analysis in ref. 34, it is found that for a particular choice of r, there is only one value of d that satisfies the Q-matching condition. Hence, for a particular cutoff wavelength, an optimal pair of r and d exists. Note that a only strongly affects the emittance at wavelengths close to or smaller than the periodicity, whereupon diffracted plane waves and surface plasmon modes start to appear. Because the enhancement in emittance is dominated by the Q-matched electromagnetic cavity modes, surface plasmons can safely be ignored in the analysis (34). In contrast, diffractive modes cause the emittance to degrade. This can be understood through the coupled-mode picture, whereby the resonances couple to a number of planewaves fixed by the period. Therefore, the cavity’s Q_rad decreases as there are more channels to couple to, resulting in suboptimal absorption. It is thus important to choose the smallest a possible for a fixed r (limited only by sidewall thickness that must be thicker than the skin-depth of the metal to preserve the wavelength selectivity of the emitter) such that multiple resonances only re-emit back into the incident channel (i.e., above the diffraction limit) in order to achieve the intended broadband high emittance. Otherwise, higher-order resonances may couple into multiple channels corresponding to diffraction, thus increasing total reflectivity. However, adequate sidewall tolerances (≃150 nm) must be included to ensure robustness to fabrication disorders, hence a would have to be slightly larger than optimal. In addition, very small sidewall thicknesses could potentially lead to breakage (due to diffusion, melting, or mechanical stress), which would destroy the connectivity of the structure, leading to a different optical response.

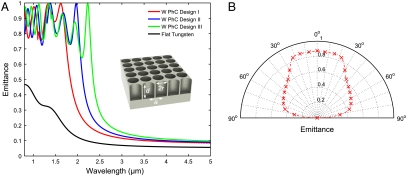
Our approach is directly applicable to any highly reflective metallic material, for instance platinum, silver, molybdenum, tantalum, etc., because the magnitude of the first emittance peak is controlled solely by Q-matching. For this investigation, we select W, firstly due to its superior ability in withstanding high temperatures (high melting point of 3,695 K, low vapor pressure of 1 Pa at 3,477 K), which makes it particularly suitable for very high-temperature applications with proper vacuum packaging. Specifically, we select 99.999% pure single crystal W to ensure superior optical performance and minimal surface diffusion at high temperatures. In addition, W has an intrinsically low emissivity at wavelengths greater than 2.5 μm as shown in Fig. 1A. Suppression of these photons is vital for higher TPV system efficiencies since these photons are generally below the bandgap of current state of the art low bandgap TPV cells. More importantly, the increasing emissivity below 2.5 μm due to interband transitions also enables us to easily enhance emission in the wavelength range 1.5–2.5 μm important for TPV energy conversion. This intrinsic wavelength selectivity is also necessary for application as an efficient solar selective absorber characterized by strong solar absorption and low thermal emittance.

Fig. 1.

(A) Simulated normal emittance for W PhC Design I (r = 0.45 μm, a = 1.10 μm, d = 1.50 μm), W PhC Design II (r = 0.55 μm, a = 1.30 μm, d = 2.10 μm), W PhC Design III (r = 0.625 μm, a = 1.40 μm, d = 2.80 μm) with the first emittance peak in the vicinity of 1.7, 2.0, and 2.3 μm, respectively. A dramatic enhancement of the emittance (i.e., near blackbody performance below the cutoff wavelength) is evident compared to flat tungsten. (B) Average emittance below the cutoff wavelength (i.e., λ ≤ 2 μm) as a function of polar angle for W PhC Design II. As can be seen, the emitter mainly radiates in the direction close to normal.

Initial design choices, guided by coupled-mode theory to select the appropriate dimensions for a particular cutoff wavelength, are followed with numerical simulations to obtain accurate emittance of the PhC, which guides us toward the optimal design. Simulations of electromagnetic properties were conducted following the same methods as outlined in ref. 18. We employ a finite difference time-domain (FDTD) simulation (35) implemented via MEEP, a freely available software package developed at MIT (36). A plane wave is launched from the normal direction and propagated through space. On each grid point of a flux plane defined at the front and back of the computational cell, the electric and magnetic fields are Fourier-transformed via integration with respect to preset frequencies at each time step. At the end of the simulation, the Poynting vector is calculated for each frequency and integrated across each plane, which yields the total transmitted and reflected power at each frequency (36). The dispersion of W is captured via the Lorentz–Drude model, fit both to room temperature (37) and elevated temperatures (38), following the procedure outlined in ref. 39. Apart from the approximations of material dispersions and grid discretization, these calculation methods are exact. The emittance of each structure can be calculated from the absorptance computed above via Kirchhoff’s law of thermal radiation, which states that the two quantities must be equal at every wavelength for a body in thermal equilibrium (40).

Additional simulations were also performed to model both structural rounding effects arising from high-temperature surface diffusion and structural imperfections arising during the fabrication process. The results on rounding effects of sharp structural edges showed that our PhC slab design is very robust with minimal changes in performance. For the case of fabrication disorders, exposure of the interference lithography patterns away from 90 ° could be captured by devising 2D periodic supercells with basis vectors separated by angles equal to the actual angular separation. Significant deviations from 90 ° were observed to change the peak separations. We also simulated elliptical holes with the eccentricity and orientation predicted for IL at those angular separations (41). However, as long as the areas of the holes were kept constant, these slight distortions were not observed to have a significant effect for angular separations close to 90 °. Furthermore, disorder was incorporated with both inclusion and removal of W at random points along the perimeter of each air hole within a supercell, designed such that the average change in air hole area is zero, and the average size of the deviation is δ. For δ < 0.05a, very little change in the ensemble-averaged emittance was observed for air hole radii r < 0.45a, which implies that our structure is robust with respect to small amounts of fabrication disorder.

To illustrate the unprecedented control that resonant Q-matching brings to shaping the thermal emission, we show in Fig. 1A three different W PhC designs that exhibit peak emittance approaching blackbody at 1.7 μm, 2.0 μm, and 2.3 μm, obtained solely by matching the radiative and absorptive rates of the first cylindrical cavity resonance. These designs demonstrate the ease of simultaneously matching the electronic bandgaps and photonic bandgaps in TPV systems utilizing gallium antimonide (GaSb), indium gallium arsenide (InGaAs), and indium gallium arsenide antimonide (InGaAsSb) photovoltaic cells (42). When optimized for these TPV systems, spectral efficiencies (ratio of useful emitted power above the bandgap to total emitted power) of ≃76% can be achieved compared to ≃35% for a greybody (e.g., silicon), which is slightly more than a factor of two improvement. For an idealized TPV system at 1,500 K, this translates to ≃19% overall heat-to-electricity efficiencies, compared to ≃9% for a greybody. In addition, they can be utilized as efficient high-temperature solar absorbers, of which the flexibility of shifting the cutoff readily enables optimization of solar thermal energy conversion systems depending on operating temperatures and solar concentration (17, 18). In particular, W PhC Design II is capable of achieving a thermal transfer efficiency (ratio of net absorbed solar radiation to total incident solar radiation) of ≃72% at 1,000 K under solar concentration of 500 suns. Regardless of the application, resonant Q-matching allows us to quickly find a near-optimal initial design, which can then be refined for a specific goal using various optimization tools.

Simulations at oblique angles shown in Fig. 1B also demonstrate the potential of our metallic PhC slabs as selective absorbers for solar thermal applications, which substantially benefit from both frequency and angular selectivity (43, 44). Frequency selectivity is strong; the location of the resonant peaks does not change with wavevector, and Q-matching is satisfied up to the diffraction threshold. Angular selectivity arises from the constancy of the resonant peaks and the decreasing diffraction threshold as a function of incident polar angle. Above the diffraction threshold, absorptance decreases because there are more channels to reflect back to, resulting in a smaller Q_rad, thus destroying Q-matching. Therefore, at larger incident polar angles, the in-band absorption region decreases and has a lower average absorptance.

Experimental Results and Discussion

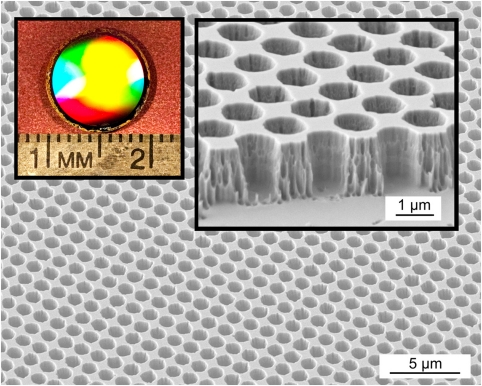
To demonstrate the performance and fidelity of our theory and computationally guided PhC design, two samples are fabricated from single crystal W to produce selective emitters with the first emittance peak at wavelengths of 1.7 μm and 2.0 μm (details of the fabrication procedure can be found in Materials and Methods). Images of the latter are shown in Fig. 2. As can be seen, long-range uniformity is achieved across a large area. In order to determine the depth of the cavities accurately, tapping mode atomic force microscopy (Veeco Nanoscope IV Multimode AFM with Nanoscience Instruments High Aspect Ratio Silicon AFM tips) is used. For the fabricated 1.7 μm (W PhC Sample I) and 2.0 μm (W PhC Sample II) peak emittance designs, the depth is found to be approximately 1.3 μm and 1.6 μm, respectively.

Fig. 2.

Scanning electron micrograph of fabricated W PhC Sample II (r = 0.55 μm, a = 1.40 μm, d = 1.60 μm) over a large area, showing excellent uniformity. Interference lithography and standard reactive ion-etching techniques are used to fabricate the samples. (Left Inset) Digital photo of the full 1-cm-diameter sample. (Right Inset) Magnified cross-sectional view of W PhC Sample II.

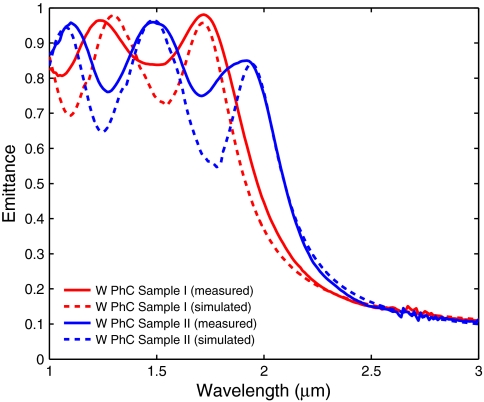
The room temperature normal emittance of the fabricated samples, approximated via Kirchhoff’s law from near-normal reflectance measurements obtained using the OL 750 spectroradiometer, are compared with FDTD simulations in Fig. 3. As can be seen, excellent agreement is seen between the measurements and the simulations; the resonant peaks match in wavelength as well as magnitude. The slight broadening and dampening of the resonances are expected due to small nonuniformities, including slightly uneven profile of the cavities and sidewall disorder due to the isotropic stochastic nature of the chemical wet etching technique used. Nevertheless, the performance is almost unaffected, and this shows the robustness of the design to fabrication disorders. In fact, this brings the emitter closer to blackbody performance below the cutoff wavelength, which translates into higher power density for energy applications. Also, due to the limitations of the RIE machine we are using, this is the deepest that we are able to etch into W, thus limiting the magnitude of the peak intended at 2.0 μm. This, however, could easily be circumvented with access to a DRIE tool.

Fig. 3.

Measured (solid lines) and simulated (dotted lines) room temperature near-normal emittance of the fabricated W PhC Sample I (r = 0.48 μm, a = 1.22 μm, d = 1.30 μm) and W PhC Sample II (r = 0.55 μm, a = 1.40 μm, d = 1.60 μm). The emittance is approximated from measurements of near-normal specular reflectance via Kirchhoff’s Law.

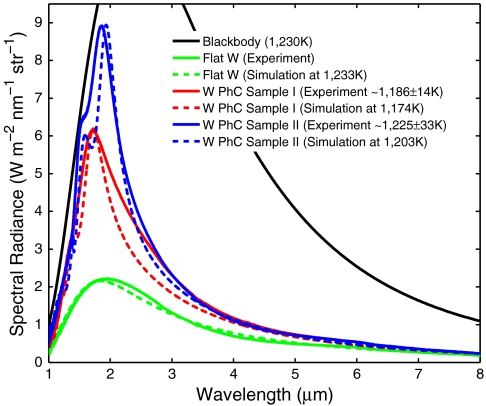
To demonstrate the viability of the approach at high temperatures, thermal emission data are also obtained by electrically heating the sample in an evacuated chamber and directing the emitted radiation into a Fourier transform infrared spectrometer (FTIR) (for more details, please refer to Materials and Methods). The raw measurements are calibrated by obtaining emission measurements from a calibrated blackbody source (Omega BB-4A) at two temperatures, which then allows the instrument response function and background radiation at each wavelength to be calculated and, more importantly, the absolute normal spectral radiance of the samples to be extracted (45). We then only need to know the surface temperature to compare the experimental measurements to simulations.

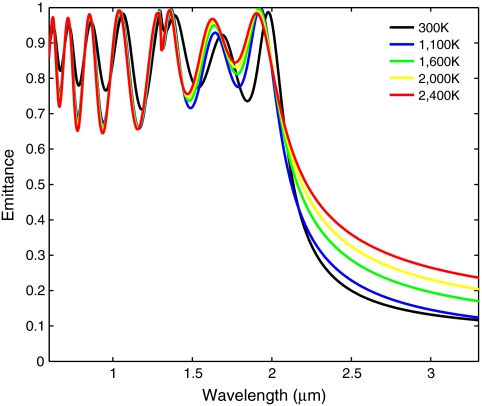
An accurate measurement of surface temperature using physical methods is extremely challenging at such high temperatures (> 1,000 K) due to the large temperature gradients and small samples involved (29), leading to erroneous estimations. Nevertheless, due to the temperature insensitivity of the emittance of the 2D metallic PhCs in the vicinity of the resonance peaks, as shown in Fig. 4, we are able to rely on room temperature emittance (ϵ_room) measurements to accurately estimate the surface temperatures of our samples during the high-temperature measurements. For instance, the first resonance peak has ϵ_room ≃ 0.98, while at higher temperatures, the change in emittance of this peak, Δϵ, is not more than 0.05. This is highly unexpected as the dielectric constant of W varies significantly with temperature. In fact, the emittance of flat W at room temperature and at high temperatures can differ by more than 80% (38). However, due to the relatively deep holes of Q-matched cylindrical cavities, the change in Q_abs is small with respect to temperature. This is because deep hole modes interact more weakly with the metal’s surface. Hence, Q_abs and Q_rad are still fairly well matched. Consequently, the emittance in the vicinity of the resonances stays approximately constant with temperature. This allows us to approximate the emittance at high temperatures, ϵ, with the following:

[1]

where Δϵ is the associated uncertainty of the emittance at high temperatures given ϵ_room is used as the estimate. To determine the uncertainty in the temperature, ΔT, given the uncertainty in the emittance at high temperatures, Δϵ, we start with the definition for ϵ(λ,T), the emittance of the sample:

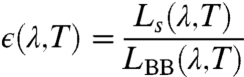[2]

where λ is the wavelength, T is the absolute temperature, and L_s(λ,T) and L_BB(λ,T) are, respectively, the spectral radiance of the sample and a blackbody. Hence, L_s is given by:

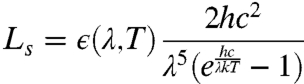[3]

where h is Planck’s constant, k is Boltzmann’s constant, and c is the speed of light. T is then given by:

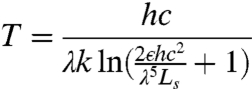[4]

Given a measurement L_s and the emittance estimate of ϵ ≃ ϵ_room around the regions of resonances, we can obtain the uncertainty in temperature using the following:

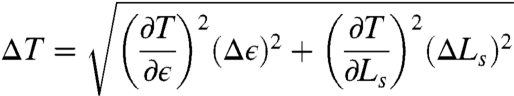[5]

Extensive calibration of our thermal emission measurement setup with a calibrated blackbody source at various temperatures showed that our spectral radiance measurements are accurate to ΔL_s/L_s < 1%. Because this is small in comparison to Δϵ/ϵ, the relative uncertainty in T can be approximated by:

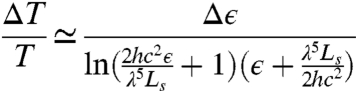[6]

The approximation scheme described can be applied, for instance, around the resonant wavelength of 2 μm for W PhC Sample II, where ϵ_room ≃ 0.85 as shown in Fig. 3. Even though the expected Δϵ as deduced from Fig. 4 is closer to 0.05 for perfectly Q-matched structures, a larger Δϵ of 0.15 is chosen here to reflect improvement in Q-matching expected for less than ideal structures. Even then, these parameters yield an estimate of the surface temperature of W PhC Sample II to within a respectable ≃3% relative uncertainty, or ≃33 K absolute uncertainty, as can be determined using Eq. 6. With these temperature estimations, we are then able to compare our experimental results to simulations. The results agree extremely well as shown in Fig. 5. Note that for temperature estimation, we have neglected the small but experimentally observable increase in the fundamental mode’s resonant frequency of ≃3% at high temperatures, because the analysis focuses on the constancy of the emittance magnitude. The increase is primarily due to the reduction of the skin depth at higher temperatures, leading to approximately 3% increase in the resonant frequency as can be seen in Fig. 4. Geometry changes due to thermal expansion can safely be neglected, because W has a very low thermal expansion coefficient of 6 μm m^-1 K^-1 (46), which results in geometry changes of less than 1%.

Fig. 4.

Comparison of simulated normal emittance of W PhC Design II at different temperatures. The simulations are performed using Lorentz–Drude parameters fitted to experimentally measured emittance of flat W at various temperatures (38). The magnitude of the emittance peaks in regions of cavity resonances are very weakly affected by changes in temperature. Hence, we are able to use the approximation that the room temperature emittance in the vicinity of the cavity resonances remains unchanged at high temperatures, resulting only in a small relative uncertainty in the temperature, which can be determined using [6].

Fig. 5.

Comparison of measured and simulated normal emitted spectral radiance of fabricated samples. The thermal emission data are obtained by electrically heating the sample to ≃1,200 K in an evacuated chamber and directing the emitted radiation with a collection angle of 5° from the normal into a Fourier transform infrared spectrometer. Simulations are performed using Lorentz–Drude parameters fitted to experimentally measured emittance of flat W at ≃1,200 K (38). The thermal emission measured from the samples agree well with simulations and demonstrates the suppression of emission above the cutoff wavelength and near blackbody performance below the cutoff wavelength.

The samples are also subjected to repeated thermal cycling (i.e., heated to ≃1,200 K for an hour) before allowing to cool to room temperature. After several thermal cycles, reflectance measurements show no measurable difference in the optical properties. Scanning electron micrographs also show the W PhC samples keeping its original microstructure, including the ≃300 nm sidewall thickness (i.e., exhibiting no evidence of surface diffusion) thus demonstrating its stability at high temperatures under vacuum. We have also performed surface diffusion simulations at 1,100 K using the level-set method (47) and surface diffusion parameters from ref. 48. Results indicate optical properties that suffer only 2% degradation over 3 yr, demonstrating its robustness to surface diffusion. Though our experiments indicate no degradation over 10 h, further work is being done to address stability issues over longer time scales (years).

Conclusion

In summary, we have demonstrated high operation temperatures of at least 1,200 K with our W PhC selective thermal emitters that are produced over large areas with macroscopic long-range order using conventional CMOS-compatible nanofabrication techniques already demonstrated at scale. The selective emitters exhibit low emittance at long wavelengths and near-blackbody emittance at short wavelengths, with a sharp cutoff in between, as predicted by numerical modeling and optimization. The spectral properties of metallic PhCs, including the cutoff wavelength and magnitude of the high emittance region, are maintained at high temperatures, demonstrating the mechanical and optical robustness of our design with respect to temperature. The emittance can be easily tailored and optimized by suitable choice of the dimensions of the cavities such that the condition for resonant Q-matching is achieved, as governed by coupled-mode theory. As an example, we have shown theory and computationally guided designs optimized for use in TPV systems employing cells with different electronic bandgaps. They are also robust with respect to experimental levels of disorder and impurities. Our PhCs provide the platform necessary to realise high-temperature nanophotonics for energy applications, ranging from efficient solar absorbers for solar thermal applications (16–19), which is characterized by good solar absorption (low reflectance for wavelengths smaller than cutoff wavelength usually in the vicinity of 1.5–2.5 μm depending on operation temperature and solar concentration) and low thermal emittance (high reflectance for wavelengths larger than the cutoff wavelength and angularly selective absorption), to highly efficient selective emitters that are important for realizing both high efficiency and high power density TPV energy conversion systems (14, 15). In addition, they can be applied as a high-efficiency near- to mid-infrared radiation source for infrared spectroscopy, night vision, as well as miniaturized on-chip for sensing applications including highly selective gas and chemical sensing (20, 21).

Materials and Methods

Fabrication of Tungsten Photonic Crystal.

The W PhC’s are fabricated through interferometric lithography using a trilayer resist process (49) with a thin layer of chrome as the hard mask for etching into W using carbon tetrafluoride (CF₄) based reactive ion etching (RIE). For this investigation, we start with single side polished single crystal W samples 10 mm in diameter (Princeton Scientific). Firstly, a thin layer of chrome (Cr) is e-beam deposited on top of the single crystal W substrate, which is then subsequently spin coated with 300 nm of BARLi antireflection coating (AZ Photoresist), followed by 20 nm e-beam deposition of silica, and finally spin coating 250 nm of THMR-iNPS4 photoresist (OHKA America). The photoresist is exposed using a Lloyd’s mirror interference lithography system with expanded beam from a 50 mW 325 nm HeCd Laser. The exposure is performed twice, with the second exposure perpendicular to the first to create a square array of cylindrical cavities. The interference angle is chosen such that we obtain the desired periodicity. After photoresist development, the diameter of the cylindrical cavities is much smaller than in the desired final structure.

Next, the holes produced in the resist layer are transferred into the silica and antireflection coating layers via CF₄ and He-O₂ based reactive ion etching (RIE), respectively, using the Plasma Therm 790. With the Cr mask now exposed, we immerse the sample into Cr-7 (Cyantek) liquid etchant. The duration of the wet etch is calibrated to obtain the desired diameter on the Cr hard mask. Note that to decrease sidewall roughness, the diameter of the holes can first be increase via isotropic etching of the photoresist with an oxygen based plasma asher. Subsequently, the silica and antireflection coating layers are removed. The Cr hard mask allows pattern transfer to the W substrate using a CF₄-O₂ based RIE. Etching of W is optimized with the following parameters: flow rate 6.7 sccm of CF₄ and 1 sccm of O₂ at 10 mTorr pressure with plasma conditions at 250 V and 90 W. The etch rate is about 10 nm of W per minute and the etch selectivity ratio to the Cr hard mask is approximately 10∶1 under these conditions. It is important to ensure complete removal of the Cr layer to ensure long-wavelength emittance remains low as predicted by simulations. Note that due to the limitations of the RIE machine we are using, we are unable to etch deeper than ≃1.6 μm. This however could easily be circumvented with access to a DRIE tool.

High-Temperature Emittance Measurements.

The W PhC sample is mounted on top of a HeatWave Labs 1-inch diameter UHV electrical heater (rated to 1,200 °C) enclosed in a vacuum chamber evacuated to a base pressure of 10^-6 Torr with a IR transparent CaF₂ window, which allows radiation to exit. While delivering power to the heater, forming gas (5% H₂-N) is flowed to achieve a process pressure of around 30 mTorr to further ensure samples do not oxidize. Radiation exiting from the CaF₂ window is then collimated into the emission port of a Nexus 870 FTIR using two parabolic mirrors with a collection angle of 5° measured from the normal. By using an aperture in between the mirrors, we ensure that the signal obtained originates solely from the W PhC sample surface. The FTIR’s Deuterated Triglycine Sulfate detector was used for the emission measurements.