Beside the point: motor adaptation without feedback-based error correction in task-irrelevant conditions

Abstract

Adaptation of movement may be driven by the difference between planned and actual motor performance, or the difference between expected and actual sensory consequences of movement. To identify how the nervous system differentially uses these signals, we asked: does motor adaptation occur when movement errors are irrelevant to the task goal? Participants reached on a digitizing tablet from a fixed start location to one of three targets: a point, an arc, or a ray. For the arc, reaches could be in any direction, but to a specific extent. For the ray, reaches could be to any distance, but in a targeted direction. After baseline reaching to the point, the direction or extent of continuous visual feedback was perturbed during training with either a cursor rotation or gain, respectively, while reaching to either the ray (goal = direction) or the arc (goal = extent). The perturbation, therefore, was either relevant or irrelevant to the task goal, depending on target type. During interspersed catch trials, the perturbation was removed and the target switched back to the point, identical to baseline. Although the goal of baseline and catch trials was the same, significant aftereffects in catch trials indicated behavioral adaptation in response to the perturbation. Adaptation occurred regardless of whether the perturbation was relevant to the task, and it was independent of feedback control. The presence of adaptation orthogonal to task demands supports the hypothesis that the nervous system can rely on sensory prediction to drive motor learning that can generalize across tasks.

over the last century, much of what we know about the underlying mechanisms of motor learning have emerged from experimental paradigms that dissociate visual and motor information during goal-directed movement. For example, reaching and throwing behavior adapts in response to altered visual feedback, as evidenced by studies using prism goggles (see Kornheiser 1976 for review) and computer-based interfaces (see Krakauer 2009 for review). In both cases, there is discordance between the visual feedback about one's actual performance and the intended performance, and task accuracy is reduced. Over time, however, one adapts to the altered visual input and can accurately perform the task. As such, the goal of adaptation could be to minimize errors in task performance, driven by the need to update behavior in response to environmental or task changes (Wolpert et al. 2001). Conceptually, this theory of motor adaptation relies on movement errors and has been defined as the modification of a movement from trial-to-trial based on error feedback (Martin et al. 1996).

The motor system may be using these seen task-based errors to drive adaptation, but more recent evidence (Mazzoni and Krakauer 2006; Tseng et al. 2007) suggests an alternate hypothesis, that such improvements in task performance could instead result from minimization of sensory prediction errors. Sensory prediction errors arise from a difference between the predicted and actual sensory consequences of a given motor command (Shadmehr et al. 2010). By dissociating the relevance of online visual feedback of a movement from the goal of the task, we tested whether adaptation occurs due to task-related errors, sensory prediction errors, or both. In this study, the “task” was operationally defined by its goal: to reach the target. While reaching to the target, subjects experienced visuomotor perturbations that were either relevant or irrelevant to the task. “Relevant” perturbations interfered with task performance, inducing errors with respect to the goal, whereas “irrelevant” perturbations theoretically did not interfere with performance by not impeding one's ability to achieve the task goal (Cusumano and Cesari 2006; Scholz and Schoner 1999). We hypothesized that if adaptation to the perturbation was driven by task-related errors, i.e., the difference between intended and actual task performance, then adaptation would only occur with task-relevant perturbations that interfered with performance. Experiencing a task-irrelevant perturbation would not disrupt execution of the intended movement, and therefore no adaptation to the perturbation would be necessary to complete the task. Alternatively, we hypothesized that if visuomotor adaptation was instead driven by sensory prediction errors that reflect the difference between predicted and actual sensory feedback, then adaptation would occur regardless of the perturbation's relevance to the task.

To test these hypotheses, we manipulated the task relevance of the perturbation through the use of a visuomotor rotation and gain (Bock 1992; Krakauer et al. 2000; Roby-Brami and Burnod 1995) that disrupted the direction and extent, respectively, of reaching movements. Until now, visuomotor rotations and gains have been used to perturb visual feedback during reaching movements to a point in space. The goal of these tasks was defined by two dimensions: a specific direction and a specific extent from a given start location. Changes in the direction or extent of visual feedback would both be task relevant, since both perturbations would interfere with task performance and subsequently require subjects to adapt. We have now developed a novel set of experiments in which the goal of the task was often unidimensional: subjects were required to reach only in a specific direction or to a specific extent. During these tasks, only the direction or the extent of visual feedback was perturbed. By doing so, movement errors were induced that were either relevant or irrelevant to task performance and tested whether adaptation occurred in task-irrelevant conditions. Some studies have assessed visuomotor adaptation either by providing feedback only after movement completion or by requiring very fast movements such that subjects did not have the opportunity to make mid-movement corrections (Hinder et al. 2010; Mazzoni and Krakauer 2006). To allow for mid-movement corrections in this study, continuous visual feedback was provided. If what we designed to be “task-irrelevant” perturbations truly were irrelevant to the one-dimensional task, then movements toward the goal would be unaltered during execution and no mid-movement corrections would be necessary. The absence of mid-movement corrections, therefore, would serve as experimental evidence that a given perturbation is irrelevant to the task.

Furthermore, if visuomotor adaptation was driven by sensory prediction errors rather than task-related errors, then adaptation would occur even when perturbations are task irrelevant. We tested the degree of visuomotor adaptation by occasionally presenting “catch trials” during training in which the task goal (target) unexpectedly changed, allowing us to probe the formation of motor memory. Catch trials in this study required control in two dimensions (direction and extent) rather than only one dimension. Significant deviations in catch trials relative to pretraining baseline behavior, even during training in task-irrelevant conditions that did not elicit mid-movement corrections, suggest that the human brain can build motor memories based on sensory prediction errors.

MATERIALS AND METHODS

Subjects

Fifteen healthy human subjects (6 female, 9 male), aged 22.7 ± 2.9 yr, participated in the experiment over the course of 2 consecutive days. All subjects were right-handed, as determined by the Edinburgh handedness inventory (Oldfield 1971). All subjects gave their informed consent, and the experimental protocol was approved by the Washington University Human Studies Committee (HRPO).

Experimental Setup

Subjects sat in a dark room in an adjustable-height chair, facing an apparatus composed of a computer monitor, a mirror, and a digitizing tablet (Intuos3; Wacom, Saitama, Japan). Subjects were instructed to comfortably hold the stylus in their right (dominant) hand, as they would a writing pen. Subjects were positioned such that they could comfortably reach the entire workspace within the tablet. All movements started at the origin of a rectangular coordinate system centered over the workspace. Positive x- and y-dimensions were defined as to the right and forward on the tablet, respectively. A start circle (0.6 cm in diameter), a cursor (0.15 cm in diameter), and a target were projected from a computer monitor onto a horizontal mirror positioned below the monitor. The mirror reflected the visual display such that the projection appeared in the same horizontal plane as the stylus. The cursor represented the two-dimensional (2-D) position of the stylus, which the subject moved along the surface of the digitizing tablet. The virtual reality display was designed and calibrated to ensure that the cursor projection accounted for the mirror (flipped) image (i.e., leftward arm movements corresponded to leftward cursor movement in the same plane) and that the cursor projection was updated in real time. Subjects moved the stylus below the mirror, without vision of the arm; thus the displayed cursor provided continuous visual feedback to the subjects during the experiment.

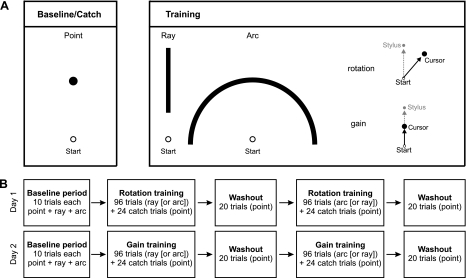
One of three targets was displayed: a point, a ray, or an arc (Fig. 1A). The point target required subjects to move in the forward direction (along subject's midline) and to a specific extent (7 cm) from the start location. The ray only required subjects to move in the forward direction, allowing them to move to any extent. In contrast, subjects were allowed to move in any direction along the arc but were required to move to a specific extent (7 cm). The task goal while reaching to the point target was therefore defined by two dimensions: a direction and an extent. The task goal while reaching to the ray or arc, however, was defined by a single dimension: direction only (ray) or extent only (arc).

Fig. 1.

A: experimental task. During baseline and catch trials, subjects reached to move a cursor to a point target displayed 7 cm from the start position with continuous veridical visual feedback (left). During blocks of training with continuous perturbed visual feedback, subjects reached to move a cursor to a ray or an arc (right). Visual feedback was perturbed by rotating the cursor position (black) clockwise from the stylus/hand position (gray) relative to the start circle or by minifying the cursor position (black) from the stylus/hand position (gray) relative to the start circle. B: diagram of training schedule.

The point target was displayed as a circle (0.6 cm in diameter). The ray was displayed as a line (0.26 cm thick), 0° relative to the start circle, and started 3.8 cm from the start circle; thus subjects were required move a minimum distance in order for us to collect adequate kinematic data. The arc was displayed as a half-circle line (0.26 cm thick) with a radius of 7 cm, centered on the start circle.

Experimental Task

Each subject was instructed to use the stylus to move the cursor from the start circle and stop on or along the target; the target was the point, the ray, or the arc. Once the cursor was held within the start circle (cursor velocity <0.02 m/s) for 1 s, the target turned from red to green, acting as a “go” signal for the movement to the target. Movement onset was defined as the time at which cursor velocity exceeded 0.02 m/s after the go signal. Once the movement was completed (cursor velocity <0.02 m/s), the target turned one of two colors based on temporal criteria: if the cursor reached the target within 750 ms from the go signal, then the target turned yellow, indicating a “correct” movement; if the movement time exceeded 750 ms, then the target turned magenta, indicating that the movement was too slow. After each trial, the subject returned the cursor to the start circle and again waited until the target turned green to begin the next movement. Before making any reaches to the ray, each subject was informed that the target was the entire line; thus the only task requirement was to place the cursor anywhere along the ray, regardless of extent. Similarly, for the arc, each subject was informed that the target was the entire line and that the cursor could be placed anywhere along the arc, regardless of direction.

Subjects participated over the course of 2 consecutive days. At the beginning of each day, subjects performed 30 trials with veridical visual feedback. This period comprised 10 trials to each target (point, ray, arc), which served as each subject's baseline performance for that day (i.e., no perturbation). Immediately following the baseline session, subjects underwent a training session in which they performed 96 movements with altered continuous visual feedback. Visual feedback was altered using either a visuomotor rotation (30° clockwise) or a minifying visuomotor gain (minifying factor of 0.7) with respect to the start location. During each training session, subjects moved to either the ray or the arc. All subjects completed sessions of rotation training and gain training to the ray (task goal = move in a targeted direction) and arc (task goal = move to a targeted extent).

All subjects underwent rotation training on day 1 and gain training on day 2. On day 1, subjects were divided into 2 different training groups: 1 group (n = 10) completed 96 trials of rotation training to the arc first, then to the ray; the other group (n = 5) completed 96 trials of rotation to the ray first, then to the arc. Training sessions were separated by 20 washout trials to the point target with veridical visual feedback to wash out any adaptation effects from the previous training session. On day 2, subjects were again divided into two training groups (arc → ray, n = 10; ray → arc, n = 5) and completed a similar schedule during gain training. All subjects, therefore, experienced a directional perturbation (rotation) and an extent perturbation (gain) of continuous visual feedback that was either relevant or irrelevant to the task goal (direction only or extent only), depending on which target they were reaching to (ray or arc).

This study was designed to test whether visuomotor adaptation would occur when perturbations of visual feedback were irrelevant to the task. To dissociate the relevance of the perturbation from the target, we reduced the target to a single dimension: direction (ray) or extent (arc). The nature of our experimental design, therefore, required the use of the point target to truly probe the formation of motor memories under task-irrelevant conditions. By interspersing catch trials in which subjects were required to move in a specific direction and to a specific extent, we were able to test whether subjects were in fact adapting. If subjects were not adapting to the perturbation when it was irrelevant to the task, then subjects would show no change in performance or “aftereffects” when reaching to the point under veridical feedback conditions. Since adaptation to the visuomotor perturbation was not necessary for accurate task performance when the perturbation was irrelevant to the task goal (i.e., experiencing a visuomotor rotation when reaching to the arc or a visuomotor gain when reaching to the ray), one might not exhibit changes in initial direction or extent of movement over the course of many trials of training compared with baseline; thus the widely accepted “performance curve” that depicts changes in behavior over the course of blocked exposure to a perturbation might not adequately reflect degrees of adaptation over time. We therefore used catch trials to determine whether visuomotor adaptation occurred during exposure to a visuomotor perturbation. Catch trials without perturbations have been used previously during dynamic adaptation to quantify the generalizability of the underlying adaptive processes (Donchin et al. 2003; Shadmehr and Mussa-Ivaldi 1994; Thoroughman and Shadmehr 2000) and are emerging as an alternative measure for visuomotor adaptation, as well (Benson et al. 2011; Haith et al. 2008; Saijo and Gomi 2010; Venkatakrishnan et al. 2011). During each training session of our study, we interspersed 24 unpredictable catch trials in which we removed the perturbation and switched back to the point target. Thus, visual feedback in these catch trials was free of any perturbation but was again relevant to both dimensions (direction and extent) of the task. The task conditions during these catch trials were identical to the baseline trials (Fig. 1A, left), enabling us to directly compare training-induced aftereffects with baseline performance before training. The complete training schedule for each day is shown in Fig. 1B.

Kinematic Data

Our custom software recorded the x-y stylus position data to compute the 2-D position of the cursor. Screen redrawing occurred fast enough to maintain the cursor centered on the stylus throughout the movement. Digital data were collected at 100 Hz using a Gateway laptop computer and were stored on disk for further analysis. Custom computer algorithms for experiment control and data analysis were written in MATLAB 7.0.

Position data were digitally convolved with Savitzky-Golay filters to smooth position and to numerically calculate velocities. The smoothing filter had an effective cutoff frequency of 6 Hz. Movement start was determined by identifying the time of peak velocity and then searching backward in time for the first point at which tangential velocity was >0.02 m/s. Movement end was similarly determined by searching forward in time from peak velocity to find the first point at which tangential velocity was <0.02 m/s. To compute average handpaths across numerous trials, we aligned the x- and y-components of velocity from each trial to the movement start time and then averaged the aligned velocities across trials. By taking the cumulative sum of these average x- and y-components of velocity, we obtained the average x- and y-coordinates of hand position, and thus the average handpath, for the trials of interest.

Analyses

Catch trials.

During catch trials, subjects were required to move to the point target with no perturbation. This task condition was identical to baseline. In both types of trials (baseline and catch), we identified the x-y position of the hand (stylus) at 50 ms following peak tangential velocity. Across subjects, peak tangential velocity occurred at 116 ± 91 ms (mean ± SE), which did not vary significantly between baseline and catch trials (P = 0.12). During rotation training, the angular deviation of this position was computed relative to 0° (straight ahead) to determine the initial direction of the movement. Negative angles were clockwise from 0°. If adaptation occurred during rotation training, then the initial direction of movement of a catch trial would be different from that of a baseline trial. During gain training, the distance of this position was relative to the start location. If adaptation occurred during gain training, then the initial extent of movement of a catch trial would be different from that of a baseline trial. The amount of adaptation during training was therefore quantified as the magnitude of these catch trial aftereffects.

Corrective responses.

To evaluate subjects' responses when experiencing rotation and gain perturbations during training, we probed online correction by quantifying the mid-movement corrections. Mid-movement corrections during rotation training were quantified as the maximum perpendicular displacement of the hand relative to the ideal straight-line hand trajectory (Levin 1996). The ideal straight-line hand trajectory (Hollerbach and Flash 1982; Morasso 1981) was defined as the line connecting the hand's x-y location at movement start and at movement termination. The magnitude of perpendicular displacement characterized the degree to which subjects corrected their movements back to the target in response to the angular perturbation; thus larger perpendicular displacements were indicative of more correction of movement direction compared with smaller perpendicular displacements.

During gain training, mid-movement corrections were quantified as the duration of the deceleration phase. Correcting errors in movement extent (i.e., overshoot or undershoot) are known to result in non-bell-shaped velocity profiles that may have multiple peaks (Crossman and Goodeve 1983; Elliott et al. 2001; Milner and Ijaz 1990), reflecting multiple mid-movement corrections before task completion (Meyer et al. 1988; Woodworth 1899). As a result, more time is spent in deceleration during reaching (Milner and Ijaz 1990). Deceleration duration is known to be highly correlated with the incidence of corrective submovements (Carson et al. 1993; Chua and Elliott 1993; Lee et al. 1997; Myall et al. 2008; Wisleder and Dounskaia 2007), particularly during reaching across different extents along a given movement direction with full visual feedback (Carlton 1981; Elliott et al. 1999; Khan and Franks 2000; Woodworth 1899). To quantify the degree of mid-movement corrections in response to gain perturbations, deceleration duration of each movement was defined as the elapsed time between peak tangential velocity and movement completion; longer deceleration durations were indicative of more correction of movement extent compared with shorter deceleration durations. The single temporal variable of deceleration duration was selected for quantifying a corrective period instead of counting submovements, which are identified based on assumptions about their amplitude and duration (Lee et al. 1997; Novak et al. 2002).

Statistical analysis.

JMP 8.0 (SAS Institute, Carey, NC) was used for all statistical analyses. For all data, the Shapiro-Wilk test was used to verify normal distribution, and the criterion for statistical significance was set at α = 0.05. To compare the degree to which subjects adapted to the perturbation during relevant and irrelevant training sessions, we first tested whether the catch trial aftereffect, averaged across all 24 catch trials that occurred during each session of rotation and gain training to the ray and arc, was significantly different from 0 across subjects. Significant aftereffects would indicate that subjects had formed an internal expectation of the visuomotor perturbation over the course of training. Paired t-tests were used to determine significant differences between conditions. For rotation training, catch trial aftereffects (measured in degrees) during training to the ray and arc were compared with baseline performance. For the gain training, catch trial aftereffects (measured in cm) during training to the ray and arc were compared with baseline performance.

To determine the degree of online trajectory modifications in response to the visuomotor perturbation, mid-movement corrections during training were compared with baseline performance. For rotation training, we compared the degree to which subjects corrected for the rotation by averaging perpendicular displacements across subjects both early in training (first 25 trials) and late in training (last 25 trials) to the ray and arc, relative to that before training. During gain training, subjects appeared to adapt in <25 trials (see results); thus deceleration durations were averaged across subjects over the first 10 trials to quantify the degree to which subjects made corrective responses early in training and were compared with before-training values. Average performances in early and late training were compared with average before-training performance using paired t-tests. All values are means ± SE. Average amounts of adaptation and mid-movement correction during training were also compared using paired t-tests to determine whether there was an effect of training schedule (arc → ray vs. ray → arc). Multiple comparisons were accounted for using the Kackar-Harville correction (Kackar and Harville 1984).

RESULTS

Behavioral Adaptation to Task-Irrelevant Perturbations

Rotation training.

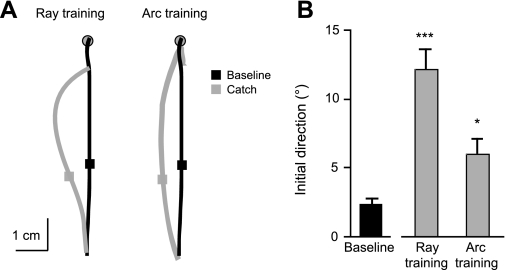
To establish baseline performance, subjects moved to the point before training. These movements were relatively straight and accurate (Fig. 2A, black line). Movements to the same point target were different, however, when they occurred as catch trials during training in a visuomotor rotation session (Fig. 2A, gray line). To adapt to the clockwise rotation of visual feedback during training, subjects moved in the counterclockwise direction, opposite to the direction of the perturbation (Fig. 2A). Although the rotation was constant in all perturbed trials, its relevance to the task differed during movement to the ray vs. the arc. By requiring movements to be made in a specific direction but to any extent, the ray constrained behavior in the dimension of the perturbation, thereby making the perturbation relevant to task completion. The arc, however, specified an extent but not a direction; since the arc provided no constraint in the perturbed dimension, the perturbation was irrelevant to reaching the arc. It is not surprising that subjects showed directional aftereffects when the perturbation was relevant to the task, given that they had to adapt to the rotation to successfully land on the ray. What is more interesting is that subjects adapted the initial direction of their movements to account for the perturbation, even when it was irrelevant to the task and not necessary to accurately land on the arc. Compared with the direction 50 ms after peak velocity during baseline movements to the point target (2.30 ± 0.44°), we observed significant directional aftereffects across subjects during rotation training to both the ray (12.13 ± 1.49°; P < .0001) and the arc (5.95 ± 1.17°; P < .05) (Fig. 2B). Directional aftereffects >1 SD above the baseline mean were observed in 100% of subjects during (relevant) training to the ray and in 60% of subjects during (irrelevant) training to the arc. Although the aftereffects due to ray and arc training were significantly different from each other (P < 0.0001), these results indicate that a lesser yet significant degree of adaptation occurred even when the perturbation was irrelevant to the task.

Fig. 2.

A: average handpaths from individual subjects for all baseline (black) and catch trial (gray) movements to the point during rotation training to the ray and arc. Squares indicate hand (stylus) position at 50 ms after peak velocity. B: mean (±SE) initial direction for all baseline (black) and catch trials (gray) during rotation training to the ray and arc across subjects. *P < 0.05; ***P < 0.0001 compared with baseline trials.

Gain training.

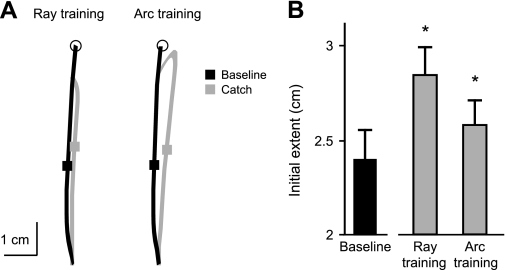
Significant catch trial aftereffects were also observed during gain training. In this case, subjects trained with a minifying gain that required them to move their hand further to move the cursor a specified distance (minifying factor = 0.7). Figure 3A shows that initial extent during catch trials (gray square) was greater than that of baseline movements (black square). By 50 ms after peak velocity, subjects had moved further in the catch trials than in the baseline trials (2.39 ± 0.15 cm) while gain training to the arc (2.55 ± 0.15 cm; P < .05) and to the ray (2.82 ± 0.15 cm; P < .05) (Fig. 3B). Extent aftereffects >1 SD above the baseline mean were observed in 30% of subjects during (relevant) training to the arc and in 60% of subjects during (irrelevant) training to the ray. The average magnitude of aftereffects in catch trials was actually somewhat larger when reaching to the ray than when reaching to the arc during rotation training, although this difference was not significant (P = .12). These catch trial aftereffects indicate that subjects were adapting to the visuomotor gain, even when the gain perturbation was irrelevant to task performance.

Fig. 3.

A: average handpaths from individual subjects for all baseline (black) and catch trial (gray) movements to the point during gain training to the ray and arc. Squares indicate hand (stylus) position at 50 ms after peak velocity. B: mean (±SE) initial extent for all baseline (black) and catch trials (gray) during gain training to the ray and arc across subjects. *P < 0.05 compared with baseline trials.

Task-Irrelevant Perturbations Induced Minimal Mid-Movement Corrections

Rotation training.

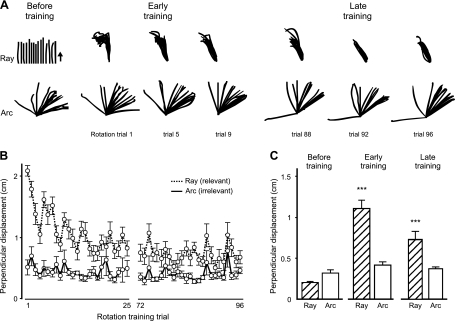
Before training, subjects reached to the ray and arc with veridical visual feedback (see Fig. 1B). When reaching with no visuomotor rotation, subjects moved to various extents along the ray and in various directions along the arc (Fig. 4A, before training). When subjects were initially exposed to the visuomotor rotation (30° clockwise), they made more mid-movement corrections when the unexpected perturbation was relevant to the task of reaching to the ray (dashed line), resulting in larger perpendicular displacement of the hand compared with when reaching to the arc (solid line) (Fig. 4B, first 25 trials). As illustrated in rotation trial 1 in Fig. 4B, subjects clearly corrected the direction of their handpaths more while reaching to the ray than to the arc. Across subjects, perpendicular displacements when reaching to the ray were significantly larger than before training (Fig. 4C, ray, before training, 0.20 ± 0.01 cm vs. early training, 1.11 ± 0.09 cm; P < .0001). By the end of training, subjects appeared to have, by and large, adapted to the visuomotor rotation while reaching to the ray, given that their handpaths were directed counterclockwise from their “before training” movements (Fig. 4A, late training) and perpendicular displacement had decreased (Fig. 4B, last 25 trials). They did, however, continue to make mid-movement corrections when reaching to the ray late in training, given that perpendicular displacement was still significantly greater than before training (Fig. 4C, ray, late training, 0.73 ± 0.10 cm; P < .0001).

Fig. 4.

A: handpaths for each subject (n = 15) with no rotation (left) as well as early (trials 1, 5, and 9; middle) and late (trials 88, 92, and 96; right) in rotation training to the ray and arc. Handpaths to the ray before training are spread for visual purposes only. Arrow indicates direction of reach. Mean (±SE) perpendicular displacement is shown across subjects for each of the first and last 25 rotation training trials to the ray (relevant) and arc (irrelevant) (B) and across all early and late training trials (C). Significant mid-movement corrections occurred during early and late training only when subjects were reaching to the ray. ***P < 0.0001 compared with before training.

Reaches to the arc did not, however, appear to be strongly affected by the perturbation. This result is consistent with the theoretical assumption that the visuomotor rotation induced errors that were irrelevant to the task, when the task did not require moving in a specified direction. With no directional task constraints, subjects chose to move in a range of directions afforded by the arc, as shown in Fig. 4A, even when their intended movement direction continued to be perturbed by the visuomotor rotation throughout the training session. Handpaths when reaching to the arc were not significantly displaced compared with before training trials (Fig. 4C, arc, before training, 0.32 ± 0.04 cm vs. early training, 0.41 ± 0.04 cm; P = .10). During reaching to the arc, movements late in rotation training continued to exhibit minimal mid-movement corrections such that perpendicular displacements were consistently low and not significantly different from those before training (Fig. 4C, arc, late training, 0.37 ± 0.02 cm; P = .30). Thus mid-movement correction in response to the visuomotor rotation occurred only when the rotation was relevant to the task and interfered with performance. Adaptation to the visuomotor rotation, however, occurred regardless of whether the perturbation was relevant or not.

Gain training.

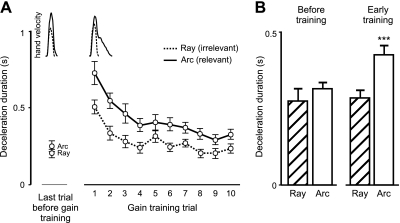
Across subjects, initial exposure to the gain perturbation elicited more mid-movement corrections during reaching to the arc (solid line) than during reaching to the ray (dashed line) (Fig. 5A, first 10 trials). Compared with reaching to the ray, deceleration durations were longer during reaching to the arc with the gain perturbation. For reference, deceleration durations averaged across subjects' last trial before gain training are shown in Fig. 5A. Differences in deceleration duration can be seen in the velocity profiles during reaching to the arc (solid line) and ray (dashed line), as shown in Fig. 5A. Deceleration durations were significantly longer during initial gain training when reaching to the arc, compared with before training (Fig. 5B, arc, before training, 0.31 ± 0.01 s vs. early training, 0.42 ± 0.02 s; P < .0001), indicating that subjects made mid-movement adjustments to the gain perturbation when the task required reaching to a specific extent. When subjects were allowed to move along the ray to any extent and the gain perturbation was irrelevant to the task, they responded minimally to the gain during an ongoing movement. Deceleration duration to the ray was marginally longer on the very first trial of gain training compared with subsequent trials (dashed line, Fig. 5A), but over the course of the first 10 training trials to the ray, deceleration durations were comparable to those before training (Fig. 5B, ray, before training, 0.27 ± 0.03 s vs. early training, 0.28 ± 0.01 s; P = .77). Subjects therefore made minimal online corrections when the gain perturbation was irrelevant to the task.

Fig. 5.

A: mean (±SE) deceleration duration across subjects for the last trial before gain training and for each of the first 10 gain training trials to the ray (irrelevant) and arc (relevant). Tangential velocity profiles inset above plots are from an individual subject reaching to the ray (dashed line) and arc (solid line) during the last trial before gain training and during the first trial of gain training. B: mean (±SE) deceleration duration averaged across all of the first 10 gain training trials compared with mean (±SE) deceleration duration to the ray and arc before training. ***P < 0.0001 compared with baseline.

No effect of training schedule.

To determine whether there was an effect of training schedule, average amounts of adaptation and mid-movement correction during reaching to the arc and ray were compared. There was no significant difference in amount of adaptation between subjects who reached to the arc first and those who reached to the ray first during rotation training (P = .81) or during gain training (P = .17). There was also no significant difference in amount of mid-movement correction between subjects who reached to the arc first and those who reached to the ray first during early (P = .72) or late (P = .86) rotation training, or during early gain training (P = .15).

DISCUSSION

The purpose of this study was to determine whether visuomotor adaptation would occur in the presence of task-irrelevant errors during reaching. We tested whether subjects would adapt to visuomotor perturbations that were irrelevant to the task goal and found that subjects adapted even when the perturbations induced errors that did not interfere with task performance. Our experimental design was unique in that the relevance of perturbation of a movement's real-time visual feedback was dissociated from the task's goal. Instead of training subjects to reach to a point that was defined by a given direction and extent from a constant start location, subjects were required to reach to an arc or a ray. The arc was defined only by a given extent and had essentially no direction constraints (see Fig. 1A). Thus the arc enabled subjects to reach across a range of directions (shown in Fig. 4A, arc), although many reaches tended to be predominantly elbow extension movements, potentially reflecting a preferred strategy used to minimize extent errors due to varying limb inertia when moving in different directions (Gordon et al. 1994). Our results clearly showed, though, that even when subjects saw the cursor deviate from their intended movement direction, they made minimal mid-movement corrections to this deviation when it was irrelevant to the task goal. Likewise, subjects did not correct their movements to the ray when they experienced task-irrelevant changes in intended movement extent (shown in Fig. 5A). In this study, the ray was defined only by a given direction and had essentially no extent constraints. By perturbing the direction or extent of movement with a visuomotor rotation or gain, respectively, the subjects' seen errors in this study were either relevant or irrelevant to the success of their task performance and resulted in varying amounts of mid-movement correction. These mid-movement corrections were not necessary, however, for adaptation to perturbations in direction due to the visuomotor rotation (shown in Fig. 2) or in extent due to the visuomotor gain (shown in Fig. 3), as indicated by significant behavioral aftereffects in catch trials where no perturbation was present.

What Drives Adaptation in Task-Irrelevant Conditions?

Before implementing this experiment, we considered what might generate a motor memory, especially in the absence of task-relevant error. Three broad classes of theories on learning are unsupervised, reinforcement, and supervised learning (Jordan and Wolpert 1999). The first arises due to organization of neural activity around natural statistics of internal firing patterns and external stimuli (Ghahramani 2004). The behavioral task presented here would not change internal patterns of firing, and exposure is brief enough (∼100 trials) to provide too short a window to build new expectations of statistics of environment.

The second class of learning is reinforcement, which adapts based on optimizing the acquisition of reward (Sutton and Barto 1998). The only instructed reward structure during perturbed trials in this study was to land on the arc or ray; either adapting or not adapting to the task-irrelevant perturbation would yield equal “reward.” Reinforcement learning, however, also typically takes thousands or hundreds of thousands of trials to obtain, which led us to bypass reinforcement as a likely computation underlying adaptation in our experimental design.

We therefore turned toward theories of supervised learning, which are usually used to explain short-term adaptation as in our experiment (Wolpert and Ghahramani 2000). Underlying supervised learning is an explicit error term. In our experiment, the only perturbation was visual: the cursor at first presented veridical hand position but then presented altered position. The presentation of cursor alone does not provide an error signal; the cursor position must be compared with an expected signal to produce any signal that would be useful for learning. Through these considerations, we hypothesized that learning in this task, if not through task-relevant error, would need to be driven by sensory prediction error.

This before-experiment consideration captured behavior on a trial-by-trial level. A subtler concern, however, could manifest within movements and could only be tested post hoc. We provided two novel task-level demands of movement: moving toward either the extent of the arc or the direction of the ray. It is possible that mid-movement behavior would be driven not by the 1-D arc or ray target but by a covert 2-D desired goal. Early in a movement, this covert goal could underlie a sensory prediction error (i.e., “the hand is appearing somewhere other than where I thought it would be”) that would drive mid-movement correction. Signals generated within mid-movement correction could, in turn, drive adaptation. This hypothetical cascade of early sensory prediction driving correction that directly drives adaptation could only be tested through actual experiment. We found that early in arc or ray training with a task-irrelevant perturbation, there was minimal mid-movement correction. Thus, in theory, adaptation was not likely driven by any mid-movement corrective signals; in reality, minimal mid-movement corrections indicated that the perturbations were in fact irrelevant to the task (i.e., our experimental design was successfully implemented). With the benefit of experiment, we then, were able to exclude the possibility that sensory prediction worked through the intermediary of feedback control, but instead motor memory could be formed directly from sensory prediction error.

Building Motor Memories From Sensory Prediction Errors

Catch trial aftereffects were indicative that motor memories were in fact being formed with repeated exposure to altered visual feedback. In previous investigations of the adaptation process using a 2-D task (i.e., point target of specific direction and extent), successful task performance was contingent on behavioral modification to reduce errors due to perturbations. As such, the paradigm of visuomotor adaptation has been limited in its ability to quantitatively dissociate whether adaptive processes are driven by task-related errors vs. sensory prediction errors. For example, Mazzoni and Krakauer (2006) discovered that by freezing online visual feedback 100 ms after movement onset and displaying knowledge of results at maximum reach extent, the motor system could minimize perturbation-induced position errors around a point in space, regardless of whether accuracy to that target was the task goal. It is important to note that in that case, the task and instructions minimized the chance to make online corrections. Results from Mazzoni and Krakauer (2006) highlighted the implicit nature of motor adaptation and suggested that the central nervous system has “the need to resolve any conflict between the predictions of a forward model and visual feedback” (p. 3645), yet did not necessarily rule out the influence of task-related errors on the adaptive process. By reducing the dimensions of the task and introducing task-irrelevant perturbations, we were able to demonstrate that sensory prediction errors arising from continuous real-time visual feedback can drive behavioral adaptation but do not necessarily evoke mid-movement corrections.

When exposed to visuomotor perturbations that did not interfere with successful task performance, subjects theoretically had no movement errors if they moved the required distance or in the required direction. In doing so, subjects did correct their reaches in these conditions (as shown in Figs. 4 and 5), yet when their motor behavior was probed using unperturbed catch trials, there was evidence of adaptation. These results reveal that the adaptation may not necessarily be driven by the need to update behavior in response to environmental or task changes (Wolpert et al. 2001). Evidence that online movement corrections are not critical to the adaptation process (Hinder et al. 2010; Noto and Robinson 2001; Tseng et al. 2007; Wallman and Fuchs 1998) has contributed to the idea that learning can be driven by forward models within the central nervous system that predict the sensory consequences of a set of motor commands. Sensory prediction errors arise from a difference between the predicted and actual sensory consequences of a given motor command (Shadmehr et al. 2010). When subjects in our study were exposed to task-irrelevant perturbations in visual feedback, they did not make online corrections to the degree that they did when moving with task-relevant perturbations. It is likely that the catch trial aftereffects observed during task-irrelevant training were the result of adaptation driven by sensory prediction errors that emerged regardless of what the extrinsic task goal was.

In our novel experimental design, the relevance of perturbation of a movement's real-time visual feedback was dissociated from the requirement of the task itself. Results provided evidence of adaptation regardless of whether perturbations in visual feedback were relevant to the task. Wei and Kording (2009) have proposed a model of adaptation that determines how relevant a motor error is to the motor plant by estimating whether the error was caused by relevant (motor plant) factors or by irrelevant (environmental) factors. An error's relevance, in this case, is defined with respect to the motor system, rather than with respect to the goal of the task like in our study. They hypothesized that the nervous system disregards movement errors that are induced by environmental factors, since the environment can transiently disturb task performance within a given trial. Irrelevant errors, which were unlikely attributable to the motor plant, resulted in minimal adaptation in the model of Wei and Kording (2009). Our study extends this idea by showing that even when motor errors are experienced yet are irrelevant to the task goal, they can still drive behavioral adaptation.

Although behavioral adaptation occurred in both the relevant and irrelevant conditions, the amount of adaptation appeared to differ between conditions, as indicated by the magnitude of catch trial aftereffects. Exposure to task-irrelevant rotated visual feedback when reaching to the arc resulted in catch trial aftereffects of ∼6°. Cressman and Henriques (2010) recently reported a similar amount of visuomotor adaptation when people were passively exposed to rotated visual feedback while reaching to a point. In this case, subjects merely saw a misaligned cursor as a robot passively moved their arm along a linear path to a set of targets, yet shifted their reaches 6° once the cursor was realigned. Subjects did, however, adapt more during active movement, supporting the idea that greater levels of reach adaptation can occur when sensory consequences of a movement can be actively, rather than passively, experienced. Results from our study extend this notion of additive experience for enhanced adaptation. Our data showed that, overall, catch trial aftereffects were stronger in the task-relevant conditions in which subjects made mid-movement corrections early during training. Significant aftereffects were, however, observed even with fewer mid-movement corrections in the task-irrelevant conditions, although to a lesser degree. Thus active movement and mid-movement corrections both may enhance, but may not be requisite for, motor adaptation. Alternatively, the difference in amount of adaptation between the task-relevant and -irrelevant conditions may also suggest that adaptation may be driven by both task-related errors and sensory prediction errors, rather than sensory prediction error alone. The novel paradigm introduced in this study to manipulate an error's relevance to the task may be useful in further studies for investigating the relative contributions of each type of error to the adaptation process.

Redding and Wallace have proposed that there are two distinct processes in adaptive learning (Redding et al. 2005; Redding and Wallace 2001; Redding and Wallace 2006), which may also explain the differing degrees of adaptation in this study. The first process is recalibration, which enables corrective movement by minimizing the error between the target and hand positions (Redding and Wallace 2001; Redding and Wallace 2006). The second process is realignment, by which the discrepancy between the spatial mappings of visuomotor and proprioceptive motor are corrected (Redding and Wallace 1996). This discrepancy is created when the expected position is different from the achieved. While experimentally dissociating the two processes, Redding and Wallace have observed that the effects of realignment contribute more to adaptation than recalibration (Redding and Wallace 2006). Results from our study that show motor adaptation, despite the relative lack of online correction during task-irrelevant training, are consistent with the realignment component of the Redding and Wallace model, which are thought to be responsible for any lasting effects seen in adaptive learning. Although Redding and Wallace noted that using a simulated or virtual environment, such as the cursor system used in our study, could possibly lessen the effects of alignment, our results also suggest that significant realignment effects can indeed by generated in such environments.

The demands of the arc and ray targets bear close resemblance to computational consideration of motor control within optimal feedback control (OFC) theory (Scott 2004; Todorov and Jordan 2002). This theory posits that kinematic trajectories can be generated within the nervous system by a minimization of mid-movement corrective control, without an explicit representation of an intended trajectory. Here we presented tasks that required only one degree of specificity at movement end. Our finding of minimal intervention when perturbation is orthogonal to target dimension agrees with predictions that OFC would make within a movement; there is no need to intervene if the perturbation does not affect target acquisition. If minimization of corrective control were the sole driver of behavior, however, there would be no signal driving motor memory formation that generated aftereffects in the catch trial. The presence of aftereffects instead is likely attributable to internal comparisons between expected trajectory and visually sensed trajectory. The aftereffect result, therefore, suggests that OFC considerations alone cannot underlie the present human motor adaptation; there needs to be adaptive processes that maintain values of expected trajectories.

In summary, data from this study showed that when subjects were exposed to altered visual feedback, they adapted regardless of whether such perturbations interfered with their ability to achieve the task goal. Our findings are consistent with those supporting that motor adaptation does not require error correction and can be driven by errors in sensory prediction.

GRANTS

This work was supported by National Institutes of Health Grants T32 HD007434 (to S. Y. Schaefer) and R01 NS057813 and R01 HD055851 (to K. A. Thoroughman and I. L. Shelly).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

Author contributions: S.Y.S. and K.A.T. conception and design of research; S.Y.S. and I.L.S. performed experiments; S.Y.S., I.L.S., and K.A.T. analyzed data; S.Y.S. and K.A.T. interpreted results of experiments; S.Y.S. and I.L.S. prepared figures; S.Y.S. drafted manuscript; S.Y.S., I.L.S., and K.A.T. edited and revised manuscript; S.Y.S., I.L.S., and K.A.T. approved final version of manuscript.