Impact of neural noise on a sensory-motor pathway signaling impending collision

Abstract

Noise is a major concern in circuits processing electrical signals, including neural circuits. There are many factors that influence how noise propagates through neural circuits, and there are few systems in which noise levels have been studied throughout a processing pathway. We recorded intracellularly from multiple stages of a sensory-motor pathway in the locust that detects approaching objects. We found that responses are more variable and that signal-to-noise ratios (SNRs) are lower further from the sensory periphery. SNRs remain low even with the use of stimuli for which the pathway is most selective and for which the neuron representing its final sensory level must integrate many synaptic inputs. Modeling of this neuron shows that variability in the strength of individual synaptic inputs within a large population has little effect on the variability of the spiking output. In contrast, jitter in the timing of individual inputs and spontaneous variability is important for shaping the responses to preferred stimuli. These results suggest that neural noise is inherent to the processing of visual stimuli signaling impending collision and contributes to shaping neural responses along this sensory-motor pathway.

neural pathways specialized in the detection of threats and escape must be reliable; thus it is especially important for their function to remain undisrupted by noise. Indeed, all sensory and motor systems have evolved to function with a certain amount of noise. Sensory signals are inherently noisy due to the stochastic activity of transduction channels (Baylor et al. 1980; Laughlin and Lillywhite 1982; Rieke and Baylor 2000) and the sensory input itself (e.g., photon noise; Baylor et al. 1979; Fuortes and Yeandle 1964; Scholes 1965). Because of the stochastic properties of ion channels, synaptic transmission, and other neuronal components, further noise is necessarily introduced through neural pathways (Fatt and Katz 1952; Rosenmund et al. 1993; White et al. 2000). Yet, neurons and neural circuits carry out computations reliably, and in some cases, optimally (Beck et al. 2008; Laughlin 1981; Osborne et al. 2005; Sengupta et al. 2010; for related energy constraints, see Niven et al. 2007).

The organization of a neural circuit can reduce noise levels in specific circumstances. If individual neurons of a population carry independent noise, then averaging will lower its level (Field and Rieke 2002; Laughlin et al. 1987). Depending on specific circumstances, nonlinear transformations such as spike thresholding and feedback loops could amplify or dampen noise (Faisal et al. 2008). Since such neural components, both noise reducing and amplifying, are widespread and interwoven in neural circuits, it is hard to predict a priori how noise levels, and conversely, neural signal reliability, will change through a processing pathway.

Thus we investigated the effects of neural noise in a sensory-motor pathway of the locust that is specialized for detecting objects approaching on a collision course and triggering escape behaviors. Earlier studies have looked at visual response variability across several stages of a neural pathway (Borghuis et al. 2009; Kara et al. 2000). However, none of them could span from the sensory periphery to neurons with direct motor system outputs, as is possible in insects. Locusts possess a pair of identically firing visual interneurons associated with each compound eye called the lobula giant movement detector (LGMD) and the descending contralateral movement detector (DCMD; Fig. 1A) (O'Shea and Rowell 1976; Rowell and O'Shea 1976). The role of these identified neurons in detecting objects approaching on a collision course and triggering escape behaviors is well documented (Fotowat et al. 2011; Gabbiani et al. 1999; Rind and Simmons 1992; Santer et al. 2006; Schlotterer 1977). They respond vigorously to simulated approaching objects (looming stimuli) with a firing rate that rises smoothly, peaks, and then falls; the timing of the peak signaling when the stimulus has reached a threshold angular size on the animal's retina (Gabbiani et al. 1999). The LGMD receives roughly 15,000 excitatory inputs responding to luminance changes in small areas of the visual field and inhibitory inputs whose population is thought to signal the angular size of the stimulus (Gabbiani et al. 2002, 2005; Hatsopoulos et al. 1995; Strausfeld and Nässel 1981). The DCMD relays this information to motor neurons in the mesothoracic and metathoracic ganglia controlling the wings and hind legs (Burrows 1996; O'Shea et al. 1974; Simmons 1980). We also know that trial-to-trial variability in the spike trains of the DCMD can predict if and when the animal will jump (Fotowat et al. 2011). Thus variability in the LGMD/DCMD responses is relevant to the behavioral output of this circuit.

Fig. 1.

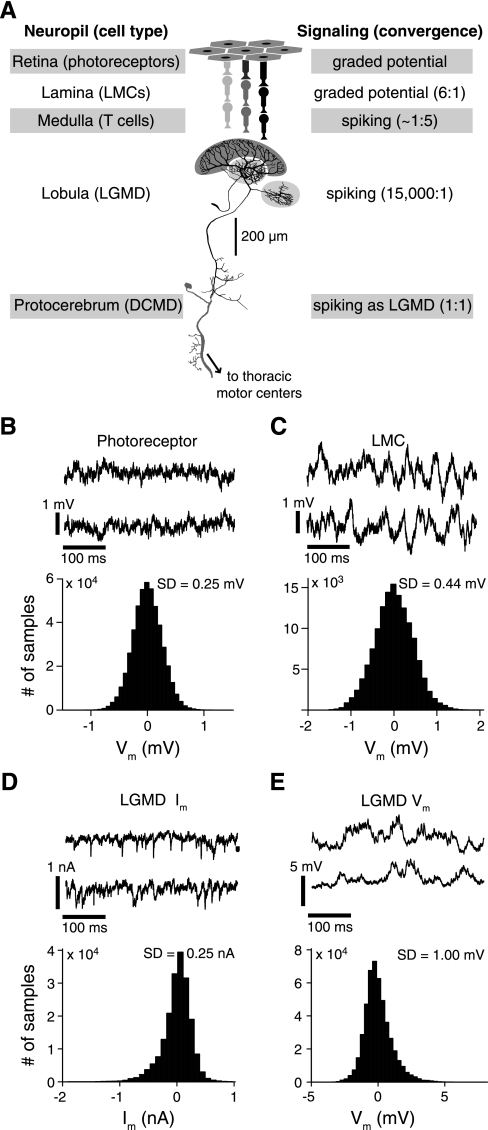
Spontaneous variability observed throughout an excitatory visual pathway involved in collision detection. A: schematic illustration of the pathway with its main anatomic and signaling properties. The excitatory input is successively relayed from photoreceptors to large monopolar cells (LMCs), which both respond in a graded manner under our stimulus conditions, and medullary T cells before impinging on the large dendritic fan of the lobula giant movement detector (LGMD; dark gray shading). The 2 smaller dendritic fields receive inhibitory inputs (light gray shading). B, top: two 400-ms long traces illustrating the spontaneous membrane potential (V_m) variability of a typical photoreceptor; bottom: histogram showing the distribution of V_m for the same cell relative to the resting potential. C: spontaneous V_m traces and histogram for a recording from a LMC. D and E: similar traces and histograms of spontaneous membrane currents (I_m; voltage clamp) and V_m (current clamp) in the LGMD. SD, standard deviation for the illustrated experiments.

The excitatory pathway converging onto the LGMD/DCMD has several features that could influence the amounts of variability observed at each stage and how it is propagated. There is a 6-to-1 convergence from the photoreceptors to the second-order visual neurons, the large monopolar cells (LMCs) of the lamina (Meinertzhagen 1976; Strausfeld and Nässel 1981). There is also a transition from graded potential to spiking responses between the LMCs' dendrites and their targets in the medulla, not unlike that between bipolar and retinal ganglion cells in the mammalian retina. Although few recordings from the medulla have been obtained (James and Osorio 1996) and little is known about its connectivity, a divergence of ∼1 to 5 is likely at this stage (Peron et al. 2009). Finally, there is a massive convergence of medullar inputs onto the LGMD. Thus we wanted to experimentally observe the effect of these cellular and network features on the propagation of variability and to understand how it influences the responses of the LGMD to looming stimuli. We find that the signal-to-noise ratio (SNR) resulting from stimulation of small parts of the visual field decreases from the periphery through the pathway and that SNRs of responses to looming stimuli are not much higher. Modeling of the LGMD and its inputs during looming suggests that jitter in the single-facet response times is important for shaping looming responses and that variability of the looming responses is largely independent of variability in the strengths of the summed inputs.

MATERIALS AND METHODS

Animal dissection and electrophysiology.

Locusts were mounted in a plastic holder and dissected as previously described (Peron et al. 2007). Sharp microelectrodes were used for intracellular recordings from photoreceptors, LMCs (80–240 MΩ, 2 M K-acetate/0.5 M KCl), and the LGMD (8–30 MΩ, 2 M K-acetate/0.5 M KCl or 3 M KCl for voltage clamp). Intracellular signals were low-pass filtered (membrane potential: 10 kHz; current: 5 kHz) and digitized (20 kHz). Photoreceptor and LGMD recordings were made using borosilicate electrodes (1.2/0.8-mm and 1.2/0.5-mm outer/inner diameters, respectively; WPI, Sarasota, FL), whereas LMC recordings were made using aluminosilicate (1.0-mm outer diameter; Harvard Apparatus, Holliston, MA). An Ag-AgCl wire was used as reference. Current-clamp recordings were made in discontinuous current clamp (DCC; at ∼25 kHz switching frequency) or bridge mode using an SEC-10LX amplifier (NPI, Tamm, Germany). Voltage-clamp recordings from the LGMD were made using discontinuous single-electrode voltage clamp (dSEVC; at ∼25 kHz). All dSEVC electrodes had <20-MΩ resistances, and electrode resistance (bridge) or capacitance (DCC/dSEVC) was fully compensated in the bath, immediately before tissue penetration. The noise levels resulting from electrodes in the bath had standard deviations (SD) of 0.15 mV for high-resistance photoreceptor/LMC electrodes, 0.06 mV for LGMD DCC, and 0.18 nA for LGMD dSEVC. These values were measured before penetration of photoreceptors and LMCs and thus represent an upper bound on the electrode noise, since the electrode resistance typically decreased following tissue penetration. We used these electrode noise levels to correct the corresponding spontaneous membrane potential noise measurements under the assumption that they add independently; that is, the measured variance equals the sum of the electrode noise variance and the cell membrane potential (or current) variance. Evoked responses were not corrected for electrode noise because it had a negligible effect on them. Intracellular recordings were obtained from the lobula and lamina through the desheathed optic lobe and from the retina through a small (∼50 × 50 μm) hole just below the dorsal rim of the eye. Photoreceptor recordings were identified by their resting potential (∼40 mV, depending on ambient light levels) and depolarizing responses to luminance increases. The photoreceptor recordings included in this study had characteristics of high-quality recordings: light-adapted resting potentials of 40–50 mV, which dropped by an average of 17 mV when background light was removed, had strong transient responses to full-contrast luminance changes (Supplemental Fig. S1) and showed no appreciable change in their resting membrane potential over ∼20 min of recording. (Supplemental data for this article is available online at the Journal of Neurophysiology website.) The extracellular potential of the lamina modulates in phase with a flashing light stimulus, allowing identification of LMCs by a resting hyperpolarization and transient, anti-phase responses to light flashes (Supplementary Fig. S1). In the fly, two subtypes of LMCs have been shown to generate small (<10 mV) spikes in response to light pulses when dark adapted (Uusitalo et al. 1995). The LMC cells presented here, recorded under light-adapted recording conditions, did not exhibit such active properties. LGMD recordings were identified by the cell's 1:1 spike correspondence with the simultaneously recorded extracellular DCMD signal (O'Shea et al. 1974). The cell was penetrated in the proximal region of the excitatory dendritic field, with spike heights varying between 20 and 50 mV. The LGMD is an electrotonically extended neuron receiving distributed synaptic inputs that are finely organized (Peron et al. 2007, 2009). Thus different visual stimulation regimes will differentially affect its local membrane resistance and impact the membrane potential noise recorded by an electrode in its main excitatory dendritic branches. One of the purposes of this study was to characterize these changes and relate them to presynaptic and LGMD firing rate variability. Stable LGMD recordings could be maintained for typically >60 min. Extracellular signals were acquired as previously described. The procedures for intracellular LGMD recordings while presenting looming stimuli were slightly different than described above and were previously described by Gabbiani et al. (2002).

Visual stimulation.

Visual stimuli were generated using custom software on a personal computer running a real-time operating system (QNX 4; QNX Software Systems, Ottawa, Canada). Looming stimuli were presented on a cathode ray tube (CRT) monitor (200 Hz, luminance range 2–90 cd/m²). The looming stimuli used were expanding dark squares on a bright background. If θ denotes the angular size of the square on the retina, the stimulus size follows θ(t) = 2tan⁻¹(l/vt), where l is the half-size of the simulated object, v is the simulated approach velocity, and t is time during the approach. By convention, v is negative for an approaching object and t is 0 at the time of collision with the animal (Gabbiani et al. 1999). θ(t) is fully described by the half-size-to-speed ratio, l/|v|, with units of time. Assuming a constant simulated object size, the lower the l/|v| value, the faster the object is approaching and the more suddenly it expands.

Stimulation at single ommatidium resolution was achieved by projecting an image generated using a digital light-processing (DLP) projector (LT140; NEC, Tokyo, Japan) through a custom-built microscope (Jones and Gabbiani 2010) mounted horizontally on a vibration-isolated optical table (luminance range 4–2,530 lux). Both the CRT monitor and DLP projector were calibrated to ensure linear, 6-bit resolution control over light levels. The ambient light level for single-facet experiments was set by a ring light mounted around the objective of the microscope. This level was constant at 490 lux, equivalent to dim daylight. Locusts stimulated using the CRT monitor were adapted to a slightly different light level, determined by the brightness of the monitor (280 lux). The mean resting membrane potential values recorded under these two conditions were very similar, −40.4 and −39.1 mV for single-facet and monitor-stimulated photoreceptors, respectively.

Single-facet stimuli.

Each stimulus spot was 2 × 2 pixels (5 × 5 μm) in size, positioned in the center of each ommatidium. Each stimulus was a 1,500-ms light pulse from baseline (4 lux) to a variable maximum (≤2,530 lux). Since the looming stimuli that we want to emulate are dark objects on a light background, we focus exclusively on the responses resulting from the return of this light pulse to its dark baseline (“off” responses; Fig. 2, A and B). Luminance changes had a variable duration, ranging from instantaneous (0 ms) up to 183 ms. Their time course had the profile of a cumulative Gaussian, with a SD equal to one-quarter of the luminance change duration. This recreates the luminance change caused by an edge moving across the approximately Gaussian spatial receptive field of photoreceptors (Burton and Laughlin 2003; Wilson 1975). Multiple facets or adjacent facet pairs were stimulated when recording from the LGMD (4 maximum, with at least 2 interposed facets). Each facet was stimulated less than once per minute to avoid local habituation (O'Shea and Rowell 1976). Stimuli were presented every 5 s for LMC and photoreceptor experiments. Trial types within all experiments were pseudorandomly interleaved. Pseudolooming stimuli spanned three facet rows on the eye, each 15 facets long, with each stimulus point positioned over a single facet. The three stimulus points in each column were stimulated simultaneously, with each column being presented a more rapid luminance change, a sequence that was designed to mimic the acceleration caused by a looming edge. See Jones and Gabbiani (2010) for more details on this stimulus and LGMD responses to it.

Fig. 2.

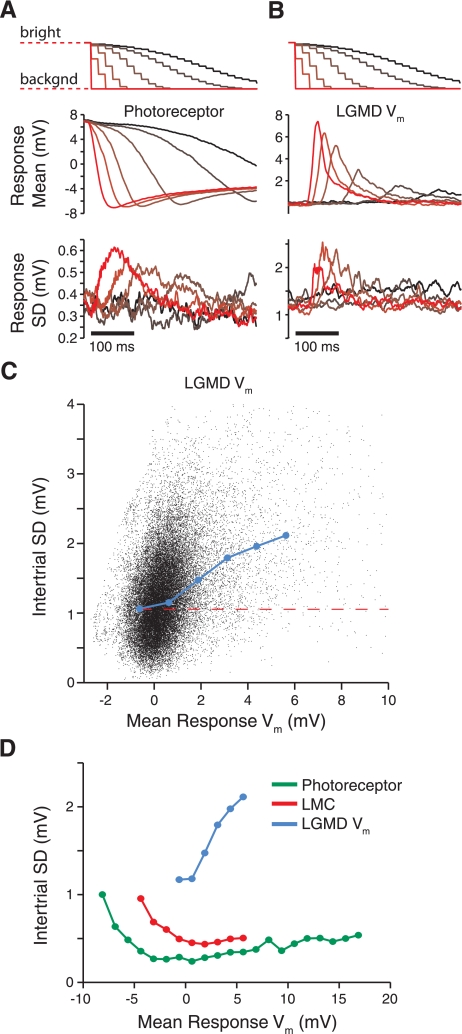
Time course and dependence of variability on V_m during single-facet stimulation. A and B: top traces show the stimulus luminance presented to a single facet over time. The luminance is initially bright and returns to its background (backgnd) value, causing the “off” response along the visual pathway. Darker colors denote slower luminance changes; brighter colors are faster. Middle traces depict correspondingly colored mean photoreceptor (A) and LGMD responses (B), averaged over all cells. The mean V_m are given relative to rest. Photoreceptors are initially depolarized, since the initial light level is above its background value. Bottom traces show the intertrial SD of the responses, averaged across recordings. C: response means and SD for the LGMD V_m (from B) plotted against each other, with each black point showing a time sample (selected at 2.5-ms intervals). The blue line shows the average resulting SD within 1.25-mV mean response bins for bins that contain >0.05% of the data. The dashed red line indicates the spontaneous noise level (Fig. 1E). D: same analysis as in C for photoreceptors (green), LMCs (red), and the LGMD V_m (blue; replotted from C).

Data analysis and statistics.

All data analysis was carried out using custom MATLAB programs (MathWorks, Natick, MA). All analyses of stimulus-evoked membrane potentials, both experimental and simulated, were performed on traces that had been median-filtered (8-ms window) to remove spikes. This window size was chosen as the shortest length able to fully exclude LGMD spikes from the traces. DCMD spikes were detected from extracellular nerve cord signals by thresholding the waveforms. Instantaneous firing rates (IFR) were calculated by convolving individual spike trains with a Gaussian window as in Gabbiani et al. (1999) (SD = 20 ms).

We utilized nonparametric statistical tests on our experimental data (Lehmann 1998). The Wilcoxon rank-sum test was employed for comparisons of two independent data sets (significance level denoted by P_RS). For comparisons of more than two conditions, we used the Kruskal-Wallis test (significance level denoted by P_KW), a nonparametric alternative to the analysis of variance (ANOVA). For the data in Figs. 4 and 5, where there are multiple cell types across several conditions, we used a two-way ANOVA to look for main effects and then verified the results with a Kruskal-Wallis test across cell types on the instantaneous (0 ms) condition and across transition durations for each cell type. Multiple comparison testing was done using Tukey's honestly significant difference (HSD) criterion to determine pairwise differences between recording types (significance level denoted by P_HSD). Because of the low number of LMCs that we were able to stably record (n = 3), we do not have the power to detect small differences in tests involving those recordings.

Fig. 4.

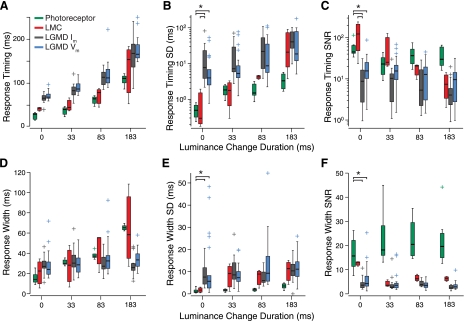
Variability of response widths and timing. A and D: distributions of latencies (photoreceptor response onset, response peak for other recordings) and response widths (FWHH) for different recording types. B and E: distributions of the SD in each experiment for these measures. C and F: corresponding SNRs for the same measures. Box plot conventions are as described in Fig. 3.

Fig. 5.

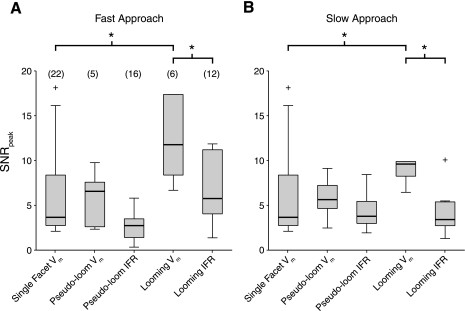
Comparison of LGMD variability for several stimulus types. Distributions of SNR_peak values are shown for single-facet, pseudolooming, and looming stimuli. A: values for looming stimuli with a half-size-to-speed ratio (l/|v|) of 10 ms and pseudolooming stimuli with an equivalent l/|v| value of 15 ms. The single-facet SNR_peak distributions for 0-ms luminance changes is plotted for comparison. B: values in response to slower approaching stimuli. Looming stimuli had an l/|v| of 40 ms for the instantaneous firing rate (IFR) measurements and 30 ms for V_m measurements. Pseudolooming stimuli had an equivalent l/|v| of 50 ms. Pseudolooming stimuli in A and B are the “fast” and “medium” speed stimuli described in Jones and Gabbiani (2010). *P_RS < 0.05. Box plot conventions are as described in Fig. 3.

Simulations.

Simulations were performed using a compartmental model of the LGMD in the NEURON simulation environment (see Fig. 6A; Hines and Carnevale 1997). The compartmental model is based on that described by Peron et al. (2009). Briefly, it has a spike-initiation zone (SIZ) segment containing potassium and sodium conductances of Hodgkin-Huxley (HH) type, as well as a voltage-gated calcium conductance and a calcium-sensitive potassium conductance mediating spike frequency adaptation. The SIZ is connected at one end with an axon containing HH-type channels, and at the other end with a passive excitatory dendritic tree (Peron and Gabbiani 2009a). An earlier model by Wang (1998) served as the basis for the functional form and parameters of the channels, with constraints specific to the LGMD derived from our previous work (Gabbiani and Krapp 2006; Peron et al. 2007). For further details on this modeling aspect, see Peron and Gabbiani (2009a, Supplemental Material). The rake-shaped dendritic tree, simplified from the actual anatomic shape, is where it receives retinotopically mapped excitatory input (Krapp and Gabbiani 2004; Peron et al. 2009). A square region of visual space from −50° to +50° elevation and 40–140° azimuth was mapped onto this dendritic tree, which has 20 straight dendritic branches, each 20 compartments in length. Excitatory input elevation is mapped across dendrites, whereas azimuth is mapped along each dendrite's length, with frontal inputs arriving more distally and posterior ones arriving proximally. Inhibitory inputs were activated in the compartments immediately proximal to the intersection of the dendritic branches but distal to the SIZ. All synaptic inputs were modeled as synaptic conductances with the time course of an α-function (e.g., chapt. 2 of Gabbiani and Cox 2010).

Fig. 6.

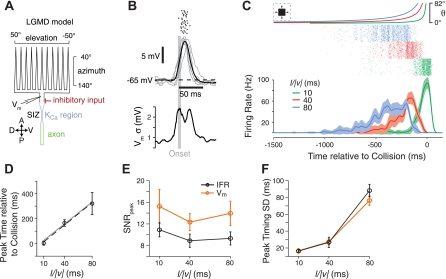
Modeling LGMD responses. A: schematic of the active compartmental model of the LGMD used. Excitatory input impinges retinotopically onto the rake-shaped dendritic tree, and inhibitory synapses are made onto the dendritic segment immediately proximal to the rake. The model is modified from the one used in Peron et al. (2009). Details can be found in materials and methods. K_Ca, calcium-sensitive potassium conductance; SIZ, spike-initiation zone. Bottom inset indicates orientation of rake relative to visual space. A, anterior; V, ventral; P, posterior; D, dorsal. B: single-facet responses from the model. Short trains of synaptic conductances (3 events at 200 Hz) from 6 inputs are triggered at the marked onset time (vertical gray line) with 6-ms temporal jitter. Individual synaptic conductances are drawn from a normal distribution with an SNR of 10 and a mean adjusted to obtain responses of a strength similar to those observed in vivo. Rasters are shown from 20 repetitions (top); the model V_m for 5 repetitions are shown (gray) with the mean model V_m (black); and the SD (σ) of the V_m are shown (bottom). Synaptic parameter values were chosen to closely match the strength and variability of responses in vivo. C: looming responses in the model. Traces (top) show the angular size of the square looming stimulus for 3 parameter values (l/|v| = 10, 40, and 80 ms in green, red, and blue, respectively). Spike trains (middle) are shown from the stimulated LGMD for 100 simulations from each stimulus. Graph (bottom) shows the Gaussian-convolved IFR with envelopes showing the SD. D: relationship of the looming stimulus parameter and timing of the peak rate. Model peak time means and SD (error bars) are shown (black) with the best-fit linear relationship (black dashed line; fit slope, 4.5; intercept, −31.0 ms; angular threshold, 25.2°). The experimentally observed linear relationship from Jones and Gabbiani (2010) is shown in gray. E: the SNR of the firing rate and V_m peaks as a function of l/|v|. F: the SD of the peak times for IFR and V_m. Error bars in E and F show bootstrapped 95% confidence intervals for plotted values.

Spontaneous synaptic activity, both inhibitory and excitatory, was generated to reproduce the level of spontaneous noise observed in LGMD current-clamp recordings. The visually driven excitatory synaptic input during looming was generated using luminance changes resulting from a looming stimulus sweeping across a simulated array of facets with realistic sampling of visual space, with six synapses per facet (Krapp and Gabbiani 2004). Each facet had a two-dimensional Gaussian receptive field (SD = 3/4°) over which it integrated stimulus luminance. The single-facet stimulation experiments were used to set the parameter values (magnitude, latency, and jitter) for individual synaptic inputs of the model. These parameters were dependent on the luminance change duration at individual facets, fitted to experimental data. In the fly, photoreceptor response dynamics have been reported to vary with location on the eye (∼20%, front vs. back and side; Burton et al. 2001). Our photoreceptor recordings were carried out on the side of the eye, which also receives the bulk of inputs caused by looming stimuli approaching from the side in our simulations. Thus slight variations in photoreceptor responses as a function of eye location are not likely to affect our modeling results. Inhibitory synaptic inputs had a time course identical to that of the area (number of facets) covered by the looming object. They were triggered with a constant delay of 70 ms after the stimulus luminance reached its midpoint at each model facet, roughly 5 ms longer than the minimal excitatory input delay. This delay is consistent with experimental inference of inhibitory timing (Gabbiani et al. 2005). Their magnitude was constant throughout the stimulus, set to produce looming responses that had firing rates and peak times similar to those in experiments. Inhibitory synaptic strength variability was set to have an SNR of 20 and jitter of 10 ms. Simulations were run 50–500 times to accurately determine the variability in the responses. For simulations shown in Fig. 8 without temporal jitter, a set of synaptic timings was generated and held constant for groups of 50 repetitions, for which response variability was measured. The results were then averaged for 10 groups of simulations and across l/|v| values. Model output was processed in the same way as experimental data. Confidence intervals (95%) were obtained for measurements of the model's responses by bootstrapping (resampling 5,000 times). Code for reproducing the model and figures using model data will be deposited on ModelDB (http://senselab.med.yale.edu/modeldb).

Fig. 8.

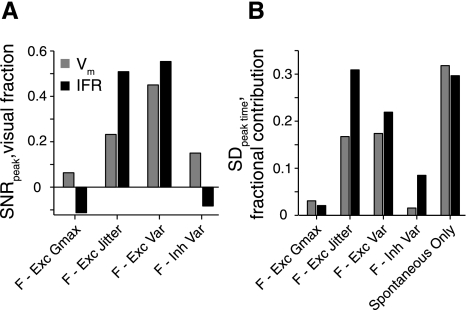
Sources of variability in the LGMD model. The model was run with specific sources of variability eliminated. “Full” (F) refers to the model with all sources of variability. Other conditions eliminate variability in excitatory synaptic maximum conductance (F-Exc Gmax), excitatory synaptic timing (F-Exc Jitter), both excitatory timing and conductance variability (F-Exc Var), the inhibitory variability (F-Inh Var), and all visually driven variability (spontaneous only). Variability was estimated for groups of 50 simulated approaches and averaged over 10 groups. A: the relative SNR_peak resulting from elimination of sources of variability. The height of each bar shows the difference from the full condition, normalized by the difference between full and spontaneous only. The SNR_peak (averaged over l/|v|) values of the full condition are 14.0 and 9.9 for V_m and IFR, respectively, whereas the SNR_peak values for the spontaneous-only condition are 19.0 and 14.0. B: the proportion that the SD_{peak time} value is decreased from that of the full condition for each condition shown. Bar height indicates the difference from full model SD_{peak time} for each condition, divided by the full model SD_{peak time} value (SD_full − SD_condition)/SD_full. SD_{peak time} values for the full model were 38.8 and 45.5 ms for V_m and IFR, respectively (averaged over all 3 l/|v| values).

RESULTS

We wanted to quantify the variability of neural responses throughout the excitatory visual pathway leading to the LGMD (Fig. 1A). Therefore, we recorded intracellularly from three cell types in the optic lobe of the locust: photoreceptors, LMCs of the lamina, and the excitatory dendritic field of the LGMD itself in both current- and voltage-clamp configurations. This allowed us to assess neural variability in LGMD responses and (directly or indirectly) at each stage in the pathway giving excitatory input to the LGMD. The intracellular recordings were selected specifically for their stable resting membrane potentials and responses for the duration of data collection. The data come from 7 photoreceptors, 3 LMCs, 22 LGMD neurons, and 28 extracellular DCMD neurons recorded in the locust Schistocerca americana. Different analyses of the data described in this article have been previously published (intracellular LGMD recordings, Gabbiani et al. 2002; other recordings, Jones and Gabbiani 2010).

Spontaneous membrane potential variability.

We first established a baseline for the variability levels by quantifying the spontaneous membrane potential noise present in the neurons. The measurements were taken from the 400-ms period immediately preceding each visual stimulus presentation (for a total of about 24 s per individual cell). We then compiled distributions of the membrane potential (V_m) relative to rest for each recording (Fig. 1, B–E). Mean spontaneous noise levels in LMCs were about twice that of photoreceptors (pooled across experiments: SD = 0.43 and 0.24 mV, respectively; corrected for electrode noise: SD = 0.40 and 0.19 mV, respectively), whereas in the LGMD it was also about twice that of the LMCs (SD = 1.05 mV pooled across experiments; unchanged after correction for electrode noise). The spontaneous noise levels for each cell type were significantly different from each other (P_RS < 0.02). The V_m distributions of photoreceptors and LMCs are quite symmetric (Fig. 1, B and C), whereas those from the LGMD are skewed in the direction of excitatory events, which is evident in the current (I_m) and V_m traces (Fig. 1, D and E). Ambient light levels during these recordings were at dim daylight levels (see materials and methods), so the noise levels reflect daytime conditions with an unchanging light level. Our results for photoreceptors and LMCs were generally consistent with earlier results obtained at similar light levels in photoreceptors (locust: Faivre and Juusola 2008, Fig. 4A; fly: Burton and Laughlin 2003) and in fly LMCs (Fig. 9 of Laughlin et al. 1987). From these recordings, we found that spontaneous membrane potential noise levels increase along the excitatory pathway leading to the LGMD.

Membrane potential variability to single-facet visual stimulation.

The unit of spatial resolution in the locust visual system is the single ommatidium (facet), with each of the eight underlying photoreceptors transducing the same light signal through a single light-collecting structure, the fused rhabdom (Land and Nilsson 2002; Shaw 1968). Moving edges in the visual world cause luminance changes in each photoreceptor's receptive field whose duration depends on the speed of motion (Burton and Laughlin 2003; Jones and Gabbiani 2010). To understand the variability caused by such stimuli in photoreceptors and downstream neurons, we repeatedly presented luminance decreases localized over single facets with a range of durations, as would result from dark edges moving through photoreceptor receptive fields at different speeds (Fig. 2, A and B, top). These stimuli thus mimic the range of speeds experienced by photoreceptors across the retina during a looming stimulus, since the angular velocity of its edges increases rapidly near projected collision (Gabbiani et al. 1999; Jones and Gabbiani 2010). In LMCs, the same stimuli will stimulate the center of their receptive field, which can be expected to play a dominant role in their response to looming stimuli based on the detailed analysis of their properties available in flies (Dubs 1982; Laughlin 1994; Shaw 1984; Srinivasan et al. 1982). In the LGMD, each such stimulus represents an elementary component of a looming stimulus, allowing assessment of the impact that their spatiotemporal integration has on its membrane potential and firing rate noise.

As shown in Fig. 2A, middle, photoreceptor V_m changes tracked changes in light levels and hyperpolarized to luminance decreases. The slopes of their membrane potential changes depended on the duration of the luminance change (Supplemental Fig. S1, A–C; Jones and Gabbiani 2010). Under our recording conditions, LMCs are also graded potential neurons, with largely transient responses that are of the opposite polarity to those of photoreceptors (Juusola et al. 1995; Laughlin et al. 1987). They thus depolarized in response to the same luminance decreases, and the size of this transient response also varied with the duration of the luminance change (Supplementary Fig. S1, D–F; Jones and Gabbiani 2010). The LGMD responded with transient depolarization and sometimes spiking to both single-facet luminance increases and decreases (Fig. 2B, middle; Supplementary Fig. S1, G–I). The synaptic currents recorded in voltage clamp to the same stimuli were also transient and excitatory (Fig. 2F of Jones and Gabbiani 2010).

To examine the temporal profile of the variability in each cell's responses, we computed the intertrial SD of the response for each point in time. We then averaged these traces across all recordings of each type. Figure 2, A and B, bottom, show the resulting response SD in photoreceptor and LGMD recordings. The intertrial SD starts at levels slightly greater than those measured for the spontaneous period. In both cell types, variability increased with the strength of the response. To quantify the relationship between membrane potential and variability, we further plotted these two measures against each other for each point in time during the stimulus presentation. Figure 2C shows this analysis for LGMD recordings. The black cloud shows each time point, with the blue line showing the mean variability as a function of membrane potential in 1.25-mV bins. Figure 2D shows the mean variability for our photoreceptor, LMC, and LGMD recordings. This analysis reveals that the LGMD variability increases as a function of response magnitude more quickly than in photoreceptors or LMCs. The differences in baseline variability are also evident in the vertical positions of these relationships. We thus conclude that membrane potential noise in response to single-facet visual stimulation also increases along the excitatory pathway leading to the LGMD.

SNRs of specific response features along the excitatory pathway.

Although membrane potential change and variability are correlated, we could not tell from the previous analysis what aspects of the responses are variable. In addition, our goal was to focus on those aspects that are important for the encoding of looming stimuli under the bright-light, high-contrast conditions characterizing our looming stimuli. On the basis of these premises, we measured several features of single-trial responses selected for their relevance to the encoding of looming stimuli along the pathway. In photoreceptors, we measured the slope of the response, since it carries information on edge speed that is extracted in the peak LMC responses (Jones and Gabbiani 2010; Juusola et al. 1995). Accordingly, we also measured V_m peaks of LMCs, as well as V_m and I_m peaks of the LGMD. The timing of single-facet responses synchronizes inputs impinging onto the LGMD and plays a role in its tuning to looming stimuli (Jones and Gabbiani 2010). We thus measured the response onset in photoreceptors and the timing of peak responses in LMCs and the LGMD. Finally, the width of the single-facet response is one of the factors that determine their summation within the LGMD. We therefore measured the full width at half-height for the LMC and LGMD responses, as well as the response duration for photoreceptors. Examples of single-trial traces and these measurements are given in Fig. 3A. For each stimulus condition we then computed a mean, SD, and SNR such that SNR = mean/SD for each of these measures. We then compared these quantities across the different stages of the LGMD visual pathway to track changes in the encoding of their associated features. The SNRs we defined also characterize performance in related signal detection tasks (e.g., chapt. 24 and 25 of Gabbiani and Cox 2010; or chapt. 4 of Wickens 2002), although this is not central to the subsequent analysis.

Fig. 3.

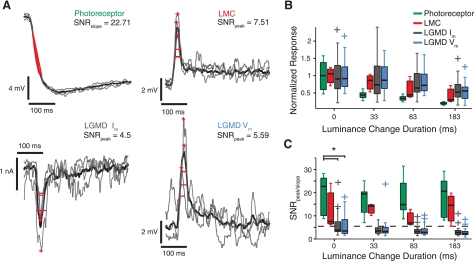
Variability and signal-to-noise ratio (SNR) of response features to single-facet stimuli. A: representative traces for each cell type showing the trial-by-trial variability of responses to an instantaneous luminance decrease at a single facet (0-ms duration). The stimulus occurs at the time the traces begin. Trial averaged responses are shown in black and 3 individual trials in gray. Measured features are depicted in red for each trial: for photoreceptor traces, they are the response slopes from 25–75% of the response height; for LMC and LGMD traces, they are the peaks (+) and response widths (full width at half-height, FWHH). The SNR is noted for the peak and slope features for the experiments shown. It is defined as the mean divided by the SD of each measured feature. B: relative response strengths (photoreceptor slopes; peak heights for other recording types) to single-facet luminance changes of varying duration. For each box plot, the central horizontal line denotes the median and the box extent depicts the 25th (p₂₅) to 75th percentile (p₇₅) data range. Whiskers show the range of data not considered outliers, and plus signs represent outliers, i.e., points >1.5 (p₇₅ − p₂₅) times away from lower (p₂₅) or upper (p₇₅) data quartile. Responses are normalized to the mean of the population distribution (at 0-ms duration) for each recording type (photoreceptors, 5.5 mV/10 ms; LMCs, 7.2 mV; LGMD I_m, 2.0 nA; LGMD V_m, 9.3 mV). C: SNR as a function of luminance change duration for the recording types. Box plots conventions are as described in B. The dashed line shows the mean SNR of the LGMD V_m peak for pseudolooming stimuli, a stimulus type that targets 45 facets in a pattern that mimics some aspects of a looming stimulus. There is a significant effect of recording type at 0-ms luminance change duration (*P_KW = 0.0023, corrected for multiple comparisons using HSD criterion). See Data analysis and statistics for definitions of probability statistics.

The normalized response strengths (slope or peak) for each condition are shown in Fig. 3B and the corresponding SNRs in Fig. 3C. Response strength fell off as the single-facet luminance changes became slower, with photoreceptor slopes dropping off more sharply than responses in downstream cells. The dependence of response strength on luminance change duration for voltage-clamp and current-clamp measures in the LGMD was quite similar. The SNRs of response strengths to single-facet stimuli were smaller for recordings further along the visual processing pathway (2-way ANOVA, P = 0), and individual comparisons yielded significant differences between photoreceptors and the LGMD I_m and V_m (P_HSD < 0.05). Photoreceptor slope SNRs were typically in the range of 10–25 (median = 22.9 across all conditions), whereas the SNR of LGMD response peaks were on average ∼5 (median = 4.0). The peak SNR, however, was not statistically dependent on the speed of the luminance change for any recording type (P_KW > 0.36). To consider the possibility that this observed SNR difference might merely be due to the response feature measured (slope vs. peak) in different recording types, we calculated the slope SNRs for our LMC and LGMD V_m responses. We did not find higher SNRs (median = 3.1 and 1.2 for LMC and LGMD, respectively). Similarly, calculating the SNR based on response peaks for photoreceptors yielded very similar values as for the slope (median peak SNR = 22.6).

The magnitudes, variability, and SNRs of the other response features, timing and width, are shown in Fig. 4. These SNRs, like those calculated from response magnitudes, provide a useful metric of how reliable their associated response features are. The two basic questions that we wanted this data to answer were 1) Does the SNR/variability of these features change through the visual pathway? If so, between which cell types? And, 2) Does the SNR/variability change with the luminance change duration? We found that the SD of response timing and width (Fig. 4, B and E) increased through the visual pathway and that the SNRs of response timing and widths (Fig. 4, C and F) changed as well (across cell types: P_KW = 1.9 × 10⁻⁵ for the SD of response timing at instantaneous luminance changes; response width SD: P_KW = 3.3 × 10⁻⁴; timing SNR: P_KW = 6.6 × 10⁻¹⁰; response width SNR: P_KW = 1.9 × 10⁻⁵). For both features, photoreceptors had lower levels of variability and higher SNRs than both LGMD I_m and V_m (P_HSD < 0.05). The LGMD I_m and V_m did not exhibit any significant differences from each other, and individual tests did not find differences with LMCs except for the LGMD I_m in the case of response timing SD and SNR (P_HSD < 0.05).

Response timings and widths increased with luminance change duration for photoreceptors and the LMCs (Fig. 4, A and D). LGMD response timings increased with luminance change duration, but response widths were constant. We observed a large dependence on both cell type and luminance change duration for the variability in response timing (Fig. 4B). Response timing variability was dependent on luminance change duration for all recording types (LMC: P_KW = 0.01, others: P_KW < 4.71.7 × 10⁻⁶). The SNRs of both measures (Fig. 4, C and F) were in most cases unchanged across the range of luminance change durations, with the only exception being the SNR of the LGMD I_m response width (P_KW = 1.7 × 10⁻⁴).

LGMD SNRs vary little with stimulus type.

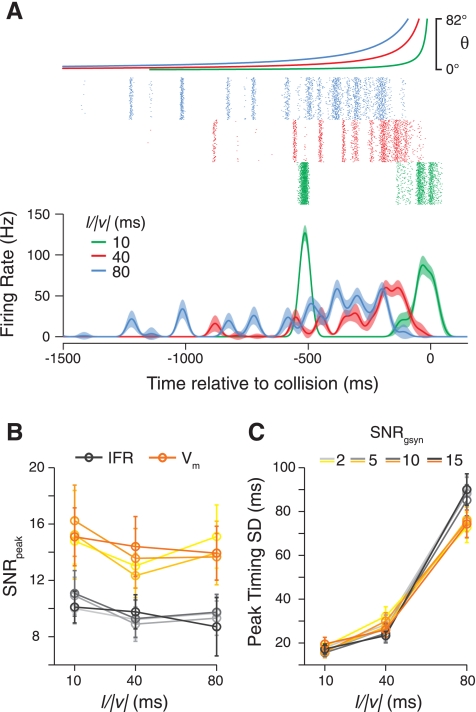
The LGMD has a much larger receptive field than cells earlier in the visual pathway and responds much more robustly to its preferred looming stimuli than to single-facet stimuli. Thus there is the possibility that it encodes its preferred stimuli more reliably, resulting in looming responses having higher SNR values than those to single-facet stimuli. To examine this possibility, we compared the SNRs of LGMD responses to single-facet stimuli (0-ms condition) with those evoked by two types of stimulated approach, looming and pseudolooming stimuli (see materials and methods). Both of these stimuli activate much larger portions of the retina and contain accelerating motion for which the LGMD is selective (Jones and Gabbiani 2010; Peron and Gabbiani 2009b; Simmons and Rind 1992). This comparison is shown in Fig. 5. The looming and pseudolooming stimuli had slightly different l/|v| values, so we grouped the responses into two speed categories, very rapid approaches and slower ones (l/|v| ≈ 10 and 40 ms, respectively). Because these stimuli produced significant LGMD spiking, we were able to compute the peak SNR for both the instantaneous firing rates and the underlying V_m, allowing us to contrast them.

The peak SNR values for firing rates were similar across stimulus types both for fast and slow approaches and were similar to those of the single-facet V_m. The SNRs for looming V_m responses were higher than for single-facet responses (slow: P_RS = 0.017, fast: P_RS = 0.008) but also higher than those for looming firing rates (slow: P_RS = 0.04, fast: P_RS = 0.002). Consequently, the peak SNR of the LGMD spiking output was no different than the peak SNR of strong single-facet responses (slow: P_RS = 0.48, fast: P_RS = 0.27). There was no significant elevation in the peak SNR values of pseudolooming responses (V_m or IFR) relative to single-facet responses. Thus the LGMD's preferred stimuli, which activate many single facets, do not evoke more reliable spiking responses than the membrane potential deflections resulting from single-facet inputs.

Modeling LGMD looming responses.

We built a model of the LGMD visual pathway to address the following question: given the variability observed in individual neurons to the single-facet signals, how reliable should the LGMD responses to looming stimuli be? The model consisted of a realistic sampling of visual space, which was used to trigger a set of appropriately timed and weighted synaptic inputs, based on the luminance time course at each model facet, to a compartmental model of the LGMD. This model had an elaborated, although simplified, dendritic structure (Fig. 6A; Peron et al. 2009). Spontaneous and visually evoked inputs were modeled independently. Spontaneous activity was randomly generated at a constant rate, excitation and inhibition balanced, to produce the level of spontaneous membrane variability found in vivo (Fig. 6B). We determined the appropriate level of excitatory drive by simulating single-facet visual stimuli and adjusting the synaptic strengths to produce responses evoking one or two action potentials, as in many of our recordings (Fig. 6B). Variability of the synaptic input strength and timing for each facet was also chosen to closely match the single-facet responses observed in vivo.

We next constructed a set of simulated looming evoked responses (Fig. 6C). The pattern of synaptic input to looming stimuli was determined using the properties of single-facet responses recorded in the LGMD under voltage clamp (Figs. 3 and 4). Specifically, excitatory inputs were triggered by luminance changes beginning at each individual facet, with magnitudes and latencies that were variable throughout the loom and based on the speed of luminance changes occurring at each individual facet in the model. Inhibitory input latencies and magnitudes were constant throughout the stimulus, triggered with a constant delay after the stimulus luminance reached its midpoint. The variability in the excitatory synaptic parameters was set to match that observed during single-facet stimulation (Fig. 6B), and the inhibitory variability was set to similar levels. Further details of the model are given in materials and methods. This pattern of synaptic stimulation preserved stimulus-induced correlations between different facet inputs to the LGMD, which have been shown to play a role in its tuning to looming stimuli (Jones and Gabbiani 2010). It does not take into account possible interactions between adjacent facet inputs, but such interactions have not been found to impact LGMD responses (Jones and Gabbiani 2010). Another dynamic lateral inhibitory interaction (O'Shea and Rowell 1975) is also likely to play a minor role in the responses of the LGMD to looming stimuli (Gabbiani et al. 2002).

We found that this simple input structure produced responses that well matched those of the LGMD. The response time course follows the same rise and fall in firing rate, with the peak time linearly related to the size-to-speed ratio (l/|v|) of the stimulus (Fig. 6D). Also, the variability in the timing of the peak firing rate increased with l/|v|, consistent with DCMD recordings (Fig. 6F; Gabbiani et al. 1999). The range of SD_{peak time} values observed in model responses was also similar to those observed in vivo. The SNR_peak of the response V_m and IFR departed slightly from the data: they were about twice as high as those observed in vivo. The relationship between the two is, however, the same, with the SNR_peak of the V_m being higher than the SNR_peak of the IFR (Fig. 6E). We thus conclude that the model adequately reproduces the LGMD responses to looming stimuli.

Impact of input variability on model output.

The model includes temporal jitter in the synaptic inputs to the LGMD, as observed in the single-facet response data (Fig. 5A). For instantaneous luminance changes, the variability of the LGMD V_m peak time was 3.9 ms (median); therefore, we set the minimum jitter of the synaptic inputs to produce a similar jitter in single-facet simulations (SD_jitter = 6 ms). This peak time variability increased when the luminance changes were slower (Fig. 4B), and we incorporated this into our model using the fitted slope of the linear relationship between the SD_{peak time} and the luminance change duration, (0.19; dimensionless since both variables have units of time). If we ignore the experimental relationship, instead setting the synaptic jitter to be constant and low throughout the looming stimulus, then the model fires bursts of spikes early in the stimulus (Fig. 7A). This contrasts with the gradual buildup seen in vivo. Such bursting behavior is consistent with LGMD responses to a modified looming stimulus in which luminance changes early in the stimulus occur more quickly than in a normal looming stimulus (“constant-rate looming” in Fig. 4 of Jones and Gabbiani 2010).

Fig. 7.

How input variability shapes LGMD model responses. A: the spiking and IFR of the LGMD model if single-facet luminance change-dependent jitter is removed. Instead, the synaptic times are jittered in the model by an amount drawn from a normal distribution with an SD set at a constant value of 4 ms. B and C: the variability of LGMD model responses is insensitive to changes in the variability of the underlying synaptic input strength. The SNR of the peak firing rate (B) and SD of the time of the peak firing rate (C) are shown for simulations where the synaptic input strength has different levels of variability, as parameterized by the SNR of the excitatory synaptic input strength (SNR_gsyn). Darker lines indicate higher SNR values. Measurements using both the V_m (orange) and IFR (grays) are shown. Values are compiled using 100 simulations per condition. Error bars show bootstrapped 95% confidence intervals on the values.

We also included variability in synaptic input strengths, as might arise from variability in quantal number, quantal size, stochastic receptor activation, or other synaptic transmission parameters. We initially set the variability of the excitatory synaptic strength (SD_gsyn = mean_gsyn /SNR_gsyn) to be roughly equal to that of the LGMD single-facet responses, SNR_gsyn = 5. However, the model's responses are quite insensitive to variability in the underlying synaptic input strengths, as shown in Fig. 7, B and C. Varying the parameter SNR_gsyn caused a significant change in the reliability of single-facet responses (data not shown) but did not cause a significant change in any of the aspects of the model's response to looming that we examined. This insensitivity can be partially explained by the number of synaptic inputs the model receives. The model LGMD, at the time of its firing rate peak, receives ∼40 independently variable synaptic inputs, resulting in the trial mean input being ∼6.3 ($\sqrt{40}$) times less variable than the individual inputs.

To further dissect which sources of variability contributed to the output variability of our model, we ran the simulations while eliminating specific sources of variability (Fig. 8). Eliminating variability in the excitatory synaptic strength (SD_gsyn = 0) changed the SNR_peak and SD_{peak time} measures very little, consistent with responses being insensitive to the value of SNR_gsyn. Keeping the synaptic timings constant made a much larger difference, which contributed most of the decrease in variability observed when both the synaptic strength and timing variabilities were eliminated. Taking away inhibitory input variability of both synaptic timing and strength also had a relatively small effect on the model's output variability. The strongest source of variability came from the spontaneous activity, accounting for about 35% of the SD_{peak time} and capping the SNR_peak at about 150% of its value in the full variability model. Thus synaptic strength variability levels within the range of those observed in vivo are not important for determining looming response SNR in the model. Instead, the firing rate SNR and variability in the timing of the peak are determined in a large part by the ongoing spontaneous activity and jitter in the timing of stimulus driven inputs.

DISCUSSION

We have shown that both spontaneous and response variability increase along the visual processing pathway that includes the LGMD and DCMD. The reliability of several aspects of responses drops, including strength, width, and timing. The variability of response timing also depends on luminance change duration, a single-facet proxy of edge speed. Increased luminance change duration, as would result from a slower moving stimulus, evokes responses with greater temporal jitter. At the level of the LGMD, summation of many inputs does boost response reliability, but spiking output from the neuron is no more reliable than the underlying V_m from single-facet inputs. Modeling the LGMD excitatory input structure as simply reflecting the properties of single-facet luminance changes, with inhibition corresponding to stimulus size, recreates many of the LGMD's looming response properties. Manipulating single sources of variability in the model identify jitter in LGMD excitatory inputs and spontaneous activity as the main drivers of LGMD's spike rate variability.

Increase in spontaneous noise through the visual pathway.

We observed that the spontaneous membrane potential gradually became more variable as we recorded farther along the visual pathway. The membrane noise increased from the photoreceptors to the LMCs. Each LMC receives input from six photoreceptors, which might cancel out a portion of photoreceptor noise, assuming their independence and adequate averaging at the level of LMCs. Although locust photoreceptors are electrically coupled within a single ommatidium, the “bumps” resulting from individually resolved photon absorption events are uncorrelated in dark-adapted conditions, suggesting functional independence (Lillywhite 1977, 1978). Additionally, in flies, electrical coupling between photoreceptor terminals within a lamina cartridge has been suggested to reduce coupling due to extracellular potential changes (Weckström and Laughlin 2010) by allowing changes in intracellular potential to match those in the extracellular space (van Hateren 1986). However, detailed studies of synaptic transmission at the photoreceptor-LMC synapse in the fly have shown it to have a high gain (Juusola et al. 1995; Laughlin et al. 1987). Furthermore, LMC cutoff frequencies are higher than those produced by photoreceptor transduction noise, meaning that both the signal and noise are subject to amplification (Laughlin et al. 1987). These factors may contribute to the noise increase observed in our experiments. We also found spontaneous noise to be larger in the LGMD than in LMCs. This most likely results from the relatively high median size of single spontaneous excitatory postsynaptic membrane potential deflections (∼0.75 mV; see Fig. S5 in Peron et al. 2009).

Decrease in single-facet SNR through the visual pathway.

We observed that the SNRs of single-facet visual responses decreased markedly as we recorded further from the visual periphery. This was true when measuring response peaks, timings, and widths (Figs. 3 and 4). These SNR decreases were mostly evident in comparisons between LGMD recordings and those from photoreceptors. This does not, however, preclude a modest change in SNR between photoreceptors and LMCs, since we were able to obtain only a small number of stable LMC recordings despite much effort (3 cells from 60 animals). The reason for their extreme difficulty is unclear; to our knowledge, their are only two reports of locust LMC recordings prior to the ones carried out here (James and Osorio 1996; Shaw 1968). Although the paucity of data from LMCs warrants caution in interpreting the results, their overall trend well fits the pattern seen along the pathway from photoreceptors to LGMD current-clamp data.

Studies in the fly visual system concluded that the SNR of their LMCs is higher than those of single photoreceptors due to an averaging of photoreceptor variability (∼160% in light-adapted conditions; Fig. 10 of Laughlin et al. 1987; Fig. 3 of de Ruyter van Steveninck and Laughlin 1996). In these studies, the SNR was defined either from sensitivity measurements for contrast steps eliciting responses close to membrane potential noise threshold (Laughlin et al. 1987) or through time-averaged wide-band random stimuli optimized to maximize information rates (de Ruyter van Steveninck and Laughlin 1996). Whereas these studies characterized contrast coding (in 2 very different regimes), the present study used light steps at a fixed maximal contrast with time-varying transition speeds. Thus our SNRs describe how reliably the luminance transition speed or duration is conveyed by various features of the neural responses at successive stages of the visual system, and cannot be directly compared with the SNRs of these studies. Furthermore, the SNR improvement observed in fly LMCs may originate from independent photoreceptor sampling related to the neural superposition structure of the eye (Braitenberg 1967; Kirschfeld 1967). The impact of the apposition structure of the locust eye and of intrafacet photoreceptor coupling (Lillywhite 1978; Shaw 1967, 1969) on signal improvement at the level of the LMCs remains to be determined.

We did not see any change in SNR between I_m and V_m within the LGMD. We know that there are active conductances in the LGMD dendrites open around the resting potential, such as hyperpolarization-activated cation channels (Dewell RB and Gabbiani F, unpublished observations). This suggests that these conductances do not introduce significant amounts of noise.

One potential source of the decrease in SNR observed throughout the pathway is the transition from graded potential to spiking neural responses at the level of the medulla. Such a decrease would be consistent with the fact that information rates measured in fly photoreceptors and LMCs are much higher than those found in spiking neurons (de Ruyter van Steveninck et al. 1997; see also DiCaprio et al. 2007 for a graded potential/spiking neuron comparison in another system). Confirmation of an eventual SNR decrease at that level will have to await electrophysiological recordings from medullary neurons synaptically connected with the LGMD. Such recordings have not proven practical up to this point but would clearly provide critical information on the functioning of the excitatory pathway leading to the LGMD.

Analogous decreases in SNR, or increases in variability, through multiple stages of a visual pathway have been observed in other systems. Kara et al. (2000) observed that the Fano factor (FF), i.e., the ratio of across-trial spike count variance to spike count mean, increases from the retina to the lateral geniculate nucleus to primary visual cortex. That study, while reporting cortical FF values that were lower than many others in the literature, measured equivalent SNR values lower than what we observe in the LGMD single-facet responses (2–3.75 at ∼40-Hz firing rate). It has also been found that along the pathway from cones to bipolar cells to retinal ganglion cells (RGCs), sensitivity to small luminance changes declines through the pathway, approximately fourfold at each stage (Borghuis et al. 2009). These declines were mainly attributed to fluctuations in synaptic vesicle release at both synapses and spike generation within the RGCs. Decreases in SNR through a processing pathways are not inevitable, however, with various studies describing behavior that seems to be limited by noise present in the sensory system, far from motor outputs (Churchland et al. 2006; Osborne et al. 2005).

Variability of looming responses.

The amount of variability observed in neuronal responses can depend on the parameters of the input it receives (Faivre and Juusola 2008). These factors include how strongly the stimulus drives the neuron (Faivre and Juusola 2008; Tolhurst et al. 1983) and stimulus dynamics (Warzecha et al. 2000; but see Schaette et al. 2005). In the LGMD/DCMD, variability has previously been analyzed mainly in the dark-adapted state, to very different stimuli from those used here (Barker 1993). We found that the peak SNR of the membrane potential in response to looming stimuli is larger than to single-facet stimuli. Since looming stimuli activate the LGMD much more robustly than single-facet stimuli, it is not entirely surprising that the SNRs of looming responses are larger than those of single-facet responses. However, the peak SNR for looming stimuli was unchanged when firing rates were considered instead of V_m. This suggests that the spike generation process within the LGMD introduces additional noise, at least during looming stimuli. Variability in spike threshold is a possible source of this additional noise (Azouz and Gray 1999; Chacron et al. 2007). Consistent with this idea, both the LGMD and our model exhibit spike frequency adaptation (SFA), which dynamically shifts the cell's frequency-current curve based on past spiking. Indeed, our model LGMD responses reproduce this drop in SNR from V_m to firing rate, and removing SFA from the model, by removing the calcium-sensitive potassium current, yields SNR values for the IFR that were higher than those for the V_m (data not shown).

Looming responses in the LGMD result from the summation of thousands of inputs over the course of the stimulus. The number of inputs activated over time, both excitatory and inhibitory, grows due to both the expanding area of the stimulus and increasing angular speed. Use of a compartmental model of the LGMD allowed us to study how variability in the individual inputs shapes the variability of the LGMD response. These simulations show that, surprisingly, the variability in the strength of individual facet inputs do not play a strong role in determining the SNR of the LGMD peak firing rate or peak membrane potential. Instead, the looming variability is largely determined by the variability from spontaneous input arriving onto the LGMD and temporal jitter of the excitatory inputs.

The model allowed us to examine the importance of LGMD input timing variability in shaping the looming responses by running the simulations with and without a luminance change duration-dependent jitter. We observed in our single-facet responses that the variability in response latency from trial to trial increased with luminance change duration (Fig. 4). Thus early on during an object's approach (or a simulated approach), the angular velocity of its edges is slow, and the object takes a long time before its edge reaches a new photoreceptor's receptive field, since locust photoreceptor receptive fields are ∼3° wide with centers separated on average by 1–2° (mean ≈ 1.5°; Krapp and Gabbiani 2004). The high amount of jitter in the synaptic inputs to the LGMD originating from different facets allows the LGMD's firing rate to climb smoothly, rather than evoke a series of bursts triggered by synchronous inputs when the stimulus reaches new visual fields. Supporting this notion, subtle bursting to stimulus changes can be observed in LGMD responses to “constant-rate” looming stimuli, a variant of a looming stimulus that stimulates each facet of the eye with a roughly equal duration luminance change that should evoke LGMD excitation with less temporal jitter than normal looming. If such bursting were to occur in vivo to looming stimuli, escape behaviors would likely be grossly mistimed (see below).

Relationship with behavior.

It was recently shown that trial-to-trial variability in the LGMD/DCMD spike trains affect jump escape responses evoked by looming stimuli (Fotowat et al. 2011). Specifically, the timing of the locust's jump correlates strongly with the time of DCMD peak firing rate such that jumps occur ∼70 ms after the DCMD reaches its peak. Additionally, after the onset of the energy storage phase preceding the jump, called co-contraction (Burrows 1996; Santer et al. 2005), both the DCMD spike count and the regularity of DCMD spiking are predictive of the animal jumping. Thus the stimulus speed dependence of temporal jitter contributes to the production of DCMD firing patterns capable of driving downstream motor neurons important for jumping. Also, the timing of the co-contraction is partially dependent on the DCMD reaching a firing rate threshold. Very bursty LGMD spike trains, like those of the model with constant jitter, are likely to cross that threshold at very different times than in the normal case, possibly evoking mistimed jumping if such spike trains were produced in intact locusts. Behavioral experiments with stimuli designed to induce such bursting DCMD firing could be carried out to further test this idea. Although there is strong evidence that the DCMD and its ipsilateral homolog play an important role in the generation of jump collision avoidance behavior to looming stimuli measured in the laboratory (Fotowat et al. 2011), other pathways will also likely contribute to escape behaviors under more natural conditions, such as those involving giant wind-sensitive neurons (e.g., chapt. 10 of Burrows 1996).

In conclusion, we have shown that neuronal response variability through a visual pathway in the locust increases and that the SNR along the pathway for single-facet signals decreases. Summation of many of these inputs within the LGMD during looming boosts the SNR slightly, but spike generation lowers it again. Modeling suggests that variability in the magnitudes of individual synaptic inputs contributes little to trial-to-trial response variability. Instead, both ongoing spontaneous activity and variability in the latencies of synaptic input shape LGMD responses. Spontaneous activity influences the SNR of the LGMD output around its peak time, whereas timing variability enables a smoothly rising firing rate during looming and helps determine the variability of the response peak, both attributes of the response important for behavioral output. Together, these results suggest that noise, especially temporal response variability, contributes to shaping the neural responses elicited by looming stimuli along this sensory-motor pathway.

GRANTS

This work was supported by grants from the National Science Foundation and the National Institute of Mental Health and by a fellowship from the National Institute for Biomedical Imaging and Bioengineering.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

Author contributions: P.W.J. and F.G. conception and design of research; P.W.J. performed experiments; P.W.J. analyzed data; P.W.J. and F.G. interpreted results of experiments; P.W.J. prepared figures; P.W.J. and F.G. drafted manuscript; P.W.J. and F.G. edited and revised manuscript; P.W.J. and F.G. approved final version of manuscript.