Task-dependent coordination of rapid bimanual motor responses

Abstract

Optimal feedback control postulates that feedback responses depend on the task relevance of any perturbations. We test this prediction in a bimanual task, conceptually similar to balancing a laden tray, in which each hand could be perturbed up or down. Single-limb mechanical perturbations produced long-latency reflex responses (“rapid motor responses”) in the contralateral limb of appropriate direction and magnitude to maintain the tray horizontal. During bimanual perturbations, rapid motor responses modulated appropriately depending on the extent to which perturbations affected tray orientation. Specifically, despite receiving the same mechanical perturbation causing muscle stretch, the strongest responses were produced when the contralateral arm was perturbed in the opposite direction (large tray tilt) rather than in the same direction or not perturbed at all. Rapid responses from shortening extensors depended on a nonlinear summation of the sensory information from the arms, with the response to a bimanual same-direction perturbation (orientation maintained) being less than the sum of the component unimanual perturbations (task relevant). We conclude that task-dependent tuning of reflexes can be modulated online within a single trial based on a complex interaction across the arms.

recent models of sensorimotor control have moved away from the concept of a desired trajectory and instead emphasize the use of flexible feedback control that drives the evolving movement. In this framework, feedback controllers are instantiated with time-varying gains and use an estimate of the current state of the motor system to generate the motor commands. One theory, termed optimal feedback control (OFC), suggests that these feedback control processes are optimally tuned to task goals, for example, optimizing a trade-off between accuracy and effort in the presence of sensorimotor noise and external perturbations, with control achieved by flexible use of sensory feedback (Todorov 2004; Todorov and Jordan 2002).

The OFC framework has led to a renewed interest in whether reflexes or “rapid motor responses” (Pruszynski et al. 2008), which represent the lower levels of feedback control, act in a way consistent with predictions of OFC. Several studies examining unimanual movements have shown that feedback gains are set in a manner consistent with predictions of OFC (Franklin and Wolpert 2008; Knill et al. 2011; Liu and Todorov 2007). While such studies have focused on how one arm responds when perturbed, there are many situations in which richer behavior can be seen. For example, Marsden et al. (1981) showed that when one arm was perturbed the cross-effector reflex response in the other arm depended appropriately on whether this arm grasped a supportive surface or a filled cup. Recent studies have shown new levels of sophistication of such bimanual reflex responses. When subjects bimanually control a single cursor, displayed midway between their hands, perturbations to one hand elicit appropriate responses in the unperturbed arm (Diedrichsen 2007; Mutha and Sainburg 2009). Although subjects can correct for a unimanual perturbation with the action of one arm alone in bimanual tasks, compensating with both arms requires less overall effort. Certain important aspects of reflex sophistication have remained unexplored. For example, in the studies described above only one arm was perturbed and the reflex gain or response could have been prespecified based on the task goals and constraints. When two arms perform some tasks, however, the gain in one arm cannot be prespecified by considering the sensory state of this arm in isolation.

We therefore examined a novel task, conceptually similar to balancing a laden tray held with both hands, where the appropriate reflex response within a single limb can only be determined after taking into consideration the sensory state of both limbs. This task is performed under an unstable rotational force field that is sensitive to rotation (tilt) and insensitive to translations of the tray. Perturbing either hand alone leads to tilt of the tray and is task relevant, whereas simultaneously perturbing both hands in the same direction has no effect on tilt and is, therefore, task irrelevant. Hence, despite the ipsilateral arm receiving the same perturbation, we can examine whether its reflex response (i.e., “cross-reflex” response) is modulated by the nature of the perturbation in the contralateral arm.

Moreover, it is unclear whether rapid cross-effector responses are sensitive to specific characteristics of the perturbing stimulus, i.e., magnitude and direction. If this was not the case, such cross-effector responses would be indistinguishable from the early release of a prespecified startlelike action or triggered reaction (Hasan 2005; Shemmell et al. 2010). If, on the other hand, these cross-effector responses are sensitive to the perturbation characteristics applied to both hands and are modulated according to the task goals, then we may also find evidence of complex, nonlinear responses to bimanual perturbations. This can be determined by specifically examining whether cross-effector reflexes produce linear or nonlinear responses to bimanual perturbations compared with the sum of the two unimanual perturbations.

MATERIALS AND METHODS

Subjects

Eleven subjects participated in the experiment (6 men and 5 women, mean age 27 ± 5 yr). All were neurologically healthy and right-handed as judged by the Edinburgh handedness questionnaire (Oldfield 1971). The study was approved by the institutional ethics committee, and subjects gave informed consent prior to participating.

Experimental Apparatus and Setup

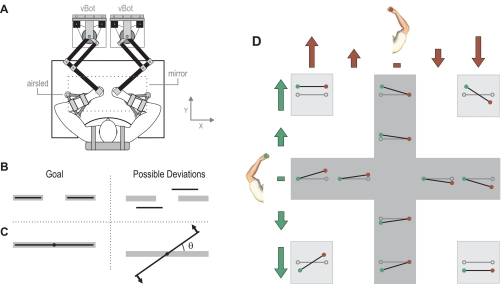
Subjects were strapped (with a 4-point racing harness) into an adjustable chair in front of a bimanual robotic rig. Each of the subject's arms rested on an airsled, and the subject grasped the handle of a vBOT robotic interface with each hand (Fig. 1A). The vBOT manipulanda are custom-built planar robotic interfaces that allow movement in the horizontal plane and can measure the position of the handles and generate forces on the hands at 1 kHz. With a mirror-monitor system subjects were prevented from seeing their own arms or robot handles, and we overlaid virtual visual feedback into the plane of the movement (Fig. 1, B and C). For full details of the robotic and virtual reality setup see Howard et al. (2009).

Fig. 1.

Experimental paradigm. A: subjects rested their arms on airsleds and grasped the handles of 2 robotic manipulanda (vBOTs). Subjects could not see their arms. Visual feedback was overlaid in the plane of movement by a mirror-monitor system. B: in the uncoupled control task, each hand independently controlled the position of a horizontal bar (black) and subjects' goal was to keep these within 2 target zones (gray rectangles). Deviations of 1 hand had no effect on the other. C: in the coupled single-object task, the manipulanda simulated the 2 hands being attached to the ends of a rigid bar (black) that was also visually displayed. The 2 hands jointly controlled the single rigid bar that could be translated and rotated. The subjects' goal was to maintain the orientation of the bar within the horizontal target (gray rectangle). However, because the target bar translated so as to track the midpoint of the bar, translations did not affect the task goal. A destabilizing rotational spring acted on the bar, generating forces (arrows) on the hand orthogonal to the bar, proportional to angular deviation from horizontal (θ) and acting to increase the angle. D: the single-object task had 12 different perturbation types: 8 unimanual (dark gray region) in which 1 arm was perturbed (2 magnitudes) while the other was clamped in place and 4 bimanual (light gray region) in which both arms were perturbed in either the same (task irrelevant) or opposite (task relevant) directions. Open circles and gray lines show the hand and bar positions prior to perturbation. Green represents the perturbations applied to the left hand and brown the perturbations to the right hand.

Electromyography

Surface electromyography (EMG) was recorded from the triceps lateralis, triceps longus, biceps brachii, and brachioradialis of each arm with the Delsys Bagnoli (DE-2.1-Single Differential Electrodes) system. The electrodes were coated with conductive gel and attached to the skin with double-sided tape. Two ground electrodes were used, one placed on each forearm just proximal to the wrist, and these electrodes were connected to the same EMG system. Prior to attachment of the electrodes, the skin was cleansed with alcohol and rubbed with an abrasive gel. The location for each electrode placement was chosen to maximize the signal-to-noise ratio while avoiding cross talk. Subjects wore latex gloves to electrically shield themselves from the robotic manipulanda. The EMG signals were band-pass filtered online through the EMG system (20–450 Hz) and sampled at 2.0 kHz.

Experimental Paradigms

Prior to the main single-object task, subjects performed a control task in which each hand independently controlled a bar that had to be placed within its own target zone (Fig. 1B). Specifically, subjects had to keep two horizontal red bars (4 × 0.2 cm), corresponding to the position of each hand, within two white target rectangles (4.4 × 0.6 cm) that were separated by 3.2 cm and ∼20 cm in front of the subject's chest (Fig. 1B). On each trial, subjects positioned the red bars within the targets and, after a pseudorandom delay (1–3 s), either the left or right hand was perturbed in either the elbow flexion or extension direction (4 perturbation conditions). Each position-controlled perturbation was a smoothly varying sixth-order polynomial (Burdet et al. 2000) with amplitude of 1.5 cm, a rise time of 150 ms, a hold time of 50 ms, and ramp back of 500 ms (reverse of initial perturbation). During the perturbation, the visual position of the red bar representing the position of the perturbed hand was frozen. Although limited by the subjects being firmly strapped into the chair, the control task was performed in part to confirm that any cross-limb reflexes seen in the single-object experiment were not due to a mechanical effect through the torso. Therefore, to avoid contributions from reflex responses due to stabilization effects (Marsden et al. 1981) the contralateral arm was free to move throughout the perturbations.

In the control task, four blocks of 100 trials (400 trials total) were performed, where each block contained each of the four perturbation conditions repeated 25 times in a pseudorandom order. Each block contained one of two background loads applied to both hands. The load conditions were either a constant load of 2 N in the elbow flexion direction or a constant load of 2 N in the elbow extension direction. The order of the two background load conditions was randomized across the first two and last two blocks. Therefore each of the four perturbations was presented 50 times for each of the two background loads.

In the main single-object task, the two robotic interfaces simulated a rigid bar, visually displayed as a red bar (12 × 0.2 cm) linking the two hands (Fig. 1C). This bar was generated by a stiff virtual spring that joined the handles together, simulating the hands acting on the end of a single solid object such as a bar, which could translate and rotate. Specifically, we simulated a two-dimensional stiff spring that acted between the handles with a spring constant of 4,000 N/m. The spring had a resting length of 12 cm and resisted any movement that changed this interhand separation, thereby simulating the hands acting on opposite ends of a 12-cm bar. If the forces exerted by either hand onto the rigid bar exceeded 1.5 N, a target rectangle changed to blue and trial progress was stopped. Subjects were instructed to keep the target white at all times. This was done to prevent subjects from stabilizing the arm-robot system by either squeezing or pulling apart the rigid object.

Subjects were required to maintain the orientation of the red bar within the white target rectangle, whose orientation was always horizontal but whose center was always aligned with the center of the red bar (i.e., it translated with the red bar). Therefore subjects were required to maintain the orientation of the red bar but were free to vary its position. To penalize deviations of the bar from horizontal we applied an unstable springlike force that was proportional to the angular deviation from horizontal and acted orthogonally to the bar in the direction of the deviation, thus destabilizing the bar's orientation (Fig. 1C). That is, we applied a rotational spring that acted in the direction of rotation, thereby generating forces on the hand that acted orthogonally to the bar and whose magnitude was proportional to angular deviation (θ) of the bar from the horizontal (θ = 0). The force applied to each hand was given by:

$$\left[\begin{array}{c}{F}_x\\ F_y\end{array}\right]=A·K·\left[\begin{array}{c}-\sin \left(\theta \right)·\theta \\ \cos \left(\theta \right)·\theta \end{array}\right]$$ (1)

where θ represents the angle between the two hands, K is the spring constant, and A is a sign transformation specific to each arm. A was set to 1 when calculating the forces applied to the left arm, and A = −1 for calculating the forces applied by the right handle. Translations of the bar had no effect on the forces produced. The spring constant K was set to 0.5 N/° for nine of the subjects. For two subjects we reduced the spring constant to 0.4 N/°, because they found the object hard to stabilize.

On each trial, subjects oriented the bar within the target rectangle, and, following a pseudorandom delay (1–3 s), either the left, right, or both hands were perturbed in an elbow flexion or extension direction. Each position-controlled perturbation was a smoothly varying sixth-order polynomial (Burdet et al. 2000) with a rise time of 150 ms and a hold time of 50 ms. There were 12 perturbation conditions: 8 unimanual and 4 bimanual. The unimanual conditions (Fig. 1D) consisted of perturbations of either a small (0.75 cm) or a large (1.5 cm) amplitude to either the left or right arm in either the flexion or extension direction. During unimanual perturbations the other hand was clamped in position by a simulated stiff spring. In the bimanual perturbation conditions only the larger perturbation was used (Fig. 1D). The perturbations were in either the same direction for both hands (translating the bar forward or backward) or opposite directions (rotating the bar either clockwise or counterclockwise). From the onset of the perturbation, visual feedback of the bar position was fixed for 200 ms to avoid any contribution of visuomotor responses to the measured force (Franklin and Wolpert 2008; Saunders and Knill 2004). The unstable field, object forces, and background loads were also not present during the perturbation. The unstable field, background load, and object forces were gradually applied (linearly from 0% to 100%) over the following 150 ms after the hold phase of the perturbation. Therefore, all task-related differences in EMG reported in our study in response to perturbations were in anticipation of an imminent unstable force field and not due to any rotary field forces per se.

All perturbations in our study were applied at the hand in Cartesian space in the positive or negative y-direction (Fig. 1A). However, because of the configuration of the arms the direction of the perturbation corresponded to either a large elbow flexion or extension, with a smaller amount of shoulder rotation. We therefore focused on the EMG responses in the elbow flexor and extensor muscles and for simplicity refer to flexor and extensor perturbations.

Subjects performed four blocks of 300 trials each (1,200 total trials). Each block consisted of 25 repetitions of each of the 12 perturbation types (which were block randomized). In addition to the unstable rotational force field that was present on every trial, each block contained one of two background loads applied to both hands. These loads were included because background loading can amplify reflex responses (Bedingham and Tatton 1984; Pruszynski et al. 2009) and to make the task more challenging, as increased muscle contraction increases kinematic variability due to signal-dependent noise (Harris and Wolpert 1998; Jones et al. 2002) that amplifies the instability of the force field (Burdet et al. 2006). The two background load conditions were either a constant load applied to both arms of 2 N in the elbow flexion direction or a load of 2 N in the elbow extension direction. The order of the two load conditions was randomized across the first two and last two blocks. Altogether each of the 12 perturbations was presented 50 times under each of the two background loads.

Data Analysis

The data were analyzed with MATLAB R14 and SPSS. Kinematic and force data were low-pass filtered with a fifth-order, zero-phase-lag Butterworth filter at 40-Hz cutoff. EMG data were high-pass filtered with a fifth-order, zero-phase-lag Butterworth filter with a 30-Hz cutoff and then rectified. All EMG data from each muscle and each subject were aligned to the onset of the perturbation. For statistical tests an α level of 0.05 was used and Tukey's honestly significant difference (HSD) test was used for post hoc comparisons.

Data normalization.

To allow for graphical display across subjects and tasks and to perform analyses to determine the onset of cross-effector responses (see Receiver operating characteristic analysis), both of which require us to combine data across subjects, each subject's EMG data were z-normalized. For each subject and muscle, we first averaged across all repetitions of the same condition, resulting in 32 EMG traces in each case (4 control + 12 experimental conditions for each of 2 background loads). Traces corresponded to a time window from 30 ms prior to perturbation onset until 200 ms after the perturbation onset. For each subject and muscle we normalized these 32 EMG traces by subtracting a single mean and dividing by a single standard deviation. The mean value was calculated by averaging across all points in the time window and across all 32 traces. The single standard deviation was calculated by taking the standard deviation at each point in the time window across the 32 traces, and then taking the mean across this time series of standard deviations.

Receiver operating characteristic analysis.

We used the unimanual perturbation trials to assess the earliest point in time at which the cross-effector reflexes in the unperturbed arm differed depending on whether the perturbed arm was extended or flexed. This was determined with receiver operating characteristic (ROC) analysis, which reflects the ability of an independent observer to discriminate between signals (Green and Swets 1966). A separate ROC analysis was performed for each muscle and background load condition. To perform one ROC analysis (for 1 muscle and background load) we calculated for each subject the mean of z-transformed EMG traces separately for the conditions in which the perturbed arm flexed or extended, leading to 22 traces (11 subjects × 2 perturbations). We used ROC discrimination criteria employed previously (Pruszynski et al. 2008, 2010) on the data to determine when different cross-effector responses could be discriminated from one another. Specifically, discrimination time was defined as the time at which ROC values exceeded 0.75 (or <0.25) for at least a period of 5 ms (ROC value of 0.5 indicates no discrimination). ROC analyses indicated that the earliest time at which cross-effector responses could be discriminated from one another was 79 ms (left triceps lateralis). Examination of the data showed little if any asymmetry between the responses of homonymous muscles of the right and left arm to equivalent mirror-symmetric perturbation conditions. Therefore, to simplify display and ROC analyses, we combined (averaged) the z-normalized data across the two arms for mirror-symmetric conditions, independently for each background load. Similar results were obtained when conducting ROC analyses using averaged EMG activity across homonymous muscles. The earliest discrimination time for cross-reflex responses was 77 ms (triceps lateralis).

Data for statistical analyses.

For all statistical analyses, the unnormalized EMG data from each muscle and each subject were first averaged across groups of five consecutive repetitions of the same condition, giving 10 EMG time series per perturbation condition, muscle (n = 8), background load, and subject. This averaging was done in order to decrease noise and facilitate an analysis requiring summation of EMG across limbs (see Nonlinear interaction analysis). For consistency, we used these averaged traces for all statistical tests.

The “R3” or “M3” reflex timing for responses from elbow muscles of the perturbed limb itself has been shown to be between 75 and 105 ms, with voluntary responses commencing at 120 ms (Pruszynski et al. 2008). It has also been shown that the transmission of signals between cortices through the corpus callosum requires at least an additional 10 ms (Cracco et al. 1989; Ferbert et al. 1992; Meyer et al. 1995; Salerno and Georgesco 1996). Therefore, because the cross-effector responses we were looking at depended on the integration of sensory information from both limbs, we determined the end of reflex time window for rapid cross-effector responses to be 105 + 10 = 115 ms. Importantly, voluntary responses in our task are likely to be slower than “voluntary” triggered responses in which the direction of the upcoming perturbation or response is known in advance, because in our study the perturbation direction was randomized. Given the ROC analysis, we therefore used the interval of 75–115 ms (which we will refer to as the R3 period) to produce data for statistical analyses.

Unperturbed arm EMG analyses.

To examine the reflex responses of the unperturbed arm to perturbations of the contralateral arm, we performed separate ANOVAs for each muscle and background load of the integrated EMG over the R3 period. Each ANOVA had a 2 × 2 × 2 design (perturbation direction × perturbation amplitude × arm: left/right), using subjects as a random variable.

Perturbed arm EMG analyses.

To examine the effects of the perturbation state of the contralateral arm on the responses of the perturbed ipsilateral arm EMG (integrated over the R3 period) we performed separate ANOVA tests for each muscle, perturbation direction of the ipsilateral arm (flexion or extension), and background load, using a 3 × 2 design (perturbation state: bimanual same direction, bimanual different direction, unimanual perturbation × arm: left/right), using subjects as a random variable.

Nonlinear interaction analysis.

To examine possible nonlinear responses, we summed the unnormalized EMG traces from unimanual perturbation conditions in order to compare the combined responses of unimanual perturbations versus the bimanual perturbation equivalents. For example, we summed the EMG from the biceps of the left arm when that arm was being extended (contralateral hand clamped) with the EMG of this same muscle when the other arm was being extended (ipsilateral hand clamped) and compared this summed signal with the EMG of the same muscle when both arms were being extended simultaneously. To remove the offset due to the summation of two channels, the median value of the clamped ipsilateral arm EMG over the 30-ms period prior to perturbation (of the contralateral arm) was subtracted from the summed EMG signal. From each of the final traces we calculated the integrated EMG over the R3 period. To test for nonlinear effects, we performed a separate ANOVA for each muscle, background load, and perturbation direction, and the design was 2 × 2 (perturbation type: bimanual perturbation, sum EMG of unimanual perturbations × arm: left/right).

RESULTS

Subjects grasped the handles of two vBOT robotic interfaces, with visual feedback overlaid into the plane of movement (Fig. 1A). In the control task the subjects had to maintain two horizontal bars within two target rectangles (Fig. 1B), and these targets were placed ∼20 cm in front of the subject's chest. In the main single-object task we simulated a rigid bar, both visually and haptically, that linked the two hands. The task was to maintain the bar's orientation horizontal, with angular deviations penalized by an unstable rotary force (Fig. 1C). Translations of the bar were allowed and had no effect on the forces experienced. During the task, each limb could either be unperturbed or rapidly flexed or extended during a trial to elicit reflex responses (Fig. 1D). Each block of trials of the single-object task began with the bar being at the same position as the target rectangles in the control task. Although translations of the bar were allowed, the subjects' hands did not deviate substantially from their original position, with standard deviation (averaged standard deviation across the subjects) for (x, y) deviations of (0.75, 1.4) cm under the extensor background load and (0.76, 1.5) cm under the flexor background load.

We found no significant difference between the responses of the muscles on the right arm compared with those of the left arm for any statistical comparison in all the experiments. Therefore, for some plotting purposes and ROC analysis, we combined the data across the arms (see materials and methods for details). All other statistical analysis was performed without combining across the arms.

Responses in Unperturbed Arm to Contralateral Perturbations

ROC analyses.

Figure 2 displays the responses of the unperturbed arm during the control and experimental (single object) task. When the flexor muscles were loaded, ROC analyses indicated that the biceps EMG of the unperturbed arm when the contralateral arm was perturbed in the flexion direction by the large-amplitude perturbation could be discriminated at 90 ms from the response of the same muscle when the other arm was perturbed in the extension direction (89 ms for smaller perturbations, Fig. 2, B and C, left). Similarly, during larger perturbations of the contralateral arm, the EMG response of the brachioradialis muscle during flexion of the contralateral arm could be discriminated from the responses of this muscle during extension of the other arm at 101 ms. No discrimination was possible during smaller perturbations for this muscle. In the control condition in which the two hands were uncoupled and each controlled its own visual bar (Fig. 1B), no discrimination of flexor EMG signals (biceps or brachioradialis) was possible during larger perturbations of the contralateral arm (Fig. 2A).

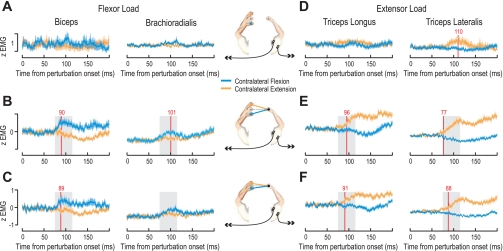
Fig. 2.

Cross-limb reflexes in the unperturbed arm elicited by contralateral perturbations: EMG traces in the unperturbed limb during perturbations of the contralateral limb. Central schematics show EMG recorded from the unperturbed right arm during perturbations of the left arm, with the intermediate hand position representing the preperturbation configuration. The EMG averages shown in the plots also include the mirror-symmetric conditions for EMG recorded from the unperturbed left arm where the right arm was perturbed. A and D: group averages of normalized EMG (see materials and methods) across all subjects in the uncoupled control task (each hand independently controlled a separate bar) when the contralateral arm was perturbed either downward (i.e., flexion, blue trace) or upward (i.e., extension, orange trace). Plots in A are for flexor muscles under the flexor background load condition and plots in D for extensor muscles under the extensor load condition. Shaded areas signify ±SE across subject means. Red vertical line indicates the earliest time at which receiver operating characteristic (ROC) analysis could discriminate between subject average traces for the 2 perturbation conditions (see results). B and E: responses in the coupled single-object task (the 2 hands controlled a single rigid bar) for the large-amplitude perturbations. Plots in B are for flexor muscles under the flexor background load condition and plots in E for extensor muscles under the extensor load background. The gray shaded areas behind the traces indicate the 40-ms period used for statistical analyses (75–115 ms). C and F: as B and E, but for the small-amplitude perturbations.

When extensor muscles were loaded, the EMG responses of both the triceps longus and lateralis during larger extension perturbations of the contralateral arm could be discriminated from responses evident during contralateral flexion perturbations, at 96 and 77 ms, respectively (Fig. 2E). During smaller-amplitude perturbations, the relative discrimination times were 91 ms for triceps longus and 88 ms for triceps lateralis (Fig. 2F). During perturbations of the contralateral arm in the control task, no discrimination of triceps longus signals was possible but the triceps lateralis responses could be discriminated at 110 ms (Fig. 2D). Note that there was essentially no movement of the unperturbed arm during contralateral perturbations in the control task, although the unperturbed arm was fully free to move. In the following analyses we examine whether the differences in EMG responses of the unperturbed arm were in the correct direction to assist in stabilizing the bar held between the two hands. For the purpose of these analyses we compared the integrated muscle activity over the interval 75–115 ms after the onset of the perturbation in the other limb.

Responses under background flexor load.

We first examine the responses of the unperturbed limb while both limbs counteracted a background flexor load in the coupled single-object task where both hands jointly controlled the orientation of a visual and haptically simulated bar (Fig. 1C). We found large effects associated with the perturbation direction of the contralateral arm for the two flexor muscles in the clamped arm (Fig. 2, B and C). We found significantly higher responses during a flexion perturbation of the contralateral arm compared with an extension perturbation of the contralateral arm for both the biceps (F_1,10 = 24.9, P = 0.001) and the brachioradialis (F_1,10 = 6.01, P = 0.034) muscles. Functionally, these responses occur in the correct direction to promote stability in the single-object task. A flexion perturbation of the contralateral arm causes a tilt of the object, which could be counteracted by increased flexor activity in the unperturbed arm.

Similarly, there was a strong effect of perturbation direction on the responses of the extensor muscles of the unperturbed arm, with significantly higher responses when the other arm was being extended rather than flexed for both the triceps lateralis (F_1,10 = 10.3, P = 0.009) and the triceps longus (F_1,10 = 17.5, P = 0.002). Similar to the flexor muscles above, the increased activation of these extensor muscles in the unperturbed arm during an extensor perturbation of the contralateral arm is appropriate to counteract the tilt of the bar. There was also a significant interaction effect of perturbation direction and amplitude for both the triceps lateralis (F_1,10 = 9.5, P = 0.012) and the triceps longus (F_1,10 = 17.3, P = 0.002) muscles, indicating that the response in the unperturbed extensor muscles was sensitive to the size of stretch in the contralateral arm. This demonstrates that the responses were appropriately graded to the size of the stretch in the contralateral arm to compensate for the differences in the amount of tilt of the object associated with the perturbation magnitudes.

Responses under background extensor load.

We now examine the responses of the unperturbed limb while both limbs counteracted a background extensor load in the coupled single-object task where both hands jointly controlled the orientation of a visual and haptically simulated bar (Fig. 1C). We found large effects associated with the perturbation direction of the contralateral arm for the two extensor muscles in the clamped arm (Fig. 2, E and F). We found significantly higher responses during an extension perturbation of the contralateral arm compared with an flexion perturbation of the contralateral arm for the triceps lateralis (F_1,10 = 32.5, P < 10⁻³) and the triceps longus (F_1,10 = 54.4, P < 10⁻³). Again, these responses function to promote stability in the single-object task. An extension perturbation of the contralateral arm causes a tilt of the object, which can be counteracted by increased extensor activity in the unperturbed arm. There was also a significant interaction effect between perturbation direction and amplitude for the triceps lateralis muscle (F_1,10 = 15.4, P = 0.003). When the contralateral arm was extending, the EMG in response to larger perturbations was higher than that during smaller perturbations, and this pattern was reversed when the contralateral arm was flexing, indicative of more suppression during the larger flexion perturbation. These effects demonstrate the appropriate grading of the responses in the unperturbed limb depending on the perturbation size and direction of the contralateral limb. When we examined the responses of the flexor muscles under this extensor loading, we found large effects associated with the perturbation direction of the contralateral arm for the biceps (F_1,10 = 7.5, P = 0.021) but not for the brachioradialis (F_1,10 = 0.31, P = 0.59). Taken together, the results indicate that the ipsilateral (clamped) arm produces stabilizing reflex responses that depend appropriately on both the perturbation direction and magnitude in the contralateral arm.

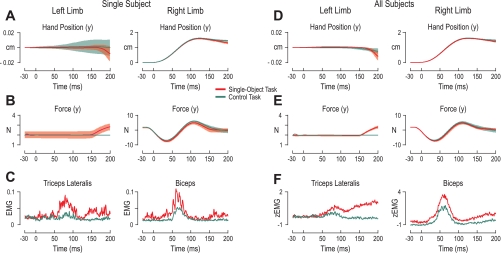
Figure 2 shows averages across subjects and arms. However, similar effects were observed in single-subject responses and for each arm. For example, Fig. 3, A–C, shows the hand position, forces, and EMG from both the left and right arm of a single subject during perturbation of the right arm in the extension direction in the control task and in the single-object task. In both tasks, little or no movement of the unperturbed hand was seen, particularly in the first 50 ms after perturbation of the contralateral arm. In the control task, perturbation of the right arm caused no appreciable change in triceps lateralis activity of the subject's unperturbed arm, although the same perturbation caused a burst of activity in the muscle around 60 ms during the single-object task (Fig. 3C, left). This burst of activity in the single-object task led to the unperturbed left hand producing a force (in the positive y-direction) at ∼150 ms (Fig. 3B, left). No such force was seen in the control task (Fig. 3B, left). The effects seen in the single subject were also found across all subjects (Fig. 3, D–F). Although it is possible to correct a unimanual perturbation with action of one arm alone in the single-object task, Fig. 3 clearly indicates that subjects distributed the work across both arms, which allows for more flexibility and overall less effort.

Fig. 3.

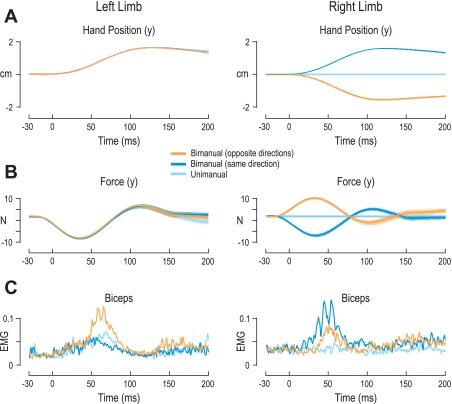
Responses during perturbation of the right arm for a single subject and across subjects. A–C are for the left and right limbs of a single subject during perturbations (onset at 0 ms) of the right hand in the arm extension direction for the extensor background load (−2 N). Red and green traces are for the single-object and control tasks, respectively. Lines represent the mean values across all repetitions of this perturbation for this single subject, and shaded areas correspond to ±1 standard deviation from the mean. A: hand position (y-axis). Note the difference in scales of y-axis for the limbs. B: forces exerted between the hand and robotic handle along the y-axis. In the single-object task the unperturbed arm was clamped into position by the robot, whereas in the control task the unperturbed arm was free to move. C: EMG in triceps lateralis of the left arm (left) and the biceps of the right arm (right). D and E: as in A and B, but lines represent averages across subject mean responses and shaded areas represent ±1 standard deviation from the mean across subjects. F: z-normalized EMG (see Data normalization) of the triceps lateralis of the left arm and biceps of the right arm across subjects.

Responses in Perturbed Arm

In the previous section we demonstrated that the perturbation state of the contralateral arm affects the responses of the unperturbed ipsilateral arm. We next examined whether the perturbation state of the contralateral arm modulates the responses of the simultaneously perturbed ipsilateral arm. Specifically, we analyzed responses in the perturbed ipsilateral arm as a function of the three possible perturbation states of the contralateral arm. Perturbations of the contralateral arm in an opposite direction lead to a marked deviation in the orientation of the object and hence to a high level of instability (Fig. 4). Conversely, perturbations in the same direction simply translate the object without causing any rotations (Fig. 4). Because our task was designed so that only changes in orientation were relevant, such a translation had no effect on task success and was task irrelevant. Finally, when the ipsilateral arm was perturbed and the contralateral arm was not, this led to an intermediate level of instability (Fig. 4). Therefore, despite the ipsilateral arm receiving the same perturbation, we can examine whether its reflex response is modulated by the nature of the perturbation in the contralateral arm.

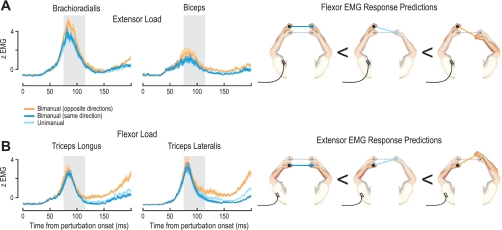
Fig. 4.

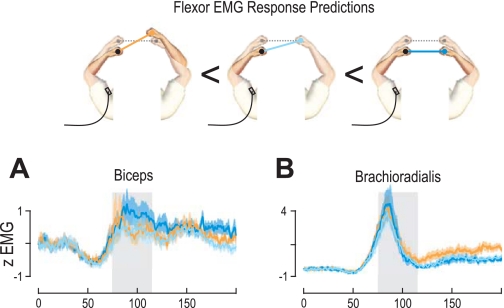
Rapid responses in the perturbed arm are modulated by contralateral perturbations: EMG traces from the perturbed limb in the coupled single-object task when the contralateral arm is unperturbed (light blue) or perturbed in the same (dark blue) or opposite (orange) direction. Schematics on right of the plots show EMG recorded from the left arm under the 3 possible perturbation conditions of the contralateral arm, with the initial bar orientation prior to perturbation represented by the gray dotted line. EMG averages shown in the plots also include the mirror-symmetric conditions for EMG recorded from the perturbed right arm under the 3 perturbation states of the left arm. A: traces represent averaged EMG (normalized) across all subjects during extension perturbations of the recorded arm in the extensor background load condition, as a function of whether the contralateral arm was unperturbed (clamped, light blue trace) or perturbed in the same (dark blue trace) or opposite (orange trace) directions. B: extensor EMG responses during flexion perturbations of the recorded arm in the flexor background load condition under 3 perturbation states of the contralateral arm. Shaded areas in trace plots signify ±SE, and the gray shaded areas behind the traces indicate the 40-ms period used for statistical analyses (75–115 ms).

Responses of stretched flexors.

When the ipsilateral arm was extended (that is, “ipsilateral” with regard to the reported EMG) we saw clear reflex responses in stretched flexor muscles across all subjects (Fig. 4A). Again, however, this reflex response was modulated by the nature of the perturbation in the contralateral arm. Specifically, during the extensor background load, there was a significant main effect of perturbation state of the contralateral arm on the responses of the stretching brachioradialis (F_2,20 = 5.47, P = 0.013) and biceps (F_2,20 = 5.46, P = 0.013) (Fig. 4A). These significant main effects were further investigated with Tukey's HSD post hoc test. We found significantly higher responses when the other arm was being flexed compared with when it was perturbed in the same extension direction (brachioradialis: P < 10⁻³; biceps: P = 0.006) or clamped (brachioradialis: P < 10⁻³; biceps: P = 0.035). In the flexor load condition, we again found a significant main effect of the perturbation state of the contralateral arm on the biceps (F_2,20 = 3.8, P = 0.039) but no significant effect for the brachioradialis (F_2,20 = 0.87, P = 0.434). A post hoc comparison on the biceps indicated significantly higher EMG when the contralateral arm was perturbed in the flexion direction compared with the extension direction (P = 0.027). Therefore, the activity of the stretched flexor muscles was modulated depending on the perturbation state of the contralateral arm. This effect was strongest when the limb was under an extensor background load, but still present for the biceps muscle under the flexor background load.

Task-dependent bimanual responses were also observed at the single-subject level. Figure 5 displays the hand kinematics, force, and unnormalized EMG responses of a single subject during the three bimanual perturbation combinations. Despite receiving the same extension perturbation, the EMG responses of the left biceps were clearly stronger when the other arm was perturbed in the opposite direction than in the same direction or unperturbed during the period of 50–80 ms after perturbation (Fig. 5C, left).

Fig. 5.

Single-subject responses to extension perturbations are modulated by contralateral perturbations: left and right limb kinematics, force, and EMG of a single subject during left arm extension perturbations (onset at 0 ms). The different traces correspond to different simultaneous perturbations of the right arm: in the same arm direction (dark blue traces), in the opposite direction (orange trances), and unperturbed (right hand clamped by robot, light blue traces). Lines represent the mean values across all repetitions of the same condition, and shaded areas correspond to ±1 standard deviation from the mean. A: hand position (y-axis). B: forces exerted between the hand and robotic handle along the y-axis. C: EMG in the biceps. Although the left arm received the identical perturbation in all combinations, its biceps EMG activity was stronger when the right arm was being perturbed in the opposite direction (orange trace), which is associated with the largest amount of rotation of the bar object and hence the highest level of instability in the single-object task. The weakest left biceps responses occurred when the 2 arms were perturbed in the same direction (dark blue trace), as this perturbation combination causes little or no tilt of the bar object.

Responses of stretched extensors.

Similarly, when the ipsilateral arm was perturbed in the flexion direction, causing a stretch in the extensor muscles, we found modulation of the extensor activity as a function of the perturbation state of the contralateral arm (Fig. 4B). Under the flexor background load, we found a significant main effect of perturbation state of the contralateral arm on the responses of the stretched triceps lateralis (F_2,20 = 4.16, P = 0.031) but not the triceps longus (F_2,20 = 2.7, P = 0.088) (Fig. 4B). The significant main effect on the triceps lateralis was further examined by Tukey HSD post hoc test, indicating significantly higher EMG when the contralateral arm was perturbed in the extension rather than the flexion direction (P < 10⁻³) or unperturbed (P = 0.014). During extensor background loading, we found significant main effects of the contralateral arm perturbation state on the responses of the stretched triceps longus (F_2,20 = 6.9, P = 0.005) and triceps lateralis (F_2,20 = 5.02, P = 0.017). Post hoc comparisons (Tukey HSD) indicated significantly higher triceps longus responses when the contralateral arm was perturbed in the extension rather than the flexion direction (P = 0.006) or clamped (P = 0.004). A post hoc comparison on the triceps lateralis also indicated significantly higher responses during bimanual perturbations in opposite directions rather than during bimanual perturbations in the same direction (P = 0.002). Therefore, similar to the stretched flexor responses above, the activity of the stretched extensor muscles was modulated depending on the perturbation state of the contralateral arm.

Responses of shortened flexors.

We now examine the results for the shortened flexors for the perturbation state of the contralateral arm. When the ipsilateral arm (that is, “ipsilateral” with regard to the reported EMG) is perturbed in the flexion direction, this causes a shortening of the flexor muscles. This shortening of flexor muscles produces the expected inhibition during the short latency interval but an excitatory response during the long latency interval (75–115 ms) for all three conditions (Fig. 6). Under an extensor background load, we found a significant modulation of the response by the state of the contralateral arm in the shortened brachioradialis (F_2,20 = 12.6, P < 10⁻³) but not the biceps (F_2,20 = 2.8, P = 0.08). A post hoc test on the significant main effect observed in the brachioradialis activity found significantly higher activity when the other arm was also perturbed in the flexed direction compared with when it was clamped (P = 0.002). Under the flexor background load, we found no significant modulation of the shortened brachioradialis muscle (F_2,20 = 2.8, P = 0.085; Fig. 6B) but a significant effect of perturbation condition on the response in the biceps (F_2,20 = 8.9, P = 0.002; Fig. 6A). The post hoc test demonstrated that there were significantly higher responses for the condition where the contralateral arm was also perturbed into flexion compared with when the contralateral arm was perturbed into extension (P = 0.002) or was clamped (P < 10⁻³). Functionally these changes in muscle activity are appropriate for the task; increased flexor responses during shortening contribute to limb stability through coactivation, but lower levels of excitation of the biceps responses were observed when the object was tilted, possibly avoiding excess tilt of the object and therefore instability.

Fig. 6.

Rapid responses from shortened flexors are modulated by contralateral perturbations. Colored traces represent averaged biceps EMG (normalized) across all subjects during flexion perturbations of the recorded arm in the flexion background load condition as a function of whether the contralateral arm was unperturbed (clamped, light blue trace) or perturbed in the same (dark blue trace) or opposite (orange trace) directions. Schematics on top of plots show EMG recorded from the left arm under the 3 possible perturbation conditions of the contralateral arm, with the initial bar orientation prior to perturbation shown by the gray dotted line. EMG averages shown in the plots also include the mirror-symmetric conditions for EMG recorded from the perturbed right arm under the 3 perturbation states of the left arm. A: responses of the shortening biceps under a flexor background load. B: responses of the shortening brachioradialis under a flexor load. Shaded areas in trace plots signify ±SE, and gray shaded areas behind the traces indicate the 40-ms period used for statistical analyses.

Responses of shortened extensors.

In the shortening extensor muscles, the results were less consistent. Under the flexor background load, extensor perturbations of the ipsilateral arm were modulated by the perturbation state of the contralateral arm for the triceps lateralis (F_2,20 = 3.78, P = 0.04) but not for the triceps longus (F_2,20 = 2.4, P = 0.114). However, the post hoc comparison indicated significantly higher responses in the triceps lateralis when the contralateral arm was perturbed in the opposite direction compared with when it was perturbed in the same direction (P = 0.004) or clamped (P = 0.009). Under the extensor background load, extension perturbations of the ipsilateral arm were not modulated by the contralateral limb state for the shortened triceps lateralis (F_2,20 = 1.9, P = 0.175), but there was such a main effect on the responses of the shortened triceps longus (F_2,20 = 5.39, P = 0.013). The post hoc comparison showed that responses were larger when the contralateral perturbation was also extended compared with when it was flexed (P = 0.001) or clamped (P = 0.039), consistent with the results from the shortened flexors.

Overall, these results show that EMG activity in the perturbed arm was systematically modulated depending on the level of task relevance associated with the contralateral arm's perturbation. That is, during muscle stretch, the highest levels of activity were seen when the contralateral arm was perturbed in the opposite direction rather than the same direction or not perturbed at all—appropriate responses for the overall task. On the other hand, in the shortened muscles, the highest levels were normally found when the contralateral arm was perturbed in the same direction as the ipsilateral arm—indicating that excitation of the shortened muscles may be avoided when they could potentially contribute to the inherent task instability.

Complex Bimanual Interactions

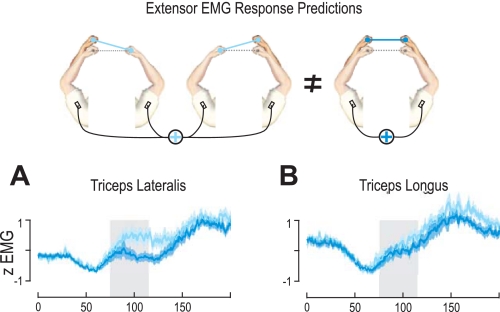
Finally, we investigated whether the nervous system can tune its sensorimotor reflexes in a complex nonlinear manner. Consider the three perturbations shown in Fig. 7, which show extension perturbations to either arm alone or to both arms simultaneously. Both single-arm perturbations are task relevant, inducing rotation of the bar (Fig. 7). In contrast, when both of these perturbations are simultaneously applied the net effect is a task-irrelevant translation of the bar (Fig. 7). Our responses to unimanual perturbations show that the stretch reflexes within a limb are larger than the cross-limb reflexes (Figs. 2 and 4). For example, when one arm is perturbed in the extension direction, there is a large flexor response in that limb and a smaller extensor response in the other limb. Therefore, if the responses simply add linearly, when both arms are extended simultaneously there will be a net flexor response in both limbs. However, the optimal response in terms of keeping the tray level and minimizing energy is to produce no response. This requires a nonlinear combination of the individual reflex responses. Therefore, we might expect a smaller (sublinear) response to the bimanual perturbation compared with the sum of each unimanual perturbation. To test whether the bimanual perturbation elicits a linear or a sublinear response, we summed the four EMG traces from the unimanual perturbations (ipsilateral and contralateral effects), which together reflect the component EMG contributions present in the bimanual perturbation (Fig. 7). We compared this to the EMG present in the bimanual perturbations summed across the arms (Fig. 7).

Fig. 7.

Rapid responses exhibit nonlinear task-dependent interactions. Nonlinear comparisons examining the response to a bimanual perturbation in the same direction compared with the sum of the responses to the unimanual components of the bimanual perturbation. Here, the light blue traces are the sum of the extensor activity from both right and left arms in the extensor load condition, during unimanual extension perturbations of either the right or left arm (corresponding color in schematics). The dark blue traces are the sum of the activity from both right and left arms during bimanual perturbations of both arms (schematics, right). A: responses of the shortening triceps lateralis under an extensor load. B: responses of the shortening triceps longus under an extensor load. Shaded areas signify ±SE, and gray shaded areas behind the traces indicate the 40-ms period used for statistical analyses.

For both extensor muscles, we found that the responses during bimanual extension perturbations were significantly lower than the summed EMG of the unimanual component perturbations (Fig. 7). Specifically, during the extensor background load condition, we found a significantly lower muscular response in the task-irrelevant bimanual perturbation in both the shortened triceps lateralis (F_1,10 = 39.9, P < 10⁻³) and the shortened triceps longus (F_1,10 = 11.4, P = 0.007) compared with the constituent unimanual conditions. Similarly, during perturbations in the flexion direction, we found a significantly lower response in the shortened brachioradialis during the task-irrelevant bimanual perturbations compared with the constituent unimanual conditions (F_1,10 = 18.5, P = 0.002). However, we found no sublinear effects on the muscles that were lengthened by the task-irrelevant bimanual perturbations within the long latency intervals (75–115 ms). Therefore, we find linear summation within the stretched muscles and a sublinear summation for shortened muscles during the task-irrelevant bimanual perturbations.

DISCUSSION

We investigated the tuning of rapid motor responses in a task conceptually similar to maintaining the orientation of a tray that has to be held horizontally with two hands. A key feature of our task is that reflex responses in one limb cannot be optimally preprogrammed based on the potential perturbations to that limb or to the other limb considered in isolation. Instead, each limb needs to take into account the ensemble of perturbations applied to both limbs, and in some situations the appropriate response should be nonlinear. We first examined reflexes in the unperturbed limb to perturbations of the other limb and found that these were tuned for both perturbation direction and magnitude (Fig. 2), thereby correcting for tilt. Second, we examined the perturbed limb and found that the magnitude of the reflex response was modulated by the nature of the perturbation in the other limb. In lengthening muscles (Fig. 4), the response magnitude was largest for perturbations that were opposite in direction, mirroring the perturbations' task relevance. In shortening flexors, the level of suppression of muscle activity also reflected the perturbations' task relevance (Fig. 6) in that the counterproductive action of these muscles in this case was inhibited more strongly during task-irrelevant perturbations. Finally, the responses of the shortening extensors were sublinear, as weaker activity was observed during bimanual perturbations in the same direction compared with the sum of unimanual perturbations (Fig. 7). However, we found no evidence of nonlinear responses in lengthening muscle. We therefore demonstrate that task-dependent tuning of reflexes can be modulated online within a single trial and such tuning is based on a complex interaction across the arms, which can involve nonlinear responses from shortening muscles.

Maintaining postural stability in a destabilizing environment presents a challenge for the sensorimotor system (Burdet et al. 2001; Franklin et al. 2007; Selen et al. 2009). A natural consequence of OFC is that sensory information should be evaluated with respect to its effect on task success, with motor responses generated only for task-relevant perturbations (Scott 2004). Indeed, the long-latency components of reflex responses vary based on prespecified task information provided explicitly by verbal instructions (Capaday et al. 1994; Crago et al. 1976; Lewis et al. 2006; Rothwell et al. 1980) or implicitly by target location (Pruszynski et al. 2008). However, OFC also predicts that an identical perturbing stimulus to one arm should give rise to widely varying responses depending on the state of the contralateral arm, that is, depending on the nature of the bimanual interaction. Bimanual interaction has been shown in the modulation of grip force in response to perturbations of the contralateral hand (Ohki and Johansson 1999; White et al. 2008). Although task-dependent cross-effector reflex responses from upper limbs have been demonstrated before (Diedrichsen 2007; Marsden et al. 1981; Mutha and Sainburg 2009), these studies only perturbed one limb. In our task we created a natural situation in which the stability of the task could not be determined by considering each arm in isolation. By considering both arms and the direction of their perturbations, we show that the reflex gain of one arm can be constructed to depend jointly on the perturbations applied to the two arms.

Previous studies of cross-effector EMG responses examined a single perturbation direction and magnitude (Marsden et al. 1981; Mutha and Sainburg 2009). Consequently, it is unclear whether cross-effector responses emerge from a feedback mechanism that takes stimulus amplitude into consideration when formulating a response, or whether such responses are the result of an early release of a prespecified command, defined as a triggered reaction (Hasan 2005; Shemmell et al. 2010). We show that cross-effector responses do indeed modulate with stimulus amplitude and direction, and this involves both amplification and suppression of responses in a manner appropriate to the task at hand. For example, larger extension perturbations of the contralateral arm were correctly associated with larger responses in the extensor muscles of the unperturbed arm. Larger flexion perturbations led to lower responses in the unperturbed extensors compared with the effects of smaller perturbations in the same direction. This suggests that these rapid motor responses are not simply triggered by the perturbation but compute the appropriate response depending on the combination of sensory information across the two limbs. In addition, both excitation and suppression of muscle activity of perturbed limbs were widely enlisted in order to maintain stability in our task. Compared with the activity present when both arms were perturbed in the same direction, the activity of lengthening muscles was heightened when the contralateral arm was perturbed in the opposite direction, whereas the activity of the shortening triceps longus and shortening flexor muscles was suppressed in this condition.

Critical to our experimental design, the visual presentation of the bar was not updated throughout the perturbation, avoiding contributions from any visuomotor responses (Franklin and Wolpert 2008; Saunders and Knill 2004). Therefore, our results isolate the response as proprioceptively driven rather than arising from visual effects. In addition, previous studies have examined such cross-effector responses during movement, in which separate reflex responses were isolated from the ongoing voluntary control (Diedrichsen 2007; Mutha and Sainburg 2009). In our study we examined the response from the limb when it was clamped in position by the robotic interface, showing that the responses are reflexive in latency and not a voluntary response to the particular perturbation.

Although most results are supportive of the OFC framework, some of our findings are incongruent with the predictions of the OFC. Specifically, we found a lack of complete suppression for task-irrelevant bimanual responses from flexor muscles, even under an extensor background load that acts in the same direction as flexion force (e.g., Fig. 4A). When both hands were perturbed in the same direction, the optimal response is to produce no force, because this perturbation is task irrelevant. In the same vein, although we show a robust main effect of perturbation state of the contralateral arm on EMG responses of the ipsilateral arm, the differentiation of activity among the perturbation states was not one of smooth gradation. That is, for lengthening muscles, there was no significant difference in EMG level between the perturbations associated with an intermediate degree of instability (i.e., single-limb perturbation) and those associated with no or little instability (i.e., bimanual perturbations in the same direction) as shown in Fig. 4. Similarly, there was no gradation of shortening biceps activity across the three perturbation states, although the activity during bimanual perturbations in the same direction was significantly higher than in any other condition (Fig. 6). It is important to point out, however, that these comparisons pertain to the time interval corresponding to the R3 component of rapid responses. At least for the lengthening triceps lateralis (Fig. 4B), appropriate gradation of activity among the three perturbation conditions was seen, albeit at longer latencies. These results suggest that, although activity from one muscle may eventually adhere to OFC predictions, there may be some nonadaptive components of the response that arise from mechanisms working in parallel with OFC [e.g., segmental feedback mechanisms (Windhorst 2007)]. For example, it has been recently shown that long-latency responses may comprise at least two overlapping processes, one of which is insensitive to task dependence (Pruszynski et al. 2011). This might also explain why there was some degree of separation between the triceps lateralis signals in the control task when the extensor muscles were loaded (Fig. 2D, right). Therefore, lower-level control processes may act to limit the extent to which a response is governed by OFC principles. That said, OFC is clearly a valuable framework for interpreting our findings for both rapid and later responses.

When we contrasted the EMG activity present when the two arms were simultaneously perturbed in the same direction with the summed EMG activity of the component unimanual perturbations, we found a nonlinear summation in shortened extensor muscles. We found no nonlinear effects in lengthened muscles. It is not clear why sublinear responses originated only from shortened muscles. We found a sublinear response in the shortened muscles during the bimanual same-direction perturbations, which would lead to a reduction in the muscle cocontraction under this condition. Cocontraction is known to be a control mechanism in the face of destabilizing environments. Because of the rotary force field applied, for the unimanual perturbations cocontraction should be high because the forces are highly destabilizing whereas for the bimanual perturbations (in the same direction) cocontraction is unnecessary because the bar does not rotate. Therefore the reduction in cocontraction in this condition is appropriate to the task demands.

Specifically, the relatively higher responses observed in the shortened muscles during the unimanual perturbations could act to increase joint stiffness relative to the bimanual perturbation conditions. This may contribute to stabilizing the limb by increasing its stiffness (Franklin and Milner 2003; Hogan 1984). However, this excitation during shortening must be balanced appropriately with an appropriate increase in activity within the stretched antagonist muscles in order to account for different degrees of instability associated with the perturbation conditions. Although the overall sign of the reflex is dominated by the large changes in the shortening muscle, excitation during muscle shortening could reflect a need to supplement required stiffness during unimanual perturbations through additional cocontraction, as more stability may be afforded when being allowed to compensate for the deviation of the rigid bar with both hands. This means that reflex responses might take into account the mechanical properties of the limbs. This is conceptually similar to the suggestion that reflex responses reflect an internal model of the limb (Kurtzer et al. 2008) and modulation of the reflex coactivation maintains a required stiffness of the limb in the face of perturbations.

Previous studies have shown that cocontraction is often used by the sensorimotor system when confronted with unstable or unpredictable environments (Franklin et al. 2003; Takahashi et al. 2001) or large errors (Franklin et al. 2008; Osu et al. 2002). This coactivation response could therefore reflect a general strategy for increasing the stiffness of the limbs through feedback modulation (Krutky et al. 2010; Shemmell et al. 2010) and highlights that reflexes do not always inhibit the shortening muscles. There are a variety of studies that show excitation in response to muscle shortening at delays within normal reflex latencies when stability is important (Crago et al. 1976; Hore and Vilis 1984; Lacquaniti and Maioli 1987, 1989). In line with previous examinations of postural responses, we found that the short-latency responses showed no sensitivity to task goals (Pruszynski et al. 2008) but that extensive modulation was observed in the longer-latency responses. Indeed, it has been shown that cortical involvement may be directly involved in reflex gain modulation (Kimura et al. 2006; Pruszynski et al. 2011; Shemmell et al. 2009). Although it has been proposed that there can be modulation of the stretch reflex within the short latency timing during reaching (Mutha et al. 2008), the study on which this is based introduced a visual shift of the target 100 ms prior to the physical perturbation. Several studies have reported that such visual stimuli [e.g., target jumps (Brenner and Smeets 2003; Diedrichsen et al. 2004), cursor jumps (Franklin and Wolpert 2008; Saunders and Knill 2004), and background shifts (Saijo et al. 2005)] can produce motor output with a latency of 110 ms. Therefore, the short-latency responses in Mutha et al. (2008) might reflect modulation based on the preceding visual shift.

In conclusion, we have developed a paradigm in which one or both arms were perturbed while subjects performed a bimanual task conceptually similar to holding a laden tray. This allowed us to investigate the behavior of the motor system when levels of task relevance are jointly determined by task goals and the instantaneous interaction between the two arms. We show that muscles of a clamped arm can produce stabilizing reflex responses that depend appropriately on the magnitude and direction of perturbations applied to the contralateral arm. In the perturbed arm, we demonstrate that reflex responses modulate with the levels of task relevance associated with the perturbation state of both arms. Last, we show that the nervous system is able to implement nonlinear interactions between the arms that may aid in producing rapid stabilizing responses. We conclude that task-dependent tuning of reflexes is an ongoing process that can be modulated during a single trial because of the interaction between the arms but may also be limited by lower-level processes.

GRANTS

We thank the Wellcome Trust for financial support.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

Author contributions: M.D., D.W.F., and D.M.W. conception and design of research; M.D. and D.W.F. performed experiments; M.D. analyzed data; M.D., D.W.F., and D.M.W. interpreted results of experiments; M.D. prepared figures; M.D. and D.W.F. drafted manuscript; M.D., D.W.F., and D.M.W. edited and revised manuscript; M.D., D.W.F., and D.M.W. approved final version of manuscript.