Non-monotonicity in the episodic random utility model

Abstract

The time trade-off is widely used in population-based surveys to estimate health-state valuations. Typically, respondents may characterize states as being better than or worse than dead. However, worse-than-dead responses can produce strongly negative mean values, so various analytic transformations of these responses have been suggested. The episodic random utility model (eRUM), operationalized using a linear regression estimator, was proposed as an alternative to these transformations, in part because of its theoretical appeal. We analyzed the eRUM estimator’s mathematical properties and found that it violates monotonicity under certain patterns of survey responses, such that improvement in some individual valuations would imply a lower overall valuation for a given health state. Consequently, it is possible that orderings of alternative strategies based on eRUM valuations could lead a decision-maker to choose a strictly dominated strategy. Re-analyzing data from a large population-based EQ-5D valuation survey in the United Kingdom, we found 27% of all time trade-off responses (63% of all worse-than-dead responses) met the conditions for violation of monotonicity, and 74% of all respondents had at least one such response. These results present some challenge to the use of the eRUM estimator in generating health-state valuations for population health measurement and economic evaluation.

1. Introduction

Health-state valuations represent important inputs to cost-effectiveness analysis and related research (Gold et al., 1996; Drummond and McGuire, 2001). Valuation approaches vary, but guidelines generally focus on elicitation methods that force respondents to make explicit choices, such as the time trade-off (TTO) and standard gamble techniques (Gold et al., 1996; NICE, 2008). The TTO is used widely in deriving valuations for generic health-state descriptions through sample surveys in the general public (Dolan et al., 1996; Tsuchiya et al., 2002; Shaw et al., 2005). A common feature in many TTO studies is that respondents may characterize states as being either better than dead (BTD) or worse than dead (WTD) (Torrance, 1982; Patrick et al., 1994; Tilling et al., 2010). Allowing for WTD valuations presents a range of conceptual, methodological and empirical challenges that have been met with varying proposed solutions, but debate persists about the most appropriate approach (Tilling et al., 2010; Robinson and Spencer, 2006; Lamers, 2007). In this paper, we present a critical evaluation of the episodic random utility framework, proposed recently as a new paradigm for understanding and analyzing health-state valuations, with particular relevance for accommodating WTD TTO responses (Craig and Busschbach, 2009; Craig and Busschbach, 2010).

2. Interpretation of Time Trade-Off Responses

One of the most widely used protocols for eliciting TTO responses was introduced in the landmark Measurement and Valuation of Health (MVH) study in the United Kingdom (MVH Group, 1994), and provides a concrete focal example for understanding the challenge of WTD responses. In the MVH protocol, valuation of a health state using the TTO begins with a question to determine whether the state is regarded as BTD or WTD. For a state deemed BTD, respondents are asked a series of binary questions to determine how many years of life lived in perfect health followed by immediate death would be equivalent to 10 years of life lived in the health state followed by immediate death. For a state deemed WTD, respondents are asked questions to determine the point of equivalence between immediate death and the alternative of some number of years spent in the health state followed by the remaining balance of a 10-year life expectancy in perfect health. For both BTD and WTD valuations, choices are offered in in ¼ year increments (MVH Group, 1994).

Precedents for the MVH protocol are found in the original formulation of the TTO (Torrance et al., 1972) and its subsequent elaboration to accommodate WTD valuations (Torrance, 1982). These seminal works also describe how individual TTO responses can be translated into valuations on an interval scale. Aggregate values for groups are typically calculated as the arithmetic mean of these individual valuations. Applying the original logic from Torrance et al. (1972) to the 10-year formulation of the TTO in the MVH, individual valuations for BTD states are calculated as $\raisebox{1ex}{$y$}\!\left/ \!\raisebox{-1ex}{$10$}\right.$, where y is the number of years spent in perfect health equivalent to 10 years in the health state. The resulting BTD valuations are thus located within the interval (0,1]. For WTD states, the formula suggested by Torrance (1982) implies a valuation of $\raisebox{1ex}{$y$}\!\left/ \!\raisebox{-1ex}{$(y-10)$}\right.$, which allows WTD values to fall in the interval [−∞, 0). In practice the lowest possible valuation using the MVH protocol would be −39 (due to the ¼ year increments), which results from a WTD response in which a person is indifferent between immediate death and an alternative of 0.25 years in the health state followed by 9.75 years in perfect health. Calculating WTD observations as $\raisebox{1ex}{$y$}\!\left/ \!\raisebox{-1ex}{$(y-10)$}\right.$, while consistent with the original interpretation of the equivalence statements elicited through the TTO, has led to unsatisfactory results when applied to survey data, with a large number of health states determined to have negative average valuations, challenging face validity (Dolan et al.,1996).

A common response to this problem has been to transform WTD observations so that they fall within the range [−1,0). The earliest proposed approach (Torrance, 1982; Torrance et al., 1982), which was later adopted by Shaw et al. (2005), was to divide all WTD observations by a constant that inflates the minimum valuation to −1 (and all other WTD valuations by the same factor). Applied alongside the MVH protocol, this transformation implies WTD valuations equal to $\left(\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$39$}\right.\right)\left(\raisebox{1ex}{$y$}\!\left/ \!\raisebox{-1ex}{$(y-10)$}\right.\right)$. Another frequently used transformation was introduced by Patrick et al. (1994) and applied in the United Kingdom MVH study and a number of subsequent studies. Describing this latter transformation, Dolan et al. (1996) reasoned that respondents were misinterpreting the WTD response scale as an interval rather than a ratio scale, citing early psychometric research (Eyman, 1967), and calculated a modified individual valuation for WTD observations, as $\raisebox{1ex}{$-y$}\!\left/ \!\raisebox{-1ex}{$10$}\right.$. In all cases the calculation for BTD valuations is unchanged, and these estimators produce final valuations that are bounded on the scale [−1,1], with minor differences between estimators due to the particular transformation used (Lamers, 2007). These transformations are pragmatic approaches for developing an estimator based on the mean of a set of individual responses, which respects the orderings in these responses (more favorable responses imply higher valuations), while also generating plausible results. However, they have been criticized for lacking a strong theoretical basis and for their reliance on ratio statistics (Robinson and Spencer, 2006; Lamers, 2007; Craig and Busschbach, 2009).

Craig and Busschbach (2009) suggest an alternate approach to calculating credible valuations directly from the unadjusted observations, by reinterpreting the source of stochastic variability in individual survey responses. This alternative is developed formally as the episodic random utility model (eRUM), whereby the reported utility (U) of an individual (i) for a health state (j) over time (t) involves a systematic component (μt) that depends on the amount of time spent in the state, and a stochastic component (ε) that does not. The eRUM differs from the traditional instant random utility model (iRUM) in its conceptualization of the error term:

$$\begin{array}{cc}{U}_{\mathit{\text{ij}}}(t)=\{\begin{array}{cc}{\mu }_{j}t+{\epsilon }_{\mathit{\text{ij}}}\hfill & \mathit{\text{eRUM}}\hfill \\ ({\mu }_j+{\epsilon }_{\mathit{\text{ij}}})t={\mu }_{j}t+{\epsilon }_{\mathit{\text{ij}}}t\hfill & \mathit{\text{iRUM}}\hfill \end{array}\hfill & (\text{Craig and Busschbach},2009)\hfill \end{array}$$

Considering the implications of the eRUM framework for deriving health-state valuations, Craig and Busschbach note that eRUM is consistent with a linear regression estimator, in which the number of years of perfect health (multiplied by −1 for WTD responses) is regressed against the number of years in a particular health state, with no constant term. Under eRUM the regression coefficient, rather than the mean of individual valuations, is the estimator for the valuation of the given health state. Craig and Busschbach have recently reiterated the regression-based operationalization as a general approach for analysis of health-state valuations, without explicit reference to the underlying eRUM model (Craig and Busschbach, 2010).

3. Non-Monotonicity of the Craig & Busschbach Estimator

Non-monotonicity is an undesirable property for an aggregate measure of social preference (Arrow, 1950). In the context of health-state valuations, if some respondents improve their valuation of a particular state, it is undesirable that the aggregate measure of value declines as a result. We hypothesized that the estimator derived from the eRUM could violate monotonicity. This hypothesis was based on the observation that, for health states that are generally valued positively, the influence of WTD scores on the slope of the regression line—constrained to pass through the origin—must decrease for increasingly negative valuations. At the extreme, if an individual were allowed to value a health state as infinitely bad (i.e. with a raw score of −10 implying an individual valuation of −∞), this observation would exert no influence on the regression line at all. Analogous to the physical concept of torque, the infinitely negative valuation produces no downward rotation of the regression line because the force is applied at zero horizontal distance to the pivot point (at the origin).

To test our hypothesis, we sought to derive the mathematical conditions that would characterize violations of monotonicity. Following Craig and Busschbach, we began by describing the eRUM estimator (μ̂) for the valuation of a particular health state in relation to the set of BTD and WTD observations, where x is the number of years spent in the health state and y is the number of years spent in perfect health (recorded as a negative value for WTD observations).

$$\widehat{\mu }=\frac{{\displaystyle \sum _i}{x}_i{y}_i}{{\displaystyle \sum _i}{x}_i^2}=\frac{{\displaystyle \sum _{\mathit{\text{BTD}}}}10y+{\displaystyle \sum _{\mathit{\text{WTD}}}}(y+10)y}{{\displaystyle \sum _{\mathit{\text{BTD}}}}{10}^2+{\displaystyle \sum _{\mathit{\text{WTD}}}}{(y+10)}^2}$$

The monotonicity condition may be understood in terms of the direction of change in μ̂ caused by a change in a single observation, so we split off one WTD observation, p:

$$\widehat{\mu }=\frac{{\displaystyle \sum _{\mathit{\text{BTD}}}}10y+{\displaystyle \sum _{\mathit{\text{WTD}}-p}}(y+10)y+y_p(y_p+10)}{{\displaystyle \sum _{\mathit{\text{BTD}}}}{10}^2+{\displaystyle \sum _{\mathit{\text{WTD}}-p}}{(y+10)}^2+{(y_p+10)}^2}=\frac{\left[{\displaystyle \sum _{\mathit{\text{BTD}}}}10y+{\displaystyle \sum _{\mathit{\text{WTD}}-p}}(y+10)y\right]+{y_p}^2+10y_p}{\left[{\displaystyle \sum _{\mathit{\text{BTD}}}}{10}^2+{\displaystyle \sum _{\mathit{\text{WTD}}-p}}{(y+10)}^2\right]+{y_p}^2+20y_p+100}=\frac{f(y_p)}{g(y_p)}$$

Next, we took the partial derivative of this expression with respect to y_p,

$$\frac{\partial \widehat{\mu }}{\partial y_p}=\frac{f\text{'}(y_p)g(y_p)-f(y_p)g\text{'}(y_p)}{g{(y_p)}^2}=\frac{f\text{'}(y_p)-\widehat{\mu }g\text{'}(y_p)}{g(y_p)}$$

Monotonicity requires that the regression estimator μ̂ must increase in y_p; that is, $\frac{\partial \widehat{\mu }}{\partial y_p}>0,\text{or}\frac{f\text{'}(y_p)-\widehat{\mu }g\text{'}(y_p)}{g(y_p)}>0$.

Noting that g(y_p) is the denominator of the original regression equation, computed as the sum of squared values and therefore always positive, we restated the monotonicity condition based only on the numerator, which led to a simple statement of the monotonicity condition.

$$\begin{array}{c}f\text{'}(y_p)-\widehat{\mu }g\text{'}(y_p)>0\hfill \\ \Rightarrow \frac{f\text{'}(y_p)}{g\text{'}(y_p)}>\widehat{\mu }\hfill \\ \Rightarrow \frac{y_p+5}{y_p+10}>\widehat{\mu }\hfill \end{array}$$

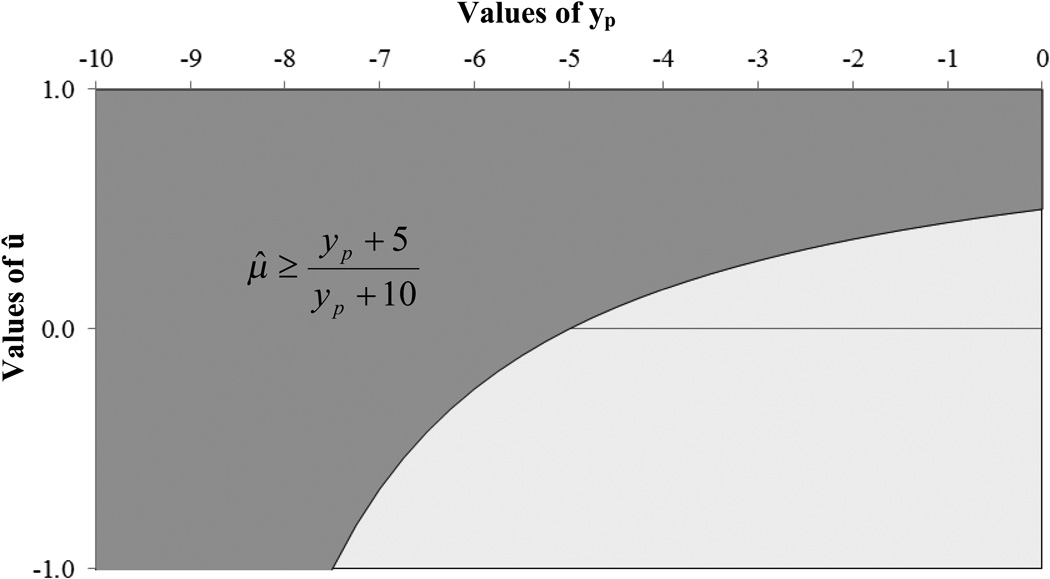
The region of the joint distribution of y_p and μ̂ where this monotonicity condition fails is shown in Figure 1. Of note, for values of μ̂ greater than 0.5, the improvement of any WTD observation will lower the value of the eRUM estimator, violating monotonicity.

Figure 1. Distribution of values of μ̂ and y_p that violate monotonicity.

μ̂ = eRUM estimator for a given health state

y_p = years lived in perfect heath from a single survey response for the given health state (multiplied by −1 for states deemed worse than dead).

Dark grey area = joint distribution of y_p and μ̂ associated with monotonicity violations.

One implication of this monotonicity violation is that a state could dominate another state by first-order stochastic dominance (Hardar and Russell, 1969) yet have a lower eRUM estimator, as shown by the stylized 4-observation example in Table I. In this example, an intervention that moved patients from Health State A to Health State B would, ceteris parabis, be judged a social welfare improvement according to the eRUM estimate, even though this makes all individuals worse-off and violates Pareto-efficiency.

Table I.

Example of possible violation of first-order stochastic dominance with eRUM

	Health State A (Dominant)		Health State B (Dominated)
Observation	x-values	y-values	x-values	y-values
1	10	10	10	9.75
2	10	9	10	8.75
3	10	8	10	7.75
4	9	−1	6	−4
eRUM estimator:	0.685		0.709

x-values = no. years spent in the health state y-values = no. years spent in perfect health

Expanding on this theoretical concern, we considered the practical implications of monotonicity violations using data from the United Kingdom MVH study (Dolan et al., 1996). The MVH study collected TTO valuations for 43 health states described using the EQ-5D. The EQ-5D system includes five domains (mobility, self-care, usual activities, pain/discomfort, and anxiety/depression), each with three possible levels. States are described in shorthand using five-digit codes reflecting levels on each domain.

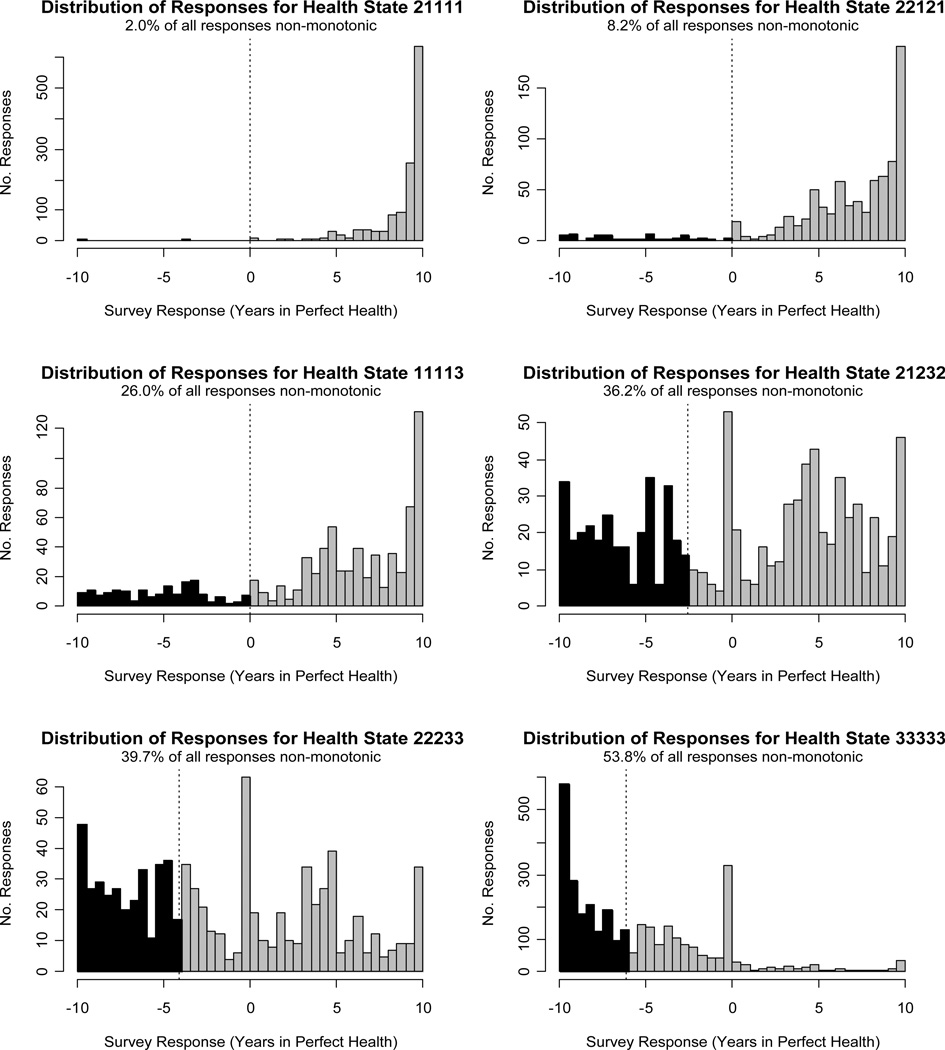
We estimated the percentage of observations in the MVH study that meet the conditions for non-monotonicity, and results are shown in Table II. Overall, 27% of all individual observations (63% of all WTD observations) fall into the region affected by non-monotonicity. For individual health states, the percentages of observations in the affected region range from 2% to 54% of all observations (58% to 100% of all WTD observations). Figure 2 shows the distribution of observations for six example health states, with the observations in the non-monotonic region shaded red.

Table II.

Percentage of observations meeting the conditions for monotonicity violations, for EQ-5D health states in the United Kingdom Measurement and Valuation of Health study.

EQ-5D health state	eRUM estimate	No. observations	Percent of observations WTD	Percent of observations in non- monotonic region	Percent of WTD observations in non-monotonic region
21111	0.88	1,319	2.0%	2.0%	100%
11211	0.87	1,347	1.7%	1.7%	100%
11121	0.85	1,324	2.6%	2.6%	100%
12111	0.85	1,322	3.6%	3.6%	100%
11112	0.84	1,318	3.5%	3.5%	100%
12211	0.79	834	4.4%	4.4%	100%
11122	0.76	827	6.3%	6.3%	100%
12121	0.76	835	4.2%	4.2%	100%
22121	0.70	837	8.2%	8.2%	100%
22112	0.70	847	6.5%	6.5%	100%
11312	0.64	832	14.7%	14.7%	100%
21222	0.63	828	12.7%	12.7%	100%
12222	0.62	837	15.4%	15.4%	100%
22122	0.62	820	14.1%	14.1%	100%
21312	0.61	816	15.7%	15.7%	100%
22222	0.60	842	16.5%	16.5%	100%
11113	0.53	832	26.0%	26.0%	100%
13212	0.52	826	22.3%	22.3%	100%
13311	0.50	816	27.1%	27.1%	100%
11131	0.43	819	37.5%	31.5%	84.0%
12223	0.40	836	37.2%	28.1%	75.6%
23321	0.39	825	40.2%	32.7%	81.3%
21323	0.38	826	39.2%	31.5%	80.2%
32211	0.37	842	40.1%	31.9%	79.6%
21232	0.33	831	46.5%	36.2%	78.0%
22323	0.30	819	47.9%	35.0%	73.2%
22331	0.27	820	52.0%	38.9%	74.9%
33212	0.26	833	52.8%	37.6%	71.1%
11133	0.25	837	55.0%	39.9%	72.6%
21133	0.22	832	57.2%	38.2%	66.8%
23313	0.22	836	55.3%	38.5%	69.7%
23232	0.21	831	59.0%	41.0%	69.6%
22233	0.15	834	62.5%	39.7%	63.5%
33321	0.15	834	63.7%	37.3%	58.6%
32313	0.14	842	64.4%	38.8%	60.3%
32223	0.11	831	65.9%	39.0%	59.1%
32232	0.09	825	69.7%	43.4%	62.3%
13332	0.07	824	69.1%	42.4%	61.3%
32331	0.05	832	73.1%	41.3%	56.6%
33232	−0.04	836	77.8%	42.1%	54.2%
33323	−0.10	844	82.0%	43.6%	53.2%
Unconscious	−0.21	3,327	96.2%	35.2%	36.6%
33333	−0.30	3,320	93.5%	53.8%	57.5%

Figure 2. Distribution of survey responses for six example health states in the United Kingdom Measurement and Valuation of Health study. Responses meeting the conditions for monotonicity violations are shaded in black.

Respondents in the MVH study were typically asked 13 TTO questions, and 74% of all respondents provided at least one response falling into the affected region; 44% provided 4 or more responses falling into the affected region. Comparing the distribution of raw scores across health states, we identified no instances where a dominated health state received a higher eRUM estimate.

4. Conclusion

This analysis investigated properties of the episodic random utility estimator (Craig and Busschbach, 2009; Craig and Busschbach, 2010) used to model survey data on health-state valuations. We found that the eRUM estimator can violate monotonicity under certain patterns of survey responses, and this potential problem pertains to a substantial proportion of all observations in a large population-based survey of health-state valuations in the United Kingdom. This problem is clearly not restricted to extreme values or outliers—for one-quarter of all observations, an incremental improvement in the individual valuation of a particular health state would result in a worsening of the aggregate valuation for that state derived using the eRUM approach. Moreover, almost three-quarters of all respondents provided at least one such response.

The eRUM approach, like the set of strategies based on transformations of WTD observations (Torrance, 1982; Dolan et al., 1996; Shaw et al., 2005), is proposed as a possible alternative to the original analytic strategy designed alongside the TTO (Torrance et al., 1972). Reacting to the implausibility of strongly-negative valuations produced by this original approach, both the eRUM and the transformation-based alternatives invoke strong assumptions to justify their particular analytic choices. Both produce the desired effect of eliminating implausibly large negative valuations, and the rankings of health states resulting from the two approaches are quite similar. This raises a reasonable question—is there really a problem with the eRUM estimator if it produces plausible results in practice? While the close concordance of health-state valuations produced by the different estimators renders the choice between them less consequential, an ideal estimator should be justifiable theoretically as well as empirically. Indeed, the eRUM is explicitly touted by its proponents as being theoretically superior to other estimators (Craig and Busschbach, 2009; Craig and Busschbach, 2010). The issues revealed by our analysis present some challenge to this position.

For the analyst weighing eRUM against the transformation approach, neither strategy emerges as clearly dominant. Both have shortcomings, and these shortcomings relate to distinct types of considerations. Arguments against the selective transformation of WTD observations have been rehearsed extensively in the literature (Lamers, 2007; Craig and Busschbach, 2009; Craig and Oppe, 2010; Shaw et al., 2010a). The regression-based estimator used in eRUM has been introduced more recently, and has not yet been subjected to the same scrutiny. In this paper, we identify an important failing of the eRUM approach, and based on empirical re-analysis of a prominent national valuation study find that this problem is highly relevant to observed, real-world response patterns. Thus, a choice between these two imperfect alternatives must ultimately depend on the relative importance that an analyst attaches to concerns about internal consistency or arbitrariness in transformation approaches vs. concerns about monotonicity violations in the eRUM estimator. Furthermore, it is worth noting that neither alternative fully reconciles known features of TTO data, such as the gap in valuations in the proximity of the dead state (Stalmeier, 2005), the greater variability of WTD observations (Dolan and Roberts, 2002), and the poor correlation between mean negative scores and overall valuations (Busschbach et al., 2003).

Additional alternatives for analyzing health-state valuation data continue to emerge, such as a strategy focusing on median rather than mean valuations (Lamers, 2007; Li and Fu, 2009; Shaw et al., 2010a), and an estimator based on directional statistics (Craig and Oppe, 2010) which—like the eRUM estimator—avoids the use of ratio statistics. At present, however, consensus on an ideal approach remains elusive (Shaw et al., 2010b). Under these circumstances, research on revised TTO question formats (e.g., Robinson and Spencer, 2006; Buckingham and Spencer, 2006; Devlin et al., 2010) and renewed consideration of ranking and other ordinal elicitation methods (e.g., Salomon, 2003; McCabe et al., 2006; Krabbe et al., 2007; Craig et al., 2009) merit continued attention in seeking to avoid or ameliorate problems with WTD health-state valuations associated with the TTO.