Sucrose in Aqueous Solution Revisited: 1. Molecular Dynamics Simulations and Direct and Indirect Dipolar Coupling Analysis

Abstract

Although the crystal structure of the disaccharide sucrose was solved more than 30 years ago, its conformational distribution in aqueous solution is still a matter of debate. We report here a variety of molecular dynamics simulations (mostly of 100 ns) using the GLYCAM06 force field and various water models, paying particular attention to comparisons to NMR measurements of residual dipolar couplings and electron-mediated spin-spin couplings. We focus on the glycosidic linkage conformation, the puckering phase angle of the fructose ring, and intramolecular hydrogen bonds between the two sugars. Our results show that sucrose is indeed a dynamic molecule, but the that crystal conformation is qualitatively the dominant one in dilute solution. A second conformational basin, populated in many force fields, is probably over-stabilized in the calculations.

1. Introduction

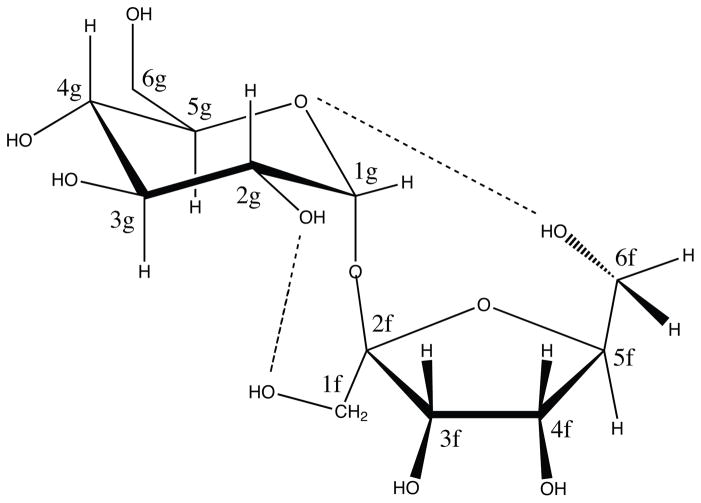
Sucrose, or table sugar, is a disaccharide with the sequence as α-D-Glu-(1→2)-β-D-Fru (see Figure 1). Although its crystal structure was reported in 1973,¹ the conformation in aqueous solution, particularly with respect to the glycosidic linkage, is still being investigated. For example, an early nuclear magnetic resonance (NMR) study of sucrose in D₂O and dimethyl sulfoxide-d₆ solvents by Bock and Lemieux ² supported a fairly rigid conformation in solution, close to crystal structure, based on the measurements of coupling constants, chemical shifts, T₁ relaxation times and nuclear Overhauser effects (NOE). This conformational rigidity was reinforced by several other NMR results, such as ¹³ C relaxation as a function of concentration, temperature, and magnetic field strength,^3,4 relaxation rates in a viscous cryosolvent (D₂O–DMSO),^5,6 and residual dipolar couplings (RDC) in dilute liquid crystal media.⁷

Figure 1.

Schematic representation of sucrose disaccharide, α-D-Glu-(1→2)-β-D-Fru. The glycosidic angles φ–ψ are defined as φ =O5_g –C1_g –O2_f –C2_f and ψ = C1_g –O2_f –C2_f –O5_f, where g and f refer to glucopyranosyl and fructofuranosyl rings respectively. The dashed lines shows the two hydrogen bonds present in the crystal structure, O2g-H1Of and O5g-H6Of with the distances of 1.85 and 1.89 angstroms respectively.¹

Other NMR studies^8–13 have questioned this single-conformation conclusion. Steady state nuclear Overhauser effects and J coupling constant studies by Perez and coworkers⁸ suggested that conformational averaging has to be included to give a good agreement between theoretical and experimental data. Poppe and Halbeek⁹ found that the interglycosidic proton-proton distances derived from NOE measurements have both temperature and magnetic field dependence which is not consistent with a rigid glycosidic linkage. Residual dipolar couplings¹³ were best fit by a model where the sugar rings have different alignment tensors, which can not be explained by a single structure. The flexibility of sucrose in aqueous solution has also been supported by optical rotation experiments¹⁴ where data were better understood by the equilibrium mixture of two conformers including the crystalline structure. Inter-residue J coupling analysis¹¹ also showed that the second dihedral of glycosidic linkage (ψ) might sample two energy minima states.

The ambiguities of NMR experiments mostly stem from the fact that interpretation of NMR observables requires structural models, especially for flexible molecules. In principle, computer simulations allow a detailed description of conformational transitions,^8,15–22 but results can depend critically on the force field used, and published results for sucrose vary a lot. Tran and Brady’s early molecular dynamics studies^15,16 found the global minimum energy conformation to be dynamically stable with no transitions away from this minimum during short (20 ps) trajectories. Later simulations (of 1 ns duration) were consistent with this model, and suggested that no direct intramolecular hydrogen bond persists in aqueous solution.^18,19 Instead the sucrose conformation is stabilized by the dynamic presence of two bridging water molecules between residues. However, other molecular modeling results combined with NMR quantities are not consistent with this single minimum.⁸

The accuracy of computer simulations, however, depends on the accuracy of force fields, the reliability of solvation models, and the difficulty of sampling all relevant conformations in a finite simulation.^23–29 Several carbohydrate force fields^30–38 are available for molecular mechanics simulations of sugars. We have chosen the GLYCAM06 model, designed for both simple monosaccharides and complex sugars and glycoproteins.³⁰ There also exists a large variety of water models for MD simulations. A recent review³⁹ compared 47 major water models and found that all these models have their advantages and deficiencies. In addition, early simulations^15–22 were limited to sub-nanosecond time scales. Recent advances in computing power, however, have made feasible direct simulations of biomolecules in explicit water to hundreds of nanoseconds or microseconds.

Using the AMBER 10 molecular simulation package⁴⁰ and the GLYCAM 06 carbohydrate force field,³⁰ we performed 100 ns MD simulations of sucrose in aqueous solution under various conditions. We evaluated these simulation trajectories via calculation of residual dipolar couplings and indirect spin-spin couplings from simulation snapshots. We mainly focused on the global conformation change from the glycosidic linkage although we also consider the analysis of local fluctuations such as intramolecular hydrogen bond and sugar puckering. In a second paper⁴¹ we will report systems with varying concentrations of sucrose in water and water-DMSO mixtures, for comparison with NMR relaxation measurements.

2. Computational Methods

1. Molecular Dynamics Simulation

Explicit solvent MD simulations were carried out using AMBER 10.⁴⁰ We used GLYCAM06,³⁰ in combination with several popular explicit water models including SPC,⁴² TIP3P,⁴³ TIP4P,⁴⁴ TIP4P/Ew,⁴⁵ and TIP5P.⁴⁶ Most simulations were carried out at 300K; for the TIP4P/Ew model, additional simulations were made at 273, 283 and 315K. In each case sucrose (in its crystal conformation¹) was solvated in a truncated octahedron of water molecules, such that the closest distance between any atom of the sucrose and the edge of the periodic box was 15 angstroms. All production simulations (100 ns) were under periodic boundary conditions in the constant volume, total energy and number of particles (NVE) ensemble. Before the production runs, equilibration processes in NVT (0.5 ns) and NPT (0.5 ns) ensemble were performed to adjust the systems into the desired temperatures and volumes. The integration time step was 0.001 ps. In all simulations, SHAKE algorithm was used to constrain bonds involving hydrogen. The non-bonded cutoff for evaluating electrostatic and van der Waals forces was set to 0.8 nm with no scaling of 1–4 interactions. To deal with long range electrostatic interactions the PME algorithm was used with the default settings, including a real space grid of 0.1 nm. We collected 100,000 conformation snapshots along each of the 100 ns trajectories.

Restrained MD simulations⁴⁷ (10 ns) were performed to analyze intramolecular hydrogen bonds as the function of glycosidic φ–ψ dihedrals and the puckering phase angle of fructose. We restrained the phase angle (via the five dihedrals from the fructose ring according to the Altona-Sundaralingam scheme ⁴⁸ as

$${\theta }_j={\theta }_{m}cos(P+4\pi (j-1)/5),$$ (1)

where θ_m is an amplitude (≈ 40° from experiment⁴⁹). P is phase angle, and j = 0, 1, 2, 3 and 4. 10 ns restrained MD simulations were carried out by retaining the phase angle (P = 0) and glycosidic dihedrals of four different free energy minima. We also did simulations with the same glycosidic dihedral restraints but various phase angle with P = 0, 18, 36, 54, 72 and 90. For all restraints we chose a force constant of 100 kcal/Rad².

2. Calculation of Residual Dipolar Couplings

Residual dipolar couplings (RDCs) arise in liquid crystalline media that partially align solute molecule so as to slightly alter the orientational averaging that eliminates direct dipolar couplings in isotropic solution. While it is always possible that the liquid crystal environment changes the conformational distribution, spectral similarities with the pure water case argue against this.⁷ The simplest analysis of RDCs is based on the assumption that the liquid crystal molecules have only steric alignment effects and do not change the internal structure of the sugar. Due to the alignment effect, sugar molecules have certain order and after transforming to the space defined by the diagonalized alignment tensor the residual dipolar coupling can be written^50,51

$$D_{ij}=-(\frac{{\mu }_0}{16{\pi }^2})\frac{{\gamma }_i{\gamma }_j\hslash }{r_{ij}^3}\kappa [S_{zz}(3{\mathit{cos}}^2{\theta }_{ij}^z-1)+(S_{xx}-S_{yy})({\mathit{cos}}^2{\theta }_{ij}^x-{\mathit{cos}}^2{\theta }_{ij}^y)],$$ (2)

where r_ij is the internuclear distance between spins, γ_i and γ_j are the gyromagnetic ratios of spins i and j. S_αα are diagonal components of alignment tensor in the molecular frame and describe the transformation from the molecular frame of reference to the laboratory coordinate system of the liquid crystal medium. κ is a scaling factor related to internal motion, and ${\theta }_{ij}^{\alpha }(\alpha =\text{x},\text{y},\text{and}\text{z})$ are the angles between the spin-spin vectors and the molecular coordinate frame defined by the diagonalized alignment tensor.

Experimental RDC data can be computed from a molecular model by treating the elements of the alignment tensor as parameters to be optimized; this leads to a set of linear equations that are usually solved by a singular value decomposition (SVD) method.⁵² Such a fit, however, may be misleading if the assumed structure model is incorrect, and we show below some of the over-fitting problems that can arise. As an alternative, the alignment tensor can be estimated from the structure of a molecule and its postulated interactions with the alignment medium. Even though such models have limited accuracy, they do ensure that the alignment tensors are qualitatively consistent with the molecular model, which need not be the case if the tensor elements are determined only by a best-fit criteria to experiment.

We used two such alternative methods to estimate alignment tensors. The PALES program⁵³ calculates the alignment tensor by a Monte Carlo simulation of molecules randomly orientated around the area close to an infinite two dimensional plate. A second method estimates the alignment tensor from the radius of gyration tensor⁵⁴ or moment of inertia.^55,56 For the former, the diagonalized alignment tensor is estimated as:

$$(S_{xx},S_{yy},S_{zz})=(-\frac{1}{2}-\frac{1}{2}\delta ,\delta -\frac{1}{2},1-\frac{1}{2}\delta ),$$ (3)

where

$$\delta =\frac{{\rho }_{yy}-{\rho }_{xx}}{{\rho }_{zz}-{\rho }_{xx}}.$$ (4)

ρ_αα (ρ_zz >ρ_yy>ρ_xx) represent characteristic lengths of the ellipsoid shape of a sugar molecule and can be obtained from the square roots of the eigenvalues of the radius of gyration tensor of the whole molecule defined as

$$R_{ij}^2=\frac{1}{N}\sum _{r=1}^N{x}_i^r{x}_j^r,$$ (5)

where $x_i^r$ are the positions of the N atoms in the molecule. Note the molecular frame in Equation 2 corresponds to the eigenvectors of Equation 5.

One would not expect these methods to work so well on a single sugar residue, which is not very anisotropic in shape; but they should work better for a disaccharide, which has a more elongated shape and hence a larger and more obvious anisotropy. Estimation of alignment tensor from the gyration tensor has been applied to construct conformational ensembles of unfolded proteins by the Blackledge group⁵⁷ and to generate statistical coil model of unfolded ensemble of proteins by Freed and coworkers.⁵⁸ More recently, the Forman-Kay group⁵⁹ has used the local alignment from a fragment size of 15 residues to derive disordered state ensembles of proteins instead of global alignment from the whole molecule. The alignment tensor estimated from gyration tensor also has been proposed to refine ensembles of unstructured proteins combining with MD simulations.⁶⁰

To evaluate the conformations sampled in MD trajectories we calculated an R factor⁶¹ between the computed RDCs for each snapshot and those reported experimentally:

$$R=\sqrt{\frac{{\sum }_i^N{(Q_i-Q_{0i})}^2}{{\sum }_i^N{Q_{0i}}^2}},$$ (6)

Here Q_i is our calculated RDC value for the i th spin nuclear pair and Q_0i is the related experimental value. The summation is over all available N experimental RDCs.

3. Calculation of indirect spin-spin coupling constants

Spin-spin couplings across the glycosidic torsion were estimated using a Karplus relation:

$$J(\theta )=A{cos}^2\theta +Bcos\theta +C$$ (7)

where θ is a C–O–C–H or C–O–C–C torsion angle connecting the two sugar rings, and the constants (A=7.49, B=−0.96, C=0.15 for C–O–C–H, A=3.70, B=0.18, C=0.11 Hz for C–O–C–C) were taken from fits to DFT data by Cloran et al..⁶² As with the RDC calculations, calculations were made for each of the 100,000 snapshots spanning 100ns of simulation.

3. Results and Discussion

1. Free energy landscapes about the glycosidic linkage

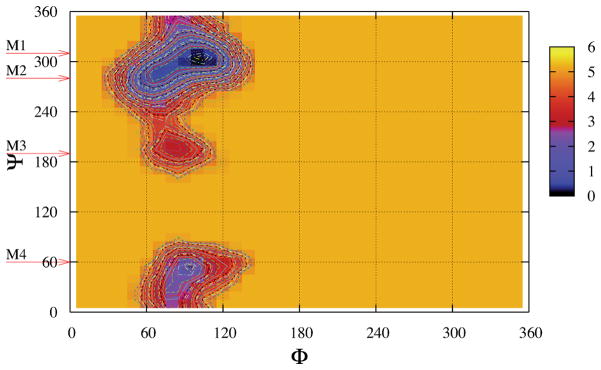
We begin by showing the free energies as a function of the glycosidic torsion angles; these were computed from the observed probabilities from 100 ns MD simulations:

$$F(\phi ,\psi )=-k_b\mathit{T}lnP(\phi ,\psi )$$ (8)

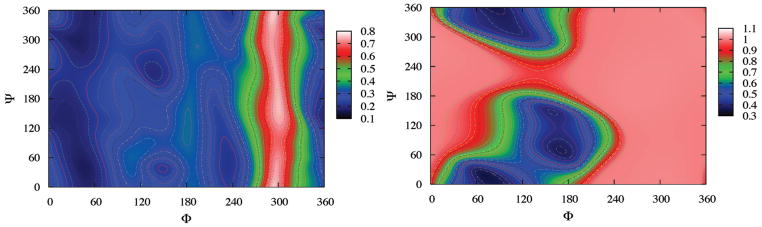
where k_b is Bolzmann’s constant and T is temperature. For convenience we also shifted all surfaces to make the values of global minima equal to 0. Figure 2 shows the free energy landscape in φ–ψ glycosidic space for the conformations of sucrose at 300K in the TIP4PEW water model; similar figures for other water models are given in the Supplementary Material. [In the Appendix, we use metadynamics and umbrella sampling to explore convergence of these landscapes, showing that at these temperatures the raw results from 100 ns simulations are converged well enough for our purposes here. These similarities also support our expectation that the NVE results shown in Fig. 2 are close to those one would obtain for a canonical (NVT) simulation, as expected for a system with a large number of degrees of freedom.] For each water model, four important minima, M1 (105°, 300°), M2 (70°, 280°), M3 (85°, 195°), and M4 (90°, 50°), can be identified. The exact φ–ψ values of these minima are listed in Table 1 and change little with water model. As we will show in Section 3, M1 is closely related to S1 and S2 conformer, M3 to S3 and S4, and M4 to S5 in the early computational work from Brady’s group.^15,16 These four minima have also been found by Freedberg and coworkers,¹³ where the potential energy landscapes were constructed by a systematic grid search with CHARMM or AMBER-type carbohydrate force fields.^34,33,35,36 Earlier work by French et al.,^21,22 combining ab initio quantum mechanics and molecular mechanics, found similar minima. Hence, the general shape of the free energy landscapes should be reliable, but the relative populations of the four basins depends on the details of the force field, and needs confirmation from experimental data.

Figure 2.

Free energy landscapes in φ–ψ glycosidic space for sucrose in the TIP4P/Ew model. Contour lines are shown from 0.0 to 5.0 kcal/mol in steps of 0.1. The local minima are identified as M1, M2, M3 and M4; see also Table 1.

Table 1.

Free energy information of four minima of sucrose in different explicit water models at T = 300K.

	SPC	TIP3P	TIP4P	TIP4P/Ew	TIP5P
positions (φ,ψ) (in degree)
M1	(104.5, 305.1)	(105.1, 304.9)	(104.9,305.2)	(104.8,305,4)	(99.8, 316.5)
M2	(69.8, 285.2)	(69.9, 285.6)	(69.4, 285.5)	(69.9, 284.7)	(65,6, 285.5)
M3	(83.9, 195.0)	(86.8, 194.9)	(85.3, 195.4)	(83.3, 196.4)	(95.2, 194.6)
M4	(90.3, 50.5)	(89.9, 51.0)	(93.6,54.9)	(94.8. 54.9)	(86.7, 38.6)
well depths (in kcal/mol)
F1	0.0	0.0	0.0	0.0	0.0
F2	0.3	0.55	0.65	0.5	1.1
F3	3.4	3.1	3.1	2.9	0.1
F4	2.3	2.7	1.6	1.8	0.4
probabilities within a radius of 20°
P1	0.581	0.634	0.605	0.577	0.341
P2	0.379	0.314	0.327	0.355	0.053
P3	0.002	0.004	0.003	0.005	0.216
P4	0.015	0.008	0.039	0.024	0.185
barriers between minima (in kcal/mol)
B12	0.4	0.6	0.7	0.6	1.3
B23	3.9	3.1	3.7	3.4	2.3
B14	2.6	3.0	2.8	2.4	0.8

Table 1 also displays the well depths and barriers for the four minima. M1 is the global minimum for all five water models and its position is close to the crystal conformation (108°, 305°).¹ The relative order of these four minima is the same for four water models (SPC, TIP3P, TIP4P, and TIP4P/Ew), but is qualitatively different for TIP5P; we don’t understand why TIP5P is an outlier here, and this probably deserves more investigation. We also integrated the probability densities within a circular region of radius of 20° around the four minima, and denoted the probabilities as P1, P2, P3 and P4 in Table 1. The probability of global minima M1 has the majority of around 60% and M2 takes more than 30% with small percentages of M3 and M4. This is similar for all models except TIP5P for which P1 only has 34% and there are significant populations of M3 and M4 (more than 15% for each). The free energy barriers (B12, B23, and B14) between different minima are also shown in Table 1. All the barriers are less than 4 kcal/mol which means that all these minima should interconvert on the simulation time scale of 100 nanoseconds. The orders of barriers are the same (B12 < B14 < B23) for all water models except TIP5P. We also notice that the barrier (B12) between M1 and M2 is rather small (≈ 0.5 kcal/mol) for the four water models except TIP5P. These small values of B12 (and low energies for M2) are consistent with other MM^16,17,20 and QM calculations.²¹ The barriers of B23 and B14 for TIP5P model are much smaller than that of other four models and result in much larger populations of M3 and M4. The relative energy differences and barrier heights between minima are quite sensitive to the force field: surveys of potential energy surface by Freedberg and coworkers¹³ showed that these quantities vary markedly in the CHARMM22, CSFF, Homans, and Accelrys force fields, although the φ–ψ values of the local minima are in good qualitative agreement. For this reason, careful comparison to experiment is an important adjunct to force field simulations.

Since not all of the relevant experiments are carried out at 300 K,^{8,9,10,11,12,13} we also computed free energy surfaces at different temperatures (273, 283, 300, and 315K). These are discussed in the Table 1S and Figure 2S of Supplementary material. The qualitative features are the same as those shown in Figure 2.

2. RDC Analysis of Conformation Snapshots

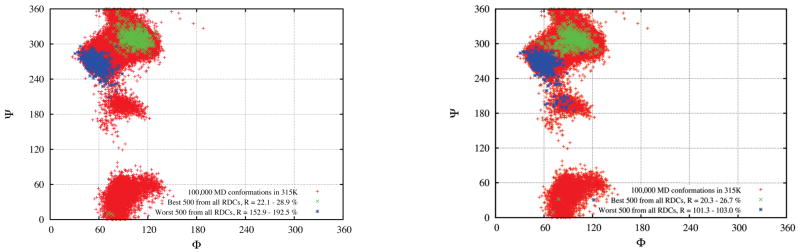
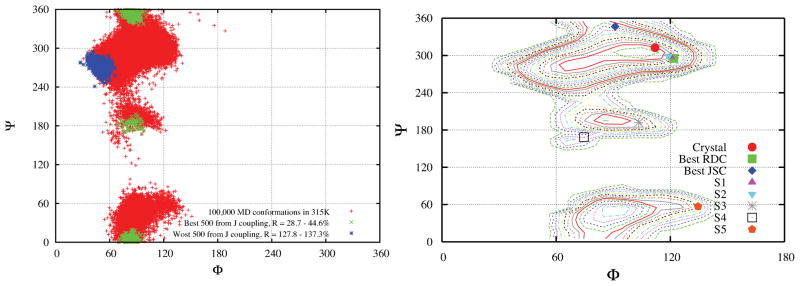
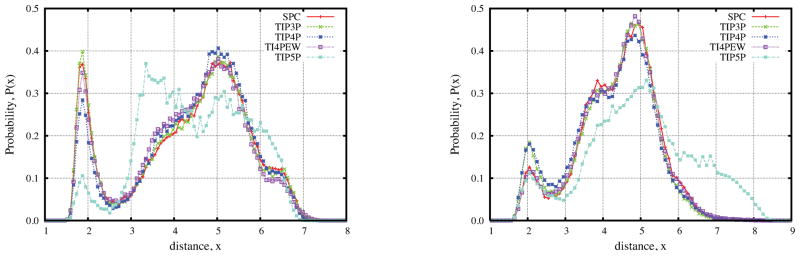
The trajectories explore many possible configurations of sucrose, and we have computed the RDCs for each of these. Figure 3 displays the best 500 and worst 500 conformations of sucrose among the 100,000 snapshots extracted from the 100 ns simulation trajectory with TIP4P/Ew waters at T = 315 K. We obtained the alignment tensor of each snapshot first from the molecular shape via the approximation of Almond⁵⁴ or PALES,⁵³ and then calculated the RDCs of each conformation. [In a separate calculation (Supporting material) we divide the RDCs into different categories: (a) all 36 nuclear pairs, (b) 8 one-bond C-H pairs, (c) 10 one-bond C-C pairs, and (d) 18 two and three-bond pairs; results were generally consistent with those for the entire data set shown in Figure 3.] Conformations around the global free energy minimum (M1) have the smallest R factors, and those near M2 have the worst agreement with experiment. Results from the Almond or PALES algorithm are consistent with each other, although the computed R factors with PALES are slightly lower, as indicated in the Figure caption. In Figure 2S and Figure 3S, we also show the similar results using a different experimental RDC data set.⁷

Figure 3.

The best 500 (green) and worst 500 (blue) conformations of sucrose among the 100,000 snapshots (red) extracted from the 100 ns simulation trajectory with TIP4PEW waters at T = 315 K. (a) The RDC ranks were produced by comparing the R factor of calculated RDCs by Almond method ⁵⁴ with respect to the experimental values. ¹³ The R factors = 22.1%~28.9% for best 500, and 152.9%~192.5% for the worst 500. (b) The same, but using the PALES ⁵³ method. All 36 proton pairs in Ref.¹³ are included. The R factors = 20.3%~26.7% for best 500, and 101.3%~103.0% for the worst 500.

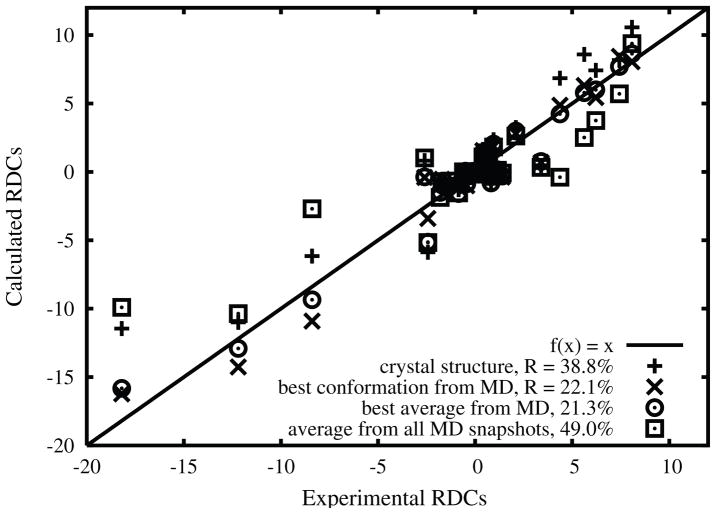
In Figure 4, we display the experimental RDCs versus calculated RDC values using Almond’s method for several structures, including the crystal structure¹ and the best MD conformation from the 100 ns trajectory with TIP4PEW waters at T = 315 K. The relatively large R factor of crystal structure (38.8%) suggests that some conformation change might happen. Allowing the (φ, ψ) values shift slightly from (108°, 305°) in crystal to (121.7°, 297.5°) reduces the R factor from 38.8% to 22.1%. Averaging over the 14 best MD snapshots slightly lowers the R-factor, as shown in the figure caption.

Figure 4.

Experimental RDCs .vs. calculated RDCs by Almond’s method for the crystal structure, the best MD conformation 100 ns trajectory with TIP4P/Ew waters at T = 315 K, and the best MD average over the top 14 in the RDC rank.

Averaging the RDCs over all 100,000 snapshots, however, yields a large R factor (49%; data is shown in Fig. 4) which implies that the simulation as a whole is not in good agreement with experiment, probably as a result of the sizable percentage of snapshots around M2, which have the worst R factors. Hence one way to improve the results would be to modify the force field and reduce the depth of the M2 conformational basin.

It is instructive to see what happens if the elements of the alignment tensor are treated as fitting parameters, rather than be estimated from the molecular structure. We rotated the crystal structure of sucrose in 1° increments about the φ and ψ dihedral angles, calculating the RDCs of each structure via best-fitting using a singular value decomposition method;⁵³ results are shown in the left side of Fig. 5. Note that in these calculations, the alignment tensors are fit to the data, and may not represent the actual shape of the molecule. There is little discrimination among conformers, with only very high energy conformers (near φ =300) excluded by the data. By contrast, the same calculation using the Almond model for the alignment tensor (Fig. 5, right) shows a sharp dependence on conformation, with only a few regions, some near the crystal structure, being favored.

Figure 5.

R-factors for RDC’s, as a function of the glycosidic dihedral angles, for the SVD (left) and Almond (right) models of the alignment tensor. See the text for details of the calculation.

We also tried to fit the alignment tensors for the two sugar rings individually as reported by Freedberg and coworkers,¹³ and obtained similar R factors, 17.6% for glucose ring and 12.7% for fructose ring, using the crystal structure to define the individual ring conformations. However, the overal (axial) alignment was not the same for the two rings (0.00016 for glucose vs. 0.00026 for fructose), indicating the no common structure could accommodate both sets of data. In these circumstances, the use of separate alignment tensors, however, provides little insight into the nature of conformational ensemble

3. Indirect spin-spin couplings

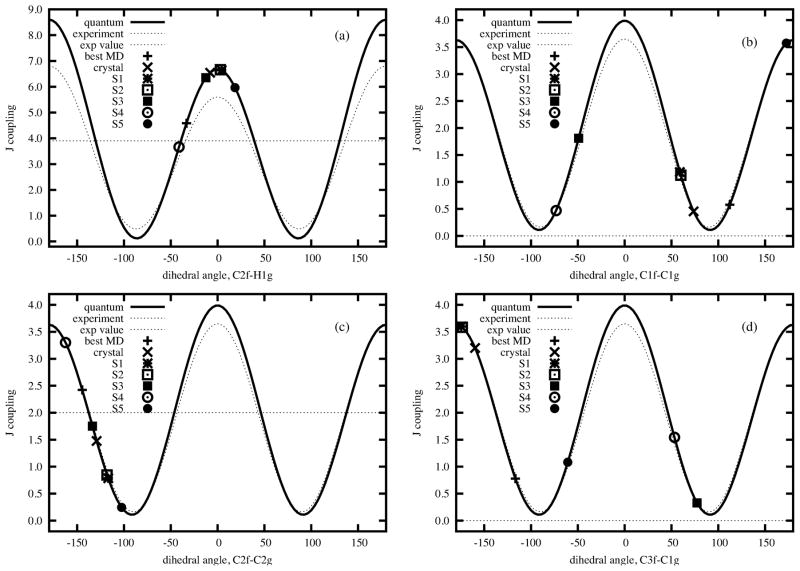
Serianni and coworkers¹¹ analyzed the indirect three-bond spin-spin couplings for four inter residue ¹³ C- ¹³ H and ¹³ C- ¹³ C spin pairs (C2f-O1g-C1g-H1g, C2f-O1g-C1g-C2g, C3f-C2f-O1g-C1g, and C1f-C2f-O1g-C1g), finding conformer S4 in Brady’s notation^15,16 to be in better agreement with the experimental J couplings than is the crystal structure (see Refs^15,16 and Table 4S). We ranked our 100,000 snapshots for agreement with this data, as we did for the RDC data. Figure 6 shows the best 500 conformers to be distributed in a region above M1 and a second region close to M3. In Table 4S and Figure 7 we list the J couplings and R factors of M1 to M4 from our MD simulation in TIP4P/Ew waters at T = 315 K, and S1 to S5 from computational results from Brady and coworkers.^15,16 We also find that M3 or S4 has a lower R factor (0.545 and 0.476 respectively) than the other three or four conformers, consistent with the conclusions of earlier work.¹¹ However we also find conformers in the M1 basin that have favorable R factors, as low as 0.287 as listed in Table 4S. The right side of Figure 6 displays the distribution of glycosidic dihedral angles from different conformers. The best MD conformer from J couplings is not very far away from the crystal structure and still belongs to the same M1 basin as the best MD conformer from the RDC analysis in Figure 3. The φ,ψ regions that best fit the RDCs are not identical to those for J-couplings, but have considerable overlap, Although the best fit region for J-couplings extends “upward” in ψ more toward the M4 region. In each case, the region that fits best to experiment is smaller and much closer to the crystal structure than is the totality of conformers visited by the MD simulation.

Figure 6.

Left: Same as Figure 3, using four inter-residue J coupling constants.¹¹ Right: Locations of glycosidic dihedral angles from different conformations on the free energy landscape constructed from the MD simulation with TIP4P/Ew at T = 315K.

Figure 7.

Individual J-couplings vs torsion angle. “Quantum” represents that the Karplus relation curve is fitted from DFT calculations,⁶² and “Experiment” for the curve fitted from experimental data.⁶⁴ Torsion angles are defined as (a) C2f-O1g-C1g-H1g, (b) C1f-C2f-O1g-C1g, (c) C2f-O1g-C1g-C2g, and (d) C3f-C2f-O1g-C1g.

4. Ring Puckering of Fructose

In addition to the variation in φ–ψ glycosidic space, another likely mode of structural flexibility originates from the ring conformation of fructose. The ring pucker describes how C3 and C4 are arranged relative to the plane defined by C2, C5 and O5. Experimental studies such as RDCs,⁴⁹ J coupling,¹¹ and optional rotation,⁶³ have showed that the pucker is confined to the NE quadrant of the pseudo-rotational wheel, with the phase angle most likely in the range of 0° to 90°.

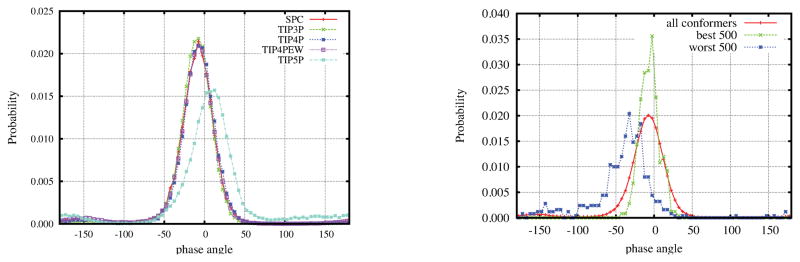
The phase angle was calculated by Altona and Sundaralingam algorithm.⁴⁸ Fig. 8(a) shows the probability density distribution of phase angle with different water models. The dependence of water models is small, and the phase angle dominantly fluctuates around −5° which is the value of crystal conformation.¹ We also noticed a slight peak presents at −150° for all models and the shift of peak for the TIP5P water model. Figure 8(b) shows the probability density distributions calculated from the best and worst 500 conformations as shown in Figure 3(a). The distributions are very similar to Figure 8(a) except that the distribution of the worst 500 shifts to more negative values. Hence, in all cases, our simulation results have large percentages of negative phase angles which are not preferred for experimental data: Optional rotation⁶³ likes the phase angle between 18° to 54°, J coupling¹¹ tends to choose values around 0° and recent RDCs predicted the range of 20° to 70°.⁴⁹ Hence adjustments of force field might be required to more favor positive phase angles.

Figure 8.

Puckering phase angle probability density distributions of the fructose monosaccharide residue of sucrose. (left) Different water models at T = 300K, (right) All 100,000 conformers, best and worst 500 from RDC rank in Figure 3.

5. Intramolecular Hydrogen Bonds

As depicted in Figure 1, there exist two intramolecular hydrogen bonds, O2g-H1Of and O5g-H6Of, in the crystal conformation.¹ Early NMR studies in aqueous solution by Bock and Lemieux² suggested that only one (O2g-H1Of) exists in solution. Molecular simulations by Engelsen and coworkers,¹⁹ however, found no intramolecular hydrogen bond presence using a revised CHARMM-type force field,³⁴ which started from the crystal structure.

Figure 9 shows the probability density distributions for the two possible hydrogen bonds shown in Figure 1 The peak around 1.9 Å corresponds to the intramolecular hydrogen bond. The distribution with TIP5P is distinguished from that of the other four water models with the significantly lower peak of the hydrogen bond. There are only slight differences for the rest four models, and TIP3P has the highest peak of hydrogen bond. Hydrogen-bond occupations were calculated by integrating the first peaks in Figure 9 and are listed in Table 5S. For the TIP4P/Ew model, the O2g hydrogen bond has an occupation of about 12%, and the O5g bond an occupation of about 5%. These two values are increased to 18% and 14% as we restrain the conformation to M1 basin region and pucker phase angle to 0 as shown below (see Table 5S also).

Figure 9.

Probability density distributions of the distances between two atoms from MD trajectories. Left: O2g and H1Of; right: O5g and H6Of.

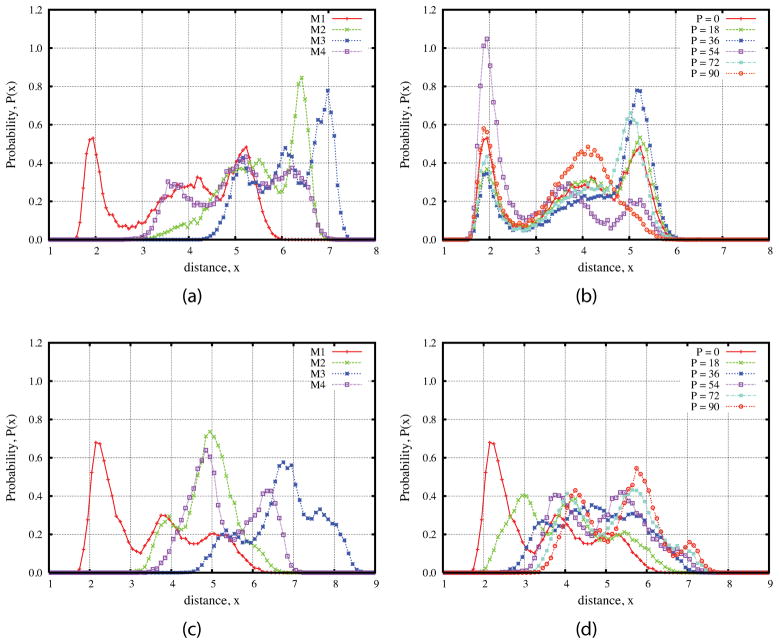
From the schematic picture in Figure 1, we can see that the distance between O2g and H1Of not only depends on the glycosidic dihedrals, φ and ψ but also depends on the dihedrals from the 1-hydroxymethyl group of fructose. To see the effects of glycosidic dihedrals and puckering phase angle on this distance, we performed the restrained MD simulations shown in Figure 10. The peak corresponding the hydrogen bond only appears when the glycosidic dihedrals are restrained to the minimum M1 which is close to the crystal conformation. This means that the hydrogen bond will be broken when the sucrose molecule transfers to the other three minima. The presence of peaks at larger distances shows that even when the molecule fluctuates around the minimum M1, the rotation of 1-hydroxymethyl group could also break the hydrogen bond between O2g and H1Of, with the occupation of about 18%.

Figure 10.

Probability density distributions of the distance between two atoms from 10ns restrained MD simulations with the TIP4P/Ew waters at T = 300 K. (a) and (b) for O2g and H1Of, (c) and (d) for O5g and H6OfO2g. For (a) and (c) the dihedrals of φ–ψ glycosidic linkage are restrained to the four different free energy minima as shown in Figure 2 and five dihedrals from the fructose ring are restrained in order to make the puckering phase angle fixed to P = 0. For (b) and (d) the values of φ–ψ are restrained to the minimum M1 but the puckering phase angle are fixed to different values (P = 0, 18, 36, 54, 72, and 90).

We also obtained the distributions with the φ-ψ dihedrals restrained to the minimum M1 but the puckering phase angle fixed to different values, P = 0, 18, 36, 54, 72, and 90. Figure 10 shows that the percentage of hydrogen-bond (35.53%, see Table 5S for other values) is greatest when P = 54. Based on Figure 10(c), similar arguments can also be reached for O5g-H6Of hydrogen bond since the distance also depends on other dihedral angles such from fructose ring and 6-hydroxymethyl group. Moreover, the O5g-H6Of is much more sensitive to the conformation of fructose ring as shown in Figure 10(d), namely the O5g-H6Of hydrogen bond breaks as the pucker angle of fructose moves to positive values, even when the glycosidic angles are restrained to crystal conformation.

4. Summary

These simulations show that the glycosidic conformation of crystal state also dominates in solution, although other free energy minima are visited. The quality of the simulation was evaluated by the calculation of residual dipolar couplings and indirect spin-spin couplings. Among the conformations sampled here, those in the M1 free energy basin (near the crystal structure, or with slightly larger values of ψ) give the best fits to both the RDC and J-coupling data. A straightforward average of RDCs and J-couplings over the entire trajectory yields poor results, mainly due to the high population near the M2 basin. Hence quantitative agreement with experiment requires a more accurate carbohydrate force field which would probably reduce the population of M2. We also note that many of the structures in the “M1 basin” fit the RDC data much better than the crystal structure itself (39% vs. 22% for the best MD conformation). This is due to the slight shift of (φ,ψ) values, from (108°, 305°) in crystal to (121.7°, 297.5°) in solution. This implies that water solvation modifies the crystal by weakening the intramolecular hydrogen bonds O2g-H1Of and O5g-H6Of.

The water solvation effects on the local structure flexibility of the fructose monosaccharide residue have also been investigated by the analysis of puckering phase angle. We found that the distribution of phase angles fluctuates around the −5° of crystal conformation. The best and worst 500 conformations from the RDC rank have similar distribution except that the distribution of worst 500 shifts to more negative values. This implies that there is only very weak correlation between the glycosidic (φ,ψ) conformation from RDCs and the local structure flexibility of the fructose from the puckering phase angles. However the large percentage of negative puckering phase angles present in our simulation results seems to disagree with experiment, suggesting that changes to the force field torsion potentials to favor positive pucker angles should be explored.

The presence of solvent water appears to have a strong influence on the intramolecular hydrogen bond patterns O2g-H1Of and O5-H6Of present in crystal structure. They are dynamic processes of breaking and reforming in solution instead of a static picture in the crystal structure. Our simulations also show that these two intramolecular hydrogen bonds can only be maintained when the system has conformations around the M1 basin (which contains the crystal structure). Furthermore, the hydrogen bonds depend not only on the conformation of glycosidic linkage but also on the rotamer population of hydroxymethyl group at C1 or C6 of fructose. Hence one strategy to stabilize the M1 basin relative to M2 would be to increase the intramolecular H-bond strength, relative to H-bonds with water. Explorations along these lines are planned.

The results presented here suggest that the question, “is sucrose rigid or flexible?” needs to be answered with care. There is almost certainly averaging within the energy basin near the crystal stucture, and probably additional flexibility about ψ to regions “above” this M1 basin, as suggested in Figs. 3 and 6. On the other hand, these regions comprise only a small fraction of the φ–ψ map, and do not include many conformations favored by the GLYCAM force field. Overall, the NMR and compuational data seem most consistent with a limited conformational ensemble centered fairly near to the crystal conformation.

Appendix

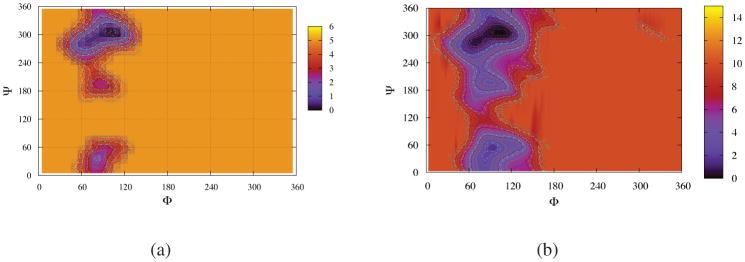
The assumption of the calculation method of free energy in Equation 8 is that the MD trajectories are long enough to visit the relevant phase space sufficiently which is a good approximation for systems with low free energy barriers. For exploring the transitions with high engery barriers, more advanced molecular dynamics techniques are required to solve the sampling probleim in the short time simulations. The adaptively biased molecular dynamics (ABMD) (Babin, V.; Roland, C.; Sagui, C. J. Chem. Phys. 2008, 128, 134101) is a recent addition to the advanced molecular dynamics techniques for accelerating simulations and is capable of overcoming these high free energy barriers and estimating the potential of mean force in the relevant space. Figure 11 and Table 2 display the free energy results of T = 283 K constructed from the 100 ns normal MD simulation and the more advanced 25 ns ABMD simulation, The ABMD method is able to explore more high energy regions but the low energy parts are similar to that of normal MD simulations. This verifies the convergences of low energy parts of normal MD simulations which are more important for the studies of pure water. Namely, although the systems in normal MD simulations will visit more high energy regions as the simulation times are increased further, we do not expect that the simulations will change the free energy landscapes of low energy parts significantly. (See our second paper ⁴¹ for more detailed ABMD results about sucorse in high viscous solvent, water-DMSO mixture.)

Figure 11.

Free energy landscapes in φ–ψ glycosidic space for sucrose in TIP4P/Ew waters at T =283 K. (a) from 100 ns normal MD simulation, the contour lines were generated from 0.0 to 5.0 KCal/mol by the difference of 0.1. (b) from 25 ns ABMD simulation, the contour lines were generated from 0.0 to 10.0 KCal/mol by the difference of 0.25. The ABMD method is able to explore more high energy regions but the low energy parts are similar to that of normal MD simulations. Note that we let all global minima have the values of zero and this results in that ABMD has different background color corresponding to the regions with higher free energy values.

Table 2.

Free energy information of four minima of sucrose in pure water at T = 283K from the 100 normal MD simulation and the 25 ns ABMD simulation resepectively.

	ABMD	Normal MD
positions (φ,ψ) (in degree)
M1	(104.5, 306.1)	(104.1, 305.4)
M2	(69.7, 283.3)	(71.2, 285.8)
M3	(88.5, 195.9)	(85.8, 194.9)
M4	(92.9, 54.3)	(84,4, 35.5)
heights (in KCal/mol)
F1	0.0	0.0
F2	0.3	0.5
F3	2.9	2.3
F4	1.4	1.8
probabilities within a radius of 20 degree
P1	0.557	0.606
P2	0.241	0.365
P3	0.003	0.008
P4	0.018	0.022
barriers between minima (in KCal/mol)
B12	0.6	0.6
B23	3.8	3.0
B14	2.5	2.4