Abstract
Diseases transmitted by mosquitoes could be controlled if vector populations were replaced with strains that have reduced vector competency. Such a strategy is being developed for control of dengue virus which is transmitted by Aedes aegypti (L.) (Diptera: Culicidae). Mosquitoes artificially infected with the bacterium, Wolbachia pipientis Hertig, are being assessed as candidates for release at the adult stage with the aim of replacement of the wild population. Wolbachia can reduce the capacity of Ae. aegypti to transmit dengue virus and has potential to be driven through the natural population via a system of cytoplasmic incompatibility. Deployment of benign mosquito strains will be influenced by population size and structure of wild-type Ae. aegypti in proposed release areas, as well as rates of gene flow among populations in the wet and dry tropical seasons. Mosquitoes from northern Queensland were screened with genetic markers to find an optimal locality for release of a benign strain of Ae. aegypti. The inland towns of Chillagoe and Charters Towers and the coastal town of Ingham had mosquito populations that were partly genetically isolated from mosquitoes in other areas across both seasons. These locations may be suitable release sites if it is important for the released strain to be restricted during initial phases of implementation. Smaller genetic differences were also evident among other regions and were consistent over two seasons (wet and dry).
Keywords: Aedes aegypti, dengue, population structure, gene flow, seasonality
Replacement of vector populations with benign strains (i.e., those that do not transmit disease) has been proposed as a strategy for vector-borne disease control. New genetic control methods incorporating this strategy are being developed for pest mosquitoes including the dengue vector Aedes aegypti (L.) (Diptera: Culicidae) (McMeniman et al. 2009). Populations of Ae. aegypti artificially infected with strains of Wolbachia pipientis that interfere with its vector competence are being backcrossed into wild mosquito genetic backgrounds from north Queensland and assessed as potential candidates for release (Yeap et al. 2011).
Mosquito strains containing Wolbachia can have a fitness benefit over wild-type mosquitoes due to cytoplasmic incompatibility (Turelli and Hoffmann 1999) and, if deployed appropriately, could replace the wild population of Ae. aegypti (Sinkins 2004). However, a successful replacement will only occur if Wolbachia mosquitoes are introduced in appropriate numbers because an unstable equilibrium point has to be exceeded for Wolbachia to spread (Turelli and Hoffmann 1999). This means that an accurate estimate of the population size of the mosquitoes is needed along with patterns of gene flow in proposed release areas. Appropriate methods of introduction (time, place and numbers released) will, therefore, be influenced by gene flow patterns and population size as well as the age structure of Ae. aegypti in proposed release areas.
For Ae. aegypti, seasonal changes in population size and movement are particularly important because modeling on a global scale suggests an increase in density during warmer months of the year (Hopp and Foley 2001). In temperate regions such as Buenos Aires, abundance of Ae. aegypti fluctuates with season and adults are not detectable in the winter presumably due to population suppression at low temperatures (Vezzani et al. 2004). In contrast, in tropical French Polynesia, populations of Ae. aegypti can be sustained by rainfall events each month so that no differences in activity between the wet and dry seasons are observed, although the wet season is thought to promote vector abundance and longevity and result in an increased risk of disease transmission (Russell et al. 2005a). Between these extremes, in subtropical Argentina, a population peak occurs in March at the time of maximum rainfall, but is reduced in winter due to low relative humidity, which affects oviposition (Micieli and Campos 2003).
Here, we consider genetic structure of Ae. aegyptiin north Queensland, Australia, in the dry season. Gene flow has previously been investigated in the wet season within this area (Endersby et al. 2009). The highest relative humidity occurs during the summer wet season (December–February) and the lowest during the winter dry season (June–August) (ABS 2002). However, some areas of north Queensland, such as Townsville and Charters Towers, have a semiarid climate. Ae. aegypti is maintained in these areas by garden watering (Canyon 2001), water tanks, and subterranean sites (Russell et al. 2002). Coastal areas of northern Queensland are generally more humid than these semiarid sites (Russell et al. 2005b). Mosquito oviposition and larval development sites in coastal towns are abundant in the form of artificial containers such as garden accoutrements, plastic containers, tires, sump pits, and flower pot bases (Canyon 2001, Kearney et al. 2009).
Knowledge of effective population size is important when considering a release of a benign strain. The number of individuals that contribute to the next generation is always lower than the census population size so numbers of individuals necessary for release can be modified accordingly. This evolutionary parameter is almost impossible to estimate by direct methods, so genetic methods are often used. Even using genetic methods, life history, sample size, number of cohorts sampled (Waples and Yokota 2007), and number of loci screened have a large influence on estimation of Ne and many methods carry assumptions about the populations under investigation (no selection, mutation or migration), which are often violated in nature (Wang and Whitlock 2003). When only data for Ae. aegypti from the wet season were available and methods of estimation used were based on microsatellite mutation models, estimates of Ne for all sampling locations were large (Endersby et al. 2009). In general, single point estimates of Ne from one generation are less precise than methods that include multigenerational data. However, methods based on temporal changes in allele frequency assume an isolated population with no immigration and estimates of Ne can be strongly biased in populations where immigration does occur (Wang 2005).
We consider the following questions: 1) Can locations be identified that are consistently genetically isolated from others, in cases where releases of mosquitoes into contained areas might be targeted? 2) Is it possible to estimate the effective population size of mosquitoes at different locations?
Materials and Methods
Ae. aegypti were sampled from three inland and nine coastal sites in far north Queensland, Australia (fig. 1; Endersby et al. 2009) in the wet season (March–June 2006) and the dry season (September–November 2006) by using collection techniques described by Endersby et al. (2009). In brief, mosquitoes were sampled using BG-Sentinel traps (Biogents, Regensburg, Germany) or by pipetting larvae from flooded containers with at least 50 live individuals targeted per location. To minimize the number of siblings in the analysis, only five adults per BG-Sentinel trap and one third- or fourth-instar larva per ovitrap or container were used. Samples were preserved in absolute ethanol and stored at −20°C before analysis.
Fig. 1.
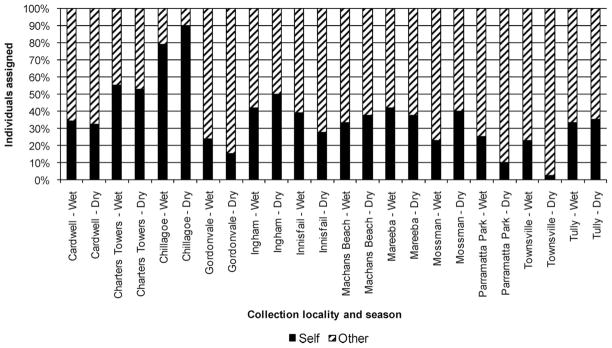
Population assignment of Ae. aegypti to “self” or “other” population in the wet and dry seasons in north Queensland, Australia.
Eight polymorphic genetic markers were used to screen for variation in populations of Ae. aegypti(Endersby et al. 2009). These included one microsatellite marker (Gyp8) and two ribosomal protein EPIC markers (Rps20b, RpL30a) developed by Endersby et al. (2009), a further two microsatellite loci developed by Slotman et al. (2007) (AC1, AG5), and three loci developed by Chambers et al. (2007) (BbA10, BbH08, BbB07). DNA was extracted using either a CTAB/chloroform method (Weeks et al. 2002) or a Chelex 100 Resin (Bio-Rad Laboratories, Hercules, CA) and polymerase chain reaction (PCR) conditions followed Endersby et al. (2009).
Analysis
A global estimate of FST (with 95% CL) (Weir and Cockerham 1984) and population pairwise measures of FST with significance determined using permutations, were obtained using FSTAT version 2.9.3 (Goudet 1995). We also estimated FIS and allelic richness (Weir and Cockerham 1984) for each population with FSTAT. Observed (HO) and expected (HE) heterozygosity were estimated using GenAlEx version 6 (Peakall and Smouse 2006) and deviations from Hardy–Weinberg (HW) equilibrium were tested using the probability test in Genepop version 3.4 (Raymond and Rousset 1995). Regression and Mantel tests of the linearized FST transformation [FST/(1 − FST)] with the natural log of geographic distance were calculated using POPTOOLS version 2.6 (Hood 2002). The Mantel tests differ slightly for the wet season to those in Endersby et al. (2009), because there were a few minor scoring errors in the geographic distance table constructed by Endersby et al. (2009). A second Mantel test of the linearized FST transformation [FST/(one − FST)] between pairs of sampling locations in the wet season versus the same estimate in the dry season was also made. Significance of Mantel tests was determined by permutation (10,000 randomizations).
Analysis of molecular variation (AMOVA) was undertaken in Arlequin version 3.11 (Schneider et al. 2000) by using pairwise FST as the distance measure, with 10000 permutations and missing data for loci set at 5%. One model for analysis partitioned variation among groups (season), among populations within groups (location) and within populations (locations). A second model was used for data within the wet and dry season separately, with groups being defined as “inland” (Charters Towers and Chillagoe) versus “coastal” (all other locations).
Several analyses to estimate the number of populations within the sample data were undertaken. First, factorial correspondence analysis using Genetix version 4.03 (Belkhir et al. 2004) was used to visualize patterns of genetic differentiation between the populations sampled. A second exploratory technique, the population assignment test in GenAlEx version 6 (Peakall and Smouse 2006), was used to see whether individuals from each of the sampled locations were assigned to their collected locality with a greater likelihood than to any of the other locations which would indicate existence of population structure (Manel et al. 2005). Parameters chosen were: assign all populations, frequency estimator = “Leave One Out”, set 0–0.01.
Geneland 3.1.4 (Guillot et al. 2008) was used to take both spatial and genetic data into account when determining population structure. Clusters are formed so that each population is in approximate Hardy–Weinberg equilibrium with linkage equilibrium between loci (HWLE). The model was run for the data from each season across sampling locations. The “uncorrelated allele frequency” option was used for all runs across the entire geographic area within a season. 500,000 iterations were used with a thinning factor of 100. Five independent runs were made for each data set with a burnin of 200 (*100). The number of pixels in the spatial design was set at 50*50.
Effective Population Size
In a previous study (Endersby et al. 2009), we used two indirect methods to estimate Ne (Kimura and Crow 1964, Ohta and Kimura 1973), the number of individuals in a theoretical ideal population having the same degree of genetic drift as the real population. These methods depended on an accurate estimate of the mutation rate of loci. The estimate of the mutation rate in Endersby et al. (2009) was made for microsatellite loci in Drosophila (Schug et al. 1997) and may be inaccurate for Ae. aegypti. Here, we have used several different indirect methods to estimate Ne that do not depend on mutation rate estimates and make use of temporal data. The temporal method using moments based F-statistics of Waples (1989) and NeEstimator (Peel et al. 2004) was used to estimate Ne for mosquitoes at each location using data from one sampling event in the wet season (nominated as generation 0) and data from one sampling event in the dry season (nominated as generation 3 because approximate generation time of 1 mo was assumed based on the observation of a maximum of 15 generations per yr; Kearney et al. 2009). All eight loci were used in this analysis.
MLNE version 1.1 (Wang 2001) uses the moment and likelihood methods developed by Wang and Whitlock (2003) to estimate Ne and immigration rate (m) jointly from temporal and spatial data on number of allele copies from focal and source populations. MLNE was run to estimate the Ne of single isolated populations with the maximum likelihood method of Wang (2001) and the moment estimator of Nei and Tajima (1981). We also used MLNE to investigate Ne around potential release sites for a Wolbachia-based release strategy (McMeniman et al. 2009). Gordonvale was a focal population with the source populations of Mossman, Mareeba, Machans Beach, Parramatta Park, and Innisfail. Townsville was investigated as another focal population with the source populations of Cardwell and Tully.
Results
Estimates of Population Genetic Parameters From Genetic Marker Data
As in the wet season (Endersby et al. 2009), data from the dry season provided no evidence of heterozygote excess/deficiency or significant inbreeding in any of the populations (data not shown). Observed (HO) and expected (HE) heterozygosities were very similar and there were no significant deviations from Hardy–Weinberg equilibrium after correcting for multiple comparisons (adjusted P value for multiple comparisons = 0.004) in samples from all locations, although samples from Tully in the wet season and Ingham in the dry both approached significance (Table 1). When data were considered by locus across seasons, there was a significant deviation from Hardy–Weinberg equilibrium for BbB07 (adjusted P value = 0.006). Endersby et al. (2009) previously indicated that null alleles are probably present at this locus.
Table 1.
Population statistics for Ae. aegypti collected in Queensland, Australia, in the wet and dry season using genetic markers
| Pop | Wet season
|
Dry season
|
Wet season
|
Dry season
|
||||||
|---|---|---|---|---|---|---|---|---|---|---|
| No. alleles | Allelic richness | No. alleles | Allelic richness | HO | HE | HW-P | HO | HE | HW-P | |
| Cardwell | 34 | 3.74 (n = 44) | 31 | 3.82 (n = 40) | 0.4795 | 0.4699 | 0.2135 | 0.4597 | 0.4574 | 0.4643 |
| Charters Towers | 35 | 4.25 (n = 29) | 38 | 4.63 (n = 40) | 0.5489 | 0.5402 | 0.1127 | 0.5247 | 0.5416 | 0.0122 |
| Chillagoe | 28 | 3.11 (n = 43) | 24 | 2.94 (n = 40) | 0.4526 | 0.4214 | 0.5083 | 0.3616 | 0.3596 | 0.2581 |
| Gordonvale | 30 | 3.53 (n = 46) | 34 | 4.15 (n = 40) | 0.5238 | 0.4979 | 0.3670 | 0.4719 | 0.4956 | 0.3310 |
| Ingham | 34 | 3.64 (n = 48) | 32 | 3.92 (n = 40) | 0.4417 | 0.4422 | 0.2826 | 0.4281 | 0.4739 | 0.0091 |
| Innisfail | 36 | 4.07 (n = 46) | 34 | 4.15 (n = 40) | 0.5062 | 0.5237 | 0.9754 | 0.4625 | 0.4832 | 0.6147 |
| Machans Beach | 32 | 3.79 (n = 48) | 33 | 4.07 (n = 40) | 0.5326 | 0.5375 | 0.1712 | 0.5244 | 0.5301 | 0.6951 |
| Mareeba | 33 | 3.63 (n = 36) | 31 | 3.83 (n = 40) | 0.4652 | 0.4503 | 0.9999 | 0.4656 | 0.4910 | 0.0292 |
| Mossman | 31 | 3.63 (n = 31) | 30 | 3.69 (n = 40) | 0.4321 | 0.4681 | 0.3378 | 0.4843 | 0.4852 | 0.7861 |
| Parramatta Park | 32 | 3.85 (n = 32) | 33 | 4.07 (n = 40) | 0.5563 | 0.5534 | 0.9804 | 0.5057 | 0.5181 | 0.2618 |
| Townsville | 31 | 3.72 (n = 35) | 34 | 4.17 (n = 40) | 0.4679 | 0.4707 | 0.2988 | 0.5009 | 0.5040 | 0.6911 |
| Tully | 32 | 3.76 (n = 45) | 33 | 4.06 (n = 40) | 0.4980 | 0.5307 | 0.0097 | 0.4625 | 0.5188 | 0.0376 |
Statistics measured included number of alleles; allelic richness (n, sample size); HO, observed heterozygosity; HE, expected heterozygosity; HW-P, 0.0042 after adjustment for multiple comparisons.
For individual population and locus comparisons in the dry season, only one significant result (P < 0.001) of 96 was observed for Ingham and BbB07 due to a heterozygote deficiency. Six of the other 11 populations showed heterozygote deficiencies at locus BbB07, but they were not significant after correcting for multiple comparisons. There was no consistent linkage disequilibrium between any loci across all populations in the wet (Endersby et al. 2009) or dry seasons (data not shown).
Tests for Population Differentiation
The estimate of FST over all populations was 0.069 (0.055–0.085; 99% CIs) in the wet season and 0.051 (0.034 – 0.069; 99% CI) in the dry season. This indicates significant population differentiation within the samples screened and suggests a slightly higher level of population differentiation in the wet season. Population pairwise comparisons of FST between all sites and seasons revealed only 49 nonsignificant comparisons out of 300 in the matrix (supp Table 1 [online only]), indicating that most populations were differentiated from others to some degree. Samples from every location except Chillagoe showed no significant genetic differentiation across seasons based on estimates of pairwise FST. The number of nonsignificant comparisons among wet season samples and among dry season samples was the same (11; supp Table 1 [online only]).
There was a significant correlation between the same pairwise FST estimates in the wet and the dry seasons indicating that degree of genetic differentiation between samples from particular localities remained consistent (Mantel r = 0.68, P < 0.0001). Linear regression showed this relationship to be positive (R2 = 0.51, P < 0.0001).
AMOVA indicated that there was no significant differentiation between seasons (percentage of variation = −0.46%, P = 0.99, Va = −0.00667, SS = 1.174, df = 1). There was significant differentiation in the dry season between inland (Chillagoe and Charters Towers) and coastal (all other) samples (percentage of variation = 3.7%, P = 0.03, Va = 0.07598, SS = 28.613, df = 1), but this difference was marginal in the wet season (percentage of variation = 2.1%, P = 0.05, Va = 0.02355, SS = 10.161, df = 1).
In a population assignment test, Chillagoe was the most genetically isolated population across both seasons. Self-assignment was 79.1% in the wet season and 90% in the dry season (Fig. 1). Charters Towers had the second highest self-assignment in both seasons and self-assignment values were similar in the wet (55.2%) and the dry (52.5%) seasons. Ingham and Mareeba had high self assignments in both seasons, with a range from 50.0% to 37.5%. In the wet season, Mossman was the least genetically isolated population; however, its self-assignment increased from 22.6% in the wet to 40% in the dry. Townsville was the least genetically isolated population in the dry season, with a self-assignment of only 2.5%.
Chillagoe, Mossman, Ingham, Machans Beach, and Tully had increases in self-assignment in the dry season compared with the wet season with increases observed for Mossman (+17.4%), Chillagoe (+10.1%), and Ingham (+8.3%). The other seven populations had decreases in self assignment in the dry season compared with the wet season with decreases observed for Townsville (−20.4%), Parramatta Park (−15.0%), Innisfail (−11.6%), and Gordonvale (−8.9%). Factorial Correspondence (data not presented) and population assignment analyses in both seasons (Fig. 1) differentiated Charters Towers, Chillagoe, and Ingham from the other populations.
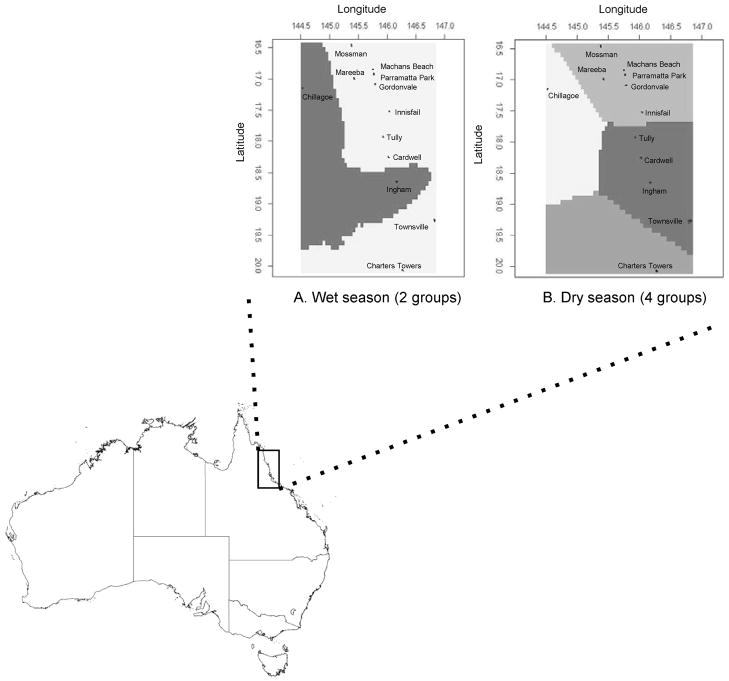
Analysis of mosquitoes from the wet season, using combined genetic and spatial data (Geneland), divided the samples into two groups (Fig. 2A). Mosquitoes from Chillagoe and Ingham comprised one group, whereas the other was made up of mosquitoes from all of the other locations. A similar analysis of mosquitoes from the dry season identified four populations in the data (Fig. 2B). Chillagoe was in a group of its own, as was Charters Towers, whereas mosquitoes from Townsville, Ingham, Cardwell, and Tully formed a single group. Mosquitoes from the remaining northeastern sites formed the fourth group.
Fig. 2.
Map of posterior mode of population membership of Ae. aegypti in north Queensland, Australia, assigned by Geneland, which takes both genetic and geographic information into account. (A) Wet season (two groups). (B) Dry season (four groups).
In the wet season, samples from Charters Towers, Innisfail, and Cardwell had the highest mean number of private alleles (0.250) followed by Mareeba and Ingham (0.125), and the remaining seven populations had none. In the dry season, Charters Towers had the highest number of private alleles (0.375) followed by Chillagoe (0.250). Gordonvale and Innisfail both had 0.125, and the remaining eight Australian populations had no private alleles in the samples taken. Allelic richness was highest in Charters Towers in both seasons and lowest in Chillagoe (Table 1).
Isolation by Distance
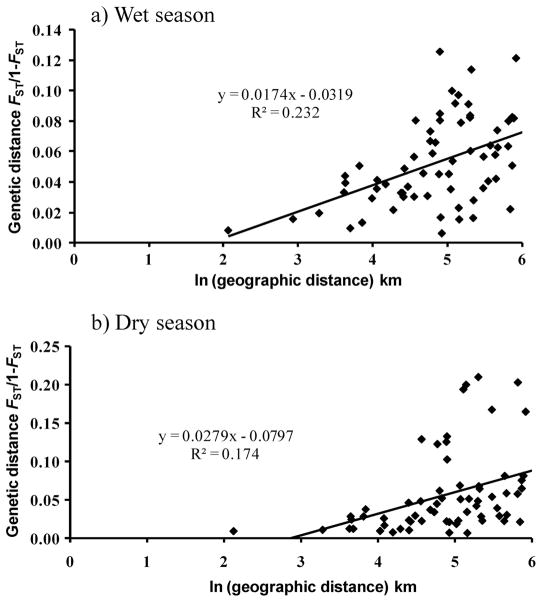
Genetic isolation by geographic distance was present in both seasons with a Mantel test showing a relationship between linearized FST estimates and the natural log of geographic distance (Mantel r = 0.481, P = 0.003, wet season; r = 0.418, P = 0.021, dry season). Linear regression showed this relationship to be positive in both seasons (wet season: R2 = 0.232, P < 0.001; dry season: R2 = 0.174, P < 0.001) (Fig. 3).
Fig. 3.
Plots of genetic isolation by geographic distance in Ae. aegypti in the wet and dry seasons in north Queensland, Australia.
Effective Population Size
Estimates of Ne from each sampling location differed between seasons and size ranking of each sample was different depending on the method used (Table 2). Using the temporal method, which took both seasons’ data into account, the smallest estimate of Ne was for Chillagoe and the largest for Charters Towers. However, upper 95% CIs for most of the estimates were reported as ∞, indicating that there is inadequate power to achieve a finite estimate of Ne under these experimental conditions. Sample size, sample interval, and number of independent alleles are all required to be large if temporal estimates of Ne are to be precise and accurate (Wang 2001). The results suggest that in many cases, our sample sizes at single locations at least were not large enough for great precision. The four sampling locations for which an upper estimate of Ne was made were Chillagoe, Mareeba, Machans Beach and Cardwell (Table 2). Estimates of Ne for the population groups suggested by Geneland were all <300 (Table 3). Upper 95% CIs were estimated for each of these putative population groupings and were all <750 individuals.
Table 2.
Estimation of Ne of Ae. aegypti from 12 locations in northern Queensland, Australia, by indirect methods
| Locality | Moments based temporal method | Lower 95% CI | Upper 95% CI | Assuming a single isolated pop
|
|||
|---|---|---|---|---|---|---|---|
| MLNE Moment | MLNE Likelihood | Lower 95% CI | Upper 95% CI | ||||
| Cardwell | 106 | 34 | 3,430 | 149 | 115 | 44 | >10,000 |
| Charters Towers | 5,564 | 60 | ∞ | 19 | 60 | 31 | 165 |
| Chillagoe | 25 | 11 | 57 | 31 | 43 | 24 | 97 |
| Gordonvale | 115 | 36 | ∞ | 151 | 833 | 86 | >10,000 |
| Ingham | 151 | 41 | ∞ | 398 | 3094 | 93 | >10,000 |
| Innisfail | 138 | 41 | ∞ | 162 | 174 | 57 | >10,000 |
| Machans Beach | 99 | 31 | 1,948 | 206 | 306 | 67 | >10,000 |
| Mareeba | 72 | 24 | 512 | 71 | 113 | 41 | >10,000 |
| Mossman | 303 | 43 | ∞ | 336 | 238 | 55 | >10,000 |
| Parramatta Park | 103 | 29 | ∞ | 137 | 284 | 58 | >10,000 |
| Townsville | 574 | 52 | ∞ | 769 | 10,000 | 116 | >10,000 |
| Tully | 1,062 | 65 | ∞ | ∞ | 10,000 | 114 | >10,000 |
Estimates of Ne for each sampling location: for moments based temporal method, Waples (1989), Peel et al. (2004), Ovenden et al. (2007); for single isolated population, Nei and Tajima (1981), Wang (2001).
Table 3.
Estimation of Ne of Ae. aegypti from 12 locations in northern Queensland, Australia, by indirect methods
| Pop | Moments based temporal method | Lower 95% CI | Upper 95% CI |
|---|---|---|---|
| Wet season grouping | |||
| 1. Chillagoe, Ingham | 92 | 40 | 238 |
| 2. Mossman, Mareeba, Gordonvale, Machans Beach, Parramatta Park, Innisfail, Cardwell, Tully, Townsville, Charters Towers | 298 | 155 | 575 |
| Dry season grouping | |||
| 1. Gordonvale, Mossman, Mareeba, Machans Beach, Parramatta Park, Innisfail | 202 | 98 | 431 |
| 2. Cardwell, Tully, Ingham, Townsville | 241 | 104 | 707 |
| 3. Chillagoe | 25 | 11 | 57 |
| 4. Charters Towers | 5,564 | 60 | ∞ |
Ne for groups identified by Geneland; methods in Waples (1989), Peel et al. (2004), and Ovenden et al. (2007).
The analysis of focal populations (planned potential release sites for a strain of benign mosquitoes) indicated that Ne for Gordonvale may be lower than that of Townsville; however, confidence intervals were extremely wide (Table 4). The estimated migration rate for the Townsville focal population had a tighter confidence interval than the estimate for Gordonvale and was <1.
Table 4.
Estimation of Ne of Ae. aegypti from 12 locations in northern Queensland, Australia, by indirect methods
| Focal pop | Source pop | ML_m | Lower 95% CI | Upper 95% CI | MT_m | MLNE moment Ne | MLNE Likelihood Ne | Lower 95% CI | Upper 95% CI |
|---|---|---|---|---|---|---|---|---|---|
| Gordonvale | Mossman, Mareeba, Machans Beach, Parramatta Park, Innisfail | 0.17 | 0.00 | >10,000 | 0.3 | ∞ | 77 | 24 | 7,388 |
| Townsville | Cardwell, Tully | 0.03 | <0.001 | 0.67 | 0.3 | ∞ | 623 | 40 | >10,000 |
Ne for focal populations from Gordonvale and Townsville; methods in Wang and Whitlock (2003). ML_m, estimated number of migrants per generation: max likelihood method; MT_m, estimated number of migrants per generation: moments based temporal method.
Discussion
The data from genetic markers indicate there is significant population genetic structure in Australian Ae. aegypti that seems relatively stable across the wet and dry seasons in 2006. Endersby et al. (2009) showed previously that populations of Ae. aegypti collected in the wet season in 2006 were structured in Australia and that there was limited gene flow that seemed to follow, somewhat, an isolation by distance model. Despite significant reduction in density of Ae. aegypti during the dry season in Australia (Montgomery and Ritchie 2002), the standing population genetic structure remains stable, with a strong positive correlation found between population pairwise FST for the wet and dry seasons. This probably reflects the limited gene flow between populations, as well as population sizes within each of the sample locations being large enough to obviate the effects of drift and inbreeding. Continuity in genetic structure of populations between seasons also could be maintained by large numbers of eggs surviving through the dry season and hatching when the wet season begins.
Although significant structure appears throughout the distribution of Ae. aegypti in Australia, several patterns are evident from the data. Chillagoe seems the most genetically differentiated of all sampled populations. This population was distinct in all analyses for both the wet and dry season data and allelic diversity was also reduced in both seasons compared with other populations. The isolation is not surprising given that Chillagoe is an inland settlement ≈100 km from the nearest town, and has a human population of only a few hundred individuals. Charters Towers and Ingham were the next most differentiated sites across seasons. Charters Towers is also an inland settlement at the southern end of Ae. aegypti’s current distribution, although the human population is considerably larger (≈8,000 people). Ingham, however, lies on the east coast of Australia and well within the continuum of sample sites on the east coast. It is not clear why this population of Ae. aegypti seems genetically distinct. Ingham is surrounded by ranges, national park and state forest on three sides, the Hinchinbrook channel in the north, and the ocean in the east. Perhaps these areas, which lack human habitation, are enough to limit natural mosquito movement into and out of Ingham.
There is also consistently low differentiation in some areas across the wet and dry seasons. The more northern coastal populations (Mossman, Mareeba, Gordonvale, Innisfail, Parramatta Park, and Machans Beach) tended to be similar in all analyses, with generally low pairwise FST estimates, although some were significantly different from zero. Similarly, the southern coastal populations (Tully, Cardwell, and Townsville) tended to have low pairwise FST estimates.
Effective population size estimates (Ne) are important to ensure that Wolbachia-infected Ae. aegyptimay be released in sufficient numbers to replace existing populations, particularly as the unstable equilibrium point may be quite high (Turelli 2010, Yeap et al. 2011). Endersby et al. (2009) used single point estimates of Ne (determined from one generation) with models for microsatellite evolution, which can be less precise than multigenerational data (Saarinen et al. 2009). In this study, we have used several temporal methods based on allele frequency changes in populations to estimate Ne (Nei and Tajima 1981, Waples 1989, Wang 2001, Peel et al. 2004, Ovenden et al. 2007).
The Ne estimates from each location were orders of magnitude lower than those made by Endersby et al. (2009) based on nontemporal approaches. The current results point to the effective population size of mosquitoes being relatively small in each location. However, 95% CIs on these estimates were generally large, and in some cases the upper limit could not be calculated. This situation was improved when Ne was estimated for groups of genetically and spatially similar samples rather than for samples from single collection locations. The methods did not produce consistent results, except that Chillagoe tended to have the lowest Ne estimates, whereas Tully and Townsville had the highest estimates.
Census sizes for Ae. aegypti have been estimated in both the wet and dry seasons. Pupal counts of Ae. aegypti per hectare in Cairns, Queensland, made by Williams et al. (2008) were ≈70 in the wet season and seven in the dry season. Surveys were taken over ≈50 km2 (Williams et al. 2008), so a rough wet season population estimate for the whole of Cairns would be 350,000 and a dry season estimate would be 35,000. Compared with the indirect Ne estimates, census size estimates seem to be orders of magnitude greater for both the wet and dry seasons. Similarly, recent surveys from Yorkey’s Knob and Gordonvale in 2009/10, areas just north and south of Cairns respectively, indicate that one to 10 females occur per house in the wet season, equating to a census size of ≈800 – 8,000 adult females per town (≈800 houses in each area; S.A.R. and P.H.J., unpublished data).
The results have implications for Wolbachia-infected Ae. aegypti replacement strategies being considered for North Queensland (McMeniman et al. 2009). Chillagoe, Charters Towers, and Ingham are the most suitable locations for the release of Wolbachia infected benign mosquitoes if it is important for the released strain to be restricted during early phases of implementation. These locations have the most genetically isolated populations of Ae. aegypti and any spread of an infected strain to other locations will, therefore, be limited. Conversely, if the goal is to spread the benign Ae. aegypti strain through its distribution, then releases should be considered in coastal regions other than Ingham. Although this study has addressed continuity of genetic structure and gene flow across a wet and dry season in Australian Ae. aegypti, further work is required to determine whether this pattern will persist across years.
In conclusion, we have shown that populations of Ae. aegyptiare genetically structured in north Queensland and this structure is maintained across wet and dry seasons. Some populations that show greater isolation may have low effective population sizes and are candidates for the initial releases of benign mosquito strains. A more targeted study of effective population size should be made in these strategic locations to answer the question of how many mosquitoes should be released to ensure that released mosquitoes constitute a substantial proportion of the natural population of Ae. aegypti.
Acknowledgments
We thank Luke Rapley for help in collecting mosquitoes. The study was funded by a grant from the Foundation for the National Institutes of Health through the Grand Challenges in Global Health Initiative and by the Commonwealth Scientific and Industrial Research Organization Cluster Collaboration Fund “Urbanism, Climate Change and Health.”
References Cited
- [ABS] Australian Bureau of Statistics. Australian Bureau of Statistics: Canberra. Australian Capital Territory; Australia: 2002. Year book Australia 2002, no. 84, ABS catalog no. 1301.0. [Google Scholar]
- Belkhir K, Borsa P, Chikhi L, Raufaste N, Bonhomme F. Laboratoire Génome et Populations. Université de Montpellier II; Montpellier, France: 2004. GENETIX 4.03, Logiciel Sous Windows™ pour la génétique des populations. [Google Scholar]
- Canyon D. A review of the dengue mosquito, Aedes aegypti (Diptera: Culicidae), in Australia. In: Canyon DV, Speare RS, editors. Rural and remote environmental health I. The Australasian College of Tropical Medicine; Townsville, Queensland, Australia: 2001. pp. 27–36. [Google Scholar]
- Chambers EW, Meece JK, McGowan JA, Lovin DD, Hemme RR, Chadee DD, McAbee K, Brown SE, Knudson DL, Severson DW. Microsatellite isolation and linkage group identification in the yellow fever mosquito Aedes aegypti. J Hered. 2007;98:202–210. doi: 10.1093/jhered/esm015. [DOI] [PubMed] [Google Scholar]
- Endersby NM, Hoffmann AA, White VL, Lowenstein S, Ritchie S, Johnson PH, Rapley LP, Ryan PA, Nam VS, Yen NT, et al. Genetic structure of Aedes aegypti in Australia and Vietnam revealed by microsatellite and exon primed intron crossing markers suggests feasibility of local control options. J Med Entomol. 2009;46:1074–1083. doi: 10.1603/033.046.0514. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goudet J. FSTAT (version 1.2): a computer program to calculate F-statistics. J Hered. 1995;86:485–486. [Google Scholar]
- Guillot G, Santos F, Estoup A. Analysing geo-referenced population genetics data with Geneland: a new algorithm to deal with null alleles and a friendly graphical user interface. Bioinformatics. 2008;24:1406–1407. doi: 10.1093/bioinformatics/btn136. [DOI] [PubMed] [Google Scholar]
- Hood G. PopTools. Commonwealth Scientific and Industrial Research Organization, Canberra, Australian Capital Territory; Australia: 2002. [Google Scholar]
- Hopp M, Foley J. Global-scale relationships between climate and the dengue fever vector, Aedesaegypti. Climatic Change. 2001;48:441–463. [Google Scholar]
- Kearney M, Porter WP, Williams C, Ritchie S, Hoffmann AA. Integrating biophysical models and evolutionary theory to predict climatic impacts on species’ ranges: the dengue mosquito Aedes aegypti in Australia. Funct Ecol. 2009;23:528–538. [Google Scholar]
- Kimura M, Crow J. The number of alleles that can be maintained in a finite population. Genetics. 1964;49:725–738. doi: 10.1093/genetics/49.4.725. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Manel S, Gaggiotti OE, Waples RS. Assignment methods: matching biological questions with appropriate techniques. Trends Ecol Evol. 2005;20:136–142. doi: 10.1016/j.tree.2004.12.004. [DOI] [PubMed] [Google Scholar]
- McMeniman CJ, Lane RV, Cass BN, Fong AWC, Sidhu M, Wang YF, O’Neill SL. Stable introduction of a life-shortening Wolbachia infection into the mosquito Aedes aegypti. Science. 2009;323:141–144. doi: 10.1126/science.1165326. [DOI] [PubMed] [Google Scholar]
- Micieli MV, Campos RE. Oviposition activity and seasonal pattern of a population of Aedes (Stegomyia) aegypti (L.) (Diptera: Culicidae) in subtropical Argentina. Mem Inst Oswaldo Cruz. 2003;98:659–663. doi: 10.1590/s0074-02762003000500013. [DOI] [PubMed] [Google Scholar]
- Montgomery B, Ritchie S. Roof gutters: key container for Aedes aegypti and Ochlerotatus notoscriptus (Diptera: Culicidae) in Australia. Am J Trop Med Hyg. 2002;67:244–246. doi: 10.4269/ajtmh.2002.67.244. [DOI] [PubMed] [Google Scholar]
- Nei M, Tajima F. Genetic drift and estimation of population size. Genetics. 1981;98:625–640. doi: 10.1093/genetics/98.3.625. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ohta T, Kimura M. A model of mutation appropriate to estimate the number of electrophoretically detectable alleles in a finite population. Genet Res. 1973;22:201–204. doi: 10.1017/s0016672300012994. [DOI] [PubMed] [Google Scholar]
- Ovenden JR, Peel D, Street R, Courtney AJ, Hoyle SD, Peel SL, Podlich H. The genetic effective and adult census size of an Australian population of tiger prawns (Penaeus esculentus) Mol Ecol. 2007;16:127–138. doi: 10.1111/j.1365-294X.2006.03132.x. [DOI] [PubMed] [Google Scholar]
- Peakall R, Smouse PE. Genalex 6: genetic analysis in Excel. Population genetic software for teaching and research. Mol Ecol Notes. 2006;6:288–295. doi: 10.1093/bioinformatics/bts460. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peel D, Ovenden JR, Peel SL. NeEstimator: software for estimating effective population size, Version 1.3. Queensland Government, Department of Primary Industries and Fisheries; Queensland, Australia: 2004. [Google Scholar]
- Raymond M, Rousset F. An exact test for population differentiation. Evolution. 1995;49:1280–1283. doi: 10.1111/j.1558-5646.1995.tb04456.x. [DOI] [PubMed] [Google Scholar]
- Russell BM, McBride WJH, Mullner H, Kay BH. Epidemiological significance of subterranean Aedes aegypti (Diptera: Culicidae) breeding sites to dengue virus infection in Charters Towers, 1993. J Med Entomol. 2002;39:143–145. doi: 10.1603/0022-2585-39.1.143. [DOI] [PubMed] [Google Scholar]
- Russell RC, Webb CE, Davies N. Aedes aegypti (L.) and Aedes polynesiensis Marks (Diptera: Culicidae) in Moorea, French Polynesia: a study of adult population structures and pathogen (Wuchereria bancrofti and Dirofilaria immitis) infection rates to indicate regional and seasonal epidemiological risk for dengue and filariasis. J Med Entomol. 2005a;42:1045–1056. doi: 10.1093/jmedent/42.6.1045. [DOI] [PubMed] [Google Scholar]
- Russell RC, Webb CE, Williams CR, Ritchie SA. Mark–release–recapture study to measure dispersal of the mosquito Aedes aegypti in Cairns, Queensland, Australia. Med Vet Entomol. 2005b;19:451–457. doi: 10.1111/j.1365-2915.2005.00589.x. [DOI] [PubMed] [Google Scholar]
- Saarinen EV, Austin JD, Daniels JC. Genetic estimates of contemporary effective population size in an endangered butterfly indicate a possible role for genetic compensation. Evol Appl. 2009;3:28–39. doi: 10.1111/j.1752-4571.2009.00096.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schneider S, Roessli D, Excoffier L. ARLEQUIN version 2.001: a software for population genetics and data analysis. Genetics and Biometry Laboratory, University of Geneva; Geneva, Switzerland: 2000. ( http://lgb.unige.ch/arlequin/) [Google Scholar]
- Schug MD, Mackay TFC, Aquadro CF. Low mutation rates of microsatellite loci in Drosophila melanogaster. Nat Genet. 1997;15:99–102. doi: 10.1038/ng0197-99. [DOI] [PubMed] [Google Scholar]
- Sinkins SP. Wolbachia and cytoplasmic incompatibility in mosquitoes. Insect Biochem Mol Biol. 2004;34:723–729. doi: 10.1016/j.ibmb.2004.03.025. [DOI] [PubMed] [Google Scholar]
- Slotman MA, Kelly NB, Harrington LC, Kitthawee S, Jones JW, Scott TW, Caccone A, Powell JR. Polymorphic microsatellite markers for studies of Aedes aegypti (Diptera: Culicidae), the vector of dengue and yellow fever. Mol Ecol Notes. 2007;7:168–171. [Google Scholar]
- Turelli M. Cytoplasmic incompatibility in populations with overlapping generations. Evolution. 2010;64:232–241. doi: 10.1111/j.1558-5646.2009.00822.x. [DOI] [PubMed] [Google Scholar]
- Turelli M, Hoffmann AA. Microbe-induced cytoplasmic incompatibility as a mechanism for introducing transgenes into arthropod populations. Insect Mol Biol. 1999;8:243. doi: 10.1046/j.1365-2583.1999.820243.x. [DOI] [PubMed] [Google Scholar]
- Vezzani D, Velázquez SM, Schweigmann N. Seasonal pattern of abundance of Aedes aegypti (Diptera: Culicidae) in Buenos Aires City, Argentina. Mem Inst Oswaldo Cruz. 2004;99:351–356. doi: 10.1590/s0074-02762004000400002. [DOI] [PubMed] [Google Scholar]
- Wang J. A pseudo-likelihood method for estimating effective population size from temporally spaced samples. Genet Res. 2001;78:243–257. doi: 10.1017/s0016672301005286. [DOI] [PubMed] [Google Scholar]
- Wang J. Estimation of effective population sizes from data on genetic markers. Philos Trans R Soc Lond B. 2005;360:1395–1409. doi: 10.1098/rstb.2005.1682. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang J, Whitlock MC. Estimating effective population size and migration rates from genetic samples over space and time. Genetics. 2003;163:429–446. doi: 10.1093/genetics/163.1.429. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Waples RS. A generalized approach for estimating effective population size from temporal changes in allele frequency. Genetics. 1989;121:379–391. doi: 10.1093/genetics/121.2.379. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Waples RS, Yokota M. Temporal estimates of effective population size in species with overlapping generations. Genetics. 2007;175:219–233. doi: 10.1534/genetics.106.065300. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weeks AR, McKechnie SW, Hoffmann AA. Dissecting adaptive clinal variation: markers, inversions and size/stress associations in Drosophila melanogaster from a central field population. Ecol Lett. 2002;5:756–763. [Google Scholar]
- Weir B, Cockerham C. Estimating F-statistics for the analysis of population structure. Evolution. 1984;38:1358–1370. doi: 10.1111/j.1558-5646.1984.tb05657.x. [DOI] [PubMed] [Google Scholar]
- Williams CR, Johnson PH, Long SA, Rapley LP, Ritchie SA. Rapid estimation of Aedes aegypti population size using simulation modeling, with a novel approach to calibration and field validation. J Med Entomol. 2008;45:1173–1179. doi: 10.1603/0022-2585(2008)45[1173:reoaap]2.0.co;2. [DOI] [PubMed] [Google Scholar]
- Yeap HL, Mee P, Walker T, Weeks AR, O’Neill SL, Johnson P, Ritchie SA, Richardson KM, Doig C, Endersby NM, et al. Dynamics of the “popcorn” Wolbachia infection in outbred Aedes aegypti informs prospects for mosquito vector control. Genetics. 2011;187:583–595. doi: 10.1534/genetics.110.122390. [DOI] [PMC free article] [PubMed] [Google Scholar]