Alkali halide clusters produced by fast ion impact

Abstract

The most abundant geometries and relative stabilities of alkali halide clusters with a (XY)_n^o configuration (e.g., LiF, NaCl, KBr) are described. Five main series were obtained: linear, cyclic, cubic, arc strips and nanotubes. The stability analysis shows that higher members are likely to be formed from the lower member of the same series and/or from two building blocks (n = 1, 2). The energy analysis (D-plot) indicates that the most compact ones (e.g., cubic and nanotubes) present higher stability when compared to the linear, cyclic and arc strip structures; moreover, relative stability between the cubic and nanotube series varies with the cluster size.

Over the last few years there has been increasing interest in studying systems at the nanometer scale, mainly because of their special electrical, magnetic and optical properties. Cluster and cluster-assembled materials have shown unique physical and chemical properties, which are quite different from those of the corresponding bulk crystals. Analysis of the cluster properties requires a detailed characterization of each member of the cluster ion series. General properties of the alkali halide clusters have been reviewed by Johnston and Martin.[1–3] Two techniques are mainly used to produce charged species out of alkali halide targets: (i) laser ablation and (ii) fast projectile sputtering.[4–7] Since LiF is transparent to visible and near UV light, absorbent materials such as Li₃N mixed with LiF powder may be employed to enhance the laser ablation. We have previously shown the advantages of using heavy ion projectiles (²⁵²Cf fission fragments at ~60 MeV) coupled to an adequate time-of-flight (TOF) analyzer for identification of large (LiF)_nLi⁺ and (LiF)_nF⁻ cluster ions (e.g., n up to 17).[8, 9]

In previous studies, we have shown that ab initio calculations including electron correlation can provide an accurate theoretical description of cluster stabilities: for instance, predictions appear to be in good agreement with gas-phase measurements of (CsI)_nCs⁺ ion clusters.[10] Although LiF nanostructures of pre-determined sizes (from a few to tens of nanometers) have been recently obtained experimentally, to the best of our knowledge, information about their structures is rather scarce. In particular, most of the stable isomers of the (LiF)_nLi⁺ series present a linear structure for small cluster size (n =1–3), while cubic cells or polyhedral structures are preferred for larger cluster sizes (n = 4–9).[11] Fragmentation energy predictions suggest that a desorbed excited (LiF)_nLi⁺ ion preferentially dissociates via (LiF)_n^o evaporation, in agreement with the slope modification in the exponential decay of the (LiF)_nLi⁺ ion abundances for n > 2. The most stable structures for the small (LiF)_nF⁻ clusters (n = 1 to 2) are linear, whereas the larger clusters (n = 4 to 6) present cubic or polyhedral structures.[11] In the present paper, we report on cluster stability and cluster formation mechanism of neutral alkali halide clusters of the form (XY)_n.

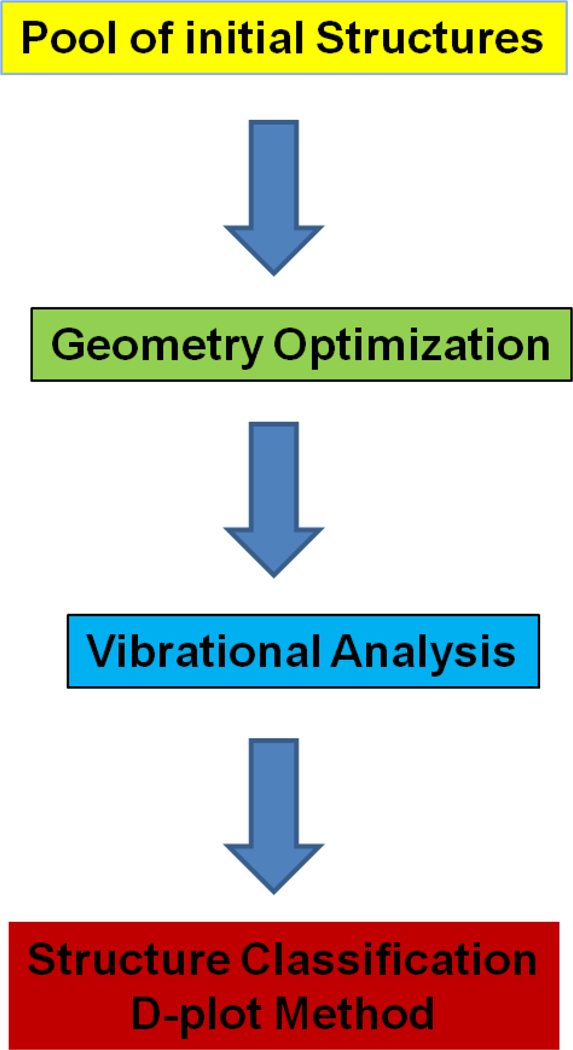
The methodology used in the search for the most stable alkali halide candidates is shown in Figure 1. A description of the theoretical approach used to generate the candidate structures can be found elsewhere.[8, 9] Briefly, the initial pool of candidate defines the diversity of the initial cluster population. Two main approaches can be used: atomistic (e.g., MD annealing cycles) or quantum (e.g., Genetic Algorithms), where the selection depends on the size and complexity of the system. In the case of the atomistic treatment, random generators create a large pool of candidate structures that can be later separated in characteristic classes and submitted to optimization. This approach is suitable in the case of limited computational resources and is recommended for large systems.[11] On the other hand, we have previously shown that genetic algorithms are advantageous for small cluster sizes. For macro-size systems (e.g., protein oligomers) the applicability of docking algorithm for the cluster generation was shown.[11]

Figure 1.

Methodology used in the search for the most stable alkali halide candidates.

Independently of the used approach, the geometry of the selected pool of candidates was optimized using Density Funtional Theory (B3LYP) and Coupled Cluster Theory (CCSD/SDD). A vibrational analysis was performed at the same level used for the geometry optimization to guarantee that all obtain structures correspond to a real minimum in the energy hypersurface. A D-plot is later used for displaying the relative stability of the clusters.[12]

The inspection of experimental results from ion impact on LiF surfaces shows that two main series are observed: (LiF)_nLi⁺ and (LiF)_nF⁻. Material ejected during the fast ion impact is mainly composed of neutral particles. Nevertheless, in the case of alkali halide targets, an odd number of atoms in the cluster can naturally generate a charge cluster (e.g., (XY)_nX⁺ or (XY)_nY⁻). We interpret that the cluster formation mechanism is based on the following considerations: i) an expanding plume is produced after each projectile impact, the main constituent of this plume being the neutral XY species; ii) although the life time of the plume is very short (tens of ps), a sufficient number of collisions may occur in this time interval to give rise to the (XY)_n clusters, where n may be up to a few tens; iii) competition for forming large clusters favors pathways having stable members.

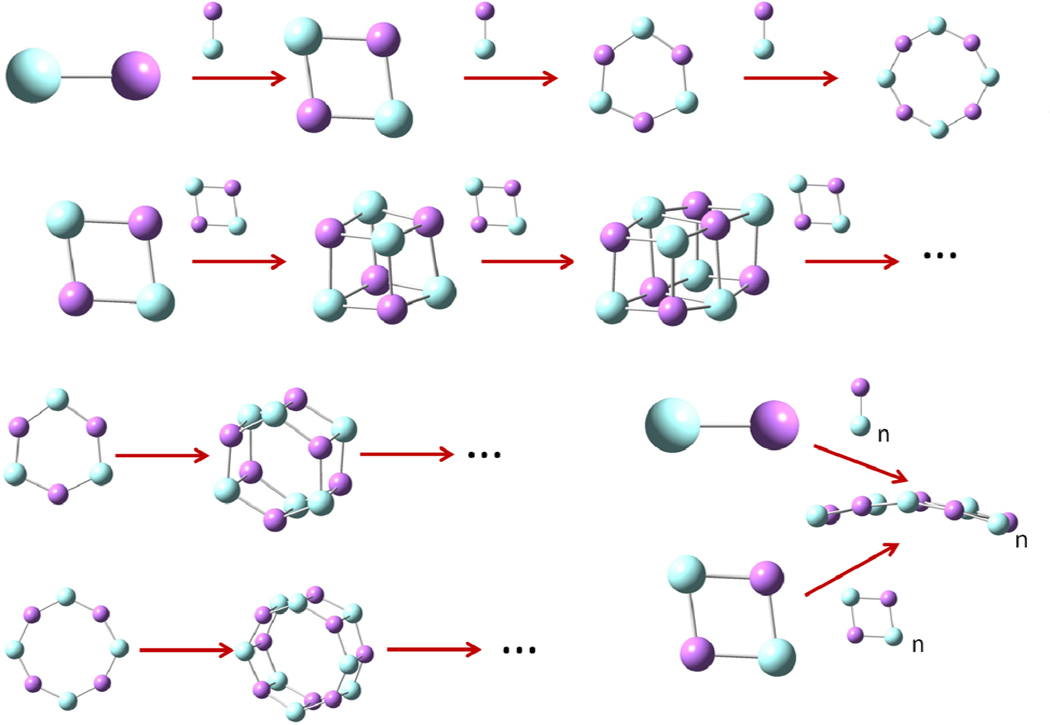
The obtained alkali halides configurations may be classified into five main series: i) linear, ii) cyclic, iii) arc strips, iv) cubic and v) nanotubes, as depicted in Figure 2. Since many of these structures are quite different from the possible debris of a crystalline solid, their formation is expected to occur from rearrangements and recombination in the initial stages of the plume expansion. For example, most of the smaller clusters, from linear to planar to cubic ones, can be generated by assembling (LiF) units. Larger clusters may result from the combination of like or different smaller units giving rise to a variety of shapes and sizes of clusters which could further rearrange into more stable structures.

Figure 2.

Formation sequence of the most abundant alkali halide series of the form (XY)_n^o.

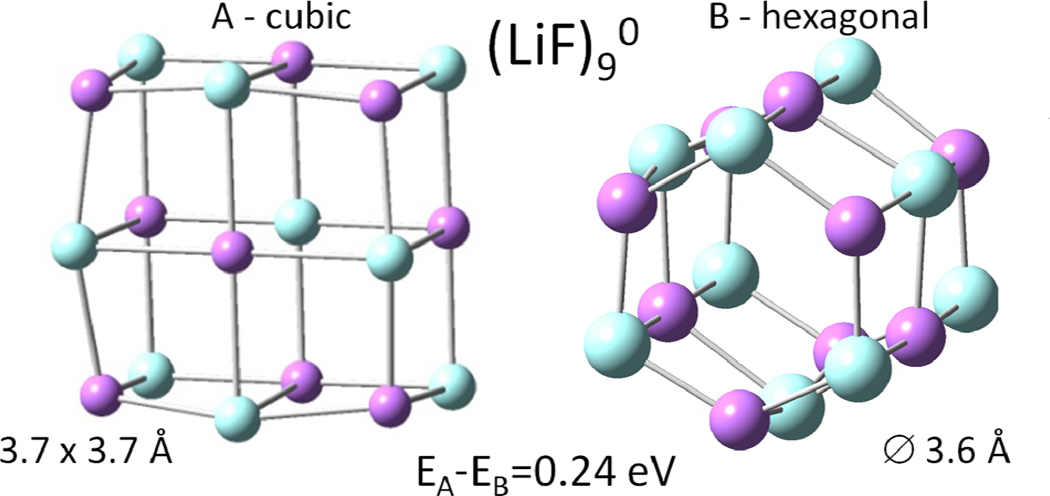
The analysis of the optimized structures shows that the most compact ones (e.g., cubic and nanotubes) present higher stability when compared to the linear, cyclic and arc strip structures. Intuitively, one could expect higher stability for the members of the cubic series since they can be directly formed from debris of a crystalline solid; nevertheless, some singularities are found. For example, the lower energy structure for the (LiF)₉^o cluster present an hexagonal geometry rather than a cubic geometry (see Figure 3). This observation is not restricted to the LiF case; some preliminary results showed that is also extensive to other alkali halides (e.g., NaCl, KBr). A more detailed description of alkali halide cluster formation of non-cubic and nanotube geometries will be described in a future paper.

Figure 3.

Lower energy structures obtained for the (LiF)₉^o series. Notice that the lowest energy structure (B) corresponds to a hexagon-based geometry, rather than the intuitively expected cubic form.

The strategy here presented for the study of alkali halide clusters allows the prediction of stable candidate structures and can be used to infer the cluster formation mechanism. The optimized structures and the associated vibration frequencies obtained offer a reliable data base for comparison with experiments. For example, future experiments involving spectroscopic measurements on alkali halide clusters trapped in noble gases matrices and gas-phase mobility measurements (analogous to ref 10) can be directly compared with the results presented here.