Detection of allosteric signal transmission by information-theoretic analysis of protein dynamics

Abstract

Allostery offers a highly specific way to modulate protein function. Therefore, understanding this mechanism is of increasing interest for protein science and drug discovery. However, allosteric signal transmission is difficult to detect experimentally and to model because it is often mediated by local structural changes propagating along multiple pathways. To address this, we developed a method to identify communication pathways by an information-theoretical analysis of molecular dynamics simulations. Signal propagation was described as information exchange through a network of correlated local motions, modeled as transitions between canonical states of protein fragments. The method was used to describe allostery in two-component regulatory systems. In particular, the transmission from the allosteric site to the signaling surface of the receiver domain NtrC was shown to be mediated by a layer of hub residues. The location of hubs preferentially connected to the allosteric site was found in close agreement with key residues experimentally identified as involved in the signal transmission. The comparison with the networks of the homologues CheY and FixJ highlighted similarities in their dynamics. In particular, we showed that a preorganized network of fragment connections between the allosteric and functional sites exists already in the inactive state of all three proteins.—Pandini, A., Fornili, A., Fraternali, F., Kleinjung, J. Detection of allosteric signal transmission by information-theoretic analysis of protein dynamics.

Early studies of cellular metabolic regulation culminated in the discovery of “allosteric transitions” within regulatory protein structures (1). This transition was characterized as a reversible conformational change: binding of a regulatory effector molecule to the allosteric site modulates the protein activity at the functional site. Since these early insights, computational and experimental evidence has added much detail at the atomic level. The currently emerging picture of allostery is that of a preexisting equilibrium among inactive and active states (2). Allosteric effectors can modulate protein function by shifting the equilibrium toward particular states (2–4). The perturbation of the free energy landscape on effector binding triggers a change in the protein that propagates from the allosteric to the functional site across the protein structure. Signal propagation has been recently argued to occur via multiple allosteric pathways, embedded in the network of residue contacts (5). Moreover, it has been recognized that the relative enthalpic and entropic contributions to the allosteric transition may vary greatly between systems. An extreme case is the purely entropically driven and dynamically mediated allosteric effect arising from rigidification of the macromolecule on binding of a ligand (6, 7). This increased understanding of allosteric regulation has suggested new directions in drug discovery. Allosteric inhibitors have been shown to be effective in targeting multiple conformational states and to be more selective than competitive inhibitors (8, 9).

While now better understood, allosteric modulation is still challenging to model. Different strategies have been recently proposed, on the basis of elastic networks (10, 11), contact maps (12–15), force distributions (16), evolutionary covariance (17), and correlations between residue motions (18–20). They generally differ in the amount of required prior information and use either single structures (10–13) or conformational ensembles (14–16, 18–20). In addition, some of them rely on the availability of data from both the inactive and active state (12, 14, 16, 18).

Here, we present a novel method to identify allosteric pathways in protein structures by an information-theoretical analysis of molecular dynamics (MD) simulations. Within the sampling limits, MD trajectories contain a wide range of molecular motions, from high-frequency harmonic oscillations to slow functional conformational transitions. However, without prior knowledge of the specific allosteric mechanism, it is still difficult to single out the residues involved in the signal propagation pathways. In our model, the dynamics of the system is reduced to a network of correlated local motions, and signal propagation is described as an information exchange through the network. Local motions are modeled as transitions between canonical states of protein fragments (21). Key residues are identified by a network topological analysis, while a time-resolved picture of their dynamical couplings is obtained from the fragment state transitions.

We report the application of the method to the receiver domains of the response regulators NtrC, CheY, and FixJ. Response regulators are part of two-component systems (TCSs), which are widespread in bacterial signal transduction (22) and control many different cellular processes, like chemotaxis (CheY; ref. 23), nitrogen fixation (FixJ; ref. 24), and nitrogen metabolism (NtrC; ref. 25). In TCSs, an external stimulus is detected by a sensor histidine kinase (the input component), which triggers a phosphotransfer reaction to the receiver domain of the response regulator (the output component). The phosphorylation promotes an allosteric conformational change that is propagated to the receiver domain interface (or signaling surface), regulating the affinity of the response regulator and, in particular, of its effector domain for the downstream targets (26). Receiver domains have a conserved fold that is coupled with >60 different effector domains, which are responsible for the specific adaptive response to the external signal (26). In this way, the same basic mechanism, a phosphorylation-induced allosteric transition, is used as a switch to modulate a variety of cellular pathways.

Since they are absent in animals, TCSs are considered as ideal candidates for the development of new antibiotics (27). However, receiver domains are of interest as prototypes of allosteric transmission within single domains (28). In particular, the role of a preexisting equilibrium in the allosteric mechanism of NtrC has been supported by strong experimental evidence (29–31).

According to our model, central network nodes are found in the signaling regions of the three receiver domains, and they are preferentially connected with the allosteric site. Analysis of the interplay between local and global motions detects strong correlations between the local dynamics around the allosteric site and the large amplitude motions of the protein.

MATERIALS AND METHODS

MD simulations

The GROMACS 4.0 program (32) was used to prepare the initial system coordinates, run the MD simulations, and analyze the resulting trajectories.

The starting coordinates for the MD simulation of unphosphorylated NtrC were extracted from the Protein Data Bank (PDB) NMR structure 1DC7. The charge of the ionizable residues was set to that of their standard protonation state at pH 7. The protein was solvated with a cubic box of simple point charge (SPC) water molecules. The initial minimal distance between the protein and the box boundaries was set to 12 Å, resulting in 9471 water molecules. The system was neutralized by adding 7 Na⁺ counterions.

The simulation of unphosphorylated CheY was started from the PDB structure 3CHY (X-ray at 1.7 Å resolution). For the residues with multiple orientations of the side chains, the A structure was selected. In particular, the orientation most exposed to the solvent was chosen for the Y106 side chain. The crystallographic water molecules and the SO₄²⁻ ions were removed. The ionizable residues were treated as in NtrC. The protein was then solvated with 8807 SPC water molecules and 4 Na⁺ counterions.

The PDB structure 1DCK (X-ray at 2.0 Å resolution) was used for the simulation of unphosphorylated FixJ. The initial coordinates were prepared the same as Roche et al. (33). The crystallographic water and PEG molecules were removed, while the protein-bound Mn²⁺ ion was modeled as Mg²⁺. The ionizable residues were treated as in NtrC. The protein was then solvated with 8646 SPC water molecules and 8 Na⁺ counterions.

The simulations were performed using the GROMOS-96 force field with the 43a1 set of parameters (34). Periodic boundary conditions were imposed. The equations of motion were integrated using the leap-frog method (35) with a 2-fs time step. The Berendsen algorithm (36) was employed for temperature and pressure regulation, with coupling constants of 0.2 and 0.5 ps, respectively. All the protein covalent bonds were frozen with the LINCS (37) method, while SETTLE (38) was used for water molecules. The electrostatic interactions were calculated with the particle mesh Ewald method (39), with a 14-Å cutoff for the direct space sums, a 1.2-Å FFT grid spacing, and a 4-order interpolation polynomial for the reciprocal space sums. For van der Waals interactions, a 14-Å cutoff was used. The neighbor list for noncovalent interactions was updated every 5 steps.

The systems were first minimized with 1000 steps of steepest descent. Harmonic positional restraints with a force constant of 4.8 kcal/mol/Ų were imposed onto the protein heavy atoms and gradually reduced to 1.2 kcal/mol/Ų in 80 ps, while the temperature was increased from 200 to 300 K at constant volume. The system was then simulated at constant temperature (300 K) and pressure (1 bar) for 100 ps. After removal of harmonic restraints, 2 ns of equilibration were run in NPT conditions. NPT production simulations were then run for 80 ns for each system. The RMSD from the starting structure calculated over C^α atoms stabilized around 4 Å after ∼45 ns for NtrC, and around 2 Å after ∼10 ns for both CheY and FixJ.

The solvation in the proximity of the allosteric site (within 4 Å of D54 or T82) at the end of the solvent equilibration phase (0–180 ps) was compared with the X-ray one for CheY and FixJ. The average distance between the crystallographic water molecules and the closest simulated ones was 1 Å in both cases.

Essential dynamics (40) was performed on the 80-ns trajectories of the 3 receiver domains. Principal components (PCs) were generated by diagonalizing the covariance matrix of C^α positions. Porcupine plots (41) were produced for PC1 and PC2 in NtrC. We defined the essential space as the subset of PCs, accounting for at least the 80% of the overall variance. It was composed of the first 9, 25, and 20 PCs for NtrC, CheY and FixJ, respectively. Convergence of the essential space was monitored by calculating the overlap (42) between the essential space PCs extracted from the first t ns and those extracted from the entire simulation. The overlap at t = 50 ns was between 0.8 and 0.91 for the 3 receiver domains, indicating that the sampling in the last 30 ns did not modify significantly the overall essential space.

Representative structures were extracted from the 3 trajectories using the clustering method of Daura et al. (43) with a 1.2-Å cutoff on C^α atoms. The most populated clusters, accounting for 31, 65, and 26% of the overall population, had the first occurrence at 41, 11, and 39 ns, and no new clusters with a population ≥5% appeared after 46, 11, and 51 ns for NtrC, CheY, and FixJ, respectively. This further confirms that no significant sampling of new regions of the conformational space occurred in the last 30 ns of simulation for all of the proteins.

To check for reproducibility of the system dynamics, two 80-ns replicas with a different set of initial velocities were run for each molecule. For NtrC, two more 80-ns replicas were run from 2 refined structures extracted from the RECOORD database (44).

The C^α root mean square fluctuation (RMSF) from the average position was calculated by superimposing each snapshot of the trajectory onto a reference structure to remove the overall rototranslational motions of the whole protein. The fragment RMSF was calculated by defining n − 3 sliding windows or fragments of 4 adjacent C^α atoms. For all of the trajectory snapshots, each fragment was superimposed onto the reference starting structure, independently from the rest of the protein, to remove local rototranslational motions. The fragment RMSF was then calculated as the quadratic mean of the RMSF values of each C^α in the window (21).

Conformational analysis of local structures

The dynamics of local structures in the MD ensembles was analyzed with a fragment-based approach. The structural alphabet (SA) M32K25 (21) was used to describe prototypical backbone conformations. The SA comprises 25 representative fragments of 4 consecutive C^α atoms. The SA was specifically designed to include the most typical local structures, as well as to correctly encode conformational transitions sampled by molecular simulations (21). Each SA fragment represents a conformational state, and it is identified by a letter (A-Y). Hence, any 4-residue-long segment in a protein structure can be labeled with a structural alphabet letter. In a so-called local fit (45) approximation, labeling is performed according to the most similar SA fragment in terms of RMSD. It follows that the conformation of a protein of n residues can be condensed to a structural string of length n − 3. We used this encoding method to translate each MD ensemble in a set of aligned structural strings. A column of this alignment describes all the conformational states sampled by a protein fragment along the simulation trajectory.

Correlation of local motions

In accordance with the proposed discrete state model, the correlation of conformational changes in a pair of protein fragments (i,j) was calculated as a normalized mutual information (MI; I_LLⁿ), Eq. 1:

$$I_{LL}^n\left(C_i;C_j\right)=\frac{I\left(C_i;C_j\right)-\epsilon \left(C_i;C_j\right)}{H\left(C_i,C_j\right)}$$ (1)

where C_i and C_j are the relevant columns in the structural string alignment, I(C_i;C_j) is the MI, H(C_i,C_j) is the joint entropy (46) and ε(C_i;C_j) is the expected finite size error (47). General expressions for the MI and joint entropy (46) of 2 random variables X and Y are presented in Eqs. 2 and 3:

$$I\left(X;Y\right)={\displaystyle \sum _{y\epsilon Y}{\displaystyle \sum _{x\epsilon X}p\left(x,y\right){\log }_2\left(\frac{p\left(x,y\right)}{p_1\left(x\right)p_2\left(y\right)}\right)}}$$ (2)

$$H\left(X,Y\right)={\displaystyle \sum _{y\epsilon Y}{\displaystyle \sum _{x\epsilon X}p\left(x,y\right){\log }_{2}p\left(x,y\right)}}$$ (3)

where x and y are the discrete states of the random variables X and Y, p₁(x) and p₂(y) are the associated marginal probabilities, and p(x,y) is the joint probability distribution.

The calculation of information theoretical quantities on finite size samples is affected by random and systematic errors (47). These are generally negligible in the case of the Shannon entropy (48) but can significantly affect the calculated MI. To improve accuracy, the systematic error on MI can be estimated and removed. In the present work, the expected error ε(X;Y) used in Eq. 1 was calculated as proposed by Roulston et al. (47):

$$\epsilon \left(X;Y\right)=\frac{B{*}_{XY}-B{*}_X-B{*}_Y+1}{2N}$$

where N is the sample size and B_XY^* B_X^*, B_X^* are the number of states with nonzero probabilities for the states of (X,Y), X, and Y, respectively.

Correlation between local and global motions

Global collective motions are usually extracted from the leading principal components (PCs) after essential dynamics (40) analysis (see above, MD Simulation). The structural change associated with a single collective motion was obtained by projection of the MD trajectory onto the relevant PC. The resulting vector contains the displacements along the PC during the simulation. These values were discretized to define a state model for the associated global motion. The correlation between the motion of a protein fragment and a given collective motion was then calculated as the normalized MI (I_LGⁿ) between the array of fragment states and the array of global motion states:

$$I_{LG}^n\left(C_i;sP{C}_j\right)=\frac{I\left(C_i;sP{C}_j\right)}{H\left(C_i,sP{C}_j\right)}$$ (4)

where C_i is the vector of states sampled by fragment fⁱ, sPC_j is the vector of global states associated with the jth PC, I(C_i;sPC_j) is their MI (Eq. 2), and H(C_i,sPC_j) is their joint entropy (Eq. 3).

The vector sPC_j was derived in the following way. The MD trajectory was first projected onto the jth PC eigenvector, producing the associated continuous collective variable (PC_j). The range of PC_j values was divided into l small bins {b¹,…,b^l} with the same size δb. Adjacent bins were then combined to produce m larger intervals, defining the global states pcs_j^k (i.e., pcs_j¹ = {b¹,…,b³}, pcs_j² = {b⁴,…,b⁸}, etc.). These states were used to discretize PC_j into sPC_j. The aggregation of bins into global states was optimized by maximizing the I_LGⁿ value, so that the resulting pcs_j^k provide the maximal estimate of the local-global correlation. A similar approach has been already used to investigate the relations between primary structure, secondary structure and sidechain surface exposure (49). From the algorithmic point of view, the global state definition can be considered as a partition problem, which can be solved by dynamic programming (49, 50). To this end, a modified version of the algorithm described in ref. 50 was implemented in C. For comparison purposes, the PC_j values were rescaled in the interval (0, 1). The optimization was performed separately for each pair (C_i;sPC_j), using a bin size δb of 0.01 and a target number of partitions m of 25, equivalent to the number of structural alphabet states.

Network model of local correlated motions

The interaction among the fragments can be inferred from the correlated state changes and modeled as a network by an undirected weighted graph, where each node represents a protein fragment labeled with its starting residue i and the correlated motion between a node pair (i,j) is recorded as an edge with weight:

$$w_{ij}=1-I_{LL}^n\left(C_i;C_j\right)$$ (5)

where I_LLⁿ(C_i;C_j) is defined in Eq. 1.

To this end, the pairwise matrix of I_LLⁿ values for all fragment pairs in a protein was calculated, and the statistically significant correlations were identified by the false discovery rate (FDR) test (51) with α = 0.001. The p values for the test were independently estimated for each pair (i,j) by generation of a random background distribution of 5000 samples. To preserve the original state probabilities (and the associated Shannon entropy; ref. 48), the randomization was performed by shuffling the letters in C_i. At the end, correlations between fragments closer than 4 Å were also excluded to remove the bias induced by fragment overlaps. The remaining values of I_LLⁿ were divided as contact (<12 Å) and noncontact (>12 Å) according to the distance of the first C^α atoms in the fragment pair. This contact cutoff (12 Å) is the upper limit of the optimal range suggested by a recent study on the reconstruction of contact maps (52). The network was built from the edges in the top 25% by I_LLⁿ value for the contact pairs and the top 5% for the noncontact pairs.

The importance of each node in the network was estimated from the number and type of its connections with other nodes using the eigenvector centrality score (53). This score is designed to emphasize the connections that are made to highly connected nodes. The centrality was obtained from the first eigenvector of the adjacency matrix, where nonzero values were set to I_LLⁿ. Nodes with higher centrality represent fragments that show correlated motions preferentially with other highly correlated fragments. These are likely candidates for contributing to global collective motions and signal transmission.

The transmission pathway of conformational changes from the allosteric site to other regions of the protein was modeled as a set of shortest paths on the network. The analysis of these paths was used to identify the protein regions that are preferentially coupled to the allosteric site. First, the shortest distances d^j_a(i) between each of the 4 fragments f^j_a (with j_a ∈ [a − 3,a]) containing the allosteric site a (D54) and all the protein fragments fⁱ (with i ∈ [1,n − 3]) were calculated with the Dijkstra algorithm (53). For each fragment f^j_a, the distribution of the shortest distances was standardized, producing the z scores:

$${\xi }^{ja}\left(i\right)=\frac{d^{ja}\left(i\right)-{\overline{d}}^{ja}}{{\sigma }^{ja}}$$

A unique z-score profile ζ^a(i) was then built by calculating the minimum value over the 4 fragments f^j_a:

$${\xi }^a\left(i\right)={\min }_{ja\epsilon \left[a-3a\right]}{\xi }^{ja}\left(i\right)$$ (6)

The fragments fⁱ with a negative z score ζ^a(i) can be considered to have a preferential dynamic connection to the allosteric site with respect to the average. We defined as “I_LLⁿ neighbors” of the allosteric site the residues in the lowest quartile (lowest 25% of data) of the z-score distribution (Supplemental Fig. S2D), resulting in a z-score threshold of −0.84, −0.94, and −1.26 for NtrC, CheY, and FixJ, respectively.

Comparison of different models of correlated motions

The network of local correlated motions was compared with other models of residue correlation. This comparison was performed to assess the methodological improvement introduced by using a discrete state representation of local dynamics. To this end a contact map, a correlation matrix of C^α positions (Γ) and a fragment correlation matrix (Γ^f) for a window of 4 adjacent C^α atoms were generated for each protein.

The contact map was calculated on the experimental structure, and residues were defined in contact if ≥2 of their nonhydrogen atoms were within a distance of 5 Å. These are the criteria reported in previous studies on allosteric modulation using contact-based approaches (12, 13). The correlation matrix Γ was calculated as described by Kormos et al. (54). To generate the fragment correlation matrix Γ^f, the RMSD ρ_i(t) of the structure of fragment i at time t from the fragment average structure was calculated after least-squares superposition. The correlation between fragments i and j was then calculated as:

$${\Gamma }_{ij}^f=\frac{\langle \left({\rho }_i\left(t\right)-{\overline{\rho }}_i\right)\left({\rho }_j\left(t\right)-{\overline{\rho }}_j\right)\rangle }{\sqrt{\langle {\left({\rho }_i\left(t\right)-{\overline{\rho }}_i\right)}^2\rangle \langle {\left({\rho }_j\left(t\right)-{\overline{\rho }}_j\right)}^2\rangle }}$$

where angle brackets and bars indicate time averaging. The absolute value of the correlations for both Γ and Γ^f was taken.

The signal-to-noise ratio (SNR) was estimated for the I_LLⁿ, Γ^f, and Γ matrices. The SNR value can be calculated as (55):

$$\text{SNR}=\frac{{\mu }_{\text{signal}}}{{\sigma }_{\text{noise}}}$$

where μ_signal is the average value of the signal and σ_noise is the standard deviation of the noise. To estimate these contributions, the data were divided into 2 groups: values > 1.5 interquartile range over the upper quartile were considered signal and the remainder data noise.

A network representation was built for each matrix. Edges were drawn for nonzero values in the contact matrices and for correlation > 0.25 in the Γ matrices (54). The networks for Γ^f matrices were built with the same contact/noncontact filtering applied to the I_LLⁿ matrix (see preceding section).

For each network, the transmission pathways from the allosteric site to the other regions of the protein were modeled by shortest paths. The connection of each position of the protein to the allosteric site was estimated with the score ζ^a(i) (see preceding section and Eq. 6).

The ability of each correlation model to correctly describe the allosteric communication pathways was assessed by a performance test. The ζ^a(i) index was used as a classifier to predict the residues of the signaling surface according to their connection with the allosteric site. For consistency, the prediction target was defined on the fragment level for both residue-based (contact map, Γ) and fragment-based (Γ^f, I_LLⁿ) networks: a position belonged to the True set if any of the residues of the associated fragment were listed in the signaling surface.

Receiver operating characteristic (ROC) curve (56) and the associated area under the curve (AUC) were calculated for each network. The ROCR library (version 1.0.2) was used for the performance analysis (57).

Software for data analysis and visualization

The R environment (58) was used for statistical data analyses. Network analyses were performed with the igraph library (version 0.5.4 for R; ref. 59). Network figures were generated with Cytoscape 2.8 (60). Protein structure images were generated with VMD 1.8.6 (61) and PyMOL 1.2 (62). The software developed for this study was implemented in C and is available online (http://mathbio.nimr.mrc.ac.uk/wiki/Software).

RESULTS

Intrinsic dynamics of NtrC

The largest structural changes experimentally observed on activation of NtrC involve its signaling region (purple spheres in Fig. 1A), namely the α4 helix and its connecting loops (refs. 25, 29, 63, 64; Supplemental Fig. S1A). In particular, β4-α4 extends, allowing the reorientation and rotation of α4, which also undergoes a register shift by partial winding and unwinding at the C and N termini, respectively. Although there is no general consensus on the type and sequence of events involved in NtrC activation (26), some key features have emerged in the literature, partly by comparison with other receiver domains. Particularly important is the interaction between the conserved T82 residue and the phosphorylated D54, together with the reorientation of the Y101 residue that fills the cavity created by the extension of the β4-α4 loop (23, 25, 26, 65).

Figure 1.

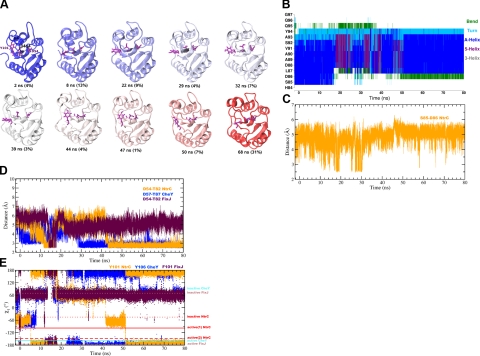
Functional and dynamical properties of NtrC mapped onto the energy-minimized NMR structure (PDB ID: 1DC7). A) Phosphorylation site (D54) and signaling surface residues (63, 78), represented as orange and purple spheres, respectively, centered on C^α atoms. B) Network of I_LLⁿ between fragment conformational transitions. Fragments that are coupled are connected with blue edges drawn between their first C^α atoms. Thick orange edges are used for the strongest 25% connections in the I_LLⁿ distribution. C) Eigenvector centrality score of the I_LLⁿ network. Per-fragment scores are mapped onto the structure by assigning to each residue the maximum value calculated over all the fragments that include it. Tube is colored (blue to red) and sized according to the eigenvector centrality.

Here, we present the results of 80 ns of unbiased MD simulation, starting from the unphosphorylated inactive conformation of NtrC. The activation of NtrC is promoted by phosphorylation of its D54 residue (orange sphere in Fig. 1A). However, experimental and theoretical evidence asserts that the unphosphorylated state exists as an equilibrium between inactive and active-like conformations (29, 66). The possibility of exchange between these forms is, therefore, part of the intrinsic dynamics of unphosphorylated NtrC. Even if the length of our simulations does not allow observation of a complete inactive-to-active transition, the trajectory analysis highlights the occurrence of active-like features (Fig. 2). Interactions between T82 and D54 are detected transiently in the 11- to 17-ns interval, and stably after 43 ns (Fig. 2D). An extension of β4-α4 is observed after 17 ns, together with a reorganization of the secondary structure of α4 that unwinds the N-terminal residues S85 and D86 (Fig. 2A, B). These residues form a transient interaction in the 10- to 31-ns interval (Fig. 2C), which has been suggested to lower the energy barrier of the activation (30, 64). Moreover, the mobile Y101 side chain visits different rotameric states, including the active-like χ₁ trans orientation (Fig. 2E). The reproducibility of these features was checked in the replicas (see Materials and Methods). The unwinding of the N-terminal α4 was observed in all cases, together with the S85–D86 interaction. The D54–T82 interaction was present in 3 of 4 replicas, while the Y101 active rotamer was found in 2. Interestingly, except for one case, these two features were generally observed together in the same simulation, suggesting a correlation between them. Moreover, in the replica where they were both absent, the unwinding of N-term α4 occurred only in the last 16 ns of simulation.

Figure 2.

Structural description of NtrC, CheY, and FixJ during the MD simulations. A) Representative structures of NtrC extracted from the cluster analysis of the MD trajectory (see Materials and Methods). Representatives of the first 10 most populated clusters are shown (cartoon), colored from blue to red according to the time order. Time (ns) of each structure is indicated, together with the relative population of the cluster (in parentheses). D54, T82, and Y101 residues are shown as magenta licorice. Note that the β4-α4 extension enhances the rototranslational movements of α4, which, at the end of the simulation, has its orientation changed with respect to the rest of the protein. In the active state, this reorientation is forbidden by the winding of the C terminus of α4, which is not observed here, most likely because of the limited simulation length. B) Evolution of the secondary structure (DSSP) of helix α4 in NtrC (residues 84–97) during the MD simulation (color code at right). The whole trajectory, including the equilibration (−2.18–0 ns) and production (0–80 ns) phases is shown. C) Distance between the S85 and D86 side chains during the NtrC simulation. Distance is calculated as the minimum over all the possible pairs of nonhydrogen atoms. D) Distance between the D54 and T82 residues (NtrC sequence) during the MD trajectories of NtrC (orange), CheY (blue), and FixJ (purple). Equivalent residues in CheY are D57 and T87. E) χ₁ torsional angle (N-CA-CB-CG) of Y101 (NtrC sequence). The equivalent residues in FixJ and CheY are F101 and Y106, respectively. Values calculated from the experimental coordinates (see Supplemental Fig. S1 for PDB IDs) are reported as horizontal lines for the active (solid line) and inactive (dotted line) structures. For NtrC, active(1) and active(2) values are derived from 1KRX and 1DC8, where 2 orientations of Y101 are found.

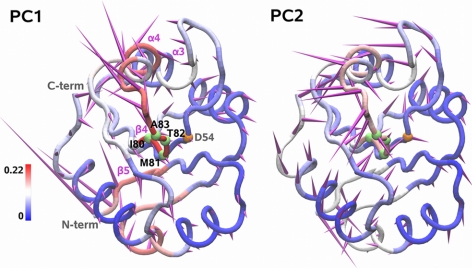
The global motions of the protein are dominated by the changes in β4-α4 and the restructuring of α4, together with the large-amplitude fluctuations of the β3-α3 loop (Supplemental Fig. S2A). Indeed, the first 2 PCs, accounting for the 64% of the overall fluctuation, describe the partial rotation of the α4 C terminus along the helix axis (PC1, PC2), together with the opening (PC2) and upward elongation (PC1) of its N-terminal turn (Fig. 3).

Figure 3.

Porcupine representation of the first and second PC (amounting to 55 and 9% of the overall fluctuation, respectively) extracted from the MD trajectory of NtrC (0–80 ns). Direction and relative amplitude of the motion of each C^α atom along the PC is represented by purple spikes. I_LGⁿ between local states and global PC states is color coded onto the tube representation of the average MD structure. C^α atoms of fragment 80 and of the phosphorylation site (D54) are represented as green and orange spheres, respectively.

Network model of local correlated motions

In the following, we present a model of signal propagation built on the analysis of local motions. These are extracted from an MD simulation by encoding the trajectory into sequences of 4-residue fragment states with the M32K25 structural alphabet (21). The communication between protein fragments is then detected by the correlation of their conformational transitions, measured by normalized MI (I_LLⁿ) between fragment encodings (Eq. 1). The fragment couplings define a network of interactions that is conveniently represented by an undirected weighted graph. The nodes (fragments) are connected by edges when their conformational transitions are correlated, and the edge weight describes the correlation strength (Eq. 5). If the I_LLⁿ is calculated over the whole simulation, the network becomes a comprehensive model of the average correlated dynamics of the protein.

We calculated the I_LLⁿ network of NtrC (Fig. 1B) from its 80-ns MD trajectory. The mapping of the network edges on the protein structure is not uniform, with weak correlations (Fig. 1B, blue) connecting the majority of the nodes and strong couplings (Fig. 1B orange) concentrated in few regions. This is reflected by the node eigenvector centrality (ref. 53; Fig. 1C and Supplemental Fig. S3), which measures the relative importance of each node in the network. High-centrality nodes have a large number of connections, preferentially with other highly connected fragments. The conformational changes of these hub fragments are likely to be involved in collective motions and allosteric signal transmission, since they can efficiently receive and transmit conformational perturbations in different parts of the molecule and possibly amplify them through their connection with other hub fragments. In NtrC, most of the high-centrality nodes are found in regions significantly involved in global collective motions (Figs. 1C and 3). Interestingly, all the top 5% nodes by centrality score (Supplemental Fig. S2C) are found on the signaling surface or close to it, namely f⁸⁰ (denoting the fragment spanning residues 80 to 83); f⁸², f⁸³, and f⁸⁵ in the β4-α4 loop; f⁹² at the C terminus of α4; and f⁶³ on the interface between α3 and α4. Thus, the functional regions can be singled out from those involved in global motions by using the topological properties of the overall network. A more detailed view can be obtained by the analysis of time-dependent couplings within selected subnetworks, as described in the following section.

Allosteric transmission across the network

We used the I_LLⁿ network to study the allosteric signal transmission in NtrC, assuming that allosteric motions may arise from the combination of local fragment couplings. To this end, we modeled the propagation of conformational changes as a path of connected edges on the network.

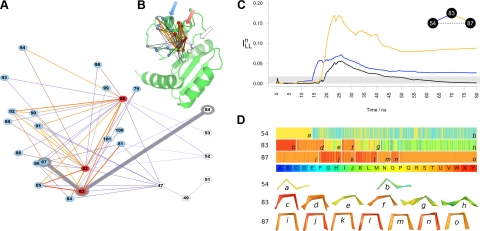
A first insight into the NtrC signal transmission was obtained from the analysis of the network connections between the allosteric site and the signaling surface. We calculated a subnetwork including only the shortest paths from the 4 allosteric fragments, containing residue D54 (f⁵¹ to f⁵⁴), to any fragment on the signaling surface (Fig. 4A). The allosteric fragments show relatively weak connections to the 3 main hubs (f⁸⁰, f⁸², f⁸³), which have stronger couplings to other fragments on the signaling surface. The subnetwork describes a 3-layer topology on the protein structure (Fig. 4B) where the hub nodes (Fig. 4B, red) in the middle layer have the role of transmitting and amplifying the signal from D54 (Fig. 4B, white) to the signaling surface (Fig. 4B, blue). These hub fragments are located on the C terminus of β4 and on the β4-α4 loop. The regions spanned by these fragments are rich in residues known to affect the allosteric mechanism. In particular, mutating T82 (f⁸⁰ and f⁸²) to residues other than serine generally abolishes the activity of receiver domains (67, 68). Indeed, the OH group in this position is considered to be involved in the signal propagation after the phosphorylation event (refs. 24, 26; see above, Intrinsic Dynamics of NtrC). Moreover, mutations of S85 (f⁸² and f⁸³) impairing its hydrogen bond donor capacity have been recently found to decrease the rate of interconversion between the NtrC inactive and active form (30). Finally, in D86N (f⁸³) mutants, the preequilibrium has been observed to be shifted toward the active conformation (30). These data support the validity of the pathways identified from the I_LLⁿ subnetwork connecting the allosteric site to the signaling surface. Indeed, they show that modifications of critical nodes in these pathways can affect the kinetics and thermodynamics of the allosteric mechanism.

Figure 4.

Analysis of the communication pathways between the allosteric site (D54) and the signaling surface of NtrC. A, B) Subnetwork of shortest paths is reported (A) along with the mapping of its fragments (spheres) on the NtrC structure (B). Fragments containing residues of the signaling surface are represented in red and blue. Hubs of the subnetwork are shown in red. Edges are colored from blue (low I_LLⁿ) to red (high I_LLⁿ); their thickness is proportional to I_LLⁿ value. Shortest path from f⁵⁴ to f⁸⁷ is highlighted in gray. Arrows (B) show the 3-layer topology of signal transmission. C) Plot of the incremental values of I_LLⁿ for the pairwise connection among f⁵³, f⁸³, and f⁸⁷. Gray bar indicates the cutoff value for edge connection (see Materials and Methods). D) Sequence of states along the trajectory for fragments f⁵⁴, f⁸³, and f⁸⁷. Legend provides color code of the structural alphabet. Same time scale as in C is used. Vertical white lines highlight transitions to ensembles of states with different composition. Each ensemble is indicated with an italic lowercase letter. Corresponding fragment structures (selected each 100 ps) are shown at bottom.

A deeper insight into the signal transmission was provided by the analysis of fragment couplings along the simulation time. We measured the incremental value of I_LLⁿ for pairs of fragments in the subnetwork to detect how the conformational transitions are propagated by consecutive fragment interactions. An example of this mechanism is provided by the signal propagation from D54 to L87 (Fig. 4C). After 14 ns, a coupling between f⁵⁴ and f⁸³ arises. This triggers a sudden increase in the correlation between f⁸³ and f⁸⁷, which generates a transient communication between D54 and L87 in the time interval 19–42 ns. The coupling f⁵⁴-f⁸³ is driven by a conformational transition of f⁵⁴ from state Q (Fig. 4D, a) to an ensemble, including state Q and E (Fig. 4D, b). This relatively modest change precedes a set of more dramatic reshapes in f⁸³, which exhibit two significant transitions (Fig. 4D, d to e and f to g) from an helical structure (mainly state U) to more extended geometries (Q and M). These transitions are responsible for the coupling with f⁸⁷ that mirrors them with more subtle changes (Fig. 4D, i to j and k to l).

The transitions undergone by f⁸³ are due to the rearrangement of the β4-α4 loop observed after 17 ns, while the f⁸⁷ transitions are related to the transient reorganization of the central part of α4 in the 17- to 50-ns time interval (Fig. 2B). The analysis of the I_LLⁿ time dependence allows detection of a direct correlation between these events, which dominate the global collective motions of the protein (Fig. 3), and the local transitions occurring at the allosteric site (f⁵⁴). Thus, the combination of path detection and time-dependent analysis provides a clear picture of signal propagation and highlights mechanisms not easily detectable with other methods.

Local and global conformational changes

We further investigated the relationship between the local conformational transitions described in the previous sections and the global collective motions of the protein. To this end, for each fragment, we calculated the normalized MI (I_LGⁿ; see Eq. 4) between the sequence of its structural states extracted with the structural alphabet (local states) and a discrete model of the most informative collective variables (PC states) derived from essential dynamics (40).

The resulting I_LGⁿ profiles per fragment are not related in a simple way to the atom displacements along the PCs (Fig. 3). Indeed, in the global motions, the conformational change of a fragment is mixed with its rigid rototranslation. Hence, regions with comparable global displacements (spike length) show different degrees of correlation with local changes (color), according to the different proportion of flexible and rigid motions contributing to the global fluctuation. This parallels the differences observed in the overall C^α and fragment RMSF (Supplemental Fig. S2A, B). When only local motions are taken into account, a general increase of the relative flexibility of β strands with respect to α helices is found (orange line in Supplemental Fig. S2B).

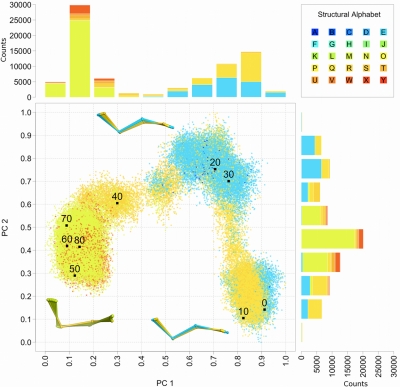
For the first two PCs (Fig. 3 and Supplemental Fig. S4), the highest I_LGⁿ values are observed on the signaling surface (β4, β4-α4 loop, and α4 termini) and, for PC1, in the α1-β2 loop. This suggests that the local state transitions found in these regions are significantly coupled to the global changes with largest amplitude. This is particularly evident for fragment f⁸⁰, which has the maximum value of I_LGⁿ. Its transition from an extended conformation (state P and partially E) to an ensemble of states dominated by E corresponds to the largest variation of the global coordinate PC2 occurring in the 10- to 20-ns interval (Fig. 5). The subsequent motion along PC1 (30–50 ns) is coupled with the fragment transition to the more angled state N. Thus, in this case different types of global motion correspond to different local transitions.

Figure 5.

Coupling of local and global motions in NtrC exemplified by f⁸⁰. MD trajectory is projected onto the space spanned by the first two PCs (Fig. 3). Each point is colored according to the encoding of f⁸⁰ (legend provides color code of the structural alphabet). Black points highlight projections selected every 10 ns. Barplots showing the letter counts in each 0.1 PC bin are colored according to the fragment letter. Three fragment ensembles are shown (ball and stick). These are representative of the 3 most populated regions of the projection, corresponding to consecutive segments of the simulation (0–18, 18–38, and 38–80 ns).

In the context of the NtrC activation process, the initial P-to-E transition of f⁸⁰ is particularly important, since it occurs in the time interval of the active-state-like interaction between the f⁸⁰ residue T82 and D54 (11–17 ns in Fig. 2D). The difference between the P and E structures is small, consistent with the relatively small f⁸⁰ global displacements along PC2 (Fig. 3). However, the strong coupling between this transition and the collective variable suggests a central role for fragment f⁸⁰ and provides a likely link between the T82–D54 interaction and the global motion along PC2.

Similarity among related allosteric proteins

To validate the results on NtrC and identify similarities with the behavior of related systems, we performed MD simulations of the homologous FixJ and CheY receiver domains. The conformational changes experimentally observed in their activation involve smaller portions of the molecule and are of lower amplitude than in NtrC (Supplemental Fig. S1). However, the signaling surface has a similar location, and the largest changes are still found in the β4-α4 loop and in the α4 helix, together with the β5-α5 loop for CheY (Supplemental Fig S1B, C; refs. 23, 24). As for NtrC, the analysis of the 80-ns MD trajectories of CheY and FixJ highlights the presence of features typical of the active state, in particular, the T82–D54 interaction (Fig. 2D) and the rotamer transitions of residue Y101 (Fig. 2E). These events were observed together also in one more replica simulation for CheY (see Materials and Methods). FixJ seemed to have a less pronounced tendency (further reduced in the replicas) to sample active site features than NtrC and CheY.

To compare the I_LLⁿ networks generated from the MD simulations, we analyzed the nodes in the allosteric site's neighborhood. In particular, we measured the length of the shortest paths connecting this site to all other fragments in the network and then defined as I_LLⁿ neighbors the nodes in the lowest quartile of the path length distribution (see Materials and Methods). These can be considered as preferentially connected to the allosteric site and, hence, more likely to be involved in the propagation of the signal.

The locations of the I_LLⁿ neighbors of the allosteric site are similar in the 3 proteins (Fig. 6). In particular, a common core can be identified, composed by β4, β4-α4, and α4 residues, together with the β3-α3 region. A significant fraction of the signaling surface is included (Fig. 6D), especially for NtrC and CheY. This suggests that the network of fragment couplings in the inactive form is preorganized to transmit the signal to the functional region. Moreover, two of the key residues in the protein activation, T82 (β4) and Y101 (β5), are preferentially connected to the allosteric site in both NtrC and CheY, as is T82 in FixJ. Fragments from β5 seem to be particularly important in the CheY network, where they are also high-centrality nodes (Supplemental Fig. S2C). The decreased functional activity of CheY mutants in the positions Y101 (Y106 in CheY numbering) and K104 (K109) has been previously related with an impairing of the transition to the active conformation (68, 69). While the role of the β3-α3 loop in the receiver domain activation is still unclear, it has been suggested that its flexibility can be modulated by phosphorylation and/or the presence of a metal ion at the allosteric site (29, 63). Changes in its conformation have been also related to a possible self-inhibition mechanism (70).

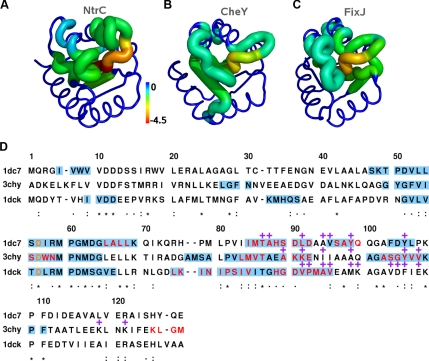
Figure 6.

Allosteric site neighbors in the I_LLⁿ networks of NtrC, CheY, and FixJ. A–C) Shortest path lengths (z scores) from the allosteric site (Eq. 6) are mapped onto experimental structures of NtrC (A, PDB ID: 1DC7), CheY (B, PDB ID: 3CHY), and FixJ (C, PDB ID: 1DCK). A sausage representation is used; tube size correlates to z-score absolute value. D) Multiple sequence alignment of NtrC (1dc7), CheY (3chy), and FixJ (1dck). The alignment was performed with T-COFFEE 7.7 (79) using default parameters. I_LLⁿ neighbors of the allosteric site (shown in orange) are highlighted in light blue; residues in fragments with the highest centrality scores (top 5% values) are in red. Purple plus symbols indicate residues of the signaling surfaces (see Supplemental Fig. S1 for mapping of the signaling surface onto the inactive structure of the 3 proteins). Degree of residue conservation is shown using asterisks (full conservation), colons (conserved substitutions), and periods (semiconserved substitutions). Sequence identity of 30% is shared between NtrC and CheY, 32% between NtrC and FixJ, and 23% between CheY and FixJ.

Finally we note that in all the proteins, the I_LLⁿ neighborhood of the allosteric site includes nearly all the fragments with a high centrality score (red residues in Fig. 6D and top 5% in Supplemental Fig. S2C). Their residues are in the same region of the receiver domain alignment. This supports the importance of the network centrality in detecting the functionally relevant regions (see above, Network Model of Local Correlated Motions). RMSF profiles seem less informative. Indeed, the top 5% residues by C^α or fragment RMSF show both weaker similarity across the proteins and a smaller overlap with the signaling regions (Supplemental Figs. S2A, B, and S5). Moreover, when considering the top-ranking C^α RMSF values, the T82 and Y101 residues are missed in all 3 cases (Supplemental Fig. S5A).

The present results suggest that the analysis of the I_LLⁿ pathways is useful to find candidate functional regions in allosteric proteins.

Comparison of different models of correlated motions

The I_LLⁿ network describes the protein dynamics with a discrete state model of local correlations. To quantify the methodological improvement provided by this approach, we compared it with a static model based on the residue contact map of the experimental structure, a model of global dynamics based on the correlation matrix of C^α positions (Γ), and a continuum model of local dynamics based on the fragment correlation matrix (Γ^f). The results are reported in Table 1.

Table 1.

Performance data from the signalling surface prediction test for the I_LLⁿ, Γ^f, Γ, and contact map matrices of NtrC, CheY, and FixJ

Protein	Matrix	SNR	Hits	Sensitivity	Precision	AUC
NtrC	ILLn	9.89	21	95.5%	28.4%	0.69
	Γf	7.86	18	81.8%	23.9%	0.57
	Γ	4.93	17	77.3%	25.0%	0.61
	Contact map	–	13	59.1%	13.0%	0.40
CheY	ILLn	11.19	21	72.4%	25.9%	0.56
	Γf	9.33	22	75.9%	24.4%	0.59
	Γ	6.96	22	75.9%	27.2%	0.62
	Contact map	–	21	72.4%	21.6%	0.50
FixJ	ILLn	9.88	19	79.2%	24.1%	0.50
	Γf	8.61	18	75.0%	16.9%	0.38
	Γ	6.09	13	54.2%	18.8%	0.48
	Contact map	–	16	66.7%	16.3%	0.46

SNR, signal-to-noise ratio. Hits, number of signaling surface fragments with ζ_a (standardized shortest path length from the allosteric site) <0. Sensitivity, percentage of hits in the total number of signaling surface fragments (22 for NtrC, 29 for CheY, and 24 for FixJ). Precision, percentage of hits in the total number of fragments with ζ_a < 0. AUC, area under the receiver operating characteristic curve. Highest values of each column are in italic.

For these matrices, the strongest correlations are separated from the bulk of the value distribution. To estimate this separation, a conventional measure of the SNR was calculated (55). In networks built on matrices with higher SNR, the dominant communication pathways are expected to be more easily singled out from the background connectivity. The SNR values are always higher in Γ^f than in Γ matrices, suggesting that part of the noise is cancelled by removal of the rigid rototranslational motions. The introduction of a discrete model further reduces the noise, so that the I_LLⁿ matrices have the highest SNR values.

In the case of allosteric modulation, the network organization should highlight preferential connections between the allosteric and the functional site. To assess the ability of the different matrices to extract the biological function, we built the associated network representation and we calculated the standardized shortest path lengths, ζ^a(i), from the allosteric site (see Materials and Methods).

A direct measure of performance is provided by the number (percentage) of fragments of the signaling region connected to the allosteric site by pathways shorter than a cutoff value (ζ^a(i)<ζ_cutoff^a). In Table 1, we reported these values as hits (sensitivity), calculated considering all the preferentially connected fragments (ζ_cutoff^a=0). For NtrC and FixJ, the I_LLⁿ network is the best performing, followed by the Γ^f model. The sensitivity of I_LLⁿ is particularly high for NtrC, where 21 of 22 fragments are recovered (95.5%). The conservative choice of ζ_cutoff^a produces for all the models a relatively low precision, i.e., the percentage of hits in all the fragments with ζ^a(i) < ζ_cutoff^a. However, the I_LLⁿ network has still the highest value for both proteins. In CheY, the sensitivity has similar values for all the models, with the Γ and Γ^f models showing slightly higher scores than I_LLⁿ and the contact map. The Γ model has the highest precision.

CheY is an interesting case in which the models based on local and global dynamics give complementary information. Indeed, the I_LLⁿ network captures the preferential connections between the allosteric site and the key residues T87 (β4), Y106 (β5), and K109 (β5-α5) better than the Γ network (Figure S6). Mutation of these residues has been shown to affect the allosteric mechanism in CheY (see preceding section). However, I_LLⁿ is less accurate in ranking the connections with residues of the signaling surface belonging to the α4 helix (magenta points in Supplemental Fig. S6A), which are instead very close to the allosteric site in the ranking from the Γ network (Supplemental Fig. S6B). These differences can be related to the fact that in CheY the α4 helix undergoes an almost pure rototranslational motion (Supplemental Fig. S2A), with minimal local changes (Supplemental Fig. S2B). On the other hand, the relevance of β5 movements, while properly recognized when considering local motions (Supplemental Fig. S2B), can be missed if only the global dynamics is analyzed (Supplemental Fig. S2A).

A stricter performance test can be obtained by assessing the correct identification of the signaling surface fragments at different values of ζ_cutoff^a. This is usually done with the ROC curve analysis, where all of the possible ζ_cutoff^a values are systematically tested. A concise measure to analyze the ROC curve results is given by the AUC, which is, in turn, the probability of reporting a correct classification (56). It should be noted that the aim of this test is only to compare the different models, which were not optimized to be used as a predictive tool. This would require an extensive parametrization and the inclusion of other descriptive indices (e.g., solvent accessibility, residue conservation, etc.). However, the overall performance reported in Table 1 is higher than expected, and in most cases better than the random model (AUC>0.5). The I_LLⁿ network is still the best performing for NtrC and FixJ, while the Γ model has the highest AUC for CheY. In all cases, the Γ model is better than Γ^f, in contrast with the SNR trend. This can be explained by a balance of precision and sensitivity.

In summary, the different tests indicate that the local models (I_LLⁿ and Γ^f) extract biologically relevant information otherwise undetected by other approaches. The discrete state representation (I_LLⁿ) has the best agreement with the experimental data in 2 of 3 cases and complements the global model (Γ) in the third one, recovering specific functional information.

DISCUSSION

In this work, we have presented a method for the detection of signal transmission in allosteric proteins and its application to the NtrC receiver domain and its homologues CheY and FixJ. Functionally implicated residues and motions were extracted in 3 steps from equilibrium simulations of the unphosphorylated state.

First, the structure ensembles are mapped onto a canonical set of representative fragments, i.e., a set of discrete states in conformational space. These were previously derived from the most populated conformations in a representative subset of the PDB database and can be considered as “low-energy” conformations (21). Unlike other approaches based on residue fluctuations in global motions (10, 11, 15, 18–20), here, the contribution of rigid fragment rototranslations is removed. Therefore, potentially relevant changes in local conformations are easily detected, even if subtle. The importance of local motions in allosteric mechanisms was demonstrated in a recent survey (71), where the majority of the residues involved in conformational changes showed significant variations in the backbone dihedral angles. In these cases, the functional interpretation is not affected by a potential loss of information from the removal of fragment rigid motions. In other cases, in which functional motions arise also from coupling between rigid rototranslations, our approach should be combined with other methods to detect collective motions. An example of a complementary approach was presented here in the comparison of the structural alphabet encoding with the global motions extracted by essential dynamics analysis (40). A unified approach with a balanced inclusion of local and global dynamics is a desirable feature of future methods.

Second, local motions are modeled as transitions between the fragment states. The introduction of discrete states removes harmonic high-frequency fluctuations, which may be considered background noise in terms of functional motion. Transitions between fragment states are able to correctly describe the extent of protein motions (21). Although rototranslation and high-frequency fluctuations have been removed at this stage, the detection of functional motions requires additional information about residue correlations.

Third, the communication between different parts of the molecule, an essential prerequisite for allosteric conformational change, is modeled by the coupling (correlation) of fragment transitions. Correlated transitions can be resolved spatially and temporally. The (time-averaged) spatial couplings over a whole trajectory are analyzed with a network model of fragment correlations to identify the most important fragments (nodes). Measures of node centrality have been previously used in the analysis of contact networks to rank the importance of residues in allosteric proteins (12, 13). The time-resolved analysis of fragment couplings between the allosteric and active sites reveals the sequence of local events along the main communication pathways. This analysis sketches out the internal workings of allosteric function and how they are encoded in the protein structure.

The results are consistent with the emerging picture of allosteric regulation (2, 5): a preorganized network of fragment couplings and connections between the allosteric and functional sites exists already in the inactive state, and fragments with high network centrality (hubs) are mostly found in functionally relevant regions. In addition, the use of discrete states from a structural alphabet allows the detection of subtle relevant motions. These can be important for the effective identification of hidden similarities, as shown for the dynamics of NtrC homologues. The methodological improvement introduced by our approach was quantified by comparison with other models of residue correlation, including contact maps, as well as global and local dynamical correlation matrices. We estimated the importance of the different elements constituting our method: the inclusion of protein dynamics is essential; the local description allows the extraction of otherwise undetectable motions, and the discrete state model significantly improves the identification of relevant correlations. Our method has the best agreement with the experimental data in 2 of 3 cases and complements the other approaches in the third one, recovering specific functional information.

We made the assumption that a signal at the allosteric site is most likely propagated through the couplings already available in the inactive state (19). Therefore, the transmission pathways are considered as an intrinsic property of the initial unperturbed state (5). This assumption is supported by the experimentally found preequilibrium between the inactive and active conformation of the unphosphorylated NtrC (29). The intrinsic dynamics of the unphosphorylated proteins was sampled by equilibrium MD simulations. The fragment state transitions proved to be particularly suitable to capture the subtle changes around the allosteric site. Thus, it was possible to detect their correlation with the motions at the functional region, even within the sampling limits of the simulations performed here. Our model could be applied to trajectories obtained from other techniques, such as enhanced sampling methods (72, 73), to explore a larger portion of the conformational space around the starting structure.

The good agreement between the experimental data and our results suggests that the approach presented could be used for functional prediction in the absence of prior information about the allosteric mechanism. In particular, the location of high-centrality fragments could indicate the regions undergoing functionally relevant conformational changes and the statistical analysis of the shortest paths could identify potential allosteric sites.

The combined information on functional dynamics and transmission pathways has been recently exploited to design allosteric inhibitors (74, 75). A detailed knowledge of the local conformational states and transitions could guide the selection or design of allosteric effectors, or alternatively guide the design of protein mutants with altered dynamical and allosteric properties.

The method presented here was primarily designed to analyze allosteric communication. However, the network of fragment correlations can help in investigating other types of distal effects in protein dynamics. An example is the emergence of drug resistance due to compensatory mutations, which are not in the proximity of the active site and do not physically interact with the ligand. Computational studies have shown that these mutations can dramatically affect inhibitor binding by modifying the functional dynamics of the protein (76, 77). The analysis of fragment correlations can shed light on these modifications and suggest the local dynamical requirements to design novel drugs.