Anti-social punishment can prevent the co-evolution of punishment and cooperation

Abstract

The evolution of cooperation is one of the great puzzles in evolutionary biology. Punishment has been suggested as one solution to this problem. Here punishment is generally defined as incurring a cost to inflict harm on a wrong-doer. In the presence of punishers, cooperators can gain higher payoffs than non-cooperators. Therefore cooperation may evolve as long as punishment is prevalent in the population. Theoretical models have revealed that spatial structure can favor the co-evolution of punishment and cooperation, by allowing individuals to only play and compete with those in their immediate neighborhood. However, those models have usually assumed that punishment is always targeted at non-cooperators. In light of recent empirical evidence of punishment targeted at cooperators, we relax this assumption and study the effect of so-called ‘anti-social punishment’. We find that evolution can favor anti-social punishment, and that when anti-social punishment is possible costly punishment no longer promotes cooperation. As there is no reason to assume that cooperators cannot be the target of punishment during evolution, our results demonstrate serious restrictions on the ability of costly punishment to allow the evolution of cooperation in spatially structured populations. Our results also help to make sense of the empirical observation that defectors will sometimes pay to punish cooperators.

1 Introduction

Explaining the evolution of cooperation is an issue of central importance to evolutionary biology as well as social sciences. Why does the competitive process of natural selection often lead to altruistic cooperation, in which individuals pay a cost to give a benefit to others? To answer this question, numerous mechanisms for the evolution of cooperation have been proposed (Nowak, 2006; Lehmann & Keller 2006; West et al. 2007), including kin selection (Hamilton, 1964; Frank 1998), direct reciprocity (Trivers 1971) and indirect reciprocity (Alexander 1987; Nowak & Sigmund 2005).

In direct reciprocity, my actions towards you depend on what you have done to me in the past. Axelrod (1984) found that the Tit-for-Tat (TFT) strategy was a winning strategy in his computer tournament. A TFT player cooperates in the first round of the repeated interaction. After the first round, a TFT player takes whatever action his opponent took in the previous round. For example, an ALLD player, who always defects in a repeated interaction, receives cooperation from a TFT player in the first round. However, the ALLD player is ‘punished’ by TFT with mutual defection in subsequent rounds. Therefore, cheating does not pay if the repeated interaction lasts long enough, and the TFT strategy can be evolutionarily stable against the ALLD strategy (Axelrod & Hamilton 1981). Numerous behavioral experiments have demonstrated that direct reciprocity can lead to stable cooperation in repeated games (Wedekind & Milinski 1996; Dal Bo 2005; Dreber et al. 2008; Dal Bo & Frechette 2009; Rand et al. 2009a; Fudenberg et al. 2010).

Another possible way to enforce cooperation is to rely on more explicit punishment (Cluttonbrock & Parker, 1995a,b, Sigmund 2007, Rand et al. 2009b). While TFT ‘punishes’ non-cooperative partners by responding to selfishness with reciprocal selfishness, explicit punishment strategies choose to inflict harm on non-cooperative partners, often at a cost to the punisher. For example, in paper wasps, subordinates that cheat by signaling an inflated status of dominance receive more aggression from other wasps (Tibbetts & Dale 2004). Similarly, monkeys that do not share food are often punished (Hauser 1992). Punishment is also known as ‘policing’ in studies of social insects, where queens or workers sometimes attack other nestmate workers that attempt to produce offspring by themselves (Ratnieks et al. 2006, Wenseleers & Ratnieks 2006). In behavioral experiments with humans, punishment has been shown to stabilize cooperation in multi-player social dilemmas (Yamagishi 1986; Ostrom et al. 1992; Fehr & Gächter 2000, 2002), leading to higher payoffs after an initial learning period (Gächter et al. 2008, Rand et al. 2009a). As a proximate explanation of such pro-social punishment, the desire for egalitarian outcomes (Fehr & Schmidt 1999; Johnson et al. 2009) and/or anger directed at norm violators (Fehr & Gächter 2002) have been recently suggested.

Under the threat of punishment, a cooperative strategy can perform better than a non-cooperative strategy, because the latter suffers the costs of being punished. Therefore cooperation may evolve in populations where punishment is prevalent. When punishment is also costly to punisher, however, we face another puzzle: how does punishment evolve? Cooperators who do not participate in punishment avoid the cost of punishment. Thus, they out-compete those who cooperate and punish. This puzzle is well-known as the ‘second-order free rider problem’ (Oliver 1980; Yamagishi 1986; Boyd & Richerson 1992; Panchanathan & Boyd, 2004).

Such ‘costly punishment’ (Fehr & Gächter 2000, 2002) has been shown to co-evolve with cooperation when, for example, cooperation and punishment are such strongly linked traits that cooperators almost always participate in punishment (Axelrod 1986; Boyd & Richerson 1992; Nakamaru & Iwasa 2005; Lehmann et al. 2007). If cooperators punish defectors, the advantage of selfish individuals is greatly reduced, and cooperation can coevolve with punishment through group selection (Boyd et al. 2003). Cooperation and punishment can co-evolve when those who punish defectors are compensated by being more likely to receive cooperation from others (Gardner & West 2004). Recent models of cultural evolution suggest that weak conformist transmission can stabilize punishment and hence promotes the evolution of cooperation (Henrich & Boyd 2001; Henrich 2004). The option to abstain from the game also favors the co-evolution of cooperation and punishment (Fowler 2005; Hauert et al. 2007; Traulsen et al. 2009). In repeated two-player games, however, it has been shown that costly punishment does not promote cooperation, as traditional tit-for-tat style direct reciprocity is sufficient (Rand et al. 2009b). In contrast to such repeated games, a credible threat of costly punishment could be effective in one-shot games, for example in the situation where resources are so scarce that a long-term reciprocal interaction, and therefore use of the TFT strategy, is unlikely.

Nakamaru & Iwasa (2005, 2006) have shown that costly punishment promotes cooperation in a two-stage game played in a spatially structured population. Nakamaru & Iwasa (2005) studied two strategies: an altruist-punisher, who cooperates with others and punishes non-cooperators, and a selfish-non-punisher, who neither cooperates with others nor punishes non-cooperators. In a subsequent paper (Nakamaru & Iwasa 2006), they included two more strategies in their analysis: an altruist-non-punisher, who cooperates but does not punish, and a selfish-punisher, who does not cooperate but punishes non-cooperators (see also Sigmund et al. 2001).

These theoretical models have studied the effect of allowing players to punish non-cooperators. In addition to such pro-social punishment, however, numerous behavioral experiments have found that a significant fraction of non-cooperators will pay to punish cooperators (Shinada et al. 2004; Denant-Boemont et al. 2007; Dreber et al. 2008; Herrmann et al. 2008; Nikiforakis 2008; Gächter & Herrmann 2009; Wu et al. 2009). For example, a series of cross cultural public goods game experiments found a great deal of cross-cultural variation in the extent to which cooperators versus non-cooperators were targeted with punishment (Herrmann et al. 2008). In the most extreme cases, participants in countries such as Greece and Oman were as likely to punish those who contributed more than them as those who contributed less. The high level of punishment directed at cooperators in this and other experiments indicates that this behavior is not merely the result of errors or lack of comprehension, but is instead a surprising aspect of human behavior requiring explanation. Throughout this paper, we refer to this punishment targeted at cooperators as ‘anti-social punishment’, in order to distinguish it from the (usual) punishment that is targeted at non-cooperators. Anti-social punishment runs counter to the common assumptions about why people choose to punish (Johnson et al. 2009; Fehr & Gächter 2000, 2002). These strategies that pay a cost for cooperators to incur a cost are often excluded from evolutionary models of cooperation and punishment. In addition to the empirical evidence for anti-social punishment, it seems most appropriate for evolutionary models to allow the full set of possible strategies (of a given complexity) and to ask what strategies emerge via natural selection, rather than restricting the strategy set to only include particularly attractive strategies.

We ask how including anti-social punishment affects the evolution of cooperation. Is this ‘dark side’ of punishment in behavioral experiments just irrational, erroneous behavior, or can it in fact be favored by natural selection? Does punishment still promote cooperation when antisocial punishment is possible? In this paper we adopt the framework used by Nakamaru & Iwasa (2005, 2006) and study the consequences of including anti-social punishment.

2 Strategies and payoffs

We consider a two-stage game with cooperation followed by punishment (as in Boyd & Richerson 1992; Sigmund et al. 2001; Nakamaru & Iwasa 2005, 2006; Boyd et al. 2003; Brandt Hauert Sigmund 2003, 2006; Fowler 2005; Hauert et al. 2007; Traulsen et al. 2009). In the first stage, each player has two choices, defection (D) or cooperation (C). Defection means doing nothing, such that all players receive zero payoffs. Cooperation means paying a cost c for another to get a benefit b (b > c > 0). In the second stage, each player can choose to punish each other player or not, conditioned on the other person’s action in the first stage. By punishing, a player pays a cost α for the other person to incur a loss β(α, β > 0). Withholding punishment results in both players receiving zero payoffs in the second stage. We do not consider mixed strategies in the following analysis, and restrict our attention to pure reactive strategies.

Since the action in the second stage is conditioned on the other players’ action in the first stage, there are four possible strategies in the second stage. A non-punisher (N) punishes no one. A pro-social punisher (P) punishes defectors only. An anti-social punisher (A) punishes cooperators only. A spiteful punisher (S) punishes both cooperators and defectors. A combination of the action in the first stage (D,C) and the strategy in the second stage (N, P, A, S) defines one’s strategy in the game. Thus we have eight possible strategies: DN, DP, DA, DS, CN, CP, CA and CS. For example, a CP-strategist cooperates in the first stage and harms defectors in the second stage (therefore deemed as a ‘strong reciprocator’ (Fehr & Fischbacher 2003; Bowles & Gintis 2004)). Table 1 summarizes these eight strategies.

Table 1.

The eight strategies considered in the present paper.

strategy	Cooperate?	Harm cooperators?	Harm defectors?
DN	no	no	no
DP	no	no	yes
DA	no	yes	no
DS	no	yes	yes
CN	yes	no	no
CP	yes	no	yes
CA	yes	yes	no
CS	yes	yes	yes

We can classify these eight strategies into two categories: strategies which do not punish other players using the same strategy (hereafter ‘self-consistent’), and strategies which do punish other players using the same strategy (hereafter ‘self in-consistent’). The strategies DN, DA, CN and CP are self-consistent. Conversely, the strategies DP, DS, CA and CS are self-inconsistent.

The 8 × 8 payoff matrix of the pairwise game is given in Eq.(1). As can be seen, the strategies DN and DA are Nash equilibria for all payoff values, and CP is a Nash equilibrium when β > c.

$$\begin{array}{cc}\hfill & \begin{array}{cccccccc}\hfill \mathrm{DN}\hfill & \hfill \mathrm{DP}\hfill & \hfill \mathrm{DA}\hfill & \hfill \mathrm{DS}\hfill & \hfill \mathrm{CN}\hfill & \hfill \mathrm{CP}\hfill & \hfill \mathrm{CA}\hfill & \hfill \mathrm{CS}\hfill \end{array}\hfill \\ \begin{array}{c}\hfill \mathrm{DN}\hfill \\ \hfill \mathrm{DP}\hfill \\ \hfill \mathrm{DA}\hfill \\ \hfill \mathrm{DS}\hfill \\ \hfill \mathrm{CN}\hfill \\ \hfill \mathrm{CP}\hfill \\ \hfill \mathrm{CA}\hfill \\ \hfill \mathrm{CS}\hfill \end{array}\hfill & \left(\begin{array}{cccccccc}0& -\beta & 0& -\beta & b& b-\beta & b& b-\beta \\ -\alpha & -\alpha -\beta & -\alpha & -\alpha -\beta & b& b-\beta & b& b-\beta \\ 0& -\beta & 0& -\beta & b-\alpha & b-\alpha -\beta & b-\alpha & b-\alpha -\beta \\ -\alpha & -\alpha -\beta & -\alpha & -\alpha -\beta & b-\alpha & b-\alpha -\beta & b-\alpha & b-\alpha -\beta \\ -c& -c& -c-\beta & -c-\beta & -c+b& -c+b& -c+b-\beta & -c+b-\beta \\ -c-\alpha & -c-\alpha & -c-\alpha -\beta & -c-\alpha -\beta & -c+b& -c+b& -c+b-\beta & -c+b-\beta \\ -c& -c& -c-\beta & -c-\beta & -c+b-\alpha & -c+b-\alpha & -c+b-\alpha -\beta & -c+b-\alpha -\beta \\ -c-\alpha & -c-\alpha & -c-\alpha -\beta & -c-\alpha -\beta & -c+b-\alpha & -c+b-\alpha & -c+b-\alpha -\beta & -c+b-\alpha -\beta \end{array}\right)\hfill \end{array}$$ (1)

For reference, consider the sub-model where punishment cannot be targeted at cooperators. In this case, the strategies A and S are not allowed in the second stage, so the payoff matrix (1) is reduced to

$$\begin{array}{cc}\hfill & \begin{array}{cccc}\hfill \mathrm{DN}\hfill & \hfill \mathrm{DP}\hfill & \hfill \mathrm{CN}\hfill & \hfill \mathrm{CP}\hfill \end{array}\hfill \\ \begin{array}{c}\hfill \mathrm{DN}\hfill \\ \hfill \mathrm{DP}\hfill \\ \hfill \mathrm{CN}\hfill \\ \hfill \mathrm{CP}\hfill \end{array}\hfill & \left(\begin{array}{cccc}0& -\beta & b& b-\beta \\ -\alpha & -\alpha -\beta & b& b-\beta \\ -c& -c& -c+b& -c+b\\ -c-\alpha & -c-\alpha & -c+b& -c+b\end{array}\right)\hfill \end{array}$$ (2)

In the following analysis, we will concentrate on the ”score-dependent viability model” (Nakamaru et al. 1997; Irwin & Taylor 2001; Nakamaru & Iwasa 2005, 2006; Sekiguchi & Nakamaru 2009) (hereafter ”viability model”). We chose to study the viability model as it has previously been shown to be very effective in promoting the co-evolution of punishment and cooperation in structured populations (Nakamaru & Iwasa 2005, 2006), and therefore presents the greatest challenge to anti-social punishment. We will compare evolutionary dynamics in unstructured populations and lattice structured populations. We will investigate the effect on the evolution of cooperation of introducing anti-social punishment into the game. We do so by expanding the strategy set to include all combinatorially possible pure strategies (shown in Eq. (1)), as opposed to making any structural changes to the game (for example creating the opportunity to retaliate as in Janssen & Bushman 2008) or increasing the complexity of the possible strategies.

3 z-mixed population model

First we study viability game dynamics in populations with no spatial structure. This viability updating rule can be interpreted as either genetic evolution or social learning. In the context of genetic evolution, an organism’s probability of death is affected by its payoff, while the probability of reproduction is random. In the context of social learning, a person’s probability of abandoning her current strategy is determined by her payoff, after which she randomly picks a new strategy from the population to imitate (a type of conformism).

Groups of size z + 1 are randomly selected from the population, and each player interacts with her z other group members to obtain a game payoff, f. In each generation a random player is given a chance to update her strategy (i.e. has some chance of death). With probability

$$d(f)=\gamma exp[-\theta f],$$ (3)

she abandons her current strategy (i.e. dies) and randomly adopts the strategy of one of the z players she just interacted with (i.e. one of the z players is randomly chosen to reproduce). This model was called ”complete mixing model” by Nakamaru et al. (1997) and Nakamaru & Iwasa (2005, 2006). However, as we will see below, this model is different from a usual ”well-mixed population” model often assumed in evolutionary game theory. To avoid potential confusion, we call the above model ”z-mixed population model”, where z represents the number of players one interacts with. Unlike the traditional well-mixed population model, agents in the z-mixed population model interact with, and compete with, only a subset of the population. The z → ∞ limit recovers the traditional well-mixed population dynamics.

Here γ,θ > 0 are constants which influence the intensity of selection. The intuitive consequence of Eq.(3) is that players with lower payoffs are more likely to change their strategies.

3.1 When anti-social punishment is not allowed

First we consider the four-strategy game, Eq.(2). It has previously been shown that in a z-mixed population, the strategies CP and CN are selected when β is large, regardless of initial frequencies of strategies (Nakamaru & Iwasa 2006). This result is surprising given that DN is always a Nash equilibrium strategy in the game, Eq.(2). The key lies in the assumptions of the viability model. In the viability model, (i) one interacts with only a subset of the population (finite z), and (ii) those whom one mimics are the same as those whom one interacts with. Such local population regulation significantly affects stability conditions of strategies, and is a common feature of many models of evolution in structured populations (Nowak & May 1992; Wilson et al. 1992; Taylor 1992; Killingback & Doebeli 1996; Szabo & Toke 1998; Hauert & Doebeli 2004; Ohtsuki et al. 2006; Santos et al. 2006). In particular, a Nash equilibrium strategy may no longer be a stable strategy in the viability model, and non-Nash equilibrium strategies may be stable.

To see how viability updating changes the stability condition, imagine the game between two arbitrary strategies, X and Y:

$$\begin{array}{c}\begin{array}{cc}\hfill \mathrm{X}\hfill & \hfill \mathrm{Y}\hfill \end{array}\hfill \\ \begin{array}{c}\hfill \mathrm{X}\hfill \\ \hfill \mathrm{Y}\hfill \end{array}\left(\begin{array}{cc}\hfill a_1\hfill & \hfill a_2\hfill \\ \hfill a_3\hfill & \hfill a_4\hfill \end{array}\right)\hfill \end{array}$$ (4)

The condition for strategy X to be a strict Nash equilibrium is a₁ > a₃, namely, X performs better than Y against X. However, in the viability model it can be shown that strategy X is stable against invasion by strategy Y when

$$(z-1)a_1+a_2>{za}_3$$ (5)

Here z is the number of others that one interacts with. See Appendix A for its derivation. Interestingly, a₂, which is the payoff of X playing against Y, appears in the stability condition. The intuitive explanation for this is that a Y-player affects the payoffs of those X players she then mimics. As z increases, the effect of a₂ diminishes, but never disappears as long as z is finite.

Using the stability condition, Eq.(5), we obtain for general z that CP is robust against invasion by DP and DN when

$$\beta >c+\frac{b+\alpha }{z}.$$ (6)

Note that CP is always neutral to CN, because there are no defectors to punish in the population of only CP and CN.

We can further extend previous analysis by introducing errors. We assume that there is a (sufficiently) small chance ε of error in execution of intended actions (Molander 1985; May 1987; Nowak & Sigmund 1989, 1992, 1993; Fudenberg & Maskin 1990; Fudenberg & Tirole 1991; Lindgren 1991; Lindgren & Nordahl 1994; Boerlijst et al. 1997; Wahl & Nowak 1999; Brandt & Sigmund 2006). More precisely, one fails to perform an intended action in the first stage and/or the second stage independently with probability ε. In the first stage, with probability ε one mistakenly chooses D though her intended action is C, and vice versa. In the second stage, with probability ε one fails to harm others though she intended to, and vice versa.

Such errors resolve the neutrality between CN and CP. In the presence of small errors, the payoff matrix between CN and CP becomes

$$\begin{array}{c}\begin{array}{cc}\hfill \mathrm{CN}\hfill & \hfill \mathrm{CP}\hfill \end{array}\hfill \\ \begin{array}{c}\hfill \mathrm{CN}\hfill \\ \hfill \mathrm{CP}\hfill \end{array}\left(\begin{array}{cc}b-c+(-b+c-\alpha -\beta )\epsilon & b-c+(-b+c-\alpha -2\beta )\epsilon +2\beta {\epsilon }^2\\ b-c+(-b+c-2\alpha -\beta )\epsilon +2\alpha {\epsilon }^2& b-c+(-b+c-2\alpha -2\beta )\epsilon +(2\alpha +2\beta ){\epsilon }^2\end{array}\right)\hfill \end{array}$$ (7)

Since ε is sufficiently small, it has an effect only when payoffs in Eq.(2) are equal (i.e. when two strategies are neutral). Neglecting ε² terms and using Eq.(5), we obtain that CP is stable against CN when

$$\beta >z\alpha .$$ (8)

Combining (6) and (8) leads to the ESS condition of strategy CP, as

$$\beta >max\{c+\frac{b+\alpha }{z},z\alpha \}.$$ (9)

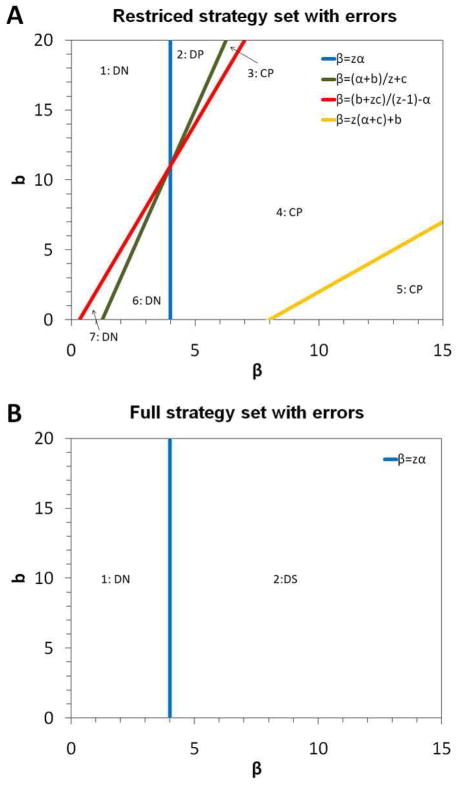
Similarly, the ESS condition for the other three strategies can be derived. Figure 1A shows the parameter regions where each strategy is an ESS. The results are equivalent to those found in the absence of error (Nakamaru & Iwasa 2006), except that CN is never an ESS. In particular, we see that the cooperative strategy CP is the only ESS when β is sufficiently large.

Figure 1.

Evolutionary stability under the z-mixed population model. The strategies that are ESS are indicated in each region of the (b, β) parameter space. We set c = 1 and α = 1. We consider small errors. (A) When anti-social punishment in not allowed, CP is ESS in regions 3, 4 and 5. (B) When anti-social punishment in allowed, CP is never ESS. Either DN or DS is the unique ESS.

3.2 When anti-social punishment is allowed

Here we allow the option of anti-social punishment, making the punishment strategies A (anti-social punisher) and S (spiteful strategy) possible in the second stage of the game. The game is thus described by the full 8 × 8 matrix given by Eq.(1).

In the absence of errors (ε = 0), we find three pairs of strategies that are neutral in addition to CN-CP. DN and DA are neutral because there are no cooperators to punish. DP and DS are neutral because they always punish themselves and each other. CA and CS are neutral because they also always punish themselves and each other. With the introduction of errors, the payoff matrices for these pairs change to

$$\begin{array}{c}\begin{array}{cc}\hfill \mathrm{DN}\hfill & \hfill \mathrm{DA}\hfill \end{array}\hfill \\ \begin{array}{c}\hfill \mathrm{DN}\hfill \\ \hfill \mathrm{DA}\hfill \end{array}\left(\begin{array}{cc}(b-c-\alpha -\beta )\epsilon & (b-c-\alpha -2\beta )\epsilon +2\beta {\epsilon }^2\\ (b-c-2\alpha -\beta )\epsilon +2\alpha {\epsilon }^2& (b-c-2\alpha -2\beta )\epsilon +(2\alpha +2\beta ){\epsilon }^2\end{array}\right),\hfill \end{array}$$ (10)

$$\begin{array}{c}\begin{array}{cc}\hfill \mathrm{CA}\hfill & \hfill \mathrm{CS}\hfill \end{array}\hfill \\ \begin{array}{c}\hfill \mathrm{CA}\hfill \\ \hfill \mathrm{CS}\hfill \end{array}\left(\begin{array}{cc}-\alpha -\beta +(b-c+2\alpha +2\beta )\epsilon +(-2\alpha -2\beta ){\epsilon }^2& -\alpha -\beta +(b-c+2\alpha +\beta )\epsilon -2\alpha {\epsilon }^2\\ -\alpha -\beta +(b-c+\alpha +2\beta )\epsilon -2\beta {\epsilon }^2& -\alpha -\beta +(b-c+\alpha +\beta )\epsilon \end{array}\right)\hfill \end{array}$$ (11)

$$\begin{array}{c}\begin{array}{cc}\hfill \mathrm{CA}\hfill & \hfill \mathrm{CS}\hfill \end{array}\hfill \\ \begin{array}{c}\hfill \mathrm{CA}\hfill \\ \hfill \mathrm{CS}\hfill \end{array}\left(\begin{array}{cc}b-c-\alpha -\beta +(-b+c+2\alpha +2\beta )\epsilon +(-2\alpha -2\beta ){\epsilon }^2& b-c-\alpha -\beta +(-b+c+2\alpha +\beta )\epsilon -2\alpha {\epsilon }^2\\ b-c-\alpha -\beta +(-b+c+\alpha +2\beta )\epsilon -2\beta {\epsilon }^2& b-c-\alpha -\beta +(-b+c+\alpha +\beta )\epsilon \end{array}\right)\hfill \end{array}$$ (12)

Taking into account Eqs.(7, 10, 11, 12), the evolutionary stability of each strategy in the game Eq.(1) under the z-mixed population model is derived.

1. DN is ESS if β < zα, and is invaded by DP, DA, and DS if β > zα.

2. DP is invaded by DN and DA if β < zα, and invaded by DS if β > zα. Thus DP is never ESS.

3. DA is invaded by DN if β < zα, and invaded by DP and DS if β > zα. Thus DA is never ESS.

4. DS is invaded by DN, DP and DA if β < zα, and is ESS if β > zα.

5. CN is always invaded by DN and DP. Thus CN is never ESS.

6. CP is invaded by CN if β < zα, and invaded by CA and CS if β > zα. Thus CP is never ESS.

7. CA is always invaded by DN and DP. Thus CA is never ESS.

8. CS is always invaded by DA and DS. Thus CS is never ESS.

Figure 1B summarizes the result. If β < zα, DN is the unique ESS. If β > zα, DS is the unique ESS. It is noteworthy that CP is never an ESS under the full strategy set. Anti-social behavior and spite destroy cooperation. As we saw above, if β > zα, CP is not invaded by CN, DN, or DP and therefore it can be ESS in the absence of anti-social punishment. When anti-social punishment is available, however, CA and CS can invade CP if β > zα. The reason for this invasion is simple. Imagine a CA (or CS)-player in a population of CP. The CA player punishes z CP players, so he pays the total cost of zα, whereas each CP player who meets the CA player incurs the loss β. If this loss is greater than the total cost the CA pays, CP is more likely to change to CA than vice versa, and therefore CA propagates in the population of CP. CA players maximize their relative fitness in a population of CP players by avoiding the punishment they would receive for defecting and by harming others to enhance the probability that they are mimicked. However, invasion by CA or CS players does not suggest maintenance of cooperation by anti-social punishment, as they are easily invaded by various defecting strategies. Thus evolution always leads to DS if β < zα.

To summarize, when punishment is sufficiently effective (i.e. β > zα), it is adaptive to punish others and increase one’s relative payoff no matter what strategy the others adopt in the first stage (see Appendix B). Hence the optimal target of punishment should be not only defectors but also cooperators, and the condition β > zα is simply the condition under which unconditional harming is adaptive in the z-mixed population model. When it was only possible to punish defectors, this power of punishment allowed CP to invade DN. Once anti-social punishment is available, however, cooperators no longer have an advantage, and spiteful defection, DS, fares best. The β > zα condition reveals that the success of spiteful punishers relies on agents interacting and competing with a limited number of others. In the z → ∞ limit of a well-mixed infinite population, DN is the unique ESS for all payoff values.

4 Lattice model

We now consider a structured population in which players are arranged on a square lattice. Each player interacts with the four players in her von Neumann neighborhood and obtains a game-payoff. Thus this lattice model is the structured counterpart to the z-mixed population model with z = 4, and is equivalent to a series of overlapping linear public goods games (e.g. Santos et al. 2008), where each player’s cooperative actions affect her four neighbors. Other features of the model are the same as the z-mixed population model as described in the previous section. Agent based simulations are used to explore the evolutionary dynamics in this structured population.

4.1 When anti-social punishment is not allowed

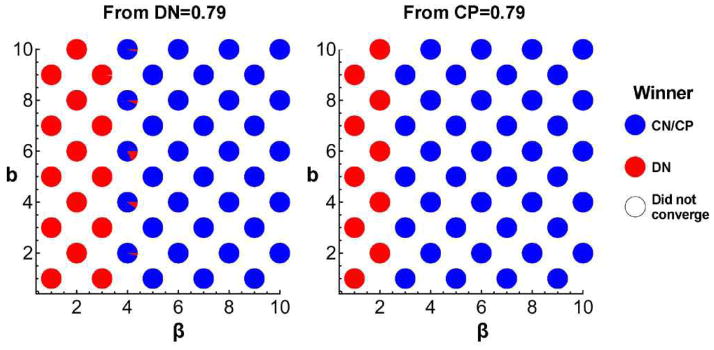
Examining the restricted four-strategy game on a lattice, we find similar results to the z-mixed population model. As Figure 2 shows, the defecting strategy, DN, is favored when β is small, and the cooperative strategies, CN and CP, are favored when β is large. Thus our inclusion of ε errors does not change results on the lattice compared to what has been found previously (Nakamaru & Iwasa 2006). In the absence of anti-social punishment, there is a large parameter region in which cooperative strategies dominate on the lattice, regardless of initial conditions.

Figure 2.

Evolutionary outcomes of the restricted strategy set without anti-social punishment on a regular square lattice. When β is small, DN wins regardless of initial frequencies of strategies; when β is large, CP wins regardless of initial frequencies of strategies. Starting from the specified initial frequency, 50 agent based simulations are run and the winning strategy is recorded. The blue portion of each circle indicates the fraction of runs where CP wins or CP and CN coexist; the red portion, the fraction of runs where DN wins; the white portion, the fraction of runs in which there was no convergence after 125,000,000 generations. We explore the (b, β) parameter space, setting c = 1 and α = 1. We consider small errors, ε = 0.01, and a 50 × 50 lattice for a total population size N = 2500. We use viability updating with parameter values γ = 0.1 and θ = 0.1. (A) Initial frequency of strategies: DN=0.79, DP=0.07, CN=0.07, CP=0.07. (B) Initial frequency of strategies: DN=0.07, DP=0.07, CN=0.07, CP=0.79.

4.2 When anti-social punishment is allowed

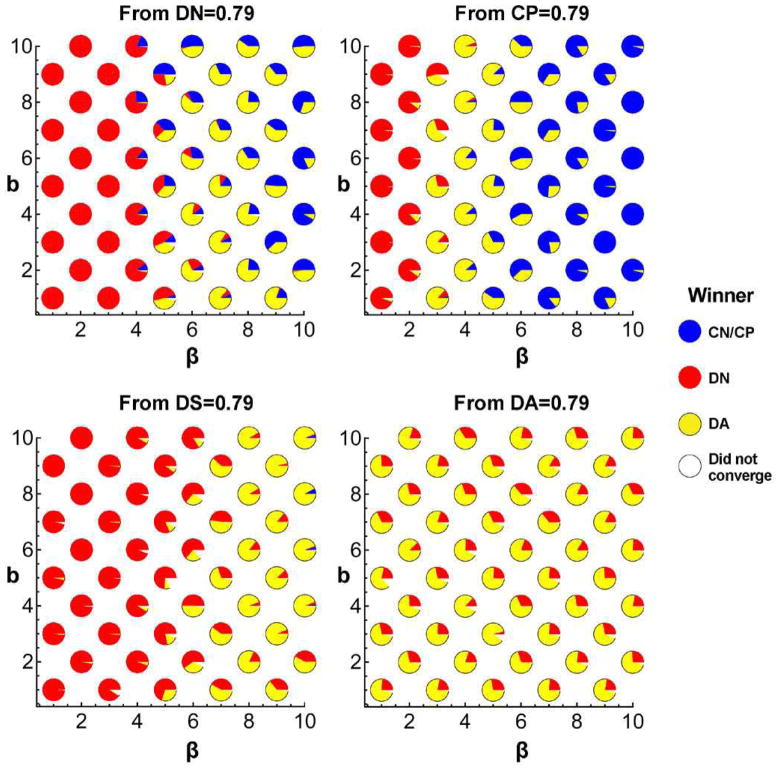
We now explore the dynamics on the lattice when strategies which punish cooperators are included, Eq.(1). Simulation results are shown in Figure 3. Results are dependent on initial strategy frequencies. When DN or CP is most abundant initially, we see a similar pattern: the majority of the time DN wins when β is small, DA wins when β is intermediate, and CP wins when β is large. When DS is most abundant initially, DN again wins when β is small, DA wins when β is large, and further simulations find that CP wins when β > 10. When DA is most abundant initially, however, the outcome is very different. Regardless of b or β, DA wins in the majority of cases. DN wins occasionally. Cooperation never invades a resident population of anti-social defectors.

Figure 3.

Evolutionary outcomes of the full strategy set on a regular lattice. Cooperation cannot invade a population of antisocial defectors, DA. Starting from the specified initial condition, 50 agent based simulations are run and the winning strategy recorded. The blue portion of each circle indicates the fraction of runs where CP wins or CP, CN, CA and/or CS coexist; the red portion, the fraction of runs where DN wins; the yellow portion the fraction of runs where DA wins; the white portion, the fraction of runs in which there was no convergence after 125,000,000 generations. DP and DS never win. We consider small errors, ε = 0.01, and a 50 × 50 lattice for a total population size N = 2500. We use viability updating with parameter values γ = 0.1 and θ = 0.1. We explore the (b, β) parameter space, setting c = 1 and α = 1. Additional simulations find qualitatively similar results for α = 0.5 and α = 1.5. Initial population density (A) DN=0.79, all others 0.03 (B) CP=0.79, all others 0.03 (C) DS=0.79, all others 0.03 (D) DA=0.79, all others 0.03.

These results are qualitatively different from what we saw in the z-mixed population. First, DS never wins on the lattice, whereas DS was the sole ESS in the z-mixed population model when β was large. A possible explanation for this difference involves spatial correlations. Since offspring disperse locally on the lattice, DS players are very likely to interact with other DS players (i.e. their ”relatives”). Because DS is self-inconsistent in the sense that one DS player harms other DS-players, the target of the DS players’ spiteful punishment tends to be other DS players. Therefore DS, as well as the other self-inconsistent strategies DP, CA and CS, cannot propagate on the lattice (see also Appendix B). A pairwise invasion analysis based on computer simulations (Table 2) shows that across β values, each self-inconsistent strategy is invaded by the first-round equivalent self-consistent strategies (i.e. DP and DS invaded by DN and DA, CA and CS invaded by CN and CP).

Table 2.

Pairwise invasion analysis in a lattice structured population. In each cell we compare two strategies, resident and mutant. The resident’s initial frequency is 0.97, and the invader’s initial frequency is 0.03. The fraction of simulations in which the invader takes over the whole population is shown. We set b = 5, c = 1 and α = 1, and conduct 50 simulations, each lasting 125,000,000 generations. We consider small errors, ε = 0.01, and a 50 × 50 lattice for a total population size N = 2500. We use viability updating with parameter values γ = 0.1 and θ = 0.1.

β = 1		Resident
		DN	DP	DA	DS	CN	CP	CA	CS
Invader	DN		1	0.24	1	1	1	1	1
	DP	0		0	0.35	0	0	1	1
	DA	0	1		1	1	1	1	1
	DS	0	0	0		0	0	1	1
	CN	0	0	0	0		0	1	1
	CP	0	0	0	0	0		1	1
	CA	0	0	0	0	0	0		0
	CS	0	0	0	0	0	0	0

β = 5		Resident
		DN	DP	DA	DS	CN	CP	CA	CS
Invader	DN		1	0.20	1	1	0	1	1
	DP	0		0	0.05	0	0	0	0
	DA	0	1		1	1	0.17	1	1
	DS	0	0	0		0	0	1	1
	CN	0	1	0	0		0	1	1
	CP	0.95	1	0	1	0		1	1
	CA	0	0	0	0	0	0		0.30
	CS	0	0	0	0	0	0	0

β = 10		Resident
		DN	DP	DA	DS	CN	CP	CA	CS
Invader	DN		1	0.21	1	1	0	1	1
	DP	0		0	0	0	0	0	0
	DA	0	1		1	1	0	1	1
	DS	0	0.03	0		0	0	1	0
	CN	0	1	0	0		0	1	1
	CP	1	1	0	1	0		1	1
	CA	0	0	0	0	0	0		0.08
	CS	0	1	0	0	0	0	0

The second major difference we observe is that on the lattice, anti-social defectors (DA) win in a large region of the parameter space, whereas DA is never an ESS in the z-mixed population. This is because DP and DS, which are potential invaders of DA in the z-mixed population model, are self-inconsistent and thus do not perform well on the lattice as discussed above. In contrast, DA is self-consistent and harms only cooperators, which protects DA from invasion by CP. The pairwise invasion analysis in Table 2 suggests that strategies other than DN cannot invade DA on the lattice. DN can occasionally invade DA, but only due to a small advantage from the ε tiny error probability (see Eq.(10)). Hence DN and DA are almost neutral. In the z-mixed population model DA can invade DN when β is large. In contrast DA never invades DN on the lattice. Again this is because in the presence of errors, DA engages in self-inconsistent punishment of erroneous cooperation.

Overall, the lattice simulation results using the full strategy set are quite different from what occurs in the restricted strategy set where anti-social punishment is not possible. When anti-social punishment is excluded, there is a wide parameter region where cooperation wins regardless of initial conditions (Figure 2). However, the introduction of anti-social punishment eliminates this region, hinders cooperation, and anti-social defectors prevail (Figure 3).

5 Discussion

Here we have analyzed the effect of anti-social punishment on the evolution of cooperation. We have studied score-dependent viability dynamics (Nakamaru & Iwasa 2005, 2006). We include all eight possible pure reactive strategies as well as tiny behavioral errors, and compare the z-mixed population model and the spatially structured lattice model.

Results in the z-mixed population model clearly demonstrate that the inclusion of anti-social punishment destroys the evolutionary success of cooperation. We found that cooperation is never ESS under the full strategy set. Spiteful defectors who always harm others (DS) are the only ESS if the punishment technology is sufficiently efficient (sufficiently large effect to cost ratio). Our lattice model analysis confirms the difficulties anti-social punishment poses for cooperation. On the lattice, cooperators can never invade a population of anti-social defectors who punish cooperators (DA). This anti-social defection strategy is highly successful across the wide parameter ranges we tested. These results show that anti-social punishment can be favored by natural selection, and highlight the dangers associated with allowing the option for costly punishment. Not only is it possible for cooperators to punish defectors, but the opposite can also occur. Together with the previous results of Nakamaru & Iwasa (2006), our results suggest that punishment only successfully promotes cooperation in structured populations if it is only possible to harm defectors but not cooperators. Our results suggest that there is an evolutionary imperative for defectors to seek out ways to punish cooperators, and thus models which exclude this phenomenon may give skewed results favoring evolution of cooperation.

At first it seems counter-intuitive that successful self-interested players would pay a cost to harm others in the second round of a two-shot game. The explanation lies in the nature of evolutionary competition in settings where you learn from the same players you interact with. Here it is not one’s absolute payoff that matters, but rather how much you have relative to others (Page et al. 2000). Although punishers (P), anti-social punishers (A), and spiteful punishers (S) in our model seem to perform spite at a level of absolute payoffs because both punisher and punishee incur immediate costs, the actual effect of these behaviors is to enhance the punisher’s probability of replacing the victims of punishment: inflicting harm which reduces the others’ payoff by more than it reduces yours improves your relative payoff. Therefore, spiteful strategies which harm others can be at an advantage in a spatially structured setting, as long as they preferentially harm agents with strategies different than their own (Hamilton 1970; Wilson 1975; Nakamaru et al. 1997; Foster et al. 2000; Nakamaru & Iwasa 2005; Lehmann et al. 2006, El Mouden & Gardner 2008). In this sense, punishment in our model does not represent genuine spite but can be classified as a selfish behavior (West & Gardner 2010). Conversely, evolution has been shown to disfavor costly punishment in repeated games played in well mixed populations (Rand et al. 2009b). The effect of costly punishment in repeated games with local interaction and competition, however, is an interesting question for future study, as is the role of anti-social punishment in games with continuous (as opposed to binary) traits (Nakamaru & Dieckmann, 2009). Furthermore, while our analysis has demonstrated that the population structure considered in this paper can favor anti-social punishment, a more explicitly structured population, such as a population subdivided into many small groups, may not, as the balance between within-group selection and between-group selection could change (Wilson 1975, Okasha 2006, Traulsen & Nowak 2006, Wilson & Wilson 2007). Similarly, incorporating explicit inter-group conflicts into our model could increase the importance of group-level selection, and therefore could change the relative importance of anti-social and pro-social punishment (Bowles 2009; Lehmann & Feldman 2008). These issues deserves further study.

We have framed the cooperative dilemma faced by players in our model as a series of pairwise interactions. However, because players are unconditional cooperators or defectors, the game we study is exactly equivalent to a z + 1-player public goods game followed by punishment (Boyd & Richerson 1992; Fehr & Gachter 2000, 2002; Sigmund et al. 2001; Nakamaru & Iwasa 2005, 2006; Boyd et al. 2003; Brandt Hauert Sigmund 2003, 2006; Fowler 2005; Hauert et al. 2007; Traulsen et al. 2009). In the z-well mixed population, a cooperator pays a cost to benefit each other member of her group, which is drawn randomly each round; this corresponds to a public goods game played under the ‘stranger matching’ protocol (Fehr & Gachter 2000, 2002). In the lattice population structure, a cooperator pays a cost to benefit her z = 4 neighbors; this corresponds to a series of overlapping public goods games with fixed group compositions. Thus the results we observe regarding anti-social punishment are not unique to pairwise interactions, but rather apply to collective action problems confronted by groups of individuals.

In our modeling framework, agents update their strategies through an evolutionary process. As opposed to prospectively calculating the strategy that would maximize one’s payoff, our agents are motivated to change strategy when their payoffs are low, and then imitate the behavior of others they observe. Thus strategies with higher payoffs tend to become more common in the population. If instead our agents picked strategies based on rational self-interest using Eq.(1) with ε errors, they would never cooperate either with or without anti-social punishment as DN is the unique Nash equilibrium. Thus in both extremes of strict imitation and strict rationality, cooperation is not stable using the full strategy set. Intermediate cases in which agents use some combination of imitation and prospective reasoning are an interesting subject for further study.

The analysis presented here raises important questions about the ability of costly punishment to promote the evolution of cooperation. Spiteful behavior including anti-social punishment is well documented aspects of human behavior (Saijo & Nakamura 1995; Denant-Boemont et al. 2007; Dreber et al. 2008; Herrmann et al. 2008; Nikiforakis 2008; Gächter & Herrmann 2009; Wu et al. 2009), and should not be ignored. Here we show that in populations with local interaction and competition, anti-social and spiteful behavior can be favored by evolution as it actually enhances actor’s relative reproductive success, and costly punishment no longer promotes the evolution of cooperation when anti-social punishment is allowed. Nonetheless, we observe cooperation throughout the natural world and human society. While many other models for the co-evolution of punishment and cooperation have been proposed, our results suggest that the effects of anti-social punishment need to be explored in these other contexts as well. If including anti-social punishment in other models gives results similar to what we have shown here, then mechanisms other than punishment could be primarily responsible for the evolution of cooperation, and punishment must have evolved secondarily for other reasons such as asserting dominance (Clutton-Brock & Parker 1995a).

Appendix A Derivation of eqation (5) in the main text

Consider the game, (4). We study the stability condition of strategy X against Y. For that purpose let ε (≪1) be the frequency of strategy Y in the population. The rest 1 − ε is the frequency of X. A Y-strategist changes to strategy X at rate

$$\epsilon \sum _{x=0}^z\left(\begin{array}{c}z\\ x\end{array}\right){(1-\epsilon )}^x{\epsilon }^{z-x}d({xa}_3+(z-x)a_4)\frac{x}{z}=\epsilon d(z{a}_3)+O({\epsilon }^2),$$ (A1)

where d(·) is given by Eq.(3). In the sum above, x represents the number of X-players with whom a Y-player interacts. With probability $\left(\begin{array}{c}z\\ x\end{array}\right){(1-\epsilon )}^x{\epsilon }^{z-x}$ the Y-player interacts with x many X-players and gains the payoff, xa₃ + (z − x)a₄. When he dies, he changes to strategy X with probability x/z. On the other hand, an X-strategist changes to strategy Y at rate

$$(1-\epsilon )\sum _{y=0}^z\left(\begin{array}{c}z\\ y\end{array}\right){(1-\epsilon )}^{z-y}{\epsilon }^{y}d[(z-y)a_1+y{a}_2]\frac{y}{z}=\epsilon d((z-1)a_1+a_2)+O({\epsilon }^2).$$ (A2)

There y represents the number of Y-players with whom an X-player interacts. With probability $\left(\begin{array}{c}z\\ y\end{array}\right){(1-\epsilon )}^{z-y}{\epsilon }^y$ the X-player interacts with y many Y-players and gains the payoff, (z − y)a₁ + ya₂. When he dies, he changes to strategy Y with probability y/z.

Comparing Eqs.(A1, A2), we obtain the stability condition of X against Y as d(za₃) > d((z − 1)a₁ + a₂), or equivalently,

$$(z-1)a_1+a_2>z{a}_3.$$ (A3)

Appendix B Conditions for DS strategy to win

An intuitive explanation of why the DS strategy wins in the z-mixed population model when β is relatively large is twofold: (i) there are no assortment effects in the z-mixed population model, such that one does not meets others with the same strategy more often than expected by global frequencies, and (ii) one learns from the same individuals one interacts with in the z-mixed population model, such that one’s payoff relative to one’s interaction partners matters.

To see that the property (i) is a necessary condition for DS to win, we compare the z-mixed population model (Section 3.1.2) with the lattice model (Section 3.2.2). Property (i) is present in the former but is absent in the latter, while property (ii) is present in both models. As we saw in the main text, DS wins in the z-mixed model but not in the lattice model, suggesting that property (i) is crucial for the propagation of DS strategy.

To see that (ii) is also a necessary condition for DS to win, we compare the z-mixed population model to a variant with ”global replacement”. In this variant, an updating player mimics the strategy of a player randomly chosen from the entire population, as opposed to a randomly selected interaction partner. Property (ii) is present in the z-mixed population model but is absent in the global replacement variant, whereas property (i) is present in both models. To compare the two models, we use agent based simulations with z = 4, population size N = 2500, b = 5, c = 1, α = 1, β = 10 and viability updating parameter values γ = 1 and θ = 1. We examine the outcome of 25 simulations lasting 125,000,000 generations, starting from an initial frequency of DS=0.79, all other strategies 0.03. Our calculations in the main text showed that DS is ESS in the z-mixed model when β > zα. Consistent with this, we find that DS wins in the majority of cases in the z-mixed population agent based simulations. Conversely, we find that DN wins 80% of the time using the global replacement model. This result suggests that property (ii) is also crucial for the propagation of the DS strategy.