Longer simulations sample larger subspaces of conformations while maintaining robust mechanisms of motion

Abstract

Recent studies suggest that protein motions observed in molecular simulations are related to biochemical activities, although the computed time scales do not necessarily match those of the experimentally observed processes. The molecular origin of this conflicting observation is explored here for a test protein, cyanovirin-N (CV-N), through a series of molecular dynamics simulations that span a time range of three orders of magnitude up to 0.4 microseconds. Strikingly, increasing the simulation time leads to an approximately uniform amplification of the motional sizes, while maintaining the same conformational mechanics. Residue fluctuations exhibit amplitudes of 1–2 Å in the nanosecond simulations, while their average sizes increase by a factor of 4–5 in the microsecond regime. The mean-square displacements averaged over all residues (y) exhibit a power law dependence of the form y ∝ x^0.26 on the simulation time (x). Essential dynamics analysis of the trajectories, on the other hand, demonstrates that CV-N has robust preferences to undergo specific types of motions that already can be detected at short simulation times, provided that multiple runs are performed and carefully analyzed.

INTRODUCTION

Native proteins are not static entities under physiological conditions. On the contrary, they undergo a broad range of motions around their native state structures, ranging from local conformational changes such as peptide bond re-orientations or amino acid side chain isomerization to global rearrangements involving entire domains or subunits. The type and size of these motions are governed by the free energy landscape near native state conditions.^1–3 In terms of functional relevance, many structural rearrangements, especially those collectively involving large substructures, are necessary for proteins to carry out their chemical and biological activities.^1–5 Therefore, in order to understand protein function, it is necessary to also examine the dynamics of proteins and not only their atomic structures. In particular, the lowest frequency internal motions, or global motions, need to be evaluated since they usually relate to the molecules’ biological functions.

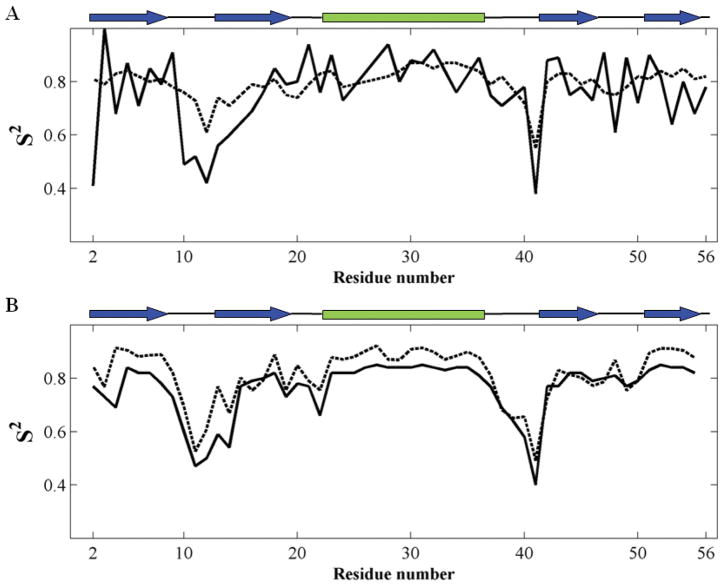
Despite the complexity of protein motions, and contrary to expectations, experimental and computational studies suggest that dynamic features that are detected computationally or experimentally at short times may explain experimental data associated with much slower processes. A typical example is the dataset of order parameters derived by Palmer and coworkers for protein G binding domain 3,⁶ based on two alternative datasets: NMR relaxation parameters for probing motions on the order of nanoseconds⁷ and residual dipolar couplings (RDCs) that probe motions on the microsecond time scale.⁸ Notably, the order parameter profiles extracted from these two datasets exhibit similar shapes,⁶ and the most ‘disordered’ residues, associated with the minima in the order parameter profiles plotted as a function of residue number (Fig. 1A), become more pronounced in the longer-time events. In contrast, the shape of the profiles, i.e., the distribution of order parameters as a function of residue index, remains essentially unchanged, suggesting that events at short time scales and those at long time scales share common features. Another example that indicates similar behavior is an NMR study of ubiquitin in which RDC and spin-lattice relaxation experiments exhibit comparable profiles that also agree with the predictions of accelerated molecular dynamics (MD) simulations, except for the amplitudes of the motions at long times.^9–11 Likewise, results for GB1 from two different length MD runs (Fig. 1B) also demonstrate that the two simulations result in comparable order parameter profiles.¹² In addition, other observations indicate a correspondence between experiments and computations, such as the relationship between MD events and catalytic turnover times observed by Kern and coworkers for adenylate kinase, even though the MD events are several orders of magnitude faster than the experimental ones.¹³ All these observations point to the existence of robust mechanism(s) of motions that underlie both short-time and long-time dynamics.

Figure 1.

Experimental and computational literature data exhibit similar motional behavior for short and long times. (A) Order parameters S² of G protein B 3 extracted from NMR data: spin-relaxation,⁷ dashed black; and RDC,⁸ solid black. (B) Order parameters S² of GB1 extracted from MD trajectories¹² of 10 ns (dashed black) and 175 ns (solid black). Secondary structure elements are depicted at the top of each panel.

Atomic motions can be divided into three basic components: the time scale of the motion, its amplitude, and its direction. In the strictest sense, characterization of protein dynamics requires the collection of thousands of time-resolved data at multiple length and time scales.⁵ As mentioned above, a broad range of experimental techniques provides information on protein dynamics, including NMR relaxation measurements,^14,15 Laue X-ray diffraction data,^16,17 infrared and fluorescence spectroscopy,¹⁸ and single-molecule studies,¹⁹ although they inform about different aspects and time scales of protein dynamics. On the computational side, structure-based methods such as MD simulations²⁰ and normal mode analysis (NMA) with elastic network models (ENMs)^21–24 have been exploited to gain insights into biomolecular systems dynamics. In particular, MD simulations are uniquely suited for examining time-resolved events in proteins at high resolution. Although extremely powerful, two shortcomings are inherent to MD simulations.²⁵ The first arises from sampling inefficiency, which becomes increasingly noticeable in large molecular systems.^25–27 Limitations of this nature can be alleviated to some extent by performing multiple independent runs for assessing convergence.^26,28–31 Second, the lengths of MD runs often remain below microseconds due to memory and computing time limitations.²⁵ Therefore, it still is an open issue whether functional motions at low frequencies can be inferred from relatively short MD runs.

The present study is carried out using cyanovirin-N (CV-N), a potent HIV-inactivating protein widely investigated in our previous studies,³² to answer the following questions: (i) How similar are the residue fluctuation profiles for different lengths runs? (ii) Do top-ranking modes from a short simulation become high frequency modes with increasing simulation time?³³ (iii) Do short MD simulations provide insights into functional motions, i.e., to what extent are the directions of motions near the native state energy minimum at short simulation times preserved at longer times? (iv) Do simulations provide information on the absolute sizes of various mechanisms of motions?

The results obtained for CV-N in combination with data reported previously for other systems, suggest that the distribution (or relative size) of residue fluctuations along the polypeptide chain is a robust quantity under equilibrium conditions, predominantly defined by the 3-dimensional architecture in the native state, while their absolute size predicted by MD simulations change with simulation duration, in the time regime (< 400 ns) investigated. The ratios of the mean-square displacements, y = <(ΔR)²>_MDk/<(ΔR)²>_MDk′ observed in two MD runs k and k′ of different durations, and that of the total simulation times, x = t_MDk/t_MDk′, are governed by a power law of the form y = x^0.26, similar to results reported by Scheraga and co-workers.^34,35 The decomposition of the trajectories into essential modes reveals that well-defined directions of the global motions, encoded by the native topology of inter-residue contacts, can be discerned even in short runs, as long as the region around the native state energy minimum is comprehensively sampled by multiple runs.

MATERIALS AND METHODS

MD simulations

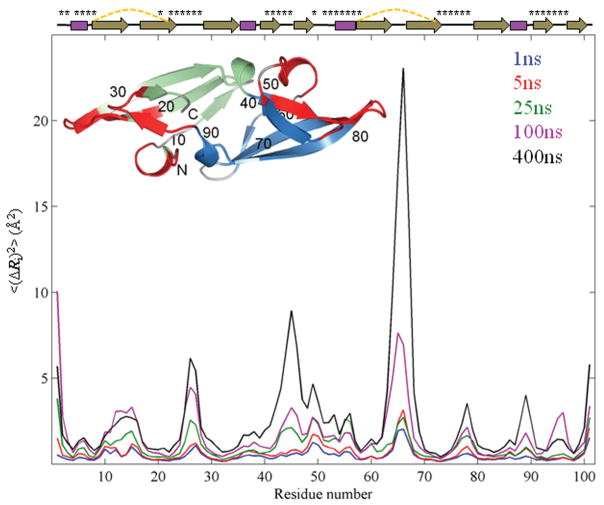
The starting CV-N structure (PDB ID: 2EZM)³² is highly anisotropic, occupying a volume of about 30 × 52 × 27 ų. The inset of Fig. 2 shows the CV-N structure. We used a simulation box of size 40 × 62 × 37 ų, which ensured a minimal water layer thickness of 5 Å for all surface residues. This thickness has been verified in our earlier simulations,³⁶ and shown in previous work,³⁷ to satisfactorily solvate the protein. The resulting system consisted of 8,159 atoms, including 2,216 TOP3P water molecules. NAMD³⁸ with the Charmm22 force field³⁹ was used with a 2 fs time step. After energy minimization and equilibration, multiple independent runs were performed at constant temperature (298 K) and pressure (1 atm).

Figure 2.

Mean-square-fluctuation profiles of CV-N from simulations with different durations. The MSFs <(ΔR_i)²> of residues averaged over twenty independent 1 ns, sixteen 5 ns, twelve 25 ns, eight 100 ns and two 400 ns runs are shown in blue, red, green, magenta, and black, respectively. Secondary structure elements of the protein are depicted at the top with disulfide bonds represented by dashed yellow lines and residues in the sugar binding sites labeled by asterisks. The inset shows the CV-N structure in ribbon representation. Domains A and B are colored green and blue, respectively, and the two sugar binding sites are colored red. Amino acid sequence positions are labeled for every 10^th residue.

Principal component analyses (PCAs) of MD trajectories and NMR models

The instantaneous position R_i(t) of each residue i is defined by the coordinates of its α-carbon atoms, which are organized into a 3n-dimensional vector of instantaneous configurations, R(t), for the protein of n residues. The configuration vector definition applies to snapshots recorded at fixed intervals from MD runs, as well as the models in the NMR structure ensemble (where t is replaced by the model index). The global changes in configuration originating from the collective fluctuations sampled in each MD run, or associated with the structural deviations observed in NMR ensemble, are identified by the same procedure, described here for MD snapshots. First, the instantaneous fluctuation ΔR_i(t) = R_i(t) − <R_i> from mean position <R_i> is evaluated for each residue, for each recorded time t (a total of m snapshots or models). This is performed after optimal superimposition of the configuration onto the starting structure so as to eliminate the rigid-body translations and rotations. The superimposition is achieved by least squares fitting to backbone heavy atoms. Second, the fluctuation vectors ΔR_i(t) (1 ≤ i ≤ n) are organized in a trajectory matrix A of dimension 3n × m, for a set of m snapshots. Multiplication of A by its transpose and division by m yields the 3n × 3n covariance matrix C for each run (or for the NMR ensemble). C may be expressed as an n × n supermatrix, the element C_ij of which is a 3×3 matrix of the form

$${\mathbf{C}}_{ij}=\left[\begin{array}{lll}\langle \mathrm{\Delta }{\mathit{X}}_i\mathrm{\Delta }{\mathit{X}}_j\rangle \hfill & \langle \mathrm{\Delta }{\mathit{X}}_i\mathrm{\Delta }{\mathit{Y}}_j\rangle \hfill & \langle \mathrm{\Delta }{\mathit{X}}_i\mathrm{\Delta }{\mathit{Z}}_j\rangle \hfill \\ \langle \mathrm{\Delta }{\mathit{Y}}_i\mathrm{\Delta }{\mathit{X}}_j\rangle \hfill & \langle \mathrm{\Delta }{\mathit{Y}}_i\mathrm{\Delta }{\mathit{Y}}_j\rangle \hfill & \langle \mathrm{\Delta }{\mathit{Y}}_i\mathrm{\Delta }{\mathit{Z}}_j\rangle \hfill \\ \langle \mathrm{\Delta }{\mathit{Z}}_i\mathrm{\Delta }{\mathit{X}}_j\rangle \hfill & \langle \mathrm{\Delta }{\mathit{Z}}_i\mathrm{\Delta }{\mathit{Y}}_j\rangle \hfill & \langle \mathrm{\Delta }{\mathit{Z}}_i\mathrm{\Delta }{\mathit{Z}}_j\rangle \hfill \end{array}\right]$$ (1)

Here, <ΔX_i ΔY_j > represents the cross-correlation between the X-component of ΔR_i for residue i and the Y-component of ΔR_j for residue j, averaged over all m snapshots. Third, the eigenvalue decomposition of C produces 3n − 6 nonzero eigenvalues and the corresponding eigenvectors. The eigenvectors define the directions of motions, and the eigenvalues scale the squared amplitudes of fluctuations. The Gaussian Network Model (GNM)^21,22 and anisotropic network model (ANM)^40,41 analyses also lend themselves to a series of eigenmodes, as described in the Supporting Information.

RESULTS AND DISCUSSION

The distribution of residue fluctuations is insensitive to the duration of simulations

We selected CV-N as our model system, based on its small size (n = 101 residues), its considerable thermodynamic stability and the large body of prior data available in our laboratory.^42–45 We compared the dynamic information retrieved from 1 ns to 400 ns MD runs. As depicted in the Fig. 2 inset, CV-N has a compact, pseudo-symmetric fold and is made up of two domains. Residues 1-39 and 91-101 form domain A (green), and 40-90, domain B (blue). The two domains share 32% sequence identity and are connected by short helical linkers. Each domain is composed of a triple-stranded β-sheet with a β-hairpin packed on top. There are two carbohydrate-binding sites located at distal positions (shown in red), one in each domain.⁴⁶ The two binding sites exhibit distinct affinities and specificities for high-mannose sugars.⁴⁷ The rotational correlation time τ_c of CV-N has been measured to be 4.5 ns.⁴⁸ Our simulations thus permit us to investigate both the sub-τ_c and supra-τ_c dynamics of CV-N under native state conditions.

Fig. 2 presents the results from a series of fifty-eight runs, adding up to a total simulation time of 2 microseconds. Multiple trajectories were generated for each simulation time (t_MDk = 1, 5, 25, 100 and 400 ns, also called the time window) to reduce inaccuracies arising from inadequate sampling of sub-states near the native state, especially for the short runs. The curves in Fig. 2 represent the mean-square-fluctuations (MSFs) in residue positions, <(ΔR_i)²> for residue 1 ≤ i ≤ n, for each time window in the range 1 to 400 ns, averaged over all runs of a given duration. Residue positions are those of the α-carbons.

As can be appreciated, the family of curves shown in Fig. 2 exhibits a striking similarity between the shapes of the residue fluctuation profiles for the different time windows. Essentially, all peaks/maxima that are noted at short time scales (e.g., 1–5 ns simulations) are amplified at longer times, with small changes in the relative sizes of the residue excursions. In principle, one might expect to detect new modes of motion at longer times, possibly changing the MSF profiles. However, only slight variations can be discerned in the profiles, such as the emergence of a peak near the helical hairpin loop around residues 65-67 in domain B in the longer time windows. Indeed, most features are robustly maintained: the loop regions usually tend to have high fluctuations, while secondary structure elements exhibit more restricted motions. Interestingly, an asymmetry in residue fluctuations can be seen, with residues in domain B exhibiting larger motions than those in domain A, consistently noted in all simulations.

A quantitative measure of the degree of similarity between these MSF profiles is provided by the correlation coefficients listed in Table I. The correlation coefficient between the MSFs for the 1 ns runs and the 400 ns runs is 0.83. Thus increasing the time window of observation by 4–5 orders of magnitude essentially leaves the shape of the fluctuation profile unchanged. A recent study of MDM2 dynamics also showed that the correlations between dihedral angle motions were conserved while the motional amplitudes changed upon binding the p53-peptide ligand,⁴⁹ which also supports the view that the conformational mechanisms are robustly maintained while the sizes of motions differ.

Table I.

Correlation Coefficients Between the MSFs of CV-N Residues Observed in MD Simulations^a and Those Predicted by the GNM

	1nsavg	5nsavg	25nsavg	100nsavg	400nsavg
5nsavg	0.96
25nsavg	0.76	0.80
100nsavg	0.71	0.76	0.79
400nsavg	0.83	0.83	0.63	0.77
GNM	0.71	0.70	0.74	0.60	0.67

^aAverages over multiple runs (see the text).

What distinguishes the different MSFs is their absolute size. The longer the simulation, the further the displacement of a residue from its mean position is. The increase in fluctuations is also evident from the root-mean-square-deviation (RMSD) profiles provided in Fig. S1. The RMSD from the original structure remains around 3.7 Å, which may be viewed as an indication of sampling the native state energy minimum even though this state may comprise narrowly distributed microstates that differ in their local conformers. But the fluctuations around the average RMSD increase with increasing simulation time, consistent with the observed dependence of <(ΔR_i)²> on the duration of the simulation. In order to uncover whether and what kind of dependency exists between the MSFs and the simulation time, we analyzed the data further (below).

The increase in residue MSFs with simulation duration obeys a power law

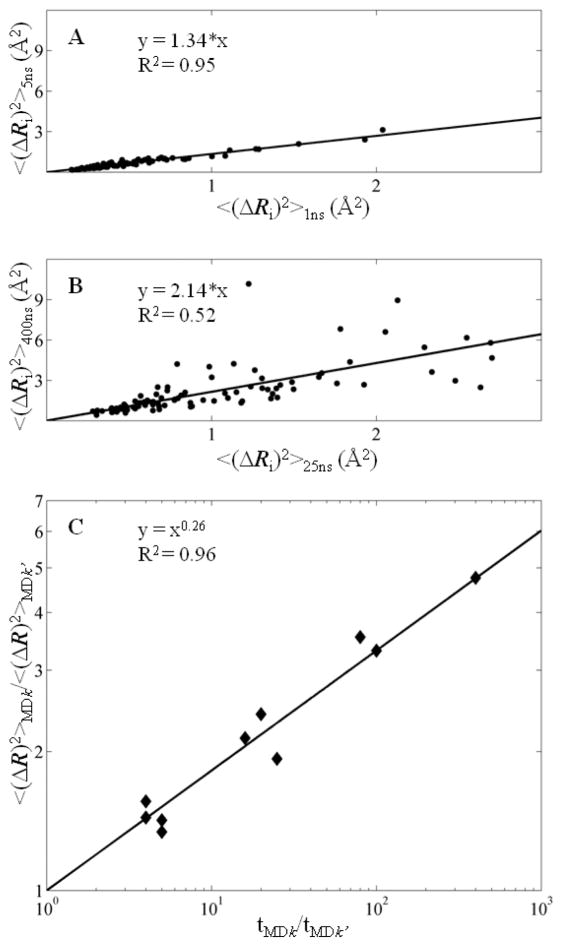
First, we consider two sets of trajectories, corresponding to two simulation times, e.g., t_MD1 = 1 ns and t_MD2 = 5 ns. Fig. 3A displays the <(ΔR_i)²> values of residues 2 ≤ i ≤ 101 for these two time windows: the abscissa represents the MSFs observed in MD1, and the ordinate, that in MD2. Linear regression of the data yields a correlation coefficient R² of 0.95, the slope of which, 1.34 in the present case, represents the average ratio of residue MSFs observed in MD2 to those in MD1. In other words, increasing the simulation time by a factor of 5 increases the residue MSFs by 34%, on average. Panel B represents a similar plot for two other time windows, t_MD3 = 25 ns and t_MD5 = 400 ns, which, in turn, yields a slope of 2.14, i.e., increasing the simulation time by a factor of 16 enhances the square displacements by a factor of 2.14.

Figure 3.

The magnitude of the fluctuations increases with increasing simulation time. (A) and (B) Comparison of MSFs for different simulations. (A) <(ΔR_i)²> of residue i in the 5 ns simulation (y axis) is plotted against <(ΔR_i)²> of the same residue in the 1 ns simulation (x axis). (B) <(ΔR_i)²> of residue i in the 400 ns simulation (y axis) versus <(ΔR_i)²> of the same residue in the 25 ns simulation (x axis). (C) The relationship between MSF and simulation time is a power function, with exponent 0.26. The MSF scaling factors for different simulations are plotted against the corresponding ratios of simulation lengths.

Repeating the same analysis for all pairwise combinations of simulation times, t_MDk for k = 1–5 (5!/3!2! = 10 of them), yields the master curve displayed in Fig. 3C. The data points show the enhancements in the MSFs accompanying the increases in the simulations, also listed in Table SI, for each pairwise combination. In other words, the ratio of MSFs for each pair of MD runs is plotted against the ratio of simulation times in Fig. 3C. Each point represents the average behavior of all residues, averaged over multiple runs, i.e., the resulting dependence represents the outcome from the complete dataset of trajectories with a cumulative simulation time of 2 μs. Note that the scales of both, abscissa and ordinate, is logarithmic and a linear relationship on such a log-log plot indicates a power law of the form y ~ x^α. The value of the exponent is evaluated from the slope of the best fit and is 0.26. Thus, the overall dependence is

$$<{(\mathrm{\Delta }\mathit{R})}^2{>}_{\text{MD}k}/<{(\mathrm{\Delta }\mathit{R})}^2{>}_{\text{MD}{k}^{\prime }}={({\text{t}}_{\text{MD}k}/{\text{t}}_{\text{MD}{k}^{\prime }})}^{0.26}$$ (2)

The subscript i in <(ΔR_i)²> has been removed since the MSFs refer to averages over all residues. Eq. (2) conveys two messages: (i) the MSFs observed in MD simulations depend on the duration of the simulations, and (ii) the dependence obeys a power law, with exponent 0.26. While this dependence seems small, it maps to displacements of <(ΔR)²>_MD1 = 0.5 Ų for t_MD1 = 1 ns, and <(ΔR)²>_MD5 = 2.6 Ų for t_MD5 = 400 ns. Thus, the square amplitudes of motions are enhanced by a factor of ~ 5 in long simulations. The major difference between short and long runs appears to be the larger excursions undertaken by the molecule around the native state energy minimum in longer runs, while the preferred directions of motions exhibit little, if any, changes.

The power law observed in present simulations (Eq. (2)) applies to CV-N equilibrium dynamics near its native state; it cannot be extended to larger scale transitions, such as those occurring during unfolding events. Evidently, the shape of the native state energy minimum defines the maximal size of fluctuations accessible to a given protein under native state conditions, and those beyond a certain range inevitably fall into new energy minima, including the unfolded state; and fluctuations in the unfolded state are limited by chain connectivity or covalent bonds. Such structural changes involving partial or complete unfolding events are beyond the range of current equilibrium simulations which maintain the native fold. The increase in the motional amplitudes simply reflects the sampling of a broader range of the global energy basin with increasing time window (up to 400 ns), and suggests that the observed MSFs simply reflect the portion of the global energy basin that is being accessed in a given run.

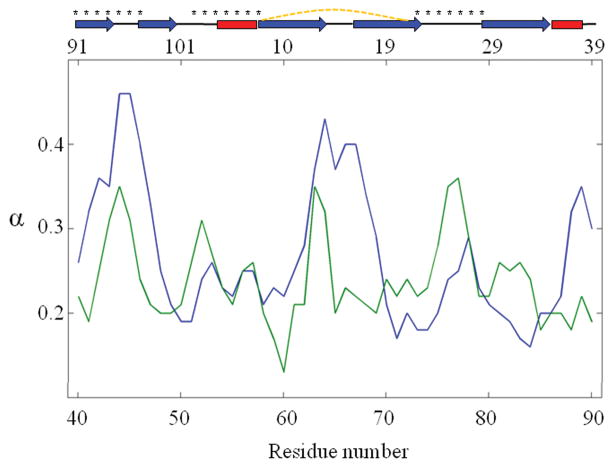
We further analyzed the behavior of each residue. Calculations yielded a range from 0.13 to 0.46, for the exponent α, depending on residue position/conformation (see Fig. 4). Larger exponents indicate a more pronounced dependence of the fluctuation sizes on the simulation time, i.e., residues with larger exponents enjoy larger conformational freedom. Examining the exponents with respect to secondary structure elements clearly indicated that loop residues possess larger exponents than their neighbors located in helices and β-strands. Another interesting observation is the distinctive distributions of exponents in the two structurally similar, but distinct, domains of CV-N. Fig. 4 suggests that in some cases it may be possible to use the exponent of individual residues or substructures to gain information on intrinsic dynamics, or conformational flexibility, which, in turn, may inform on functional properties.

Figure 4.

Power law exponents for CV-N residues. The results are shown on domain A (green), and domain B (blue). The upper abscissa displays residue positions in domain A, and the lower abscissa, the residue positions in domain B. The secondary structures with disulfide bonds (dashed yellow lines) are represented on the top, and residues comprising the binding sites are labeled by asterisks.

The above power law relationship suggests that there may be a time-dependent conformational drift throughout our simulations, even though we are exploring the neighborhood of the native state energy minimum. The deviation of the time-dependence of observed motion from that of a classical Brownian motion (where the exponent α is unity) might be attributed not only the subdiffusive motion which has been suggested to originate from the trapping in a local minimum/sub-state of the native state in the energy landscape^35,50 and from the sampling of infrequent and large jumps between such local minima,⁵¹ but also to the bounded motion of the protein constrained by native contact topology in addition to covalent bonds.

Comparison of essential modes extracted from different MD runs

Towards gaining a better understanding of the physical basis of the comparable RMSF profiles observed at different time scales (Fig. 1) and identifying the shared mechanisms that underlie the observed similarity across different time windows, we examined the principal motional modes sampled in simulations of different lengths. To this end, we decomposed the CV-N motions in each MD trajectory into a series of collective modes, each ranked by their weights. We focused on the top-ranking modes (global modes), also called essential modes, since these are usually the most collective modes and numerous applications have shown their relevance to biological function.¹

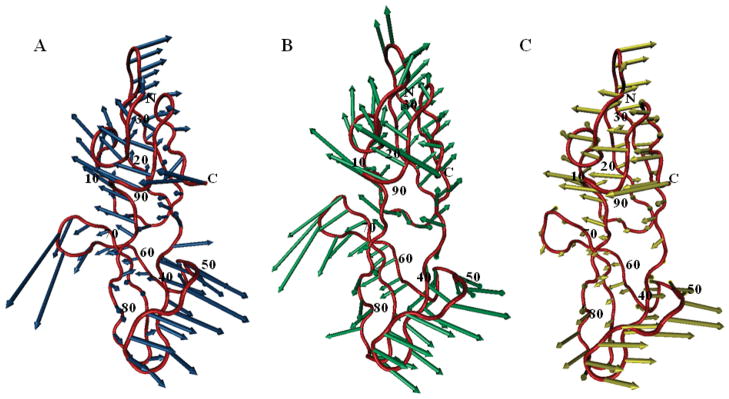
We considered two most extreme runs: the 1 ns and 400 ns simulations. The global (lowest frequency) mode obtained from two such runs is illustrated in Fig. 5, panels A and B. Strikingly, although one might expect that the longer simulations probe more collective motions that only emerge at longer time scales, the global motional behavior is remarkably similar in the two runs. The correlation coefficient between the two modes is 0.77, suggesting that the global modes at either short or long times share robust features that are uniquely defined by the structure, and can be extracted to a good approximation from short runs.

Figure 5.

Shared global mode between theory and simulations. The CV-N backbone structure is shown in tube representation (red) with the directions of the global motion for the 1 ns simulation (A) and the 400 ns simulation (B), or the second mode predicted by the ANM (C) depicted by blue, green, and yellow arrows, respectively. The correlation coefficients between pairs of modes displayed are 0.77 (blue/green), 0.69 (blue/yellow), and 0.64 (green/yellow). Primary sequence positions are labeled for every 10^th residue.

To validate these findings, the first two modes of two 400 ns simulations were compared with the global modes extracted from all other shorter simulations. The results of this analysis are presented in Table SII. Thirty-two of all fifty-six short (≤ 100 ns) simulations yielded global motions similar to those in the first 400 ns simulation, with similarity defined as a correlation coefficient > 0.6 between the two modes. A very similar result was obtained, performing the analysis for the second 400 ns simulation. Even though not all the different length simulations in our dataset converged completely, a large fraction of them share the low frequency motions with the longest runs.

The correlation between the global mechanisms of motions sampled in runs of different durations becomes even more apparent when we combine trajectories from all individual runs with the same duration, and compare the principal modes of motions computed for each combined trajectory. The results, presented in Table II, further confirm that the directions (not the size) of the global motions are effectively conserved across runs of various lengths, although the orders of the modes (shown in parentheses) may shift in some cases. This analysis also underscores the importance of carrying out multiple simulations and subjecting the compiled data to mode decomposition in order to detect the ‘consensus’ global modes and extract information on collective mechanics.^27,52

Table II.

Correlation Coefficients Between the Global Modes from MD Simulations,^a NMR Structural Ensemble, and ANM Predictions

	1nscomb	5nscomb	25nscomb	100nscomb	400nscomb
5nscomb	0.80 (1,1)
25nscomb	0.75 (2,1)	0.64 (2,1)
100nscomb	0.58 (5,3)	0.57 (2,1)	0.84 (1,1)
400nscomb	0.59 (1,4)	0.67 (1,2)	0.80 (4,4)	0.59 (1,3)
ANM	0.57 (1,1)	0.60 (2,2)	0.61 (2,3)	0.60 (2,3)	0.58 (1,4)
NMR	0.60 (2,1)	0.63 (2,1)	0.57 (2,2)	0.56 (2,2)	0.47 (2,2)

^aThe MD global modes refer to the combination of multiple trajectories of a given simulation length. Entries in parentheses represent the mode numbers, e.g. the 2^nd mode of the combined 25 ns simulations (total of 12 runs) displays a correlation coefficient of 0.75 with the 1^st mode of the combined 1 ns simulations (20 runs).

Given that the top-ranking modes of motions from long simulations can be extracted to a good approximation from short simulations (provided that multiple runs are combined), insights into biological motions of low frequencies may be gained via multiple short simulations. The explanation for such unexpected behavior may lie in the nature of the folding energy landscape. The energy space may be described in terms of an orthogonal basis set, with each basis vector defining a different mode of motion. If the global modes of motion in long and short simulations, respectively, display the same patterns, this suggests that the molecule tends to move along the same direction or to sample the same subspace, in both cases, although the amplitudes of the displacements differ.

Both ENM and NMR results are consistent with the MD simulation results

As further verification of the relevance of our findings to CV-N dynamics, we performed the GNM^21,22 analysis of the PDB structure 2EZM, the NMA^53,54 of the same structure using the ANM,⁴⁰ and the PCA of the NMR ensemble of 40 structural models for CV-N.³² ANM modes have been observed in previous studies to correlate with the structural dynamics intrinsically accessible to enzymes^1,55,56 and with the microseconds dynamics of G-protein coupled receptors.²⁷ The distribution of NMR models also provides information on structural variabilities, which may be compared to those observed in MD runs.^36,57,58

The correlations between the distribution of MSFs predicted by the GNM, <(ΔR_i)²>_GNM, and those observed in different MD runs are presented in Table I. The correlations vary from 0.60 (with <(ΔR_i)²>_100ns,avg) to 0.74 (with <(ΔR_i)²>_25ns,avg). Here the subscript designates that the MSFs refer to the averages over multiple MD runs of a given duration (e.g., 12 runs of 25 ns each, or eight runs of 100 ns, etc). These results are consistent with our previous findings where correlations of 0.64 ± 0.04 were obtained³⁶ between GNM-predicted MSFs and the MSFs inferred from multiple 10 ns MD simulations. The results presented in Fig. 5C, Table II row 5 and Table SIII further show that the global modes predicted by the ANM correlate with the global modes derived from MD simulations, irrespective of the length of the simulation.

Tables II also displays the correlations between the principal modes of structural deviations inferred from NMR models (last row) and global modes observed in MD simulations. The correlations between the NMR principal modes and MD global modes, 0.55 ± 0.06, are not as high as those among MD runs with different lengths, 0.68 ± 0.11 (Table II). This may be attributed to the fact that there are only 40 models in the NMR ensemble, which may not provide a complete description of the accessible reconfigurations. The level of agreement appears to decrease with increasing simulation duration, presumably be due to the inadequate sampling of the accessible (larger) conformational subspace by fewer independent runs. Finally, we examined the subspace spanned by the first ix global modes extracted from MD simulations, the NMR ensemble, and ANM predictions. As observed in Table SIV, there are large overlaps between these subspaces, with an average RMSIP (root mean-square inner product)⁵⁹ of 0.59 ± 0.11. The observed subspace similarities at the low frequency region suggest the global motions observed in MD simulations and those predicted by the ANM share robust features uniquely encoded by the equilibrium structure.

The conformational dynamics usually consists of a continuous spectrum of motions, with varying frequencies and amplitudes. As such, it can hardly be divided into two distinctive groups, fast and slow. However, in the literature, for simplicity, two time regimes have been defined, sub-τ_c and supra-τ_c, to describe fast and slow motions, respectively. τ_c is the correlation time deduced from T₁/T₂ ratio measured by NMR spectroscopy. ^{12, 60} In the case of CV-N, the experimentally measured τ_c is 4.5 ns.⁴⁸ Therefore, the time scale of present simulations includes motions in the ‘fast’ regime, as well as ‘slow’ regime. The frequency range of slow motions varies by two orders of magnitude up to 0.4 microseconds time scale. The conclusions drawn therefore apply to this time regime. Yet, it is worth noting that the most cooperative (global) modes of internal motions derived from short and long simulations share close similarities (compare, for example, panels A and B in Fig. 5). Furthermore, these global motions exhibit reasonable agreement with the results from ANM calculations, and NMR data, which also supports the robustness of the results from simulations and the fact that these robust modes are uniquely defined by the architecture.

CONCLUSION

In the present work, we have analyzed the amplitudes and directions of residue motions in multiple MD runs of durations varying in the range 1 ns – 400 ns. The simulation conditions were identical in all runs, except for the lengths of the simulations. Our data show that the distribution of residue fluctuations, or the MSF profile, is insensitive to the simulation length, while the amplitudes increase with simulation time. The square amplitudes exhibit a power law dependence on the simulation time, while the correlation times are linearly dependent. These findings suggest that the types of motions, but not their absolute size scales, can be accurately extracted from MD runs in the observed time regime, which includes both sub- and supra-τ_c motions up to hundreds of nanoseconds. Accurate assessment of the distribution of residues, however, and extraction of the global modes that predominantly define the common features of the RMSFs observed at various time windows, require performing multiple simulations and decomposing (by PCA) the trajectories to identify consensus modes.

The present study also explains why and how simulations that sample several order of magnitude faster events may provide insights into the conformational mechanics of much slower processes. Our in-depth examination of the spectra of essential modes retrieved from the different simulations suggests that highly robust and usually functional modes that persist (or fully evolve) at longer times can be discerned even in short simulations provided that the dominant modes are extracted by a PCA of the combination of multiple trajectories. The motions are robustly defined by the shape of the native state energy minimum, which apparently governs protein fluctuations not only in the close neighborhood but also during relatively large excursions away from the minimum. The fact that the GNM and ANM results are consistent with MD simulation results also points to the dominance of shape of the energy landscape near the native state minimum in defining the accessible routes/modes of reconfiguration.

The observations made here for CV-N are consistent with different levels of coverage of the native state energy well, shorter simulations covering the bottom only, while longer simulations reaching distant locations while remaining in the same well. CV-N’s high stability at room temperature⁶¹ made it a good candidate for performing extended simulations without the risk of significant structural changes or large conformational drift. In principle, the shape of the energy landscape would affect the observed shifts in fluctuation profiles. One might expect to see a broad range of excursions under native state conditions when that the structure’s stability is mainly entropic in nature, i.e., when the structure has access to multiple microstates while maintaining its native fold. In such cases, the observed size of fluctuations would exhibit a relatively more pronounced dependence on the simulation duration. This behavior is evidenced by the higher exponent observed in loop regions that enjoy multiple conformations. It remains to be seen if the residue fluctuation profiles of proteins predominantly stabilized by enthalpic interactions (native state characterized by a deep, but not necessarily broad energy, minimum), exhibit any shifts similar to those observed here for CV-N prior to the onset of their unfolding.