Abstract
In this study, we report the formation of ribose sugar radicals in high yields (85 – 100%) via photo-excitation of adenine cation radical (A•+) in Ado and its ribonucleotides. Photo-excitation of A•+ at low temperatures in homogenous aqueous glassy samples of Ado, 2′-AMP, 3′-AMP and 5′-AMP forms sugar radicals predominantly at C5′- and also at C3′-sites. The C5′• and C3′• sugar radicals were identified employing Ado deuterated at specific carbon sites: C1′, C2′, and at C5′. Phosphate substitution is found to deactivate sugar radical formation at the site of substitution. Thus, in 5′-AMP, C3′• is observed to be the main radical formed via photo-excitation at ca. 143 K whereas in 3′-AMP, C5′• is the only species found. These results were supported by results obtained employing 5′-AMP with specific deuteration at C5′-site (i.e., 5′,5′-D,D-5′-AMP). Moreover, contrary to the C5′• observed in 3′-dAMP, we find that C5′• in 3′-AMP shows a clear pH dependent conformational change as evidenced by a large increase in the C4′ β–hyperfine coupling on increasing the pH from 6 to 9. Calculations performed employing DFT (B3LYP/6-31G*) for C5′• in 3′-AMP show that the two conformations of C5′• result from strong hydrogen bond formation between the O5′-H and the 3′-phosphate dianion at higher pHs. Employing time-dependent density functional theory [TD-DFT, B3LYP/6-31G(d)] we show that in the excited state, the hole transfers to the sugar moiety and has significant hole localization at the C5′-site in a number of allowed transitions. This hole localization is proposed to lead to the formation of the neutral C5′-radical (C5′•) via deprotonation.
Introduction
A number of recent efforts have established that photo-excitation of one-electron oxidized bases in DNA-RNA systems 1 – 8 at low temperatures results in sugar radical formation. The excitation effectively results in hole transfer to the sugar which quickly deprotonates to produce a neutral carbon centered sugar radical. This was found to occur in both guanine and adenine containing DNA systems with formation of specific sugar radicals dependent on the base and structural features.1 – 9 For example, we observed that photo-excitation of one-electron oxidized adenine in 2′-deoxynucleosides resulted in near complete conversion to sugar radicals, predominantly C5′• with a small contribution of C3′•.9
The precursor to the sugar radical is the DNA base cation radical for guanine containing systems and was assumed to be the deprotonated species for adenine containing systems.9 This is because the adenine cation radical (A•+) from dAdo has been reported by Steenken and coworkers to have a pKa of ≤ 1 in aqueous solutions at ambient temperature.10, 11 In agreement, a number of ESR and ENDOR studies reported that A•+ is deprotonated even at 4 K in single crystals.12 We note here that the deprotonation of the hole formed initially in the parent structure leads to its localization on a single base and thus, the deprotonated one-electron oxidized adenine moieties are detected in single crystals.12b
Thus, on the basis of these previous results10–12 it was assumed that one-electron oxidized dAdo in our work, that the adenine moiety exists in its de-protonated state as A(–H)• at pHs ranging from 5 to 12.9 Our method employs aqueous (H2O or D2O) solutions of LiCl at room temperature which are cooled at 77 K to form homogenous aqueous glasses that soften on annealing to allow for diffusion.1 – 4, 8, 9, 13, 14 In our experimental system (i.e. in homogenous aqueous glasses at low temperature), radicals show similar properties as found in aqueous solutions at room temperature. For example, in the case of G•+ (dGuo), we found that the site of deprotonation is N113 which had also been suggested by pulse radiolysis in aqueous solution at room temperature.10, 11 Moreover, we also found that in aqueous glasses at 150 K, the pKa of G•+ (dGuo) is ca. 5 to 6 13 - which is just ca. 1.5 units higher than the pKa value of 3.9 of G•+ in aqueous solution at room temperature.10, 11
A recent report from our laboratory shows that the assumption that deprotonation occurred at pH 5 was incorrect and that adenine cation radical is actually stable at 150 K in aqueous glasses of dAdo up to pH 8 and to pD 8.5.14 In these systems dAdo associates on cooling and the adenine cation radical is stabilized by charge-resonance interactions within adenine stacks thereby resulting in the higher pKa value of ca. 8 for the adenine cation radical in H2O glasses at 150 K.14 Theoretical calculations point out that the adenine dimer cation radical, A2•+, shows delocalization of the hole over both bases and is stabilized by ca. 12–16 kcal/mol relative to the monomers, A•+ and A.14 The delocalization of the hole in adenine stacks is suggested to raise the pKa from ≤1 for monomer cation radical 10, 11 to ca. 8 for the adenine cation radical in the stacked system.14 These experimental results are supported by theoretical calculations of the pKa of the adenine monomer cation, A•+ (pKa ca. -0.3) and dimer cation radical, A2•+ (pKa ca. 7).14 The calculations also show for the amine deprotonated adenine radical (A(-H)•) that the unpaired spin is localized only on the A(-H) moiety even when stacked with A, i.e., AA(-H)• 5, 7, whereas the spin is delocalized in stacked A2•+.14 These results indicate that stacks of A in DNA will tend to stabilize the hole from deprotonation and allow for hole transfer even over long distances.14 In agreement with this proposition, studies of hole transfer through A stacks show that such transfer is apparently not hindered by deprotonation. 15 – 20 In fact, it has been suggested that hole delocalization should extend over to 3 to 4 adenine bases in such A tracts.21
In this study, we investigate one-electron oxidized Ado and various derivatives and we establish that at the native pH/pD (ca. 5) of 7.5 M LiCl glass, one-electron oxidized adenine in each case exists as adenine cation radical at 150 K as found for dAdo14. We also investigate sugar radical formation via photo-excitation of the adenine cation radical in glassy systems of Ado and its nucleotides. It is well known that sugar radicals can adopt numerous conformations22 – 25 defined by its pseudo-rotation cycle 26. This makes sugar radical identification difficult based on their hyperfine splittings alone. 22 – 25, 27 – 29 As a result, following our previous studies with Guo,8 in this work we have used selective deuterium substitution at C1′, C2′ and at C5′ in the sugar moiety of Ado, and at C5′ in 5′-AMP to identify the site of the sugar radical produced by photo-excitation of A•+ and assign their proton hyperfine couplings to these sites. These studies show that we observe production of C3′• and C5′•, but do not find formation of C1′•, C2′• or C4′• via photo-excitation of the adenine cation radical in Ado. Thus, we find that both Ado and dAdo nucleosides form the same radicals suggesting little effect of the C2′-OH group during formation of sugar radicals from the excited cation radical. The reasons for this unexpected result are discussed in terms of the distribution of the hole over the sugar ring in the excited state.
Materials and Methods
Compounds
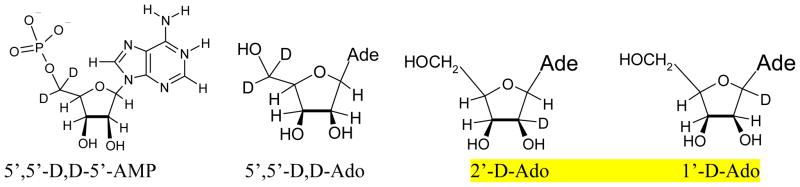
Adenosine (Ado), Adenosine 2′-monophosphate (2′-AMP), Adenosine 3′-monophosphate (3′-AMP), Adenosine 5′-monophosphate (5′-AMP), Adenosine 2′, 3′-cyclic monophosphate (2′,3′-cAMP) and lithium chloride (99% anhydrous, SigmaUltra) were obtained from Sigma Chemical Company (St Louis, MO). Potassium persulfate (crystal) was obtained from Mallinckrodt, Inc. (Paris, KY). 1′-D-adenosine (1′-D-Ado), 2′-D-adenosine (2′-D-Ado), 5′,5′-D,D-adenosine (5′,5′-D,D-Ado), and 5′,5′-D,D- adenosine 5′-monophosphate (5′,5′-D,D-5′-AMP) (see scheme 1) were purchased from Omicron Biochemicals, Inc. (South Bend, IN). The stereospecificity of the deuteration at the specific site of the sugar moiety in Ado was maintained in these compounds as these deuterated derivatives were synthesized by Omicron from D-Ribose.2, 8 All chemicals were used without further purification.
Scheme 1.
Isotopically substituted compounds used:
Glassy sample preparation
As per our earlier work with deoxynucleosides, deoxynucleotides, DNA-oligomers,1 – 4, 9, 13, 14 Guo, its deuterated derivatives and RNA-oligomers containing guanine moieties,8 glassy samples of Ado, its deuterated derivatives, and its nucleotides were prepared by dissolving ca. 3 mg of compound in 1 mL of 7.5 M LiCl in D2O or H2O in the presence of 5 mg K2S2O8. Whenever required, we have adjusted pH/pDs of these solutions by quick addition of adequate amount (in μL) of 1 M NaOH or 1 M HCl in H2O or D2O under ice-cooled condition. As per our previous studies,9, 13, 14 Following our previous works regarding preparation of glassy solutions, 1 – 4, 8, 9, 13, 14 we have used 7.5 M LiCl in D2O or H2O in this work as well. We have used pH papers for pH/pD measurements of these solutions. Thus owing to the high ionic strength and the use of pH papers, these pH/pD values should be considered as approximate. 9, 13, 14 These homogenous solutions were bubbled thoroughly with nitrogen gas at room temperature. Subsequently, following our earlier works,1 – 4, 8, 9, 13, 14 the transparent glassy samples were prepared by drawing the solution into Suprasil quartz tubes (4 mm diameter, cat. no. 734-PQ-8, WILMAD Glass Co., Inc., Buena, NJ) followed by cooling to 77 K and were stored at 77 K in liquid nitrogen in the dark. As per our earlier work,1 – 4, 8, 9, 13, 14 we note that our glassy sample containing Ado or its derivative being dissolved homogenously in 7.5 M LiCl are not crystalline solids but are glassy homogeneous super-cooled liquids. These glassy solutions, on annealing, soften to allow for molecular migration and solution phase chemistry.
γ-Irradiation
As per our earlier works,1 – 4, 8, 9, 13, 14, 30 all glassy samples of Ado and its nucleotides and the deuterated derivatives of Ado were γ− irradiated with an absorbed dose of 2.5 kGy under liquid nitrogen at 77 K using a model 109-GR9 irradiator, containing a shielded 60Co source.
Annealing and photo-excitation of samples
Following our earlier works,1 – 4, 8, 9, 13, 14, 30 we have produced the one-electron oxidized adenine species by annealing γ-irradiated glassy samples in a variable temperature assembly (Air Products) in the dark with the aid of cooled nitrogen gas. The glassy samples were annealed for 12 – 20 min at 148 to 152 K where the glass softens sufficiently to allow for molecular migration which leads to the disappearance of Cl2•− with the concomitant formation of one-electron oxidized adenine as described in our earlier work.9, 13, 14 The same temperature assembly was used for photo-excitation of adenine cation radical for our glassy samples. Similar to our work in 2′-deoxynucleosides/tides and in DNA-oligomers, 1 – 4, 9, 13, 14 and also in Guo and in RNA-oligomers,8 we have not observed sugar radical formation by the direct attack of Cl2•− on the sugar moiety in these glassy samples of Ado and its nucleotides as well.
The glassy samples of Ado and its nucleotides were photo-excited 143 K (±2 K) using tungsten lamp (250 W). This temperature was necessary to prevent radical migration which starts at ca. 148 K. Also, photo-excitation of the glassy samples of 5′,5′-D,D-Ado were carried out at 77 K employing tungsten lamp (250 W). Photo-conversion rates are found to be slower at 77K and in some cases the radical distribution changes with temperature. Both effects have been attributed to conformational flexibility allowed at higher temperatures in these glasses.2, 4 During photo-excitation, the IR and UV components of this light were cut off by a water filter and a 310 nm cut off filter, respectively. We note that ca. 60 mW of the total lamp intensity is effective in causing sugar radical formation via photo-excitation.9
Electron Spin Resonance
As per our earlier works,1 – 4, 8, 9, 13, 14 the glassy samples of Ado and its nucleotides were immediately immersed in liquid nitrogen after (i) γ-irradiation at 77 K, (ii) annealing to 148 – 152 K, and (iii) photo-excitation at 143 K. We have recorded the ESR spectra of these samples at 77 K and at 40 dB (20 μW) employing a Varian Century Series ESR spectrometer operating at 9.2 GHz with an E-4531 dual cavity, 9-inch magnet and with a 200 mW klystron. Following our work,1 – 4, 8, 9, 13, 14, 30 we have used Fremy’s salt (g (center of the spectrum) = 2.0056, AN = 13.09 G) for field calibration.
Analyses of ESR spectra
The fraction that a particular radical contributes to the overall spectrum has been estimated employing doubly integrated areas of benchmark spectra because the number of spins of each radical species (i.e. moles of each radical) is directly proportional to these doubly integrated areas. Using programs developed in our laboratory (ESRADSUB, ESRPLAY) that use least square fittings of benchmark spectra of the radicals, we have obtained the fractional contribution of these radicals in an experimentally obtained ESR spectrum.1 – 4, 8, 9, 13, 14, 30
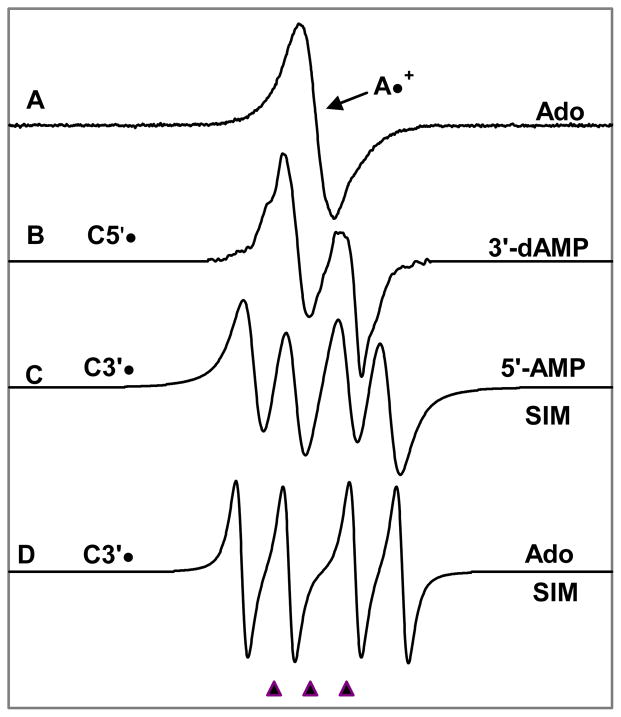
In Figure 1, we have presented the benchmark spectra employed to analyze the ESR spectra shown in this work. Spectrum 1A is the benchmark spectrum of adenine cation radical in Ado and in its nucleotides. In Figure 1B, the benchmark spectrum of C5′• is shown (an anisotropic doublet owing to C5′-αH (ca. -21 G) and this spectrum has been obtained from 3′-dAMP9 and this is in good agreement with the literature.12f,g In Figures 1C and 1D we have presented the benchmark spectra for C3′• obtained with the aid of simulation based on isotropic hyperfine and g parameters given in Table 1. Figure 1C was used for analyses of ESR spectra from 5′-AMP samples and Figure 1D has been used to analyze the ESR spectra in Ado samples. We note that the C3′• for Guo 8 was found to be identical to that found here for Ado. We have found in our earlier work with deoxyribonucleosides and –tides that the hyperfine couplings for C3′• vary slightly with compound and also with temperature.2, 9 Therefore, we note that the hyperfine coupling constants for the two β-H atoms (β-proton couplings) – one at C2′ and the other at C4′ could vary slightly with compound for these two C3′• spectra shown in Figures 1C and 1D.
Figure 1.
(A) A•+, produced from Adenine moiety in Ado via one-electron oxidation by Cl2•−. (B) C5′•, formed via photo-excitation of A•+ in 3′-dAMP (7 M LiCl glass/D2O).9 (C) Isotropically simulated spectrum for C3′• in 5′-AMP with the following parameters: 1βH = 15 G, 1βH = 34 G, line-width = 8.5 G, and giso =2.0027 (see text and Table I) (D) Isotropically simulated spectrum for C3′• using two β-hydrogen hyperfine couplings (simulation parameters: C2′-βH = 41 G, C4′-βH = 17 G, line-width = 4.5 G and giso =2.0028) (see text, Table I). This C3′• characterized from Ado was found to be identical to that found for Guo.8
Table I.
Hyperfine couplings and g-values for ribose radicals in Ado and its derivativesa
| Name of the radical a | Compound | Hyperfine coupling constants (G) | g-value (apparent)b |
|---|---|---|---|
| C3′• | Ado, 2′-AMP, 3′-AMP |
ca. 41 (C2′-βH) ca. 17 (C4′-βH), |
2.0028 |
| C3′• | 5′-AMP, 5′,5′-D,D-5′-AMP | ca. 15 (1 βH), ca. 34 (1βH) | 2.0027 |
| C5′• | Ado, 2′-AMP, 3′-AMP pH 5 | ca. 21 (C5′-αH) | 2.0023 |
| 3′-AMP pH 9 | ca. 21 (C5′-αH), ca. 34.5 (C4′-βH) |
HFCC values are for the sugar radicals produced via photo-excitation of the adenine cation radical at 143 K in the frozen aqueous (7.5 M LiCl D2O) glassy solution with native pD (ca. 5). These values are obtained from the spectra recorded at 77 K.
The apparent g-value is the experimental center of the spectrum.
We also note here that subtraction of a small singlet “spike” from irradiated quartz at g = 2.0006 has been carried out from the recorded spectra before analyses as in our previous work. 1 – 4, 8, 9, 13, 14
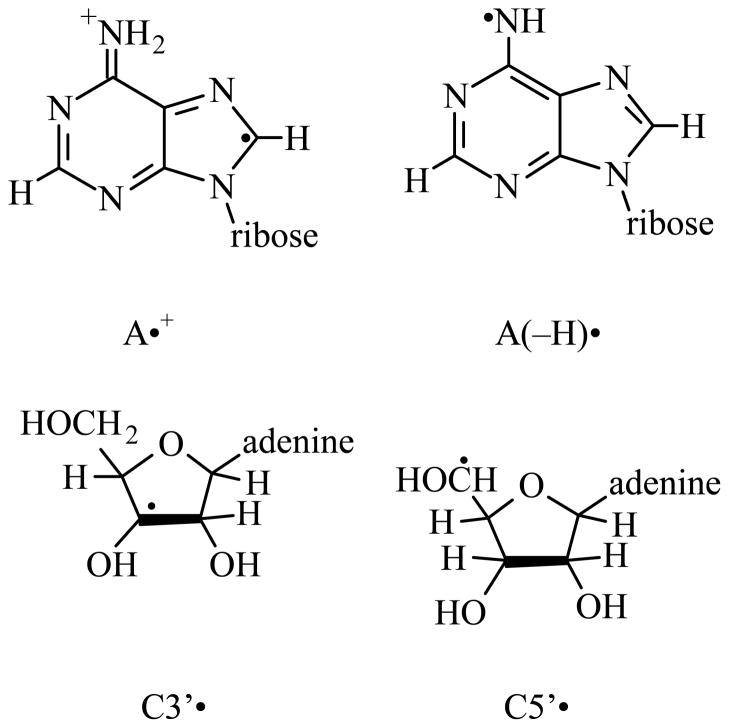
In Table I, we have also mentioned the hyperfine coupling constant (HFCC) values and the apparent g-values of the sugar radicals. In scheme 2, we have presented the structures of the radicals described in this work.
Scheme 2.
Radicals described in this work.
Theoretical (DFT) calculations
Calculations for C5′• in 3′-AMP have considered two different protonation states of the phosphate (PO4) moiety, viz. monoprotonated (PO4−1) and its deprotonated form (PO4−2). Geometries of C5′• in 3′-AMP in PO4−1 and PO4−2 states have been optimized in the presence of 3 to 4 water molecules near the phosphate group to mimic experimental conditions to some extent. The calculations were preformed using B3LYP functional and 6-31G* basis in the set as implemented Gaussian03 suite of programs.31a The molecular structures are plotted using freely available molecular modeling program JMOL.31b
In order to obtain reliable values of isotropic HFCCs, calculations require an appropriate basis set.32 Recently, HFCCs of several neutral radicals as well as cation and anion radicals using DFT method and different basis sets (6-31G*, TZVP and EPRIII) have been computed.33 These calculations show that B3LYP/6-31G* method gave the HFCCs which are comparable to the experimental values. Also, our work using B3LYP/6-31G* method predicted HFCCs of hydrated guanine radicals and sugar radicals that are in agreement with experiment.2, 9, 13
We have carried out excited state calculations of Ado radical cation using TD-DFT (time dependent density functional theory) for determining the transition energy and the nature of the molecular orbitals involved in transitions. Calculations were performed using the TD- B3LYP/6-31G(d) method as implemented in Gaussian 03.
Results and Discussion
State of protonation of one-electron oxidized adenine in Ado and in its nucleotides
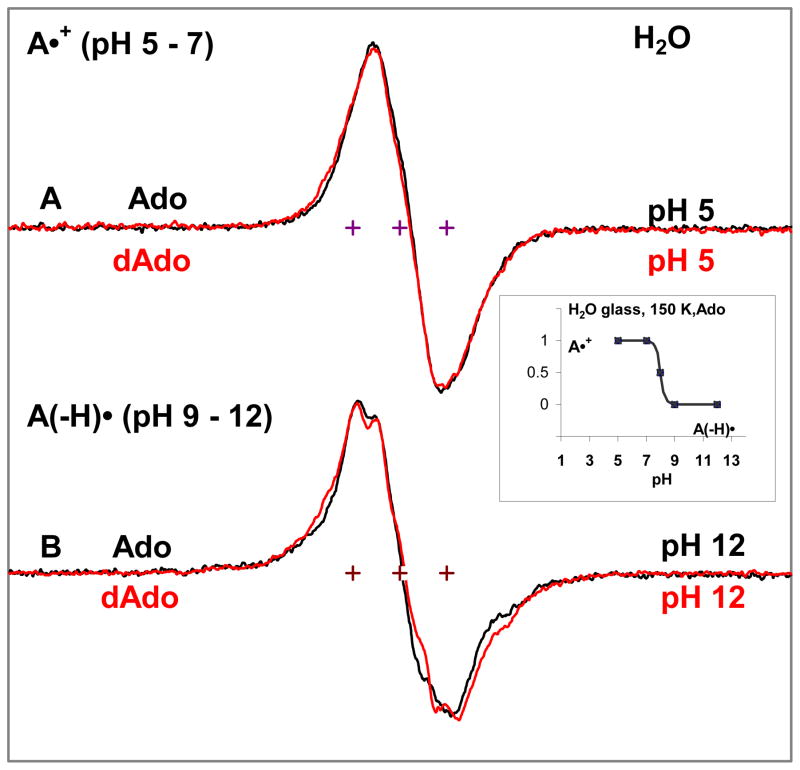
To determine the acid base nature of the Ado cation radical, the spectra of one electron oxidized Ado was investigated in glassy samples (7.5 M LiCl/H2O). The line-shape, hyperfine splitting and the g-values of one-electron oxidized Ado shown in Figure 2A (black color), is found to be identical to those found in the ESR spectra of one-electron oxidized dAdo in glassy samples shown in red.14 The spectrum for dAdo has been recently shown to be due to the adenine cation radical (A•+) with the spin density localized to the adenine ring. In Figure 2B we reported the spectrum of one electron-oxidized Ado at pH ca. 12 which is also identical to that found for dAdo (in red). This spectrum is that from the N-6 deprotonated species A(-H)•. A(-H)• is found at pH 9 and above. A study as a function of pH shows the pKa value of the adenine cation radical in glassy samples of Ado at 150 K is ca. 8 (see insert of Figure 2), which is identical to that found for the adenine cation radical in dAdo under similar conditions14. Thus, at the native pH/pD (ca. 5) of 7.5 M LiCl, we conclude that one-electron oxidized Ado exists as the cation radical (A•+) in these glassy samples of Ado.
Figure 2.
ESR spectra of one-electron oxidized adenine formed in Ado (Black) and dAdo (red, ref. 14) respectively in H2O in 7.5 M LiCl glass (see experimental). Spectra in (A) found at pH 5. Spectra in the pH range 3 to 7 are identical. Spectra in (B) were found at pH 12 and spectra in the pH range 9 to 12 were identical. All ESR spectra are recorded at 77 K. The spectra in A and B are assigned to A•+ and its deprotonated species to A(-H)•, respectively. The Figure (insert) shows that up to pH 7, one-electron oxidized adenine in Ado remains as the cation radical, and at pH ca. 9 and above, it exists as A(-H)•. These results show that A•+ in Ado and dAdo have indentical pKa values at 150 K (ca. 8)14.
Photo-excitation of adenine cation radical in the glassy sample of Ado and of derivatives of Ado having deuteration at specific sites in the sugar moiety
Ado
In Figure 3A, we present the ESR spectrum of A•+ formed via one-electron oxidation of Ado by Cl2•− in 7.5 M LiCl glass after annealing at ca. 152 K for 10 – 20 min in the dark and is recorded at 77 K. This spectral shape, g-value, and hyperfine splitting are identical to that of the adenine cation radical in the glassy samples of dAdo under the same conditions.9, 14 Hence this spectrum shown in Figure 3A is used as a benchmark spectrum in Figure 1A regarding our analyses for A•+ in Ado.
Figure 3.
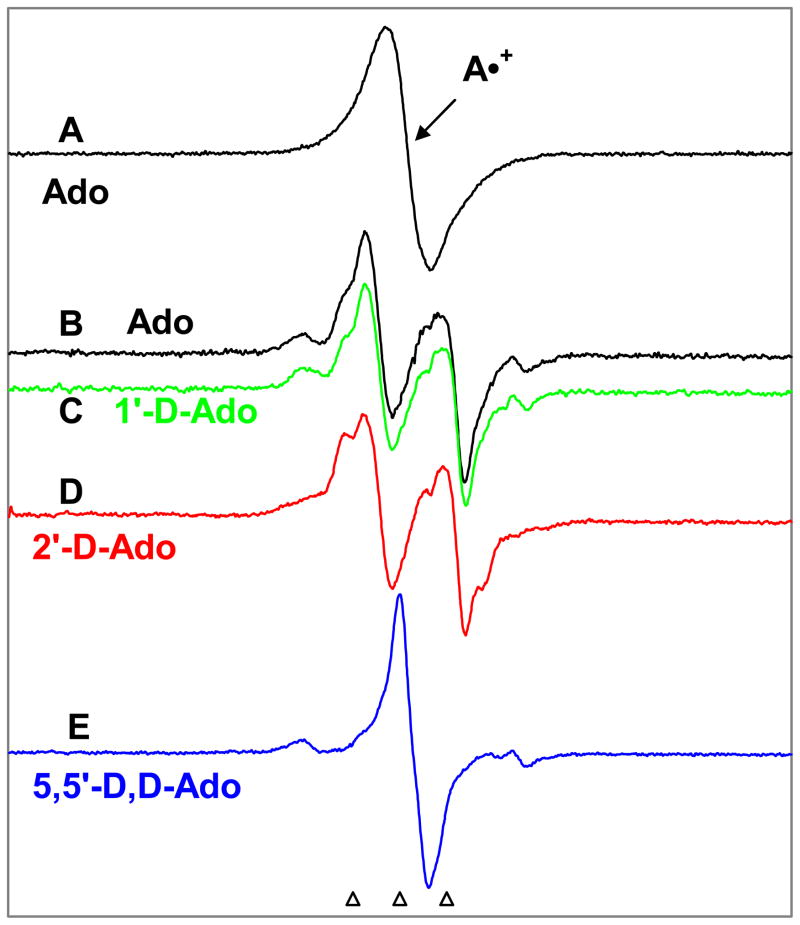
(A) Spectrum of A•+ in Ado in 7.5 M LiCl glass/D2O before illumination. (B) Spectrum after visible illumination at 143 K of the same sample used in (A) shows a nearly complete conversion to sugar radicals (Table II). A central doublet assigned to C5′• is present and a prominent quartet assigned to C3′• is also observed at the wings. (C) Spectrum after visible illumination at 143 K of A•+ in 1′-D-Ado. No change in spectra in B and C is noted. (D) Spectrum obtained after visible illumination at 143 K of A•+ in 2′-D-Ado. The central doublet from C5′• remains, but the end lines of the quartet assigned to C3′• are lost. (E) After visible illumination at 143 K of A•+ in 5′,5′-D,D-Ado. The central doublet assigned to C5′• has collapsed to a singlet. Photo-excitation was carried out for 140 min for each sample. All ESR spectra are recorded at 77 K.
Figure 3B shows the spectrum after 140 min of visible light illumination at 143 K. Analysis of the spectrum shown in Figure 2B using the benchmark spectrum of A•+ and those of the sugar radicals shown in Figure 1 (Spectra 1B and 1D) reveals that (i) photo-excitation of A•+ at 143 K in glassy samples of Ado leads to almost complete (ca. 95%) conversion to sugar radicals, and (ii) the spectrum in Figure 3B is a composite of C5′• (ca. 85%), C3′• (ca. 10%) and A•+ (ca. 5%) (Table II) (see also Figure 4).
Table II.
Extent of formation of sugar radicals via photo-excitation of A•+ in Ado and in its nucleotides at 143Ka,b,c
| Name of the Compound | Percent converted d | C3′• e | C5′•e | |
|---|---|---|---|---|
| Ado | 95 | 10 | 90 | |
| 2′-AMP | 95 | - | 100 | |
| 3′-AMP | 100 | - | 100 | |
| 5′-AMP | 87 | 85 | 15 | |
| (77 K) | 70 | 30 | 70 | |
| 5′-dAMP | 100 | 50f | 50f | |
| (77 K) | 30 | 30 | 70 | |
| 2′,3′-cAMP | 95 | – | 100 | |
Percentage expressed to ±10% relative error.
We have prepared all the glassy samples using 7.5 M LiCl (the native pH of 7.5 M LiCl is ca. 5) unless mentioned otherwise in table.
Samples were photo-excited at 143 K except as noted and all the spectra were recorded at 77 K.
Percentage of A•+ that converts to sugar radicals via photo-excitation. Within experimental uncertainties, we have found that the total spectral intensities before and after illumination were the same.
Each calculated as percentage of total sugar radical concentration - which sum to 100%.
From our published work.9
Figure 4.
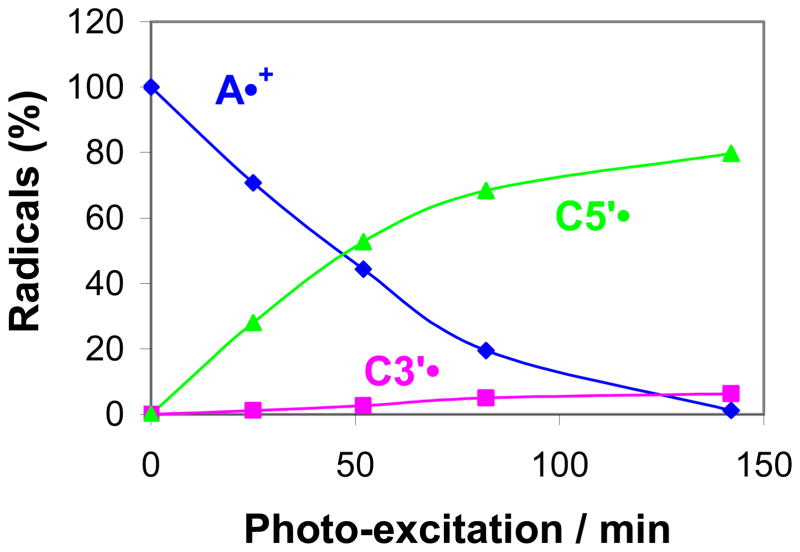
Extent of formation of C3′• and C5′• sugar radicals by excitation of A•+ (Ado) as a function of photo-excitation time at the native pD (ca. 5) of 7.5 M LiCl/D2O at 143 K in glassy samples of Ado.
1′-D-Ado
Using the same procedures used for glassy samples of Ado above, photo-excitation of A•+ has also been carried out using 1′-D-Ado resulting in the spectrum in Figure 3C. We find that the spectrum shown in Figure 3C for 1′-D-Ado shows no significant changes from the spectrum shown in Figure 3B for Ado samples. As a result of the smaller magnetic moment of deuterons, couplings from deuterium are only 15% (1/6.514) that of protons in the same site.13, 14 For this reason, any beta-proton coupling at C1′ would be lost owing to deuteration at that position. The fact that the spectra obtained via photo-excitation of A•+ in the glassy samples of Ado and 1′-D-Ado (i.e., Figures 3B and 3C) are identical makes it clear that no sugar radicals formed in Ado via photo-excitation of A•+ have a significant beta-proton coupling to the hydrogen at C1′-site. This eliminates the possibility of C2′• as a contributor to the spectrum of the sugar radical cohort in the spectrum 3B. The fact that the C2′• is not formed in Ado via photo-excitation of A•+ is unexpected as theory shows that in RNA and in its model systems (e.g., nucleoside), C2′-H bond is one of the weakest in the ribose moiety.22
2′-D-Ado (Identification of C3′•)
After photo-excitation of A•+ in the glassy samples of 2′-DAdo at 143 K, the resulting spectrum is shown in Figure 3D. In this case, the overall features of the central doublet in the spectrum in Figure 3D are the same as for Ado (Figure 3B) and for 1′-D-Ado (Figure 3C). However, comparison of wings in the spectrum 3D with those of spectrum 3B (for Ado) show the loss of the two outermost lines of the quartet assigned to C3′•. Following our work with Guo,8 and from the similarities observed between the spectra of sugar radical cohort from the samples of 2′-D-Ado and 2′-D-Guo (see supporting information Figure S1), analysis of the spectrum 3D shows that the larger coupling was lost for C3′•, and we, therefore, assign that the 41 G (1βH) hyperfine coupling is due to the hydrogen at C2′ and the 17 G (1βH) hyperfine coupling to the C4′-hydrogen atom. We have simulated this quartet ESR spectrum (see Figure 1) using these above-mentioned hyperfine couplings with a line-width of 4.5 G.8 We note here that the overall hyperfine splitting and the individual hyperfine couplings for the C3′• reported above matches very well with our findings in Guo samples.8
5′,5′-D,D-Ado (Identification of C5′•)
The spectrum found after photo-excitation of A•+ in 5′,5′-D,D-Ado at 143 K is shown in Figure 3E. As can be seen, the central (ca. -21 G) doublet observed in all the spectra 3B – 3D is replaced by a singlet. Comparing the A•+ spectrum shown in 3A with the singlet in spectrum 3E, we note that the singlet does not originate with any remaining A•+, as it differs considerably in shape and in the g-value (center of the spectrum) from the A•+ spectrum. Most importantly, the characteristic visible absorption associated with A•+ is lost after 140 min of photo-excitation.
The collapse of the central doublet to a singlet in 5′,5′-D,D-Ado but not in 1′-D-Ado and/or in 2′-D-Ado restricts the choice of radicals giving rise to the doublet to either C4′• or C5′•. C4′• is not a likely choice for a number of reasons:
In our earlier studies an unequivocal assignment of the identical doublet in dAdo to C5′• was made using 13C substituted dAdo with 13C substitution at C5′ position in the sugar moiety.9
for both 5′,5′-D,D-Guo 8 and 5′,5′-D,D-dGuo 2, we also found the collapse of a similar doublet (ca. 19 G) which we have assigned to C5′•. Deuteration at C3′ in 3′-D-Guo had no effect on the doublet spectrum in keeping with C5′• but not C4′•. 2
For these reasons, we assign the doublet in spectra 3B – 3D and the corresponding singlet in 3E to C5′•.
Formation of sugar radicals with photo-excitation time
In Figure 4, we have presented the data regarding formation of C5′• and C3′• with time via photo-excitation of the adenine cation radical in glassy samples of Ado. Using the benchmark spectrum of A•+ (Figure 1A) and those of the sugar radicals shown in Figure 1 (i.e. Figures 1B and 1D), we have obtained the radical percentages of A•+, C5′•, and C3′• at various photo-excitation times. Figure 4 clearly shows that, unlike Guo where C1′• was found,8 we do not observe formation of C1′• via A•+ during photo-excitation in glassy samples of Ado. Both in short and in long photo-excitation times, excitation of A•+ in glassy samples of Ado, produces C5′• and C3′• only with C5′• formed at ca. 15 times the rate of C3′• formation.
Photo-excitation of A•+ in glassy samples of adenine nucleotides
In Figure 5A, we present the ESR spectrum of one-electron oxidized adenine in 3′-AMP formed via oxidation by Cl2•− at pD 6. This spectrum shown in Figure 5A and the spectra of similarly one-electron-oxidized 2′-AMP, 5′-AMP, 5′,5′-D,D-AMP, and 2′,3′-cAMP at the native pD (ca. 5) of 7.5 M LiCl glass (not shown) match nicely with the spectrum of A•+ shown in Figure 3A (for Ado) and 1A (benchmark spectrum of A•+). Thus, via one-electron oxidation, each of the nucleotides is oxidized at the adenine moiety to produce A•+. As expected, 12a – 12c, 12e this similarity between the spectrum in 5A and that in 3A shows that during formation of A•+ in adenine ribonucleotides, oxidation does not occur at the sugar or phosphate moieties i.e., neither sugar nor phosphate radicals are formed on oxidation of AMPs.
Figure 5.
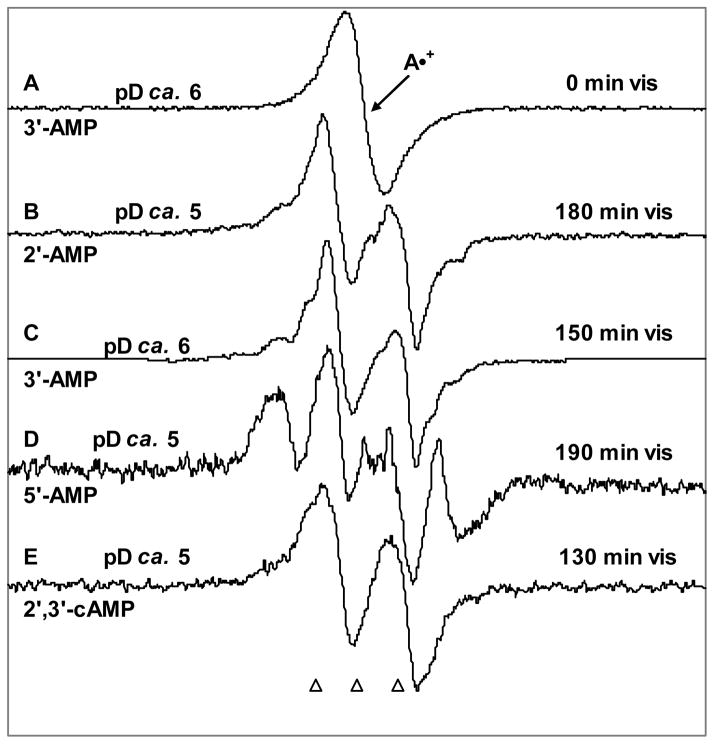
(A) ESR Spectrum from A•+ in 3′-AMP in a 7.5 M LiCl glass/D2O at pD ca. 6. (B) After illumination of A•+ in 2′-AMP for 180 min, C5′• is produced (see text). (C) Illumination of A•+ in 3′-AMP for 150 min at pD 6, this resulting spectrum is assigned to C5′•. (D) Spectrum after illumination of A•+ in 5′-AMP at pD ca. 5 for 180 min containing C3′• and C5′• found by subtraction of ca. 13% of the A•+ benchmark spectrum (Figure 1A). (E) Spectrum found after illumination of A•+ in 2′,3′-cAMP at pD ca. 5 for 180 min. This spectrum is assigned to C5′•. Each of the spectra (B), (C), (D) and (E) has an appropriate amount of A•+ spectrum (Figure 3A) subtracted (ca. 5%, 10%, 13% and 5% respectively) from the final spectra obtained after photo-excitation. All illuminations have been carried out with visible light at 143 K and all spectra were recorded at 77 K.
Figures 5B, D and E show the effect of visible illumination of A•+ in 2′-AMP, 5′-AMP and in 2′,3′-cAMP, respectively at the native pD (ca. 5) of 7.5 M LiCl glass whereas in Figure 5C, the effect of visible illumination of A•+ in 3′-AMP at pD ca. 6 in 7.5 M LiCl is presented.
Photo-excitation of A•+ in 2′-AMP
In Figure 5B, the ESR spectrum obtained after 180 minutes of visible light illumination at 143 K at the native pD (ca. 5) of the LiCl glass and after subtraction of A•+ (ca. 5%) in 2′-AMP is shown. The hyperfine splitting, line-shape and g-value shown in spectrum 5B is nearly identical to those found for the C5′• spectrum shown in Figure 1B (and in other works2, 9) and is also assigned to C5′• (see supporting information Figure S2).
Photo-excitation of A•+ in 3′-AMP
In Figure 5C, we present the ESR spectrum found in 3′-AMP samples at pD ca. 6 after photo-excitation of A•+ for 150 minutes. Note that subtraction of remaining A•+ (ca. 10%) was performed. This spectrum is also shown in Figure 6A. The spectrum shown in Figure 5C has the prominent doublet (ca. -21 G) at the center and further small line components at the wings as found for 2′ AMP and is assigned to C5′•.
Figure 6.
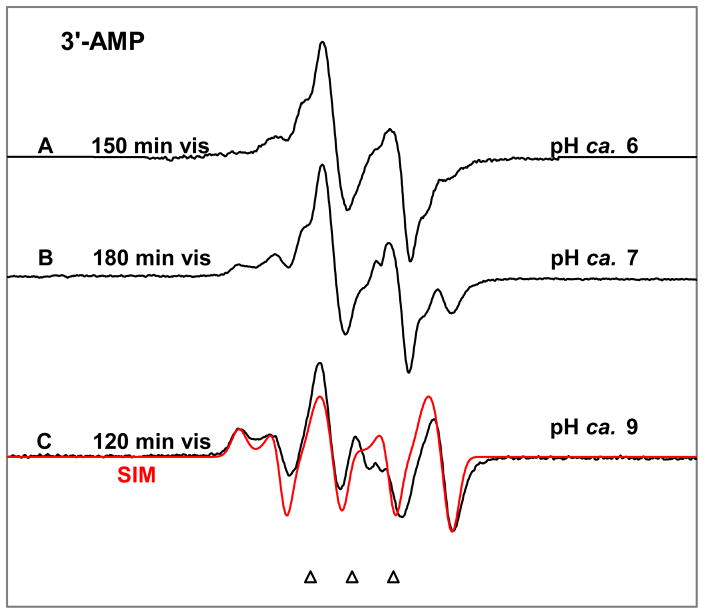
Spectra obtained after illumination of one-electron oxidized 3′-AMP in 7.5 M LiCl/D2O glass at pD 6, 7 and 9. The remaining A•+ has been subtracted from each spectrum. All spectra are attributed to C5′• which changes its conformation with increasing pD to show coupling to the C4′-H atom. With increase in pD of the glassy solution, the line components at the wings in spectrum become more visible (see spectrum C). Spectrum (C) is simulated (red color) using the parameters: 1αH (9.0, 15.0, 33.0) G, 1 βH (34.5, 34.5, 34.5) G, (2.0032, 2.0020, 2.0049), 4.5 G line-width with Lorentzian/Gaussian = 1.
pH dependence in the C5′• spectrum formed in 3′-AMP
In Figure 6, we report the ESR spectra of the C5′• formed via photo-excitation of A•+ in the glassy (7.5 M LiCl/D2O) samples of 3′-AMP at various pDs. The spectrum in Figure 6A obtained at pD ca. 6 is clearly the spectrum of the C5′• (see supporting information Figure S2). It is evident from the wings of the spectra shown in Figures 6B and 6C with respect to the wings in Figure 6A that as the pD of the solution is increased, along with the 21G anisotropic alpha coupling a new 34 G hyperfine beta-coupling arises which is assigned to the C4′-proton. At pD ca. 7, we have found that the spectrum 6B is a combination of spectrum 6A (65%) and spectrum 6C (35%) (see supporting information Figure S3). We assign this change in hyperfine coupling (spectrum 6A vs. spectrum 6C) to deprotonation at the phosphate moiety in 3′-AMP at the higher pD which leads to a conformational change in the C5′-radical induced by formation of a hydrogen bond between the 5′-OH and the phosphate dianion (see theory section). The pKa value for the first dissociation in the phosphate group of 5′-AMP has been reported in the literature as 6.21 in aqueous solution at ambient temperature.34, 35 Assuming the pKa value of the phosphate group in 3′-AMP to be close to that in 5′-AMP, and following our work showing that pKa of G•+ in these glassy samples at low temperature is ca. 1.5 unit higher than the pKa of G•+ in aqueous solution at ambient temperature,13 we predict that the pKa value of the phosphate group in 3′-AMP in our system (i.e., in glassy solution at temperature ca. 150 K) would be ca. (6.2 +1.5 = about 7.7). The relative concentrations of the two forms for C5′• (i.e., spectrum 6A and spectrum 6C) in Figure 6B indicates that the pKa of the phosphate group in the glassy solution of 3′-AMP at 150 K is ca. 7.5 and this value matches well with the expected value (ca. 7.7). Therefore, we assign the spectrum 6A (at pD ca. 6) and spectrum 6C (at pD ca. 9) to the C5′• containing monoacidic (charge = −1) and dibasic (charge = −2) forms of the phosphate group at C3′ respectively. We have simulated spectrum 6C using the parameters: 1αH (9.0, 15.0, 33.0) G, 1 βH (34.5, 34.5, 34.5) G, g = (2.0032, 2.0020, 2.0049), line-width (4.5, 4.5, 4.5) G and Lorentzian/Gaussian = 1. The simulation (red color) matches the experimental spectrum (black color) in Figure 6C well. The spectrum found in 6A is in accord with a conformation of the radical site in the C5′ radical that has a torsion angle of ca. 90° between the z-axis of the p-orbital at the C5′-radical site and the H-C4′ bond (see Figure 8C). Therefore, in this particular conformation of C5′• in 3′-AMP, the beta C4′-proton is in the nodal position of C5′-radical p-orbital which results in a small hyperfine coupling. On the other hand, the spectrum 6C corresponds to a conformation of the C5′• in 3′-AMP where the torsion angle between the z-axis of the C5′-radical p-orbital and the H-C4′ bond becomes ca. 36° (vide infra). In this conformation of C5′• in 3′-AMP a large beta C4′-proton hyperfine coupling is found (see Figure 8D). The -21 G alpha coupling is consistent with a C5′-radical site in a near-planar conformation as an alpha coupling decreases rapidly with radical site nonplanarity. For dAdo, 13C substitution at C5′-atom also gave 13C couplings consistent with a near planar conformation for C5′• in dAdo.9 For comparison, a similar study of C5′-radical in 3′-dAMP was performed. In this case, we did not observe a pH dependence.
Figure 8.
B3LYP/6-31G* optimized geometries of C5′-radical in (A) mono-protonated phosphate (PO4H−1) in the presence of 4 waters and (B) deprotonated form (PO4−2) in the presence of 3 waters. The atoms O5′, C5′, H5′, and C4′ are constrained in the same plane in (A) and (B). In (A) the dihedral angle H4′-C4′-C5′-O5″ was constrained to 0° whereas in (B) it is 54°. Figures (C) and (D) are the exposed views of the atoms O5′, C5′, H5′, and C4′ shown in Figures (A) and (B). Figure (C) shows that the C4′-H atom in Figure (A) is in the nodal plane of the p-orbital of C5′-radical; whereas, Figure (D) points out that it is lifted significantly out of the nodal plane and results in a large beta proton hyperfine coupling from the C4′-H atom in the C5′-radical.
Photo-excitation of A•+ in 5′-AMP
In Figure 5D, we present the ESR spectrum recorded at 77 K at the native pD (ca. 5) of 7.5 M LiCl/(D2O) glassy sample of 5′-AMP after photo-excitation of A•+ at 143 K for 190 minutes followed by subtraction of remaining A•+ (ca. 13%). This spectrum has far less of the central doublet (ca. 15% of total spectral intensity) as found in the spectra shown in Figures 5B and 5C. The spectrum is clearly dominated by a quartet. Subtraction of the C5′• doublet (ca. 15%) isolates the quartet (see supporting information Figure S4). The quartet results from two couplings of 34 G (1βH) and 15 G (1βH). A simulation using these couplings with g = 2.0027 and a line-width of 8.5 G is shown in supporting information Figure S4. We assign this quartet to C3′• for 5′-AMP. This justification for this assignment is presented below.
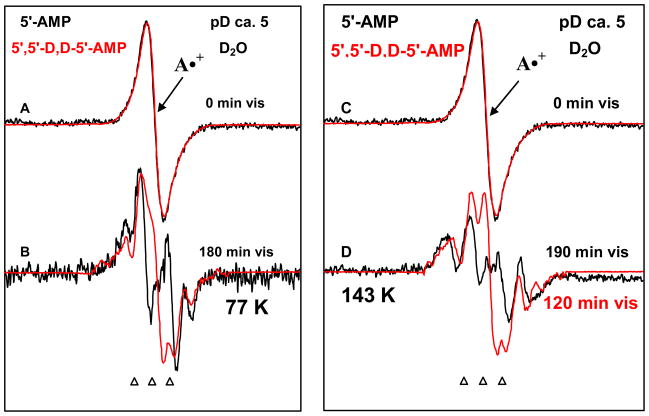
Photo-excitation of A•+ in 5′,5′-D,D-5′-AMP
In Figures 7A and 7C, we show the ESR spectrum of A•+ formed by one-electron oxidation reaction with Cl2•− in identically prepared, and handled samples of 5′-AMP (black color), and 5′,5′-D,D-5′-AMP (red color). Since the spin and charge are always located in the adenine moiety in these systems, it is expected and found in spectra 7A and 7C that the deuteration of both hydrogen atoms at C5′ in the sugar moiety of 5′,5′-D,D-5′-AMP does not show any effect on the A•+ spectrum.
Figure 7.
(A) and (C) Spectra of A•+ formed in identically prepared and handled samples of 5′-AMP (Black) and 5′,5′-D,D-5′-AMP (Red) before illumination. After visible illumination (B) at 77 K and (D) at 143 K of A•+ in 5′-AMP (Black) and 5′,5′-D,D-5′-AMP (Red) respectively. The spectra (B) and (D) of sugar radical cohort in 5′-AMP samples (Black) are obtained after subtraction of the adequate amount (ca. 30% (for 77 K) and ca. 13% (for 143K)) of A•+ spectrum (Figure 1A). After visible illumination at 77 K as well as at 143 K of A•+ in 5′-D,D-5′-AMP, the central doublet from C5′• has collapsed to a singlet, but the quartet assigned to C3′• is present in the sugar radical cohort. All ESR spectra are recorded at 77 K.
The spectra found after photo-excitation at 77 K of A•+ in 5′-AMP (Black) as well as of A•+ in 5′,5′-D,D- 5′-AMP (Red) followed by subtraction of the remaining A•+ (ca. 30% of the original spectrum in 5′-AMP samples), is shown in Figure 7B. In Figure 7D, we present the spectra obtained after photo-excitation at 143 K of A•+ in 5′-AMP (Black) as well as of A•+ in 5′,5′-D,D- 5′-AMP (Red) followed by subtraction of the remaining A•+ (ca. 13% of the original spectrum in 5′-AMP samples). As can be seen from Figures 7B and 7D, the central (ca. -21 G) doublet assigned to C5′• is converted to a singlet. We note here that the central singlet assigned to the 5-deuterated C5′• in Figures 7B and 7D do not originate with any remaining A•+, since it differs considerably in shape and g-value (i.e., the center of the spectrum) from the A•+ spectrum (Figure 7A, 7C).
It is evident from Figures 7B and 7D that the line components of the quartet are not affected owing to the deuteration at C5′ site in the sugar moiety in 5′,5′-D,D-5′-AMP samples. This eliminates the possibility of assignment of this quartet to C4′• since coupling to the C5 protons would be expected. Since deuteration at C1′- in Ado has established that C2′• is not formed, but, we still found the same C3′• signal (see Figures 3B and 3C). Therefore, we can confidently assign this quartet to C3′•.
Photo-excitation of A•+ in 2′,3′-cAMP
In Figure 5E, the ESR spectrum obtained after 130 minutes of visible light illumination at 143 K and after subtraction of A•+ (ca. 5%) in 2′,3′-cAMP is shown. This spectrum contains only a central doublet which is tentatively assigned to C5′•.
Theoretical calculations for C5′• in different states of phosphate (PO4H−1 and PO4−2) in 3′-AMP
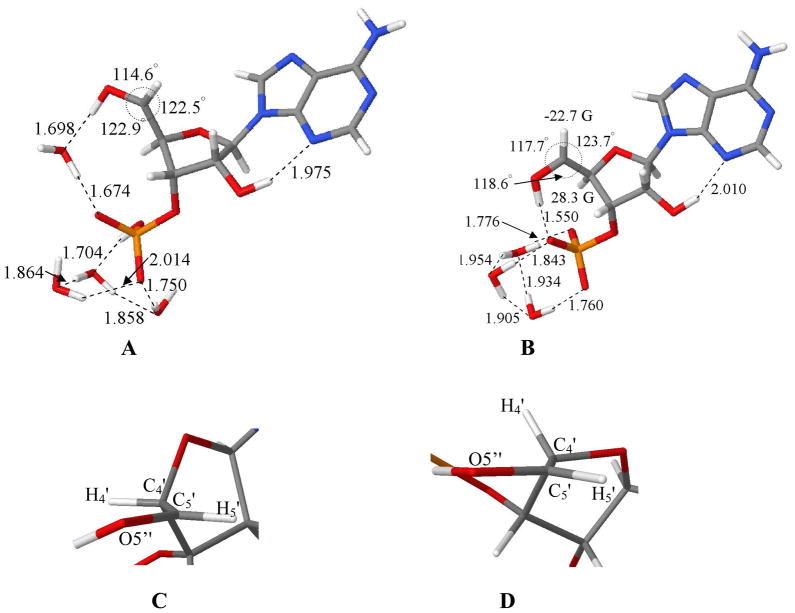
The B3LYP/6-31G* optimized geometries of C5′• in two protonation states of phosphate (PO4H−1 and PO4−2) in 3′-AMP are shown in Figure 8A and B, respectively. Our experimental findings using 13C-substitution at C5′-site in dAdo 9 and the C5′-radical α-coupling of ca. -21 G in both dAdo9 and in Ado (this work) clearly establish that conformation of C5′-radical site is near planar. Therefore, the C5′-radical site has been constrained to the planar conformation during geometry optimization in these calculations (i.e., C5′, C4′, O5″, and H5′ atoms are in a plane (see Figures 8A and B)).
A strong and direct hydrogen bonding between O5′–H----(PO4−2) apparently holds the C5′-radical in the conformation shown in Figure 8B. However, a weaker hydrogen bonding (1.7 Å) between O5′–H----(PO4H−1) is found (see supporting information Figure S5) that allows for competition with water hydrogen bonding and likely leads to variety of possible conformations of the C5′-radical. Therefore, we have introduced a water molecule between O5′–H and PO4H−1 and have optimized the whole structure as shown in Figure 8A. The hydrogen bond distances between O5′–H and water molecule as well the water molecule and PO4 moiety are both found to be ca. 1.7 Å (see Figure 8A). This tends to confirm that water can compete with direct hydrogen bonding between O5′–H----(PO4H−1).
The isotropic hyperfine coupling constants (HFCC) of C5′ (αH)-radical for structures 8A and 8B are found to be ca. -21 to -23 G and are not significantly dependent on the protonation state of the PO4 moiety. This theoretical isotropic HFCC value of the C5′ (αH) coupling is in good agreement with experiment which is (-)21G (Table I).
The isotropic HFCC of β (C4′–H) atom in C5′-radical with PO4H−1 in presence of 3 and 4 water molecules (Figure S5) were found to be 29 and 23 G, respectively. However, the HFCC value obtained for β (C4′–H) atom in C5′-radical in Ado and 3′-AMP in this work and in previous work with dAdo,9 dGuo,2 3′-dAMP9 clearly shows that the β (C4′–H) atom in C5′-radical has a HFCC of ca. 0 to 5 G. This small HFCC value clearly establishes that the beta C4′-proton is in the nodal position of C5′-radical p-orbital (see Figures 8C, D). This HFCC is therefore, is far lower than the corresponding theoretically calculated value. Thus, in order to mimic the experimental conformation the dihedral angle H4′-C4′-C5′-O5′ was constrained to 0°, for C5′-radical with PO4H−1 and we represent this conformation in Figure 8A. This conformation is approximately 1.2 kcal mol−1 higher in stability than the conformation shown in supporting information Figure S5 in which the dihedral angle H4′-C4′-C5′-O5″ was relaxed and is clearly accessible in a fully hydrated system.
The isotropic HFCC of β (C4′–H) atom in C5′-radical with PO4−2 in presence of 3 water molecules (Figure 8B) was found to be 28.3 G. This is reasonably close to the experimentally observed HFCC value of ca. 34.5 G.
We note here that a variety of conformations for C5′-radical with PO4H−1 likely exist in addition to the dominant contribution shown in Figure 8A. In fact, some small components in the spectra shown in Figure 5B, C as well as in 6A and B likely are contributions from such conformations. However, the strong hydrogen bonding between O5′–H and the PO4 moiety in C5′-radical with PO4−2 forces the C5′-radical site to adapt a single conformation where the β (C4′-H) proton has a large HFCC.
TD-DFT calculations
TD-DFT (B3LYP) calculations were preformed in Ado cation radical employing 6-31G(d) basis set and the 13 lowest transition energies were calculated. The molecular orbital involved in each electronic transition, along with their transition energies (in eV) are shown in supporting information Figure S6 and supporting information Table T1. We have shown the dominant molecular orbitals involved in these excitations in Figure S6 and a representative transition in Figure 9.
Figure 9.
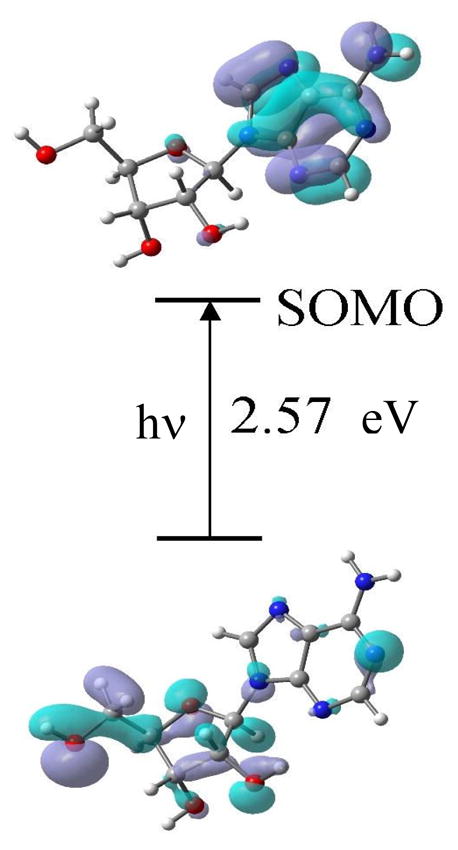
Representative TD-B3LYP/6-31G(d) calculated electronic transition (10th) occurring from inner core doubly occupied molecular orbital (62β) to 70 β SOMO (singly occupied molecular orbital). This transition as most others show significant hole localization at C5′ in the excited state. After the transition the lower figure represents the SOMO showing the hole moves from base to sugar.
From molecular orbital plots shown in Figure 9 and S6, it is clearly evident that, in the ground state, SOMO is localized on the adenine base in Ado cation radical in agreement with experiment. During electronic excitations, the hole transfers from adenine base to the sugar moiety. In most of the transitions shown in Figure S6 we found that the hole is largely is localized on C5′ in the sugar moiety. C5′ is the major site of radical formation as observed experimentally in Figure 3. However, other sugar sites in the excited state including C3′ as well as C1′ and C2′ (see electronic transitions S4, S5, S10, S11, S13 in Figure S6) also show some extent of hole localization; however, apart from C5′•, the other only experimentally observable sugar radical is C3′•.
Conclusion
(i) Formation and nature of A•+ formed in Ado and in its nucleotides via one-electron oxidation
We attribute the formation of A•+ in Ado, in deuterated derivatives of Ado, and in the nucleotides of Ado studied here in homogenous aqueous glassy solutions at low temperature to the cation radical A•+ based in part upon previous results for dAdo.14 The deprotonated species (A(-H)•) for Ado in this and previous work14 is found only at pH ca. 8 and above. In aqueous solutions at ambient temperature the pKa of A•+ was <1,10,11 thus A(-H)• would be expected from pH 1 and above (see Introduction). This stabilization found in our system at low temperatures is attributed to association with other Ado molecules which allows for a sharing of the hole via a charge-resonance interactions.
This work and our earlier work with guanine and adenine deoxynucleotides2, 8, 9 have shown that on one-electron oxidation, localization of the hole in these compounds always takes place in the base moiety. In adenine nucleotides investigated in this work one-electron oxidation also results in hole localization on the adenine moiety. Theoretical calculations 12e and references therein also predict that localization will be on the base except when the phosphate is left as a negatively charged without counterion or solvation in which case localization occurs at the phosphate. The latter situation would only be applicable to the gas phase.12e
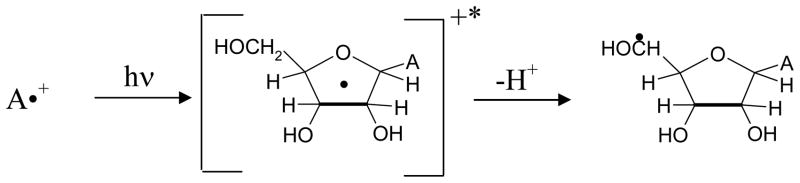
(ii) Mechanism of formation of sugar radicals in Ado and in its nucleotides via photo-excitation of A•+
In this work, we have observed neutral sugar radical formation in Ado and in its nucleotides at specific sites in the sugar moiety via deprotonation of the excited A•+ as shown in scheme 3.
Scheme 3.
Formation of a sugar radical e.g., C5′• via photo-excited A•+.
Neutral sugar radical formation by photo-excitation of an one-electron oxidized base is now shown to be well established mechanism in deoxynucleotides, DNA oligos, DNA1 – 7, 9 and guanine ribonucleotides and RNA8.
(iii) Identification of sugar radicals formed via photo-excitation of A•+ in Ado
In Table II, we have summarized our experimental data regarding formation of sugar radicals via photo-excitation of A•+ in Ado and in its nucleotides. It is evident from Table II that in Ado, on photo-excitation of A•+, C3′• and C5′• are formed without significant contributions from other sites. We note that the gas phase ONIOM-G3B3 calculations of the C–H bond energies for the adenosine ribose moiety in Ado give the following relative energies in kcal mol−1: C4′ (0.0) < C5′ (0.1) < C1′ (0.4) < C2′ (1.2) < C3′ (2.8).22 As can be seen, the bond energies at each site (except at C3′-site) are within 1 kcal/mol and would suggest no preference except that formation of C3′• would be the least favored. In fact, we do not observe C1′•, C2′•, or C4′• production in the sugar radical cohort and only C5′• and C3′• are formed. Clearly bond energy arguments fail to account for the specific formation C3′• and C5′• in Ado.
Our work with 3′-dGMP,2 5′-dGMP,2 3′-dAMP,9 5′-dAMP,9 and 5′-GMP8 demonstrates that the substitution of phosphate at C3′- and at C5′-sites lead to deactivation in the formation of C3′• and C5′• as found in this work (Table II). Theoretical calculations carried out in our laboratory23, 24 and the more recent ONIOM-G3B3 calculations22 also show that substitution of phosphate at a site leads to a significant higher bond energy and deactivation at that site. However, C-H bond energies are obviously not the dominant overall factors underlying radical formation in adenine nucleotides, since C2′• would be then be the predominant radical formed and we find no observable spectrum of C2′•. Thus, the lack of C2′• formation in the adenine nucleotides again points to the relevance of the effect of spin and charge distribution on the sugar moiety in the excited hole. Our TD-DFT calculations do show that C5′-site in adenosine cation radical is the major site for hole localization in the excited state of the cation and deprotonation from this site we believe is a dominant mechanism for radical formation on photoexcitation. We note on excitation of A•+ and hole transfer to the sugar component that the availability of proton acceptor sites around the sugar are likely to be involved in the formation of sugar radicals. Of course, thermodynamic factors such as C-H bond energies are likely to contribute but the lack of significant deuterium isotope effects on the relative radical production (see Figure 3) suggests that this is not a dominant factor. Thus the deprotonation leading to neutral sugar radical production is kinetically rather than thermodynamically controlled. Hole distribution in the excited state is apparently the dominant driving force for neutral sugar radical production.
(iv) Temperature dependent formation of C5′• on photo-excitation of A•+ in 5′-AMP samples
In agreement with our previous works 2, 8 with 5′-dGMP and 5′-GMP on photo-excitation of G•+ at 77 K, we have observed that C5′• production dominates on photo-excitation of A•+ in both 5′-AMP and 5′-dAMP samples (see Table II) at 77 K. On the other hand, similar to the results found in 5′-dGMP 2 and in 5′-GMP,8 C5′• is found not to be the predominant radical in the sugar radical cohort formed via photo-excitation at 143 K. These results, therefore, clearly establish that the site of deprotonation in the excited cation radical changes with temperature. We attribute this to softening of the aqueous glass at 143 K which allows for molecular relaxation in the excited state and may provide alternative deprotonation pathways for each conformation as the hole distribution would likely differ with structural form. Recent experimental findings showing increases in excited state proton transfer rates with decreasing viscosity in protic media36 would explain the greater efficiency in deprotonation found at 143 K vs. 77 K (Table II).
(v) Prediction of the pKa of the phosphate moiety in the C5′• of 3′-AMP
The experimental results presented in Figure 6 and the theoretical results shown in Figure 8 clearly establish the two different conformations of C5′• in 3′-AMP, i.e., one where the beta C4′-proton in the nodal position of C5′-radical p-orbital (i.e., spectrum in Figure 6A and structure in Figure 8A) and, (ii) one with a conformation that gives a large beta C4′-proton hyperfine coupling (spectrum in Figure 6C and the structure in Figure 8B)). The first conformation is assigned to the species with the monoprotonated phosphate (i.e., PO4H−1) and the second to the species (i.e., PO4−2) after deprotonation. The relative contributions of these two conformations with pH, directly yield the pKa of the phosphate group in the C5′-radical of 3′-AMP at 150 K as ca. 7.5. This value compares well with that expected (ca. 7.7) for a nucleotide in our system and suggests that the C5′• does not have a significant influence on this pKa. This conformational dependence of C5′• with pH is not observed in 3′-dAMP.
Supplementary Material
Acknowledgments
This work has been supported by the NIH NCI under grant no. R01CA045424. We are grateful to Arctic Region Supercomputing Center (ARSC) for a generous grant of CPU and facilities. Computational studies were also supported by a computational facilities grant NSF CHE-0722689. We are grateful to Omicron Biochemicals Inc. for timely syntheses of the deuterated Ado derivatives used in this work. We also thank S. Collins for his assistance in the experiments.
Footnotes
Supporting information available:
Supporting information include the following. Figure S1 showing the similarities of sugar radical cohort formed in glassy samples of 2′-D-Ado and of 2′-D-Guo via photo-excitation of A•+ and G•+ respectively. Figure S2 represents the similarities in the ESR spectra of C5′• observed in 3′-AMP (this work), 3′-dAMP (ref. 9), and 3′-dGMP (ref. 2). Figure S3 shows that ESR spectyrum of C5′• in 3′-AMP formed at pD ca. 7 has about 35% contribution from C5′• in 3′-AMP formed at pD ca. 9. Figure S4 represents the isolation of C3′• radical spectrum in 5′-AMP samples as well as its isotropic simulation. Figure S5 shows the B3LYP/6-31G* optimized geometries of C5′-radical in PO4H−1 in the presence of 4 waters. Figure S6 shows the TD-B3LYP/6-31G(d) calculated electronic transitions from inner core molecular orbitals to 70 β SOMO (singly occupied molecular orbital) in Ado cation radical. Table T1 represents the output of TD-B3LYP/6-31G(d) calculated electronic transitions. Finally, a full reference 30a is given. This information is available free of charge via the internet at http://pubs.acs.org/.
References
- 1.Shukla LI, Pazdro R, Huang J, DeVreugd C, Becker D, Sevilla MD. Radiation Research. 2004;161:582–590. doi: 10.1667/rr3167. [DOI] [PubMed] [Google Scholar]
- 2.Adhikary A, Malkhasian AYS, Collins S, Koppen J, Becker D, Sevilla MD. Nucleic Acids Res. 2005;32:5553–5564. doi: 10.1093/nar/gki857. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Adhikary A, Kumar A, Sevilla MD. Radiation Research. 2006;165:479–484. doi: 10.1667/rr3563.1. [DOI] [PubMed] [Google Scholar]
- 4.Adhikary A, Collins S, Khanduri D, Sevilla MD. J Phys Chem B. 2007;111:7415–7421. doi: 10.1021/jp071107c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Kumar A, Sevilla MD. J Phys Chem B. 2006;110:24181–24188. doi: 10.1021/jp064524i. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Becker D, Adhikary A, Sevilla MD. In: In Charge Migration in DNA: Physics, Chemistry and Biology Perspectives. Chakraborty T, editor. Springer-Verlag; Berlin, Heidelberg, New York: 2007. pp. 139–175. [Google Scholar]
- 7.Kumar A, Sevilla MD. In: Radiation Induced Molecular Phenomena in Nucleic Acid: A Comprehensive Theoretical and Experimental Analysis. Shukla MK, Leszczynski J, editors. Springer-Verlag; Berlin, Heidelberg, New York: 2008. pp. 577–617. [Google Scholar]
- 8.Khanduri D, Collins S, Kumar A, Adhikary A, Sevilla MD. J Phys Chem B. 2008;112:2168–2178. doi: 10.1021/jp077429y. [DOI] [PubMed] [Google Scholar]
- 9.Adhikary A, Becker D, Collins S, Koppen J, Sevilla MD. Nucleic Acids Res. 2006;34:1501–1511. doi: 10.1093/nar/gkl026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Steenken S. Chem Rev. 1989;89:503–520. [Google Scholar]
- 11.(a) Steenken S. Free Rad Res Commun. 1992;16:349–379. doi: 10.3109/10715769209049187. [DOI] [PubMed] [Google Scholar]; (b) Steenken S. Biol Chem. 1997;378:1293–1297. [PubMed] [Google Scholar]
- 12.(a) Close DM, Nelson WH. Radiation Research. 1989;117:367–378. [PubMed] [Google Scholar]; (b) Nelson WH, Sagstuen E, Hole EO, Close DM. Radiation Research. 1992;131:272–284. [PubMed] [Google Scholar]; (c) Hole EO, Sagstuen E, Nelson WH, Close DM. Radiation Research. 1995;144:258–265. [PubMed] [Google Scholar]; (d) Kar L, Bernhard WA. Radiation Research. 1983;93:232–253. [Google Scholar]; (e) Close DM. J Phys Chem B. 2008;112:8411–8417. doi: 10.1021/jp804243k. [DOI] [PubMed] [Google Scholar]; (f) Close DM. In: Radiation Induced Molecular Phenomena in Nucleic Acid: A Comprehensive Theoretical and Experimental Analysis. Shukla MK, Leszczynski J, editors. Springer-Verlag; Berlin, Heidelberg, New York: 2008. pp. 493–529. [Google Scholar]; (g) Bernhard WA, Close DM. In: In Charged Particle and Photon Interactions with Matter Chemical, Physicochemical and Biological Consequences with Applications. Mozumdar A, Hatano Y, editors. Marcel Dekkar, Inc; New York, Basel: 2004. pp. 431–470. [Google Scholar]
- 13.Adhikary A, Kumar A, Becker D, Sevilla MD. J Phys Chem B. 2006;110:24171–24180. doi: 10.1021/jp064361y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Adhikary A, Kumar A, Khanduri D, Sevilla MD. J Am Chem Soc. 2008;130:10282–10292. doi: 10.1021/ja802122s. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Giese B. Ann Rev Biochem. 2002;71:51–70. doi: 10.1146/annurev.biochem.71.083101.134037. [DOI] [PubMed] [Google Scholar]
- 16.Giese B, Amaudrut J, Köhler A-K, Spormann M, Wessely S. Nature. 2001;412:318–320. doi: 10.1038/35085542. [DOI] [PubMed] [Google Scholar]
- 17.Kawai K, Majima T. In: Charge Transfer in DNA: From Mechanism to Application. Wagenknecht H-A, editor. Wiley-VCH Verlag GmbH & Co. KGaA; Weiheim: 2005. pp. 117–151. [Google Scholar]
- 18.Lewis FD, Daublain P, Zhang L, Cohen B, Vura-Weis J, Wasielewski MR, Shafirovich V, Wang Q, Raytchev M, Fiebig T. J Phys Chem B. 2008;112:3838–3843. doi: 10.1021/jp710718p. [DOI] [PubMed] [Google Scholar]
- 19.Augustyn KE, Genereux JC, Barton JK. Angew Chem Int Ed Engl. 2007;46:5731–5733. doi: 10.1002/anie.200701522. [DOI] [PubMed] [Google Scholar]
- 20.Joy A, Ghosh AK, Schuster GB. J Am Chem Soc. 2006;128:5346–5347. doi: 10.1021/ja058758b. [DOI] [PubMed] [Google Scholar]
- 21.Shao F, O’Neill MA, Barton JK. Proc Natl Acad Sci USA. 2004;101:17914–17919. doi: 10.1073/pnas.0408128101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Li M-J, Liu L, Fu Y, Guo Q-X. J Phys Chem B. 2006;110:13582–13589. doi: 10.1021/jp060331j. [DOI] [PubMed] [Google Scholar]
- 23.Colson A-O, Sevilla MD. Int J Radiat Biol. 1995;67:627–645. doi: 10.1080/09553009514550751. [DOI] [PubMed] [Google Scholar]
- 24.Colson A-O, Sevilla MD. J Phys Chem. 1995;99:3867–3874. [Google Scholar]
- 25.Guerra M. Res Chem Intermed. 2002;28:257–264. [Google Scholar]
- 26.Sänger W. Principles of Nucleic Acid Structure. Springer-Verlag; New York: 1984. pp. 18–21.pp. 48pp. 55pp. 62–63. [Google Scholar]
- 27.Parr KD, Wetmore SD. Chem Phys Lett. 2004;389:75–82. [Google Scholar]
- 28.Wetmore SD, Boyd RJ, Eriksson LA. J Phys Chem B. 1998;102:7674–7686. [Google Scholar]
- 29.Guerra M. Phys Chem Chem Phys. 2001;3:3792–3796. [Google Scholar]
- 30.Shukla LI, Adhikary A, Pazdro R, Becker D, Sevilla MD. Nucleic Acids Res. 2004;32:6565–6574. doi: 10.1093/nar/gkh989. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.(a) Frisch MJ, et al. Gaussian03, Revision B.04. Gaussian, Inc; Pittsburgh, PA: 2003. (For complete Reference, see supporting information) [Google Scholar]; (b) An Open-Science Project © 2004. Jmol development team; http://jmol.sourceforge.net. [Google Scholar]
- 32.(a) Malikin VG, Malkina OL, Eriksson LA, Salahub DR. In: In Modern Density Functional Theory, A Tool for Chemistry. Seminario JM, Politzer P, editors. Elsevier; New York: 1995. p. 273. [Google Scholar]; (b) Engels B, Eriksson LA, Lunell S. Adv Quantum Chem. 1996;27:297. [Google Scholar]
- 33.(a) Hermosilla L, Calle P, García de La Vega PM, Sieiro C. J Phys Chem A. 2005;109:1114–1124. doi: 10.1021/jp0466901. [DOI] [PubMed] [Google Scholar]; (b) Hermosilla L, Calle P, García de la Vega JM, Sieiro C. J Phys Chem A. 2006;110:13600–13608. doi: 10.1021/jp064900z. [DOI] [PubMed] [Google Scholar]
- 34.Sigel H, Massoud SS, Corfu NA. J Am Chem Soc. 1994;116:2958–2971. [Google Scholar]
- 35.Mucha A, Knobloch B, Jeżowska-Bojczuk M, Kozlowski H, Sigel RKO. Chem Eur J. 2008;14:6663–6671. doi: 10.1002/chem.200800496. [DOI] [PubMed] [Google Scholar]
- 36.Yushchenko DA, Shvadchak VV, Klymchenko AS, Duportail G, Pivovarenko VG, Mély Y. J Phys Chem A. 2007;111:10435–10438. doi: 10.1021/jp074726u. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.