Genome-wide association of an integrated osteoporosis-related phenotype: is there evidence for pleiotropic genes?

Abstract

Multiple musculoskeletal traits assessed by various methods at different skeletal sites serve as surrogates for osteoporosis risk. However, it is a challenge to select the most relevant phenotypes for genetic study of fractures.

Principal component analyses (PCA) were conducted in participants of the Framingham Osteoporosis Study on 17 measures including BMD (hip and spine), heel ultrasound, leg lean mass (LLM), and hip geometric indices, adjusting for covariates (age, height, BMI), in a combined sample of 1,180 men and 1,758 women, as well as in each sex. Four principal components (PCs) jointly explained ~69% of the total variability of musculoskeletal traits. PC1, explaining ~33% of the total variance, was referred to as the component of “Bone strength”, since it included the hip and spine BMD as well as several hip cross-sectional properties. PC2 (20.5% variance) was labeled as “Femoral cross-sectional geometry“; PC3 (~8% variance) captured only ultrasound measures; PC4, explaining ~7% variance, was correlated with LLM and hip geometry.

We then evaluated ~2,5 mil SNPs for association with PCs 1, 2, and 4. There were genome-wide significant associations (p < 5 × 10⁻⁸) between PC2 and HTR1E (that codes for one of the serotonin receptors) and PC4 with COL4A2 in women. In the sexes-combined sample, AKAP6 was associated with PC2 (p= 1.40 × 10⁻⁷). A SNP in HTR1E was also associated with the risk of non-vertebral fractures in women (p= 0.005). Functions of top associated genes were enriched for the skeletal and muscular system development (p < 0.05).

In conclusion, multivariate combination provides genetic associations not identified in the analysis of primary phenotypes. Genome-wide screening for the linear combinations of multiple osteoporosis-related phenotypes suggests that there are variants with potentially pleiotropic effects in established and novel pathways to be followed up to provide further evidence of their functions.

INTRODUCTION

Age-related osteoporotic fractures are common in the U.S. and represent a major public health threat that is likely to increase in importance as the population ages⁽¹⁾. Osteoporotic fracture is heritable; however, the fracture phenotype is a difficult one to study genetically: fractures typically do not occur until later in life, and are influenced by factors outside of the skeleton. Therefore, risk factors for osteoporotic fracture (proxy phenotypes), such as bone mineral density (BMD), bone quantitative ultrasound (QUS), and bone geometry are traditionally investigated, since these quantitative traits predict risk of osteoporotic fractures^(2–5) and may be reliably measured at any age. Studies over the last decades have documented the major contribution of genes to BMD^(6–7), QUS⁽⁸⁾, and bone geometry^(9–10). Since fracture is a product of both bone strength and forces applied to the skeleton, muscle mass has also been considered to be a risk factor for fractures⁽¹¹⁾; moreover, it is characterized by a shared heritability with bone strength properties^(12–13).

It is important to realize that none of these proxies is a perfect phenotype of osteoporosis, especially for a genetic study. There might be some unique information obtained from each risk factor, however, since these phenotypes are correlated and partially redundant, a study of the commonality of genetic associations among these traits may prove useful in obtaining a more complete understanding of the mechanisms underlying fracture susceptibility. Genetic markers that influence highly correlated traits can be detected by several methods. One approach to extract non-redundant information is to apply principal component analysis (PCA) to the data. PCA transforms the original phenotypes to an equal number of orthogonal factors (PCs), each defined as a specific linear combination of the original phenotypes.

In earlier work, we applied PCA to BMD and heel ultrasound measures; we identified two independent heritable PCs, which were linked to several chromosomal regions⁽¹⁴⁾. QTLs for these integrated phenotypes were further replicated by a large-scale meta-analysis of BMD⁽¹⁵⁾, attesting to the power and merits of this approach. PCA analysis has been applied by others to multiple bone-related traits in mice^(16–17). We hypothesized that using a composite measure of several correlated phenotypes may provide new and complementary insights into the genetics of osteoporosis, by both reducing the measurement error of several related variables and improving genetic signals through an integrated phenotype definition. Correlated musculoskeletal phenotypes should therefore point towards gene networks that may contribute to these phenotypes^(18–19).

MATERIALS AND METHODS

Sample

The sample used for our analyses was derived from two cohorts of the population-based Framingham Heart Study (FHS). FHS is a large, longitudinal population- and family-based study with multiple well-characterized phenotypes that began in 1948 in Framingham, MA, with the enrollment of 5,209 men and women ages 28 to 62 years (Original Cohort). In 1971 the FHS Offspring Study was initiated by enrolling 5,124 adult children of the Original Cohort and their spouses. Details and descriptions of the Framingham Osteoporosis Study are provided elsewhere^(20–23) as well as publicly available through the Database of Genotype and Phenotype (dbGaP) at http://view.ncbi.nlm.nih.gov/dbgap. In brief, the Original and the Offspring Cohorts in the Osteoporosis Study represent adult members of two-generational (mostly nuclear) families. The Osteoporosis Study was approved by the Institutional Review Boards for Human Subjects Research of Boston University and Hebrew SeniorLife and all participants provided written informed consent.

Osteoporosis-related musculoskeletal phenotypes

The following measures were available in members of both Framingham Cohorts:

Bone mineral density (BMD)

The participants underwent bone densitometry by dual energy x-ray absorptiometry (DXA) with a Lunar DPX-L (Lunar Corp., Madison, WI) between 1996–2001. The coefficients of variation (CV) in normal subjects for the DPX-L have been previously reported to be 0.9% for the lumbar spine (LS), 1.7% for the femoral neck (FN), and 2.5% for the trochanter BMD⁽²⁰⁾.

Quantitative ultrasound (QUS)

calcaneal broadband ultrasound attenuation (BUA) and speed of sound (SOS) were measured with a Sahara® bone sonometer (Hologic, Inc., Waltham, MA), between 1996–2001. Based on duplicate, same-day measurements on 29 subjects, CVs for BUA and SOS were 5.3% and 0.4%, respectively⁽²⁴⁾.

Hip geometry

DXA scans were measured with an interactive computer program⁽²⁵⁾. The program derived a number of proximal femoral structural variables, including (a) gross anatomic measures, such as femoral neck length (FNL), neck-shaft angle (NSA), and subperiosteal diameter (width, cm), and (b) cross-sectional indices, such as cross-sectional bone area (CSA, cm²), section modulus (Z, cm³), and Buckling Ratio (unitless) at the two femoral regions (narrow neck, NN, and the femoral shaft, S). CVs were previously reported to range from 3.3% (NN outer diameter) to 9.1% (FNL)⁽²⁵⁾.

Body composition

Whole body DXA scans were obtained from the study participants with the same Lunar DPX-L machine used for BMD and at the same visit. The scans were collected at medium speed for all subjects regardless of weight or body thickness. Regions of interest were analyzed using the standard Lunar software for body composition. Leg lean mass (LLM, kg) was derived by subtracting regional bone mineral content from the fat-free mass of the lower extremities.

Non-Vertebral fractures

Using the assessment protocol in the Framingham Osteoporosis study that has been reported previously⁽²⁶⁾: incident fractures were reported in the Offspring, by interview at each examination (conducted every 4 years) or by telephone interview for participants unable to attend examinations. Fractures included hip, wrist, pelvis, femur, humerus, rib, sternum, lower arm, ankle and lower leg fractures, and were confirmed by review of medical records and radiographic and operative reports, when available. Whenever possible, fractures due to high trauma (e.g. a fall from higher than standing height, severe traffic accidents) were excluded; multiple simultaneous fractures in different sites were counted as one fracture. The Offspring cohort's participants were followed for fractures from the date of the DXA scan through December 31, 2007.

Other measurements (covariates)

Information on age, sex, height, body mass index (BMI), and in women, menopausal status and estrogen use, were obtained for each participant at the time of the musculoskeletal measurement. Details for these measurements are available elsewhere^(20,27).

Genotyping, Quality Control, and Imputation

Genotyping was conducted through the FHS SHARe (SNP Health Association Resource) project initiated in 2007 on all Framingham Study participants with DNA available, using the Affymetrix 500K (250K Sty and 250K Nsp) mapping array and the Affymetrix 50K supplemental gene-centric array (50K MIP). A total of 549,827 SNPs were genotyped in 9,274 FHS subjects. We excluded 793 individuals with an average SNP call rate < 0.97. We also excluded SNPs with call rate < 0.95 (34,868 SNPs); Hardy-Weinberg equilibrium test p-value < 10⁻⁶ (8,531 SNPs); minor allele frequency (MAF) < 0.01 (66,829 SNPs); or unknown genomic annotation (6,089 SNPs). Genotyping from 433,510 SNPs in 8,481 individuals passed these quality control measures.

SNP imputation in the FHS was performed on all 8,481 individuals, using MACH2, which outputted imputed dosages for all autosomal 2,543,887 SNPs on HapMap CEU release 22, build 36. Imputation of 57,197 SNPs for the X chromosome was performed with the program IMPUTE. SNPs with the imputed variance ratio < 0.3 were excluded.

Population Substructure

A principal component analysis was performed using EIGENSTRAT⁽²⁸⁾ to model differences of individuals' ancestral genetic background (to infer axes of variation) using a subset of 425,173 SNPs with MAF ≥0.01, HWE p ≥10⁻⁶, and call rate ≥0.95. SNP weights for 10 principal components (EIGENSTRAT-PCs) were calculated using a maximal set of independent individuals (n=882); the PCs for the remaining individuals were computed using the SNP weights obtained from this subset of unrelated individuals. EIGENSTRAT-PCs that were significantly associated with musculoskeletal PC phenotypes (p<0.05) were adjusted for in our GWAS analyses to minimize spurious associations due to population substructure.

Statistical analysis

Principal component analysis (PCA) of the musculoskeletal traits

Measures including BMD (hip and spine), heel ultrasound, leg lean mass, and hip geometric indices were adjusted for covariates: age, height, BMI (and sex in combined sample). PCA was conducted in a combined sample of 1,180 men and 1,758 women who had all the studied traits measured (non-missing), using the information from the entire correlation coefficient matrix of these phenotypes (provided in Supplementary Table 3). Our analyses were also performed in men and women separately, because musculoskeletal traits, especially BMD, bone geometry and muscle mass, are sexually dimorphic. PCA was conducted in order to (a) examine the inter-relationship among the variables and (b) produce a substantially smaller number of independent (uncorrelated) hypothetical underlying factors⁽²⁹⁾. This analysis produces linear combinations of the original measures that capture most of the information (variance) of these measures. The first principle component (PC1) accounts for as much of the variability in the data as possible. The analysis was performed in two stages: 1) factor extraction and 2) rotation of the principal components using the Varimax option. Those factors with eigenvalues > 1.0 were retained for further investigation. We calculated PCs using weights from PCA of unrelated subjects in our data. To obtain representative estimates of the weights for the rest of the sample, we used averages from 10,000 PCAs of re-sampled unrelated subjects.

Genome-Wide Association Study

We performed GWAS analyses of musculoskeletal PCs using population-based additive linear mixed effects (LME) models⁽³⁰⁾ with ~2.5 mil SNPs, in sexes-combined sample, as well as in the women-only subsample. In addition to adjusting for covariates, LME regression models account for correlations due to family relationships in pedigrees of arbitrary sizes and varying degrees of relationship. Since all the SNPs were imputed, we used the expected dosages (number ranging between 0 and 2) in our regression models. Further, to minimize missing genotypes in our data, we used only well-imputed SNPs in our analyses. SNP associations at p<5 × 10⁻⁸ were considered to be genome-wide significant (GWS); SNPs with p<5 × 10⁻⁵ were considered “suggestive” associations ⁽³¹⁾.

SNP Association with the Non-Vertebral Fractures

Using logistic regression, each GWS SNP was tested for association with the non-vertebral fractures outcome using an additive genetic model. The mean dosage of one of the alleles (a value between 0 and 2) was the predictor variable, in the sex-combined sample (adjusting for sex) and in women-only sample. We used generalized estimating equations (GEE) to account for familial correlations. Since we assessed associations between top SNPs identified for PCs with fracture risk, significance was set with Bonferroni adjustment for the number of tests.

Bioinformatic Analysis

Annotation

for the SNPs associated with PCs at p<5 × 10⁻⁵, gene annotation was based on the UCSC table browser for all RefSeq (hg18) genes. If a SNP was located outside known genic regions, the nearest RefSeq gene was assigned as the gene annotation. The distance between non-genic SNPs to the nearest gene ranged from 99 bp to 1514 kbp.

Identification of Enriched Physiological Function in Identified Genes

To better understand potential functional roles and the biological validity of the top associated genes on a gene-level as well as a gene network level, we inferred novel gene networks for each PC using Ingenuity Pathways Analysis (IPA) Software (Ingenuity Systems, Redwood City, CA, USA). In IPA, there are 43 high-level physiological functional categories, and “skeletal and muscular development and function” is one of these categories. Each high-level physiological function contains a number of lower level (or more specific) physiological functions. The functional analysis identified the biological functions that were significantly associated with the data set. Annotated genes associated with biological functions and/or diseases in Ingenuity's Knowledge Base were considered for the analysis. Right-tailed Fisher's exact test was used to calculate a p-value determining the probability that the “skeletal and muscular development and function” assigned to that data set was due to chance alone. P-values <0.05 were considered significant.

Gene Network Inference via Knowledge-Based Data Mining

We next analyzed biological interactions among identified genes using the IPA tool. The gene annotations from the GWAS SNPs were entered into the IPA analysis tool to construct the biological networks of the top associated genes. Networks are generated from the gene set by maximizing the specific biological relationship of the input genes, which represents their interconnectedness with each other relative to other molecules they are connected to in Ingenuity's Knowledge Database. All biological relationships are supported by at least one reference from the literature or from canonical information stored in the Ingenuity Pathways Knowledge Base. Networks were limited to 35 molecules each to keep them to a functional size. The p-value of probability for the genes forming a network was calculated with the right-tailed Fisher's Exact Test based on the hypergeometric distribution. To gain biological insights on whether this novel gene network was associated with any known canonical pathways, we further overlaid the gene network with canonical pathways using IPA.

RESULTS

Characteristics of the sample are provided in Table 1, by cohort and gender. In each cohort, men and women were of similar age. As expected, male participants were heavier, taller and in general had greater average BMI, leg lean mass, BMD, QUS, and geometric measures than females (but lower for shaft buckling ratio). Due to missing values for some musculoskeletal traits, 1,180 men and 1,758 women were included in the final analysis. Of the total 1,758 women, there were 641 postmenopausal women, mostly from the Offspring Cohort, who were not on estrogen.

Table 1.

Characteristics of the studied sample, by Cohort and gender.

	Original Cohort		Offspring Cohort
	Males	Females	Males	Females
Variable	Mean ±S.D	Mean ±S.D	Mean ±S.D	Mean ±S.D
N*	144	261	962	1362
Age (yrs)	77.3 ±3.6	77.7 ±4.0	61.3 ±9.2	60.3 ±9.3
Height (meter)	1.70 ±0.07	1.56 ±0.06	1.74 ±0.07	1.61 ±0.06
Weight (kg)	79.2 ±12.4	65.8 ±12.1	86.6 ±13.0	70.8 ±14.2
BMI (kg/m2)	27.4 ±3.8	27.0 ±4.9	28.4 ±3.8	27.3 ±5.3
Premenopausal or Currently on Estrogen, N (%)	-	19 (7.28%)	-	625 (45.88%)
BMD (g/cm2)
Femoral neck	0.866 ± 0.125	0.723 ± 0.119	0.966 ± 0.132	0.868 ± 0.140
Total Femoral	0.937 ± 0.141	0.760 ± 0.129	1.036 ± 0.140	0.911 ± 0.147
Trochanter	0.826 ± 0.133	0.624 ± 0.121	0.877 ± 0.136	0.714 ± 0.133
Lumbar spine	1.313 ± 0.213	1.053 ± 0.211	1.311 ± 0.197	1.153 ± 0.197
Quantitative Ultrasound
BUA (dB/MHz)	77.78 ± 22.43	53.37 ± 16.53	83.14 ± 19.03	71.40 ± 18.44
SOS (m/s)	1546.25 ± 38.19	1513.49 ± 30.12	1559.73 ± 34.27	1549.60 ± 35.14
Bone geometry
NSA (degrees)	131.7 ±6.2	128.0 ±5.5	129.4 ±4.9	127.5 ±5.2
FNL (cm)	5.4 ±0.8	4.6 ±0.6	6.0 ±0.8	5.2 ±0.6
Narrow Neck Outer diameter (cm)	3.4 ±0.3	2.9 ±0.3	3.8 ±0.5	3.3 ±0.4
Narrow Neck CSA (cm2)	2.4 ±0.4	1.8 ±0.4	2.8 ±0.4	2.3 ±0.4
Narrow Neck Section modulus (cm3)	1.4 ±0.3	0.9 ±0.2	1.8 ±0.4	1.3 ±0.3
Narrow Neck Buckling Ratio	12.9 ±3.2	13.6 ±4.7	11.4 ±6.2	10.4 ±6.0
Shaft Outer diameter (cm)	3.2 ±0.2	3.0 ±0.2	3.5 ±0.4	3.2 ±0.4
Shaft CSA (cm2)	4.2 ±0.6	2.8 ±0.5	4.5 ±0.6	3.3 ±0.5
Shaft Section modulus (cm3)	2.6 ±0.4	1.6 ±0.3	2.8 ±0.5	1.9 ±0.4
Shaft Buckling Ratio	3.6 ±0.9	4.7 ±1.3	3.9 ±1.1	4.7 ±1.5
Muscle mass
Leg Lean mass (kg)	17.04 ±2.23	11.53 ±1.54	17.21 ±2.21	11.57 ±1.57

^*number of subjects for all available participants with both genotypes and phenotypes.

PCA of Osteoporosis-related Phenotypes

We conducted PCA in sexes-combined as well as in 1,180 men and 1,758 women, separately. In sexes-combined analysis as well as in women, the PCA found four components above the 1.0-eigenvalue threshold, which jointly explained 69.3% of the total variability of musculoskeletal characteristics, in each sample (Table 2a). In men, the PCA revealed an additional principal component with an eigenvalue > 1.0 (cumulatively explaining up to 71.8% variance, Table 2b). Based on the loadings of the musculoskeletal phenotypes, principal component 1 (PC1), explaining 33.9% of the total variance in the combined sample (33.5% in women and 33.2% in men), may be referred to as representing “Bone strength”, since it correlates with BMD and several hip cross-sectional properties, such as narrow neck and shaft CSA and section modulus (also, inversely correlated with buckling ratio). PC1 weights were very similar in all 3 analyses for most variables except for shaft section modulus, shaft buckling ratio, and leg lean mass in men.

Table 2.

Component loading matrix after Varimax rotation.

a) sexes combined
	PC1	PC2	PC3	PC4
	Bone strength	Femoral cross-sectional geometry	Heel ultrasound	Femoral shaft stability
Total body BMD	88	−11	24	−15
Femoral Neck BMD	84	−5	19	−20
Trochanter BMD	82	−11	24	−7
LS BMD	63	−2	29	−1
Heel ultrasound/BUA	30	2	89	4
Heel ultrasound/SOS	30	2	90	0
Femoral Neck Length	8	62	−2	−7
Femoral Neck-Shaft Angle	−10	−15	9	50
Narrow Neck Outer diameter	−10	89	4	5
Narrow Neck CSA	81	34	10	−11
Narrow Neck Section Modulus	49	72	7	−6
Narrow Neck Buckling Ratio	−35	10	9	48
Shaft Outer diameter	−13	91	−1	−6
Shaft CSA	84	9	6	23
Shaft Section modulus	59	61	1	20
Shaft Buckling Ratio	−55	67	−5	−16
Leg Lean mass	22	−1	−17	69
Eigenvalue	5.75	3.49	1.38	1.15
Explained variance (%)	33.9	20.5	8.15	6.75

b) Men
	PC 1	PC 2	PC 3	PC 4	PC 5
	Bone strength	Femoral cross-sectional geometry	Heel ultrasound	Femoral shaft stability	Femoral neck geometry
Total body BMD	88	−12	27	9	−10
Femoral Neck BMD	88	−6	19	2	−4
Trochanter BMD	82	−12	26	13	−7
LS BMD	65	3	27	1	18
Heel ultrasound/BUA	26	0	91	6	−3
Heel ultrasound/SOS	28	2	91	3	−1
Femoral Neck Length	1	49	6	12	− 57
Femoral Neck-Shaft Angle	−8	−5	0	7	89
Narrow Neck Outer diameter	−12	89	5	3	−4
Narrow Neck CSA	84	30	12	13	1
Narrow Neck Section Modulus	52	74	8	8	−2
Narrow Neck Buckling Ratio	− 50	11	14	22	10
Shaft Outer diameter	−10	91	−4	−7	−13
Shaft CSA	68	0	19	54	−11
Shaft Section modulus	45	61	9	40	−13
Shaft Buckling Ratio	−42	73	−14	−32	−4
Leg Lean mass	1	−4	1	83	4
Eigenvalue	5.98	3.63	1.84	1.30	1.09
Explained variance (%)	33.2	20.2	10.2	7.2	6.0

c) Women
	PC 1	PC 2	PC 3	PC 4
	Bone strength	Femoral cross-sectional geometry	Heel ultrasound	Femoral shaft stability
Total body BMD	87	−13	24	−16
Femoral Neck BMD	83	−5	20	−21
Trochanter BMD	80	−12	25	−6
LS BMD	64	−3	29	1
Heel ultrasound/BUA	30	1	89	3
Heel ultrasound/SOS	30	1	89	−1
Femoral Neck Length	7	63	−2	−1
Femoral Neck-Shaft Angle	−5	−8	11	56
Narrow Neck Outer diameter	−7	90	2	3
Narrow Neck CSA	77	38	8	−18
Narrow Neck Section Modulus	49	70	5	−11
Narrow Neck Buckling Ratio	−28	9	6	54
Shaft Outer diameter	−13	91	0	−3
Shaft CSA	87	12	2	15
Shaft Section modulus	63	58	−3	16
Shaft Buckling Ratio	− 59	65	−3	−10
Leg Lean mass	20	−4	−27	64
Eigenvalue	5.69	3.48	1.47	1.15
Explained variance (%)	33.45	20.46	8.64	6.75

values are multiplied by 100 and rounded to the nearest integer.

The highest weights (≥0.5) are marked in bold.

PC2 can be labeled as “Femoral cross-sectional geometry“ component (explaining 20.5% variance in sexes-combined and women, and 20.2% variance in men), since this PC correlated with femoral neck length, narrow neck and shaft outer diameters and section moduli, and shaft buckling ratio.

PC3, explaining 8.15% total variance, was labeled a “Heel ultrasound” component, since it was strongly correlated only with the two measures of QUS (and slightly inversely, with LLM in women). PC4, explaining 6.75% variance, was correlated with NSA and leg lean mass in the combined sample (less strongly with narrow neck buckling ratio, NN BR) and was thus deemed “Femoral shaft stability” factor. This PC was characterized with most sex-specificity: thus, in women, it was strongly correlated with NN BR, while in men, it was strongly correlated with leg lean mass and shaft CSA, but not with NSA. Finally, there is an additional PC5 in men, explaining 6.0% of the total variance, which can be labeled “Femoral neck geometry” (since it correlated with FNL and NSA).

In the ensuing genetic analysis we decided to focus on PC1, PC2 and PC4, since these components explained a large proportion of the total variability in multiple musculoskeletal traits, while PC3 is only a factor of heel ultrasound. Also, we performed GWAS in both sexes-combined and women-only analyses, given a smaller size and weaker power of men-only sample.

Genome-wide association study

Since some resulting musculoskeletal PCs showed correlation with the ancestry principal components (EIGENSTRAT-PCs), we adjusted PC1 for EIGENSTRAT-PCs 2, 3 and 4 in the SNP association analyses; similarly, PC4 was adjusted for EIGENSTRAT-PCs 1, 2, and 3. After this adjustment the inflation factors (λ_GC) were ≤ 1.015 for GWAS of all musculoskeletal PCs.

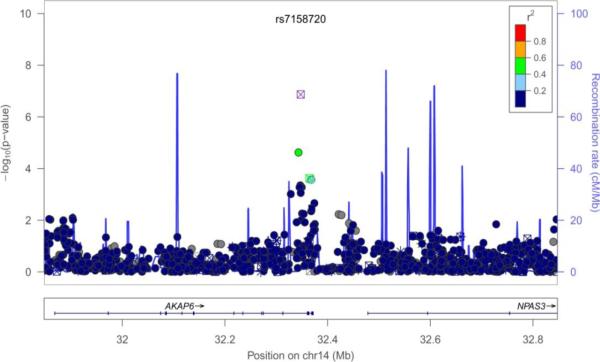
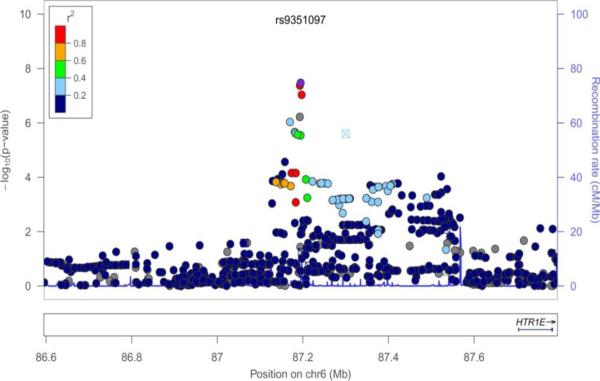
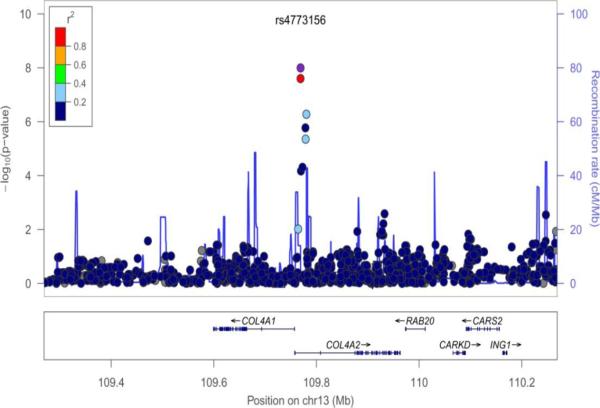
GWAS of the PCs 1, 2, and 4 in the sexes-combined sample did not produce genome-wide significant associations (p < 5 × 10⁻⁸). The best signal was between SNP rs7158720 within the A kinase anchor protein 6 (AKAP6) gene on chr. 14 and PC2, with p-value 1.40 × 10⁻⁷. Notably, rs7158720 within AKAP6 gene was also associated with PC2 in women, with p = 4.1 × 10⁻⁵ (Table 3). In the sample of women, genome-wide significant associations (p < 5 × 10⁻⁸) were observed for PC2 with two SNPs in linkage disequilibrium (r² = 0.935) on chr. 6: rs9351097 and rs9362321, both in the 5-hydroxytryptamine (serotonin) receptor 1E (HTR1E) gene. There are several other SNPs, some in high LD, in the vicinity of the HTR1E gene, among which two SNPs were associated with PC4 in sexes-combined analysis at p<3.2 × 10⁻⁵. Finally, 2 SNPs in the COL4A2 gene were highly significantly associated with PC4 in women (rs4773155, p = 2.50 × 10⁻⁸, and rs4447275, p=5.30 × 10⁻⁸). These SNPs are in LD (r² ~ 0.5); there was no suggestive association of this region within the sexes-combined sample.

Table 3.

Top SNPs associated with PCs in combined-sexes and women-only sample

PC, sample	SNP	Chr	position	Code d allele	Non-Code d allele	Coded allele frequenc y	LD	pval	beta	h2q	In/near gene*
PC2, women	rs9351097	6	87194834	T	G	0.175	--	3.40 * 10−	0.252	0.0164	HTR1E
PC2, women	rs9362321	6	87192966	T	C	0.174	0.838	4.30 * 10−8	0.246	0.0162	HTR1E
PC2, women	rs9362322	6	87197144	A	T	0.196	0.838	9.30*10−8	0.242	0.0154	HTR1E
PC2, women	rs9362320	6	87192883	T	C	0.018	0.096	6.00*10−7	0.648	0.0135	HTR1E
PC2, women	rs6919366	6	87169891	G	T	0.337	0.336	9.30*10−7	0.176	0.0130	HTR1E
PC4, combined	rs6911565	6	87557585	A	C	0.137	0.178	1.10*10−5	−0.19	0.0081	HTR1E
PC4, combined	rs12665525	6	87553199	C	T	0.117	0.178	3.20*10−5	−0.18	0.0073	HTR1E
PC2, combined	rs7158720	14	32347622	A	C	0.209	--	1.40*10−7	0.161	0.0086	AKAP6
PC2, women	rs7158720	14	32347622	A	C	0.208	--	4.10*10−5	0.167	0.0091	AKAP6
PC2, combined	rs10148694	14	32343262	T	C	0.358	0.464	2.40*10−5	0.112	0.0055	AKAP6
PC4, women	rs4773155	13	109780420	A	C	0.432	--	2.50 * 10−8	0.356	0.0204	COL4A2
PC4, women	rs4447275	13	109769067	G	A	0.462	0.533	5.30*10−7	−0.272	0.0166	COL4A2

LD: linkage disequilibrium with the most-significant SNP

h²q - variance explained by a SNP

^*distance from the nearest gene was assumed not to exceed 500kb.

At the suggestively-significant threshold p < 5 × 10⁻⁵, there were 186 and 182 SNPs associated with PC1 in the sexes combined and women-only analyses respectively; 161 and 121 SNPs associated with PC2, and 115 and 177 SNPs with PC4. SNP associations with the most significant p-values are provided in Table 3, and regional plots are shown in Figure 1. Table 3 also shows the variance explained in PCs by each of the top SNPs, which ranged from 0.55% to 2.04%.

Figure 1.

Regional plots of SNP-PC phenotype association (index SNPs are marked). A: Combined PC2 (rs7158720); B: Women PC2 (rs9351097); C: Women PC4 (rs4773156).

Further, each GWS SNP was tested for association with non-vertebral fracture outcomes, in sex-combined sample and in female-only sample (n=1984 and 1208, respectively), using logistic regression. SNP rs6919366 in HTR1E was significantly associated with non-vertebral fractures in women, even after Bonferroni correction for number of test (Table 4).

Table 4.

Top SNPs associated with PCs in combined-sexes and women-only sample: association with the non-vertebral fractures.

SNP	Chr	position	Coded allele	Non-Coded allele	In/near gene	Sexes combined*		Women-only**
						OR	p-value	OR	p-value
rs9351097	6	87194834	T	CD	HTR1E	1.1277	0.2883	1.2089	0.1417
rs9362321	6	87192966	T	C	HTR1E	1.1257	0.2868	1.2084	0.1359
rs9362322	6	87197144	A	T	HTR1E	1.0541	0.6487	1.1310	0.3392
rs9362320	6	87192883	T	C	HTR1E	0.8604	0.6738	0.8254	0.6523
rs6919366	6	87169891	G	T	HTR1E	1.2084	0.0446	1.3451	0.0051
rs6911565	6	87557585	A	C	HTR1E	0.8686	0.2903	0.9746	0.8617
rs12665525	6	87553199	C	T	HTR1E	0.8416	0.1971	0.9269	0.6081
rs7158720	14	32347622	A	C	AKAP6	1.0406	0.7051	1.0214	0.8585
rs10148694	14	32343262	T	C	AKAP6	1.0864	0.3660	1.1020	0.3561
rs4773155	13	109780420	A	C	COL4A2	1.0595	0.6942	1.0363	0.8366
rs4447275	13	109769067	G	A	COL4A2	0.9053	0.4274	0.9145	0.5371

^*Sample size = 1984

^**Sample size = 1208

Bioinformatics analyses

In the sexes-combined sample, 186, 161, and 115 SNPs suggestively associated with PC1, PC2, and PC4 were mapped and annotated to 48, 36, and 41 genes, respectively. All of these gene lists were significantly associated with the skeletal and muscular system development and function (“high-level function”; p < 0.05 (Table 5)). For example, PC1 was significantly associated specifically with the functional annotation of osteopenia and osteoporosis (p < 0.05). PC2 was significantly associated with the functional annotation of ossification, fracture of bone, development of osteoblast and formation of osteophyte (p < 0.05). PC4 was significantly associated with the function annotation of development of skeleton, arrest in growth and differentiation of bone cell lines (p< 0.05). In a sample of women, 182, 121, and 177 SNPs associated with PC1, PC2, and PC4 were mapped and annotated to 58, 32, and 43 genes, respectively. Similarly to the sexes-combined results, all of these gene lists were significantly associated with the skeletal and muscular system development and function (p < 0.05) in women.

Table 5.

Gene networks associated with skeletal and muscular system development and function inferred from GWAS of principal components.

PC	p-value*	# of molecules in the network
PC1 (combined)	9.05*10−5 − 8.72*10−3	4
PC2 (combined)	2.55*10−3 − 7.54*10−3	6
PC4 (combined)	7.71*10−5 − 4.08*10−3	8
PC1 (women)	4.64*10−4 − 1.51*10−2	6
PC2 (women)	7.57*10−4 − 1.05*10−2	8
PC4 (women)	4.66*10−3 − 4.17*10−2	4

^*p-value for enrichment analysis; ranges correspond to the different specific lower level functions or sub-categories (e.g. osteopenia, ossification and mineralization) that are classified within the “skeletal and muscular system development and function”

Novel Gene Network Inference

To better understand potential functional roles and the biological validity of the top genes on a gene-level as well as a gene network level, we inferred novel gene networks for each PC using IPA. For each PC, we ranked genes by connectivity in each network, since highly-connected proteins, or hub genes, are likely to be more essential to biological function and survival, and potentially represent therapeutic targets^(18,32). The novel gene network inferences are provided in supplementary table 1 (attached at the end), and the hub genes/molecules (defined arbitrarily as those with greater than 9 connections with other members in the network, i.e. ~25% of other 34 molecules, excluding self-regulatory connection) are provided in supplementary table 2.

Gene networks inferred from top genes in each PC were significantly associated with skeletal and muscular system development and function (all p < 0.05; supplementary table 1). There were in total 11 genes or molecules identified as “hubs” in the six top gene networks. Two of them, HNF4A and GPCR, appeared as hubs in more than one gene network (supplementary table 2).

DISCUSSION

Genome-wide association studies offer an unbiased approach to identify new genetic pathways for a complex disease such as osteoporosis. Although genetic factors substantially contribute to the risk of osteoporotic fractures, the fracture phenotype presents a challenge for a genetic association study since non-traumatic fractures typically do not occur until later in life. An abundance of multiple surrogate phenotypes assessed by various methods at different skeletal sites makes a focused genetic search similarly challenging.

We hypothesized that a composite summary measure of several correlated phenotypes may provide a comprehensive outlook on the genetics of osteoporosis. One approach to extract essential non-redundant information is to apply principal component analysis to the correlation coefficient matrix of related phenotypes. PCA transforms the original phenotypes to a number of orthogonal PCs, each defined as a specific linear combination of the original phenotypes. Of note, while the PCs capture specific constructs underlying musculoskeletal traits, biological interpretation of the resulting phenotypes may not be obvious⁽¹⁶⁾. In a sample of adult participants of the Framingham Osteoporosis Study, we found that independent PCs jointly explained 69.3% of the total variability of musculoskeletal characteristics in sexes-combined analysis (similarly, 76.9% of the total variability in men and 69.3% in women). The first two factors, PC1 (“Bone strength”) and PC2 (“Femoral cross-sectional geometry“), explained most of the total variance (~33–34% of the variance for PC1 and about 20-for PC2). PCs 3 and 4 explained ~8.2% and ~6.8% of the total variance. Notably, PC3 was strongly correlated only with two measures of QUS, therefore has less appeal for the study of the musculoskeletal system as a whole. It is important to emphasize that biological interpretation of the resulting PC constructs is not straightforward; therefore the labeling we chose is an over-simplification in order to make the constructs more intuitive. Further, using bioinformatic and pathways analyses we found that the PCs could be linked to biologically-meaningful functional annotations.

We screened the whole genome for associations with the integrated phenotypes represented the three PCs (PC1, PC2 and PC4), since PC3 explained only variability in heel ultrasound. Genome-wide significant associations (p < 5 × 10⁻⁸) were observed between PC2 in women and two SNPs in linkage disequilibrium (r² = 0.935) on 6q14-q15, both in the HTR1E gene. This signal was supported by several suggestively-associated SNPs in the same region. The HTR1E gene codes for one of the several receptors for 5-hydroxytryptamine (5-HT or serotonin), a biogenic hormone that functions as a neurotransmitter and a mitogen. The activity of the 5-HT1E receptor is mediated by G-coupled proteins. Recently, it has been demonstrated that gut-derived serotonin binds to the Htr1b receptor present on osteoblasts and inhibits its proliferation⁽³³⁾. In addition, Oury et al. showed that brain-derived 5-HT binds to Htr2c receptor expressed on neurons of the hypothalamic ventromedial nucleus and favors bone mass accrual by inhibiting the activity of sympathetic neurons⁽³⁴⁾. Our earlier work⁽³⁵⁾ demonstrated that the same HTR1E SNP rs9362321 was associated with FNL in Framingham women (p = 5.57 × 10⁻⁷). Here we extended this finding to the integrated phenotype, which included measures of cross-sectional proximal femoral geometry, such as narrow neck and shaft's outer diameters and section moduli. Also, SNPs in the vicinity of HTR1E gene were suggestively associated with PC4 (regarded as “Femoral shaft stability” factor) in the sexes-combined sample. PC4 was mostly correlated with leg lean mass in both sexes, pointing to a possible effect on non-geometric properties of the femur.

Further, in order to substantiate the value of understanding the genetic contributions to the integrated phenotype constructs, we assessed associations between top SNPs identified for PCs with fracture risk over ~8 years follow-up. Indeed, SNP rs6919366 in HTR1E was significantly associated with non-vertebral fractures in women. This finding of association with fracture risk is especially important, since it supports the value of knowing an individual's genetic predisposition to risk factors measured in midlife (the subjects were ~63 years old on average at the baseline), for predicting a late-life event, such as osteoporotic fracture. Taken together, serotonin and its 5-HT receptor might play an important role in bone metabolism, although their precise function in bone metabolism has yet to be elucidated.

Another gene, suggestively associated with PC2 in the sexes-combined analysis (less strongly in women), was the AKAP6 gene on chr. 14, which codes for a protein kinase A (PRKA) anchor protein 6. This protein is highly expressed in various brain regions, cardiac and skeletal muscle. Notably, both AKAP6 and 5-HT are associated with the cyclic adenosine monophosphate (cAMP) signaling pathway. Since 5-HT exerts its effect through the cAMP effector pathway⁽³⁶⁾, which is coordinated by AKAP6⁽³⁷⁾, the crosstalk between AKAP6 and HTR1E on bone metabolism warrants further investigation. The third gene, whose SNPs were highly suggestively associated with PC4 in women only, was the COL4A2 gene. This gene encodes one of the six subunits (alpha 2) of type IV collagen, the major structural component of basement membranes and extracellular matrix organization, which is expressed in muscle. However, SNPs in neither AKAP6 nor COL4A2 were associated with non-vertebral fractures.

We further examined whether candidate regions obtained by GWAS for BMD (reported by Rivadeneira et al.⁽³⁸⁾ and by Kung et al.⁽³⁹⁾), for association with our PCs. In Supplementary Table 4, we provide best association p-values for the 21 candidate intervals. There were suggestive associations (p < 5 × 10⁻⁵) of PC1 with WLS (GPR177) and SHFM1 and of PC2 with the MEPE locus (including SPP1 and IBSP); this is not surprising, given that PC1 is heavily loaded on BMD measures and PC2 on Femoral cross-sectional geometry.

Despite the fact that we have identified a gene HTR1E that was significantly associated with PCs and confirmed suggestive associations with other osteoporosis-related genes, it is difficult to directly replicate our findings, because we have measured a number of musculoskeletal phenotypes that are not available collectively in many cohorts. Instead, we performed a bioinformatics analysis to see if biological information supports our most significant findings. We therefore performed gene set enrichment analysis and observed that genes having the most significant associations with the PCs were significantly associated with the “skeletal and muscular system development and function.” We further inferred a gene network from the annotated genes associated with each PC. All gene networks were highly scored, suggesting there are strong and non-random connections between several top genes in each PC. Previous work suggested that hub genes (those abundantly connected to other members of the network⁽¹⁸⁾) are likely to be more essential to biological function and survival; therefore we also identified the hub genes in each gene network. Interestingly, all identified hub genes are known to be associated with osteoblast development and differentiation (Supplementary Table 1), except for HNF4A, which encodes for hepatocyte nuclear factor-4 alpha, a transcription factor that regulates the expression of several hepatic genes. Mutations of HNF4A have been associated with monogenic autosomal dominant non-insulin-dependent diabetes mellitus type I ⁽⁴⁰⁾, while recent studies demonstrated the importance of insulin signaling in osteoblast that affects both bone remodeling and glucose metabolism⁽⁴¹⁾. Therefore it is possible that HNF4a affects bone metabolism through regulation of insulin secretion.

Because musculoskeletal traits and fracture risk are characterized by a marked sexual dimorphism, our principal component analyses were performed also in men and women, separately. Minor differences between genders were evident in PCA. However, since the proximal femur can be represented as a cantilever beam, a pronounced sex difference in femoral neck length might reflect distinct biomechanical demands and therefore, dictate a relationship between the femur shape and muscle mass. Since our sample size for men was modest, - we decided not to focus on the analysis of men and to focus on analyses in women. As results of GWAS confirmed, there was some advantage in performing a women-specific analysis, since it revealed GWS associations and further, associations of a SNP in HTR1E with non-vertebral fractures in women.

One of the merits of principal components analysis is a potential increase in power. Notably, our simulations of individual traits revealed low statistical power to detect SNPs with effects on a trait's variance of 0.55% to 2%, for a significance level α =5 × 10⁻⁸. Our simulations indicated that in women we had from 11% power (for a SNP explaining 1% variance) to 64% power (2% variance), while in the combined sample, we had power ranging from 5% to 49% (0.5% to 1% variance, respectively). Power for <0.5% effect was close to 0%. Our finding of a GWS association in a sample of 1,758 women with the HTR1E gene provides some evidence for greater power with the use of the PCA method. Both theoretically and empirically, PCA is predicted to be more powerful than an analysis of multiple traits one at a time⁽⁴²⁾; it also prevents inflation of experiment-wise type I error rates by avoiding testing numerous non-independent phenotypes.

The PCA method is suitable for the studies similar to ours, in which multiple surrogate traits, but not endophenotypes, are measured. For example, Saless et al. recently performed a PCA in a reciprocal intercross of the recombinant congenic mice strains HcB-8 and HcB-23 with multiple phenotypes encompassing body size, femoral diaphysis size and shape, and femoral biomechanical performance. Similar to us, they achieved substantial dimensional reduction of the data, accounting for 80% of the phenotypic variance within the first 4 PCs. Furthermore, their linkage mapping identified a QTL that was undetected in the study of individual phenotypes⁽¹⁶⁾. Previously, biomechanical performance, anatomy, and BMD of the femur were studied by Koller et al. in C57BL/6J and C3H/HeJ inbred mice⁽¹⁷⁾. They similarly revealed pleiotropic QTLs on chromosomes 4 and 14 influencing nearly all of the bone phenotypes measured, and found QTLs on chromosomes 1, 8, 13, and 17 with effects restricted to either bone density or bone structure/biomechanical phenotypes.

There is therefore a practical importance of using PCA for data reduction and “phenomic” outcomes. We analyzed many available musculoskeletal phenotypes, since none is a perfect proxy for osteoporotic fracture. Combinations of BMD measures from more than one region⁽⁴³⁾, as well as composite use of BMD with QUS⁽³⁾ or BMD with hip geometry⁽⁴⁴⁾, have been suggested as the way to improve osteoporotic fracture prediction. Here we show that there are genetic predispositions to a combination of BMD traits with hip cross-sectional properties, such as cross-sectional areas and section moduli. Interestingly, by applying a different approach, a Bayesian block clustering⁽⁴⁵⁾, to GWAS results of the above musculoskeletal traits, we obtained very similar results. In that study, by examining each phenotype independently and combining the results afterwards, we found a strong cluster consisting of 10 traits (BMD at several skeletal sites; ultrasound measures; cross-sectional areas and section moduli of femoral neck and shaft). Gene-set enrichment analyses indicated biological pathways associated with these clustered phenotypes, similar to ones found here⁽⁴⁵⁾. This “confluence” of results obtained by two different approaches is encouraging. As well, loading of both leg lean mass and proximal femoral geometric traits on the same factor (PC4) in this study supports the notion that there are shared genetic contributions to both osteoporosis and sarcopenia⁽¹³⁾.

There are shortcomings worthy to be mentioned. There is a complex relationship of bone measurements with age. In particular, the measurement error of the DXA-derived hip geometry phenotypes is higher than that of BMD, since subperiosteal bone margins may not be detected accurately in osteoporotic bone (thereby underestimating outer diameter of bone), especially in old persons with cortical porosity and very low mineral density. Further, estimates of average cortical thickness and buckling ratio in the HSA method are based on assumptions about bone shape and the assigned fractions of cortical and trabecular bone, which might change with aging (reviewed by us previously⁽⁴⁶⁾). Furthermore, the biological interpretations of GWAS results are limited by the information provided in Ingenuity's Knowledge Database, which is not focused around the musculoskeletal system's interactions and has preponderance of non-bone-related datasets. With the targeted bioinformatic tools⁽⁴⁷⁾, new biological pathways relevant to the skeleton may emerge for further pursuit. With these limitations and without replication, we consider findings of this study to be hypothesis generating rather than definitive. In particular, inferred gene networks are preliminary, until further evidence is obtained by replication and molecular study.

In conclusion, in this study we grouped osteoporosis-related traits into composite phenotypes, which were studied for genome-wide association. We were able to decrease the number of variables that could have been used individually for GWAS to focus on essential information from an ever-growing number of phenotypes that have become available for genetic study with advances of the measurement techniques. We pointed out associations between integrated musculoskeletal traits and three genes, one of which - HTR1E – was also associated with non-vertebral fractures risk. We thus provided direction for future studies to confirm functional evidence to substantiate roles of newly-found genes in etiology of osteoporotic fracture. The method of multivariate combination is a potentially powerful tool for genomic discovery since it provides additional insight into the biology of a complex condition that could not always be obtained from studying the primary (directly measured) surrogate phenotypes. This knowledge may also prove helpful in prioritizing the phenotypes to be utilized in genetic studies of osteoporosis.