An Approach for Balancing Diagnostic Image Quality with Cancer Risk: Application to Pediatric Diagnostic Imaging of ^99mTc-Dimercaptosuccinic Acid

Abstract

A recent survey of pediatric hospitals showed a large variability in the activity administered for diagnostic nuclear medicine imaging of children. Imaging guidelines, especially for pediatric patients, must balance the risks associated with radiation exposure with the need to obtain the high-quality images necessary to derive the benefits of an accurate clinical diagnosis.

Methods

Pharmacokinetic modeling and a pediatric series of nonuniform rational B-spline–based phantoms have been used to simulate ^99mTc-dimercaptosuccinic acid SPECT images. Images were generated for several different administered activities and for several lesions with different target-to-background activity concentration ratios; the phantoms were also used to calculate organ S values for ^99mTc. Channelized Hotelling observer methodology was used in a receiver-operating-characteristic analysis of the diagnostic quality of images with different modeled administered activities (i.e., count densities) for anthropomorphic reference phantoms representing two 10-y-old girls with equal weights but different body morphometry. S value–based dosimetry was used to calculate the mean organ-absorbed doses to the 2 pediatric patients. Using BEIR VII age- and sex-specific risk factors, we converted absorbed doses to excess risk of cancer incidence and used them to directly assess the risk of the procedure.

Results

Combined, these data provided information about the tradeoff between cancer risk and diagnostic image quality for 2 phantoms having the same weight but different body morphometry. The tradeoff was different for the 2 phantoms, illustrating that weight alone may not be sufficient for optimally scaling administered activity in pediatric patients.

Conclusion

The study illustrates implementation of a rigorous approach for balancing the benefits of adequate image quality against the radiation risks and also demonstrates that weight-based adjustment to the administered activity is suboptimal. Extension of this methodology to other radiopharmaceuticals would yield the data required to generate objective and well-founded administered activity guidelines for pediatric and other patients.

The goal of every nuclear medicine study is to obtain the maximum diagnostic information as cost-effectively and in as short a period of time as possible and with the lowest patient radiation exposure (1). Children are generally more sensitive to radiation and have their entire lifetimes to manifest radiation effects, so these considerations are even more pressing in pediatric populations. Consensus pediatric dosing guidelines for diagnostic studies in nuclear medicine have recently been published in the United States (2). These update previously described guidelines (1,3–9). Administered activities (AAs) in pediatric nuclear medicine have been developed empirically, taking into account the whole-body radiation absorbed dose, type of examination, available photon flux, instrumentation, and examination time: high AAs, which do not directly result in improved diagnostic sensitivity or accuracy, or low AAs, which do not permit adequate examination, result in unnecessary radiation exposures. AA estimates for pediatric patients based on adult AAs corrected for body weight or body surface area are generally used for children over 1 y of age. Premature infants and newborns require special consideration, and the concept of minimum total AA should be considered. Minimum total AA can be defined as that AA of the radiopharmaceutical below which the study will be inadequate regardless of the patient’s body weight or surface area.

In this work, we used modeling-derived biodistribution data to simulate images generated using different AAs or imaging durations (i.e., different image count densities) for 2 simulated 10-y-old girls having the same weight but different body morphometry. The resulting images were evaluated for task-based diagnostic quality and, combined with the corresponding calculated absorbed and effective doses, were used to define the tradeoff between diagnostic image quality and risk to the patient of radiogenic cancer.

MATERIALS AND METHODS

Pharmacokinetic Modeling and Dosimetry

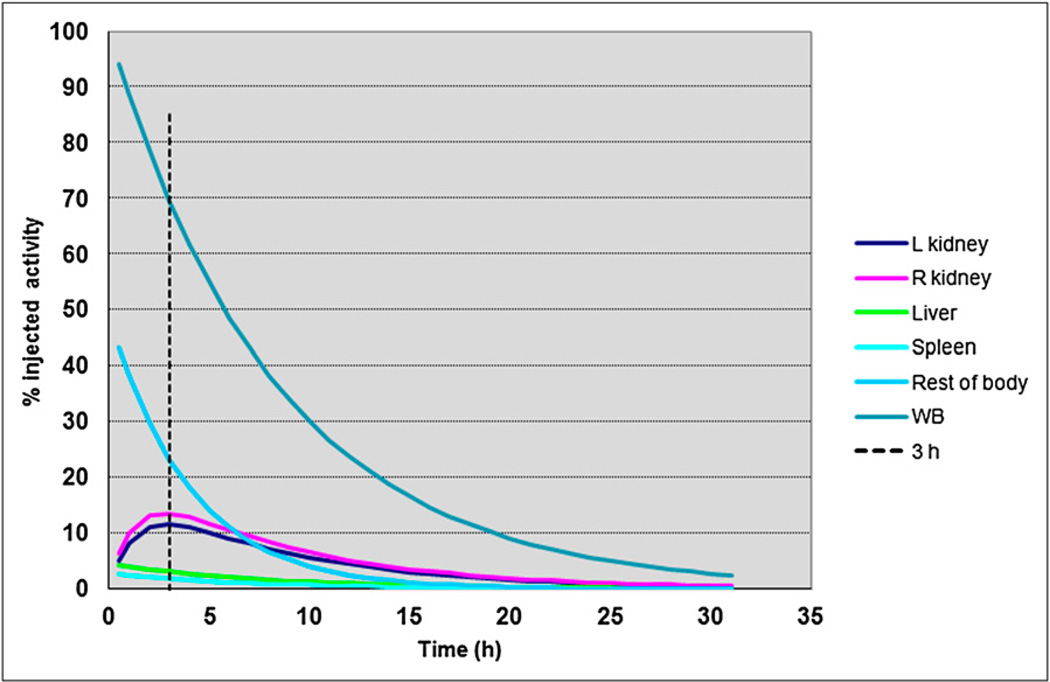
The pharmacokinetics of dimercaptosuccinic acid (DMSA) in children of various ages have already been characterized (10,11). The whole-body clearance rate, λ_eff, was not explicitly listed in these references; it was calculated from the urine data provided by fitting a monoexponential function to the complement of the urine data (100% excreted) at each time point. These parameters (Table 1) were used with the appropriate exponential expressions to generate the kinetic data used in the imaging simulations and also in the dosimetry calculations of the present study (Fig. 1).

TABLE 1.

^99mTc-DMSA Pharmacokinetic Parameters for Pediatric Patients

	Left kidney			Right kidney			Liver		Spleen
	Am(1 −exp(−λ+t)) × exp(−λ−t)*			Am(1 −exp(−λ+t)) × exp(−λ−t)*			A0 × exp(−λefft)		A0 × exp(−λefft)		Urine (% excreted)		Whole body exp(−λefft)
Age	Am (%)	λ+ (/h)	λ− (/h)	Am (%)	λ+ (/h)	λ− (/h)	A0 (%)	λeff− (/h)	A0 (%)	λeff− (/h)	6 h	24 h	λeff− (/h)
Newborn	2.1E+1	7.2E−1	9.0E−3	2.1E+1	6.4E−1	8.0E−3	5.7E+0	1.4E−1	1.6E+0	1.6E−1	6.6E+0	1.3E+1	1.2E−1
1	2.0E+1	6.0E−1	1.4E−2	2.0E+1	7.2E−1	1.3E−2	3.2E+0	1.3E−1	1.5E+0	1.4E−1	1.2E+1	2.1E+1	1.2E−1
5	2.1E+1	7.2E−1	1.7E−2	3.3E+1	7.2E−1	1.4E−2	5.0E+0	1.5E−1	1.3E+0	2.1E−1	1.1E+1	1.9E+1	1.2E−1
10	2.0E+1	6.6E−1	8.0E−3	2.2E+1	7.2E−1	6.0E−3	4.5E+0	1.3E−1	2.8E+0	1.4E−1	1.6E+1	2.3E+1	1.2E−1
15	2.2E+1	6.8E−1	5.0E−4	2.2E+1	8.0E−1	0.0E+0	5.2E+0	1.2E−1	3.0E+0	1.3E−1	1.1E+1	1.7E+1	1.2E−1

^*Biologic (decay corrected) uptake and clearance rates, λ₊ and λ₋, respectively, are listed for kidneys; clearance rates for other organs are effective. Fitted equations are listed below each organ.

A_m = maximum % uptake; A₀ = initial uptake (backextrapolated to t = 0).

FIGURE 1.

^99mTc-DMSA time–activity curves for 10-y-old. Vertical dotted line corresponds to time after injection at which DMSA imaging is performed. WB = whole body.

The analytic expressions were integrated from zero to infinity to give the number of nuclear transformations (NTs) in individual organs for the absorbed dose calculations. NTs were also provided for lungs and heart with contents. These were obtained by apportioning a calculated blood NT concentration to each organ according to its blood volume. Blood NT was obtained from the work of Treves (1) wherein clearance of DMSA from blood is described as following a single exponential function with a 56-min half-life. Absorbed doses were calculated according to the MIRD Committee methodology as described in MIRD pamphlet 21 (12). The working expression for absorbed dose is:

$$D(r_T)={\displaystyle \sum _{r_S}}\mathit{Ã}(r_S)·S(r_S\leftarrow r_T).$$ Eq. 1

The radionuclide and anatomic model-dependent portion (i.e., the term to the right) of Equation 1 is designated the S value and is indexed by source (r_S) and target region (r_T) (12,13). The S value is given as:

$$S(r_T\leftarrow r_S)={\displaystyle \sum _i}\frac{{\mathbf{\Delta }}_i·\mathrm{\varphi }(r_T\leftarrow r_S,E_i)}{M(r_T)},$$ Eq. 2

wherein a sum over all radionuclide emissions is included. The numerator in this expression is the product of the energy emitted per disintegration of the radionuclide for emission i, Δ_i, and the fraction, ϕ(r_T←r_S, E_i), of this emitted energy that is absorbed by the target tissue r_T, when emissions with energy E_i originate in source tissue r_S. The denominator is the mass of the target region, M(r_T).

The time-integrated activity Ã(r_S) (or number of NTs) in source tissue r_S is given by:

$$\mathit{Ã}(r_S)={\displaystyle {\int }_0^{\mathrm{\infty }}}A(r_S,t)\mathit{\text{ dt}}.$$ Eq. 3

Organ-absorbed doses obtained in this way were used to calculate both the tissue-factor-weighted organ-equivalent dose, H(r_T), and the effective dose, E:

$$w_{T}H(r_T)=w_T{\displaystyle {\sum }_R}{w}_R{D}_R(r_T)\text{ and }E={\displaystyle {\sum }_T}{w}_{T}H(r_T),$$ Eq. 4

where the first weighting parameter, w_R, is related to the biologic effectiveness of different types of radiation particles for stochastic effects and is equal to 1 for ^99mTc emissions. The second weighting parameter—the tissue-weighting factor w_T—is defined by International Commission on Radiological Protection Committee (ICRP) 1 and represents the proportion of total radiation detriment attributed to individual tissue r_T in the body. Radiation detriment is defined in ICRP publication 60 (14) and more recently publication 103 (15) and includes a variety of stochastic endpoints such as cancer mortality, cancer morbidity, and years of life lost.

Cancer Risk Estimation

To balance the risk of an imaging procedure with the image quality needed for accurate diagnosis, we examined several alternatives to evaluating risk from the absorbed and effective dose calculations. As noted in ICRP 103, effective dose is appropriate in assessing radiation detriment, which includes cancer incidence risk for workers and the general population (15). Risk assessment for medical diagnosis is “best evaluated using appropriate risk values for the individual tissues at risk and for the age and sex distribution of the individuals undergoing the medical procedures.” Consistent with this recommendation and to further optimize AA recommendations for pediatric diagnostic imaging, we used sex- and age-specific cancer incidence risk estimates, expressed as lifetime attributable risk (LAR), as tabulated in the National Academy of Science’s BEIR VII report (16). Although these risk estimates have high uncertainties for individual patients, they can be used collectively in optimizing values of AA and resulting organ-absorbed dose to classes of pediatric nuclear medicine patients. In the case illustrated in this work, the product of organ-absorbed doses and corresponding LAR for a 10-y-old girl was summed over all organs to give the overall risk for cancer incidence. This approach was compared with a risk estimate based on sex- and age-averaged LAR values and with an overall radiation detriment derived from the effective dose using ICRP 103 tissue-weighting factors (15). The latter comparison was made using a detriment-adjusted nominal risk coefficient for cancer incidence for the whole population that is reported in ICRP publication 103 as 5.5 × 10⁻² Sv⁻¹. This value was multiplied by the effective dose to give an effective dose–derived overall risk for radiation detriment, which includes cancer incidence. The organ LAR and ICRP 103 weighting factors used in the calculations are shown in Table 2.

TABLE 2.

Organ w_T and Lifetime Attributable Risk (LAR) Used in Risk Calculations

Target organ	ICRP 103 Organ weighting factor, wT	BEIR VII LAR cancer incidence*
		10-y-old girl	Sex- and age-averaged
		Colon	0.12	158	135
Lungs	0.12	504	244
Stomach wall	0.12	72	42
Ovaries	0.08	73	45
Urinary bladder wall	0.04	152	104
Esophagus	0.04	—	—
Liver	0.04	20	21
Brain	0.01	—	—
Salivary glands	0.01	—	—
Skin	0.01	—	—
Remainder	0.12	—	—
Red bone marrow	0.12	86	92
Bone surface	0.01	—	—

^*No. of excess cases for population of 100,000 receiving organ-absorbed dose of 0.1 Gy.

Pediatric Phantom

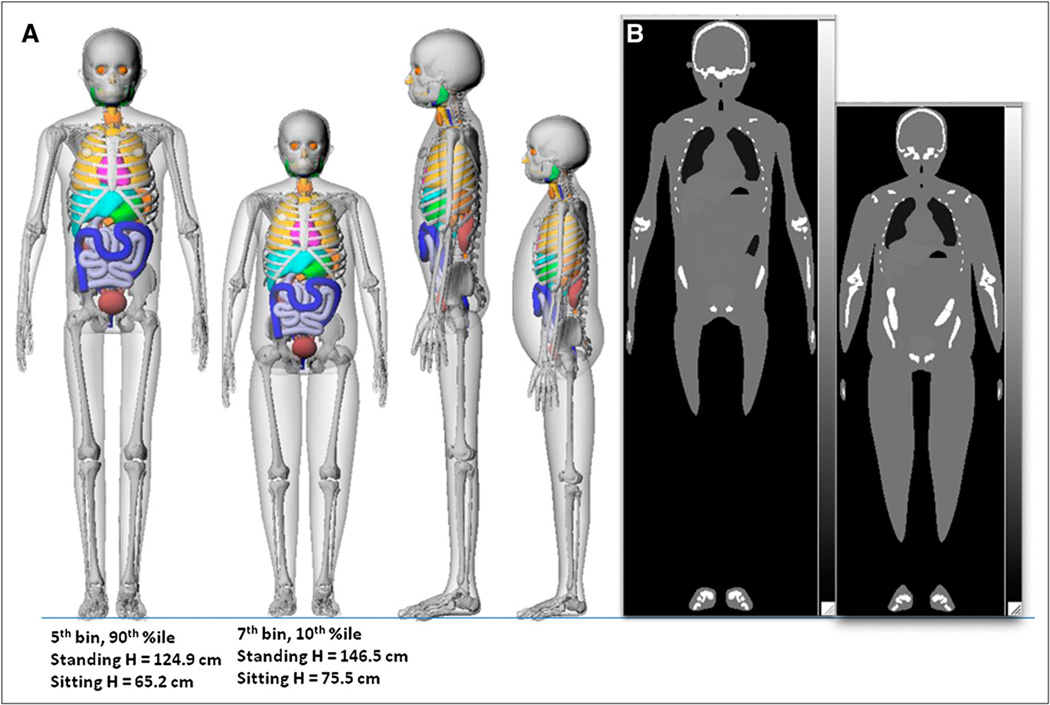
The implications of administering the same weight-based activity to a tall, thin child and a short, heavy child both of the same weight were examined using 2 versions of the 10-y-old female phantom. The Advanced Laboratory for Radiation Dosimetry Studies (ALRADS) UF NHANES–based phantom series (17,18) was used to select a 90th weight-percentile (fifth height bin) child and a 10th weight-percentile (seventh height bin) child. The 2 phantoms are shown in Figure 2. To calculate S values, the phantoms were voxelized at 1.6- and 1.5-mm isotropic resolutions, respectively; 1.2-mm voxelization was used for the image simulations. An in-house MATLAB (The MathWorks, Inc.) code, Voxelizer 4 described previously by Lee et al. (19), was used to perform the voxelization. The resulting hybrid voxel phantom was imported into the radiation transport code MCNPX 2.5 (20). Photon and electron emission spectra from ^99mTc were then abstracted from a recently updated decay scheme monograph published by the MIRD committee (21). Two Monte Carlo simulations were thus run—one for photon emissions (x and γ rays) and another for electron emissions (β, IC, and Auger electrons)—each with 5 × 10⁶ particle histories yielding this number of histories per source–target region pair. Photon and electron components of the S value were then combined to yield total spectral S values as listed in Table 3. Source organs correspond to those in the biokinetic model of ^99mTc-labeled DMSA. Target tissues were those assigned values of w_T in the ICRP 103 definition of effective dose, which includes the collective target region remainder tissues. This approach—direct sampling of radionuclide emission spectrum in MCNPX—yields higher S value convergence with fewer Monte Carlo histories than does the traditional approach, in which monoenergetic values of specific absorbed fractions are assembled and then spectrum-weighted.

FIGURE 2.

Ten-year-old female phantoms weighing 32 kg: anatomic depiction (A) and coronal slice through corresponding attenuation map (B), generated from anatomic description of A. %ile = percentile; H = height.

TABLE 3.

w_T-Weighted Equivalent Organ Doses, Absorbed Doses, and LAR Values for Two 32-kg Pediatric Patients for ^99mTc-DMSA Renal Imaging Studies

	Short, stout (fifth bin 90th percentile, 125-cm height)				Tall, thin (seventh bin 10th percentile; 147-cm height)
			LAR*				LAR†
Target organ	wT H(rT)/A0 (mSv/MBq)	D(rT)/A0 (mGy/MBq)	10-y-old girl	Sex- and age-averaged	wT H(rT)/A0 (mSv/MBq)	D(rT)/A0 (mGy/MBq)	10-y-old girl	Sex- and age-averaged
Colon	7.81E–04	6.51E–03	0.6	0.5	4.94E–04	4.12E–03	0.2	0.2
Lungs	1.86E–03	1.55E–02	4.6	2.2	1.45E–03	1.21E–02	1.8	0.9
Stomach wall	2.16E–04	1.80E–03	0.1	0.0	1.52E–04	1.27E–03	0.0	0.0
Ovaries	3.79E–06	4.74E–05	0.0	0.0	3.74E–06	4.68E–05	0.0	0.0
Urinary bladder wall	2.57E–05	6.43E–04	0.1	0.0	2.16E–05	5.40E–04	0.0	0.0
Esophagus	9.22E–06	2.31E–04	–	–	5.40E–06	1.35E–04	–	–
Liver	2.97E–03	7.43E–02	0.9	0.9	2.16E–03	5.40E–02	0.3	0.3
Brain	6.53E–06	6.53E–04	–	–	1.59E–05	1.59E–03	–	–
Salivary glands	3.85E–07	3.85E–05	–	–	1.10E–06	1.10E–04	–	–
Skin	1.28E–04	1.28E–02	–	–	9.97E–05	9.97E–03	–	–
Remainder	7.57E–03	6.31E–02	–	–	4.96E–03	4.13E–02	–	–
Red bone marrow	5.26E–04	4.38E–03	0.2	0.2	4.09E–04	3.41E–03	0.1	0.1
Endosteum	9.22E–05	9.22E–03	–	–	7.18E–05	7.18E–03	–	–
Effective dose	1.42E–02				9.84E–03

^*No. of excess cancer incidence cases for population of 100,000 receiving AA of 1.85 MBq/kg (=59.2 MBq).

^†No. of excess cancer incidence cases for a population of 100,000 receiving AA of 0.93 MBq/kg (=29.6 MBq)

Imaging and Observer Simulations

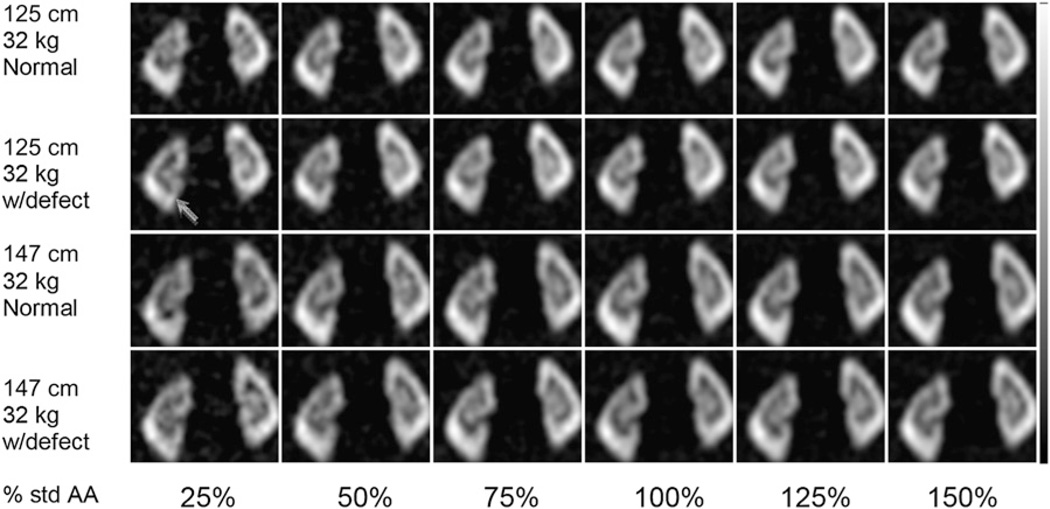
The 1.2-mm voxel representation of the two 10-y female UF phantoms was used as input to an analytic projection code that models attenuation, the spatially varying collimator–detector response (22), and object-dependent scatter (23). Organ uptake was based on values from the pharmacokinetic modeling, with imaging at 3 h after injection. From the models, we estimated the percentage injected activities in the left and right kidneys, spleen, liver, and body. In each kidney we distributed the activity to the cortex, medulla, and pelvis on the basis of observed image intensity ratios in pediatric SPECT images. The total activity in the phantom was based on the 32-kg weight of the phantom times a dose of 1.85 MBq per kg, the standard dosing at Boston Children’s Hospital. Projection data were simulated using an analytic projection code that models attenuation, detector, and scatter. This code has been extensively validated for imaging of a variety of isotopes by comparison to Monte Carlo and experimental projection data. We modeled a low-energy, high-resolution collimator, 128 × 128 projection images, a 360° body-contouring orbit, 120 projection views, and a 0.22-cm projection bin size. Organ uptake was varied randomly with a uniform distribution over a range of ± 10% of the modeled values. We created defects with uptake reduced by uniformly distributed random amounts in the range of 15%–25% relative to the activity concentration of surrounding normal kidney, giving defect–to–background activity ratios of 0.15–0.25. In each kidney, the defects were placed in the inferior, lateral, and superior positions, with a size resulting from the intersection of a 2.2-cm-radius sphere centered on the defect location within the cortex of the kidney. We created 50 random uptake variations for each defect location and images with and without the defect, for a total of 600 phantom projections. The projections were scaled to represent the count level that would be obtained using a low-energy, high-resolution collimator (sensitivity of 85.6 counts/s/MBq) and a 30-min acquisition using a dual-camera system. The images were then scaled to represent 25%, 50%, 75%, 100%, 125%, and 150% of this count level (corresponding to a change in the AA by the same proportion), and Poisson noise was additionally simulated. There was an average of approximately 31 kilo counts in the projection data for one 0.22-cm-thick slice in the region over the kidneys for the 100% count level. The resulting projections were reconstructed using filtered backprojection followed by an order 5 3D Butterworth filter with a cutoff frequency of 0.73 cm⁻¹. This filter was chosen because it subjectively gave the best image quality, but the filter was not otherwise optimized. Sample coronal images for the different body morphometry and count levels are shown in Figure 3.

FIGURE 3.

Example of set of simulated coronal ^99mTc-DMSA SPECT images through kidneys used in CHO study. Images are from 2 phantoms with body weight of 32 kg and with heights of 125 and 147 cm. In this example, images are shown with and without single defect (defect–to–kidney activity ratio, 0.2) (arrow). Noise levels correspond to 25%–150% of standard AA (std AA) of 1.85 MBq/kg and 30-min scan with dual-camera SPECT system.

We then extracted 64 × 64 coronal images centered on the defect centroids and used these to perform a channelized Hotelling observer (CHO) study. This CHO methodology has been described previously (24). It is a computer simulation–based procedure for diagnostic task–based evaluation of images to generate receiver-operating-characteristic (ROC) curves. It has been shown to predict human observer performance in the detection of a myocardial perfusion defect (25), including an investigation of the effects of reduced count levels (26). We used difference-of-mesa channels with octave widths in the frequency domain and a starting frequency of 0.5 cycles per pixel, giving a total of 6 frequency domain channels. The CHO for each phantom and noise level was trained and tested using a leave-one-out strategy in which 599 of the images were used to train the observer; the resulting CHO was then tested on the remaining phantom, yielding a single test statistic value. We applied this strategy using each of the 600 images, thus producing 600 CHO test statistic values for each phantom and noise-level combination. The test statistics were then analyzed using LAB-ROC4 (27) and CLABROC (28). The LABROC4 code performs maximum-likelihood estimation of the ROC curve parameters and computes the area under the ROC curve (AUC) and its SD from continuously distributed rating data assuming a binormal model. The method used does not require that rating data themselves be binormally distributed but rather that there exists a monotonic transformation (which may be unknown) of the rating data that produces binormally distributed data. The program CLABROC performs hypothesis testing of the AUC values assuming paired rating data. It takes advantage of the correlations in the data to improve the statistical power, and thus the p-values are not estimated directly from the SD of the AUC produced by LABROC4.

RESULTS

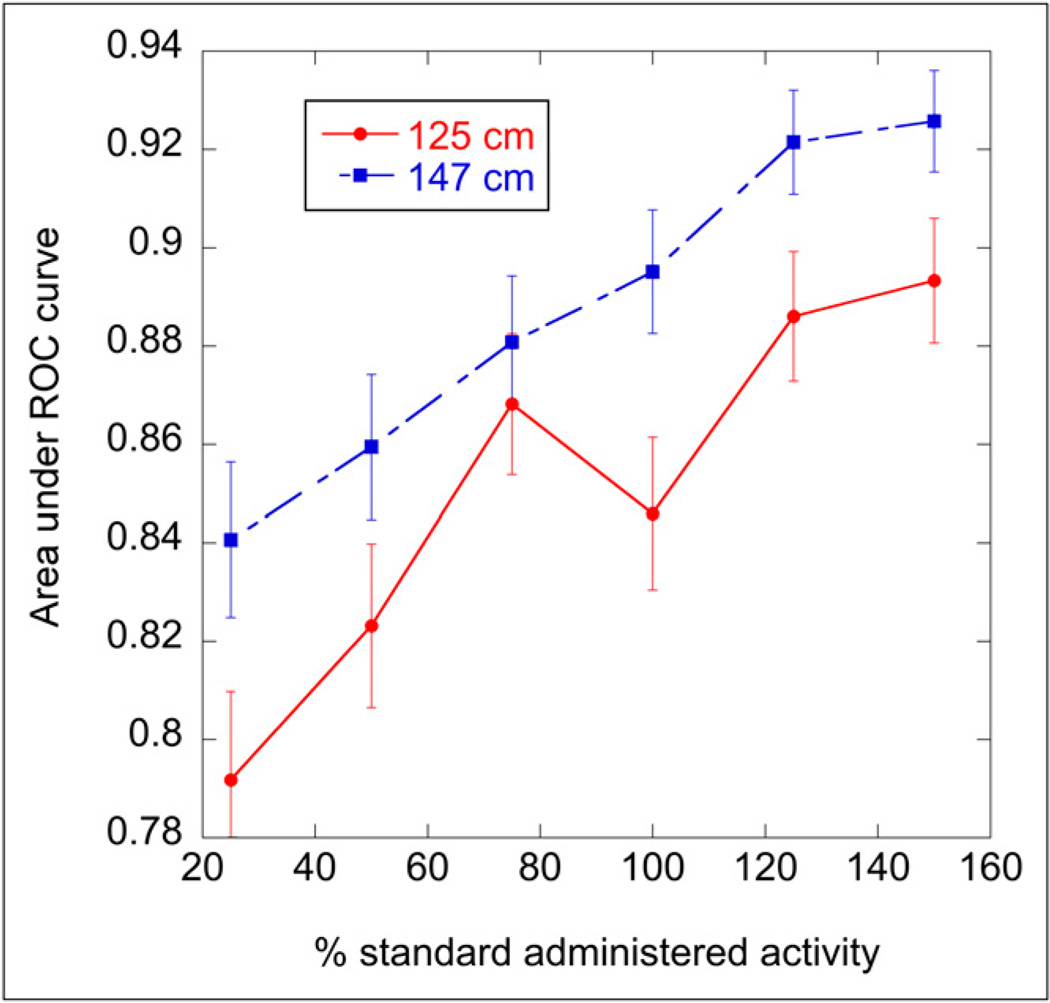
The results of the CHO study and area under the ROC curve (AUC) values for both phantoms at the various count levels are shown in Figure 4. The error bars for the AUC values were obtained from LABROC4. We tested the significance of differences in the AUC for the 2 phantoms at the same noise levels, taking into account the paired nature of the data (using CLABROC). The 1-tailed p-levels for the percentage AAs were 0.017, 0.046, 0.28, 0.008, 0.024, and 0.017 (ordered by increasing AA). Thus, the only AA not significant at a p-level of 0.05 was for the 75% AA. For the remaining cases, we can reject the null hypothesis that the AUC for the tall, thin patient is less than or equal to the AUC for the shorter–stouter patient at the p-level of 0.05.

FIGURE 4.

Plot of AUC as function of relative AA for 2 different simulated phantoms. AUC provides measure of detectability of regions with reduced kidney function, with higher AUC indicating better performance. AUC curve for taller (147 cm) patient is approximately same as that for shorter (125 cm) patient if AAs for taller patient are scaled by factor of 2, indicating that same image quality can be obtained for taller patient in same acquisition time, with one half of AA.

In interpreting the importance of the difference in AUC values, one should note that the curves would be roughly equivalent if the curve for the 147-cm phantom were shifted to the left by 50% of the standard AA. In other words, for the 147-cm-tall phantom, the same performance in terms of identifying the defect could have been obtained with half of the standard weight-based injected activity normally used for the 125-cm-tall patient. This result indicates that body morphometry, and not just weight, is a significant factor in determining image quality for a given AA. The difference in image quality was due to a combination of 3 factors: the 125-cm patient had about 10% fewer photons escaping the body, required a 10% larger average camera orbit radius resulting in poorer resolution, and a 10% higher scatter-to-primary ratio, resulting in slightly higher noise, poorer resolution, and poorer contrast for the shorter patient.

To evaluate the dose implications, ^99mTc S values were generated for the same 2 phantoms. Model-derived residence times for each source organ of a 10-y-old were used to calculate organ-absorbed doses for selected target tissues listed in ICRP 103. The tissue-weighting factors were applied to the absorbed doses, and tissue-factor-weighted equivalent doses were obtained for each phantom. The resulting effective doses per unit AA were 1.42 × 10⁻² mSv/MBq and 9.84 × 10⁻³ mSv/MBq for the short, stout and tall, thin phantoms, respectively. Organ LAR values were also applied to obtain the overall risk for cancer incidence in these 2 hypothetical pediatric patients. The consensus weight-based AA of 1.85 MBq/kg for ^99mTc-DMSA (2) was applied to obtain the organ and overall risk values for the short, stout patient; half of this AA was used for the tall, thin patient to take into account the fact that the same image quality could be obtained with 50% of the AA. Individual organ results are summarized in Table 3, and overall cancer incidence risks are compared in Table 4. For this particular agent, and its corresponding organ dose distribution, a difference between age- and sex-averaged risk and patient-specific risk can be noted. The lower AA needed for the tall, thin child translates into overall cancer incidence risk values that are less than half of those for the short, stout child.

TABLE 4.

Summary of Risk Calculations

Body morphometry	Cancer incidence risk at equal diagnostic image quality*
	AA (MBq)	ICRP 103†	10-y-old girl	Sex- and age-averaged
Short–stout	59.2	5	6	4
Tall–thin	29.6	2	2	1

^*No. of excess cases for population of 100,000.

^†ICRP describes risk of radiation detriment rather than risk of cancer incidence.

DISCUSSION

Consensus guidelines for pediatric AA in nuclear medicine imaging have been recently published (2). The guidelines describe the consensus of expert practitioners in the field. The challenge in identifying the appropriate AA in pediatric nuclear medicine imaging is to balance the long-term concern of radiation risk with the immediate need to obtain images that are diagnostically adequate. The Dosimetry and Pediatrics Committees of the European Association of Nuclear Medicine (8,9,29) developed a method that addresses this challenge. In that approach, each radiopharmaceutical considered was assumed to be uniformly distributed in one of the age-specific, Oak Ridge National Laboratory–stylized phantoms (30), and the complement of the whole-body absorbed fraction (1 minus the whole-body absorbed fraction) was taken as proportional to the photon flux that would be observed by an imaging device. The ratio of this value to the equivalent value obtained for the adult male phantom was used as the normalization factor for photon flux.

The methodology described in the present study is similar in principle to that used by the European Association of Nuclear Medicine Dosimetry Committee but with the following differences. First, in place of calculated photon flux as the measure of image quality, simulated patient images were generated and evaluated by computer observers to obtain a task-based measure of image quality. Second, instead of a uniform whole-body distribution, pharmacokinetic model–based realistic activity distributions were used in the simulated images. As shown in this work, this approach makes it possible to consider anatomic variations for a specific age and weight. Such variations can substantially influence the activity required to obtain good-quality diagnostic images. The approach could ultimately be used to obtain a dataset to help establish pediatric dosing guidelines across a wide spectrum of ages, weights, and body types, bringing us closer to achieving the goal of deriving the maximum diagnostic information in the shortest time and with the lowest patient radiation exposure.

For this rather extreme example (only 10% of the pediatric population at that weight falls into these 2 categories), the effective dose per AA to the short, stout pediatric patient is 44% greater than that to the tall, thin patient. This is reflected in the lower values of the entries in the D(r_T)/A₀ column (Table 3) for the tall, thin patient than those corresponding to the short, stout patient. The distances between source and target organs in the short phantom are less than those in the tall phantom. There are also organ mass differences that will affect the absorbed dose. Larger target organs will absorb more energy, but the energy will be divided by a larger mass; consequently, it is difficult to predict in advance the impact on each organ.

To better understand the cancer incidence risks for pediatric patients associated with imaging at different AAs, organ-absorbed doses were used to calculate LAR values. Because effective dose calculations use sex- and age-averaged tissue-weighting factors, we examined the effect of using averaged values versus sex- and age-specific values. In the case of ^99mTc-DMSA, the dose distribution gave overall risk values that were greater than those obtained by averaging (Table 4). As shown in Table 2, however, the effect of age and sex averaging is strongly dependent on the organ dose profile, and, in particular, for agents that localize to marrow the LAR can differ by almost 2-fold. In most cases, age- and sex-specific risk estimation would allow less AA for equal cancer risk than age- and sex-averaged risk estimation, suggesting that both sex and age, in addition to body morphometry, should be considered when defining optimal pediatric dosing.

CONCLUSION

We present a methodology that balances image quality with cancer risk in evaluating the appropriate AA level for pediatric patients. Using this method, we show that weight-based adjustment alone can lead to unnecessarily high AAs in a certain portion of the pediatric patient population. We also demonstrate age- and sex-specific evaluations of overall cancer incidence risk and examine the implications of using sex- and age-averaged risk parameters. The techniques developed in this work can lead to pediatric imaging AA guidelines that rigorously and transparently balance image quality with associated excess radiation-induced cancer risks. Extension of this methodology to other radiopharmaceuticals would yield the data required to generate objective and well-founded AA guidelines for pediatric and other patients.