On Average: Data Exploration Based on Means Can Be Misleading

INTRODUCTION

On the basis that “a picture is worth a thousand words,” data are often presented graphically in order to convey some of the information that they contain. Modelers use graphical representations of data for numerous purposes, two of the most important being, to inform and drive the modeling process and to communicate with their clients who are the end users of their models. However, it is not always clear which graphic should be used for a particular set of data and for a particular purpose. As such, it is very well possible that choosing the wrong graph may mislead rather than enlighten, which is obviously a situation to be avoided if at all possible. Part of the difficulty lies in the fact that exploratory data analysis (EDA), which incorporates graphical exploration of the data, is perceived to be as much an art as it is a science. The artistic aspect of EDA is based on human creativity and intuition, and it is our intuition that can sometimes fail on us.

One of the most intuitive graphs is one in which the data are averaged in some way and the averages plotted. This use of averages is so intuitive that it is frequently used without very much thought or consideration. It must be acknowledged that in many cases, this proves to be a good strategy though there are occasions when it can be misleading. This paper examines some commonly encountered situations in which such graphics may be misleading. The reasons why they are misleading are explored and explained. In addition, an alternative strategy is suggested.

In order to maintain the confidence of the end users in a model, it is important that any apparent contradiction between the model and the graphical presentation of the data is carefully explained. It is hoped that the following sections will go some way in helping with that explanation.

For the purposes of the following discussion, it will be assumed that the response variable (Y) is recorded on a continuous scale. The independent variable (x) may be continuous or discrete.

The next section describes a general approach to building a mixed effects model. The following two sections discuss the use of data averages and their limitations. An alternative to data averaging is introduced in the following section. The data averaging and alternative methods are compared by means of a simulated trial and a real case example. The paper finishes with a discussion.

MIXED EFFECTS MODEL

When the data are grouped in such a way that observations within a group are correlated, the model needs to take account of such correlation. Longitudinal data are, of course, grouped and correlated in this way because repeated observations on the same subject (experimental unit) are correlated. This correlation is due to the fact that such observations reflect the individual characteristics of the subject. There are several options available for modeling correlated data (1), one of which is the use of a mixed effects model incorporating both random and fixed effects. The use of mixed effects models is limited to situations where the correlation between observations within a group is positive, which is the case for many datasets. These mixed effects models are widely used in pharmacometrics and will form the basis of our discussion.

Consider a situation where data were collected from n subjects with m_i observations being made on the ith subject. For the sake of simplicity, a single discrete valued independent variable will be considered with r distinct values denoted by x_kk = 1,2,…,r. Note that it is not being assumed that each subject has one observation at each distinct value of x, and consequently, m_i is not necessarily equal to r. If x is continuous, it can be discretized using intervals that span the range of x with x_k being the middle of the kth interval. Let the observations be denoted by Y_ij where the subscript i represents the subject and the subscript j indicates a particular observation recorded for that subject. The vector of random effects associated with the ith subject will be denoted by η_i. These random effects are constant across all observations for a particular subject but vary from subject to subject and are included in the model to account for the positive correlation between observations within a group and for the variation between groups.

The modeling objective is to construct a suitable model of the general form

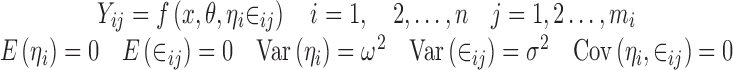1

where θ is a vector of fixed effect parameters and the random part of Y_ij is described by the random effect η_i and by the noise ∈_ij. The E(.) notation stands for the expected value (mean or average) of a random variable, while Var(.) and Cov(.) represent the variance and covariance, respectively (2). In addition to Eq. 1, the model usually includes some distributional assumptions about the random effects and the noise. Note that the number of observations that each subject has at any particular value of x is not specified and might vary from subject to subject.

The first problem is to find a function f(.) which would be suitable to describe the data under consideration. The most common approach is to select a function based on knowledge of the processes giving rise to the data, or based on previous experience with similar data. The choice of a function is frequently supported by plotting the data to show that it conforms to the general shape of the function selected. When no information is available about the processes giving rise to the data and there is no previous experience to call upon, the data are plotted and an empirical or a semi-mechanistic function that describes the shape of the plot is selected. In all of these scenarios, the plot used is frequently the one which uses the average value of Y at each distinct value of x, plotted versus x. The question to be addressed is whether or not such a plot is appropriate in any given situation.

THE AVERAGE

The problem of finding a suitable function f(.) for the data can be somewhat simplified by dividing it into two steps. The first step consists of identifying the appropriate function to use to describe the non-random part of the model. This amounts to deciding what function to use to describe noise-free data (∈_ij = 0) from a typical subject (η_i = 0). The second step is to decide how the random effects (η_i, ∈_ij) enter the function f(.).

The first step amounts to considering a simplified problem in which the random effects (η_i, ∈_ij) are replaced by their means, both of which are zero. Essentially, what we are trying to do here is to identify the function f(x, θ, 0, 0). If the value of f(x, θ, 0, 0) were known for each value of x, then plotting f(x, θ, 0, 0) versus x would indicate the shape required and would hopefully suggest a suitable function or set of functions for f(x, θ, 0, 0) and/or might be used to justify the use of a particular function. Of course, the value of f(x, θ, 0, 0) is unknown but might be estimated at each distinct value of x, and the estimates plotted versus x to produce the required graph. Since f(x, θ, 0, 0) represents the model for Y_ij in Eq. 1 with η_i and ∈_ij replaced by their mean values of zero, it seems intuitive to use the sample mean of the Y_ij, averaged across i and j as an estimate of f(x, θ, 0, 0). These sample means (one for each value of x_k) are written as 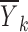where

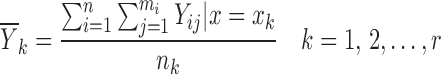2

and n_k is the number of observations in the dataset with x = x_k. A plot of the 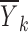values against the independent variable x_k is used as an indicator of the shape of f(x, θ, 0, 0) and also to suggest suitable functions that might be used or to support the use of a particular function for f(x, θ, 0, 0).

The second step is to decide how the random effects (η_i, ∈_ij) enter the function f(.). The choice of a model for the noise is largely empirical (3). Some commonly employed structures (4) are the additive error model

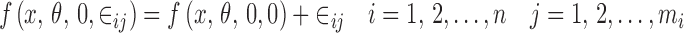3

the proportional error model

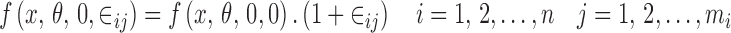4

and the multiplicative error model

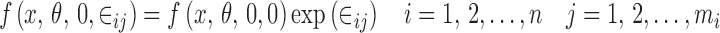5

The multiplicative error model can be approximated by the proportional error model. Finally, the random subject effects are usually based on the idea of between-subject variation of the parameters defining the shape of f(x, θ, 0, 0). For example, if

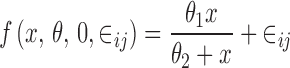then the model

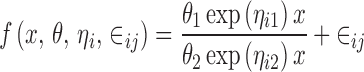or

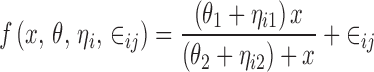6

might be considered because each of them describes subject to subject variation in the elements of θ.

THE MODEL FOR THE AVERAGE

Now, let us examine in more detail the use of 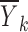as an estimate of f(x_k, θ, 0, 0). This step was described above as “intuitive,” but we will look at it from a statistical point of view and assess how good an estimate of f(x_k, θ, 0, 0) the data average 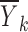really is.

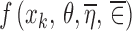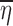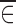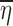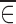The rationale for averaging lies in the fact that we are interested in f(x_k, θ, 0, 0) which is the model in Eq. 1 with η_i and ∈_ij replaced by their mean values of zero. If we could compute where and represent sample averages of η_i and ∈_ij, respectively, and if we could assume that both and are close to zero, then we have an estimate of f(x_k, θ, 0, 0).

The first consideration is the linearity of f(x, θ, η_i, ∈_ij) in terms of η_i and ∈_ij. It is well-known (1,5,6) that if the function is nonlinear in these random variables, then the mean of the function is not equal to the same function of the means. Consider the logarithm as an example of a nonlinear function. The mean of the natural logarithm of data values (5, 62, 37, 18, 46) is 3.2 while the natural logarithm of the mean of these data values is 3.5, which demonstrates that the mean of the logarithm is not equal to the logarithm of the mean. 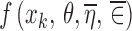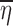Averaging the values of the response variable Y_ij at a fixed x corresponds to averaging f(x, θ, η_i, ∈_ij) at a fixed x across values of η_i and ∈_ij and is not equal to where and 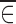represent the averages of η_i and ∈_ij, respectively, when the function is nonlinear in η_i and ∈_ij. Because this property of the average has been well documented (1,5,6), we will not dwell on it here except to point out that nonlinearity is one reason why plotting data averages could be misleading.

The function f(x, θ, η_i, ∈_ij) can be approximated by means of a first-order linearization as follows:

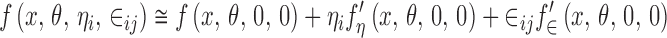7

where the prime denotes partial differentiation with respect to the subscript. If the function f(.) is linear in η_i and ∈_ij, the approximation is exact. How good this approximation is depends on the form of the function f(.) and on the size of the variances of η_i and ∈_ij (6). In the following discussion, it will be assumed that the linear approximation is at least “reasonable” if not exact. Substituting Eq. 7 into Eq. 1 gives

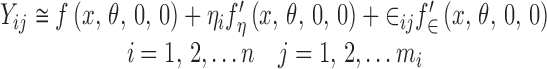8

Substituting this into Eq. 2 will give us a model for 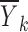. Let us proceed in steps by summing over the j subscript first.

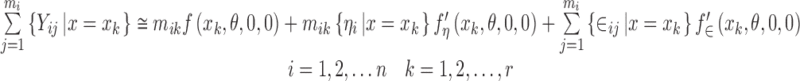9

where m_ik represents the number of observations recorded for the ith subject with x = x_k. Now sum over the i subscript to get

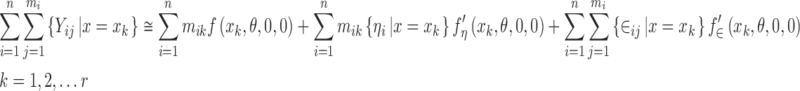10

Now dividing across by n_k and noting that 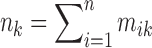yields

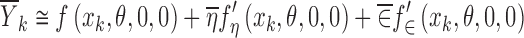11

where

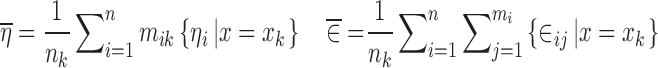12

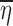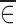If both and are close to zero, then 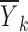would be approximately equal to f(x_k, θ, 0, 0). Consequently, we can see that there are two conditions for the data averages to be used as estimates of f(x_k, θ, 0, 0), namely

1. The model should be linear or approximately linear in both the random effects and the residual error.

2. The mean values 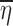and 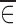in Eq. 12 should be expected to be close to E(η_i) = 0 and E(∈_ij) = 0, respectively.

This latter condition can be examined by considering 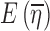, which is the mean of the sampling distribution of 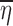. This mean can be derived (2) from Eq. 12 as

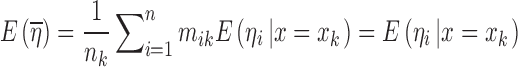13

where 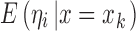is the mean of η_i conditional on x = x_k and is also described as the regression function of η_i on x (7). If η_i and x are independent of each other, we can write

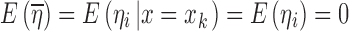14

i.e., the conditional mean of η_i is equal to its marginal mean which is zero and we could expect 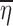to be close to E(η_i) = 0. However, when η_i and x are dependent on each other, Eq. 14 does not hold and 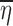could be different from zero.

Similarly, we can write

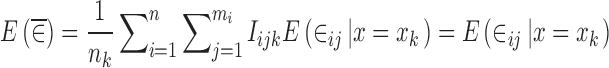15

where I_ijk is an indicator variable taking a value of 1 for each observation with x = x_k and a value of zero otherwise. When ∈_ij and x are independent of each other, then

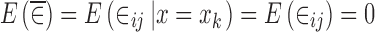16

and 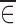would be expected to be close to zero. On the other hand, when ∈_ij and x are dependent on each other, 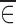could be different from zero.

The results in Eqs. 11, 14, and 16 show that in a situation where the model is approximately linear in both the random effects and the residual error and both the random effects and the residual error are independent of x, plotting 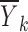versus x_k would give a reasonable representation of the function f(x, θ, 0, 0). However, when these conditions do not hold, the plot could be misleading.

An example of a situation in which the random effects are correlated with x is a dose titration study in which the drug dose administered to a subject at each dosing occasion is represented by x and is dependent on the response of the subject to earlier doses. Because the response to earlier doses depends on the individual subject’s random effects, there will be a correlation between the dose administered and the random effects. Consequently, in this circumstance one should not expect 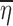to be close to zero and plotting 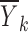versus x_k would not be expected to yield a reasonable representation of the function f(x, θ, 0, 0).

AN ALTERNATIVE APPROACH

Combining Eqs. 1 and 7 gives Eq. 8 which can be written as

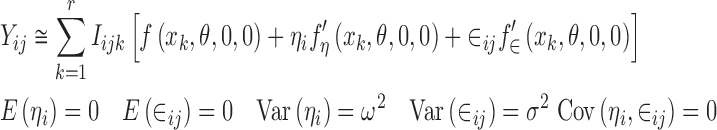17

where I_ijk is as defined in Eq. 15. Since interest centers on estimating f(x_k, θ, 0, 0), we can think of the values of this function at the discrete values of x as parameters to be estimated. In other words, the values of f(x_k, θ, 0, 0) k = 1, 2,…,r become parameters that can be written as

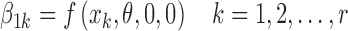18

At this stage of the model building process, we do not know the form of the function f(.), and as a result, we have no information about the random effects. Consequently, we use a single random effect which acts as a surrogate for all of the random effects. The derivatives with respect to the random effect and the residual error at the discrete values of x can also be considered as parameters and written as

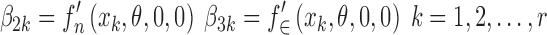19

Combining Eqs. 17, 18, and 19 gives a linear mixed effects model

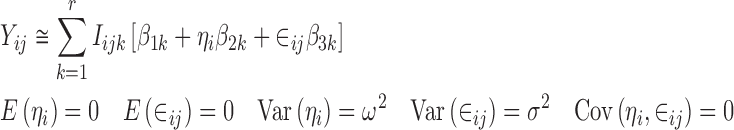20

which can be fitted to the data in order to estimate the values of all of the β parameters. However, the model in Eq. 20 is over-parameterized because the variance of the random effect (ω²) and the residual variance (σ²) cannot be uniquely estimated. This is due to the fact that the variance of Y_ij includes a term that is equal to β_2k²ω² and a term equal to β_3k²σ², and only these products are estimable (identifiable), not the individual components, and consequently, ω² and σ² cannot be uniquely estimated. This over-parameterization can be dealt with by fixing the values of the two variances. Once the β parameters have been estimated, the required plot can be produced by plotting 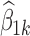versus x_k.

SIMULATION STUDY

In order to demonstrate the effects described above, a dose–response study was simulated with two treatment arms. The doses studied ranged from 10 to 50 mg in 10 mg increments. Each subject received ten doses of drug, and their response was recorded on a continuous (arbitrary) scale following each dose. In one treatment arm, the subjects underwent a forced dose titration following every second dose, i.e., their first two doses were 10 mg, the next two were 20 mg, etc. In the other treatment arm, a controlled dose adjustment regimen was used. In this arm, subjects were administered a 10-mg dose on the first dosing occasion. All subsequent doses were dependent on the responses to the previously administered doses. If the responses were below a pre-determined threshold, the dose was escalated by 10 mg, and once a subject recorded at least one response above the threshold, their dose was maintained at that level for the rest of the trial. The model used to simulate the jth response for the ith subject was an E_max model and can be described by

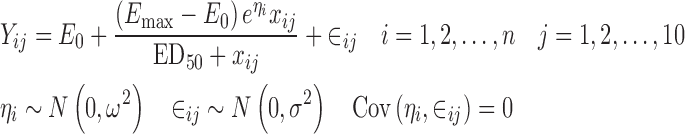21

where Y_ij is the response and x_ij represents the dose administered. The maximum effect varies from subject to subject and may be described as the sensitivity of the subject to the drug because subjects with large values of E_max experience greater responses than those with smaller E_max values. Note that this model is nonlinear in the random effect, and as a consequence, the alternative approach, described above, is based on a linear approximation. In order to minimize the effect of sampling variation on the results, a very large sample of 10,000 subjects was simulated in each arm with E₀ = 20, E_max = 100, ED₅₀ = 30, ω² = 0.08, and σ² = 100. In the controlled dose adjustment arm, the threshold response was 50 units.

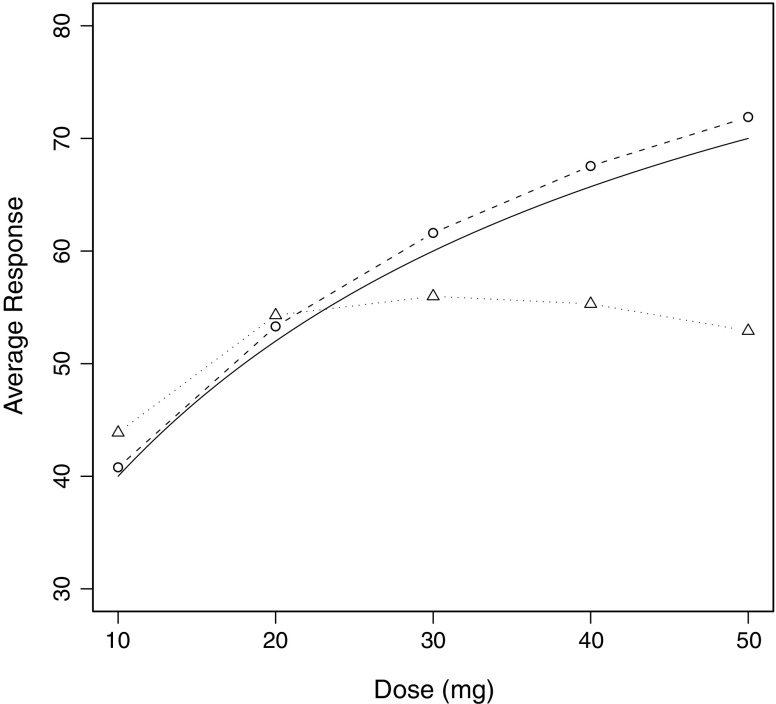
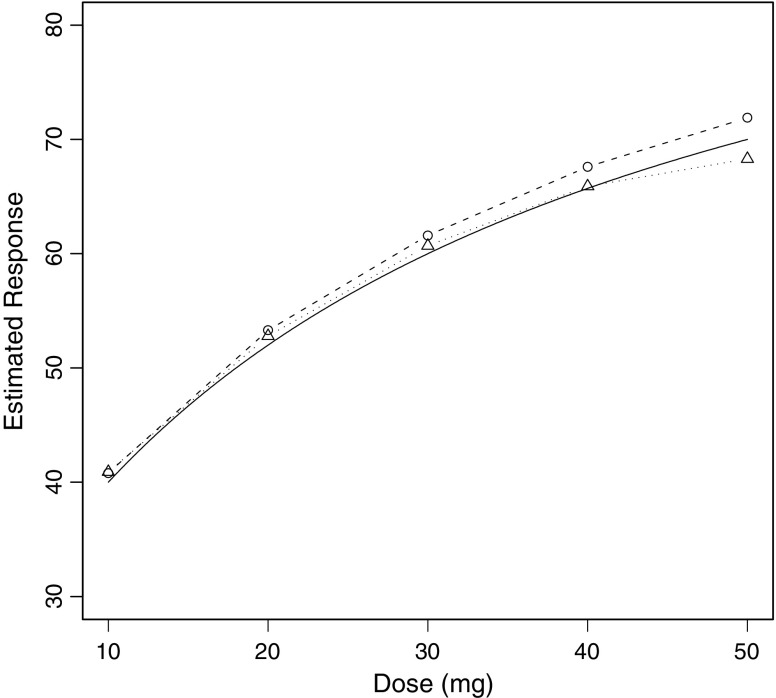
The result of plotting the average response at each dose versus dose is shown for both treatment arms in Fig. 1 along with the noise-free dose–response curve for a typical (η_i = 0) subject. Then the mixed effects model of Eq. 20 was fitted to each dataset using NONMEM® VI (8) and the estimates of 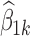were plotted versus x_k for each treatment arm, and the results are illustrated in Fig. 2 which also includes the noise-free dose–response curve for a typical (η_i = 0) subject for reference purposes.

Fig. 1.

The noise-free dose–response relationship for the typical subject along with mean response plotted versus drug dose for each arm of the simulated trial. The solid curve with no symbols represents the noise-free dose–response relationship for the typical subject, the circles with dashed lines refer to the forced titration arm, and triangles with dotted lines correspond with the controlled dosage adjustment arm

Fig. 2.

Estimates of the β _1k parameters in Eq. 20 plotted versus drug dose for each arm of the simulated trial. Circles with dashed lines refer to the forced titration arm, and triangles with dotted lines correspond with the controlled dosage adjustment arm. The noise-free dose–response relationship for the typical subject is represented by the solid curve with no symbols

EXAMPLE

Data collected during a phase 3 study of an ER formulation of tapentadol hydrochloride, which has been developed for the management of moderate to severe chronic pain in patients 18 years or older, will be used to illustrate the points discussed above. This centrally active analgesic agent has an apparent dual mode of action, being both a mu-opioid receptor agonist and an inhibitor of norepinephrine (re)uptake. The study was a randomized, multicenter, double-blind, parallel-group trial with controlled dose adjustment regimens of tapentadol ER, placebo, and active comparator (oxycodone CR) in subjects with moderate to severe chronic pain due to osteoarthritis of the knee. The eligible populations included opioid naïve and opioid experienced subjects who presented with moderate to severe pain based on pain intensity scores. The trial consisted of five periods: screening, washout, titration, maintenance, and follow-up. The doses of tapentadol investigated ranged from 100 to 250 mg twice daily (b.i.d.). Doses of tapentadol 50 mg were used for the purpose of titration only.

Throughout the trial, each individual subject recorded twice daily (morning and evening) their average pain intensity over the previous 12 h using an 11-point (0–10) numerical rating scale (NRS). Following screening, subjects proceeded to a washout period lasting 3 to 7 days. At completion of the washout period, subjects were randomized to their double-blind treatment arm (tapentadol, oxycodone or placebo). Determination of baseline pain intensity was defined as an average of the pain intensity score measured over the last 3 days prior to randomization with an average NRS score of ≥5 required for randomization. Following randomization, subjects were individually titrated over 3 weeks to the optimal individual dose of the investigational drug. The optimal dose is defined as the dose providing a meaningful improvement of pain with acceptable side effects in the subject’s perception. Subjects initiated treatment with tapentadol ER (base) 50 mg b.i.d., oxycodone CR 10 mg b.i.d., or placebo b.i.d. After 3 days, the dose was increased to tapentadol ER 100 mg b.i.d., oxycodone CR 20 mg b.i.d., or placebo b.i.d., respectively. This was the minimum dose allowed for the remainder of the trial. Upward titration at a minimum of 3-day intervals (six consecutive doses) in increments of tapentadol ER 50 mg b.i.d., oxycodone CR 10 mg b.i.d., or placebo b.i.d. was permitted. The maximum doses of active treatment allowed were tapentadol ER 250 mg b.i.d. and oxycodone CR 50 mg b.i.d. Downward titration (not below the minimum dose) was also permitted using the same decrements without a time restriction. Subjects continued their investigational drug intake for a 12-week maintenance period. Medication could be adjusted up or down in increments of tapentadol ER 50 mg b.i.d., oxycodone CR 10 mg b.i.d., or placebo b.i.d. Adjustment of dose took place in agreement with the investigator, with a minimum of 3 days between each dose adjustment. A post-treatment follow-up period of 2 weeks followed treatment discontinuation.

Along with the twice daily NRS pain scores and the baseline pain score, the doses of medication administered, the patient’s age, body weight, gender, and opioid experience were also recorded. Because each pain score represents the average pain in the 12-h time period immediately preceding the recording of the pain score, the dose associated with each pain score was that administered 12 h prior to the recording of the pain score.

Consider a modeling exercise whose objective is to establish a dose–response model for tapentadol based on the pain scores recorded in the morning (for the sake of simplicity). For this purpose, the data collected for subjects who received the active comparator do not contain useful information and are ignored.

Because of the titration and dose adjustment nature of the trial design and the fact that subjects were blinded to the medication received, the placebo was administered at different “dose” levels, each identical in appearance with the corresponding tapentadol tablet. Consequently, the data collected from placebo-treated subjects also includes dose information corresponding with the dose that the subject believed had been administered, i.e., five “dose” levels of placebo were used in the study (50, 100, 150, 200, and 250 mg). This aspect of the study design must be taken into account when modeling the data.

The controlled dose adjustment nature of the study implies that subjects have varying sensitivity to their medication and this ought to be part of the random subject effect. Following the early doses (50 and 100 mg of tapentadol or placebo), the dose of medication administered to a subject depends on that subject’s responses to previous doses which in turn depends on the subject’s sensitivity to the medication. Consequently, the dose administered is correlated with the subject’s sensitivity to the medication. For example, a very sensitive subject will receive a meaningful improvement of pain with acceptable side effects at low doses and will seldom if ever be administered the higher doses. On the other hand, a relatively insensitive subject will very rapidly escalate the dose of medication to the higher dose range and will be administered few low doses and lots of high doses.

The dataset was divided into four subsets as follows:

1. Opioid naïve subjects administered the placebo

2. Opioid experienced subjects administered the placebo

3. Opioid naïve subjects administered tapentadol

4. Opioid experienced subjects administered tapentadol

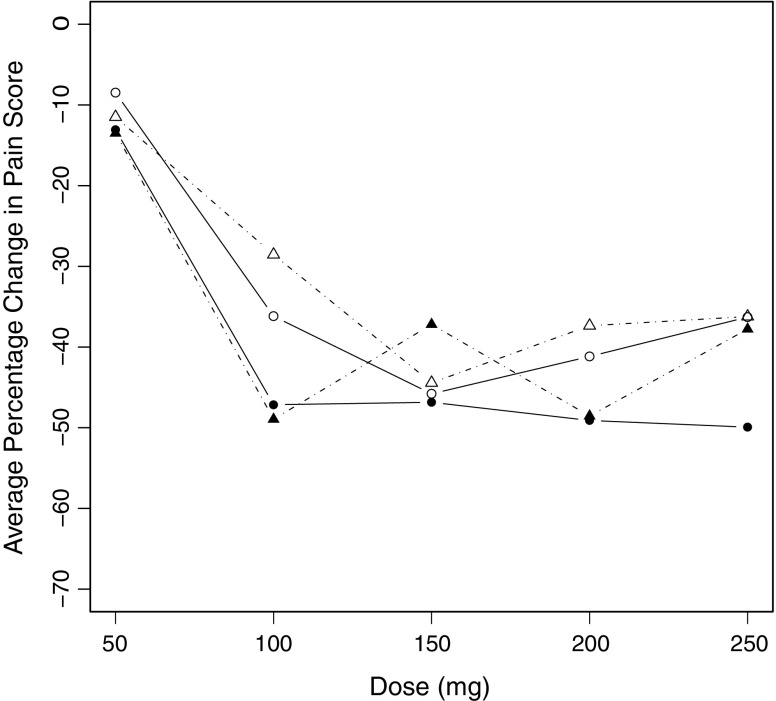
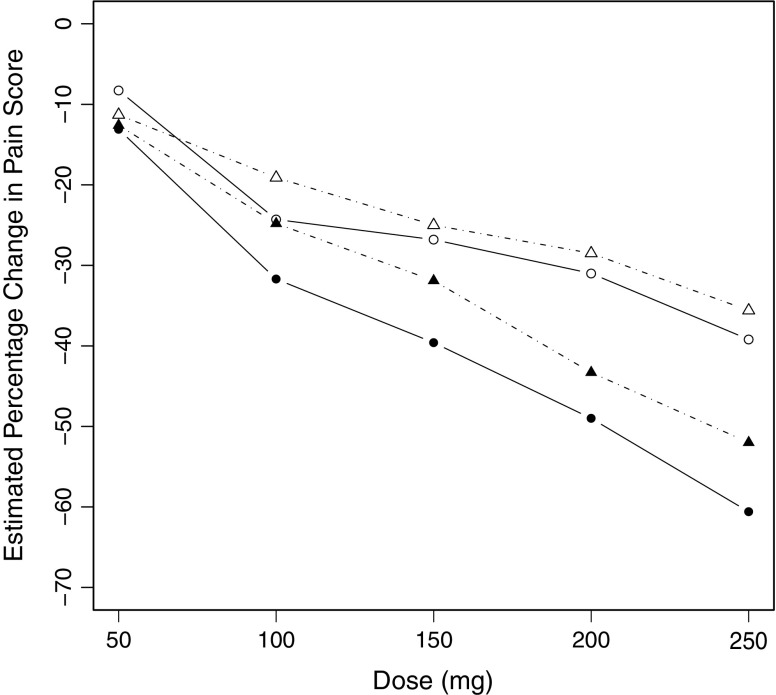
Since interest centers on dose–response relationships, the dose of medication was treated as x in the analyses conducted. Percentage change from baseline pain score was the response variable (Y) with negative values corresponding with a reduction in pain score. Each dataset was first analyzed by computing the mean of all responses at each dose level from 50 to 250 mg in increments of 50 mg. The mean response was plotted versus dose, and the results are shown in Fig. 3 where the plots for the four datasets are overlaid. Then the linear mixed model of Eq. 20 was fitted to each dataset using NONMEM® VI (8), and in each case, the estimates of 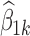were plotted versus x_k and these four plots are overlaid in Fig. 4. An extract from the code used is given in the “Appendix.”

Fig. 3.

Mean percentage change in pain score from baseline (negative values correspond with a reduction in pain score) plotted versus dose of medication for each of four groups of subjects. Open symbols refer to placebo-treated subjects, and solid symbols refer to tapentadol-treated subjects. Opioid naïve and opioid experienced subjects are indicated by circles and triangles, respectively

Fig. 4.

Estimates of the β _1k parameters in Eq. 20 plotted versus dose of medication for each of four groups of subjects. Open symbols refer to placebo-treated subjects, and solid symbols refer to tapentadol-treated subjects. Opioid naïve and opioid experienced subjects are indicated by circles and triangles, respectively

DISCUSSION AND CONCLUSIONS

The results of the simulated trial in Fig. 1 clearly illustrate a big difference between the plots for the two arms of the trial. In the forced titration arm, the dose administered is independent of the random subject effects and the residual error because the doses were administered according to a fixed schedule incorporated into the trial design. Consequently, Eqs. 14 and 16 indicate that we can expect that plotting the average response versus dose would give a good representation of the noise-free dose–response curve for the typical subject. This expectation is borne out by the results plotted in Fig. 1. The difference between the curve describing noise-free data in a typical subject and the means based on the forced titration arm was shown to be due to the fact that the model is nonlinear in the random effect (results not shown).

The plot in Fig. 1 for the controlled dose adjustment arm is clearly misleading in terms of the dose–response relationship and demonstrates the potential to introduce a selection bias into the dose–response analysis of the data, if such analysis does not take proper account of the controlled dose adjustment design. Use of such a design is likely to result in only the least drug sensitive subjects receiving the highest doses. As a result of their low sensitivity, the responses recorded for these doses would be less than would be expected in the general population. On the other hand, the most sensitive subjects will receive most of the lower doses administered because they will reach the threshold response at a low dose and continue with that dose for the remainder of the trial. Consequently, as we move from left to right in Fig. 1, not only is dose increasing but subject sensitivity is effectively decreasing, although this is not shown on the graph. A naïve interpretation of the mean responses in Fig. 1 attributes the high level of response in the more sensitive subjects and the low response in the least sensitive subjects to the dose rather than the subjects receiving that dose. The association between the dose administered and the subject’s drug sensitivity implies that these two are correlated, and the dose–response analysis needs to take this fact into account. The ICH guideline on dose–response (9) highlights this issue and points out that a crude analysis of such data can give a misleading inverted “U-shaped” curve. Such a curve is clearly illustrated in Fig. 1. The FDA Guidance for Industry on exposure–response relationships (10) echoes these same points. This issue is also discussed by Ting (11) who points out that the disadvantage of a controlled dose adjustment design is the difficulty in data analysis.

Using the alternative approach contained in Eq. 20 takes subject to subject variation in drug sensitivity into account thus allowing for the fact that only the least sensitive subjects receive the higher doses, etc. Figure 2 demonstrates that this approach is useful and that it produces results that are very similar to those of the forced titration study.

The tapentadol example illustrates the results of data averaging and the alternative approach using four different treatment groups in a real dataset. It is noteworthy that in this trial, there was an initial forced dose titration from the 50-mg dose to the 100-mg dose and controlled dose adjustment thereafter. Consequently, the dose–response relationship from 50 to 100 mg is quite clear in Fig. 3; however, there is no apparent relationship at higher dose levels. On the other hand, Fig. 4 clearly shows a dose–response relationship in all four treatment groups, and this illustrates the advantage of the alternative strategy based on Eq. 20. It is obvious from Fig. 4 that placebo-treated subjects exhibit a clear relationship between their response and the “dose” of placebo administered. Furthermore, the tapentadol-treated subjects also have an obvious dose–response relationship with larger reductions in their pain scores than the placebo-treated subjects. It is also clear that for each treatment, the opioid naïve subjects have greater reductions in their pain scores than opioid experienced subjects. In fact, Fig. 4 is in remarkably close agreement with the results of an independently conducted modeling exercise (unpublished work) and was used to support the choice of model.

Both the simulated results and those of the tapentadol trial confirm the assertion that plotting data-averaged responses versus a variable of interest (dose in these examples) can result in a very misleading graph. When the underlying model is either linear or approximately linear in the random effects and the residual error, the suggested alternative plot may be a useful way to view the relationships inherent in the data.

The methodology presented in this paper is not particular to dose–response relationships, it applies generally. For example, the independent variable could be “time,” and the recording of a response variable may depend on the response itself.

Appendix

The following is an extract from the NONMEM® code used to fit Eq. 20 to the data.