Covariate Pharmacokinetic Model Building in Oncology and its Potential Clinical Relevance

Abstract

When modeling pharmacokinetic (PK) data, identifying covariates is important in explaining interindividual variability, and thus increasing the predictive value of the model. Nonlinear mixed-effects modeling with stepwise covariate modeling is frequently used to build structural covariate models, and the most commonly used software—NONMEM—provides estimations for the fixed-effect parameters (e.g., drug clearance), interindividual and residual unidentified random effects. The aim of covariate modeling is not only to find covariates that significantly influence the population PK parameters, but also to provide dosing recommendations for a certain drug under different conditions, e.g., organ dysfunction, combination chemotherapy. A true covariate is usually seen as one that carries unique information on a structural model parameter. Covariate models have improved our understanding of the pharmacology of many anticancer drugs, including busulfan or melphalan that are part of high-dose pretransplant treatments, the antifolate methotrexate whose elimination is strongly dependent on GFR and comedication, the taxanes and tyrosine kinase inhibitors, the latter being subject of cytochrome p450 3A4 (CYP3A4) associated metabolism. The purpose of this review article is to provide a tool to help understand population covariate analysis and their potential implications for the clinic. Accordingly, several population covariate models are listed, and their clinical relevance is discussed. The target audience of this article are clinical oncologists with a special interest in clinical and mathematical pharmacology.

INTRODUCTION

The analysis of pharmacokinetic (PK) data using a population approach has many advantages over traditional methods, and key strengths are the potential for dosing individualization and simulating dosing algorithms for a certain drug under different conditions, e.g., organ dysfunction or combination chemotherapy (1). Inclusion and quantification of individual-specific covariates facilitates our understanding of the overall dose–exposure–response relationship, and helps determine if covariate-based dose individualization is required to normalize exposure and minimize variability in therapeutic outcomes or adverse events across population subgroups. Resulting parameter estimates might have a clear pathophysiological or mechanistic meaning, e.g., the volume of blood or plasma that is cleared of the drug, and this is indeed the most common case with modeling drug concentration–time data. However, highly mechanistic models might also include more hypothetical processes of drug ADME (absorption, distribution, metabolism and elimination), such as blood flow, organ size, chemical or molecular interactions between specific drugs. The latter is often referred to as physiological-based PK (PBPK) modeling. A population model quantifies interindividual variability in the model parameters, a process that is crucial to be able to obtain an accurate description of the typical individual within a population. In fact, decisions in drug development are increasingly being made on model-based population analyses, and this approach is also encouraged by the regulatory agencies (2). One of the most popular software tools for doing nonlinear mixed-effects (NLME) modeling is NONMEM (3,4). However, there are other software tools such as Phoenix (5), SAS (6), Monolix (7), PKBUGS (8), and others. Guidelines on population pharmacokinetics have been issued by the US Food and Drug Administration (FDA) (9) and by the European Medicines Agency (EMA) (10).

When modeling population PK data, identifying covariates is important in explaining interindividual variability and thus increasing the predictive value of the underlying model (11–15). Nevertheless, covariate modeling is often of only limited clinical use, and its main value is to provide a coherent and rational framework for describing and predicting the dose–concentration–response relationship and other key features such as disease progression. Whereas a parameter is a fixed quantity estimated according to the model, a covariate is an independent variable that contains information on a parameter, i.e., the parameter depends on the covariate. Accordingly, a covariate model can be used for identifying patient subpopulations at risk for subtherapeutic or toxic effects and to subsequently individualize drug treatment. Furthermore, such a model is useful for identifying the need for and aiding the design of new studies in the process of drug development. The covariate selection process can be univariate or multivariate, and is regularly built with stepwise inclusion with a predefined level of significance for accepting covariates as part of the model. A well-known problem with the stepwise procedure is selection bias resulting in overestimation of the importance of a certain covariate (see “METHODOLOGICAL CONSTRAINTS: PARAMETER SHRINKAGE, SELECTION BIAS, AND COLLINEARITY” section). Even though data are limited at present, previous investigations have indicated that selection bias might not be a problem that is clinically relevant (16). Various methods for covariate selection have been described, including the classical stepwise covariate modeling method (11), and newer strategies such as the Lasso method (17) and the Wald’s Approximation Method (WAM) (18).

A methodological challenge with identifying the true and most important covariate is the potential correlation between the covariates themselves (19) that can potentially result in a further increase of the covariate selection bias. In fact, the level of significance of one covariate in a respective drug model does not inform the investigator about the clinical relevancy of the covariate identified. Accordingly, a covariate with strong predictive value might not be selected by the investigator due to the potential loss of a mechanistic meaning of the covariate model (19). This procedure of filtering these covariates with no physiological relationship to the parameters of interest is a key element of PK modeling, and supports the development of clinically reasonable models. Another issue is that parameter estimates can also be affected by collinearity when entering new covariates into the structural model in NONMEM, and correlations among covariates greater than 0.5 should be a warning to the investigator, because the accuracy of the parameter estimates themselves may be biased, and the precision of the estimates might be inflated due to ill-conditioning (20). The purpose of this review is to provide a tool to help understand population covariate analysis and their potential implications for the clinic. Accordingly, several population covariate models are listed, and their clinical relevance is discussed. The target audience of this article are clinical oncologists with a special interest in clinical and mathematical pharmacology (Tables I and II).

Table I.

Covariate Effects of Most Common Individual Characteristics on the Pharmacokinetics of Major Anticancer Drugs

Drug	Major covariates	Mathematical association	Recommended dosing	Clinical relevance	Reference
Busulfana	WT	CL = 4.04 L/h/20 kg·(WT/20) 0.74	1.1 mg/kg for children ≤12 kg	Improve target AUCbusulfan	(56)
			0.8 mg/kg for children >12 kg	(900–1,350μmol h/L)
Docetaxelb	HEPc	CL = BSA(36.8–4.6·AAG-0.14·AGE)·(0.58·HEP)	~60% dose in pts with elevated	Avoid (febrile) neutropenia	(39)
			Liver enzymesc
Melphalana	WT, GFR	D(mg) = 9·(0.34·WT + 0.038·GFR)	Proposed nomogram	Improve target AUCmelphalan (9μg h/mL)	(62)
Methotrexate	COM, GFR	CL = 8.8 + 0.04·(87 − GFR) − (2.45·PPI) − (1.46·NSAR)	Avoid NSAR	Avoid nephrotoxicity, mucositis and myelosuppression	(75)
			Potentially avoid PPI
Paclitaxelb	SEX	VMEL = 37.4·1.2Sex·(BSA/1.8)0.84·(Age/56)0.35	200 mg/m2 in male patients	Avoid severe neutropenia	(73)
			175 mg/m2 in female patients
Pemetrexed	GFR	CL = 43 + 47.2·(GFR/92.6)	Avoid when GFR <45 ml/min	Avoid severe neutropenia	(76)
Temozolomide	BSA	ln(CL) = ln(4.87) + 1.14·ln(BSA)d	150 mg/m2 for 5/28 days	Avoid severe neutropenia	(65)
Topotecan	GFR, WT	CL = (5.7 + 12.8·GFR/70)·(WT/70)0.75	0.75 mg/m2 for 5/28 days	Avoid severe neutropenia	(80)
			if GFR 20–40 ml/min

Ref reference, WT weight, HEP hepatic enzymes, AUC area under-the concentration–time curve, SEX patient gender, BSA body surface area, PPI proton pump inhibitors, NSAR nonsteroidal antirheumatic drugs, CL drug clearance (liters per hour), D dose, GFR glomerular filtration rate (ml/min/1.73 m²), VM _EL maximum elimination capacity (micromoles per hour), COM comedication

^aIn children

^bAnalysis performed in patients receiving 3-weekly docetaxel/paclitaxel

^cEither GGT, alkaline phosphatase, ALT, AST

^dFor male patients

Table II.

Covariate Effects of Specific Genotypes on the Pharmacokinetics of Major Anticancer Drugs

Drug	Genotype	Mathematical association	Recommended dosing	Pharmacological relevance	References
Docetaxela	ABCB1 1236C>T	CL = 56.5·(1.0HETZ)·(0.72HOMZ)	–	28% Lower drug clearance in homozygous mutant patients	(30)
Gemcitabine	CDA*3	CL = 73·BSA·(1–0.64·HOMZ)·(1–0.17·HETZ)	–	64% Lower CL in HOMZ 17% lower CL in HETZ	(78)
Gemcitabine	CDA*2	CL = 171·(0.79HETZ)b	–	21% Lower CL in HETZb	(91)
Imatinib	ABCG2-421 C > A	CL = 7.3·(WT/54)0.56·(AGP/1.13)−0.65·(ALB/38)0.66·0.77HETZb	No dose adaptation needed	23% Lower CL in HETZb	(92)
Indisulam	CYP2C9*3	CL = 46·(1–Θ1·HETZ + 2·Θ2·HOMZ)	50–100 mg/m2 dose reduction	27% Lower Vcmax	(29)
	CYP2C19*3		per mutated allele	38% Lower CLc
Letrozoled	CYP2D6	CL/F = 1.03·(WT·1 + HETZ·0.84 + HOMZ·0.45)	No dose adaptation needed	14% Lower CL/F in HETZ	(93)
				55% Lower CL/F in HOMZ
6-MPe	TPMT*3A,3B,3 C	FM3 = 0.019·(2.56)TPMT	40% dose reduction in HETZ	Overproduction of 6-TGN in the presence of TPMT*3A,3B,3 C	(94)
			90% dose reduction in HOMZ

Ref reference, HOMZ homozyous mutant, HETZ HETZ heterozygous mutant, CL drug clearance (liters per hour), D dose, GFR glomerular filtration rate (ml/min/1.73 m²), VM _EL maximum elimination capacity (μmol/h), 6-MP 6-mercaptopurine, TPMT thiopurine S-methyltransferase (presence of at least one TPMT gene mutation), FM ₃ fractional metabolic transformation of 6-MP into 6-Thioguanine nucleotide (6-TGN)

^aAnalysis performed in patients receiving 3-weekly docetaxel/paclitaxel

^bNo homozygous mutant patients in this population

^cFinal PK-model included linear (CL) and nonlinear Michaelis–Menten (V _max) elimination (95)

^dJapanese healthy postmenopausal women

^eIn children with acute lymphoblastic leukemia

COVARIATE MODEL-BUILDING

Various parameters can have an impact on drug PK, including patient anthropometrics such as weight and body surface area (BSA), organ dysfunction, patient age, comedication that can interfere with the drug under investigation, other therapeutic interventions, or the presence of drug pathway-associated gene polymorphisms among others. While a covariate model usually describes parameters of the structural (fixed effects) model, this has also some influence on the random effects distribution, e.g., the magnitude of the interindividual or residual error (21), or the probability that an individual belongs to a certain subpopulation (e.g., poor or good metabolizers) (22,23). Covariates are usually treated as independent variables and included in the model as if they were measured without any error.

Principally, all variability in a population model can be viewed as predictable in the case a very large number of latent variables are included, with the latter being unmeasured or unknown parameters. The actual covariates, however, are measurable and are partly correlated with the latent variables. A true covariate is usually seen as one that, among the investigated covariates, carries unique information on a structural model parameter (19). However, the amount of data that can be used for building the covariate model, and the study design itself can have significant impact on the probability of selecting a covariate from competing covariate models (15). In a simulation study by Han and colleagues, it was shown that incorporating stratification into the study design and applying a wide covariate range can facilitate the process of defining parameter–covariate relationships (15). Therefore, the design of population PK studies is essential to enable the estimation of PK parameters as well as covariate effects (parameter identifiability), and a minimum of data points is usually required. As a rule of thumb, for each PK parameter to be estimated, at least one drug concentration–time point is needed. The chosen time points are also important with, e.g., drug concentrations during absorption of an oral drug being important for identifying the absorption constant, or concentrations around peak of an infusion being important for identifying the volume of distribution. These aspects are discussed in the drug case studies at the end of the article if indicated.

BINARY AND CATEGORICAL COVARIATES

A binary or dichotomous covariate only attains two discrete values, e.g., patient sex. Categorical covariates attain three or more discrete values or levels, and they are either called nominal if there is no sequence in the data (e.g., religion, nationality), or ordinal if there is some ordering or sequence in the data (e.g., social class or treatment outcome). Discrimination between nominal and ordered data however is only appropriate if the covariate has more than two levels. In NONMEM, the binary covariate of patient sex (SEX) may be coded on drug clearance (CL_D) as follows:

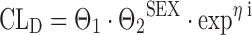1

where CL_D is the individual drug clearance, Θ₁ the mean population value for drug clearance, SEX being patient sex taking the values of 0 or 1, ηi represents the interindividual error that is assumed to be normally distributed with mean 0 and variance ϖ², and Θ₂ is a fixed-effects parameter in the structural model, giving the proportional increase or decrease for the patient subgroup with sex equaling one. Accordingly, a categorical covariate with three levels can be replaced by two dummy covariates, the first dummy being 1 if the original covariate is 1 and 0 otherwise, the second dummy being 1 if the original covariate is 2 and 0 otherwise:

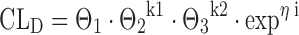2

where Θ^k1₂ represents the proportional change in drug clearance in patients belonging to category 1, and Θ^k2₃ represents the proportional change in drug clearance in patients belonging to category 2.

CONTINUOUS COVARIATES

Continuous covariates contain markedly more information compared to binary or categorical data. Therefore, covariates in a respective trial setting should be coded and collected as continuous data if possible. The analysis of a respective covariate in a continuous compared to a categorical manner improves the chances of detecting a correlation with the PK parameter that is described, provided there is such a correlation. The effect of a continuous covariate such as creatinine clearance or patient age on a specific PK parameter is often expressed relative to its median, and this scaling results in much improved interpretability of the covariate formula. The most common functional forms of covariate relations are linear, piece-wise linear, power function, and exponential (11). We may code a linear relationship between a covariate (BSA in this case) and drug clearance (CL_D) as follows:

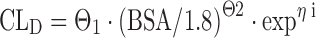3

where CL_D is the individual drug clearance, Θ₁ the typical population value for drug clearance, patient BSA being the continuous covariate centered to the population mean of 1.8 m², and Θ₂ being a fixed-effects parameter in the structural model, giving the proportional deviance of the individual drug clearance from the population typical value. Again, η_i represents the interindividual error.

TIME-DEPENDENT COVARIATES

Time-dependent covariates are frequently observed in clinical studies, can provide additional information to that obtained from time-constant covariates, and should therefore be considered in the process of covariate model building. This is especially true for patients with advanced cancer, frequently suffering from changes of organ function, body composition (cancer cachexia), and performance status over time. However, the analysis of time-dependent covariates adds an additional layer of complexity to the model, why often it is chosen to treat intraindividual variation the same way as interindividual variation in a respective covariate.

The magnitude of the effect of the change in a covariate may differ between patients. For example, a certain degree of cholestasis may result in a substantial decrease of drug elimination in one patient but not necessarily in another patient. As a consequence, individual dose adjustments based on a prespecified covariate should account for such interindividual variability when predictions are made on some target PK parameters such as drug exposure.

Waehlby and colleagues described two models for time-dependent covariates (24). In the first model, different covariate–parameter relationships were estimated for within- and between-individual variation in covariate values, by splitting the standard covariate model into a baseline covariate (BCOV) effect and a difference from the baseline covariate (DCOV) effect, as exemplified in Eq. 4 (24):

4

In which BCOV is the baseline value of the covariate and DCOV is the individual difference (at each time point) in the covariate from baseline (COV–BCOV). Θ_DCOV describes the effect of covariate variation within an individual, and is the fractional change in ρ_POP with individual changes in COV. If Θ_BCOV and Θ_DCOV are similar, there may be no indication of distinctive inter- and intraindividual covariate models. The modeler may fix either BCOV or DCOV to 0, and test the performance of the respective models against each other. By doing so, the reduced models provide information on whether the data support relationships with BCOV or DCOV or both (24). Information in the observed data related to the parameter “P,” as well as the variability in the values of BCOV and DCOV, determine the precision (SEs) of Θ_BCOV and Θ_DCOV.

In the second model, the magnitude of the covariate effect was allowed to vary between individuals, by the inclusion of interindividual variability in the covariate effect (24):

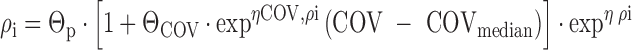5

where η^COV,ρi is a random variable with a mean of 0 and variance ϖ², which allows the magnitude of the covariate effect to differ between individuals. Accordingly, a change of one unit in the covariate may cause substantial alterations in the parameter in some individuals, whereas the effect may be moderate or absent in others. To ensure that P_i remains positive when this model is implemented, the parameters may need to be constrained, e.g., by logit transformation. In the above model, COV could be replaced by DCOV, and additional interindividual variability in DCOV if appropriate.

SPECIAL CASE: PHARMACOGENETIC COVARIATE MODELING

Pharmacogenetics studies the influence of variations in DNA sequence on drug absorption, disposition, and drug effects (25,26). The EMA has acknowledged the relevancy of pharmacogenetics in the evaluation of clinical pharmacokinetics (27). Although pharmacogenetic data are mainly studied using noncompartmental methods followed by analysis of variance (ANOVA) on the individual PK parameters (28), NLME models have many advantages over ANOVA-type calculations. In particular, NLME allows to perform an integrated analysis of the knowledge accumulated on the drug PK and pharmacogenetic data, and it is applicable with less samples per patient as compared to less sophisticated analytical methods. With respect to PK aspects, the highest penetrance of genetic polymorphism is registered at the level of drug metabolism, where about 40% of phase I metabolism of clinically used drugs is affected by polymorphic enzymes. Well-known polymorphic cytochrome P450 (CYP) enzymes include CYP2D6, CYP2C19, and CYP2C9. Regarding phase II enzymes, the genetic variability of UDP-glucuronosyltransferases, N-acetyltransferase-2, and some methyltransferases are known to play a role in the interindividual variability in drug PK. The additional contribution of polymorphisms in drug transporters has recently been recognized. In practice, genetic variations are demonstrated by the identification of single-nucleotide polymorphisms, insertions/deletions, and variation in gene copy number (copy number variation) (27). Respective study designs should include adequate estimations of the number of patients of each genotype in order to obtain valid data for population analysis. Accordingly, the EMA recommends some kind of power calculations before the initiation of respective studies to ensure a sufficient population size (27). If a genotype is rare, studies with selected inclusion of patients carrying this rare genotype may be considered. Another strategy to deal with rare genotypes is pooling of study data. In general, studies looking at the (quantitative) impact of genotypes on drug PK should focus on genetic alterations that are known to be functionally relevant (candidate gene approach), and that clearly affect the respective drug metabolic pathway.

Because the respective functional gene mutations concern germline mutations as analyzed in peripheral blood mononuclear cells, NONMEM coding is analogous to what has been described for categorical covariates, with some special considerations to be taken into account. Most importantly, the analysis of genotype covariates should be constrained to evaluate pathophysiologically reasonable relationships. The quantitative impact of allelic variants in the population model may be coded as follows:

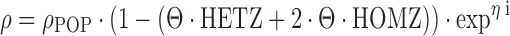6

where the PK parameter ρ has a typical value of ρ_POP in wild-type patients. The typical value of heterozygous mutant patients (HETZ) is equal to ρ_POP reduced by “Θ · 100%”, and homozygous mutant status (HOMZ) is assumed to result in twice the impact as compared to the heterozygous mutant status, with the typical value of ρ reduced by “2 · Θ · 100%” as compared to the wild-type status (29). Obviously, there might not be a perfect gene dose effect, in that, e.g., a normal allele compensates for a mutated allele in heterozygous patients, or the presence of one mutated allele might result in a profound disruption of enzyme activity that cannot be compensated by the remaining wild-type allele. If similar conditions are expected for a certain genotype, a separate fixed effect on ρ_POP might be adequate for carriers of the heterozygous and homozygous state, respectively. For example, such a model has been used by Bosch and colleagues for docetaxel (30):

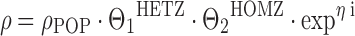7

where HETZ is one for a carrier of the heterogeneous trait and zero otherwise, and HOMZ is one for a carrier of the homogeneous trait and zero otherwise. The fixed-effects parameters Θ₁ and Θ₂ are the proportional factors by which ρ deviates from ρ_POP in carriers of the heterogeneous and homogeneous mutant trait, respectively. There are also pathophysiological situations where a binary gene dose effect may be reasonable, e.g., the comparison between wild-type versus heterozygous/homozygous mutant patients, or the comparison between wild-type/heterozygous versus homozygous mutant patients:

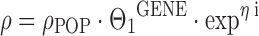8

Where GENE = 0 for wild-type (wild-type and heterozygous mutant) patients and 1 for heterozygous/homozygous (homozygous) mutant patients, respectively. By comparing Eq. 6 to 8, it becomes evident that the assumption of a quantitative gene dose effect results in a lower chance of finding a significant correlation between genotype and the respective PK parameter. Another less frequently used coding for the association between heterozygous and homozygous mutant traits on drug clearance has been described by Chou and colleagues (31):

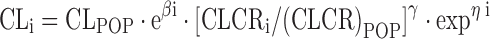9

where CL_i is the individual drug clearance; CL_POP is the population value for drug clearance; βi is separately estimated for patients with wild-type, heterozygous, and homozygous mutant status; CLCR_i is the individual creatinine clearance; CLCR_POP is the population value for creatinine clearance; and γ is the scaling factor for the individual renal function. Equation 9 may be adequate for drugs that undergo elimination mainly by the kidneys, as the respective drug clearance is scaled to renal function. For the special case in which a quantitative or continuous gene expression has been measured (e.g., tumoral mRNA expression), a coding such as illustrated in Eq. 3 should be preferred, as it contains more information as compared to binary or categorical genotype data.

Ideally, pharmacogenetic–pharmacokinetic modeling will result in dose recommendations for the case a clinically relevant impact of the respective genotype on drug PK has been found. According to the recommendations by EMA, alternatives to account for genotype effects include dose titration regardless of the genotype, specific upfront dosing based on the genotype, or optional gene-based dosing (27).

SELECTION AND INTERPRETATION OF COVARIATES

Not all significant covariates included in a population model are necessarily clinical relevant, and not all significant covariates are always included in the final model. Therefore, understanding the process of covariate selection and interpretation is important. These two interrelated topics are covered in this section.

Stepwise covariate modeling (SCM) dominates model selection in NLME modeling (11). The stepwise-automated covariate procedure steps through possible covariate–parameter combinations in a forward fashion, and evaluates their importance in the population model. Covariates that are significant with regards to a predefined p value are retained in an intermediate or full forward covariate model before undergoing stepwise backward elimination. This approach uses less runs and computational capacity and is practical for models with relatively short run times (11). The starting point of the forward inclusion covariate procedure is the base population model without any covariates. In the first step, the improvement of the fit relative to the basic model is compared when each of the covariate models are added univariately, and the model with the largest improvement is kept for the next evaluation step, given there is some overall statistical significance supporting the inclusion of the respective covariate. This stepwise forward inclusion of covariates is repeated, until there are no more significant parameter/covariate combinations to be added to the full model. Thereafter, a backward elimination procedure is started, during which each covariate model is replaced by the next lower in the model hierarchy. The model that contributes the least to the data fit, given that it is not significant, is dropped and a new current model is formed. The backward elimination continues until no more terms can be dropped. The goodness-of-fit between hierarchical models is measured by the difference in the objective function value (OFV) as produced by NONMEM. The difference in OFV between two hierarchical or nested models is approximately chi-square distributed, with n variable degrees of freedom (df). Accordingly, the OFV is used to obtain the significance level for the difference between two nested models (16,32). Often, a p value of 0.01 is used for the forward inclusion procedure, and a more stringent p value of 0.005 is often used for the backward elimination procedure.

In drug development, model-based population analysis is often used in an exploratory manner, but model-based confirmatory analysis is also increasingly applied (2). Whereas a confirmatory analysis wants to test a predefined hypothesis, an exploratory population analysis is a hypothesis-generating process. Often, the model is developed in several stages. In the first stage, the structural model is developed, starting with a simple model and expanding the complexity when supported by the data. Highly influential or prespecified covariates can be included in the model. In a next step, covariate relations that may explain part of the interindividual variability of a parameter can subsequently be included in the model. In a final stage, the completeness of the stochastic model is re-evaluated and checked for its stability. Usually, a single NLME model is chosen from the different covariate models, and this model is called the final model (33). Depending on the purpose of the model, the criteria for final covariate selection include several items such as:

1. Pathophysiological and mechanistic plausibility and prior beliefs

2. Exploratory goodness-of-fit plots (34–36)

3. Statistical significance (11,16)

4. Clinical relevance (37)

5. Predictive performance from internal or external validation (38–40)

6. Parameter precision (20,41)

7. Reduction of unexplained parameter variability

There is general uncertainty about the definition of a significant reduction in unexplained variability between patients (vii). This issue has been covered more extensively by Duffull and colleagues, where a reduction of unexplained variability by 30% has been proposed to be clinically significant (42). Very often, reduction of interindividual variability per covariate by <20% is seen.

The SCM approach often selected within NONMEM has extensively been investigated, and there are some known limitations such as the phenomenon of multiple comparisons. Often, several covariates are investigated, possibly on a number of structural model parameters such as drug clearance and volume of distribution, using different parameterizations. In this case, multiple comparisons usually call for a Bonferroni correction, where the overall type I error accepted for statistical significance is divided by the number of simultaneously tested covariates (43). Besides Bonferroni correction, another way to correct for overfitting is to use a stricter p value in the covariate selection process, as is often used with NONMEM. The way in which Bonferroni-like correction is done during a respective covariate selection process might also be dependent on whether the selection process has prospectively been defined or not. For example, the testing of a pathophysiologically based drug pathway-associated candidate gene on drug clearance might have more weight than the testing of a genotype that has no physiological relationship with the PK of the drug. Translating the general advice in traditional statistics (44) to covariate selection in NLME modeling indicates that it often harms the predictive performance of a model if more than one covariate parameter per 10–20 individuals in the dataset is investigated on each structural model parameter. Fewer covariate parameters should be investigated for parameters on which information is sparse or when categorical covariates are investigated. Importantly, biological plausibility requires that the chosen covariate makes pathophysiological sense, for example, impaired renal function results in lower clearance of a renally excreted drug. If a certain covariate is considered clinically relevant, this implies that drug dosing should be modified according to this respective covariate. These aspects are covered in the following section. Finally, the predictive performance of population models for achieving, e.g., therapeutic plasma drug concentrations or a predefined area under the concentration–time curve (AUC) should be evaluated, both with the inclusion of the respective covariate and without the covariate. This can be done using various methods such as the posterior predictive check (45) or the visual predictive check (35) and helps interpretation of the potential benefit of using a specific covariate.

An attractive newer method to overcome some of the shortcomings of the conventional SCM is the “least absolute shrinkage and selection operator” or Lasso method. Lasso is an algorithm that results in shrinkage of the uncertain covariate coefficients towards a lesser effect than indicated by the actual dataset, with a subsequent decrease of the estimation error and selection bias, and an increased external validity of the covariate estimates (17). The covariate model is determined by cross-validation that is superior for predictive model selection compared to the p value in small or moderate-sized datasets. A further benefit of Lasso is that it investigates all possible covariate relations, similar to the WAM (18), but the selection with Lasso is simultaneous, continuous and within NONMEM. Within Lasso, all covariates are standardized to have 0 mean and a standard deviation of 1. Subsequently, the model containing all potential covariate–parameter relations is fitted with the sum of the absolute covariate coefficients being smaller than the predefined parameter “t.” This restriction will force some coefficients towards zero, while the others will undergo some shrinkage. Therefore, covariate testing for inclusion and estimation of the covariates run in parallel. The Lasso algorithm has been outlined in detail by Ribbing and colleagues (17). In their comparison of the Lasso shrinkage algorithm with conventional SCM, Lasso predicted external data better than SCM at different p values, though the benefit decreased with increasing number of patients, and was negligible for large datasets (17).

METHODOLOGICAL CONSTRAINTS: PARAMETER SHRINKAGE, SELECTION BIAS, AND COLLINEARITY

The individual parameter estimates in NONMEM are estimated using the Bayesian methodology, and they are generally referred to as empirical Bayes estimates (EBE) (46). Bayesian methodology estimates the prior distribution from the data and uses them as if they were known to obtain the posterior distribution. At one extreme, with no observations available, the patient will be regarded as a typical patient. At the other extreme, when data for an individual goes towards infinity, the prior will have marginal impact; in between these extremes, both factors will contribute, and depending on the relative variability (including interindividual and residual unexplained variability), individual estimates could be closer either to the population mean or to the true individual parameter value (47). When data are uninformative at the individual level, the EBE distribution will shrink towards zero (η-shrinkage, quantified as 1-SD(ηEBE)/ω), IPRED towards the corresponding observations, and IWRES towards zero (ε-shrinkage, quantified as 1-SD(IWRES)) (47). Accordingly, shrinkage issues should be considered, because if not, this may impede decision making, increase the time for data analysis, decrease the reliability of the model, and finally result in inappropriate models.

In the presence of substantial shrinkage, EBE-based diagnostics may indicate false relationships or hide true relationships when used for covariate screening. If only certain parameters are screened for covariates, it may happen that EBE would indicate false parameter–covariate relationships, which may even turn out to be significant when tested directly in the model, while the covariate was truly related to other parameter. Therefore, whenever single parameters are screened for covariate relationships, and a certain covariate appears to be significant, the relationship between the significant covariate and other parameters should also be tested for potential correlations. There are no guidelines as to what level of shrinkage may be acceptable and what not. According to an extensive data simulation study, Savic and Karlsson found that the power of EBE-based diagnostics decreased when either η- or ε-shrinkage were at a level of 20–30% (47). Therefore, it seems rational to provide values for shrinkage whenever EBE-based diagnostics are used for communicating model quality. In cases were substantial shrinkage is present, a model building process involving more direct testing and less or no reliance on EBE-based diagnostics should be considered. Additionally, other types of diagnostics ought to be used in these cases, for example, simulation-based diagnostic (48) or conditional-weighted residuals (49).

Identification of covariates and quantification of their impact on specific PK parameters is one of the primary objectives of population PK modeling. The covariate model is regularly built in a stepwise manner, as has been outlined in the chapter on “SELECTION AND INTERPRETATION OF COVARIATES.” With methods such as SCM, selection bias may be a problem if only statistically significant covariates are accepted for inclusion into the final model (19). Competition between multiple covariates may further increase selection bias, especially when there is a moderate to high correlation between the respective covariates. This may result in a relevant loss of power to identify the true covariates. In an extensive simulation study, Ribbing and colleagues were able to show that selection bias can be substantial when working with small datasets (≤50 subjects) that—at the same time—harbor true covariates with a weak impact on the target PK parameter (19). If selected under these circumstances, the covariate coefficient is on average estimated to be more than twice its true value, making the covariate model less adequate for predictive purposes. In the same simulation analysis, competition from false covariates resulted in a substantial loss in the analytical power to select the true covariate, but the already high selection bias increased only marginally (19). Therefore, any potential bias resulting from covariate competition is negligible if statistical significance is also required for covariate selection. However, selection bias may well harm the predictive performance of the covariate model, if low-powered, false covariates are selected. For the same reason, these low-powered covariates may falsely appear to be clinically relevant when selected. The following methodological pitfalls have nicely been summarized by Ribbing and colleagues (19), and deserve special attention when working on covariate models:

• The power of selecting a true covariate decreases with increasing correlation to any false covariate, at least in small/moderate-sized datasets.

• Selection bias is also a problem for true covariates with a weak effect in small/moderate-sized datasets. This may also result in the identification of covariates as being clinically relevant when they are not.

• The predictive performance of the covariate model may decrease when selecting true but low-powered covariates.

• Stricter p values may not avoid selection bias, but will decrease the risk of selecting false covariates.

• The predictive performance of low-powered covariates may be improved by using alternative selection criteria or by avoiding selection bias.

It is well-known that correlation among the covariates in linear regression will affect the precision of the regression parameter estimates, possibly leading to parameter estimates that are artificially nonsignificant. This effect is referred to as “collinearity.” When two correlated covariates enter into a linear model simultaneously, compared to the case where either variable is entered in the model alone, one or more of the following may occur: (1) Regression parameter estimates may become statistically nonsignificant; (2) Regression parameter estimates may exhibit a sign change that may or may not be physically possible; (3) Regression parameter estimates per covariate may differ substantially. Collinearity can also affect parameter estimates in the NLME model building process when covariates are entered into the structural PK model (20).

SELECTED EXAMPLES OF DRUG-SPECIFIC COVARIATE MODELS

This chapter does not claim to give a complete overview on population covariate models in oncology, rather it wants to illustrate where covariate testing resulted in an improved understanding of the drug PK, and sometimes even allowed this to be applied in clinical practice. An important controversy concerns BSA-guided dosing of anticancer drugs, and several covariate models have contributed essentially to improve our understanding on the value of BSA-based dosing (50). The concept of BSA dosing originates from experiments showing that the maximum tolerated dose (MTD) in non-rodents and LD₁₀ in mice correlated to the MTD in humans when dose was expressed per BSA (in square meter) (51,52). By correcting for BSA, it was generally assumed that cancer patients would receive a dose of a certain cytotoxic drug that is associated with acceptable toxicity without reducing the drug’s therapeutic effect. However, in many cases of anticancer drug treatment, the use of BSA did not reduce interindividual variability in drug PK, why flat-fixed dosing regimens have been suggested in some cases (50,53,54). The value of BSA as a covariate on drug elimination and the respective use of BSA-guided dosing is discussed if indicated. Important anthropometric and biochemical as well as pharmacogenetic covariate effects of major anticancer drugs have been summarized in overview tables. Some recommendations from population covariate models have been included into the Summary of Product Characteristics (SPC) of the respective drugs, and this is discussed if appropriate.

ALKYLATORS

Due to their primary toxicity being myelosuppression, alkylators such as busulfan, melphalan, cyclophosphamide, or thiotepa are the most important molecules for high-dose myeloablative treatment (HDT). Accordingly, the study of the PK of these substances is important to allow for therapeutic drug monitoring (TDM) and adequate treatment individualization.

Busulfan is characterized by a highly variable absorption following oral administration, hepatic elimination via glutathione-S-transferase (UGT), and a small therapeutic window, with low AUC potentially resulting in engraftment failure (55), and high exposure putting patients at risk for veno-occlusive disease or seizures. The PK of busulfan were studied in children with leukemia in various clinical studies (56–58). Hassan and colleagues studied 20 children undergoing HDT, and found that CL_busulfan was 42% higher in children with inherited disorders as compared to children with leukemia, and that elimination was induced over repeated doses (57). A potential cause for the higher CL_busulfan in children with leukemia might be induction of hepatic phase I metabolism, as these patients are pretreated with various enzyme-inducing molecules. In a registration study for i.v. busulfan, Booth and colleagues assessed dosing of i.v. busulfan to achieve a target AUC between 900 and 1,350 μmol h/L in 24 pediatric patients (56). By exploring body weight, age, gender, and BSA as potential covariates on the PK of busulfan, the authors were able to define an optimal dose of 1.1 mg/kg for children ≤12 kg of weight and 0.8 mg/kg for those >12 kg of weight. The authors used data simulations on the final model to test the performance of different weight cutoffs, and found the two-step dosing algorithm as described above to achieve a 56% success rate for target AUC_busulfan (900–1,350 μmol h/L) (56). Importantly, even accounting for age as an important covariate resulted in a “success rate” (equal to patients within the target AUC_busulfan) of <60%, suggesting that additional TDM with subsequent fine tuning of the dose of busulfan would be necessary. Based on a retrospective population PK analysis in 102 patients, a recommendation to dose busulfan according to the adjusted ideal body weight rather than the actual weight or BSA in adults has been included into the drug’s SPC (59). In children, busulfan dosing according to the actual body weight (five weight categories from <9 to >34 kg) is recommended (60).

Melphalan is another alkylating agent that is mainly used for HDT in children with neuroblastoma or sarcomas, and in adults with multiple myeloma. Nath and colleagues developed a population covariate model of high-dose melphalan in children (61,62), and derived a dosing algorithm to achieve a target AUC_melphalan of 9 μg h/mL based on patient weight, glomerular filtration rate (GFR) and concomitant administration of carboplatin (62):

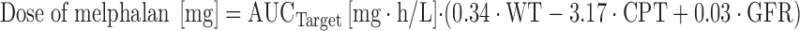10

where WT is patient weight (in kilograms), CPT concurrent treatment with carboplatin (0 = no, 1 = yes), and GFR (ml/min/1.73 m²).

Cyclophosphamide is a widely used alkylator, and its activation and elimination is mediated by various polymorphic drug-metabolizing enzymes, including CYP2C9, CYP2B6, CYP3A4, CYP2C19, and GSTA1. Timm and colleagues found a quantitative gene dose effect of the CYP2C19*1/*2 gene variant on the elimination of cyclophosphamide when given at doses ≤1,000 mg/m² in 60 patients with various malignancies (63). Cyclophosphamide constant of elimination (k_e) decreased from 0.109 in CYP2C19*1/*1 (wild-type) carriers to 0.088 in heterozygous CYP2C19*1/*2 carriers and 0.076 in three homozygous CYP2C19*2/*2 carriers. Cyclophosphamide doses >1,000 mg/m² resulted in increased elimination of the drug due to well-known autoinduction (64), and no effect of CYP2C19 genotype was seen in patients receiving high-dose cyclophosphamide (63). This example nicely illustrates the importance of considering drug regimen, anthropometrics, and potentially drug pathway-associated genetic variability to have an understanding of the interplay between the different covariates. This information has not been introduced into the drug’s SPC to our knowledge.

Temozolomide is an orally available alkylator, and the most important drug for treating high-grade astrocytoma. The PK of temozolomide were described by a one-compartment model with first-order absorption and elimination (65). Body surface area was the only significant covariate in a large population PK analysis of 445 patients receiving different doses of temozolomide for anaplastic astrocytoma, glioblastoma multiforme, or malignant melanoma (65). In the analysis by Jen and colleagues, covariates were introduced into the structural model as linear additive terms of their log-transformed values, e.g., in the case of BSA:

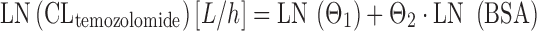11

where CL_i is the individual CL_temozolomide, Θ₁ is the typical value for CL_temozolomide. As a special note, log transformation is sometimes used in the case of non-normally distributed PK parameters, as is the case in Eq. 11. However, for sufficiently large sample sizes (n ≥ 10), the means are normally distributed regardless of the shape of the original distribution, according to the Central Limit Theorem, and we have not to care too much about non-normal parameter distribution as long as we make inferences on parameter means. In the analysis by Jen and colleagues, patient age, sex, creatinine clearance, liver enzymes, smoking status, and selected comedication were not chosen as covariates on CL_temozolomide. The results of this study support BSA-guided dosing of temozolomide. In a similar study performed in 39 children, BSA and patient age were significant covariates on CL_temozolomide (66). Temozolomide elimination increased with increasing BSA and age according to Eqs. 12 and 13:

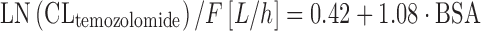12

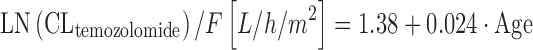13

where F is the bioavailability of the drug. Equation 12 implies that dosing of temozolomide according to BSA is adequate, although clearance of the drug shows only small changes with increasing BSA (e.g., +9% for BSA going from 1.8 to 2.0 m²). In Eq. 13, CL_temozolomide is normalized to BSA. This normalization assumes a significant association between BSA and the respective drug in the first place, that is not the case for many anticancer drugs (50). Furthermore, most anticancer drugs are dosed according to BSA, and this already implies some scaling, hence normalization to BSA may not be necessary in Eq. 13. By using multivariate integration of Eqs. 12 and 13, interpretability of the formula is much improved. The information that clearance of temozolomide is not decreased in the elderly patient has been included into the UK’s electronic Medicines Compendium (eMC) (67).

TAXANES

Docetaxel is an important drug in patients with breast cancer, prostate cancer, and non-small-cell lung cancer, among others. An early population covariate analysis in 26 solid cancer patients receiving docetaxel at various dosages, BSA and patient age were significant covariates, resulting in the following equation (68):

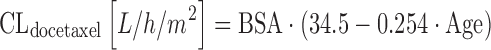14

Equation 14 allows BSA to be expressed in square meters. The analysis by Launay-Iliadis suggests a rather marked association between patient age and CL_docetaxel, with the latter decreasing from 43 to 28 L/h when patient age doubles from 35 to 70 years. Larger population PK studies confirmed a negative association between increasing patient age and a decrease of docetaxel elimination, but with a roughly 7% decrease for a 71-year-old patient as compared to the population mean (69), this effect is not suggested to be of substantial clinical relevance. Subsequent studies showed that elevated liver enzymes are also important, as they predict for a lower CL_docetaxel in both the 3-weekly (39,69) and weekly docetaxel regimens (70). In the latter study, investigators also found CYP3A4 activity as assessed by the erythromycin breath test (1/t_max) to be another significant covariate as follows:

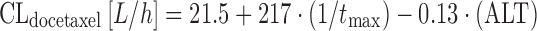15

where ALT is alanine aminotransferase. What stands out in Eq. 15 is the fact that both ALT and the erythromycin breath test are surrogates for liver function, and this limits the clinical plausibility of Eq. 15. Based on population PK studies with single-agent docetaxel 100 mg/m², a dose reduction to 75 mg/m² is recommended in patients with elevations of ALT or AST greater than 2.5 times the upper limit of normal according to EMA’s SPC (71). Similarly, a starting dose of 55 mg/m² docetaxel (instead of 75 mg/m²) is recommended in breast cancer patients ≥60 years of age in combination with capecitabine (71).

Similar covariates as with docetaxel were also found to predict CL_paclitaxel in solid cancer patients (72,73). A population covariate analysis in 168 cancer patients resulted in the following equation, with VM_EL being the maximum elimination capacity of paclitaxel:

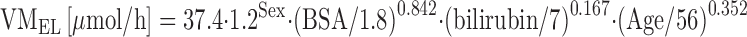16

Typically, male patients had a 20% higher VM_EL as compared to female patients; a 0.2 m² increase of BSA resulted in a 9% increase of VM_EL; a 10-year increase of patient age led to a 5% decrease of VM_EL; and a 10-μmol increase of total bilirubin led to a 14% decrease of VM_EL. The same covariate set was confirmed in a group of 35 patients with impaired liver function (72). These data might support upfront individualization of paclitaxel dosage based on patient gender and patient age, and this approach is actually studied in a randomized clinical study in patients with non-small-cell lung cancer (EUDRACT 2010-023688-16).

ANTIFOLATES

Methotrexate at doses ≥1 g/m² (high-dose methotrexate, HDMTX) is the backbone for treating diseases such as primary central nervous system lymphoma, osteosarcoma, or acute lymphomatous leukemia. Methotrexate undergoes renal elimination, and elimination of MTX is prolonged in patients with renal impairment or third-space fluid collections (74). An extended covariate analysis in 76 patients receiving HDMTX at doses up to 12 g/m² showed that creatinine clearance and comedication with nonsteroidal antirheumatic drugs (NSAR) or benzimidazoles (proton pump inhibitors, PPI) are significant predictors of CL_MTX as follows (75):

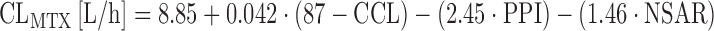17

where PPI or NSAR are defined as “one” in the case of concurrent treatment, and “zero” in the case of no concurrent treatment. These data suggest a marked reduction of CL_MTX in the case of concurrent treatment with PPI (−27%) or NSAR (−16%) (75), and the respective comedication should be avoided.

Pemetrexed is the second clinically important antifolate that has its place in the treatment of malignant pleural mesothelioma and non-small-cell lung cancer. Creatinine clearance was similarly found to be an important covariate on CL_pemetrexed. In practical terms, a 63% decrease in CCL resulted in a 32% decrease in CL_pemetrexed, and a 45% increase in AUC_pemetrexed (76). In the FDAs SPC, it is stated that pemetrexed AUC is increased to 165%, 154%, and 113% in patients with creatinine clearances of 45, 50, and 80 ml/min, respectively, and compared to a creatinine clearance of 100 ml/min (77). Nevertheless, this information has not translated into quantitative dosing recommendations in patients with impaired renal function. Rather, the recommendation is to avoid pemetrexed in patients with a creatinine clearance <45 ml/min (77).

DEOXYNUCLEOSIDE ANALOGS

The deoxynucleoside analogs are frequently used anticancer drugs that mimic deoxycytidine (gemcitabine, cytosine arabinoside) and adenosine (clofarabine), respectively. These drugs undergo rapid deamination by cytidine deaminase (CDA), and predominantly renal elimination. Deoxynucleoside analogs typically undergo intracellular activation by phosphorylation to the active triphosphate compound. Sugiyama and colleagues described the pharmacokinetics of gemcitabine in 250 Japanese cancer patients receiving gemcitabine at 800 or 1,000 mg/m² over 30 min by a linear two-compartment model (78). Major contributing factors for gemcitabine clearance were the mutational status of CDA 208A > G (CDA*3) and CDA −31delC according to the subsequent equation (78):

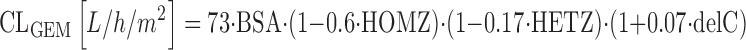18

where CL_GEM is the clearance of gemcitabine, HOMZ is 1 for homozygous CDA*3 status and 0 otherwise, HETZ is 1 for heterozygous CDA*3 status and 0 otherwise, and delC is the number of CDA −31delC alleles in the individual patient (delC = 0,1, or 2). These data suggest a substantial 64% decrease for gemcitabine clearance in carriers of the homozygous mutant CDA*3 genotype, and a moderate 7% increase for gemcitabine clearance per CDA -31delC mutant allele (78).

To describe the pharmacokinetics of clofarabine, Bonate and colleagues have pooled data from three pediatric studies in a total of 40 patients (79). The elimination of clofarabine has been described as follows:

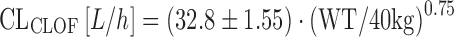19

where CL_CLOF is the clearance of clofarabine, and WT is the individual patient’s weight in kilograms. In this case, patient weight was an important predictor of all primary PK parameters of clofarabine, and the analysis confirms the utility of BSA or weight-adapted dosing of clofarabine, particularly in pediatric patients (79).

TOPOTECAN

Topotecan is a topoisomerase-I inhibitor that is used in advanced small-cell lung cancer, ovarian, or cervical cancer. Up to roughly 75% of the drug undergoes renal excretion, with 50% of the drug being excreted as parent compound or hydrolyzed topotecan. In 2002, Mould and colleagues pooled data from nine clinical studies and 245 patients receiving daily i.v. topotecan at doses ranging from 0.2 to 2.0 mg/m² for 5 days on a 3-week cycle (80). The PK of topotecan were described with a linear two-compartment model, and drug clearance was categorized into renal clearance and non-renal clearance. Compromised renal function, low body weight, and poor ECOG performance status were determinants of a lower CL_topotecan. On the basis of the estimates of clearance obtained with the use of the final model, the percentage of total clearance attributed to renal CL_topotecan in individual patients ranged from 20.7% to 85%. Creatinine clearance had the greatest influence in explaining interpatient variability in CL_topotecan. The inclusion of this covariate reduced the interpatient variability on total topotecan clearance from 49% to 40%. Body weight was also found to account for a proportion of interpatient variability, reducing the variability from 40% to 35%. ECOG status accounted for only 2% of the interpatient variability of CL_topotecan, reducing the interpatient variability to a final 33%. This model is exemplary in that it successfully differentiates between renal and non-renal clearance. Accordingly, the UK’s eMC recommends that daily i.v. topotecan is reduced from 1.5 to 0.75 mg/m² in patients with a creatinine clearance between 20 and <40 ml/min (81). Although significant in the model by Mould and colleagues, implementation of the ECOG performance status had only a small effect on CL_topotecan and respective dose adaptation is not recommended in official guidelines.

PROTEIN KINASE INHIBITORS

The protein kinase inhibitors are a growing class of oral anticancer agents that have various cellular targets such as the epidermal growth factor receptor (EGFR) for erlotinib or lapatinib, vascular endothelial growth factor for sunitinib or sorafenib, BCR-ABL for imatinib or farnesyl transferase (FTase) for tipifarnib. While toxicity differs substantially between the different drugs, virtually all protein kinase inhibitors are metabolized by CYP3A4, resulting in a high interindividual variability of drug clearance, and rendering them susceptible for drug–drug interactions.

Pharmacokinetics of imatinib were analyzed in 371 patients with CML receiving 400 mg imatinib once daily (82). While the impact of the covariates on CL_imatinib as outlined in Eq. 18 was not impressive, there was the interesting finding that CL_imatinib decreased during the first 4 weeks of treatment, for reasons that are unclear so far. This was included into the covariate formula by using a fixed parameter for treatment cycle as follows:

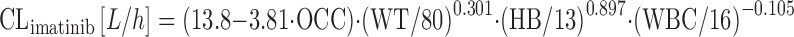20

where OCC is 0 for treatment day 1 and 1 for treatment day 29, WT is patient weight, HB is hemoglobin (grams per deciliter) and WBC is white blood count (grams per liter). This corresponds to a 25% drop of CL_imatinib from cycles 1 to 2. The pathophysiological meaning of the relationship between the covariates HB, WBC, and CL_imatinib is unclear, but could reflect the fact that 10–25% of imatinib undergoes distribution to blood cells (83). The time-dependent decrease of CL_imatinib has been confirmed in patients with gastrointestinal stromal tumor (GIST), and plasma α1-acid glycoprotein was additionally found to be a significant covariate on CL_imatinib, with the latter decreasing at higher concentrations of AAG (84). Contrary to the studies by Schmidli (82) and Debaldo (84), CYP3A4-activity was introduced in the structural model in an approach to predict individual clearance of EGFR tyrosine kinase inhibitors (85). In the study by Li and colleagues, CL_midazolam was taken as a surrogate for CYP3A4 activity, and steady-state plasma concentrations of unbound gefitinib were found to vary substantially with regards to CL_midazolam:

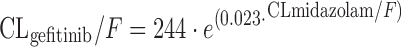21

The findings from the covariate model were further translated to derive steady-state gefitinib plasma concentrations corresponding to individual CL_midazolam, with unbound gefitinib plasma concentration varying between approximately 2 and 60 μg/L after oral dosages of 250 or 500 mg/day (86). This study shows that a simple probe drug approach with assessment of midazolam elimination could allow for improved dosing of gefitinib, as 60% of the variability of unbound gefitinib plasma concentration was explained by individual CYP3A4-activity (86).

Erlotinib, the other important EGFR TKI, is also undergoing hydroxylation that is mediated by CYP3A4 and also CYP1A2, the latter being subject to significant induction in smoking patients. Accordingly, CL_erlotinib was found to be 24% higher in current smokers as compared to former or never smokers (85). Current smokers should be advised to stop smoking, as plasma concentrations of erlotinib are reduced in smokers as compared to nonsmokers, and the degree of reduction is likely to be clinically significant, as stated in EMA’s SPC (87).

Houk and colleagues pooled data from 590 subjects receiving sunitinib to identify the impact of potential covariates on the variability in exposure following oral administration of the drug (88). Separate models were developed for sunitinib and the main metabolite SU12662, each using a two-compartment model with first-order absorption and elimination. Not only gender and ethnicity had an impact on the elimination of sunitinib, but also the type of disease (GIST = gastrointestinal stromal tumor, mRCC = metastatic renal-cell cancer, OTH = other solid tumors), according to Eq. 22:

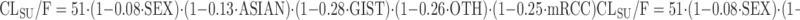where SEX is coded 0 for male and 1 for female patients, ASIAN as 0 for non-Asian ethnicity and 1 for Asian ethnicity, and disease state (GIST, mRCC, OTH) as 0 for absence and 1 for presence. These important data support a lower elimination of sunitinib in patients with Asian ethnicity, potentially as a result of a lower CYP3A4 activity. Currently, no initial dose adaptations are recommended with regards to patient gender or ethnicity (89).

CONCLUSION

Covariate models have improved our understanding of the pharmacology of many anticancer drugs, including busulfan or melphalan that are frequently part of high-dose pretransplant treatments, the antifolates methotrexate and pemetrexed whose elimination is strongly dependent on GFR and comedication, the tyrosine kinase inhibitor gefitinib whose elimination is strongly dependent on the activity of cytochrome p450 3A4 (CYP3A4), erlotinib whose elimination is susceptible to CYP1A2 induction in smoking patients, lung cancer, or the multiple kinase inhibitor sunitinib whose elimination is lower in Asian as compared to Caucasian patients. Although population PK analyses are increasingly recognized for decision making by regulatory agencies (2), covariate models have resulted in direct dosing recommendations in only a limited number of anticancer drugs so far (59,71,81). This is related to the fact that academic groups have little influence on official posology as outlined in the drug’s SPC, and the responsibility of the regulatory agencies to prevent treating oncologists from using anticancer drugs in situations in which there are limited safety data available. This is especially true for patients with impaired organ function, patients at the outer extremes of age (children, elderly) or body size (obesitas, BSA >>2.0 m²), and patients using interacting drugs (e.g., CYP3A4 inducers or inhibitors while using tyrosine kinase inhibitors). Still, covariate models have been very useful to give recommendations for quantitative dose adjustments, e.g., in children receiving busulfan (59), patients with impaired renal function receiving topotecan (81) or patients with impaired hepatic function receiving docetaxel (71). In the future, it will be very important to use information from population covariate models for assessing dosing algorithms in prospective clinical studies. Respective simulation tools are part of most PK software packages and are potent instruments for the design of clinical studies, similar to what has been suggested by Bruno and colleagues for anticancer drug activity (90).