Abstract
It is well known that object recognition requires spatial frequencies exceeding some critical cutoff value. People with central scotomas who rely on peripheral vision have substantial difficulty with reading and face recognition. Deficiencies of pattern recognition in peripheral vision, might result in higher cutoff requirements, and may contribute to the functional problems of people with central-field loss. Here we asked about differences in spatial-cutoff requirements in central and peripheral vision for letter and face recognition.
The stimuli were the 26 letters of the English alphabet and 26 celebrity faces. Each image was blurred using a low-pass filter in the spatial frequency domain. Critical cutoffs (defined as the minimum low-pass filter cutoff yielding 80% accuracy) were obtained by measuring recognition accuracy as a function of cutoff (in cycles per object).
Our data showed that critical cutoffs increased from central to peripheral vision by 20% for letter recognition and by 50% for face recognition. We asked whether these differences could be accounted for by central/peripheral differences in the contrast sensitivity function (CSF). We addressed this question by implementing an ideal-observer model which incorporates empirical CSF measurements and tested the model on letter and face recognition. The success of the model indicates that central/peripheral differences in the cutoff requirements for letter and face recognition can be accounted for by the information content of the stimulus limited by the shape of the human CSF, combined with a source of internal noise and followed by an optimal decision rule.
Keywords: Pattern recognition, Peripheral vision, Letters, Faces, Spatial-frequency bandwidth, Ideal observer
I. INTRODUCTION
People sometimes need to function near the spatial-resolution limit for pattern recognition. Examples include recognizing letters on a distant traffic sign while driving, or recognizing a familiar face across the street. In these cases, spatial resolution is limited by visual acuity. Factors besides acuity may also limit spatial resolution such as fog, low-resolution display rendering, refractive error or damage to the visual pathway from eye disease. The current study aims to address pattern recognition under conditions of low resolution.
Reading and face recognition are among the most common human visual activities. Besides their ecological significance, there is also theoretical importance for selecting these two categories in studying human pattern recognition. It is thought that faces are recognized holistically (e.g., Farah, 1991; Tanaka & Farah, 1993; Gauthier & Tarr, 2002), while letters are thought to be recognized based on simple features (e.g., Pelli, Burns, Farell, & Moore-Page, 2006). These two categories of objects are exemplars of two important kinds of pattern recognition.
Previous studies of letter and face recognition have shown that the human visual system requires spatial frequencies extending beyond some critical value, e.g., 1–3 cycles per letter (CPL) (Ginsburg, 1978; Legge, Pelli, Rubin & Schleske, 1985; Parish & Sperling, 1991; Alexander, Xie & Dracki, 1994; Solomon & Pelli, 1994; Gold, Bennett, & Sekuler, 1999; Chung, Legge, & Tjan, 2002) and 3–16 cycles per face width (CPF) (Harmon, 1973; Harmon & Julesz, 1973; Ginsburg, 1980; Fiorentini, Maffei & Sandini, 1983; Hayes, Morrone, & Burr, 1986; Costen, Parker, & Craw, 1994; Gold, Bennett, & Sekuler, 1999). The wide range of estimates for faces may be due to methodological differences across studies such as filtering techniques and number and type of faces (e.g., faces with or without hair).
Previous studies of spatial-frequency requirements for pattern recognition have employed psychophysical methods to determine the ranges of frequencies that yield optimal recognition performance. For example, Gold et al. (1999) investigated the center frequencies critical for letter and face recognition. They measured contrast thresholds required to recognize two-octave wide band-pass filtered letters and faces in the presence of external white noise at 67% accuracy level and defined the critical frequency as the bandwidth showing the largest ratio of ideal to human contrast threshold energy. Although methods requiring measurement of contrast thresholds for letters and faces in the presence of masking noise have yielded useful theoretical insights, they do not characterize recognition in the more ecologically common case of reduced spatial resolution. Moreover, little is known about how the minimum spatial-frequency requirements for pattern recognition differ in central and peripheral vision.
It is known that reading in peripheral vision is slow (Chung, Mansfield, & Legge, 1998; Rubin & Turano, 1994) and face recognition in peripheral vision is poor (Mäkelä, Näsänen, Rovamo, & Melmoth, 2001) even with adequate magnification. People who lose their central vision due to diseases such as age-related macular degeneration (AMD) have to rely on their peripheral vision to read and recognize faces. It is important to gain a better understanding of what aspects of pattern recognition in peripheral vision differ from central vision for both theoretical and clinical reasons.
The primary goal of the present study is to examine whether there are differences in spatial-frequency requirements between central and peripheral vision for letter and face recognition. We measured recognition performance as a function of the cutoff frequency of a low-pass spatial-frequency filter. Minimum spatial-frequency cutoffs yielding criterion recognition accuracy (i.e., 80%) for 26 letters of the English alphabet and 26 celebrity faces were measured in both central and peripheral vision. We call this minimum spatial-frequency cutoff the critical cutoff, which represents the minimum spatial resolution allowing for reliable letter and face recognition. The critical cutoff for object recognition can be expressed in both retinal spatial frequency (cycles per degree, CPD) or object spatial-frequency (cycles per object, CPO). In this paper, cutoffs are usually expressed as object spatial frequencies. In order to find the critical cutoff for object recognition, one could fix angular object size, and allow retinal and object spatial frequency to covary. In this study, we, however, preferred to fix retinal spatial frequency and vary object spatial frequency by changing image size. This choice was made because an upper-bound on retinal spatial frequency is often imposed by physiology (e.g., the acuity limit). A retinal spatial frequency (1.5 CPD) was chosen as the cutoff because it could be studied in both foveal and peripheral vision (see more details in the Method section.)
There are at least four reasons to expect that the spatial-frequency requirements of object recognition may be different in central and peripheral vision. First, because of acuity limitations, larger letters (or faces) are usually required for peripheral recognition. It has been shown that the optimal spatial frequency band shifts to higher object frequency (CPL) when letter size increases (Alexander et al., 1994; Majaj, Pelli, Kurshan, & Palomares, 2002; Chung, Legge, & Tjan, 2002).
Second, there are studies showing that the human visual system can make use of both grayscale resolution (i.e., contrast coding) and spatial resolution for pattern recognition, (Farrell, 1991; Kwon & Legge, Under review). If this is the case, the lower contrast sensitivity of the periphery (i.e., reduced range for contrast coding) might mean that the very low resolution stimuli that can be recognized in the fovea might not be recognizable in the periphery. Evidence for an interaction between contrast coding and spatial resolution in face recognition also comes from the work of Mäkelä et al. (2001). They measured contrast sensitivity for face identification in order to see if foveal and peripheral performance would become equivalent by magnification of image size only. They found that to achieve equivalent performance, however, both the size and contrast of images needed to increase in the periphery.
Third, pattern recognition in peripheral vision is known to suffer from crowding (Bouma, 1973), i.e., impairments in recognition performance due to interference from nearby flankers. Martelli, Majaj, and Pelli (2005) demonstrated that crowding occurs not only at the object level (e.g., face), but also at the part level (e.g., eye, nose, mouth). The crowding effect can be reduced by increasing spacing between parts of an object. Increasing spacing can be achieved by increasing the size of the object as a whole or by increasing the separation between parts while keeping the size of each part intact. These manipulations would result in a larger object size, which in turn might lead to a higher critical cutoff requirement in peripheral vision. Furthermore, Chung and Tjan (2007) showed that the human visual system shifts its sensitivity toward a higher spatial-frequency channel when identifying crowded letters, compared to single letters.
A fourth factor differing between central and peripheral vision and potentially affecting critical cutoffs for pattern recognition is the shape of the human contrast sensitivity function (CSF). Previous studies have demonstrated that the shape of the human CSF helps to explain the spatial-frequency characteristics of letter recognition and reading (Gervais, Harvey, Jr., & Roberts, 1984; Legge, Rubin, & Luebker, 1987; Chung et al., 2002; Chung & Tjan, 2009).
A secondary goal of the present study was to examine whether the difference, if any, in spatial frequency requirements in central and peripheral vision for pattern recognition can be accounted for by the human CSF. For this purpose, we implemented a model, similar to the CSF-ideal-observer model introduced by Chung, Legge and Tjan (2002). We incorporated human CSFs for central and peripheral vision in the model, and asked if its performance in letter and face recognition resembled our human data.
II. METHOD
2.1. Subjects
Eighteen (letter recognition) and twelve (face recognition) college subjects (ages ranging from 19 to 25) were recruited from the University of Minnesota campus. They were all native English speakers with normal or corrected-to-normal vision and normal contrast sensitivity. The mean acuity (Lighthouse distance acuity chart) was − 0.09 logMar (Snellen 20/16), and ranged from −0.24 (Snellen 20/11) to 0.04 (Snellen 20/22). The mean log contrast sensitivity (Pelli-Robson chart) was 1.84, and ranged from 1.65 to 2.05. Subjects were either paid $10.00 per hour or granted class credit for their participation. The experimental protocols were approved by the Internal Review Board (IRB) at the University of Minnesota and written informed consent was obtained from all subjects prior to the experiment.
2.2. Stimuli
Letter images
The 26 lower-and upper-case Courier font letters of the English alphabet were used for the letter recognition experiment. The letter images were constructed in Adobe Photoshop (version 8.0) and MATLAB (version 7.4). Letter size defined as x-height varied from 14 to 47 pixels (0.45° to 1.5° at a viewing distance of 60 cm). A single black letter was generated on a uniform gray background of 250 × 250 pixels.
Face images
Images of 26 well-known celebrities (13 females and 13 males) were selected from the Google image database. The set of 26 faces was selected from a larger set of 50 celebrity faces using a familiarity survey administered to fifteen college students. Survey respondents were given a 2 × 2 inches photo of a celebrity’s face. They had to fill out the name of each celebrity and rank how familiar they were with the celebrity on a five-point scale. If they did not name the celebrity correctly, then the familiarity score was set to 1. The familiarity score was averaged across the 15 respondents. The 26 celebrities with the highest scores were selected.
The faces were all smiling and viewed from the front. There were two versions of each face: with hair and without hair. Faces with hair are ecologically more valid. On the other hand, faces without hair allowed us to examine face recognition without a hairline, known to be a major external cue for human face recognition (Sinha, Balas, Ostrovsky, & Russell, 2006). In both versions, however, we tried to eliminate any conspicuous external cues such as glasses, beard, and hair accessories.
The size of a face image was determined by the edge-to-edge width of the face at eye level. For a given size condition, all the 26 faces were scaled in size to equate them for the width of each face. We used various sizes of faces ranging from 16 to 155 pixels (0.5° to 5°) for faces with hair and from 46 to 279 pixels (2° to 9°) for faces without hair. All the face images were placed on a uniform gray background of 400 × 400 pixels. The faces were resized in Adobe Photoshop (version 8.0) and MATLAB (version 7.4).
The ranges of pixel gray-scale values of face images were similar across the 52 different face images (26 faces with hair and 26 faces without hair): the minimum values ranged from 0 to 33 with median value of 1 and the maximum values ranged from 200 to 255 with median value of 241.
All subjects were shown the set of 26 faces prior to the experiment to confirm familiarity and to inform the subjects about the set of possible target faces.
Image filtering
The images were blurred using a 3rd order Butterworth low-pass filter in the spatial frequency domain. The filter was radially symmetric with a cutoff frequency of 1.5 CPD for letter or face), equivalent to 1.5 CPO for a 1° letter size. The filter function was as follows:
| (Eq. 1) |
where r is the component radius, c is the low-pass cutoff radius and n is the filter’s order.
The filter’s response function is shown in Fig. 1. Fig. 2 shows sample letters and faces for both normal (top panels) and blurred images (bottom panels).
Figure 1.
The response function of the 3rd order Butterworth filter with the cutoff frequency of 1.5 CPD, equivalent to 1.5 CPL for a 1° letter size.
Figure 2.
Sample letters and faces for unfiltered (top row) and low-pass filtered images (bottom row).
Image display on screen
To present the filtered images on the monitor, we mapped the luminance values of the letters to the 256 gray levels. The DC value of the filtered image was always mapped to the gray level of 127, equivalent to the mean luminance of the monitor (40 cd/m2). The stimuli were generated and controlled using MATLAB (version 7.4) and Psychophysics Toolbox extensions (Mac OS X) (Brainard, 1997; Pelli, 1997), running on a Mac Pro computer. The display was a 19” CRT monitor (refresh rate: 75 Hz; resolution: 1152 × 870, subtending 37° × 28° visual angle at a viewing distance of 60 cm). Luminance of the display monitor was made linear using an 8-bit look-up table in conjunction with photometric readings from a MINOLTA CS-100 Chroma Meter. The image luminance values were mapped onto the values stored in the look-up table for the display.
2.3. Measuring critical cutoff frequencies for letter and face recognition
Face and letter recognition measurements were conducted in separate experiments on different subject groups. Both experiments, however, used the same procedure.
Recognition performance was obtained for six cutoff frequencies specified in CPO. This was achieved by fixing the cutoff retinal spatial frequency at 1.5 CPD and using six image sizes. For example, for a letter size of 1°, the cutoff frequency in CPO was 1.5 CPL. It is also possible to find the critical cutoff frequency by fixing letter size and varying the retinal spatial-frequency cutoff of the filter. In order to check the consistency of our method, we also obtained critical cutoffs by measuring recognition accuracy by fixing stimulus size and varying retinal frequency. We obtained critical cutoffs for the uppercase foveal condition from three subjects. We found that the mean critical cutoff is 1.21 (±0.07) CPL for this condition, which is not statistically different from the critical cutoff frequency obtained by fixing retinal frequency and varying image size. (p = 0.084). This finding convinced us to believe that the two different procedures yield approximately the same results.
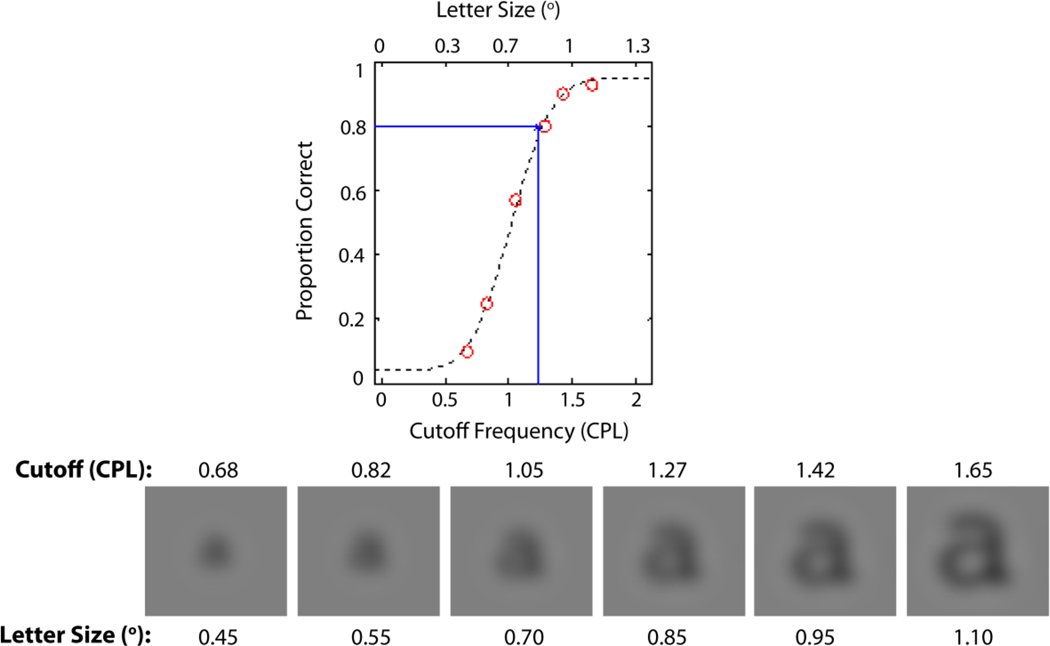
The critical cutoff was estimated from the resulting psychometric function, a plot of percent correct letter recognition as a function of cutoff (Fig. 3). Best-fitting (least squares) cumulative Gaussian functions (Wichmann & Hill, 2001) were fit to the data and threshold was defined as the cutoff yielding 80% correct responses (Fig. 3). The parameters alpha and beta are related to the mean and variance of the underlying Gaussian distribution, and determine the psychometric function’s location on the x-axis (alpha) and steepness (beta). Trials with six different cutoffs in CPL (or CPF) were randomly interleaved. Each cutoff was presented 100 times, so there were 600 trials for each psychometric function.
Figure 3.
An example of a psychometric function for letter recognition. Recognition performance was obtained for six cutoff frequencies as measured in CPO. This was achieved by fixing the cutoff retinal spatial frequency at 1.5 CPD and using six image sizes. The images below the psychometric function show a sequence of images, all with the same cutoff frequency of the filter measured in CPD (i.e., 1.5 CPD) but different cutoff frequencies measured in CPO depending on the size of the stimulus image.
In each trial, subjects were presented with a blurry letter (a – z or A – Z) for 150ms. Next, the displays were set to average luminance, and after a brief pause (500 ms), a set of 26 thumbnail versions of the letter images (56 × 56 pixels in size) appeared on the screen. Then, subjects identified the target stimulus by clicking the mouse on one of 26-letter answering keys forming a clock face. To prevent subjects from using any image matching strategy, a different font (Arial) and the opposite lettercase were used for the response key.
The location of each letter on the response key was shuffled every block to avoid any response bias induced by specific location. Subjects were given approximately 30 practice trials before the experimental test. A small cross in the center of the stimulus served as a fixation mark to minimize eye-movements throughout the experiment. A chin-rest was used to reduce head movements and to maintain the 60 cm viewing distance. Subjects were instructed to fixate on the fixation point on the computer screen during trials. The experimenter visually observed subjects to confirm that these instructions were being followed. The exposure time (150 ms) was too brief to permit useful eye movements.
Each letter and face recognition experiment consisted of four blocks: 2 lettercases (lower vs. uppercase letters) × 2 face types (faces with hair vs. without hair) × 2 visual field locations (fovea vs. periphery (10° lower visual field)). Thus, within a block, subjects were aware of both the type of target object and target location. The order of blocks was counterbalanced across subjects.
III. RESULTS
3.1. Letter recognition in fovea and periphery
Fig. 4 shows one subject’s psychometric functions from fovea and periphery (left panel for lowercase and right panel for uppercase). As described in the Method section, a critical cutoff was estimated from a psychometric function and defined to be the cutoff yielding 80% correct responses. Critical cutoffs were larger in the periphery than the fovea for both letter cases (0.92 CPL vs. 1.10 CPL for lowercase; 1.06 CPL vs. 1.40 CPL for uppercase). The slope of the curve decreased from the fovea (black asterisks) to the periphery (red asterisks) for both lower-and uppercase letters. (The peripheral condition refers to 10° eccentricity in the lower visual field.) This pattern of results was fairly consistent across all the subjects.
Figure 4.
Psychometric functions for subject 3: (a) lowercase letters and (b) uppercase letters. Data from the fovea are shown as black asterisks and periphery as red crosses. The dotted lines are the best fits of a cumulative Gaussian function.
We performed an analysis of variance (ANOVA) on cutoff (CPL) — 2 (visual field: fovea, periphery) × 2 (lettercase: lower, upper) repeated measures ANOVA with visual field and lettercase as within-subject factors. There was a main effect of visual field (F(1, 17) = 119.08, p < 0.001), indicating that critical cutoffs are significantly larger in the periphery than the fovea (20% larger on average). There was also a main effect of lettercase (F(1, 17) = 351.15, p < 0.001), indicating that uppercase letters have larger critical cutoffs than lowercase letters. We also found a significant interaction effect between lettercase and visual field location (F(1, 17) = 7.59, p = 0.014), indicating that the difference in critical cutoff between central and peripheral visual field is more pronounced for uppercase than lowercase letters.
As shown in Fig. 5, the mean critical cutoff for lowercase letters significantly increased from 0.90 CPL (±0.01) in the fovea to 1.06 CPL (±0.02) in the periphery and also increased for uppercase letters from 1.14 CPL (±0.02) in the fovea to 1.36 CPL (±0.02) in the periphery (all p < 0.05).
Figure 5.
Critical cutoffs in the fovea and the periphery for lowercase and uppercase letters (n=18).
Table 1 summarizes mean and standard errors for critical cutoffs. These differences are qualitatively unchanged for different threshold criteria ranging from 50% to 90%.
Table 1.
Critical cutoffs (defined as the minimum cutoff to achieve 80% recognition accuracy) and parameter values of the psychometric functions for four different stimulus conditions (n =18).
| Critical Cutoff (CPL) |
α (scale parameter) |
β (shape parameter) |
|
|---|---|---|---|
| Lowercase in the fovea | 0.90 (±0.01) | 0.47 (±0.004) | 0.15 (±0.006) |
| Lowercase in the periphery | 1.06 (±0.02) | 0.55 (±0.011) | 0.19 (±0.008) |
| Uppercase in the fovea | 1.14 (±0.02) | 0.63 (±0.007) | 0.15 (±0.005) |
| Uppercase in the periphery | 1.36 (±0.02) | 0.73 (±0.013) | 0.21 (±0.007) |
Changes in critical cutoffs could result from two possible influences on the psychometric function: 1) a horizontal shift of the curve along the cutoff axis, characterized by parameter alpha; or 2) a change in steepness of the curve, characterized by parameter beta. Our findings indicate that most of the effects on critical cutoff were due to changes in the slopes of the psychometric functions.
For both lowercase and uppercase letters, the slopes of the curves decreased substantially from the fovea to the periphery, as indicated by a significant increase in β value. There was a 32% increase in β value for lowercase letters in the periphery (Table 1). Even larger changes for uppercase letters were found, 35% increase in β value.
3.2. Face recognition in fovea and periphery
Fig. 6 shows subject 2’s psychometric functions for the fovea and the periphery (left panel for face with hair and right panel for face without hair). Critical cutoffs were larger in the periphery than the fovea for both face types (1.97 CPF vs. 3.06 CPF for face with hair; 3.89 CPF vs. 5.07 CPF for face without hair). The slope of the curve decreased from the fovea (black asterisks) to the periphery (red asterisks) for both face types. This pattern of results was fairly consistent across all the subjects.
Figure 6.
Psychometric functions of subject 2: (a) faces with hair and (b) faces without hair. Data from the fovea are shown as black asterisks and periphery as red crosses. The dotted lines are the best fits of a cumulative Gaussian function.
We performed an analysis of variance (ANOVA) on cutoff (CPF) — 2 (visual field: fovea, periphery) × 2 (face type: face with hair, face without hair) repeated measures ANOVA with face type and visual field as within-subject factors. There was a main effect of visual field (F(1, 11) = 18.63, p = 0.001), indicating that critical cutoffs are significantly larger in the periphery than the fovea. There was also a main effect of face type (F(1, 11) = 38.54, p < 0.001), showing that faces without hair require larger critical cutoffs than faces with hair. We also found a significant interaction effect between face type and visual field (F(1, 11) = 9.50, p = 0.01), indicating that the difference in critical cutoff between central and peripheral visual field is more pronounced for faces without hair.
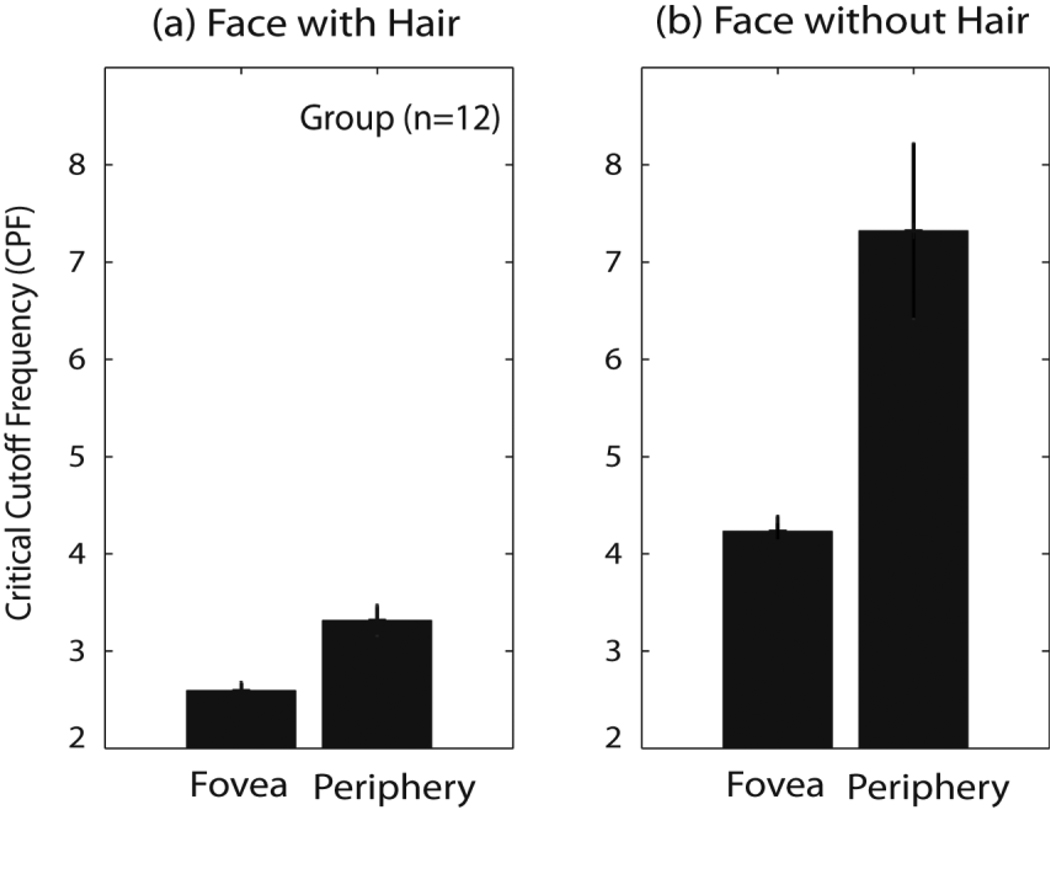
As shown in Fig. 7, the mean critical cutoffs for faces with hair increased from 2.59 CPF (±0.10) in the fovea to 3.31 CPF (±0.16) in the periphery and also for faces without hair from 4.23 CPF (±0.15) in the fovea to 7.32 CPF (±0.90) in the periphery. Table 2 summarizes mean and standard errors for critical cutoffs obtained from threshold criteria at 80% accuracy. The pattern of result stayed unchanged for different threshold criteria ranging from 50% to 90% accuracy.
Figure 7.
Critical cutoffs in the fovea and the periphery for faces with hair and faces without hair (n =12).
Table 2.
Critical cutoffs and parameter values of psychometric functions for four different stimulus conditions (n=12).
| Cutoff (CPF) |
α (scale parameter) |
β (shape parameter) |
|
|---|---|---|---|
| Faces with hair in the fovea | 2.59 (±0.10) | 1.64 (±0.07) | 1.13 (±0.06) |
| Faces with hair in the periphery | 3.31 (±0.16) | 1.83 (±0.10) | 1.76 (±0.19) |
| Faces without hair in the fovea | 4.23 (±0.15) | 2.75 (±0.09) | 1.76 (±0.13) |
| Faces without hair in the periphery | 7.32 (±0.90) | 4.02 (±0.30) | 3.92 (±0.82) |
For both face types, slopes of the psychometric functions were shallower in the periphery, accounting for the larger value of the critical cutoff. There was a 27% increase in β value for faces with hair in the periphery. Even larger changes for faces without hair were found, 75% increase in β value.
IV. MODEL DESCRIPTION AND COMPARISON WITH HUMAN PERFORMANCE
4.1. Model Overview
We now describe the implementation of a CSF-noise-ideal-observer model (hereafter the model) for letter and face recognition in central and peripheral vision. The aim of our modeling was to determine if our human results could be accounted for by a small set of assumptions about early visual processing combined with an optimal decision rule. To the extent that human performance matches model performance, we can pinpoint stimulus-based factors that may account for central-peripheral changes in human pattern recognition.
In principle, an ideal observer is able to perform with 100% accuracy in a recognition task if the stimuli are noise free. For this reason, many prior studies comparing human performance to an ideal observer have included noise-perturbed stimuli so that ideal performance drops below ceiling. In our study, no external noise was added to the stimulus. Instead, we constructed the model to have a source of additive noise following stimulus encoding and prior to the decision process (hereafter we call the stimulus with added noise “noisy input stimulus” for convenience).
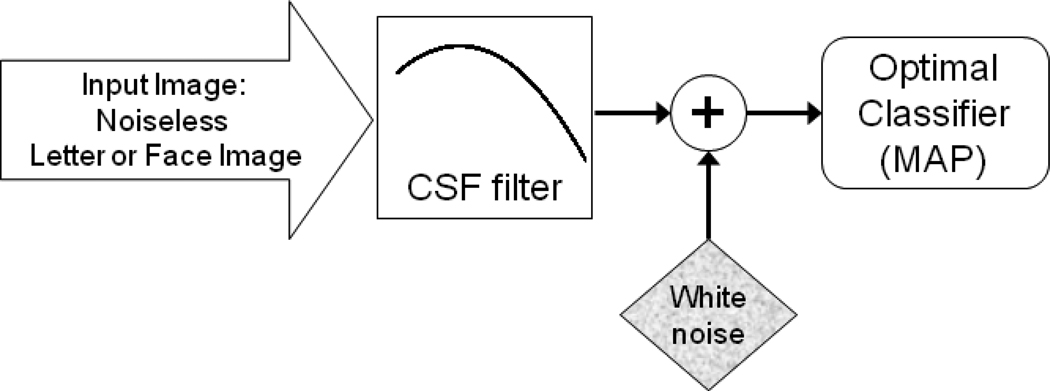
The model contained a CSF filter 1 and additive noise source placed between the stimulus and an optimal classifier as depicted in Fig. 8. The CSF filter was a linear filter with a shape identical to a human CSF.
Figure 8.
A schematic diagram of the CSF-noise-ideal-observer model.
The decision process in the model knows the exact pixel representations of the set of possible low-pass-filtered stimulus images and the probability of occurrence of the letters (the 26 letters are equally probable). The model also knows the statistics of the added luminance noise and the weighting associated with the CSF filter. In each simulation trial, the input to the model is a low-pass filtered letter or face image. The model makes full use of task-relevant information and makes a recognition response to maximize performance (percent correct) via a strategy of choosing the maximum posterior probability of the input being a particular target given the noisy image available to the decision process (Tanner & Birdsall, 1958; Green & Swets, 1966). The computation of finding the maximum posterior probability is equivalent to minimizing the Euclidean distance between the noisy input stimulus and its stored noiseless template (e.g., 26 letters or faces), often called template matching (Details of this computational derivation are provided in Appendix A).
The model’s performance was based on Monte Carlo simulations of 21,000 trials per psychometric function. Recognition performance of the model was measured for input stimuli with seven cutoff frequencies, yielding performance levels from 10% correct to 95% correct. There were 3000 trials for each cutoff level. A psychometric function, a plot of recognition accuracy vs. cutoff, was created by fitting the data with a cumulative Gaussian function. The critical cutoff was defined as the spatial frequency yielding 80% correct on the psychometric function.
Our model used empirical CSFs from Chung and Tjan (2009). Their CSFs were measured in the fovea and at 10° in the lower visual field (Fig. 9) using stimulus parameters similar to those of our study. 2
Figure 9.
Contrast sensitivity functions (CSFs) of human observers in the fovea (unfilled circles) and at 10° eccentricity (filled circles) (Adapted from Chung & Tjan, 2009)
4.2. Comparing Model and Human Recognition
4.2.1. Fitting the model to human recognition data by varying the noise parameter
We constructed plots of the model’s recognition accuracy as a function of spatial-frequency cutoff for comparison with human data (cf., Fig. 10). The steepness and position along the frequency axis of the model’s psychometric function depend on both the amplitude of the model’s internal noise and the featural similarity of the test targets. Before comparing human and model performance, we briefly discuss how these factors interact in determining the shape of the model’s psychometric functions.
Figure 10.
Letter recognition for the model in the fovea (black asterisks) and the periphery (red crosses), and for human observers (green open squares). Data were fitted with a cumulative Gaussian function.
It has been proven that in a pattern recognition task among N targets, percent correct (or d-prime) is monotonically related to mean Euclidean distance between all pairs of targets (Luce, 1963; Geisler, 1985). Given a fixed level of noise, a set of targets with greater separation in feature space will yield better performance than a set of more similar targets. Putting this another way, the more similar the stimuli, the lower the noise amplitude required to push down recognition performance to a criterion threshold level. In our study, recognition performance is influenced by three factors: 1) the intrinsic featural similarity of the target stimuli (e.g., uppercase letters have a higher featural similarity than lowercase letters which contain distinctive ascenders and descenders, and faces without hair have a higher similarity than faces with hair); 2) increasing blur produces increased similarity by filtering out distinguishing fine pattern details; and 3) the amplitude of added noise. In our empirical procedure, spatial-frequency cutoff (blur) was the independent variable used for generating a psychometric function. We would expect that the position of our subjects’ psychometric functions on the spatial-frequency axis would depend on both the similarity of their perceptual representations of the stimuli and their internal noise. For our ideal-observer model, the position of the psychometric function is determined by the similarity of the digitally filtered stimulus images and the model’s internal noise.
The only free parameter in the model is the amplitude of the internal noise which we varied to seek a good match between human and model performance. As shown in Table 3, a separate value of the model’s noise parameter was obtained for each experimental condition. To summarize: 1) For both letters and faces, central vision required a smaller noise value than the periphery. This is likely because the human internal noise is higher in the periphery than in central vision. 2) A lower noise level was required for uppercase than lowercase letters, and also a lower noise level for faces without hair than for faces with hair. This is likely due to differences in stimulus similarity rather than differences in internal noise. 3) A much larger noise level was required for faces than letters. While this difference might reflect higher internal noise in the human face processing system, we believe that the difference is more likely due to factors related to perceptual similarity of faces. We will return to this issue.
Table 3.
Noise parameter values (N0) used for the best fits of the model.
| Stimulus Condition | Noise (σ2) = N0 | |
|---|---|---|
| Letter | Lowercase in the fovea | 0.43 |
| Lowercase in the periphery | 0.61 | |
| Uppercase in the fovea | 0.35 | |
| Uppercase in the periphery | 0.50 | |
| Face | Face with hair in the fovea | 3.18 |
| Face with hair in the periphery | 3.85 | |
| Face without hair in the fovea | 2.31 | |
| Face without hair in the periphery | 2.87 | |
We tested whether the model fits are significantly better when separate noise values were used for different stimulus conditions by comparing the models with separate noise levels for the 8 different sets of stimuli and models with fewer independent noise levels (e.g., the eight noise levels were reduced to two levels: one for the fovea and the other for the periphery by using the mean noise levels for the four sets of central stimuli and four sets of peripheral stimuli). Statistical tests (i.e., the nested model test and a goodness of fit test) suggested that having different internal noise levels for different stimulus conditions was required for the model to satisfactorily explain human recognition data.3 Appendix B also addresses whether the inclusion of the CSF in the ideal observer model is important for accounting for our human data. As the appendix illustrates, the model fits are much better when the CSF is included.
Letters
Fig. 10 compares the letter recognition performance of the model to human observers. Except for the uppercase foveal condition, it is evident that the model provides a good account of human letter recognition data. Particularly, in the case of lowercase letters (Fig. 10. a), the data from the model nearly aligned with those of human observers. The quantitative analysis using a goodness of fit test (χ2 test) confirmed that the model provides a good account of human letter recognition performance for three of the four stimulus conditions (all p > 0.05). The exception is the uppercase foveal condition. What caused the poorer model fit for this condition is uncertain. Similar to humans, the model had larger critical cutoffs in peripheral vision than central vision for both letter cases (0.88 CPL in the fovea and 1.02 CPL in the periphery for lowercase letters; 1.12 CPL in the fovea and 1.34 CPL in the periphery for uppercase letters). The larger critical cutoff in peripheral vision appeared to result primarily from changes in the slope of the psychometric function, a consequence of the higher noise level required for the model to fit the human data in the periphery.
Faces
We also found that the model provides a satisfactory account for human face recognition data (Fig. 11). A goodness of fit test (χ2 test) further confirmed that the model provides a good account of human face recognition performance for all four stimulus conditions (all p > 0.05). Similar to humans, the model had larger critical cutoffs in peripheral than central vision for both face types: 2.29 CPL in the fovea and 3.24 CPL in the periphery for faces with hair; 4.09 CPL in the fovea and 7.14 CPL in the periphery for faces without hair. As is evident from Table 3, the model required much higher levels of noise to match the human face-recognition data than the human letter-recognition data. A consequence is the substantially higher critical cutoff frequencies for faces.
Figure 11.
Face recognition performance of the model in the fovea (black asterisks) and the periphery (red crosses) and for human observers (green open squares). Data were fitted with a cumulative Gaussian function.
4.2.2. Model performance with fixed noise
As discussed above, the location and shape of the model’s psychometric function depend on both the amplitude of internal noise and the similarity of the set of stimuli. In the preceding subsection, we treated the model’s noise amplitude as a parameter and found that noise values could be selected to provide a good match between the model and human data. But this leaves unclear the impact of pattern similarity within our four sets of stimuli. We addressed this issue by fixing the noise amplitude to determine how the model’s psychometric functions depend on the nature of the stimulus sets.
In Fig. 12, the model’s psychometric functions are shown for the four sets of stimuli in central vision with the noise value held constant. The fixed noise value was 0.43, the value required to provide a match to the human data for lowercase letters. The corresponding human psychometric functions are also shown. As expected from the selection of the fixed noise level, the human and model psychometric functions coincide for the lowercase letters. The model’s psychometric function shifts slightly rightward for the uppercase letters compared to the lowercase letters as expected from our intuition that uppercase letters have greater featural similarity than lowercase letters. The human psychometric function shows a similar rightward shift. Surprisingly, however, the model’s psychometric functions for the two sets of face stimuli (with and without hair) are quite similar to the psychometric functions for the letters (e.g., critical cutoffs of 0.9 CPL for lowercase letters, 1.2 CPL for uppercase letters., 0.56 CPF for faces with hair, and 1.02 CPF for faces without hair). This implies that for the model, the featural similarity of the sets of faces is not very different from the sets of letters. On the other hand, the human psychometric functions for the faces are displaced substantially rightward on the spatial-frequency axis, and have much higher critical cutoffs for faces than letters. The discrepancy in Fig. 12 between the human and model psychometric functions for faces implies that either the human face-recognition system has much higher internal noise than the letter-recognition system, or that the encoding of faces in human perception results in the loss of distinguishing features that remain available for the model’s optimal classifier.
Figure 12.
Psychometric functions for the model with noise level of 0.43: (a) lowercase letters, (b) uppercase letters, (c) faces with hair and (d) faces without hair. Data from human observers are shown as black asterisks and the model as red circles. The dotted lines are the best fits of a cumulative Gaussian function.
As indicated in Table 3, we found that in order to make the model fit the human data in the periphery, the noise parameter value of the model had to be increased by a factor of approximately 1.4 compared to the value in the fovea. Since the same two stimulus sets were used between central and peripheral vision, this finding can be explained by attributing 40% greater internal noise to the periphery at 10°.
Consistent with the findings in central vision shown in Fig. 12, if we fix the peripheral noise level at the amplitude required to fit the lowercase letter data Fig. 13, there is a large discrepancy between human and model psychometric functions for faces (e.g., critical cutoff frequencies of 1.05 CPL for lowercase letters, 1.5 CPL for uppercase letters, 0.67 CPF for faces with hair, and 1.3 CPF for faces without hair).
Figure 13.
Psychometric functions for the model with the noise parameter value of 0.61: (a) lowercase letters, (b) uppercase letters, (c) faces with hair and (d) faces without hair. Data from human observers are shown as black asterisks and the model as red circles. The dotted lines are the best fits of a cumulative Gaussian function.
V. DISCUSSION AND CONCLUSIONS
In the current study, we asked whether properties of peripheral vision might result in higher spatial-frequency-cutoff requirements for pattern recognition. Our secondary goal was to assess the impact of the human CSF in accounting for central and peripheral differences. We implemented the CSF-noise-ideal observer which incorporates empirical CSFs into an ideal observer model. We summarize our findings as follows:
We found that the critical cutoffs of human observers are significantly larger in peripheral than central vision, by an average of 20% for letters and 50% for faces. Our model analysis showed that even after taking the CSF into account, peripheral vision requires a larger critical cutoff for object recognition. This can be explained by an approximately 40% increase in noise from central vision to peripheral vision. This difference in critical cutoff between central and peripheral vision may contribute to the reading and face-recognition difficulties of people with central-field loss.
-
Our results showed that high levels of object-recognition accuracy are possible with quite low cutoffs. Despite the wide range of estimates among studies (cited in the Introduction), there has been a growing consensus that the spatial frequencies of 2–3 CPL and 8–16 CPF are the most crucial for identifying letters and faces respectively. However, we have found that people can achieve 80% recognition accuracy even with spatial-frequency cutoffs of 0.9 CPL and 2.6 CPF. These discrepancies between our findings and the previous studies are probably due to the distinction between the minimum spatial-frequency cutoffs required for pattern recognition (our study) and the optimal bands of spatial frequencies for pattern recognition identified in other studies (e.g., Gold et al., 1999). Data reported in Loomis (1990) also showed that low-pass filtered letters with a cutoff frequency of approximately 0.9 CPL yield reliable recognition performance (85 – 90% accuracy). Evidence that low object spatial-frequencies can support pattern identification has also been reported by Bondarko and Danilova (1997).
The low cutoffs may seem to contradict the conventional idea that letter recognition relies on the shape and arrangement of individual features (such as line segments and curves). This is because the cutoff frequency of 0.9 CPL has an equivalent sampling rate less than 2×2 samples per letter 4 (Shannon, 1949), and fewer than 4 binary samples would permit discrimination among fewer than 16 patterns, not adequate for discriminating among 26 letters. In a follow-up study (Kwon & Legge, under review), we addressed this apparent discrepancy by testing the hypothesis that the human visual system relies increasingly on grayscale coding (contrast coding) for letter recognition when spatial resolution is severely limited.
-
Uppercase letters have higher critical cutoff frequencies than lowercase letters, and faces without hair have higher critical cutoffs than faces with hair. This was true for our human observers and also our ideal-observer model. What accounts for these differences? Lowercase letters have more spatially distinctive features, such as ascending and descending strokes, than uppercase letters. Similarly, faces with hair have more distinguishable cues than faces without hair. A reduced set of distinctive spatial features appears to necessitate a larger critical cutoff frequency.
Our model analysis with a fixed noise level showed that the model requires much higher critical cutoffs for uppercase letters than lowercase letters and for faces without hair than faces with hair. The results are consistent with those of human observers. This suggests that differences in spatial frequency requirements between uppercase and lowercase letters and between faces with and without hair are mostly driven by the inherent properties of stimuli (especially the featural similarity of members of a set of stimuli).
-
The increase in the critical cutoff frequency for pattern recognition from central to peripheral vision appears to generalize across different kinds of complex pattern recognition. It is often thought that there is a large difference between face recognition and letter recognition in terms of featural vs. holistic processing respectively. Our data show that despite these different types of processing, both letter and face recognition exhibited larger cutoff requirements in peripheral vision than central vision.
How general are our results? We acknowledge that using different sets of letters (e.g., fonts), or face images (e.g., a larger number of faces, or different face poses) might have resulted in different critical cutoff frequencies. Nonetheless, to the extent that the model explains our results, we expect that most other stimulus sets would show the same pattern – increase in the critical cutoff frequency from central to peripheral vision. It is also noteworthy that for low-pass letters, channel frequency for letter recognition does scale exactly with letter size (Majaj et al., 2002). This evidence might speak to generalization of our results to other cutoff spatial frequencies and letter sizes.
Recognition performance of the CSF-noise-ideal observer model nearly matched human recognition performance when the model was fit to the human data using one free parameter (the amplitude of the additive noise). The results of our modeling suggest that the minimum spatial-resolution requirements of human pattern recognition can be accounted for by a simple front-end sensory model which contains the properties of the stimulus, combined with the filtering properties of the human CSF and a source of internal noise, and followed by an optimal decision rule.
Our ideal-observer model’s performance exhibited one marked difference from human performance. When the model had a fixed noise level, its critical cutoffs for face recognition were lower than those for letter recognition. Humans showed the opposite – higher critical cutoffs for faces than letters. What accounts for this discrepancy?
Humans may have a much less detailed representation of faces than letters, so that the effective stimulus similarity in our sets of faces was greater than for our sets of letters. In our experiment, we compelled subjects to choose from among a set of 26 faces. But, in the real world, people must encode information about a much larger set of faces. The strategies for representing a large number of faces may take advantage of configural data distributed more broadly across the frequency spectrum with sparser representation of low-frequency information. But coarse low-frequency features that survive severe blur may be effective for letter recognition which needs to distinguish only among 26 letters.
It is also possible that the discrepancy arises because the human face-recognition system is much noisier than the letter-recognition system. Higher noise would translate into a larger critical cutoff frequency for a given criterion level of performance.
In conclusion, our results show that the spatial-frequency-cutoff for pattern recognition is higher in peripheral than central vision. This difference can be accounted for by the CSF-noise-ideal observer model. In the context of the model, the central/peripheral differences can be traced to differences in the CSF and the overall amplitude of internal noise. The greater spatial-frequency requirements for human face recognition than letter recognition implies either a greater level of internal noise in human face processing or differences in human coding strategies for letters and faces.
► We asked about differences in spatial-frequency requirements in central and peripheral vision for human pattern recognition. ► We found that the minimum ranges of spatial frequencies for reliable letter and face recognition are larger in peripheral vision than central vision. ► The shape of the human contrast-sensitivity function and a source of internal noise can account for these differences.
ACKNOWLEDGEMENTS
We thank Susana Chung and Bosco Tjan for sharing their CSF data with us. We thank Meredith Sherritt and Jennifer Mamrosh for helping with screening face images. We also thank Rachel Gage for help with data collection. This work was supported by NIH grant R01 EY002934.
Appendix A. Decision rule of the CSF-noise-ideal observer for the recognition task
The CSF-noise-ideal observer has to solve the inverse optics problem, which is to figure out the most probable target signal (Ti) out of all possible 26 target signals (T) for a given input retinal image R, arrays of luminance pixel values. The problem can be expressed as P(Ti|R) and can be solved using Bayes’ rule as follows:
| (A.1) |
Since the denominator P(R), which is just a normalizing constant can be removed from the equation, P(Ti|R) can be reduced to the product of the likelihood function P(R|Ti) and the prior probability P(Ti) of a target signal.
| (A.2) |
Since the prior probabilities of the 26 signals (letters or faces) are equal in our experiment, P(Ti) = 1/26, the problem of finding maximum posterior probability can be expressed as a maximum likelihood function:
| (A.3) |
Therefore, the ideal observer’s goal is to find the maximum likelihood function of a given noisy input image R as a function of all possible 26 noiseless templates Ti and choose the highest possible Ti as its recognition response. The input image R is represented as an array of luminance pixel values and is added to zero-mean Gaussian luminance noise, σ. Thus, let’s say there is the m number of pixels in the input image R and Rj be the jth pixel in the image R. Then, at each pixel, we can compute the possible probability value of the noiseless signal Tij in noisy input Rj since it has a Gaussian probability density function as follow:
| (A.4) |
Since the luminance noise at different pixels is a random sample which is identically and independently distributed, i.i.d., the probability of the entire input image R is the product of the probabilities of all the pixels.
| (A.5) |
| (A.6) |
| (A.7) |
After removing terms that do not depend on i or j from Eq. A.7, the likelihood function is P(R|Ti) is reduced to the following exponential function:
| (A.8) |
Inspection of Eq. A.8 tells us that the likelihood function P(R|Ti) is monotonically related to ‖R − Ti‖2. In other words, maximizing Eq A.8 is the same as minimizing the Euclidean distance ‖R − Ti‖2 between the input image R and a template Ti. In other words, the ultimate job of the ideal observer, which is to find the maximum posterior probability is equivalent to finding the smallest Euclidean distance between the noiseless template Ti and noisy input image R.
Appendix B. Model selection
We compared one version of the ideal-observer model using a CSF and one without the CSF to see if inclusion of the CSF provides a better description of human performance data.
As described earlier, a wide range of white noise (σ2) levels was applied to the stimulus to find the noise level providing best fit to human recognition data. For each model, a family of psychometric functions from 8 different noise levels was built for each given stimulus condition. For each model, we selected the best fit psychometric function to that of human observers among a family of eight curves. Then, the two best psychometric functions from each model were compared using statistical F-test in which the model with a least mean squared error value was chosen as a superior model. Each psychometric function was constructed based on seven cutoffs. There was one free parameter, the constant noise N0 for each model.
1) Model Selection for Letter Recognition
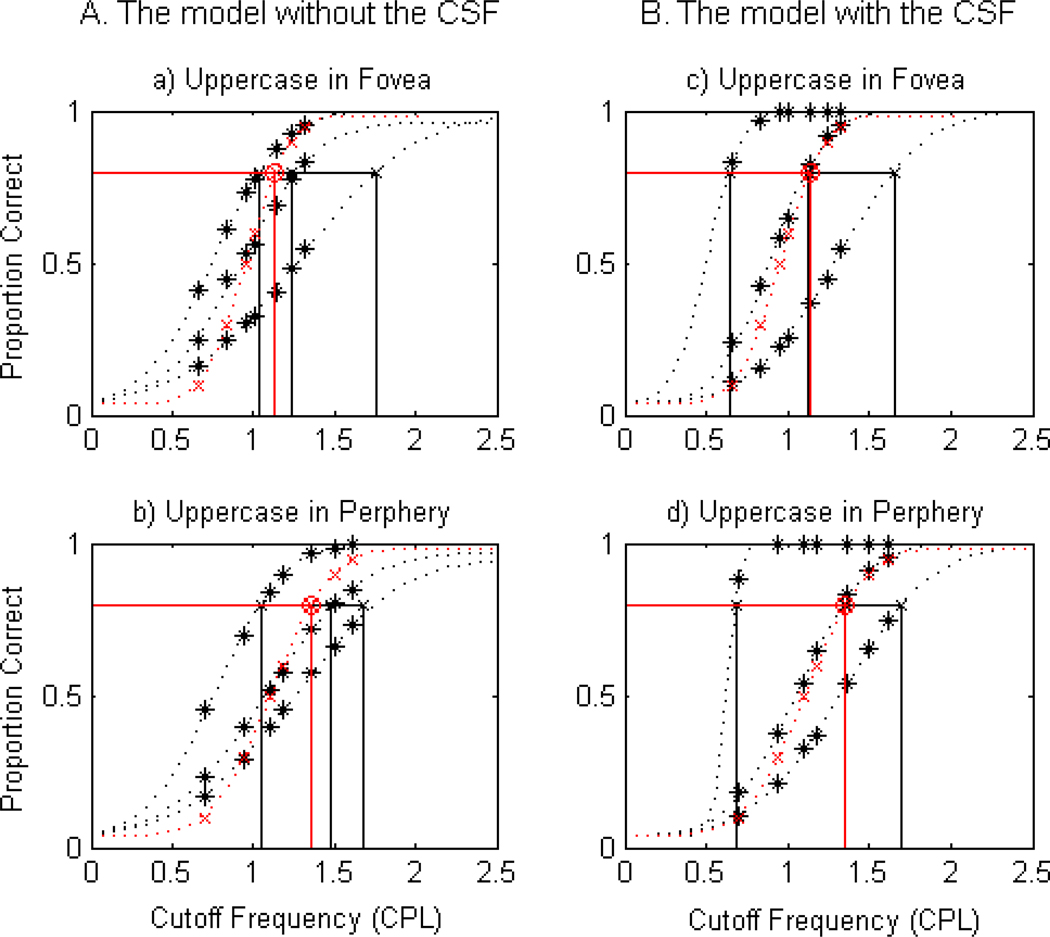
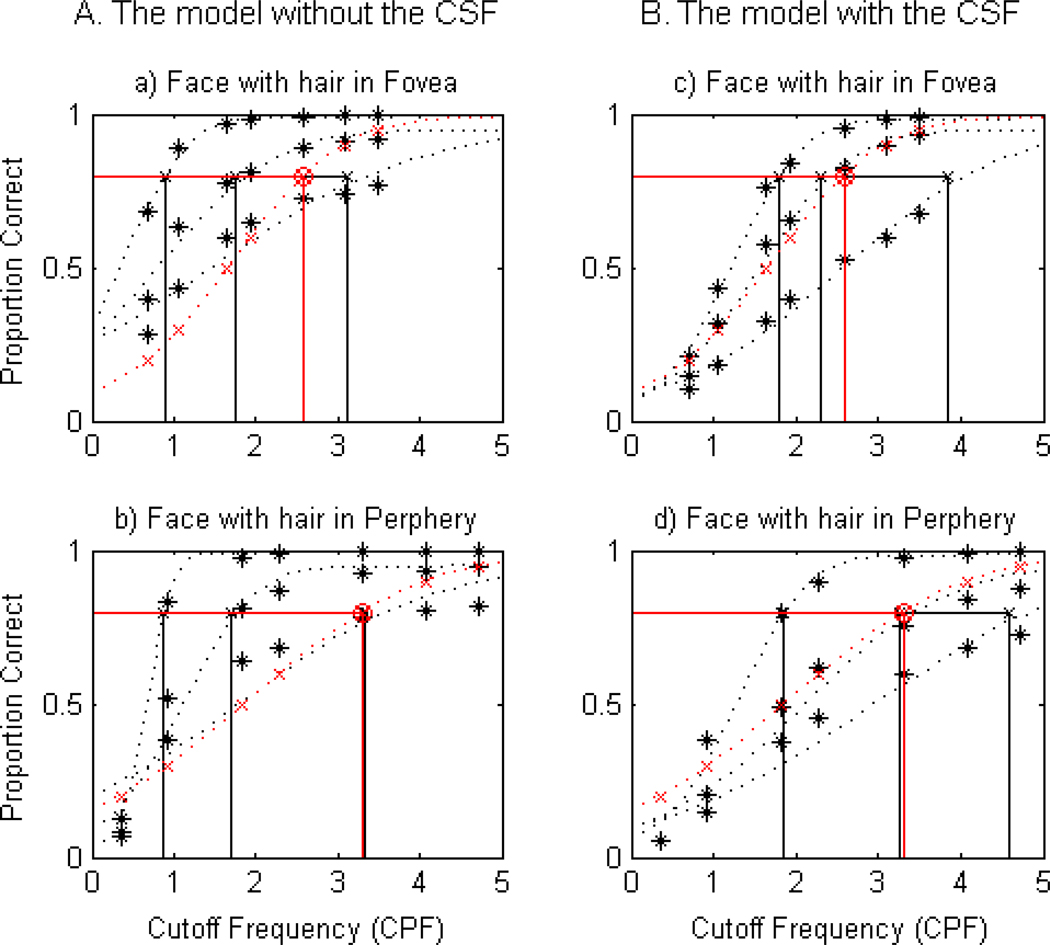
Figs B.1 and B.2 demonstrate the goodness of fit of each model to human data (left column from the model without the CSF vs. right column from the model with the CSF. Each panel contains four psychometric functions: three from the ideal (black) and one (red) from humans. For convenience, we only plotted three of them from the family of eight curves and compared them with those for human observers. The middle curves in the set of three in each panel are considered to be the best model fit to human recognition data.
Figure B.1.
Lowercase letter recognition of the models (A. The model without the CSF; B. The model with the CSF) in comparison with human recognition performance in the fovea (top row) and the periphery (bottom row).
Figure B.2.
Uppercase letter recognition of the models (A. The model without the CSF; B. The model with the CSF) in comparison with human recognition performance in the fovea (top row) and the periphery (bottom row).
Figs. B.1. and B.2. clearly demonstrate that the model with the CSF is superior to describe the human data for all four stimulus conditions. For example, as shown in Figs. B.1. c. and B.1.d. from the lowercase letter, the curves from the model with the CSF completely aligned with those of humans. In the case of the uppercase letter, the fit was not as good as lowercase letters, but the model with the CSF was still better than the model without the CSF. Quantitative analysis using F-test further confirmed that the model with the CSF was a better model than the model without the CSF for all four stimulus conditions (all p < 0.002). Table B.1. summarizes residual sum of squares from the two models.
Table B.1.
Residual Sum of Squares (RSS) of the two models for letter recognition.
| Lowercase in the fovea |
Lowercase in the periphery |
Uppercase in the fovea |
Uppercase in the periphery |
|
|---|---|---|---|---|
| RSSmodel without CSF (df = 6) | 0.108 | 0.071 | 0.330 | 0.151 |
| RSSmodel with CSF (df = 6) | 0.004 | 0.001 | 0.056 | 0.022 |
Based on our model selection analysis, we used the best fit data from the model with the CSF to examine spatial-frequency requirements in the fovea and the periphery in comparison with human recognition data.
2) Model Selection for Face Recognition
Consistent with letter recognition data, the model with the CSF provided a better account of the human recognition data for all four stimulus conditions. For example, as shown in Figs. B.3.c. and B.4.d. the curve from the model with the CSF nearly overlapped with that from humans. The quantitative analysis using F-test further confirmed that the model with the CSF is superior to the model without the CSF for all four stimulus conditions (all p < 0.002). Relatively larger variance in human face recognition data might have contributed to slightly less satisfactory fit between humans and the model. Table B.2 summarizes residual sum of squares from the two models.
Figure B.3.
Face with hair recognition of the ideal observers (A. The model without the CSF; B. The model with the CSF) in comparison with human observers’ performance in the fovea (top row) and the periphery (bottom row).
Figure B.4.
Face without hair recognition of the ideal observers (A. The model without the CSF; B. The model with the CSF) in comparison with human observers’ performance in the fovea (top row) and the periphery (bottom row).
Table B.2.
Residual Sum of Squares (RSS) of the two models for face recognition.
| Lowercase in the fovea |
Lowercase in the periphery |
Uppercase in the fovea |
Uppercase in the periphery |
|
|---|---|---|---|---|
| RSSmodel without CSF (df = 6) | 0.347 | 0.245 | 0.448 | 0.211 |
| RSSmodel without CSF (df = 6) | 0.013 | 0.041 | 0.005 | 0.037 |
Given the fact that the model with the CSF gives a better account of human face recognition, we used the best fit data from this model to examine spatial-frequency requirements in the fovea and the periphery in comparison with human data.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
| (Eq. 2) |
The CSFs were measured using an orientation discrimination task for sine-wave gratings windowed by Gaussian profiles with 150 ms exposure duration (see more details in Chung & Tjan, 2009). The threshold values and the general shape of our CSFs are comparable to those reported in previous grating detection studies (DeValois, Morgan, & Snodderly, 1974; Virsu & Rovamo, 1979).
The eight noise levels were reduced into two: one for the fovea and the other for the periphery by using the mean noise levels. The mean noise levels across the foveal conditions (N0 =1.5688) and across the peripheral conditions (N0 =1.9575) were obtained and used for the ideal-observer model. Then the resulting data from the model were fitted to human recognition performance data. In order to see if models with fewer of independent noise levels provide a better description of human performance data, we performed a nested model test (F-test) between the model with different noise levels and if models with fewer of independent noise levels. The nested-model test revealed that the model with separate noise levels was a better model than models with fewer of independent noise levels for all eight stimulus conditions (all p < 0.000001). A goodness of fit test further confirmed that models with fewer of independent noise levels are significantly different from human performance data for all stimulus conditions (all p < 0.000001). These results suggest that the reduced noise level model is not sufficient enough to account for human recognition performance data.
In signal processing, the Nyquist rate is the maximum sampling rate which can be transmitted through a channel, which is equal to two times the highest frequency contained in the signal.
REFERENCES
- Alexander KR, Xie W, Derlacki DJ. Spatial-frequency characteristics of letter identification. Journal of the Optical Society of America. 1994;11:2375–2382. doi: 10.1364/josaa.11.002375. [DOI] [PubMed] [Google Scholar]
- Bondarko VM, Danilova MV. What spatial frequency do we use to detect the orientation of a Landolt C? Vision Research. 1997;37:2153–2156. doi: 10.1016/s0042-6989(97)00024-2. [DOI] [PubMed] [Google Scholar]
- Bouma H. Visual interference in the parafoveal recognition of initial and final letters of words. Vision Research. 1973;13:767–782. doi: 10.1016/0042-6989(73)90041-2. [DOI] [PubMed] [Google Scholar]
- Brainard DH. The psychophysics toolbox. Spatial Vision. 1997;10:433–436. [PubMed] [Google Scholar]
- Chung STL, Legge GE, Tjan BS. Spatial-frequency characteristics of letter identification in central and peripheral vision. Vision Research. 2002;42:2137–2152. doi: 10.1016/s0042-6989(02)00092-5. [DOI] [PubMed] [Google Scholar]
- Chung STL, Mansfield JS, Legge GE. Psychophysics of reading. XVIII. The effect of print size on reading speed in normal peripheral vision. Vision Research. 1998;38:2949–2962. doi: 10.1016/s0042-6989(98)00072-8. [DOI] [PubMed] [Google Scholar]
- Chung STL, Tjan BS. Shift in spatial scale in identifying crowded letters. Vision Research. 2007;47:437–451. doi: 10.1016/j.visres.2006.11.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chung ST, Tjan BS. Spatial-frequency and contrast properties of reading in central and peripheral vision. Journal of Vision. 2009;9:1–19. doi: 10.1167/9.9.16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Costen NP, Parker DM, Craw I. Spatial content and spatial quantization effects in face recognition. Perception. 1994;23:129–146. doi: 10.1068/p230129. [DOI] [PubMed] [Google Scholar]
- De Valois RL, Morgan H, Snodderly DM. Psychophysical studies of monkey vision. 3. Spatial luminance contrast sensitivity tests of macaque and human observers. Vision Research. 1974;17:7581. doi: 10.1016/0042-6989(74)90118-7. [DOI] [PubMed] [Google Scholar]
- Farah MJ. Patterns of co-occurrence among the associative agnosias: Implications for visual object representation. Cognitive Neuropsychology. 1991;8:1–19. [Google Scholar]
- Farrell JE. Grayscale/Resolution Tradeoffs in image quality. In: Morris Robert A, Andre Jacques., editors. Raster imaging and digital typography II. New York: Cambridge University Press; 1991. pp. 65–80. [Google Scholar]
- Fiorentini A, Maffei L, Sandini G. The Role of High Spatial Frequencies in Face Perception,”. Perception. 1983;12:195–201. doi: 10.1068/p120195. 1983. [DOI] [PubMed] [Google Scholar]
- Gauthier I, Tarr MJ. Unraveling mechanisms for expert object recognition: Bridging brain activity and behavior. Journal of Experimental Psychology: Human Perception and Performance. 2002;28:431–446. doi: 10.1037//0096-1523.28.2.431. [DOI] [PubMed] [Google Scholar]
- Geisler WS. Ideal observer theory in psychophysics and physiology. Physica Scripta. 1985;39:153–160. [Google Scholar]
- Gervais MJ, Harvey LO, Jr, Roberts JO. Identification confusions among letters of the alphabet. Journal Experimental Psychology: Human Perception and Performance. 1984;10:655–666. doi: 10.1037//0096-1523.10.5.655. [DOI] [PubMed] [Google Scholar]
- Ginsburg AP. Ph.D. Thesis. Cambridge University: Aerospace Medical Research Laboratory Report AMRL-TR-78_129. USAF, Wright-Patterson AFB, OH; 1978. Visual information processing based on spatial filters constrained by biological data (Vols. I and II) [Google Scholar]
- Ginsburg AP. Specifying relevant spatial information for image evaluation and display design: an explanation of how we see certain objects. Proceedings of the SID. 1980;21:219–227. [Google Scholar]
- Gold J, Bennett PJ, Sekuler AB. Identification of bandpass filtered letter and faces by human and ideal observers. Vision Research. 1999;39:3537–3560. doi: 10.1016/s0042-6989(99)00080-2. [DOI] [PubMed] [Google Scholar]
- Green DM, Swets JA. Signal detection theory and psychophysics. New York: John Wiley and Sons; 1966. [Google Scholar]
- Harmon LD. The recognition of faces. Scientific American. 1973;229:70–83. [PubMed] [Google Scholar]
- Harmon LD, Julesz B. Masking in Visual Recognition: Effects of 2-Dimensional Filtered Noise. Science. 1973;180:1194–1197. doi: 10.1126/science.180.4091.1194. [DOI] [PubMed] [Google Scholar]
- Hayes T, Marrone MC, Burr DC. Recognition of positive and negative bandpass filtered images. Perception. 1986;15:595–602. doi: 10.1068/p150595. [DOI] [PubMed] [Google Scholar]
- Kwon M, Legge GE. Trade-off between spatial resolution and contrast coding for letter recognition. Journal of Vision. (under review) [Google Scholar]
- Legge GE, Pelli DG, Rubin GS, Schleske MM. Psychophysics of reading. I. Normal vision. Vision Research. 1985;25:239–252. doi: 10.1016/0042-6989(85)90117-8. [DOI] [PubMed] [Google Scholar]
- Legge GE, Rubin GS, Luebker A. Psychophysics of reading. V. The role of contrast in normal vision. Vision Research. 1987;27:1165–1171. doi: 10.1016/0042-6989(87)90028-9. [DOI] [PubMed] [Google Scholar]
- Loomis JM. A model of character recognition and legibility. Journal of Experimental Psychology: Human Perception and Performance. 1990;16:106–120. doi: 10.1037/0096-1523.16.1.1066. [DOI] [PubMed] [Google Scholar]
- Luce DR. Detection and recognition. In: Luce DR, Bush RR, Galanter E, editors. Handbook of mathematical psychology. vol. I. New York: John Wiley and Sons; 1963a. pp. 103–188. [Google Scholar]
- Majaj NJ, Pelli DG, Kurshan P, Palomares M. The role of spatial-frequency channels in letter identification. Vision Research. 2002;42:1165–1184. doi: 10.1016/s0042-6989(02)00045-7. [DOI] [PubMed] [Google Scholar]
- Mäkelä P, Näsänen R, Rovamo J, Melmoth D. Identification of facial images in peripheral vision. Vision Research. 2001;41:599–610. doi: 10.1016/s0042-6989(00)00259-5. [DOI] [PubMed] [Google Scholar]
- Martelli M, Majaj NJ, Pelli DG. Are faces processed like words? A diagnostic test for recognition by parts. Journal of Vision. 2005;5:58–70. doi: 10.1167/5.1.6. [DOI] [PubMed] [Google Scholar]
- Parish DH, Sperling G. Object spatial frequencies, retinal. Vision Research. 1991;31:1399–1416. doi: 10.1016/0042-6989(91)90060-i. [DOI] [PubMed] [Google Scholar]
- Pelli DG. The VideoToolbox software for visual psychophysics: Transforming numbers into movies. Spatial Vision. 1997;10:437–442. [PubMed] [Google Scholar]
- Pelli DG, Burns CW, Farell B, Moore-Page DC. Feature detection and letter identification. Vision Research. 2006;46:4646–4674. doi: 10.1016/j.visres.2006.04.023. [DOI] [PubMed] [Google Scholar]
- Rubin GS, Turano K. Low vision reading with sequential word presentation. Vision Research. 1994;34:1723–1733. doi: 10.1016/0042-6989(94)90129-5. [DOI] [PubMed] [Google Scholar]
- Shannon CE. The Mathematical Theory of Communication. Urbana, IL: University of Illinois Press; 1949. [Google Scholar]
- Sinha P, Balas BJ, Ostrovsky Y, Russell R. Face recognition by humans: 19 results all computer vision researchers should know about. Proceedings of the IEEE. 2006;94(11):1948–1962. [Google Scholar]
- Solomon JA, Pelli DG. The visual filter mediating letter identification. Nature. 1994;369:395–397. doi: 10.1038/369395a0. [DOI] [PubMed] [Google Scholar]
- Tanaka JW, Farah MJ. Parts and wholes in face recognition. Quarterly Journal of Experimental Psychology. 1993;46A:225–245. doi: 10.1080/14640749308401045. [DOI] [PubMed] [Google Scholar]
- Tanner WP, Jr, Birdsall TG. Definitions of d0 and g as psychophysical measures. Journal of the Acoustical Society of America. 1958;30:922–928. [Google Scholar]
- Virsu V, Rovamo J. Visual resolution, contrast sensitivity, and the cortical magnification factor. Experimental Brain Research. 1979;37:475–494. doi: 10.1007/BF00236818. [DOI] [PubMed] [Google Scholar]
- Wichmann FA, Hill NJ. The psychometric function: I. Fitting, sampling and goodness-of-fit. Perception and Psychophysics. 2001;63:1293–1313. doi: 10.3758/bf03194544. [DOI] [PubMed] [Google Scholar]