In Vivo 3D Whole-Brain Pulsed Steady State Chemical Exchange Saturation Transfer at 7T

Abstract

Chemical exchange saturation transfer (CEST) is a technique to indirectly detect pools of exchangeable protons through the water signal. To increase its applicability to human studies, it is needed to develop sensitive pulse sequences for rapidly acquiring whole-organ images while adhering to stringent amplifier duty cycle limitations and SAR restrictions. In addition, the interfering effects of direct water saturation (DS) and conventional magnetization transfer contrast (MTC) complicate CEST quantification and need to be reduced as much as possible. It is shown that for protons exchanging with rates of less than 50–100 Hz, such as imaged in amide proton transfer (APT) experiments, these problems can be addressed by using a 3D steady state pulsed acquisition of limited B₁ strength (~1 μT). Such an approach exploits the fact that the DS width, MTC magnitude, and SAR increase strongly with B₁, while the size of the CEST effect for such protons depends minimally on B₁. A short-TR (65 ms) steady state sequence consisting of a brief saturation pulse (25 ms) and a segmented EPI train allowed acquisition of a 3D whole-brain volume in approximately 11 s per saturation frequency, while remaining well within SAR and duty cycle limits. MTC was strongly reduced, but substantial saturation effects were found at frequencies upfield from water, which still confound the use of MT asymmetry analysis. Fortunately, the limited width of the DS signal could be exploited to fit it with a Lorentzian function allowing CEST quantification. APT effects ranged between 1.5 and 2.5% in selected white and gray matter regions. This power and time-efficient 3D pulsed CEST acquisition scheme should aid endogenous CEST quantification at both high and low field.

Introduction

Chemical exchange saturation transfer (CEST) (1–7) is a contrast mechanism based on the saturation of low-concentration exogenous or endogenous pools of protons that are in constant exchange with the bulk water pool. One type of CEST imaging, amide proton transfer (APT) of mobile cellular peptides and proteins (8,9), has a unique contrast that increases for brain tumors (8,10) and reduces when pH is lowered during acute ischemia (9,11). Currently, applicability of CEST/APT MRI in the clinic is limited by sensitivity (effect of a few percent) and by amplifier duty cycle and specific absorption rate (SAR) restrictions that prohibit use of lengthy saturation schemes. In addition, CEST/APT quantification and image appearance may differ between hospitals due to the interference of competing saturation phenomena such as direct water saturation (DS) and conventional magnetization transfer contrast (MTC), the contributions of which depend on local hardware properties (coils, amplifiers) and on the pulse sequence parameters used. As such there is a need to develop sensitive pulse sequences for rapidly acquiring quantitative whole-organ images while adhering to amplifier and SAR limitations.

The relative magnitude of CEST and conventional MT contrast can be weighted by varying the saturation length, t_sat, and strength, B₁ (12). It is not always appreciated that this weighting can be optimized for the particular exchange rate range of interest. Rapidly exchanging protons such as in paraCEST agents and hydroxyl- or amine-based diaCEST compounds require high B₁ fields to allow sufficient saturation efficiency α (2,13,14):

$$\alpha \approx \frac{{(\gamma B_1)}^2}{{(\gamma B_1)}^2+{(k_{sw})}^2},$$ [1]

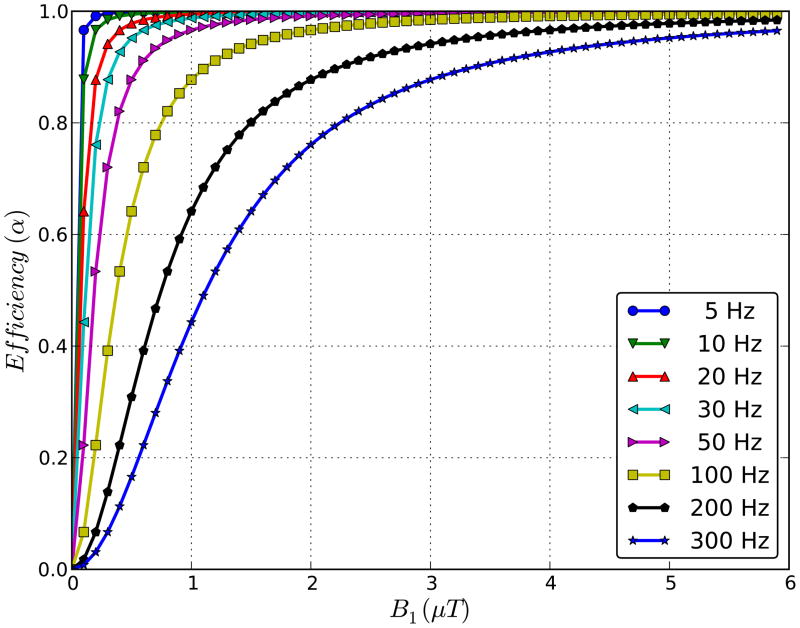
in which γ = 267.5 × 10⁶ rad/Ts and k_sw the exchange rate from solute to water. For slower rates, such as those of amide protons in tissue (k_sw ~ 28 Hz (9,13)), only limited B₁ strength is needed (Figure 1). On the other hand, the DS width (15–17), MTC magnitude (18–20), and SAR decrease strongly when reducing B₁. This suggests the opportunity to design a low-B₁ pulse sequence for APT in which maximum CEST saturation efficiency can be retained under conditions of strongly reduced MTC effects and a narrowed DS line shape.

Figure 1.

Saturation efficiency as a function of saturation field strength (B₁) for protons with a range of exchange rates (Calculated using Eq. [1]). Notice that maximum efficiency can be reached at low B₁ for slow exchange rates.

CEST volume acquisitions have been performed using multi-slice (21–23) and 3D (24) approaches, with the latter having the advantage of the saturation being distributed equally over the volume. CEST imaging has been accomplished using long block pulses (10,25) or a series of short pulses (8,26–28) such that the saturation efficiency of the pulse train of pulses is similar to that of the long hard pulse. Alternatively, one can use steady state approaches (22,29) with alternating brief saturation and image acquisition. It is expected from experience with MTC studies (18,30,31) that power deposition and thus scan times can be reduced using pulsed steady state acquisitions. Here we use the Bloch equations to simulate the relative contributions of CEST, MTC and DS as a function of saturation pulse length and strength with the goal of finding suitable 3D steady state CEST/APT acquisition parameters that have reduced DS and MTC interference and are not limited by amplifier duty cycle and SAR restrictions. In addition, we show that such acquisition removes the need for asymmetry analysis of the saturation effects with respect to the water frequency and allows quantification of CEST/APT effects.

Materials and Methods

Theory

We focus on one type of endogenous CEST, namely amide proton transfer (APT) of mobile cellular peptides and proteins (8,9), for which the exchangeable protons of interest resonate around 3.5 ppm downfield from water (8). CEST effects can be predicted accurately by the Bloch equations, which can include CEST, DS, and MTC effects in a 3-compartment model. However, Bloch simulations are often not that transparent. As the amide proton exchange rate is only about 28 Hz (9,13), it is possible to also use the analytical equations to verify results. The pure amide proton transfer ratio can then be described by (2,9,13):

$$\mathit{APTR}=x_s·\alpha ·k_{sw}·T_{1w}\left(1-e^{-t_{\mathit{sat}}/T_{1w}}\right)$$ [2]

in which T_1w is the longitudinal relaxation time of water and x_s the ratio of solute proton and water proton (111.2 M) concentrations. CEST/APT quantification requires the removal of competing effects of DS, which has been approached by measuring saturation effects as a function of offset frequency (so-called Z-spectra (32) or CEST spectra (25)) and processing such data using so-called MT ratio asymmetry (MTR_asym) analysis with respect to the water resonance frequency. For the amide proton transfer signals at 3.5 ppm from water this is:

$${\text{MTR}}_{\text{asym}}(3.5\text{ppm})=\{{\text{S}}_{\text{sat}}(-3.5\text{ppm})-{\text{S}}_{\text{sat}}(3.5\text{ppm})\}/{\text{S}}_0$$ [3]

However, such analysis is complicated by inherent asymmetries in the MTC effect (33–35) and by possible occurrence of so-called Nuclear Overhauser Effects (NOEs (2,36)) upfield (i.e. at negative frequency offsets) from water. Thus, the MTR_asym measured in tissue is a convolution of multiple effects:

$${\mathit{MTR}}_{\mathit{asym}}(3.5\mathit{ppm})=\mathit{APTR}+{\mathit{PTR}}^{\mathit{endo}}(3.5\mathit{ppm})+{\mathit{MTR}}_{\mathit{asym}}^{\mathit{MTC}}(3.5\mathit{ppm})+{\mathit{MTR}}_{\mathit{asym}}^{\mathit{NOE}}(3.5\mathit{ppm}),$$ [4]

in which PTR^endo accounts for endogenous proton transfer effects other than due to amides. In general it is assumed that MTR_asym = APTR and images are called APT images, but it would be more correct to use APT-weighted for the terminology. Each of the contributions in Eq. [4] depends differently on B₁ and t_sat, and, consequently, MTR_asym(3.5ppm) effects may vary (between −5% and 5%) between laboratories or even between different experiments in the same laboratory. Of course saturation effects can only be positive, because additional water signal can unfortunately not be created, and negative or asymmetries are due to larger saturation effects upfield from water. In a practical approach (24,37), APT images are often acquired using saturation parameters that provide approximately zero MTR_asym(3.5ppm) for normal tissue, thereby highlighting lesions. This is not a major problem when using APT to determine relative contrast between affected and normal tissue such as in tumors or ischemia, but it may be an issue for diseases where lesions are less clear. Here we investigate the convolved effects of MTC, DS and APT during steady state, which reveal some troubling aspects when applying asymmetry analysis, leading to the need to analyze data without this approach.

Pulse Sequence and Simulations

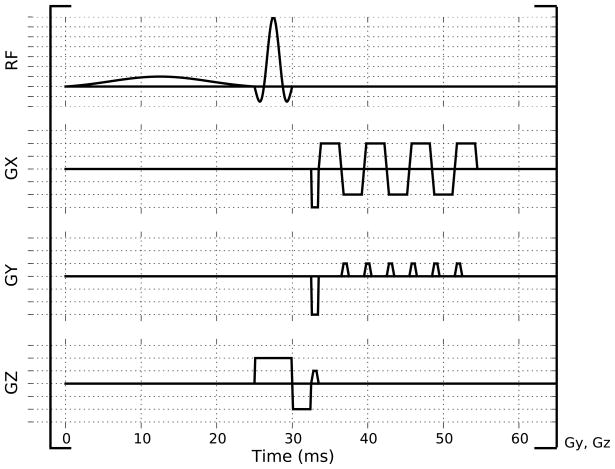
In Figure 2, a 3D CEST technique is shown in which chemical exchange transfer is built up over multiple saturation pulses. After every short saturation pulse a segmented EPI readout is acquired. This fast readout and short TR (65 ms) result in an efficient whole brain CEST acquisition of less than 11 s per irradiation frequency, allowing a full Z-spectrum to be acquired in a clinically reasonable time. The rapid scanning leads to a magnetic steady-state situation.

Figure 2.

Pulsed CEST acquisition consisting of a frequency selective sinc-Gauss saturation pulse followed by a short partial EPI readout. This TR interval is repeated continuously (166 times for the pulse sequence parameters described in the Methods section) with the saturation pulse applied at one frequency in order to fill 3D k-space, starting with the high frequency region of k-space during steady state build up. No inter-volume delay is used when acquiring the multiple frequencies for a Z-spectrum.

To obtain insight into this, CEST, MTC and DS effects for white matter were simulated using the Bloch equations for a 3-pool model (38,39) consisting of macromolecular, amide and bulk water protons. For convenience, the MTC effect was assumed to be symmetric so that MTR_asym(3.5ppm) equals the APT effect. These simulations were used to determine (a) the optimum B₁ and duration of the saturation pulse for maximum APT effect and (b) the number of saturation pulses needed to obtain steady state. The situation of macromolecular and amide protons exchanging with the bulk water pool was modeled for 7T based on previously published relaxation and exchange rates for free water and amide pools summarized in Table 1 (31,38). Note that exchange rates, concentrations and chemical shifts in ppm are not field dependent. The T₂ values were estimated from 3T literature (13,18) by assuming a reduction of 40% with respect to 3T. For convenience all T₁ values were set at 1.7 s. An offset frequency of 3.5 ppm was used for amide protons, while 0 ppm was used for all other protons. The APT and MTC effects were simulated as a function of saturation pulse power (0.1 μT to 5 μT in steps of 0.1 μT) and duration (5 ms to 65 ms in steps of 5 ms) to determine parameters to maximize APT and minimize MTC. A 40 ms delay after each saturation pulse was simulated during which exchange and relaxation occur. This delay was based on the shortest possible TR (65 ms). The simulated signal was quantified at 301 saturation frequencies linearly spaced between −10 and 10 ppm. To determine the number of consecutive pulses required to reach steady-state, the signal intensity after each sinc-gauss pulse (applied on the APT frequency of 3.5 ppm) was plotted as a function of time post sequence onset. For comparison, a Z-spectrum was simulated with a continuous saturation pulse of duration 2500 ms and 1 μT at the same saturation frequencies as in the pulsed scheme. This length of pulse is similar to previous CEST work (24,27) and was intended to be comparable to 100 repetitions of pulsed saturation.

Table 1.

Parameters used in the 3-pool Bloch equation simulations.

	T1 (s)	T2 (ms)	Exchange Rate (s−1)	Chemical Shift (ppm)	Proton Concentration (mM)	Ref
Macromolecule	1.7	0.01	4.6	0	7,150	(30)
Amide	1.7	33*	28	3.5	72	(13)
Bulk Water	1.7	48*	-	0	111,200	(18)

^*Estimated based on the listed references, but adjusted for field strength assuming a reduction of 40% with respect to 3T. Note that the value of T₂ is needed for the Bloch simulation but will not strongly affect the CEST effect.

Data Acquisition

The study was approved by the Johns Hopkins Medicine IRB and performed on six normal controls who provided informed consent. MRI data was acquired on a 7T Philips Achieva system (Philips Healthcare, Best, The Netherlands) using a quadrature transmit head coil and a 32 channel Novamedical phased array receive coil. High dielectric pads (40) were placed on either side of the head by the temporal lobes for padding to minimize movement and to flatten the signal intensity across the head (40). Third order shims were optimized over the brain. Imaging data were acquired using the 3D multi-shot gradient-echo (EPI factor 7) sequence of Figure 2 with TR/TE/FA =65 ms/7.2 ms/12° across 40 slices at 2×2×2 mm isotropic resolution across a FOV of 220×220 mm. The multi-shot EPI used a linear readout so the zero k-space profile was acquired half way through the volume acquisition. The parallel imaging SENSE factor was set to 2×2 (RL × AP). The saturation pulse was a 1 μT, 25 ms single-lobe sinc-gauss pulse. The TR of 65 ms was the shortest duration possible given the saturation pulse duration, readout and delay imposed by the pulse sequence to allow for RF and gradient duty cycles. The time for whole brain acquisition per irradiation frequency at 2×2×2 mm resolution was 10.9 s. No inter-volume delay was used after each volume acquisition. Following two dummy acquisitions, an unsaturated volume was acquired followed by 77 volumes at saturation frequency offsets of 0.0, ±0.2, ±0.4, ±0.6, ±0.8, ±1.0, ±1.2, ±1.4, ±1.6, ±1.8, ±2.0, ±2.2, ±2.4, ±2.6, ±2.9, ±3.1, ±3.2, ±3.3, ±3.4, ±3.5, ±3.6, ±3.7, ±3.9, ±4.1, ±4.4, ±4.6, ±4.8, ±5.0, ±5.5, ±6.0, ±6.5, ±7.0, ±7.5, ±8.0, ±8.5, ±9.0, ±9.5, ±10.0 ppm (relative to the water frequency). Total acquisition time was 14 min 24 s. The unsaturated reference was acquired using the same sequence as the saturated volume (including the TR) except the RF saturation pulse was turned off.

Data Processing

All data was registered to the first volume (unsaturated) using the rigid body (6 degrees of freedom) registration algorithm FLIRT (FSL, FMRIB Centre, University of Oxford) with the normalized mutual information cost function and sinc resampling. All further data processing was done using Python, Scipy and Numpy (www.python.org, scipy.org and numpy.scipy.org, respectively) using code written in-house.

A confound in selective frequency saturation is the underlying variability in the B₀ inhomogeneity due to local susceptibility-induced field shifts. These frequency variations can be as high as 1 ppm in regions near the nasal cavity and ear canals, while smaller variations are seen across the whole brain. The advantage of Z-spectra is that signals are acquired at many saturation offset frequencies, allowing the minimum signal (maximum direct water saturation) in each voxel to be found and then shifted to the assigned water frequency of 0 ppm for referencing. No obvious MTC effects could be discerned in the steady state Z-spectra allowing us to fit the direct saturation contribution using a Lorentzian line shape (15) in each voxel:

$$L(A,b,{LW}_{1/2},f_{\mathit{shift}})=100-A\left(\frac{{({LW}_{1/2})}^2}{{({LW}_{1/2})}^2+4{(f_0-f_{\mathit{shift}})}^2}\right)+b$$ [4]

where A is the amplitude, LW_1/2 is the water linewidth, f_shift is the frequency shift of the Z-spectrum due to magnetic field inhomogeneities and b is a baseline offset. The Lorentzian fit was based on points from the Z-spectrum around the water frequency (|f_shift| < 1 ppm) and points above 6 ppm from water (f_shift ≥ 6 ppm), where limited endogenous CEST and NOE effects are expected. Such Lorentzian fitting has been used previously in paraCEST imaging (41) when occurrence of CEST effects at positive and negative frequencies with respect of water prohibited the use of asymmetry analysis. However, for the B₁ needed in paraCEST imaging, this would not be precise in vivo because MTC effects cause the water saturation line-shape to be non-Lorentzian. The Lorentzian curve was used to shift the acquired data to correct for B₀ inhomogeneity and to determine the CEST/APT effects. Two types of analysis were done for measuring APT numbers: (i) standard asymmetry analysis for the range 3.3 – 3.7 ppm according to Eq. [3] and (ii) Lorentzian difference analysis (LDA), in which the acquired data were subtracted from the Lorentzian curve and the mean signal around from 3.3–3.7 ppm was quantified without the need to use the upfield side as a control.

Regions were drawn on a mid-axial slice through representative white and gray matter regions and CSF. The mean MTR_asym(3.5ppm) and APT signals within each region were calculated and displayed. A t-test was used to test the hypothesis that these quantities differed between regions.

Results

Simulations

In Figure 3a, the 3-pool Bloch simulation of the APT effect is shown as a function of saturation B₁ and duration. Maximal APTR (1.7%) was found for a 1 μT, 25 ms saturation pulse and a TR of 65 ms. When simulating only the MT and DS effects for these saturation settings (Fig. 3b), it can be seen that MTC and DS effects are very small at 3.5 ppm. These optimized saturation parameters were subsequently used to simulate the signal intensity as a function of saturation pulse number (Fig. 3c). For the first volume, signals at 3.5 ppm and −3.5 ppm were within 1% of the final steady-state signal by the 60^th and 57^th TR interval, respectively, assuming an initial fully relaxed signal. For a TR of 65 ms, this would correspond to 3.9 s and 3.7 s of scanning time, which is approximately 1/3 of the k-space volume. When acquiring a Z-spectrum, the signal can be in steady state with far fewer pulses (and therefore much faster) by having no delay between the volume acquisitions at different frequencies. This is shown in Figure 3c by the dotted and dash-dotted lines for which the previous saturation point was 0.1 ppm away from the APT and control frequencies. When simulating steady-state Z-spectra with inter-volume delays of 0 s (Fig. 3d) and 7 s (Fig. 3e), there was negligible difference, giving an APTR of 1.7% in both cases. It can be seen that Z-spectra simulated using a continuous 1 μT hard pulse of length 2 s show strongly increased contributions from MTC and DS (dashed lines) compared to those simulated in steady state (solid lines). The APTR quantified from the continuous hard pulse Z-spectra was 1.3% for both 0 s and 7 s inter-volume delays. This reduced APT sensitivity compared to the steady-state approach is likely due to the larger competing contributions from MTC and residual DS at the 3.5 ppm offset. Another Z-spectrum was simulated (for the 0 s inter-volume delay) using a continuous 0.4 μT hard pulse (length 2 s) to match the expected APTR of a 25 ms 1 μT sinc-gauss pulse (Fig. 3c dotted line). The saturation-matched Z-spectrum and difference compared well to that from the pulsed sequence.

Figure 3.

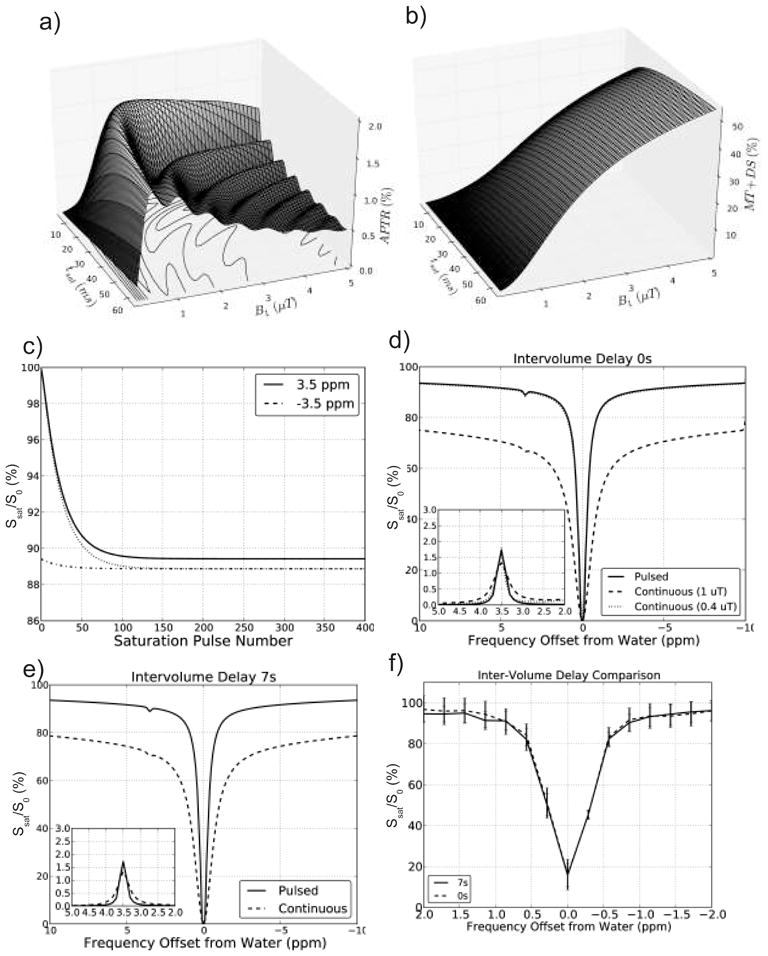
Simulations of the effect of saturation strength and duration on the pulsed steady state APT effect for a 3-compartment model of semi-solid macromolecular protons, solute amide protons, and bulk water protons (Table 1). a) APTR for TR = 65 ms, showing a maximum at t_sat = 25 ms and B₁ ~ 1 μT. b) MTC+DS effect at 3.5 ppm for TR = 65 ms using zero APTR. A strong reduction with decreasing B₁ can be seen, leading to very small MTC for t_sat = 25 ms at B₁ values of 1 μT or less. c) Normalized water signal intensity (S/S₀) as a function of number of TR intervals to determine the number of saturation pulses needed to reach steady state. Simulations for saturation at 3.5 ppm (APT frequency) and −3.5 ppm (control frequency) for an initially fully relaxed signal (solid and dashed lines, resp.) and for a previously obtained steady state at a frequency differing by 0.1 ppm (dotted and dash-dotted lines, resp). d) Comparison of Z-spectra for pulsed steady-state CEST (solid curve), continuous saturation CEST (dashed line) with a 0 s inter-volume delay and continuous saturation with B₁ (0.4 μT) designed to match pulsed saturation (dotted line). The inset shows the MTR_asym for both simulations. e) as d) but with a 7 s inter-volume delay. f) Mean signal intensity (and standard deviation) of an in vivo region in white matter (major forceps) acquired from one acquisition with 0 s inter-volume delay (dashed line) and one acquisition with 7 s inter-volume delay (solid line). This pair of acquisitions was used to corroborate the simulations that showed little effect of the minimal inter-volume delay.

Human Studies

To corroborate the negligible dependence of the saturated steady state signal on inter-volume delay, an in vivo experiment was done. A single volunteer was scanned twice using the pulsed CEST sequence with saturation offsets ranging from −1 ppm to 1 ppm (21 step acquisition), both with a 7 s and a 0 s inter-volume delay. White matter Z-spectra from the major forceps were quantified (Figure 3f). A spill-over effect from one saturation frequency to the next would skew the shape of the Z-spectrum acquired with 0s inter-volume delay to the positive side, but this was not the case. This is consistent with the simulated results in Figures 3d and 3e. Therefore, all in vivo data acquired for APT quantification used the 0s inter-volume delay. The added benefit is that the acquisition is much faster and the number of TR intervals to get into steady state significantly reduced (as seen in the simulated data of Figure 3c).

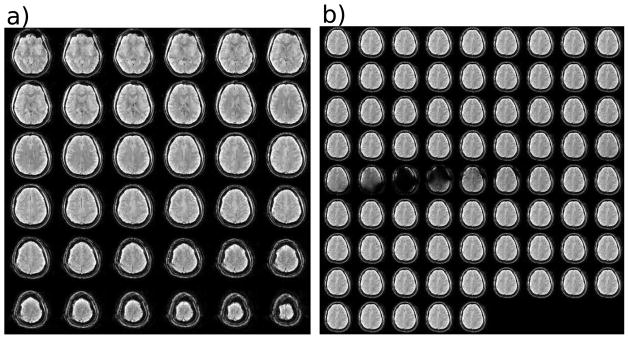
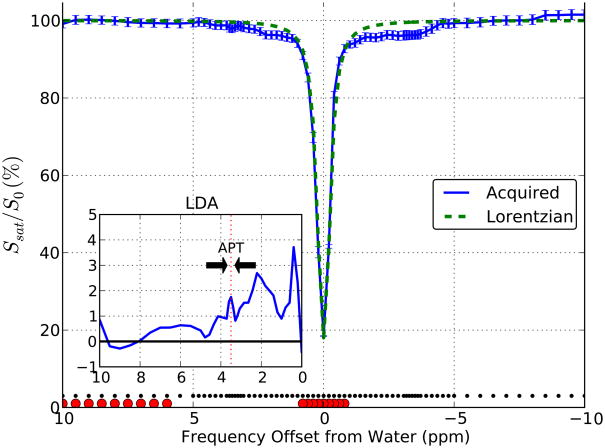
In Figure 4a, an example slice stack is shown for the unsaturated volume of the steady state acquisition. Images as a function of saturation frequency for one anatomical slice are shown in Figure 4b, indicating that there was sufficient saturation as reflected in the images near direct water saturation. Figure 5 shows a Z-spectrum acquired data using 77 frequency offsets in the major forceps. The normalized signal intensities above 6 ppm are indistinguishable from 100%, suggesting negligible MTC effects. In addition, the saturated water line shape is very narrow. These features allowed the use of Lorentzian fitting to points between ±1 ppm and above |frequency offset| of 6 ppm (dashed line). This fit can be assumed to be dominated by direct water saturation effects and was used in each voxel to correct for the frequency shift of the Z-spectrum due to B₀ field inhomogeneities. The difference between the Lorentzian curve and acquired data should represent signal related to chemical exchange between tissue solute protons and bulk water. The downfield difference (shown in the inset in Figure 5) revealed a broad group of resonances between 0 and 5 ppm that may be attributed to exchangeable protons. The range around 3.5 ppm was previously assigned to APT (42–44). Interestingly, there are appreciable saturation effects at frequencies lower than water (between 0 and −5 ppm). This is the range where Ling et al. (36) suggested the presence of NOE signals, which can probably be attributed to exchange-relayed NOEs (2,45). Such signals complicate the use of MTR_asym(3.5 ppm) calculations for the amide protons. Fortunately, the minimal MTC effects in the low-power pulsed CEST data allow the use of Lorentzian Difference Analysis (LDA) to estimate the APT effects from the difference between the Lorentzian fit and the acquired data (see Methods).

Figure 4.

a) Slices of one volume (unsaturated) of the pulsed 3D acquisition to show the excellent image quality. b) The saturated volumes of one slice for saturation offset frequencies ranging from −10 ppm to 10 ppm. The images near the middle are dark because of direct water saturation.

Figure 5.

In vivo Z-spectra for a region in white matter (major forceps). Z-spectrum acquired at frequencies denoted by the small black dots along the bottom. The lack of detectable saturation at frequencies > 8 ppm and < −8 ppm confirm the expected negligible MTC for the steady state acquisition. The acquired data for the frequencies indicated by the large red circles were fitted to a Lorentzian function. The difference between the Lorentzian (green dashed line, assumed to be based only on direct water saturation) and acquired data indicate that exchange effects occur both at positive and negative frequencies with respect to water. Inset: the mean signal between the Lorentzian fit and data acquired between 3.3 and 3.7 ppm was used to calculate the APTR.

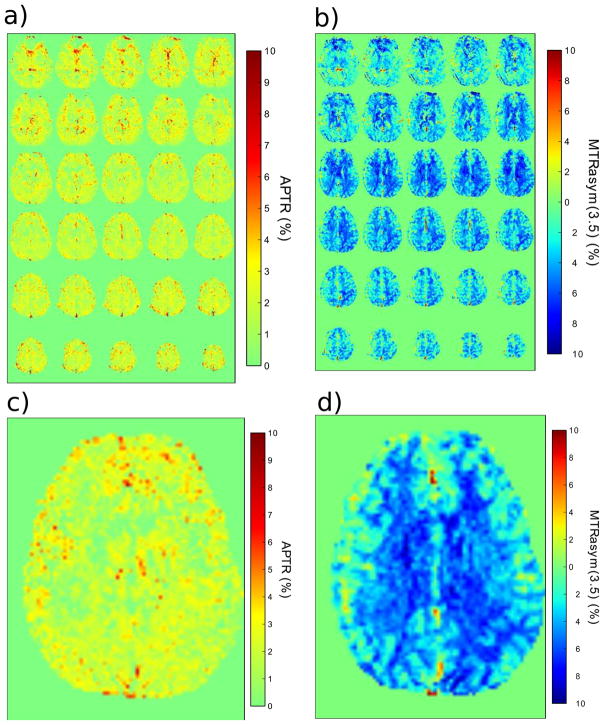
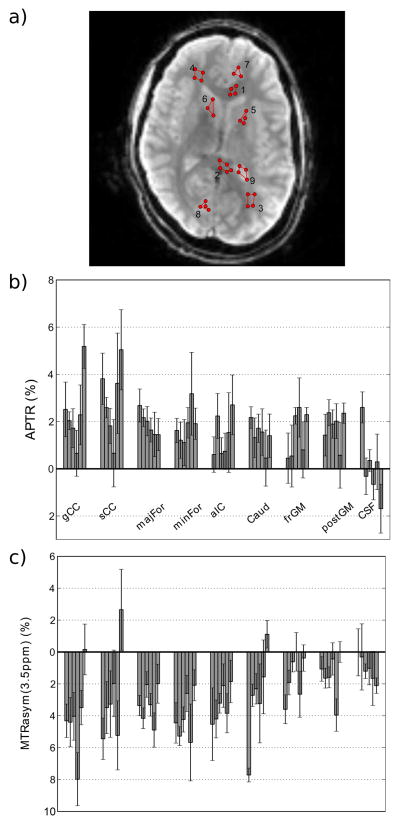
Spatial maps of the B₀-corrected APTR between 3.3 and 3.7 ppm created using this LDA technique are shown in Figure 6a. For comparison a traditional APT-weighted (asymmetry) map calculated using Eq. [3] is shown in Figure 6b. The most important difference is that the signal in the new APTR map is positive, whereas it is mostly negative in the traditional asymmetry map, due to interference of the exchange-relayed NOE signals. The mean APTR from six normal controls was quantified for nine brain regions (Figure 7a–b, Table 2). There was no statistical difference (p > 0.01) between any tissue region (WM or GM). APTR values in all WM and GM regions were statistically different from the APT in CSF (p < 0.01), except for the frontal gray matter. The lack of a statistical difference between frontal gray matter and CSF could be due to partial volume effects with CSF in the cortex. For comparison, the MTR_asym at 3.5 ppm was calculated (Fig. 7c, Table 2), which is commonly used to determine APT differences in patients. Again, none of the tissues showed statistical differences (all p > 0.01). The only deviation from the mean was the CSF measure from volunteer 1, which we attribute to partial volume effects due to small ventricles. The other CSF values were close to zero.

Figure 6.

a) An amide proton transfer ratio (APTR) map quantified from the mean signal between 3.3 and 3.7 ppm in the difference plot (Figure 5 inset) on a per voxel basis. b) MTR_asym(3.5ppm) map based on asymmetry analysis of the same data as in a). c) Slice 20 of the APTR map in a). d) Slice 20 of the MTR_asym(3.5ppm) map in b). Note the negative signal intensity in the MTR asymmetry method.

Figure 7.

a) Example regions drawn on a single slice of one control where 1 = genu of corpus callosum (gCC), 2 = splenium of CC (sCC), 3 = minor Forceps (minFor), 4 = major Forceps (majFor), 5 = anterior internal capsule (aIC), 6 = caudate nucleus (Caud), 7 = frontal Cortical gray matter (frGM), and 8 = posterior Cortical GM (postGM), and 9 = CSF. b) The mean and standard deviation of the APTR (%) for each volunteer organized by region. c) The mean and standard deviation of the MTR_asym(3.5ppm) (%) for each volunteer organized by region.

Table 2.

APT effects quantified for nine brain regions (n = 6) in normal controls.

Region	APTR (3.3 – 3.7 ppm)	MTRasym (3.5 ppm)
gCC	2.4 ± 1.4 %	−4.0 ± 2.4 %
sCC	2.9 ± 1.4 %	−2.8 ± 2.7 %
majFor	1.9 ± 0.4 %	−3.3 ± 1.0 %
minFor	1.8 ± 0.7 %	−4.1 ± 1.3 %
aIC	1.4 ± 0.8 %	−3.3 ± 1.0 %
caudate	1.4 ± 0.5 %	−2.7 ± 2.6 %
frGM	1.5 ± 0.9 %	−1.5 ± 1.3 %
posGM	1.8 ± 0.6 %	−1.5 ± 1.3 %
CSF	0.1 ± 1.3 %	−1.1 ± 0.7 %

Standard deviation is given. Abbreviations: genu of corpus callosum (gCC), splenium of CC (sCC), major Forceps (majFor), minor Forceps (minFor), anterior internal capsule (aIC), caudate nucleus (Caud), frontal Cortical gray matter (frGM), posterior Cortical GM (postGM), and CSF.

Discussion

We developed a fast low-B₁ pulsed CEST steady state acquisition able to acquire 3D whole-brain volumes in less than 11 seconds per frequency offset at a 2 mm isotropic resolution. Bloch equation simulations were used to optimize the saturation pulse parameters with respect to reducing contributions from MTC and DS at 3.5 ppm while retaining close to maximal APT effects. The resulting parameters allowed acquisition within amplifier duty cycle limitations and well within SAR guidelines, even at 7T (SAR was approximately 1.5 W/kg). Interestingly, the resulting Z-spectra for pulsed CEST showed prominent upfield exchange transfer effects, which confounded analysis of CEST effects using the commonly used approach of asymmetry analysis. The resulting data were therefore processed using Lorentzian fitting of the direct water saturation contribution and subtracting this from the experimental Z-spectrum. This was possible due to the narrow appearance of the DS line shape, which was a consequence of the low B₁ power used. To better facilitate such DS fitting, the sampling frequency of the Z-spectrum around the water frequency was increased, which did not cause a major increase in overall scan time due to the short 3D volume acquisition time. Lorentzian difference analysis allowed quantification of the APT effect without being affected by potential MTC and exchange-based asymmetries with respect to the water frequency. The resulting LDA-based APTR maps differed strikingly from the MTR_asym(3.5 ppm) based images (Figure 6) in that the range of values was more restricted (2.1 +/− 0.6% versus −3.9 +/− 1.6%, respectively) and positive. The most likely explanation is that the asymmetry measures vary due to intensity differences in the upfield region of the spectrum where the pulsed CEST acquisition showed significant signal saturation from −1 ppm to −5 ppm.

The magnitude of both CEST and NOE effects is a function of saturation strength and duration and will most likely differ for different coil setups. Thus, absolute quantification of CEST effects will always require specification of B₁, t_sat and the pulse sequence timing details, as corroborated by other papers (e.g., Refs. 28,36). The finding of a negative MTR asymmetry is probably not restricted to pulsed style acquisition and it is clear that one must be careful in interpreting APT (and CEST) effects based on MTR asymmetry analyses. Importantly, saturation effects cannot be negative because this would correspond to an increase in water signal. Thus the asymmetry analysis data cannot be a correct value for APTR. Using LDA, the effect size measured in selected white and gray matter regions reflects well the values found based on Bloch equation simulations (Fig. 3). Using the values in Table 1 for the exchange rate, T_1w, and the ratio x_s of solute protons versus water protons (111.2 M), the maximum effect (infinite saturation time t_sat) for a B₁ of 1 μT (267.5 rad/s) as based on the analytical solution is 1.4%, in good agreement with the simulation results (1.7%). Experimental APTR values (Table 2) varied from the same range to slightly higher, but such small discrepancies can easily occur based on differences in relaxation and exchange parameters between the simulations and experiments. We therefore conclude that, when MTC effects are small and the DS line shape sufficiently narrow, the LDA approach provides a suitable alternative for quantifying APT. One surprising aspect of the results was that the MTC contribution was lower than simulated. We attribute this to B₁ loss in the cables between the amplifier and the coil. Note that this should not affect the saturation efficiency for APT, but will affect MTC strongly (Figures 3a,b). For systems with more efficient power transfer, an even more reduced B₁-setting may therefore be possible. Another potential factor affecting APTR is B₁ inhomogeneity. Again however, as shown in Fig. 1, this is not a main issue for slowly exchanging protons as long as variation is not more than 10–20% from the optimal B₁. It is a major issue for paraCEST and amine and OH protons.

It is clear that the low-power steady-state pulsedCEST acquisition reveals additional information in the Z-spectrum, which may provide information complementary to amide proton exchange. Most prominent are saturation effects upfield from water (−1 ppm to −5 ppm), which are in the range where Nuclear Overhauser Effects (NOEs) can be expected (2,36). These could be due to both direct protein-water (36) or exchange-relayed (2) NOEs, with the latter more likely based on the known time scale of such transfers for mobile proteins (43,45,46). These signals may offer new information for protein/peptide content or pH quantification independent of the amide proton peak at 3.5 ppm. We are currently investigating this in more detail. In addition, there is abundant CEST signal difference between 0 ppm and 3 ppm from water. This is where other amides, amines and hydroxyl groups resonate. It is important to realize that the relative contributions of these different groups to the signal will vary with the saturation parameters. For instance, high-B₁ approaches will allow detection of fast-exchanging protons, while for low-power approaches, such as used in the pulsed steady state CEST here, slowly exchanging protons such as the amides will be more visible (Figure 1). It should be clear from this discussion that CEST and APT quantification are dependent on the pulse sequence parameters. In addition, changing the saturation power will affect both the direct saturation and MTC contribution in the Z-spectrum. Until standardization of CEST approaches occurs, one must therefore be careful in comparing numbers between different sites.

Technical Details

The data acquisition took 14 minutes and 24 seconds. This is mostly because of the very high spectral resolution (77 saturation frequencies) and we expect that this number can be reduced based on specific experimental needs. A more important detail is that the acquisition time was 11 s per 40-slice 3D volume. The first in vivo APT measurements (10,37) were single slice experiments with 1.5 × 1.5 × 5 mm³ resolution, taking approximately 30 s per slice. A recent multi-slice CEST FISP (28) sequence allowed acquisition of 13 slices in approximately 10 s. The only other 3D readout (24) used a GRASE sequence and was a 2.2 × 2.2 × 4.4 mm³ acquisition with 30 slices per volume and each volume acquired in 20 s. Thus the current sequence is the fastest per volume and has more slices per volume.

A single lobe sinc-Gauss pulse was used for saturation and we found this simple pulse to provide good saturation and power tradeoffs with minimal side-lobe contamination. Z-spectra simulated with short square-shaped pulses had large alternations in signal due to side lobes because of the sinc-like profile in frequency space (data not shown). Other saturation pulses with more optimized shaped should be possible but were not tested in this work.

The short-TR pulsed CEST technique requires a sufficient duration to build up the saturation-transfer steady state for amide protons exchanging with the water peak. For the 3D technique proposed here we set the readout to begin at the high frequency end of k-space to allow a sufficient number of saturation pulses to be applied before the phase encoding scheme encoded near the center of k-space. Based on the simulations and the tissue parameters approximately 50 TR intervals are required for the steady state to be reached (Fig. 3c). This will be dependent on T_1w as well as TR. When performing lower resolution acquisitions this may be problematic as the number of phase encodes reduces, and therefore, the number of saturation pulses may not be sufficient to reach steady state within the first one or two frequencies of the Z-spectrum. It should be noted that fewer TR intervals would be required to reach steady state at 3T, due to the decreased T_1w with respect to 7T. Initially, we included an inter-volume delay to reduce the possibility of saturation from one frequency bleeding over into the subsequent volume (saturated at a different frequency). For the work here we found minimal bleed over, even without delay between volumes. The likely reason for this is the placing of the initial 50–60 saturation pulses at the high frequency k-space lines.

Fat/lipid saturation may cause chemical-shift based artifacts such as banding around the brain (24) or through the brain when using EPI-type imaging (47). This generally becomes an issue when performing asymmetry analysis, which is not necessary to get APTR here. However, even the MTRasym(3.5ppm) images seem to be free of any lipid banding effects so such artifacts seem to be absent. We have no certain explanation for this, but it may be due to the overall low power used being insufficient for the lipid saturation (similar to the low MT effect). Other metabolites in principle can give NOEs in the upfield region, the size of which will vary depending on molecular motion and pulse sequence timing. We are currently looking into this.

In the simulations, all T₁ values were conveniently set at 1.7s. This is not expected to affect the results appreciably, because the exchange rates correspond to average life times of about 200 ms for the macromolecular protons and 35 ms for amide protons, both small relative to T₁. In addition, T₂s were estimated and thus not precise. However, this rate affects mainly the saturation efficiency (Zhou 2004 theory paper) and is generally negligible (neglected in Eq. [1] too).

The pulsed CEST sequence should also be suitable for lower field strengths such as 3 Tesla, where body coil excitation is used. We confirmed this experimentally (results not shown).

The direct saturation line shape of the Z-spectrum was fit using a Lorentzian function, but other interpolation options are possible, such as a spline (1) or high-order polynomial (13). The Lorentzian was chosen because it properly describes the DS curve during steady state (15) and uses physically intuitive parameters. A more exact representation would require fitting of the whole Z-spectrum to the Bloch equations (e.g., Refs. 9,14,20) based on three pools (bulk water, macromolecular and amide). In normal brain tissue it may be possible to estimate the pool parameters, but this would likely be more difficult in the presence of pathology (e.g,. tumor, stroke, lesions).

Conclusions

We showed that a pulsed saturation, steady-state 3D whole brain CEST experiment is feasible on a high field (7 Tesla) imaging system. The pulse amplitude and duration were optimized for maximal amide proton transfer and strongly reduced MTC and width of the DS line shape. The narrow DS line could be fitted using Lorentzian line shape analysis, allowing us to quantify the APT effect independent of assumptions about exchangeable protons upfield from water. This technique is expected to be a highly efficient and clinically feasible method to acquire whole brain CEST data for slowly exchanging protons (k_sw < 50–100 Hz)