Conditions Leading to High CO₂ (>5 kPa) in Waterlogged–Flooded Soils and Possible Effects on Root Growth and Metabolism

Abstract

• Aims Soil waterlogging impedes gas exchange with the atmosphere, resulting in low P_O2 and often high P_CO2. Conditions conducive to development of high P_CO2 (5–70 kPa) during soil waterlogging and flooding are discussed. The scant information on responses of roots to high P_CO2 in terms of growth and metabolism is reviewed.

• Scope P_CO2 at 15–70 kPa has been reported for flooded paddy-field soils; however, even 15 kPa P_CO2 may not always be reached, e.g. when soil pH is above 7. Increases of P_CO2 in soils following waterlogging will develop much more slowly than decreases in P_O2; in soil from rice paddies in pots without plants, maxima in P_CO2 were reached after 2–3 weeks. There are no reliable data on P_CO2 in roots when in waterlogged or flooded soils. In rhizomes and internodes, P_CO2 sometimes reached 10 kPa, inferring even higher partial pressures in the roots, as a CO₂ diffusion gradient will exist from the roots to the rhizomes and shoots. Preliminary modelling predicts that when P_CO2 is higher in a soil than in roots, P_CO2 in the roots would remain well below the P_CO2 in the soil, particularly when there is ventilation via a well-developed gas-space continuum from the roots to the atmosphere. The few available results on the effects of P_CO2 at > 5 kPa on growth have nearly all involved sudden increases to 10–100 kPa P_CO2; consequently, the results cannot be extrapolated with certainty to the much more gradual increases of P_CO2 in waterlogged soils. Nevertheless, rice in an anaerobic nutrient solution was tolerant to 50 kPa CO₂ being suddenly imposed. By contrast, P_CO2 at 25 kPa retarded germination of some maize genotypes by 50 %. With regard to metabolism, assuming that the usual pH of the cytoplasm of 7·5 was maintained, every increase of 10 kPa CO₂ would result in an increase of 75–90 mm HCO₃⁻ in the cytoplasm. pH maintenance would depend on the biochemical and biophysical pH stats (i.e. regulatory systems). Furthermore, there are indications that metabolism is adversely affected when HCO₃⁻ in the cytoplasm rises above 50 mm, or even lower; succinic dehydrogenase and cytochrome oxidase are inhibited by HCO₃⁻ as low as 10 mm. Such effects could be mitigated by a decrease in the set point for the pH of the cytoplasm, thus lowering levels of HCO₃⁻ at the prevailing P_CO2 in the roots.

• Conclusions Measurements are needed on P_CO2 in a range of soil types and in roots of diverse species, during waterlogging and flooding. Species well adapted to high P_CO2 in the root zone, such as rice and other wetland plants, thrive even when P_CO2 is well over 10 kPa; mechanisms of adaptation, or acclimatization, by these species need exploration.

‘What is known about this?’ said the King.

‘Very little’ said Alice.

‘That is very important’ said the King.

(paraphrased from Alice's Adventures in Wonderland by Lewis Carroll)

INTRODUCTION

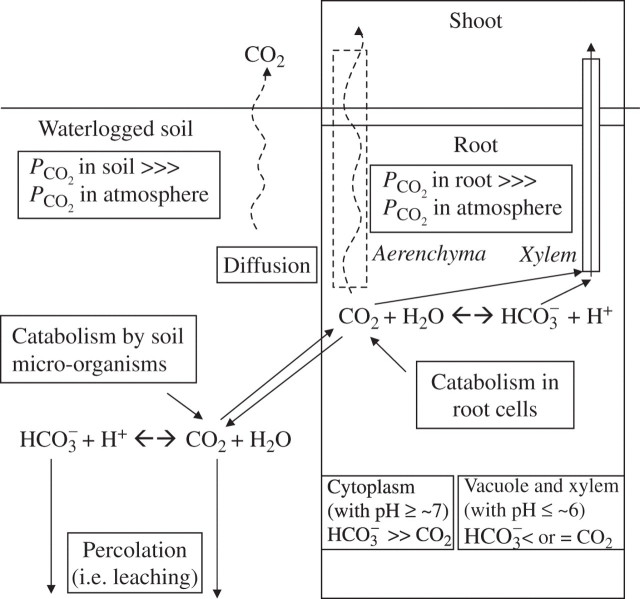
Owing to the 10⁴ times slower gas diffusion in water than in air, waterlogged soils are usually anoxic and by inference the slow gas diffusion will lead to accumulation of large amounts of dissolved inorganic carbon (Fig. 1; Armstrong, 1979; Jackson and Drew, 1984). Consequently, many waterlogged soils are likely to increase in P_CO2 to maxima between 10 and 40 kPa (equilibrium pressure; see Appendix 1 for abbreviations and definitions of terms used within the text) and sometimes higher, but these maxima would be reached much slower than the concurrent decrease in P_O2 of the soil, owing to the combination of a ∼34-fold higher solubility of CO₂ than of O₂ in aqueous media (Armstrong, 1979) and the conversion of a substantial proportion of CO₂ to HCO₃⁻, which will be particularly prominent at higher soil pH (Fig. 2). Hence, the present theme is clearly relevant to long-term flooding in marshes and wetlands, as well as in rice paddies; nevertheless, substantial P_CO2 may also be reached in some types of soil during transient waterlogging lasting longer than several days.

Fig. 1.

High partial pressures of CO₂ occur in many waterlogged and flooded soils, particularly when pH < 7·0. Lack of ventilation leads to build up of high concentrations of dissolved inorganic carbon derived from catabolism by micro-organisms in the soil and by plant roots. CO₂ and HCO₃⁻ levels in the roots will depend on the equilibrium between the input of CO₂ and pathways which remove inorganic carbon to the shoots, i.e. diffusion in the gas phase of the roots and in some species by convective gas flow through rhizomes, as well as CO₂ and HCO₃⁻ in the xylem stream. In species with rapid ventilation, and in a soil P_CO2 of 40 kPa, P_CO2 in roots is assessed at 13–26 kPa (see section in text on P_CO2 in roots and rhizomes, and Table 3). Percolation may also remove dissolved inorganic carbon, at least in puddled rice soils and then would contribute substantially to mitigation of rises in soil P_CO2. In some cases CO₂ removal by diffusion to the atmosphere may become substantial, e.g. when P_CO2 is 40 kPa and the rate of soil production is relatively low (e.g. 15 × 10–12 mol cm^–3 s^–1) (Appendix 2c and main text). CO₂ may also be converted to CH₄ (not shown), depending on soil redox (see text). Assumed is a pK_a of 6·3 in the soil water. If pH of soil <6·3; then HCO₃⁻ < CO₂ and increases in P_CO2 will be relatively rapid. If pH of soil >6·3 than HCO₃⁻ > CO₂ and increases in P_CO2 will be relatively slow.

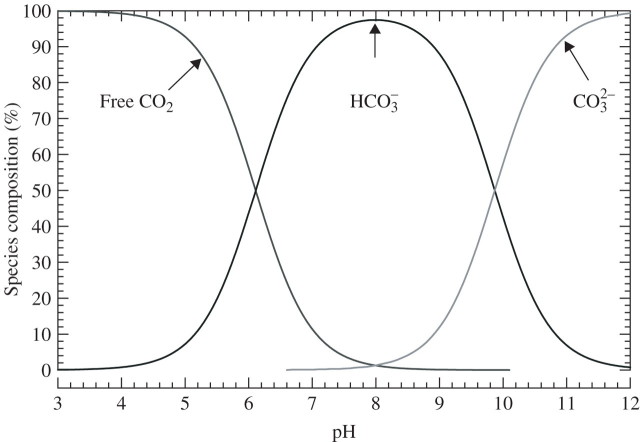
Fig. 2.

Carbonate speciation for total carbonate in a closed system, as influenced by pH. Note that at pH < 4, 100 % of the total dissolved inorganic carbon is H₂CO₃ (CO₂ + H₂O), at pH 8·0 HCO₃⁻ is at maximum and at high pH (i.e. >12) CO₃^2– is at maximum. (courtesy of Dr John R Chipperfield, Emeritus Reader in Inorganic Chemistry, Department of Chemistry, University of Hull, Kingston upon Hull, UK). Based on the Henderson–Hasselbalch equation (Segel, 1976): pH = pK_a + log(HCO₃⁻/CO₂). pK_a assumed for the calculation = 6·11, and pK_a2 = 9·87. The locations of the curves relative to the pH scale will depend on the ionic strength of the solution (Yokota and Kitaoka, 1985). The example shown is for the assessed ionic strength of 0.1 m in the cytoplasm (Appendix 2a). The pK_a may become ∼6·3 at the low ionic strength in some soil solutions and floodwaters. In an open system, the species distributions would vary as shown, but, of course, there may be increases in dissolved inorganic carbon, so that the molar concentration of CO₂ can be relatively high even when pH is above ∼7·0.

In waterlogged soils, the cortical gas-space continuum in plants provides the principal pathway for O₂ flow from the air to the roots, while in many cases zones receiving sufficient O₂ for oxidative phosphorylation are adjacent to anoxic zones (Jackson and Armstrong, 1999; Gibbs and Greenway, 2003). O₂ movement and anaerobic metabolism have been reviewed elsewhere (for aeration: Jackson and Armstrong, 1999; Armstrong and Drew, 2002; Colmer and Greenway, 2005; for anaerobic metabolism: Armstrong and Drew, 2002; Gibbs and Greenway, 2003; Greenway and Gibbs, 2003; Jackson and Ricard, 2003). The present review evaluates the occurrence of high CO₂ in waterlogged soils and the consequences for growth and metabolism of roots in such soils; as well as possible acclimatizions and adaptations to P_CO2 in the range of 5–50 kPa, which have been measured in several flooded soils (Boru et al., 2003; IRRI, 2005).

Surprisingly, plant responses to high P_CO2 in waterlogged-flooded soils have hardly been studied. As a gross observation, wetland plants clearly thrive during flooding. For example, paddy rice in a field at IRRI (Philippines), with water depths maintained between 50 and 100 mm above the soil surface until 7 d before maturity, yielded up to 9·3 t ha^–1 (Ying et al., 1998); this soil had a pH of 6·6 and 1·4 % organic matter and, as will be described shortly, would presumably have been at high P_CO2, at least when rice was in its tillering stage.

A preliminary model, presented in this review, predicts that, even at 40 kPa CO₂ in the soil, P_CO2 in the roots would not often rise above 13–26 kPa. Nevertheless, even in plant organs surrounded by air some tissues may reach high P_CO2 owing to restricted ventilation, as found in the xylem of stems of several tree species. Maximum values are particularly relevant to our theme, as these indicate what P_CO2 the cells surrounding the xylem have to tolerate. These maximum values for CO₂ in the xylem depend on the species; the range for maxima in different species was found to be 4–26 kPa CO₂ (McGuire and Teskey, 2004). High P_CO2 can also occur in some seed pods; in chickpea, CO₂ during part of the day was zero, but 7–11 kPa CO₂ was reached during the night (Ma et al., 2001). These data indicate that some germinating seeds might be tolerant to high P_CO2 during flooding, because they require tolerance to high P_CO2 during their formation.

Mechanisms by which wetland plants acclimatize to high P_CO2 in the root zone have not been elucidated, and it is not clear to what extent there are adverse effects on non-wetland plants. Nevertheless, we can speculate on the consequences of the acid load exerted by high P_CO2. Taking for the quasi steady state an example of a moderate P_CO2 of 10 kPa, either HCO₃⁻ in the cytoplasm would be 75–90 mm (Table 1b), running the risk of adverse effects on metabolism, or the cytoplasm would have to be below the usual value of pH 7·5 (Table 1b). By analogy, a new set point for pH of the cytoplasm (pH_cyt) has been suggested for energy-deficient cells (Felle, 1996, 2005; Greenway and Gibbs, 2003). Under anoxia, pH_cyt usually decreases to between 6·9 and 7·1, even in anoxia-tolerant tissues (Greenway and Gibbs, 2003); the known exception is Potamogeton pectinatus in which pH_cyt only decreased to 7·3 upon imposition of anoxia (Summers et al., 2000). So, in most species, the HCO₃⁻ concentrations in the cytoplasm, at a given P_CO2, should be 2·5–4 times less for anoxic than for aerobic cells. In wetland species, with root systems containing large volumes of aerenchyma, the vast majority of cells would be expected to receive adequate O₂ for oxidative phosphorylation (Armstrong and Drew, 2002; Colmer and Greenway, 2005), so whether these cells would also have a lower set point for pH_cyt than when the roots are in an aerobic soil/medium is an intriguing question.

Table 1.

Information on CO₂ and HCO₃⁻ in aqueous solution The table gives values at a P _CO2 of 10 kPa; a pressure at the lower end of the range of P _CO2 to be expected in waterlogged–flooded soils and the root tissues in these soils. Detail on the derivations is given in Appendix 2a. The influences on pK_a of ionic strength and temperature are from Yokota and Kitaoka (1985)

a. CO2 concentrations in equilibrium with 10 kPa CO2 in the gas phase, and pKa of the CO2–HCO3− equilibrium
	Temperature (°C)
	15	20	25	30
CO2 (mm)	4·4	3·8	3·3	2·9
pKa	6·19	6·14	6·12	6·10

b. HCO3− in cytoplasm and vacuole (mm), calculated using the Henderson–Hasselbalch equation (see caption to Fig. 2)
Compartment	pH	Temperature (°C)
		15	20	25	30
Cytoplasm	7·5	90	86	80	73
	7·3	51	49	44	41
	7·0	28	27	25	23
Vacuole	6·0	2·8	2·7	2·5	2·3
	5·0	0·3	0·3	0·3	0·2

The scarce information on the effects of P_CO2 higher than 5 kPa on metabolism is also reviewed here. Substantial information is available on exposure of fruits to high P_CO2, but the relevance of these data to our theme is tenuous as these responses are confounded by effects of the climacteric.

We conclude that studies on growth and metabolism of roots at high P_CO2 are required for wetland and non-wetland species, both for tissues with sufficient O₂ for oxidative phosphorylation and for anoxic tissues.

P_CO2 IN WATERLOGGED SOILS

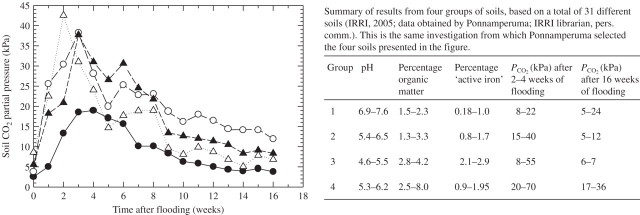
Few P_CO2 values have been measured in waterlogged field soils. In one study, P_CO2 increased from 1 to 30–35 kPa after 2 weeks of flooding (Boru et al., 2003; crop was soybean, pH of soil, temperature and water depth above the soil were not reported). Changes in P_CO2 of soils in pots have been evaluated, with the most comprehensive data set for 31 paddy-field soils without plants (IRRI, 2005; republished data obtained by Ponnamperuma in the 1960s). As expected, rises in P_CO2 were rather gradual, while P_CO2 declined again after 2–4 weeks of flooding (Fig. 3). This study indicated some trends for different groups of soil (table with Fig. 3). Peaks in P_CO2 remained lower when soil pH started on the alkaline side, with maxima between 8–22 kPa in the alkaline soils and 15–40 kPa in mildly acidic soils (group 1 vs. group 2 in table with Fig. 3). There are also indications that during the first weeks of flooding, P_CO2 may reach as high as 55 kPa in some soils that had an initial pH of between 4·6 and 5·5 and 70 kPa in some soils with a high percentage of organic matter (groups 3 and 4, respectively, in table with Fig. 3). P_CO2, in all the types of soils, declined after prolonged flooding, although some soils still contained 24–36 kPa after 16 weeks of flooding (table with Fig. 3). There are also some experimental data from pots with plants. In an experiment with rice, trends in P_CO2 upon flooding were similar to those shown in Fig. 3 (Cho and Ponnamperuma, 1971). Furthermore, the importance of soil pH was demonstrated: liming a sandy loam increased the original pH of 4·8 to 6·2; the average P_CO2 over 2–4 weeks of flooding was ∼40 kPa for the limed soil and ∼60 kPa for the unlimed soil (Cho and Ponnamperuma, 1971; average of the soils at 20 and 30 °C). The data of Cho and Ponnamperuma (1971) were obtained by titrations using methyl orange as an indicator, and so more direct measurements of P_CO2 are required. In an experiment with wheat, the P_CO2 in soil following waterlogging to the soil surface rose over 6 d from 2 to 10 kPa; after another 4 d it had risen to 14 kPa – temperature was 14 °C, organic matter was 3·3 % and initial pH was 6·3 (Trought and Drew, 1980a; P_CO2 measurement using a sample of soil solution and measuring the equilibrium CO₂ in the gas head-space by gas chromatography). Rises in P_CO2 after the start of waterlogging were much more gradual than the decreases in P_O2; P_O2 commonly decreases from ∼ 21 to 0 kPa within 1–1·5 d after the start of waterlogging (Trought and Drew, 1980a). A fast decline in soil P_O2 after the onset of waterlogging is consistent with calculations showing that sealing the surface would deplete the O₂ present in a (previously) well-aerated soil within 2 d (Payne and Gregory, 1988).

Fig. 3.

P_CO2 in flooded rice soils in pots without plants (Ponnamperuma, 1984), temperature unknown. P_CO2 was calculated based on the Henderson–Hasselbalch equation; the data were obtained by sampling the soil solution and assessing HCO₃⁻ concentration using titration with methyl orange (pH range 3.0–5.0), and the pK_a from the ionic strength in the soil solution. Such procedures may be in error if the soil solution contains weak acids other than CO₂ (IRRI, 2005). It is not clear if, and in what way, the P_CO2 values were corrected for the presence of organic acids; we have therefore not included in the table the few extremely high values measured for some soils. The value of 8 kPa in one of the soils before it was flooded (time 0) implies the soil had a very low gas-filled porosity under the experimental conditions.

The increase in P_CO2 in waterlogged soils (as shown for flooded soils in Fig. 3) would be associated with CO₂ evolution during catabolism by micro-organisms, mediated by organic electron acceptors, as in alcoholic fermentation (Kirk, 2004). Additional CO₂ evolution would be derived from conversion of end products of anaerobic catabolism to CO₂, mediated by inorganic electron acceptors, sequentially NO₃⁻, Mn(III/IV) and then, as a principal acceptor, Fe(III) (Kirk, 2004). Usually, the CO₂ production by the soil slows with time of flooding, and CO₂ production is outstripped by factors decreasing P_CO2, as shown after 2–4 weeks of flooding in Fig. 3.

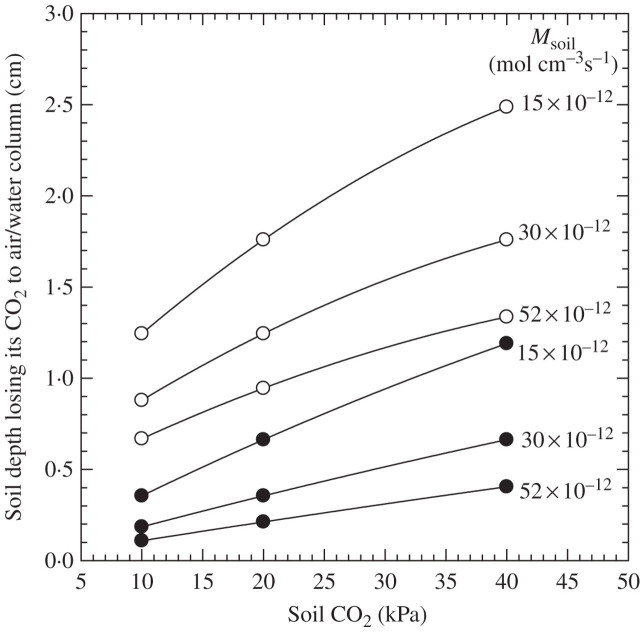
One cause of CO₂ removal would be loss to the atmosphere. The soil depth from which CO₂ production is lost to the atmosphere would be greater the lower the CO₂ production by the soil and the higher the P_CO2 in the soil (Fig. 4). The percentage production lost from the soil profile can be derived by dividing the depths shown in Fig. 4 by the depth of the soil profile producing CO₂. Taking a soil depth of 200 mm, as in rice paddies, then at 40 kPa in the soil the losses would be 12·5 and 6·5 % for CO₂ production rates of 15 and 52 × 10⁻¹² mol cm^–3 s^–1, respectively; at 10 kPa these losses would be only 6·2 and 3·5 %, respectively. Removals would be lessened for flooded soils. For example, CO₂ removals would be reduced by at least half in rice paddies, with say 100 mm stagnant water on the soil surface. Reductions would be larger the higher the rate of CO₂ production by the soil and at 10 vs. 40 kPa CO₂ in the soil (Fig. 4). As an example, for a P_CO2 in the soil of 10 kPa, and a production rate of 52 × 10⁻¹² mol cm^–3 s^–1, losses from a 200-mm soil layer would become trivial, i.e. ∼0·5 % of the rate of production. These estimates are based on a D_soil = 0·2D₀, D_soil is the effective CO₂ diffusion coefficient in the soil and D₀ is the CO₂ diffusion coefficient in solution. Given that the thickness of the soil layer from which the CO₂ is lost to the atmosphere varies with the square root of D_soil, losses from a soil with a D_soil of 0·33, a usual figure for a rice paddy, would be 1·3 times greater than given above.

Fig. 4.

Soil depth losing CO₂ to the atmosphere as related to soil production rates and CO₂ pressures in the soil, for soils saturated to the surface (open circles) or with 100 mm of stagnant water on the soil surface (filled circles). Predictions were based on the protocols in Appendix 2c. M_soil = metabolic rate of soil organisms = CO₂ production rate in soil. The percentage of CO₂ production in the soil lost to the atmosphere by diffusion would be the depth of the layer from which CO₂ is lost, divided by the depth of the soil profile producing CO₂.

In addition to atmospheric losses, other important factors causing CO₂ in the soil to decline would be precipitation of inorganic carbon as complexes of Fe (Kirk, 2004) and, in soils acidic at the start of flooding, increases in soil pH. The pH of the solution of rice paddy soils after 2 weeks of flooding usually ranges between 6·5 and 7·0, although there were cases reported when pH remained as low as 5·0 or as high as 8·0 (Ponnamperuma, 1984), so that CO₂/HCO₃⁻ ratios would have been 25 and 0·02, respectively. Soils that are acidic at the start of waterlogging are likely to develop high P_CO2 upon waterlogging faster than more alkaline soils (table with Fig. 3). In a survey of soils from paddy fields in Asia, the mean soil pH was ≤ 5·5 in five of 11 countries (De Datta, 1981). Soils with a pH 5·5 or lower, including acid sulfate soils which occur in the deltas of south-east Asia (De Datta, 1981), would be particularly prone to develop high P_CO2, particularly as some acid soils still had a pH of between 4·5 and 6·2 at 2 weeks after the start of flooding (Ponnamperuma, 1984). Furthermore, as discussed further below, CO₂ exposure of rice roots growing in acidic soils would be increased due to biogeochemical reactions following radial loss of O₂ from the roots to the soil, resulting in a lower pH in the rhizosphere and hence higher CO₂ concentrations relative to the bulk soil. Thus, inorganic carbon accumulation as a result of flooding would intensify any acid load imposed by the acidity of these soils.

The time sequences for changes in P_CO2 in the rice paddy soils shown in Fig. 3 can be compared with the known CO₂ production rates in 16 anaerobic rice soils in a laboratory experiment at 30 °C (Yao et al., 1999). We deduce that the lowest CO₂ production rates over the first 14 d of waterlogging would be 1·6 µmol g^–1 d. wt soil d^–1 and these rates would result in an increase in P_CO2 of 4·0 kPa d^–1, with about double that value for the mean production rate of the 16 soils (for procedures see Appendix 3b). By comparison, the observed increases were, on average, 1·6 kPa d^–1 for the four rice paddy soils studied by Ponnamperuma (1984) with a range of 0·7–2·5 kPa (Fig. 3). This discrepancy may to some extent be due to the assumption of a soil porosity of 50 % (in Appendix 3b), while some paddy soils had total porosities of 61–62 % (Painuli et al., 1988) and heavy textured soils may change into a gel-like structure upon puddling and then increase in total porosity (Greenland, 1981); values of 60–70 % are typical for these soils (G. J. D. Kirk, pers. comm.). A total porosity of 70 rather than 50 % would reduce the assessed increase in P_CO2 of 4·0 kPa d^–1 to 2·9 kPa d^–1. The remaining substantial discrepancy between the data on CO₂ production and the observed increases in P_CO2 of soils can be resolved only in comprehensive experiments designed to assess CO₂ production rates, pH changes during waterlogging, total porosity of the particular soils, as well as monitoring any losses of CO₂ from the soil.

The key data on soil P_CO2 of Ponnamperuma (Fig. 3 and its table) were only for fallow soils, so it is crucial to obtain data for soils in the field carrying stands of rice. Roots would make a substantial contribution to the changes with time in P_CO2 of the soil, in the early phase after the start of flooding CO₂ production may contribute to the rate of rise in dissolved inorganic carbon in soils. Of equal importance, in the quasi steady state, the gas-space continua in the plants might vent, to the atmosphere, considerable amounts of CO₂ that enter from the soil, in addition to the CO₂ produced by the root's catabolism. Some indication for the importance of this venting can be gained from data on CH₄ emissions: in a field ‘covered with rice’, cutting the rice stems below the water surface showed that up to 94 % of the methane emissions from the soil–root system was via the gas-space continua from roots to shoots (Holzapfel-Pschorn et al., 1986). In this quasi steady state, soil P_CO2 will be determined by both the CO₂ production by the soil and ventilation via the root system. That ventilation via plants depends on the density of roots of the stand was indicated by the very similar CH₄ emission rates between soil with paddy rice and bare soil during the first 7 weeks after transplanting, when there would not yet be a dense stand (Holzapfel-Pschorn et al., 1986). Even when the bulk soil has reached a P_CO2 of 40 kPa, the amounts of CO₂ removed via the air space continuum would tend to be less than 10 % the CO₂ production, as long as the density of roots is low (for details see next section).

The need for comprehensive data on P_CO2 in waterlogged soils is amplified by further factors affecting P_CO2, which make extrapolation of the data by Ponnamperuma (1984) to field soils quite uncertain. First, CO₂ production is strongly dependent on organic matter (Rowell, 1988). Secondly, in rice soils, there is often some percolation, reaching 5–10 mm d^–1, which would remove part of the produced CO₂ (Rowell, 1988). Other percolation rates were 1–8 mm d^–1 in montmorrilonitic clay at IRRI, Los Banos, as affected by different degrees of puddling and amounts of water use during puddling (Painuli et al., 1988) and 0·5–4·5 mm d^–1 for six paddy soils in the Philippines (Kirk, 2004). That removal of dissolved inorganic carbon by percolation may be a major factor in limiting increases in P_CO2 in the root zone is assessed for a 200-mm soil layer in a puddled rice field, by assuming that the soil is fallow, is at 30 °C and that percolation, at 5 mm d^–1, would be the only cause of CO₂ removal. Using the calculation given in Appendix 2c, assuming a pK_a of 6·3 in the Henderson–Hasselbalch equation (caption to Fig. 2), it is assessed that a soil at 40 kPa CO₂ would lose by percolation 8, 12 and 24 × 10⁻¹² mol cm^–3 s^–1 at pH 6·5, 6·75 and 7·0, respectively, i.e. removal would exceed or at least be a substantial proportion of the CO₂ production rates of 15–50 × 10⁻¹² mol cm^–3 s^–1 assumed below in Table 3. The leaching would also slow down the increases in P_CO2 with time and be more important at lower temperatures because of the higher solubility of CO₂ (Table 1a). In contrast to observations for methane, ebullition would make only a small contribution to CO₂ removal, because CO₂ is ∼ 20 times less volatile than methane (Kirk, 2004). Thirdly, CO₂ may be converted to CH₄, with the redox potential for the equilibrium at −125 mV for a soil with pH of 5·0, and at −245 mV for a soil with pH of 7·0 (Rowell, 1988). In rice paddy soils in the quasi steady state, the ratio between production of CO₂ and CH₄ ranged between 0·28 and 0·93 (Yao et al., 1999). Nevertheless, even gas bubbles from marshland in the USA with 20–70 kPa CH₄ still contained 5·5–10 kPa CO₂ (Shannon et al., 1996), indicating that the bulk soil had about the same P_CO2.

P_CO2 IN ROOTS AND RHIZOMES

When the rhizosphere is high in dissolved inorganic carbon, its uptake into root cells will be dominated by the high permeability of plant membranes to CO₂, as CO₂ is a weak acid and plant cells rapidly take up many weak acids in the undissociated form (Guern et al., 1991; for CO₂ see Heber et al., 1994). The presence of an undissociated acid in the medium is called an ‘acid load’ (Bown, 1985; Guern et al., 1991), as the dissociation of weak acids in the cell will tend to acidify the cytoplasm. Intensity of the ‘acid load’ imposed by exogenous total dissolved inorganic carbon in the soil solution will depend on the pH of the soil solution, as pH determines the HCO₃–CO₂ equilibrium (Fig. 2). This crucial point was demonstrated using carnation (Dianthus caryophyllus) callus cells; O₂ uptake was stimulated two-fold by adding pure CO₂ to a solution buffered at a pH of 5·7, resulting in a P_CO2 of 5·5 kPa (Palet et al., 1991). Similarly, addition of HCO₃⁻+K⁺ increased O₂ uptake, but this stimulation decreased with increasing pH_ext and became negligible when pH_ext was 7·8, when the CO₂/HCO₃⁻ ratio would be 0·03 (Palet et al., 1991). However, to conclude from these results that the effects on metabolism were due to CO₂, rather than to HCO₃⁻ (Drake et al., 1997), is misleading. Whether the metabolic consequences of high P_CO2 are due to the ensuing high concentrations of endogenous CO₂ or to the inevitable rises in HCO₃⁻ in the cytoplasm needs further experimentation.

The only data on P_CO2 in roots of plants in waterlogged soils have been published for whole root systems of Quercus nigra (water oak) and Fraxinus pennsylvanica (green ash), at 9 months after flooding to 100 mm water depth. The highest value was 10 kPa CO₂ for green ash (Good and Patrick, 1987). However, this value would be an over estimate because inorganic carbon was extracted in a solution with a pH of 2·5; taking this into account, our estimates of P_CO2 in these root systems, based on the data provided by Good and Patrick (1987), are between 2·8 and 5·4 kPa (for details see Appendix 4a). Obtaining reliable data on P_CO2 in roots of plants in waterlogged soils is a high priority for future research.

Measurements of P_CO2 in gas sampled from lacunae of rhizomes, petioles and culms of partially submerged wetland species have shown that P_CO2 in these organs is at least several kPa (Table 2). Stem internodes near the soil surface of rice growing in 0·8 m of water reached 4–10 kPa CO₂ (Table 2). Most of this CO₂ had presumably emanated via diffusion from the roots; the only other possible source was from catabolism within the stem, as the floodwater was ruled out given that the P_CO2 of the floodwater was 1·5–3 kPa when P_CO2 in the internodes was 8–10 kPa (Setter et al., 1987). In this system, P_CO2 in the soil will be high, so that there will be a diffusion gradient between the roots and the internodes, i.e. roots would be substantially higher in P_CO2 than the internodes. Rice has no substantial convective flow (Beckett et al., 1988), so the venting of CO₂ to the atmosphere via the internodes and shoots would be dependent on diffusion. Regardless, even in species with convective gas flow through their rhizomes, high P_CO2 values have been observed (i.e. despite the potential of rapid ventilation); in one case P_CO2 reached 10 kPa (Table 2). In the floating-leaved water lily, Nuphar luteum, in 1·2 m of water, 85 % of the CO₂ flowing up the petiole was fixed by photosynthesis (Dacey and Klug, 1982a). Photosynthesis using CO₂ derived from the roots is not further reviewed herein.

Table 2.

Measured values of P _CO2 and P _O2 in rhizomes, or stems, of wetland plants

Species and water depth	Organ	PCO2 (kPa)	PO2 (kPa)	Reference
Phragmites australis; water 20 cm above soil surface. Observations 14 d after installing the needles for sampling, which would have disturbed the steady-state PCO2	Rhizomes, 0–20 cm depth	2·5	15	Brix (1988)
	Rhizomes, 50–80 cm depth	7·2	3
Nuphar (water lily) a floating leaved species; in a lake with 1.5 m of water	Rhizomes, 4–6 cm under sediment	8·2–10·3	8·7–5·6	Dacey (1981)
Nuphar; in pond with 1 m of water	surface	2·1–3·4	10–15.3	Dacey and Klug (1982b)
Deep-water rice in field with 0.8 m water	Stem internodes, near soil surface	4–10	8–12	Setter et al. (1987)

In the absence of reliable data, the value of P_CO2 that may occur in roots of waterlogged plants can be speculated for two cases: (1) when P_CO2 in the soil is higher than in roots, which is probably the case in soils that are waterlogged for longer than ∼7 d; and (2) when P_CO2 in the roots is higher than in the soil, which would occur at least at the start of waterlogging. Before discussing these two cases it is relevant to discuss the possibility that root tissues in the mature zones of many wetland species may be ‘insulated’ from the soil, due to a ‘barrier’ to gas diffusion in the external cell layers, as found for O₂ (Armstrong, 1979; Colmer, 2003a).

Roots with a low permeability to radial gas diffusion in basal zones

Basal zones of roots of many wetland species have a rather tight barrier to radial O₂ loss (Armstrong, 1979; Colmer, 2003a), for example in rice roots at more than 20 mm from the apex (Colmer, 2003b). The key question for our theme is whether this barrier would also have a high resistance to CO₂ diffusion. The layers with very low permeability to radial O₂ loss are presumably associated with suberin in the exodermis. Further information on how solutes and water permeate through these layers, if at all, is scant. There are data on water permeability for rice roots, on isolated outer parts of the roots, which did contain suberin in their exodermis (Ranathunge et al., 2004). However, these data are of doubtful relevance to our theme as these roots were raised in aerated nutrient solution and therefore presumably had no strong barrier to O₂ exchange. More relevant are some data for roots of Phragmites australis, which in their zone of very low permeability to O₂ contained some passage areas (‘windows’) of about 1 mm in diameter, which did show significant radial O₂ loss (Armstrong et al., 2000); such areas are likely to be also entry areas for water uptake. The radial O₂ diffusion to the medium would be opposite to the water flow, and occur via diffusion whereas the water movement occurs via mass flow. Thus, it is reasonable to assume that when CO₂ is higher in the root than in the environment (case 2, discussed below), CO₂ loss to the root environment would, as for O₂, be greatly restricted. By contrast, when CO₂ is higher in the soil than in the root, CO₂ entry into these root sections may be higher than predicted (case 1, discussed below), as fast water flows during the day may conceivably facilitate CO₂ uptake by mass flow, i.e. restrictions to CO₂ influx may be pronounced only at night. Such CO₂ flow would be particularly prominent if water flow was through aquaporins, which may also have a high permeability for CO₂ (Tyerman et al., 2002). On the other hand, if aquaporins have a low permeability to CO₂, the high permeability of the lipid bilayer to CO₂ would be dominant (Tyerman et al., 2002), while the effect of water flow on CO₂ intake would be greatly reduced.

Case 1: P_CO2 higher in the soil than in the root

Values for P_CO2 that may occur in roots in waterlogged soil have been assessed using a preliminary model as described in Appendix 3a, and the predictions are shown in Table 3. These calculations also provide the diameter of the soil core from which CO₂ would flow from the soil into the root. The latter is relevant to ecosystems during long-term flooding, as the wider the core from which CO₂ flows to a root, the more likely it is that cores around several roots will overlap and hence gradually lower the P_CO2 in the soil, owing to ventilation to the atmosphere via the gas-filled channels in the roots.

Table 3.

Predictions for development of root CO₂ partial pressures in waterlogged soils with a bulk soil P_CO2 of 40 kPa as a result of root and soil CO₂ production

Column number	1	2	3	4	5	6	7	8	9	10
Effects of different characteristics	Soil CO2 production rates			Root radius	Root length and initial tip CO2		Root porosity			Temperature
Root radius (cm)	0·06	0·06	0·06	0·03	0·06	0·06	0·06	0·06	0·06	0·06
Root porosity (%)	35	35	35	35	35	35	35	16	4.2	35
Root length (cm)	10	10	10	10	30	30	10	10	10	10
Soil temperature (°C)	30	30	30	30	30	30	30	30	30	15
Soil CO2 production rate (10–12 mol cm–3 s–1)	52	30	15	30	30	30	30	30	30	15
Initial CO2 in root tip (kPa)	10	10	10	10	10	20	10	10	10	10
CO2 input into root from soil (10–12 mol s–1)	97·2	88·5	79·6	58·8	74·9	52·9	88·5	79·8	52·1	90·3
R(si)PCO2 in root required to ventilate influx from soil (kPa)	3·6	3·3	2·9	8·7	8·3	5·9	3·3	6·5	16·1	3·5
Resultant RPCO2 in 10 mm root tip (kPa)	13·6	13·3	12·9	18·7	18·3	25·9	13·3	16·5	26·1	13·5
Radius of soil core from which influx is derived (cm)	0·90	0·97	1·30	0·79	0·89	0·75	0·97	0·92	0·75	1·39

The radius of the soil core from which CO₂ flows into the root is also predicted. These two predictions are shown in the two bottom rows. Bulk soil at 40 kPa CO₂, and effective soil CO₂ diffusivity (D_soil) = 0.2D₀. Effects of D_soil other than 0.2D₀ are shown in Fig. 6. The default data set in column 2 is given in bold type, and changes in parameters from the default values are shown also in bold type for the various other columns. Columns 1–3 show the effects of differences in soil CO₂ production rate [assessed from Yao et al. (1999); see Appendix 3b]; column 4 (cf. column 2), effects of decreased root radius; column 5 (cf. column 2), effects of increased root length; column 6 (cf. column 5), effects of increased root length and initial root tip CO₂ concentration; columns 7–9, effects of root porosity; column 10 (cf. column 2), effects of soil temperature (lower temperature decreasing soil CO₂ production and altering CO₂ diffusivities and solubilities in root and soil). Data are from our own preliminary model (see text and Appendix 3a).

The preliminary model is based on the assumption that CO₂ influx occurs only into the 10-mm root tip; this assumption was made for several reasons. It is the simplest model, and the predictions are particularly relevant for wetland species including rice, which, as argued earlier, might have a layer of low permeability to CO₂ in the mature root zones. Furthermore, the predictions are the most conservative possible, therefore giving the minimum values of P_CO2 likely to occur in roots of plants in waterlogged soils at a given P_CO2 in the soil; these are the best values in a review which argues the unproven notion that roots in waterlogged–flooded soils often contain high CO₂.

In Table 3, we have used an example where D_soil is given by the relationship D_soil/D₀=0·2, where 0·2 is the product of the fractional porosity (ɛ) and a gas-space tortuosity factor (τ < 1). Results with other values of D_soil/D_o are considered after discussing the values presented in Table 3. Another assumption for Table 3 is that P_CO2 in the bulk soil is 40 kPa. This value was chosen because the few data available indicate that this P_CO2 would prevail in several waterlogged–flooded soils, at least for several days, so the plants need at least to survive at this particular level. Three rates of CO₂ production in the soil were chosen, to evaluate the impact of this parameter on the resulting P_CO2 in the root. These rates are based on the rare, but comprehensive, set of data for CO₂ production in the laboratory, for 16 anaerobic rice paddy soils, from China, the Philippines and Italy, at 30 °C (Yao et al., 1999). CO₂ production rates chosen were 15, 30 and 52 × 10⁻¹² mol cm^–3 soil s^–1, as observed between 8 and 10 d after the start of anaerobiosis, when soil below pH 7·0 will be approaching high levels of P_CO2. Subsequently, CO₂ production declined and in the quasi steady state reached 0·38–5·41 × 10⁻¹² mol cm^–3 soil s^–1 (calculated from Yao et al., 1999). It remains unknown whether this decline is due to feedback by the high P_CO2 attained, depletion of readily decomposable organic matter or other causes.

The estimated P_CO2 in the root which would be required to ventilate the CO₂ influx from the soil (^R(si)P_CO2) to the atmosphere should be added to an estimate for P_CO2 associated with ventilation of CO₂ produced by the root's own catabolism (^R(rc)P_CO2), to obtain total P_CO2 in roots (^RP_CO2). The minimum value for ^R(rc)P_CO2 can be assessed by assuming a respiratory quotient of 1·0. If there were no net CO₂ flux between the root and the soil, the P_CO2 gradient in the gas-space continuum would be of the same magnitude as the observed P_O2 gradient, but of course in the opposite direction. Any anaerobic CO₂ evolution, as in ethanolic fermentation, would increase these levels of CO₂.

Overall, the predictions show that the P_CO2 in the root (^RP_CO2) generated by a combination of net influx of CO₂ from the soil (^R(si)P_CO2) and CO₂ produced by the root catabolism (^R(rc)P_CO2) is greatly influenced by the percentage gas-filled porosity of the roots, and to a lesser extent by root diameter and length. Surprisingly little effect arises from three-fold differences in the rate of CO₂ production in the soil. The effects of different effective diffusion coefficients for CO₂ in soil will be discussed after considering cases 1·1 and 1·2.

Case 1·1: predictions for roots of wetland species with high root porosity, when in flooded soil

Most of the cases given are for rice, with the gas-filled porosity in the roots set at 35 %. Furthermore, it was assumed the roots were 100 mm long and their diameter was 0·6 mm, unless stated otherwise. Predictions for various conditions are:

(1) Soil production increases of CO₂ by as much as 3·5-fold only increased the predicted ^RP_CO2 in the 10-mm root tip from 12·9 to 13·6 kPa (Table 3, columns 1–3). By contrast, the diameter of the soil core from which CO₂ flows into the root is 45 % larger at the lower CO₂ production rate in the soil (Table 3, columns 1 and 3).

(2) Smaller root diameters of 0·3 mm would increase ^RP_CO2, for example in the 10-mm tip of a 100-mm-long root to 18·7 kPa compared with 13·3 kPa for a root diameter of 0·6 mm, while decreasing the predicted diameter of the soil core from which CO₂ flows into the root by ∼20 % (Table 3, columns 2 and 4).

(3) Rice roots can reach a length of ∼ 300 mm in flooded fields (Kirk, 2003), for which ^RP_CO2 in the 10-mm root tip would be 18·3 kPa, rather than the 13·3 kPa predicted for a 100-mm-long root (Table 3, columns 5 and 2).

(4) The conclusion in condition (3) was based on the assumption that the CO₂ production rate of 300-mm-long roots would result in an ^R(rc)P_CO2 of only 10 kPa in the 10-mm tip. However, in 300-mm-long roots, the P_O2 in the 10-mm root tip is more likely to be close to zero and hence the ^R(rc)P_CO2 at which CO₂ ventilation in the gas-space continuum balances the CO₂ production in catabolism is assessed at 20 kPa. Then, still assuming the bulk soil P_CO2 is at 40 kPa, the ^RP_CO2 would be 25·9 rather than 18·3 kPa (Table 3, columns 5 and 6), while the ^R(si)P_CO2 (i.e. the component of ^RP_CO2 due to influx from the soil) would drop from 8·3 to 5·9 kPa CO₂ (Table 3, columns 5 and 6), as a result of the smaller concentration gradient between the bulk soil and the root.

(5) Because many wetland species thrive in cool climates, predictions on ^RP_CO2 were also made for 15 vs. 30 °C. For this comparison, the lowest rate of CO₂ production 15 × 10⁻¹² mol cm^–3 soil s^–1 was used for the value of 15 °C, as the rate of CO₂ evolution from soil has a Q₁₀ of ∼2 (Yao and Conrad, 2000; Bouma et al., 1997). The predicted P_CO2 in the 10-mm root tip was nearly identical at 15 and 30 °C (Table 3, column 10 vs. 3): in the soil solution a 20 % lower diffusion coefficient at 15 than at 30 °C is outweighed by the 50 % increase in solubility of CO₂, while diffusion in the gas-space continuum is 10 % slower at 15 than at 30 °C (Armstrong, 1979).

Overall, these predictions for roots of rice and other wetland plants, which have in their mature zones an impermeable barrier to O₂, and hence possibly to CO₂ exchange, indicate that when the bulk soil P_CO2 is 40 kPa, the 10-mm tips of their roots, which have no impermeable barrier to gas exchange, would reach at least 13 kPa and rise to 26 kPa P_CO2 in some cases. Equally importantly, the model predicts that P_CO2 in the roots of these species would remain well below the 40 kPa CO₂ in the soil: the P_CO2 assumed in Table 3 to be in the bulk soil.

Case 1·2: predictions for roots with porosities lower than 35 %, when in flooded soil

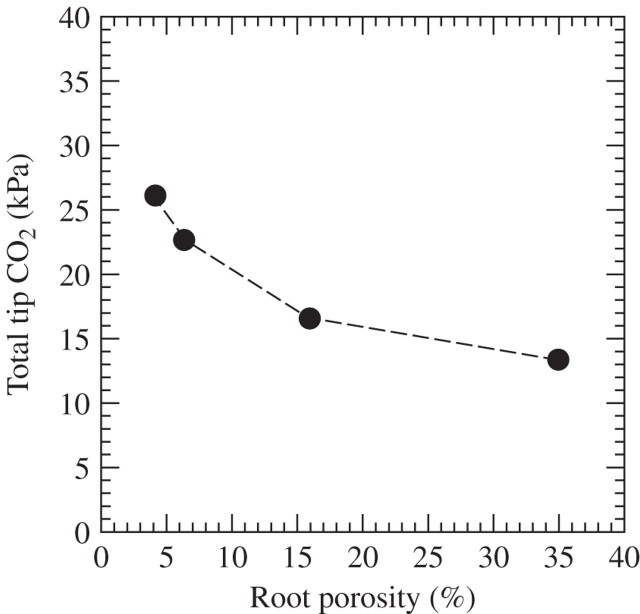
Gas-filled porosities in roots of several species are smaller than in rice (Justin and Armstrong, 1987; Colmer, 2003a). ^RP_CO2 was estimated for 100-mm-long roots and the bulk soil at 40 kPa; porosities of ∼ 15 % would still limit ^RP_CO2 to 16·5 (Fig. 5). At lower porosities, ^RP_CO2 rises rather steeply, although even at the low porosity of 4 %, ^RP_CO2 is still about 14 kPa below the P_CO2 in the bulk soil. These lower porosities would be representative for non-wetland plants in waterlogged soil; for example, maize reaches a root porosity of 16 % (Yu et al., 1969). Importantly, as with other non-wetland species, maize lacks a barrier to O₂ exchange along its roots (Darwent et al., 2003). So, the predicted ^RP_CO2 will be substantially above the 16·5 kPa given for a root porosity of 16 % in Fig. 5, where it is assumed that only the 10-mm tip is permeable to CO₂. These considerations show that roots of non-wetland species are likely to reach substantially higher internal P_CO2 during waterlogging–flooding than those of wetland species. High root porosity leads to larger radii for the soil cores from which CO₂ flows into the root (Table 3, columns 7–9); the amount of CO₂ lost from the soil would be 1·7 times higher at a root porosity of 35 % than at 4·2 %.

Fig. 5.

Relationship between root porosity and ^RP_CO2, when the bulk soil is at 40 kPa P_CO2. Predictions were derived using the protocols in Appendix 3a. Conditions assumed are: CO₂ production by the soil of 30 × 10⁻¹² mol cm^–3 s^–1, P_CO2 in the root required to ventilate CO₂ production in the root of 10 kPa, root radius of 0·6 mm, root length of 100 mm and soil temperature of 30 °C. Other conditions are as in Table 3. Note that the P_CO2 in the root due to influx from the soil would be the values shown minus 10 kPa.

In conclusion, when P_CO2 in the soil is higher than in the roots, P_CO2 in the roots can be surprisingly much lower than in the soil: depending on the P_CO2 in the bulk soil and plant characteristics such as percentage gas-filled porosity, root length and resistance to CO₂ movement across the external cell layers of roots, the estimated P_CO2 in the roots ranged between 13 and 26 kPa. Variations in CO₂ production rates in the soil have little effect on P_CO2 in the roots, as these are compensated for by changes in the soil volume from which CO₂ flows into the roots (Table 3, columns 1–3). Nevertheless, soil CO₂ production rates remain relevant to the ecosystem of flooded fields because (1) at the start of waterlogging high rates of CO₂ production will lead to rapid increases in P_CO2 of the soil, and hence in roots, and (2) in the longer term the radius of the soil core from which CO₂ enters roots would determine the impact that vegetation has on soil P_CO2; soils with low rates of CO₂ production and therefore a larger radius of soil core from which CO₂ enters roots (Table 3, columns 1–3) might, when root density becomes high, intensify any gradual removal of CO₂ produced in the soil via gas-space continua in the roots to the atmosphere. Let us assume that in a stand of rice, young, 100-mm-long roots would be 26 mm apart. This figure is chosen because at 40 kPa CO₂ in the soil and a production rate of 15 × 10⁻¹² mol cm^–3 s^–1 the cores from which CO₂ flows into the root would be just touching. At this root density, the removal of CO₂ to the atmosphere from a 200-mm soil layer with a P_CO2 of 40 kPa would be 1·1 and 4 % of the CO₂ produced at rates of 50 and 15 × 10⁻¹² mol cm^–3 s^–1, respectively (protocols given in Appendix 2d). Such losses will be much lower if the P_CO2 in the bulk soil has reached only 20 kPa, always assuming the same root density; for example, at 15 × 10⁻¹² mol cm^–3 s^–1 the removal via the gas space continua would only be 1·6 % of the rate of production (assessed using the protocols given in Appendix 3a). These calculations are based on a simplified case; in reality, CO₂ would also enter via lateral roots and the removal as a percentage of that produced by the soil would tend to increase. Nevertheless, this increase would be mitigated by the decrease in CO₂ concentration gradient between the tip and the atmosphere, associated with the entry of CO₂ into root sections closer to the surface.

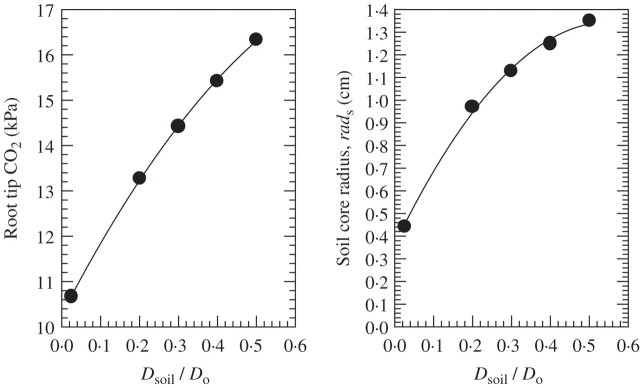
Effect of soil porosity (ɛ) and tortuosity (τ). There is, at present, insufficient information on the effective diffusion coefficient for CO₂ in waterlogged soils. Different values of the effective diffusion coefficient (D_soil) than the 0·2 taken in the calculations presented in Table 3 would give substantial changes in ^R(si)P_CO2, as affected by the various characteristics of the soil and root systems; nevertheless, these changes would be only in degree, not in kind. Total porosities (ɛ) range between 40 % for sands and 50 % for clays (Ahuja et al., 1999), while in some puddled rice soils ɛ can be as high as 60–70 % (Kirk, 2004). Assuming these materials are not ‘cemented’, the tortuosity factor (τ) would be ∼ 0·66 (Penman, 1940), and similar values of 0·5–0·7 were found for the impedance factor in rice soils based on diffusion of ³⁶Cl⁻ (Kirk et al., 2003; the impedance factor is close to the tortuosity factor, τ). Tortuosity will increase (i.e. τ will decrease) with decreasing soil porosity (ɛ) (Kirk et al., 2003). D_soil is derived by multiplying the product of τ and ɛ with D₀, from the diffusion coefficient in aqueous solution. The product of τ and ɛ (i.e. D_soil/D₀) is 0·28 for sands, 0·33 for clays and 0·3–0·5 for the puddled rice soils. Taking the mean value of D_soil/D₀ for the puddled rice soils of ∼0·4, ^R(si)P_CO2 would be 57 % higher than at a D_soil/D₀ of 0·2, and the radius of the soil core from which CO₂ flows into the root would increase by ∼25 % (Fig. 6); nevertheless, ^RP_CO2 would increase only from 13·3 to 15·4 kPa. By contrast, at least for the drained state, Currie (1965) has shown that crumbs (aggregates) in clays are in a ‘consolidated-cemented’ state and that these crumbs have a mean D_soil/D₀ of ∼0·1 (range 0·025–0·156). If these crumbs persisted following waterlogging, the pathway of CO₂ diffusion may be mainly through these crumbs to root surfaces, which line these crumbs. If the D_soil/D₀ was 0·1, rather than 0·2, there would be a reduction of 42 % for ^R(si)P_CO2 (calculated according to Appendix 3a), while the reduction in ^RP_CO2 would be only 10 %, with a 30 % smaller radius of the soil core from which CO₂ flows into the root (Fig. 6).

Fig. 6.

Plots for root tip CO₂ (^RP_CO2 in kPa) and soil core radius (rad_s) from which CO₂ enters roots in waterlogged soil as predicted using the model presented in Appendix 3a, for a range of values of D_soil/D₀, and the following conditions: root length = 100 mm, site of entry into the root only the 10-mm root tip, CO₂ production rate = 30 × 10⁻¹² mol cm^–3 soil s^–1, root fractionial porosity = 0·35. This is the combination of soil and plant characteristics shown in column 2 of Table 3. The substantial effects of D_soil/D₀ (i.e. the product of soil porosity and tortuosity) on ^RP_CO2 at the combination of soil and plant characteristics used would also apply to other combinations of characteristics of the soil–plant system (shown in Table 3); the magnitude of the effects on ^RP_CO2 will differ in degree, but not in kind.

Role of HCO₃⁻ diffusion in the soil on CO₂ entry into roots. This theme will only be considered qualitatively, as more precise analysis will require detailed modelling of the complex interplay between HCO₃⁻ and CO₂ diffusion. Possible relevance of HCO₃⁻ diffusion depends upon both the soil and the rhizosphere pH. Assuming first that pH is uniform between the bulk soil and rhizosphere, then any HCO₃⁻ diffusion would not alter the picture derived by considering CO₂ diffusion alone, as the rate constant of the uncatalysed rate of CO₂ hydration is 0·037 s^–1 (Raven and Newman, 1994), i.e. much faster than the rate of diffusion prevailing in the soil. However, radial O₂ loss, as occurs from root tips and laterals in many wetland plants (Armstrong, 1979; Colmer, 2003a), would complicate the picture. Radial O₂ loss will tend to lower the pH of the rhizosphere, by oxidation of Fe²⁺ to Fe³⁺, which will precipitate, and by NH₄⁺ removal, either by its uptake or by nitrification with subsequent uptake of NO₃⁻ by the roots (Begg et al., 1994; Kirk, 2004). Both oxidation of Fe²⁺ to insoluble Fe(III) and NH₄⁺ removal will reduce the cation concentration in the rhizosphere and hence lower pH (Gerendas and Schurr, 1999). The Henderson–Hasselbalch equation shows that under such conditions, P_CO2 would be higher in the rhizosphere than in the bulk soil, while a gradient in HCO₃⁻ towards the root surface would be equal in magnitude to the CO₂ gradient from rhizosphere to bulk soil, i.e. CO₂ will tend to diffuse from the rhizosphere to the bulk soil, while HCO₃⁻ would flow towards the root (Begg et al., 1994). (Note that, for convenience, this deduction has assumed an absence of CO₂ uptake by the root.) Thus, the boundary conditions postulated for the model in Appendix 3a would no longer apply. Here we consider only the extreme case where the presented model would give grave errors. In Iloilo sand with rice plants, the pH at 3 d after the start of waterlogging was 5·0 at the root surface compared with 6·5 at 10 mm from the root surface (Begg et al., 1994). The Henderson–Hasselbalch equation predicts that at equilibrium, P_CO2 would be 2·5 times greater at the root surface than in the bulk soil, while during CO₂ uptake by the root, the diffusion of dissolved inorganic carbon to the root will presumably nearly entirely depend on the large HCO₃⁻ gradient in the direction of the root surface. Consequently, CO₂ uptake by the rice roots in Iloilo sand is likely to be substantially faster than predicted by the model used in the present paper, albeit by less than expected from the high CO₂ level in the rhizosphere because the diffusion of HCO₃⁻ is 40 % slower than that of CO₂ (Kirk, 2004). The application of these deductions to the present model are uncertain because it is as yet unknown what the pH gradient would be around the 10-mm extending root tip. Nevertheless, substantial pH gradients might be expected despite the shorter exposure of the soil to the influence of the root, associated with the continued extension of the root tip, as this shorter exposure would be counteracted by high rates of processes tending to reduce the pH of the rhizosphere, such as vigorous uptake of NH₄⁺ (either as the cation or as NO₃⁻ after nitrification) (see Colmer and Bloom, 1998) and oxidation of Fe²⁺ (Kirk, 2004), stimulated by the substantial radial O₂ loss to the rhizosphere surrounding the apex (Armstrong, 1979; Colmer 2003a). Note that this complication is much less serious in better-buffered soils; for example, in Maahas soil the pH was 7·24 at 10 mm from the root and 7·1 next to the root (Kirk, 2004).

Effects of xylem flow along roots, and of convective gas-flows through aerenchyma in rhizomes. P_CO2 in roots might be lower than indicated above because the CO₂ efflux to the shoot may be increased due to rapid transpiration. For the xylem stream, the amount of dissolved inorganic carbon removed from the roots can be calculated using the flow rates and anatomy given by Armstrong (1979), while the amount would also depend on the pH of the xylem sap (Table 1b). In a survey of three tree species, pH of the xylem sap ranged between 5·6 and 6·5 (McGuire and Teskey, 2004). In Ricinus communis the pH of the xylem sap fluctuated between 6·0 round midnight and 5·3 at midday (Gerendas and Schurr, 1999). At pH 5·3, the ratio of HCO₃⁻/CO₂ would be 0·1; even so, substantial dissolved inorganic carbon would be removed at fast transpiration; assuming that roots had a P_CO2 of 10 kPa, the xylem stream would remove 40 % of the CO₂ produced in aerobic catabolism. Substantially more dissolved inorganic carbon might exit in the xylem stream if its pH was higher; for example, at pH 6·5 the HCO₃⁻/CO₂ ratio would be 1·6 (cf. equation in caption to Fig. 2), and then nearly all the CO₂ produced by the root's aerobic catabolism would be removed in the xylem stream. Estimates of the same order of magnitude can be derived from transpiration ratios presented by Ludlow (1976); dissolved inorganic carbon removal was estimated to range between 20 and 100 % of production (procedures given in Appendix 2b). As the combination of CO₂ production by the roots and CO₂ influx from the soil may give rise to as much as 26 kPa P_CO2 in the root (Table 3, column 6), much higher than the example of 10 kPa used above, substantial diurnal fluctuations in P_CO2 may occur when transpiration is high during daylight hours as compared with when transpiration is low during the night.

Possible diurnal fluctuations in P_CO2 in roots, as dependent on xylem flow, would be accentuated in species with convective gas flow through their rhizomes; for example, Phragmites australis has a P_CO2 in its rhizomes close to 0 kPa during the day, whereas at night, when gas movement is by diffusion, P_CO2 was 6 kPa (Chanton et al., 2002). Similar fluctuations for CH₄ (Chanton et al., 2002) demonstrated that these diurnal changes were due to differences in gas flow, not related to photosynthesis. During darkness lasting 50 h, P_CO2 in rhizomes of P. australis increased, but only in those at depths of 0–60 cm, not when the rhizomes were at greater depths in the mud (Brix, 1988). Furthermore, the deductions made here require a caveat; as discussed earlier CO₂ influx into roots may become substantial during rapid water flow, and if so, the predicted fluctuations in CO₂ would be dampened. Thus, the hypothesis that diurnal cycles of transpiration cause diurnal cycles in P_CO2 in the rhizomes and root system needs testing; a comprehensive test would include rates of transpiration, pH of the xylem sap and convective gas flow through rhizomes, in addition to internal P_CO2 measurements.

Case 2: P_CO2 lower in the soil than in the root

This situation is likely to occur at the start of waterlogging before P_CO2 in the soil builds up, or when O₂ deficiency occurs in swelling clays, with a low gas-filled porosity which can be aggravated by soil compaction (Blackwell et al., 1985). In such compacted soils CO₂ might still be ventilated through the inter-crumb pore space, as the water-filled soil capillaries can be relatively short; thus, diffusive fluxes can still be substantial, and much faster for CO₂ than for O₂ in view of the earlier mentioned 34-fold higher solubility of CO₂ versus O₂, so that the ΔP_CO2 will be much smaller than the ΔP_O2 (Greenwood, 1973; Payne and Gregory, 1988). Similarly, with low P_CO2 in the soil, effluxes of CO₂ from roots will only require relatively small differences in ΔP_CO2 between the gas-space within the roots and the external solution. This crucial point is best demonstrated using data for excised maize roots, in which the only fluxes are between root and external solution. In these roots, the ΔP_O2 between solution and the middle cortex was 21·1 – 14·4 kPa=6·7 kPa (Gibbs et al., 1998). Let us assume that the respiratory quotient is 1·0, the flow of both O₂ and CO₂ is through the same pathway though in the opposite directions, while the main resistance would be in the liquid steps (i.e. through cells and through any water in extracellular spaces). Then, the required efflux of CO₂ to the root medium would only require a ΔP_CO2 of 6·7/26·5 = 0·25 kPa; the denominator is 26·5 rather than 34 because in water the ratio of diffusion coefficients of CO₂ to O₂ is 0·78 (Armstrong, 1979). Similarly, only low ΔP_CO2 between cortex and stele are predicted; based on the ΔP_O2 of 4 kPa between inner cortex and outer stele in aerated maize roots (Gibbs et al., 1998), the ΔP_CO2 would be only 0·15 kPa.

In conclusion, detailed modelling of the factors determining P_CO2 in plant roots is clearly needed, but will be warranted only when data on P_CO2 in soils and root tissues become available. Such measurements, combined with modelling, would elucidate the question of to what extent the root tissues of waterlogged plants experience high P_CO2.

EFFECTS OF HIGH P_CO2 ON ROOT GROWTH

Effects of high P_CO2 on root growth have been studied in solution culture for flooding-tolerant rice, and the much less flooding-tolerant soybean (Boru et al., 2003). Treatments were imposed at 14 d after germination and continued for another 14 d. Rice grew as well with its roots in anaerobic as in aerated solutions. Response to CO₂ was only studied for plants in anaerobic solutions. Root dry weight of rice was not affected by 15 kPa CO₂, but was reduced by 25 % at 50 kPa CO₂ (Boru et al., 2003). The longest roots, a more refined indicator of root growth than dry weight, were 15 % shorter at 15–30 kPa CO₂ than with anaerobiosis alone. The length was reduced by a further 15 % at 50 kPa CO₂. These rice roots have a large volume of aerenchyma and hence would receive large amounts of O₂ from the shoot, so might not experience a combination of high P_CO2 and anoxia. Consistent with the results for rice given by Boru et al. (2003), rice plants survived exposure of their roots to 100 kPa CO₂, even at pH 4·0 (Tanaka and Navasero, 1967); nevertheless, dry weight of similarly treated rice roots was decreased by ∼45 %, compared with a mere 7 % due to anoxia without CO₂ (Rao and Mikkelsen, 1977).

In contrast to rice, soybean (under the same experimental protocol) root length reduced by 60 % in anaerobic solutions, while this inhibition was increased to 78, 89 and 94 % when the anaerobic flushing gas contained 15, 30 and 50 kPa CO₂, respectively (Boru et al., 2003). Consistent effects, although usually less severe, were found for dry weight and various characteristics of shoot growth. It is relevant that a much larger part of the root system of soybean than of rice might have been anoxic. It would also be of interest to establish whether high P_CO2 was adverse to the zones receiving sufficient O₂ for oxidative phosphorylation, to the anaerobic zones or to both. As pointed out by Boru et al. (2003), part of the adverse effect of high P_CO2 during anaerobiosis of the nutrient solution could be related to its inhibition of ethylene action, as indicated by a pronounced reduction in the number of adventitious roots in soybean. Consistently, 10 kPa CO₂ reduced aerenchyma in adventitious roots of rice by 8–40 % (Jackson et al., 1985). Confirmation of the results reported by Boru et al. (2003) is important for several reasons. Foremost, Boru et al. (2003) applied the high P_CO2 suddenly; it has been discussed above that such sudden increases are quite atypical for soils in the field and, as shown in a later section, sudden increases in P_CO2 will result in transient, drastic, decreases in pH_cyt, followed by at least partial recovery. Severe adverse effects during the ‘shock’ of sudden exposure to high P_CO2 may well occur, and these might have long-term repercussions on growth; indeed, it is impressive that rice tolerated the combination of these shocks, and subsequent exposure to 50 kPa CO₂ for 14 d. A second important limitation of using solution culture, for the evaluation of the consequences of high P_CO2 in waterlogged soil, is that these solutions are usually flushed with gas and hence are turbulent. Consequently, the endogenous P_CO2 in the roots will be fairly close to the exogenous P_CO2; so this technique is unsuitable to ascertain the tolerance of various species in waterlogged soils, as the soil solution will be stagnant, and therefore the endogenous P_CO2 will be lower the larger the gas-space continuum in the roots (Fig. 5), which is species-dependent. Summing up, the available data make a convincing case for tolerance to high P_CO2 for rice roots. On the other hand, whether intolerance to high P_CO2 in soybean roots is a component of the well-known intolerance to waterlogging of this species needs to be tested with more gradual increases in P_CO2.

Of particular relevance to our theme are the few investigations on the interaction between high P_CO2 and low P_O2. Studies on wheat show that adverse effects of high P_CO2 on root growth either did not occur, or were not as severe, at low compared with at ambient P_O2 (Huang et al., 1997). Exposure of wheat roots to 10 kPa CO₂ at 20 kPa O₂ reduced total root length by ∼30 %; however, at 5 kPa O₂ the 10 kPa CO₂ did not aggravate the adverse effects of 5 kPa O₂ (Huang et al., 1997). Interestingly, with the combination of 10 kPa CO₂ and 5 kPa O₂, the length of the axes of the seminal roots was reduced less than at either 10 kPa CO₂ or 5 kPa O₂ alone (Huang et al., 1997); in other words, at 5 kPa O₂, 10 kPa CO₂ stimulated seminal root elongation by 25–35 %. Similarly, 10 kPa CO₂ did not aggravate the already large growth reductions of wheat roots in N₂-flushed nutrient solution (Trought and Drew, 1980b). The results from Huang et al. (1997) present an enigma because, at 5 kPa O₂, substantial parts of the roots would still receive sufficient O₂ for oxidative phosphorylation; for 6-mm root tips of wheat this proportion was assessed at ∼50 % (Thomson et al., 1989). It is not clear why these aerobic zones, which presumably are critical to the performance of the roots, would not be impaired in their function by high P_CO2, even though high P_CO2 clearly reduced growth in aerated solutions. A similar mitigation of the adverse effects of high P_CO2 by concurrent exposure to low P_O2 was found for germinating maize (Table 4). Interestingly, a genotypic difference in tolerance to 25 kPa CO₂ was consistent with their tolerance to flooding (Cerwick et al., 1995). This is so far the only recorded case in which differences in flooding tolerance within a species were associated with the ability to cope with high P_CO2 rather than with low P_O2 in the medium. In contrast to these responses by wheat and maize, in soybean the earlier described adverse effect of 30 kPa P_CO2 on growth in anaerobic solutions (Boru et al., 2003) was not found in soil flushed with gas mixtures containing 30 kPa CO₂ and 20 kPa O₂ (Grable and Danielson, 1965). Thus, in soybean, high P_CO2 may have adverse effects only when the roots are in anaerobic solution, and this possible interaction needs to be tested in the same experiment and with the same genotype.

Table 4.

Germination of maize in rolls of moistened paper at 25 kPa P _CO2 at 5 and 20 kPa O₂

Treatment	Flooding-tolerant genotype	Flooding-intolerant genotype
Percentage germination relative to controls
25 kPa CO2 + 20 kPa O2	81	47
25 kPa CO2 + 5 kPa O2	97	77
5 kPa O2	98	96

Data are expressed as percentage of germination at 20 kPa O₂ and 0 CO₂ in the flushing gas (data from Cerwick et al., 1995).

The genotypes are assigned as being ‘tolerant’ or ‘intolerant’ data based on experiments in soil flooded for 72 h, when germination of the tolerant genotype was reduced by 40 % and of the intolerant genotype by 85 %.

The interaction between high P_CO2 and low P_O2 requires comprehensive information on the effects of high P_CO2 on aerated roots; unfortunately there is very little information on this topic. In flooding-tolerant Rumex palustris, exposure to 10 kPa CO₂ for 2 h in aerated solution reduced the elongation rate of primary roots by 20 % (Visser et al., 1997). By contrast, dramatic injury resulting from exposure to modest P_CO2 (∼2 kPa) has been reported for roots of some cacti. The cortical cells of the cacti were considered to be dead within 3–6 h following exposure to CO₂ as low as 2 kPa (Nobel and Palta, 1989; Palta and Nobel, 1989). The same period of exposure to anoxia was not fatal. Based on these and other data, Nobel and Palta (1989) concluded the extreme intolerance of these species to P_CO2 of 1–3 kPa was the likely reason for their restriction to well-aerated sandy soils. Enigmatically, in the leaves of the same and a related species as used by Nobel and Palta (1989), P_CO2 increased to 1·3–2·5 kPa during the day, when CO₂ is liberated from malate, which is part of the normal circadian rhythm (Luettge, 2002). In view of this apparent difference in tolerance between leaf and root tissues, confirmation of the results of Nobel and Palta would be useful (some further reservations on the experiments by Palta and Nobel are given in Appendix 4b).

Further information on the tolerance of roots to high P_CO2 is scant and contradictory. In experiments lasting a few days, P_CO2 of 6·5–8·5 kPa stopped root growth in pea, bean, sunflower and broad bean (Stolwijk and Thimann, 1957) and cell division in broad bean (Williamson, 1968). By contrast, P_CO2 at 5–6·5 kPa had little effect on roots of oat (Stolwijk and Thimann, 1957) and soybean (Grable and Danielson, 1965). Possible reasons for these discrepancies include differences in tolerance between various species, contamination of ethylene in the CO₂ supply (suggested by M. Cramer) and insufficient prevention of CO₂ enrichment of the air around the shoots (Cramer, 2002). So, new experiments are needed to evaluate the effects of high P_CO2 in the root zone on plant growth.

EFFECTS OF HIGH P_CO2 ON METABOLISM

We have found no information on the effects of high P_CO2 on root metabolism of waterlogging-tolerant species, and with the exception of large reductions in CO₂ evolution in the roots of the cacti mentioned earlier (Nobel and Palta, 1989; Palta and Nobel, 1989) no information on non-wetland species (for further comments on the experiments on cacti, see Appendix 4b).

Responses of fruit and vegetables exposed to high CO₂ during storage might provide an indication of the likely responses by plant cells. In harvested fruits and vegetables, respiration was usually reduced by high P_CO2, while injury was postulated in the cases when respiration was increased (Herner, 1987; Mathooka, 1996). Such data are not reviewed in detail here because the results for the vegetables are merely descriptive and the results for the fruits may be confounded by delay in the climacteric and possible interactions with ethylene (Mathooka, 1996). More relevant might be some papers on the response of non-growing cell cultures and protoplasts of pear fruit (Kerbel et al., 1990 and Lammertyn et al., 2001, respectively). Decreases in respiration of these cells and protoplasts were 25 and 40 % for 5 and 15–20 kPa CO₂, respectively, and this degree of inhibition was not affected by P_O2 between 2·5 and 21 kPa (Lammertyn et al., 2001); this is a similar response to that described earlier for growth of roots of intact wheat plants. As these preparations were derived from pear fruits, there is still the confounding possibility of physiological changes associated with the climacteric. Consistently, these cultures responded similarly to the intact fruit, in respect both to high P_CO2 (Kerbel et al., 1990L; ammertyn et al., 2001) and to ethylene (Brady and Romani, 1988).

Substantial data are available on the effects of 10–50 kPa CO₂ on photosynthesis by leaves of a range of species (Heber et al., 1994); high CO₂ was used to simulate acid rain. This response of photosynthesis to high P_CO2 is only peripheral to our theme, because submerged leaves are seldom exposed to P_CO2 higher than 10 kPa. In a flooded rice field, the P_CO2 was 3 kPa at 0600 h, but due to increases in pH of the waters associated with CO₂ uptake during photosynthesis, CO₂ concentrations became very low at midday (Kirk, 2004); the effects of high P_CO2 on photosynthesis will thus be transient. Furthermore, as shown in a large survey of ‘CO₂-rich’ freshwater streams in Denmark, the highest values of CO₂ (1·5–3 kPa) occurred only in 2 % of the streams (Sand-Jensen and Frost-Christensen, 1998). However, in sheltered, slightly polluted lakes in the Netherlands P_CO2 ranged between 3·5 and 10 kPa (Prince and de Guia, 1986). Furthermore, leaves may not respond to high CO₂ in the same way as roots, given that adverse effects on CO₂ fixation may be particularly severe as the pH of the stroma of the chloroplasts is ∼8·0 (Alberts et al., 2002), i.e. at a given P_CO2 the HCO₃⁻ concentrations would be approx. three-fold higher than in the cytoplasm (Table 1b). Nevertheless, in view of the scarcity of studies on metabolic responses to high P_CO2, this seminal paper by Heber et al. (1994) remains valuable to this review, as it provides ideas on how plant metabolism may cope with high dissolved inorganic carbon. In some experiments by Heber et al. (1994), CO₂ was added at the start of a light period, quasi steady-state rates of photosynthesis in leaves of Symphytum officinale were then reached at 1 min after transfer to 2 kPa CO₂, but this lag was 15–30 min after transfer to 20 kPa CO₂. There were remarkable differences in tolerance to high CO₂ among species; times to reach a new quasi steady-state photosynthesis were sometimes much longer than in Symphytum officinale. Furthermore, quasi steady-state rates of photosynthesis of spruce and barley leaves were not affected by 20 kPa CO₂, while in maize leaves photosynthesis was inhibited by 40 and 80 % at 10 and 20 kPa CO₂, respectively (Heber et al., 1994), values consistent with intolerance to 25 kPa CO₂ of some maize genotypes during germination (Table 4).

Changes in metabolism are now be discussed, first in relation to the imposed acid load (i.e. a tendency to acidify the cytoplasm) and then in relation to direct effects of CO₂ and/or HCO₃⁻ on enzymes.

Acid loads

At equilibrium, the vacuole, which usually has a pH of 5–6 (Guern et al., 1991), would contain a mere 0·3–2·5 mm HCO₃⁻ for each 10 kPa CO₂ (Table 1b). By contrast, pH_cyt is usually ∼7·5 in aerobic cells (Xia and Roberts, 1996; Ratcliffe, 1997), so each increase of 10 kPa P_CO2 in the roots would result in an additional 75–90 mm HCO₃⁻ in the cytoplasm (Table 1b). Hence, 10 kPa P_CO2 presents a large ‘acid load’ as the buffering capacity of the cytoplasm in cells, other than leaf cells, is 20–80 meq l^–1 (pH unit)^–1 (Kurkdjian and Guern, 1989).

The response to high P_CO2 will be first considered for the quasi steady state, when high P_CO2 is predicted for most roots in waterlogged soil, provided soil pH is not too far above the pK_a of the CO₂–HCO₃⁻ equilibrium, say not above ∼7·0. Subsequently, responses to sudden changes in P_CO2 will be considered. Responses to such rapid changes in P_CO2 of the environment are seldom relevant to waterlogging in the field, because as discussed earlier P_CO2 in soils only increases by 0·05–0·1 kPa h^–1 (calculated from Fig. 3 and Trought and Drew 1980a), which would result in an increase of a mere 0·45–0·9 mm HCO₃⁻ h^–1 in the cytoplasm, assuming its pH was 7·5. Nevertheless, responses to sudden changes in P_CO2 remain of interest for four reasons:

1. Rather rapid fluctuations in dissolved inorganic carbon in plant tissues might occur, as argued earlier, due to fluctuations in transpiration, as well as in convective gas flows through rhizomes.

2. Sudden exposure to high P_CO2 would occur during the planting of paddy rice in puddled fields, already flooded for 2–3 weeks (Rowell, 1988). Presumably, the roots would be suddenly exposed to high P_CO2 and this shock would coincide with a need for healing of the root systems.

3. Data obtained following sudden changes in P_CO2 provide evidence that pH stats have become engaged (as discussed below).

4. Sudden changes in exogenous P_CO2 have been the practice in nearly all nutrient solution experiments, making discussion of the consequences of such ‘shocks’ relevant to interpretation of these experiments.

Mechanisms of acclimatization to high P_CO2

There are three possible mechanisms of acclimatization to high endogenous P_CO2, all related to either mitigating or coping with formation of HCO₃⁻ in the cytoplasm. By contrast, the only way to minimize CO₂ concentrations in cells of roots exposed to high soil P_CO2 is, as discussed earlier, via rapid ventilation to the shoots in the root gas-space continuum (Table 3 and Fig. 5). First, the biochemical pH stat, i.e. removal of organic acids, or production of organic cations, would provide cation balance for the increased level of HCO₃⁻. Secondly, a biophysical pH stat would via uptake of cations (usually K⁺) provide the charge to balance the HCO₃⁻, as discussed in general for pH regulation by Ullrich and Novacky (1990). These two mechanisms would not change the HCO₃⁻ concentration, which will be determined by the pH of the cytoplasm and the CO₂ concentration attained in the tissues, as determined by rates of production during catabolism, influx from the environment and ventilation via the gas-space continua within roots. The third mechanism would mitigate the increases in HCO₃⁻ in the cytoplasm by a decrease in the set point of the pH of the various cytoplasmic compartments, which would greatly reduce the formation of HCO₃⁻ at a given CO₂ concentration (Table 1b) and hence reduce its possible effects on metabolism. At moderate P_CO2, such a mechanism may avoid the need to engage the pH stats, provided the cytoplasm had a high buffering capacity. All three mechanisms have their limitations and it is therefore likely that in tissues reaching 30–40 kPa CO₂, the three mechanisms may have to act in concert if acclimatization is to be achieved.

(1) The quasi steady-state

(a) A decrease in the set point of pH_cyt. A decrease in pH_cyt would greatly lessen the increase of HCO₃⁻ by decreasing the ionization of H₂CO₃ (Table 1b). For the CO₂–HCO₃⁻ equilibrium, even a relatively small decrease in pH from 7·5 to 7·3 would result in a decrease of 45 % in the equilibrium HCO₃⁻ concentration (Table 1b). In embryos of Artemia, the brine shrimp, pH_cyt was reduced by increases in P_CO2, but even the smallest decrease from pH 7·9 to 7·3, due to an increase in P_CO2 by 10 kPa, reduced respiration by 50 % (Busa and Crowe, 1983). Accordingly, these authors concluded that decreases in pH_cyt in Artemia triggered metabolic arrest, which is well established during anoxia for this and some other animal species (Hofmann and Hand, 1990). Whether the set point in pH_cyt can decrease without slowing metabolism remains unknown. Regardless, lowering the set point of pH_cyt will have a limit: in anoxic plant tissues substantial decreases of pH_cyt below ∼7·0 are associated with compromised metabolism and eventual death (Xia and Roberts, 1996; Greenway and Gibbs, 2003).

(b) The biochemical pH stat. This stat would merely replace endogenous organic acids by HCO₃⁻ and therefore have few further repercussions for metabolism. The maximum amount of organic acids that could be removed would be about 80 meq ml^–1 of cytoplasm; this value is based on the K⁺ level in the cytoplasm of barley roots (Leigh, 2001), which is mainly balanced by organic anions, but a lower value is likely as some of the organic anions would be essential for intermediary metabolism.

(c) The biophysical pH stat. For each rise of P_CO2 by 10 kPa, such a stat would have to increase the concentration of monovalent cations by 75–90 mm, mainly K⁺, assuming the set point of pH_cyt remained at 7·5. However, the increase in cation concentration is unlikely to cope completely with the large acid loads likely to occur in a number of situations for roots in waterlogged soils: K⁺ in the cytoplasm of barley roots was 80 mm (Leigh, 2001), and substantial increases in K⁺ above this concentration have adverse effects on metabolism. For example, 170 mm K⁺ (as acetate) gave a 80 % reduction in ³⁵S-methionine incorporation into proteins by an isolation from wheat germ (Flowers and Dalmond, 1993). This paper is particularly relevant to the present theme, because it indicates genetic diversity in tolerance to high K⁺ concentrations, with K⁺ optima of 100–150 mm in five non-halophytes, 125–200 mm in two halophytes and 200–275 mm in the extreme halophyte Suaeda maritima (Flowers and Dalmond, 1993). Such data need further scrutiny, as the isolations were supplemented with post-ribosomal supernatant of wheat germ and showed polypeptide elongation, but little initiation of new polypeptide chains (Flowers and Dalmond, 1993).

A biophysical pH stat would have the disadvantage of an increase in ionic strength, which would decrease the pK_a of the HCO₃–CO₂ equilibrium and hence increase the HCO₃⁻ concentration. We estimate that an increase in ionic strength from 0·1 to 0·19 m would result in only a 13 % increase in HCO₃⁻ concentration at any particular CO₂ concentration (calculated from Yokota and Kitaoka, 1985). A more serious disadvantage may be associated with the essential osmotic balance between cytoplasm and vacuole. Briefly, a rise of 90 mm in HCO₃⁻, balanced by monovalent cations in the cytoplasm, would increase its osmotic pressure by 0·43 MPa, requiring a similar increase of osmotic pressure in the vacuole, and if P_CO2 fluctuates in the tissues (Chanton et al., 2002) osmotic pressure would have to fluctuate accordingly.

(2) Acclimatization to fluctuations in P_CO2

The acid load exerted by high P_CO2 was demonstrated for cultured cells of Acer pseudoplatanus; using ¹⁴C DSMO, a chemical pH probe with a pK_a of 6·3, the pH of the cytoplasm decreased by 0·7 units within 3 min after addition of 5 kPa CO₂, while engagement of a pH stat was indicated by partial recovery of pH_cyt over the next 25 min (Kurkdjian et al., 1978); exposure to 5 kPa CO₂ was not continued long enough to establish the new steady state. Acclimatization was also very rapid in leaf discs of Symphytum officinale; after a sudden increase to 20 kPa CO₂ in the dark, ∼30 min exposure before switching on the light reduced the lag in photosynthesis from ∼15 to 6 min. As stated earlier, CO₂ penetration will be rapid, so we can speculate on the likely initial decreases in pH_cyt; using as an example the sudden increase of 50 kPa CO₂ in the root medium at 25 °C as imposed in experiments by Boru et al. (2003), pH_cyt would be expected to decrease to 6·25, 6·56 and 6·69 respectively, for buffering capacities of 20, 50 and 80 mm pH^–1 unit (as given by Kurkdjian and Guern, 1989). It is unknown for what length of time such low pH_cyt can be tolerated.

We postulate that the biochemical pH stat is indicated by sudden increases in P_CO2, for example the large increases in respiration by cultured cells of carnation during the first 10 min following sudden increases in P_CO2 (Palet et al., 1991). This biochemical pH stat would remove 0·09 µmol H⁺ g^–1 f. wt min^–1, as judged by the increase in O₂ consumption when the cells were challenged with ∼5·5 kPa CO₂ (Palet et al., 1991). Support for the hypothesis that the increase in respiration is associated with the acid load comes from inhibition of the stimulation of O₂ uptake by SHAM, an inhibitor of the alternative oxidase (Palet et al., 1991). SHAM also inhibited CO₂ and/or HCO₃⁻ stimulation of O₂ uptake in tissues of several other species (Palet et al., 1991). The acid load would activate the biochemical pH stat, which usually involves decarboxylations of organic acids, as proposed by Davies (1986). Such decarboxylations would be facilitated by engagement of the alternative oxidase pathway, so as to accelerate removal of the TCA cycle acids derived from, for example, malate. Assuming all the putative decarboxylations were from the cytoplasmic pool, which is plausible given that the vacuolar pH would not be changed appreciably by the high P_CO2, and a cytoplasmic volume of 10 %, the biochemical pH stat could remove carboxylate groups at 0·9 meq ml^–1 cytoplasm min^–1, being within reach of the observed pH recovery following addition of 5 kPa CO₂ (Kurkdjian et al., 1978). The biochemical pH stat may not always be able to cope completely with diurnal fluctuations in CO₂ concentration; these were as large ∼1·8 kPa h^–1 during diurnal changes in convective gas flow (Chanton et al., 2002), resulting in, at a cytoplasmic pH of 7·5, changes of 0·25 meq HCO₃⁻ ml^–1 cytoplasm min^–1. It should be noted that our interpretation, that the stimulation of the alternative pathway was due to the acid load imposed by CO₂ addition, differs from that by Palet et al. (1991), who postulated that stimulation of the alternative pathway provided an, albeit inefficient, compensation for the reduced ATP formation due to the inhibition of cytochrome c oxidase by high CO₂–HCO₃⁻ (this inhibition is discussed in the next section). The results obtained with the inhibitors used by Palet et al. (1991) need to be confirmed using ¹⁸O₂ (Ribas-Carbo et al., 2005) to test the suggestions on different tolerance of the cytochrome c and alternative pathways to CO₂ and/or HCO₃⁻.

To achieve a functional biochemical pH stat able to cope with an increase in P_CO2, malic enzyme (l-malate: NAD oxidoreductase-decarboxylating), which is part of the classical pH stat (Davies, 1980, 1986), should not be inhibited by high HCO₃⁻ and/or CO₂. Interestingly, during studies in vitro, 5 mm HCO₃⁻ reduced malate decarboxylation by 50 % when pH was 7·5; however, at pH 7·2, 50 % inhibition occurred only at 30 mm HCO₃⁻, while at pH 6·5 there was hardly any inhibition with HCO₃⁻ up to 40 mm (Neuburger and Douce, 1980). Thus, malic enzyme can still function in the pH stat even at high levels of HCO₃⁻ provided pH_cyt decreases by a few tenths of a unit, conditions likely to prevail in tissues exposed to high CO₂ and low O₂ concentrations. That only small changes in pH are required to trigger the pH stat was shown for Crassulacean acid metabolism when a decrease in pH_cyt from 7·5 to 7·2 could account for the profound decrease in activity of phosphoenolpyruvate carboxylase, during the light cycle (Hafke et al., 2001).

A biophysical pH stat was postulated by Heber et al. (1994) to explain results following sudden exposure of leaves to high CO₂. Their argument is based on the rapid acclimatization of photosynthesis, in about 10 min, which they assume is feasible because data related to H⁺ transport during photosynthesis have shown an H⁺/K⁺ exchange between cytoplasm and vacuole as high as 6·6 µmol ml^–1 cytoplasm min^–1 [derived from assessment by Heber et al. (1994) on a chlorophyll basis and converted by us to volume of cytoplasm using data from Winter et al. (1993)]. Their main argument is perceptible acidification of the vacuole (assessed using a fluorescent probe with a pK_a of 4·8) during acclimatization to high P_CO2; this acidification is consistent with a biophysical but not with a biochemical pH stat.

The biophysical pH stat would involve energy consumption, as the cation uptake to balance the HCO₃⁻ would require H⁺ extrusion. Before discussing the energy requirement for this H⁺ extrusion, we argue that this requirement will be related to the capacity for energy production; both the amount of HCO₃⁻ formed in the roots and the capacity within these tissues for ethanol formation and hence ATP formation would presumably be closely related to the cytoplasmic volume (the latter is supported experimentally by correlations between maximum catalytic activity of ADH and soluble protein in root tissues of different age; Andrews et al., 1994). Hence, the balance between the requirements for energy of the biophysical pH stat and the capacity to produce energy would be similar in slightly and highly vacuolated cells. A high rate of K⁺ uptake from the medium would be 10 µmol g^–1 f. wt h^–1. Assuming the cytoplasmic volume is 10 % of the cell volume, then an increase of 100 mm K⁺ may be achieved at ∼1 h after sudden transfer to high CO₂. The cost of the associated H⁺ extrusion of 100 µmol H⁺ h^–1 ml^–1 cytoplasm may require only 50 µmol ATP h^–1 ml^–1 cytoplasm, as the stoichiometry of the H⁺-ATPase under energy deficits may be 2 rather than 1 (Warncke and Slayman, 1980). This expenditure of ATP would be of serious concern only if there was concurrent imposition of anoxia, because then even the lower ATP requirement would be somewhat above the assessed hourly ATP production via ethanolic fermentation in slightly vacuolated, 2-mm maize root tips (from Saglio et al., 1988, assuming that in these tips cytoplasm contributed 50 % to the cell volume). Energy requirements in terms of µmol ATP (unit of time)^–1 ml^–1 cytoplasm would be much higher when there was the fast H⁺/K⁺ exchange between cytoplasm and vacuole as proposed by Heber et al. (1994); their tissues were in air, and it is very unlikely that such rapid production of energy could be achieved during an energy deficit. Any energy requirements for acclimatization to fluctuations in P_CO2 would be particularly serious at the start of anoxia when the processes involved in acclimatization to anoxia would also require large amounts of energy.

In conclusion, no comprehensive study on the response to sudden increases in P_CO2 has been made, so it needs to be determined whether all plant tissues depend on a combination of the biochemical and biophysical pH stats, or whether the action of these stats is species-specific. Of particular interest is the acclimatization to the diurnal cycles in acid load, predicted on the basis of the earlier discussed transport of dissolved inorganic carbon in the transpiration stream, possibly intensified in some species by fast convective gas flow through the rhizomes during the day, but not during the night. For such diurnal fluctuations, the least likely mechanism would be the biophysical pH stat, as this stat would require energy for H⁺ transport as well as for fluctuations in osmotic pressure of the vacuole.

POSSIBLE EFFECTS OF HIGH CO₂ AND/OR HCO₃⁻ ON RESPIRATORY ENZYMES INCLUDING CYTOCHROME OXIDASE

The preceding discussion has shown the importance of metabolism of tolerance to high CO₂ and HCO₃⁻. The earlier described reductions in respiration during long-term exposure to high P_CO2 (e.g. Herner, 1987; Mathooka, 1996; Lammertyn et al., 2001) may be due to reduced utilization of ATP, or be primary effects of high CO₂–HCO₃⁻ on the metabolic pathways. Inhibition of the respiratory pathways leading to oxidative phosphorylation would be particularly serious to functioning of roots in waterlogged soils, as the zones receiving sufficient O₂ for oxidative phosphorylation presumably need to compensate for low ATP production by any anoxic zones (Armstrong and Beckett, 1987; Colmer and Greenway, 2005).

The adverse effects on enzymes may be due to carbamation of proteins or to other types of inhibition of enzyme activity, for example competitive inhibition between substrate and HCO₃⁻ or CO₂, as shown for cytochrome oxidase (Miller and Evans, 1956) and succinic dehydrogenase (Cerwick et al., 1995). Carbamation converts amine and amide groups into a negatively charged carbamate: RNH₂ + CO₂ ↔ RNHCOOH ↔ RNHCOO⁻ + H⁺ (Mitz, 1979; Lorimer, 1983). Furthermore, CO₂ may have profound effects on lipids, with possible changes in membrane permeability (Mitz, 1979). So far, knowledge on carbamation effects in plants during prolonged exposure to high P_CO2 is lacking. It needs to be elucidated whether the effects of carbamation on proteins and lipids persist in the longer term and whether activities of some enzymes are inhibited due to carbamation, i.e. similar to the reduced affinity of O₂ for haemoglobins following their carbamation (Lorimer, 1983).

Considering the known effects on metabolic reactions, a possible reduction in glycolysis at high P_CO2 was indicated for pear fruit and cultured cells from pear fruit; changes in glycolytic intermediates at 20 kPa P_CO2 were consistent with a reduction in the carbon fluxes through the phosphofructokinases (PFKs; Kerbel et al., 1990). Consistently, activities of PFK (ATP) and PFK (PPi) on a protein basis were reduced by 50 % at 20 kPa CO₂ (Kerbel et al., 1990). However, these reductions occurred only at 2–3 d, but not at 1 d, after imposing the high P_CO2, so it seems likely that these responses are consequences of effects of HCO₃–CO₂ on other parts of metabolism, rather than direct effects of HCO₃–CO₂ on the PFKs.

Other possible lesions are in the TCA cycle, or in the electron transport chains. For mitochondria isolated from fruit of apple, oxidations of fumarate, pyruvate and succinate were suppressed by 30 % in equilibrium with 5·8 mm CO₂ and ∼70 mm HCO₃⁻, while reductions were smaller for several other substrates (Shipway and Bramlage, 1973). Succinic dehydrogenase was also strongly inhibited in isolated mitochondria from maize mesocotyls by 10–20 mm HCO₃⁻ (Cerwick et al., 1995); the pH during assay is uncertain, so the HCO₃⁻/CO₂ can only be approximated at between 15 and 40 mm. In both these cases the inhibition due to high HCO₃⁻ and/or CO₂ might be associated with inhibitions either of transport of organic acids into the mitochondria or of enzymes oxidizing the organic acids; this uncertainty makes their relevance equivocal, as inhibition of uptake of succinate by the mitochondria would not be relevant to in vivo effects. Such complications were avoided, using mitochondria disrupted by transferring them from 0·5 to 0·05 m sucrose, by comparing the effects of NaHCO₃ with those of NaCl (Bendall et al., 1960). These authors concluded that responses to high HCO₃⁻ and/or CO₂ were specific for succinic dehydrogenase, but effects by HCO₃⁻ on NADH oxidase and cytochrome oxidase were merely due to ionic strength, or to the high Na⁺ balancing the HCO₃⁻ (Bendall et al., 1960).

The high sensitivity of succinic dehydrogenase to high HCO₃⁻ is particularly noteworthy given that mitochondria have 0·5–0·6 higher pH than the cytosol (Rottenberg, 1975). Thus, at a given P_CO2, succinic dehydrogenase, like other TCA cycle enzymes, would be presumably exposed to approx. three-fold higher HCO₃⁻ concentrations than the enzymes in the cytosol. Yet, rapid functioning of succinic dehydrogenase in vivo is implied by the experiments of Palet et al. (1991), because, following sudden CO₂ addition, O₂ uptake was transiently increased rather than decreased in their cultured cells, implying a large flow of carbon through the TCA cycle, and consistent with the cessation of O₂ uptake when both the cytochrome and the alternative oxidase pathways were inhibited (Palet et al., 1991). Nevertheless, these fast rates of succinic dehydrogenase at high P_CO2 are not all that enigmatic, as most of the gradient for H⁺ transport in the mitochondria depends on the membrane potential, so that the pH gradient is a much smaller component of the free energy gradient for the H⁺ flux generating ATP than in the chloroplasts.

Contrary to the conclusion by Bendall et al. (1960) that cytochrome c is not inhibited by high HCO₃⁻ (discussed above), Palet et al. (1991) present evidence that the cytochrome oxidase pathway is inhibited by high HCO₃⁻ and/or CO₂. In the key experiment by Palet et al. (1991), the cytochrome pathway, which had been stimulated by 1·6-fold, following addition of the uncoupler CCCP, was inhibited by 50 % when 20 mm (HCO₃⁻+K⁺) was added (Appendix 4c describes the experiments using SHAM and CN⁻, which support this conclusion). Isolated cytochrome c oxidase from these carnation cells at a pH of 7·2 was also inhibited by 40 % at 10 mm HCO₃⁻ (Palet et al., 1991). Other experiments with root extracts also showed that isolated cytochrome c oxidase was inhibited more by NaHCO₃ than by equivalent amounts of NaCl, with competitive inhibitions of ∼60 % for soybeans and 35 % for spinach at 100 mm HCO₃⁻ and 0·2 mm CO₂ (Miller and Evans, 1956). Inhibition of the cytochrome oxidase chain by CO₂ and/or HCO₃⁻ may substantially reduce ATP synthesis by cells and tissues, but only if there is fast respiration due to a high requirement for ATP, as shown by studies with isolated turnip mitochondria; cytochrome oxidase had a high flux control coefficient of 0·47–0·66 provided the mitochondria were in state 3, i.e. had fast ATP synthesis and O₂ uptake (Padovan et al., 1989). The large inhibition of the uncoupled rate by high CO₂, as observed by Palet et al. (1991), also implies inhibitions by high CO₂ would be most prominent in tissues with fast ATP consumption, i.e. those growing rapidly, or involved in energy-dependent solute transport to the xylem. Such tissues are also those most likely to face an energy deficit under hypoxia (reviewed by Greenway and Gibbs, 2003), which may therefore be exacerbated by high P_CO2.

The possible inhibition of cytochrome c oxidase raises the question of whether acid loads lead to ethanolic fermentation, as uncoupling of oxidative phosphorylation did in early experiments by Beevers (1953). A substantial number of papers related to fruit ripening do report formation of acetaldehyde and ethanol at high P_CO2 (e.g. Mathooka, 1996), although in most studies P_CO2 was usually 60–80 kPa; this dramatic metabolic perturbation may therefore be relevant to roots in some soils that either have an initial low pH or a very high percentage organic matter (table with Fig. 3). Furthermore, lettuce leaves exposed to 20 kPa P_CO2 showed distinct increases in acetaldehyde and ethanol concentrations (Mateos et al., 1993). The response of ethanol production in roots to increases in HCO₃⁻ and/or CO₂ has not been studied.

Causes of the effects of high P_CO2 on respiration need to be further explored, and in particular there needs to be a focused investigation on the putative inhibition of the cytochrome oxidase pathway, as there is reasonable evidence that this may be a key reaction inhibited by high HCO₃–CO₂, while any inhibition in vivo may be of crucial importance to roots in waterlogged soil. Such an investigation may include exposures to more gradual increases in P_CO2 than used by Palet et al. (1991), and study of isolated enzymes, which may be the best system to test whether the inhibitory effects of high P_CO2 are due to high CO₂, high HCO₃⁻ or both.

RESPONSES TO INCREASES IN P_CO2 FROM 0·03 TO 1·0 kPa

Effects on plants of increases in CO₂ between 0·03 and 1·0 kPa are outside the theme of this review, but need some discussion given that they show the need for a relevant baseline ‘control’ for studies of elevated CO₂ in roots and leaf tissues. Responses to increases in the CO₂ range to 1 kPa influence the interpretations of existing data obtained at high P_CO2, when the ‘control’ was P_CO2 of ∼0·033 kPa. In contrast to this level of CO₂ in air, in soils P_CO2 at 30 cm depth ranged between 0·08 kPa in winter and 1 kPa in summer (Johnson et al., 1994), so use of atmospheric P_CO2 as a control level for studies of roots seems inferior to use of levels more typically experienced by roots in soils.

For leaves there is abundant evidence that even when the current CO₂ concentration in air is only doubled, i.e. to about 0·066 kPa, respiration is reduced by 20–30 % and that these inhibitions are partly due to direct effects, i.e. elicited within minutes after increase in P_CO2 (Amthor, 1997; Drake et al., 1997, 1999). In his key review, Amthor (1997) emphasized that a substantial number of these observations, on the response of respiration to doubling or trebling ambient CO₂, could be due entirely, or largely, to artefacts, such as leakage of CO₂ from the respirometer and dark fixation of CO₂. Nevertheless, Amthor (1997) considers some of the list of observations he reviewed as genuine decreases in CO₂ production.

In roots of intact Douglas fir, decreases of 37 % in CO₂ production were found when CO₂ was increased from 0·03 to 0·17 kPa (Qi et al., 1994). There were no checks on whether the increase in exogenous CO₂ increased dark fixation, although leakage from the cuvette was unlikely as reference cuvettes were used and the inhibition of CO₂ production increased only slightly when CO₂ was raised from 0·33 to 0·7 kPa. In contrast to these findings with roots of pine, increases in P_CO2 from 0·02 to 0·25 kPa in the medium did not affect respiration by roots of citrus and beans (Bouma et al., 1997); these authors could find no reason why their results differed from responses obtained by others. Qi et al. (1994) emphasized that the substantial reductions in respiration to P_CO2 in the range 0·03–1 kPa are irrelevant to roots in most soils, which, even when drained, have substantially higher P_CO2 than 0·1 kPa. Furthermore, higher CO₂ in roots than in leaves is to be expected, as ventilation of the CO₂ from roots to the surrounding solution has a much higher boundary layer resistance than diffusion between leaves and air; in an earlier section the likely gradient of P_CO2 to ventilate CO₂ evolved during respiration in excised maize roots was assessed at ∼0·25 kPa.

CONCLUSIONS

Soils

In waterlogged soils, the well-known slow diffusion of gases would result in increases in dissolved inorganic carbon. This increase in inorganic carbon would result in gradual increases in soil P_CO2. The suggestion that P_CO2 in soils during waterlogging and flooding often reaches 10–40 kPa and sometimes even 70 kPa remains quite tenuous, as it is based on only three experiments with soils in pots and a single field observation, with only one set of data for soil waterlogging without flooding. Furthermore, all the detailed observations (Fig. 3; Cho and Ponnamperuma, 1971) were based on titration of the soil solution and therefore are quantitatively insecure (see caption to Fig. 3). Thus, new experiments using direct measurement of CO₂ are needed for a range of soil types (with flooding versus waterlogging also as a variable) at the surface and at different depths below the surface. Measurements of P_CO2 in various waterlogged–flooded soils in the field should also be a high priority. There are also indications that the actual timing and the maximum P_CO2 reached depend on several factors, such as temperature, percentage organic matter, pH of the soil, ‘active’ iron and density of the vegetation, but these indications require further rigorous testing preferably by manipulations with a given soil type.

Response by plants to P_CO2 above 5 kPa

Reassuringly, the suggestion that P_CO2 in flooded soils is often high is supported by the remarkably high tolerance of rice to high P_CO2 in solution culture (Boru et al. 2003); the inference is that rice is adapted to high P_CO2, which therefore presumably occurs during at least some critical phases of its growth in paddy fields. Importantly, the 50 kPa P_CO2 used by Boru et al. (2003) was approximately twice as high as the highest P_CO2 predicted for rice roots in the preliminary model, which assumed the bulk soil was at 40 kPa CO₂ (Appendix 3a and Table 3), indicating that adverse effects of high P_CO2 on this species are unlikely. By contrast, the main root system of soybean has less gas-space continuum than in rice, and is therefore likely to experience higher P_CO2, so that the data of Boru et al. (2003) indicate, but do not prove, that this species might be adversely affected by high P_CO2 in the soil. Further evidence for genetic variability in tolerance to high P_CO2 comes from experiments on responses of leaf tissues to 10–50 kPa CO₂ (Heber et al., 1994).

The present paper has reinforced the view that tolerance to waterlogging is a multifaceted adaptation. The model predicting P_CO2 gradients that would occur when the sum of the CO₂ production by the root and influx from the soil is balanced by ventilation of CO₂ via the aerenchyma to the shoot shows that during waterlogging a large gas-space continuum would not only supply substantial O₂ to roots but also retain relatively low P_CO2. Possible metabolic adaptations are less firmly established. Growth of rice was not adversely affected by as high as 50 kPa P_CO2, even in turbulent solutions when endogenous P_CO2 would have been fairly close to exogenous P_CO2; hence, by inference, metabolism in rice plants presumably shows a higher tolerance to high CO₂/HCO₃⁻ than waterlogging-intolerant species. The predictions on high P_CO2 in roots need testing in representative ecosystems, with as the main variables different rates of CO₂ production and effective porosity of the soil, and different densities and percentage gas-filled porosities of the root systems.

‘Bulk’ P_CO2 measurements in soils and roots would provide valuable data. In soils, these could be readily supplemented using the ‘semi-microelectrodes’ that have been so successful in studies on P_CO2 in the xylem sap of trunks of trees (McGuire and Teskey, 2002, 2004). Information is also needed on the extent to which P_CO2 in the soil affects P_CO2 in the roots, and on possible diurnal cycles of P_CO2 prevailing in root sections with a tight barrier to radial O₂ loss. In waterlogged soils, different responses of genotypes might be associated with the volume of the gas-space continuum in roots, which will determine P_O2 and P_CO2 in the root tissue. For plant tissues, suitable CO₂ micro-electrodes with 2-µm tips have been developed to measure P_CO2 in stomatal cavities (Hanstein et al., 2001). These micro-electrodes are unsuitable for impaling cells (H. Felle, pers. comm.) but their application to studies in, for example, aerenchyma and xylem of plant roots, would nevertheless be an exciting advance in understanding the physiology of plants. Such measurements would be key evidence to evaluate possible effects on metabolism, as P_CO2 in the cells can be inferred in view of the high permeability of cell membranes to CO₂, while HCO₃⁻ in the cytoplasm can be assessed as long as pH_cyt is also measured.

Knowledge of responses of roots and rhizomes to the very high P_CO2 that are likely in many waterlogged soils is slender. In studies to elucidate this question there are three key issues:

(1) Use of gradual increases in P_CO2, particularly since such gradual increases are the norm in the field. These are, among others, required to test rigorously whether rice and soybean (cf. Boru et al., 2003) differ in long-term response to high exogenous P_CO2, or in ability to withstand the shock of the sudden increase in P_CO2, or both. The crucial importance of acclimatization in evaluating tolerance to a change in environmental conditions has been highlighted during studies on anoxia, when effects were much more severe following anoxic shock, than when anoxia was imposed following a hypoxic acclimatization (Drew, 1997; Gibbs and Greenway, 2003).

(2) It should be established whether any inhibitions observed at 5 kPa and higher P_CO2 present a real ecological response, i.e. the key comparisons should not be with 0·03–0·06 kPa CO₂ as found in the atmosphere, but with a P_CO2 of ∼1 kPa known to occur in drained soils.

(3) Evaluation of responses of excised, healed roots, as using roots of whole plants cannot establish tissue tolerance to high P_CO2 beyond doubt, because of possible interaction between shoots and roots.

Metabolic acclimatization

Responses to high CO₂ by zones receiving sufficient O₂, as well as possible interactions between high P_CO2 and low P_O2 in root tissues, need to be elucidated. Assessments need to be made on the relative importance of the mechanisms known to be of value for acclimatization during periods of high P_CO2, i.e. biophysical and biochemical pH stats and the lowering of the set point of pH_cyt, the latter being the only means to retain relatively low HCO₃⁻ at a given CO₂ concentration. Because optimum functioning of the cells at pH_cyt below 7·0–7·2 is unlikely (Greenway and Gibbs, 2003; Felle, 2005), high concentrations of HCO₃⁻ in the cytoplasm presumably remain inevitable in roots with a high P_CO2. This amplifies the need for studies on responses of metabolism to high concentrations of CO₂–HCO₃⁻ in roots. One of the priorities would be to establish to what extent the cytochrome oxidase pathway is inhibited by 5–40 kPa P_CO2 and/or by HCO₃⁻ in the range 100–200 mm. The indication that, in extracts, the degree of inhibition of cytochrome c oxidase by high HCO₃⁻ is species-specific is promising and should be tested for wetland and non-wetland plants. Such studies need to separate effects on metabolism of high P_CO2 and high HCO₃⁻ concentrations, as the former will always be high, while increases in HCO₃⁻ concentrations could be kept in check by lowering the set point of pH_cyt. Such issues are important even for roots of wetland species containing large volumes of aerenchyma because, in most waterlogged situations, roots are likely to experience at least 5–15 kPa P_CO2 during waterlogging lasting at least 2–3 weeks, even when part of the CO₂ will be ventilated via the aerenchyma, and also be removed in the xylem stream when plants are transpiring.

Appendix 1a. Abbreviations

PCO2	partial pressure of CO2
SPCO2	PCO2 in soil
RPCO2	PCO2 in the root in the quasi steady state
R(rc)PCO2	PCO2 component in the root associated with CO2 evolved in root catabolism
R(si)PCO2	PCO2 component in the root associated with CO2 influx from the soil
PFK (ATP)	phosphofructokinase – ATP dependent
PFK (PPi)	phosphofructokinase – PPi dependent
PPi	pyrophosphate
pHcyt	pH of cytoplasm
pHvac	pH of vacuole
pHext	pH in medium
pHstat	biochemical or biophysical reactions, which return pH to a set point, following a perturbation
D0	self-diffusion coefficient in water
ɛ	fractional porosity
τ	tortuosity of a pathway
Δ	difference in concentration between two locations

Appendix 1b. Definitions

Acid load: exposure of a tissue to a weak acid, when net uptake of its undissociated form will tend to decrease pH of the cell and cytoplasm.

Effective diffusion coefficient: the diffusion coefficient in aqueous solution multiplied by the product of fractional soil porosity (ɛ) and a tortuosity factor (τ, <1·0), which is a measure for reduced diffusion through the network of soil pores.

Set point: a value of a biological characteristic which will be restored, despite conditions which will tend to alter the value. Set points may be part of the prevailing biochemical networks, i.e. can shift if these networks change.

Waterlogging: when soil is saturated with water. This term is used for both waterlogged soils (i.e. soil can be saturated to the surface, or to any depth below the soil surface within the root zone) and flooded soils (i.e. when water is above the soil surface).

Flooding: when free water is above the soil surface.

Appendix 2a. Information on the conventions used to calculate HCO₃⁻ levels in Table 1b

HCO₃⁻ was calculated using the Henderson–Hasselbalch equation (see caption to Fig. 2). The influences on pK_a of ionic strength and temperature are from Yokota and Kitaoka (1985), who derived these values from Harned and Bonner (1945). Table 1a gives predictions for plant cell fluids; the pK_a values are for an ionic strength of 0·1 m, which was based on the following:

1. K⁺ at 80 mm (Leigh, 2001).

2. Mg²⁺ at 1·5 mm as soluble ions in cytoplasm (Zhang et al., 1997).

3. Anions as divalent species: 15 mm based on a buffering capacity of maize leaves between pH 7 and 8 (Heber et al., 1994).

4. 53 mm monovalent anions.

For soils, we have assumed a low ionic strength and hence a pK_a value of 6·3.

Appendix 2b. Assessment of possible fluctuations in P_CO2 in roots due to transpiration

Transpiration ratios for C₃ plants are 628 g H₂O g^–1 of dry matter produced (Ludlow, 1976). The water flow in the xylem per millilitre of fresh weight of root can then be assessed assuming a shoot-to-root ratio of 2, a fresh-to-dry weight ratio of the roots of 13, relative growth rates of 0·1 or 0·2 d^–1 and transpiration for 12 h d^–1. The values for the rate of water flow to the shoot were used to estimate the exit of dissolved inorganic carbon in the transpiration stream, in a similar way as was done in the text using water flow data taken from Armstrong (1979).

Appendix 2c. Assessment of CO₂ removal from rice paddy soils by percolation and by diffusion to the atmosphere

Percolation. Percolation would remove dissolved inorganic carbon (i.e. both HCO₃⁻ and CO₂); the sum of these is taken for this example as 1 mm. Assuming a percolation rate of 5 mm d^–1 (Rowell, 1988), the amount of dissolved inorganic carbon in the percolation water will be 0·5 µmol cm^–2 d^–1. Also assuming a 200-mm-deep layer, there would be removal of 0·25 × 10⁻¹² mol cm^–3 s^–1.

Diffusion to the atmosphere. Diffusion would be in the form of CO₂.

The appropriate equation is based on Armstrong (1982, eqn 10·5):

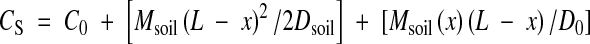where L is the total height through which the CO₂ moves (soil plus depth of water), x is the height of any water level above the soil surface, so L – x is the depth of soil from which CO₂ is escaping, C_S is the concentration in the bulk soil and C₀ the CO₂ in the atmosphere, M is the rate of CO₂ production in the soil and D_soil is the effective diffusion coefficient of the soil and D₀ the diffusion coefficient in water.

Once the depth of soil from which the produced CO₂ is lost to the atmosphere is established (i.e. L – x), the removal can be expressed as a percentage of the CO₂ production by dividing (L – x) by the depth of the soil profile which is producing CO₂.

Appendix 2d. Assessment of CO₂ removal via the roots to the atmosphere

These calculations refer to the model described in Table 3 and Appendix 3a. We can calculate the CO₂ removed from the soil from the size of radii from which CO₂ flows into the root. The percentage of the CO₂ produced in the soil profile vented through the air-space continuum of the root will depend on the root density. For example, assume a root density in which the roots are 26 mm apart; this density is chosen because with a soil production rate of 15 × 10⁻¹² mol s^–1 and a P_CO2 of 40 kPa in the bulk soil, the radii of the soil core from which the produced CO₂ flow into the root would be just touching (Table 3, column 3). Also assume 100-mm-long roots in a 200-mm-deep soil profile. The percentage lost from the soil core with a radius of 13 mm, relative to that produced in a 200-mm soil profile, would then be 5 % of the soil production. Allowing for ‘dead spaces’ between the cores, the 5 % removal from the whole soil profile would then be (3·14/4) × 5=∼4 %. For the same radius of soil core of 13 mm the percentage lost at CO₂ production rates different from 15 × 10⁻¹² mol cm^–3 s^–1 is inversely related to the rate of production.

Appendix 3a

Protocols for a preliminary model to estimate P_CO2 in the root gas-space continuum (^RP_CO2) attained when CO₂ ventilation to the shoot will balance the sum of CO₂ produced by root catabolism and the entry from CO₂ produced in the soil.

For Table 3 it is assumed that CO₂ in the soil (^SP_CO2) = 40 kPa > ^RP_CO2 and that the effective diffusion coefficient (cm² s^–1) for CO₂ in the waterlogged soil (D_soil) is derived by multiplying D₀, the diffusion coefficient in aqueous solution, by the fractional porosity (ɛ) and tortuosity (τ) of the network of pores. In Table 3, D_soil/D₀ (i.e. the product of ɛ × τ) is taken as 0·2. Effects of other values of D_soil/D₀ are shown in Fig. 6. Note that it is assumed that in no case are the soil cores from which CO₂ flows into the roots overlapping.

The protocol is then:

(A) Using eqn 1 (Armstrong, 1979) preliminary estimates are first made of the radius of the soil core (rad_s) from which CO₂ flows from the soil into the 10-mm-long root tip; reasons for choosing this site of entry are given in the text. Influxes of CO₂ over larger sections of the root would give higher P_CO2 values in the roots, but effects of other characteristics such as root porosity and length of roots would differ not in kind, only in degree.

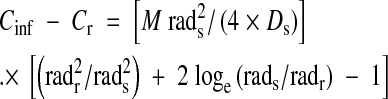(1)

C_inf is the liquid-phase CO₂ concentration (mol cm^–3) at rad_s, C_r is the liquid-phase CO₂ concentration at the root surface (and in equilibrium with the gaseous CO₂ in the root), M is the rate of CO₂ production in the soil core (mol cm^–3 s^–1), rad_r is the radius of the root and rad_s, the parameter to be determined, is the radius of the soil core from which CO₂ will flow into the root. Equation (1) is solved as follows: (1) assumptions are made on the initial ^R(rc)P_CO2 and hence C_r that would occur if the CO₂ was only via root catabolism (for conversion of P_CO2 to CO₂ concentration, see Table 1a); (2) the radius of the soil that will supply CO₂ to the root (rad_s) is then found by establishing at which rad_s the left and right sides of eqn (1) become equal.

(B) Having derived rad_s, the CO₂ production rate (mol s^–1) of a 10-mm length of this soil core (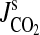) can then be calculated and this is the preliminary prediction for the CO₂ that flows from the soil into the 10-mm root tip.

(C) The next step is to calculate ^R(si)C_gr, the gas-phase CO₂ concentration in the root tip that would be required in the root to ventilate the influx, i.e. 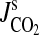, by diffusion through the root gas-space to the atmosphere, where

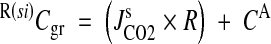(2)

where C^A is the CO₂ concentration in air, i.e. ∼0·033 kPa, and R, the gas-phase diffusive resistance of the root between root tip and atmosphere = L/(D_effective × A_x) in which L is the length of the root, D_effective = D₀ɛτ where D₀ is the diffusion coefficient of CO₂ in the gas phase of the root (Armstrong, 1979), ɛ is the fractional gas-filled porosity, τ the gas-space tortuosity (taken as 1) and A_x is the cross-sectional area of the root.

(D) By converting ^R(si)C_gr to the equivalent partial pressure of CO₂ in the tip (^R(si)P_CO2) (using Boyle's law) an initial estimate of the total CO₂ partial pressure in the tip (^RP_CO2 ) can now be made as: ^RP_CO2 = ^R(rc)P_CO2 + ^R(si)P_CO2.

(E) However, this ^RP_CO2 will be an overestimate as an increase in endogenous CO₂ will reduce the CO₂ concentration gradient between the soil and the root and hence reduce the flux; hence, steps A to D need to be repeated, after first converting ^RP_CO2 to a new liquid-phase CO₂ concentration to substitute for C_r in eqn (1). The steps are repeated until convergence to a constant ^RP_CO2 is reached when the sum of CO₂ produced in the root and the CO₂ influx into the root balances the outflow through the gas-filled porosity of the root.

Appendix 3b

Procedures to calculate CO₂ production, and to compare rates of measured CO₂ production by soil with increases in ^SP_CO2 with time

(1) Production rates in soils. The available data were given by Yao et al. (1999) in µmol g^–1 d. wt of soil d^–1 for 16 paddy soils. For our calculations, to be used in Table 3, we expressed these rates per cm^–3 of soil, using a total soil porosity of 50 % (mean value for clays of three large surveys reported by Ahuja et al., 1999) and a density of soil solids of 2·6 g cm^–3 (Nobel, 1974).

(2) Comparison with measured increases of P_CO2 in soils. Comparisons between soil production rates and ^SP_CO2 require, into addition to the rates as calculated in part 1 of this appendix, an assumption on the soil pH at the time of the ^SP_CO2 measurements. Other data show that pH in waterlogged soils is usually between 6·7 and 7·0, unless the soil is very low in reducible iron (Ponnamperuma, 1984). For the calculation of the dissolved inorganic carbon in the soil in pots of Ponnamperuma, assumptions were: a soil with a pH of 6·75 at 10–14 d after the start of flooding, and a pK_a of 6·3 for the CO₂–HCO₃⁻ equilibrium.

Appendix 4a. Paper by Good and Patrick (1987)

(1) Procedure to calculate CO₂ in the roots

The extract obtained at pH 2·5 will include unknown amounts of dissolved inorganic carbon present in vivo as HCO₃⁻. This procedure would not introduce a serious error due to HCO₃⁻ present in the vacuole, which will be very low as in five of six cases pH_vac of roots was 4·6–5·6 (Kurkdjian and Guern, 1989), i.e. nearly all the dissolved inorganic carbon would be present as CO₂. However, much of the dissolved inorganic carbon in the cytoplasm will be in the form of HCO₃⁻; and this would lead to substantial overestimates of P_CO2, when the roots are extracted at low pH. Assuming a pH_cyt of 7·5 and volumes of either 5 or 10 % of the cell, then 46 or 72 % of the extracted inorganic carbon would have been in the form of HCO₃⁻ and P_CO2 would have been 5·4 or 2·8 kPa, rather than the reported 10 kPa.

(2) Comment on assessed P_CO2 values

The CO₂ pressures assessed in section 1 are quite low, presumably, at least partly due to the 9 months of flooding, as P_CO2 in flooded soils typically reaches a maximum during the first 2–4 weeks of flooding (Fig. 3).

Appendix 4b. Papers by Palta and Nobel (1989) and Nobel and Palta (1989)

Survival

The second criterion used by Palta and Nobel (1989) to assess survival, that the CO₂ evolution was zero when the roots were returned from 2 to 0·1 kPa CO₂, needs verification as no detailed data were given, i.e. the time over which the observations were taken was not reported. (Use of neutral red staining was the first criterion.)

Measurement of respiration

Any new experiments of these adverse responses of respiration to CO₂ as low as 2 kPa by roots of cacti (Nobel and Palta, 1989; Palta and Nobel, 1989) would preferably include measurements on O₂ uptake, to complement the CO₂ data, for several reasons.

O₂ uptake would be a more direct measurement of respiration and avoids confounding by: (1) CO₂ dark fixation, which would lower the respiratory quotient, i.e. underestimate respiration; (2) possible CO₂ efflux to the shoot either in the gas-space continuum, or in the xylem stream, leading to underestimates of respiration, which would increase with increasing exogenous CO₂ concentration. The gas-space continuum would of course also reduce the measurements on O₂ uptake from the medium, but that underestimate would not be dependent on exogenous CO₂, unless high CO₂ reduced respiration. Data on porosities of these roots would reveal whether substantial ventilation to the shoot is likely.

In view of these complications, it would be preferable to obtain measurements on excised roots, which are healed, i.e. incubated until the trauma of excision is overcome.

Appendix 4c. Experiments by Palet et al. (1991)

(1) In the key experiment by Palet et al. (1991) on inhibition of cytochrome oxidase, the SHAM-sensitive chain (i.e. alternative oxidase pathway) was inhibited prior to addition of the uncoupler CCCP, while addition of 1 mm cyanide at the end of the experiment showed the cytochrome oxidase pathway had remained operational (Palet et al., 1991).

(2) In Palet et al.'s experiments, increases in the rate of O₂ uptake elicited by adding CO₂ were higher than the rate increases following addition of HCO₃⁻, pH_ext before addition was 5·7 and we estimate the P_CO2 in the experiment with added HCO₃⁻ at ∼30 kPa, i.e. much higher than the 5·5 kPa imposed by addition of CO₂. This discrepancy is presumably associated with slow conversion of CO₂ to H₂CO₃, as supported by experiments with addition of carbonic anhydrase in Palet et al. (1991).