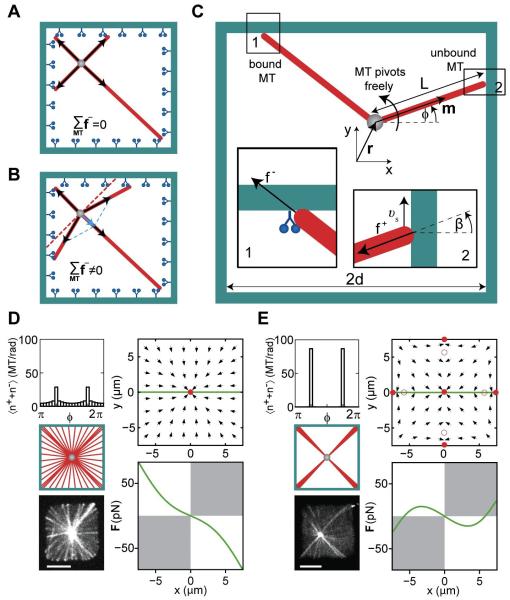
Figure 6. Theory of aster positioning.

Cartoon showing the net pulling force without (A) and with MT slipping (B). (C) Schematic representation of a MT organizing center at r=(x,y) in a confining geometry. The MT orientation is described by the angle φ, the MT length is denoted by L. Inset 1 shows a MT under pulling force f⁻. Inset 2 shows a MT under pushing force f⁺, which slips along the wall with velocity ν_s. The angle between the MT orientation and the normal to the boundary is β. (D,E) Angular MT distributions and the corresponding force direction fields for a MT organizing center in a chamber with (D; k_b=0.02 s⁻¹) and without dynein (E; k_b =0 s⁻¹). Full and hollow red circles show the stable and unstable force-balanced states, and the green line indicates the positions for which the forces are shown below. White quadrants indicate where the force is centering. Other parameters (see Box 1) are k_cat = 10⁻⁴ s⁻¹, k_off = 10⁻³ s⁻¹, = 5 pN, ζ = 5·10⁻⁵ N·s/m, κ = 3.3·10⁻²³ Nm², M=50. For comparison, images of a MT aster in a microfabricated chamber with (D), and without dynein (E) are shown. Scalebars indicate 5 μm.