Onset of Sheath Extension and Duration of Lamina Extension are Major Determinants of the Response of Maize Lamina Length to Plant Density

Abstract

• Background and Aims Plants regulate their architecture strongly in response to density, and there is evidence that this involves changes in the duration of leaf extension. This questions the approximation, central in crop models, that development follows a fixed thermal time schedule. The aim of this research is to investigate, using maize as a model, how the kinetics of extension of grass leaves change with density, and to propose directions for inclusion of this regulation in plant models.

• Methods Periodic dissection of plants allowed the establishment of the kinetics of lamina and sheath extension for two contrasting sowing densities. The temperature of the growing zone was measured with thermocouples. Two-phase (exponential plus linear) models were fitted to the data, allowing analysis of the timing of the phase changes of extension, and the extension rate of sheaths and blades during both phases.

• Key Results The duration of lamina extension dictated the variation in lamina length between treatments. The lower phytomers were longer at high density, with delayed onset of sheath extension allowing more time for the lamina to extend. In the upper phytomers—which were shorter at high density—the laminae had a lower relative extension rate (RER) in the exponential phase and delayed onset of linear extension, and less time available for extension since early sheath extension was not delayed.

• Conclusions The relative timing of the onset of fast extension of the lamina with that of sheath development is the main determinant of the response of lamina length to density. Evidence is presented that the contrasting behaviour of lower and upper phytomers is related to differing regulation of sheath ontogeny before and after panicle initiation. A conceptual model is proposed to explain how the observed asynchrony between lamina and sheath development is regulated.

INTRODUCTION

Understanding how plants regulate their leaf area in response to density is of great importance for a range of problems such as determination of optimal sowing density or understanding crop–weed competition. The major types of density regulation include the repression of tillering and the variation of leaf size. In maize, tillering is inhibited even at low population densities (Tetio-Kagho and Gardner, 1988; Moulia et al., 1999; Maddonni et al., 2002). As a consequence, regulation of leaf expansion is the major degree of freedom via which maize plants adapt their leaf area in usual and high population densities.

Individual leaf area is determined by regulation of its width and length, and a limited number of studies have investigated how each of these two components changes with density (Sonohat Popa, 1997; Sonohat and Bonhomme, 1998; Bos, 1999; Fournier, 2000; Pommel et al., 2001). Leaf width is always reduced at higher density, but length shows a more complex behaviour, with the length of the leaves of earlier phytomers increased (or possibly remaining unchanged for the very lowest leaves), and that of higher phytomers decreased. For higher densities, the greater length of the lower leaves is probably partly due to photomorphogenetic responses to enrichment in far-red light (Casal et al., 1987; Kasperbauer and Karlen, 1994; Ballaré and Casal, 2000). On the other hand, at higher density, the extension of the upper leaves occurs with a lower level of PAR light per unit leaf area (Fournier and Andrieu, 1999), thus possibly reducing carbohydrate availability for the growth zone. However, there is substantial evidence, reported below, that effects are more complex than individual leaf extension rate responses to its growth environment, and this study aims at a better identification of the processes involved.

It has been observed in maize (Smith, 1981) and barley (Skinner and Simmons, 1993) that manipulation of light quality resulted in changes in the rate of leaf extension without changes to the duration of extension. On the other hand, Bos (1999) found that an increase in the duration of extension played the major role in the increased length of maize leaves in response to density or shading. A possible explanation for these conflicting results is that, in grasses, the length of the sheath tube formed by the lower leaves plays a role in determining the extension of the new leaves that grow inside. Artificial lengthening or shortening of the sheath tube results in large changes in the final lamina and sheath length of growing leaves (Davies, 1983; Wilson, 1985; Casey et al., 1999). B. Andrieu (unpubl. res.) found that this also occurred in maize. This occurs through a change in the size of the elongation zone, and possibly also because the emergence of the lamina out of the sheath tube may trigger the differentiation of the sheath–lamina boundary (Skinner and Nelson, 1994, 1995; Arredondo and Schnyder, 2003; Fournier et al., 2005). In maize, high density (Fournier, 2000 and results reported herein) and low irradiance (Fournier and Andrieu, 2000) result in an increase in the sheath length for phytomers 1– 6. Thus, the response of sheath and lamina length to density is likely to include a response to the enlarged sheath tube, and thus to the environment perceived during the growth of the earlier phytomers, that confounds with the direct responses of the leaf to the external environment it perceives.

For leaves of upper phytomers, a response to lower light availability may or may not be part of the response to density. Very low carbohydrate concentrations do limit the rate of grass leaf extension (Kemp, 1981), and numerous studies (e.g. Bos and Neuteboom, 1998, for wheat; Bos, 1999, for maize) have shown a decrease in the rate of leaf appearance at lower values of photosynthetic photon flux density (PPFD). This effect is, however, only significant for the range of values of PPFD generally found in plant cabinet conditions rather than in field conditions. Tardieu et al. (1999) showed that leaf extension is largely independent of carbon budget when the leaf is autotrophic. Even when the growing zone of a leaf is an important sink for carbohydrate, the plant is able to mobilize pools of resources and adapt leaf specific area and width so that the leaf extension rate is highly buffered against changes in plant carbohydrate availability (Lattanzi et al., 2004). Fricke (2002) reduced the carbohydrate availability by various means in barley leaves, and found that although the rate of extension of leaves was affected, a nearly invariant final length was achieved through compensation between a lower extension rate and a longer duration. Finally, the shorter length of leaves of upper phytomers in maize grown at high density does not appear to be a straightforward consequence of what is known about the regulation of leaf extension by carbohydrate availability.

In order to obtain a better understanding of how maize leaf length is regulated with density, a detailed analysis of the extension of successive laminae and sheaths along the shoot was performed in two contrasting density treatments. The kinetics of extension can be viewed as resulting from a succession of phases in the functioning of the growing zone. In a previous report (Hillier et al., 2005), the arguments for such a view were reviewed and the methodological aspects related to the estimation of the parameters of multiphase models for organ extension were presented. In the current work, these methods are used to investigate how these parameters vary for successive leaves along the shoot and are how they are modulated with plant density.

MATERIALS AND METHODS

Experiments were carried out at the INRA campus of Thiverval-Grignon, France (48 °51′N, 1 °58′E) on a silty loam soil (Typic Eutrochrept, Soil Survey Staff, 1996, silt 70 %, clay 23 %, sand 7 %), fertilized with 140 kg ha⁻¹ N, 100 kg ha⁻¹ P₂O₅, 100 kg ha⁻¹ K₂O, before sowing. The hybrid Zea mays L. ‘Déa’ was sown on 15 May 2000, at two contrasting densities: 9·5 and 30·5 plants m⁻². They will be referred to below as normal density (ND) and high density (HD), respectively. Plots were irrigated regularly and weeds were carefully controlled by application of 0·8 kg ha⁻¹ of atrazine and 0·5 kg ha⁻¹ of Diplome (Bayer) at sowing, and then later manually. Complementary 30 kg ha⁻¹ N was applied as a spray on both treatments on 23 June 2000 (340 °Cd after sowing, corresponding to leaf stage 10·6). It is assumed that this late spray did not significantly interfere with leaf extension: in ‘Déa’, consistent with what is reported on other maize varieties (Vos et al., 2005), it was observed in parallel experiments (unpubl. res.) that plants grown in contrasted nitrogen treatments (application of 180 kg ha⁻¹ N vs. 40 kg ha⁻¹ N at sowing) did not differ in the rate of tip and collar appearance, and differed by <5 cm in leaf length. To illustrate that the results presented are representative of the effect of density, data from three other experiments on the same location and soil will be shown when available.

Monitoring plant development

Fifteen plants in each treatment were tagged at the time at which leaf 3 was exposed. Leaves are counted acropetally, with leaf 1 being the first complete leaf. Cotyledon and coleoptile are not taken into account. Plants were chosen so that their development was close to that of the median plant for that treatment. Two or three times a week, the number of visible and collared leaves, the exposed length, L_e, of the two youngest visible leaves and the length of the youngest mature laminae were measured for each of the tagged plants. L_e was measured as the distance from leaf tip to the V formed by the previous leaf. The median values for these lengths served as references to select between two and four (usually three) plants, which were dissected to enable measurement of the length of all sheaths, laminae and internodes. Internode data are not shown herein, as they were used only to estimate the time at which the plant apex reached the soil level or when leaf tips emerged from the sheath tube. Destructive measurements took place on the same days as non-destructive measurements from stage V3 until the end of extension. They were performed under a binocular microscope (maximum magnification 50×) for the early stages of development, and with a ruler once the dimension of the organ exceeded 1 cm.

Meteorological measurements and calculation of thermal time

In both treatments, the temperature of the soil at 3·5 cm depth, within a row and within 1–2 cm of a plant, was monitored in four places with thermocouples. Once the apices reached the level of the soil, the temperature of the growing zone was estimated using two thermocouples per treatment, inserted behind a sheath, and repositioned regularly to maintain them at the height of the shoot apex (as controlled by dissection of similar plants). The thermocouples were inserted on the north part of the stem, to avoid direct sunlight on the sheath enclosing the thermocouple. The temperature measured in this way is representative of that of the growing zone (Birch et al., 2002; Fortineau et al., 2002). Data from equivalent thermocouples were consistent and were averaged. The temperature of the leaf growing zone was assumed to be that of the soil when the apex was below soil level, and thereafter that monitored within the sheaths. Thermal time was calculated on an hourly basis, considering a linear dependence with temperature and T_base = 9·7 °C. Unless otherwise specified, it is given as the thermal time from sowing.

Decimal leaf stage and decimal plastochron index

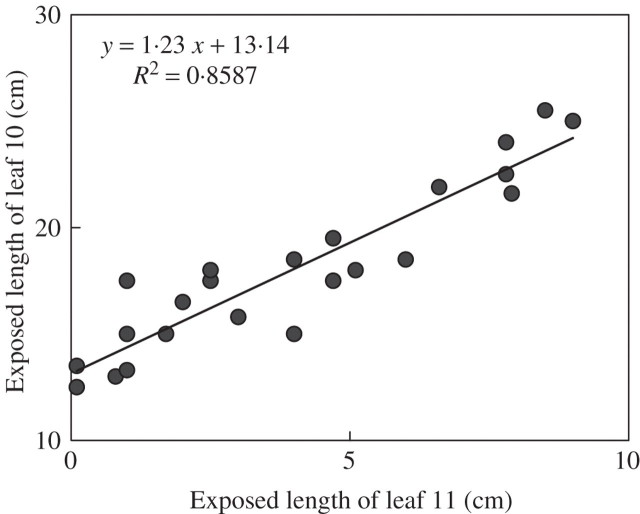
A decimal leaf stage (DLS) index was derived to ensure continuity of the index between successive leaf appearances. At each date, the exposed lengths of the two youngest visible leaves were measured on tagged and collected plants. It was then verified (data not shown) that L_e could be approximated as a linear function of thermal time. Scatter plots of L_e(n) vs. L_e(n + 1) were calculated for every pair (n, n + 1) of phytomers and a linear model L_e(n) = L_e0(n) + a L_e(n + 1) was fitted. Coefficients of determination, r², were generally higher than 0·8 (see Fig. 1 for n = 10). The intercept L_e0(n), representing the exposed length of leaf n when the tip of leaf n + 1 is just visible, was estimated for each leaf position in each treatment. The DLS was calculated as DLS = n + L_e(n)/L_e0(n), where n is the number of visible leaves. DLS is equal to n when leaf n is just exposed, and then increases linearly with the length of the exposed part of leaf n to obtain the value n + 1 when L_e(n) = L_e0(n) – which corresponds to leaf n + 1 being just exposed.

Fig. 1.

Scatter plot of the length of the exposed part of lamina 10 vs. the length of the exposed part of lamina 11, for hybrid maize ‘Déa’ at normal density.

The plastochron index (PI; Erickson and Michelini, 1957) was calculated in order to have a decimal count of the number of leaves formed by the apex. This requires the definition of a length L_min at which a leaf is considered to be formed. It was possible to distinguish leaf primordia from a size of approx. 25 µm, but L_min = 250 µm was chosen to allow an accurate estimate. Independently of treatment, a constant ratio was observed between lengths of successive leaves in the early stages of growth [L(n) = 2·03 L(n + 1), r² = 0·85]. Thus PI = n + [log(L(n)) − log(L_min)]/log(2·03), where L_min is the reference size, n is the number of leaves longer than L_min, and L(n) is the length of the youngest leaf. PI takes the value n when n leaves have been formed and the youngest of them is exactly the reference size. PI then increases continuously with L(n) and tends toward n + 1 when L(n)/L_min tends to 2·03, meaning that the next leaf primordium is about to reach the reference size L_min.

Selection of homogeneous plants

The analysis presented does not aim at representing the average characteristics of the crop, but the behaviour of a ‘median’ plant. Thus, the selection process described below was made to ensure that measurements were taken from plants following the more frequent behaviour.

When dissected, the plants were checked for homogeneity of mature leaf size and final leaf number. Before leaf 10 was fully grown, plants were disregarded if the length of the youngest mature lamina differed by >10 % from the average for that leaf over tagged plants. After lamina 10 was fully grown, the selection was based on the length of lamina 10. After panicle initiation, it was possible to establish the final number of leaves—which was found to vary between 14 and 16, being 15 in 70 % of the samples. Thus, after panicle initiation, only data from plants having produced exactly 15 leaves were considered for analysis.

DLS and date of collar appearance were calculated from a subset of five plants per treatment, out of the 15 plants initially tagged and non-destructively monitored. The criteria for selecting that subset was that the plants produced 15 leaves, and that mature size of leaves and thermal time of flag leaf appearance were close to the median for that treatment.

Parameterization and fitting

The choice of models and the fitting procedures are described in Hillier et al. (2005), and for detailed information on these matters, reader are referred to that paper. Only a brief description is given here. A model possessing two distinct growth phases was used to describe lamina and sheath extension as functions of thermal time, the first phase being exponential in character, the second linear. The model includes a plateau, corresponding to the period where extension is complete. The phases are given explicitly as follows,

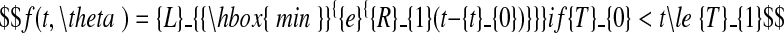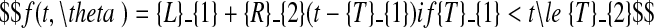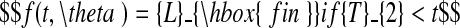T₀ (°Cd) is the point in thermal time at which the model begins, which corresponds to the moment when L = L_min; L_min was taken to be 0·25 mm for laminae and 3 mm for sheaths. T₁ and T₂ ( °Cd) are respectively the thermal time of the change from exponential to linear extension, and of the end of extension. R₁ ( °C⁻¹ d⁻¹) is the relative extension rate (RER) during the exponential phase and R₂ (cm °C⁻¹ d⁻¹) is the linear extension rate (LER) during the linear phase. L_fin is the final length of the organ.

The following constraints ensure continuity of the model function at the two phase transitions

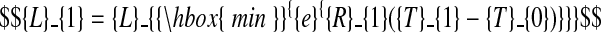(C.1)

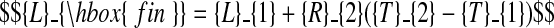(C.2)

For laminae, but not for sheaths, the data also suggested continuity of the first derivative at T₁ (the exponential-to-linear phase change). This constraint, when imposed, may be expressed thus:

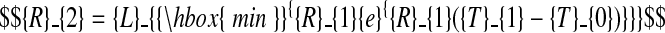(C.3)

For laminae, T₀ was not estimated along with the other parameters: it was instead calculated from the linear regression of the PI with thermal time. This means that for sheaths, there were five parameters to be estimated: T₀, R₁, T₁, R₂ and T₂, whereas for laminae there were only three: R₁, T₁ and T₂, since R₂ is also given by the constraint C.3. These parameters have been estimated where possible for sheaths and laminae according to the criterion of maximum likelihood and using the function gnls in the statistical software package ‘R’ (R, http://www.r-project.org; see, for example, Ellner, 2001; Ripley, 2001).

Statistical analysis

For the estimates of model parameters, as well as for combinations of parameters, such as the final length L_fin (calculated from Equation C.2) or the phase durations, calculated as T₁ − T₀ and T₂ − T₁, confidence intervals at the 5 % level were calculated using a non-parametric Bootstrap method (Efron and Tibshirani, 1993). Details of the procedure are given in Hillier et al. (2005). For those phytomers for which the model could not be fitted, final organ lengths were calculated from measurements of mature organs only, and confidence intervals at the 5 % level were calculated considering a Student distribution.

For DLS, data given are means calculated over the subset of five median plants per treatment, selected out of the 15 plants initially tagged. Confidence intervals at the 5 % level were calculated considering a Student distribution of measurements. For collar appearance, data are from the same subset of plant as for DLS. Thermal time of appearance of the collar of leaf n was estimated as the mean between the thermal time at the first day of measurement where a collar had appeared on >50 % of plants and that of the previous day of measurement. Confidence intervals were estimated as ± half the thermal time difference between these two dates. Data for the PI represent measurements on individual plants so confidence intervals could not be estimated.

Complementary data

The agronomic treatments in these experiments were similar to those in 2000, except that no late spray of nitrogen was applied. Data collection and analyses were highly similar to those for 2000, except for the differences listed below.

Mature lamina and sheath length were collected for ‘Déa’ sown on 28 April 1999 at a density of 30 plants m⁻². Data are means calculated over 10–20 plants with 15 leaves, out of 30 plants identified as close to the median of the plot and tagged at the time at which leaf 4 was exposed.

The kinetics of leaf tip and collar appearance were collected for hybrid ‘Nobilis’ sown on 15 May 2000 at a density of 9·5 plants m⁻². Data are from ten plants with 15 leaves, out of 15 plants identified as close to the median of the plot and tagged at the time at which leaf 4 was exposed. Data collection and processing, including the measurement of organ temperature, were as for the main experiment.

The kinetics of lamina and sheath extension were monitored for hybrid ‘Nobilis’ sown on 6 May 1998 at a density of 9·5 plants m⁻². The data collection and processing were identical to those for the main experiment, except that organ temperature was not monitored. Thermal time up to the appearance of leaf 13 was estimated from leaf stage, using the thermal time–leaf stage relationship established for that cultivar in 2000 (see above). At late stages of development, apex temperature is very close to the temperature measured in a Stevenson screen. As such, the accumulation of thermal time after appearance of leaf 13 was calculated based on the measurements at the meteorological station. This allowed the parameters of the multiphase models of extension to be fitted; however, because of possible biases between actual and estimated temperature sums, only results that are not expressed in thermal time units will be shown.

RESULTS

Rate of shoot development and final size of organs

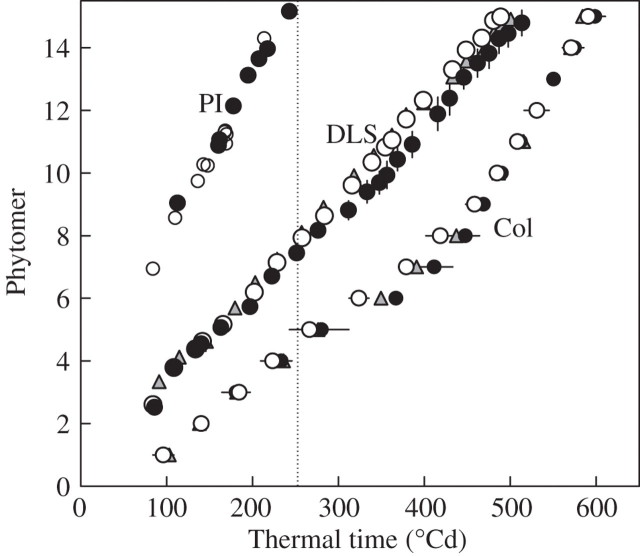
Figure 2 shows the thermal time course of the PI, DLS and number of collared leaves. Germination (radicle between 0·5 and 1 cm) occurred in all treatments 50 °Cd after sowing.

Fig. 2.

Plastochron index (PI), decimal leaf stage (DLS) and timing of collar appearance (Col) as functions of thermal time since sowing. Data are for ‘Déa’ at normal density (open circles) and high density (filled circles), and ‘Nobilis’ at normal density in 2000 (triangles). The dotted line shows the time of panicle initiation. For DLS, vertical bars show confidence intervals (±2 s.e.), when larger than the size of the symbols. For timing of collar appearance, horizontal bars show the thermal time interval between two successive dates of measurements.

The DLS curve shows that, in all treatments, the first three or four leaves appeared at a higher rate than the upper ones. DLS then progressed linearly with thermal time from stages 4·5 to 12·5 in all ND treatments (r² = 0·998). For the upper two or three leaves, the slope of DLS against thermal time tended to decrease, and the estimation of DLS was also less accurate due to variability in the shape of the whorl.

In the ND treatments, the phyllochron within the range [4·5 < DLS < 12·5] was 33·2 °Cd, being identical in ‘Nobilis’ and ‘Déa’. In the HD treatment, the appearance of leaf 9 was delayed (Fig. 2), but thermal time intervals between the appearances of other leaves were the same as in the ND treatment.

The PI was calculated for ‘Déa’ only and found to be linearly related to the DLS, in agreement with the results of Lejeune and Bernier (1996). No difference was found between treatments. Consistent with the identical rate of DLS for lower leaves, the PI was identical in all treatments (19·2 °Cd). Panicle initiation in ‘Déa’, estimated as the moment when the apex reached 0·5 mm, occurred 237 ± 10 °Cd after sowing (DLS = 7·2) in ND and HD treatments.

Timing of collar appearance was found to be nearly identical between density treatments for the bottom phytomers (1–4) and, more remarkably, for the highest phytomers (10–15). However, collars of intermediate leaves appeared later in HD compared with ND, differences being larger than the confidence intervals for leaves 6 and 7. How the timing of collar appearance relates to the kinetics of leaf extension will be discussed later.

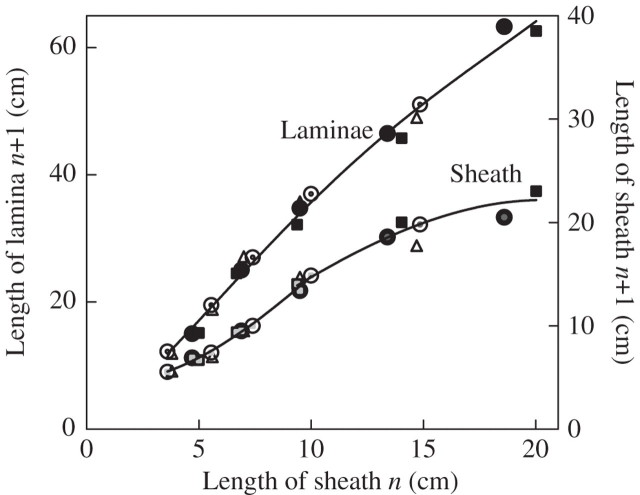
Figure 3 presents the lengths of mature laminae and sheaths as a function of leaf number. Each point is the measured length averaged over between 15 and 30 mature leaves. When a model could be fitted (see below), calculation of L_fin yielded the same results to within a few millimetres. The lengths of laminae 1–7 and sheaths 1–5 were identical in all ND treatments, differences between ‘Déa’ and ‘Nobilis’ occurring for laminae 9 and above and for sheath 6 and above—being longer in ‘Déa’ than in ‘Nobilis’. The effect of density was, however, significant from the first leaf on sheaths and laminae (P < 0·001). In agreement with what has been reported in previous studies, lower phytomers were longer in HD than in ND, whereas for upper phytomers (from sheath 7 and lamina 10) the opposite occurred. Figure 4 compares the mean final length of the sheath or lamina of leaf n + 1 with the mean final length of the sheath of the previous leaf (n) for n = 1–5. It shows that the relationships hold independently of density and cultivar, except for a slightly lower plateau in ‘Nobilis’ than in ‘Déa’ for the relationship between sheath n and sheath n + 1.

Fig. 3.

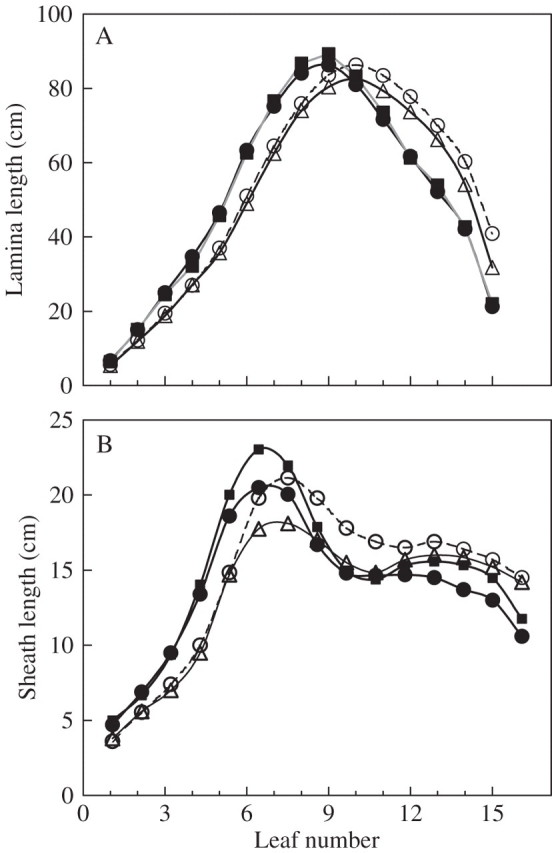
Final length of (A) laminae and (B) sheaths of successive phytomers along the shoot. Data are for ‘Déa’ at normal density (open circles) and high density (filled cicles), for ‘Nobilis’ at normal density in 1998 (triangles) and ‘Déa’ at high density in 1999 (squares). Confidence intervals (±2 s.e.) are smaller than the size of the symbols.

Fig. 4.

The final length of sheaths and laminae 2–6 plotted against the length of the sheath in the preceding leaf (1–5). Data are for ‘Déa’ at normal density (open circles) and high density (filled circles), for ‘Nobilis’ at normal density in 1998 (triangles) and ‘Déa’ at high density in 1999 (squares). Confidence intervals (±2 s.e.) are smaller than the size of the symbols.

Kinetics of laminae extension

The two-phase kinetics models were attempted for the HD and ND treatments in ‘Déa’ in 2000 and in ‘Nobilis’ in 1998. The models could be appropriately fitted to the extension of laminae 4–15 in all treatments. Phytomers 1–3 could not be fitted due to insufficient data. Similar values of model parameters were found in ND treatments for both cultivars. Those differences in parameter values might partly result from the indirect estimation of growing zone temperature for ‘Nobilis’ in 1998. For this reason, only ‘Déa’ data sets will be considered for the analysis of the kinetics of leaf extension.

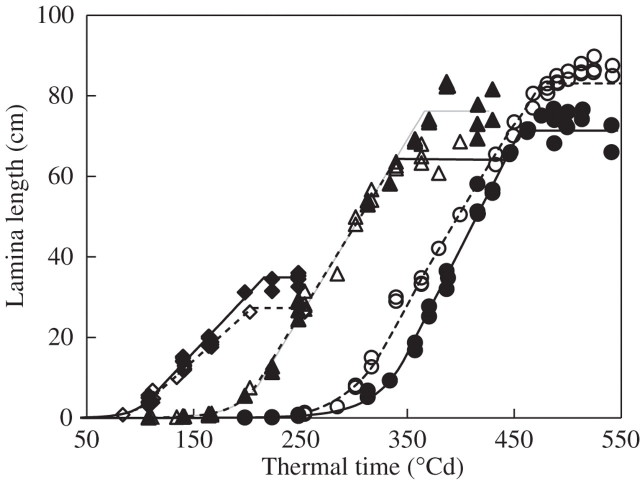
Figure 5 shows the kinetics of lamina extension for phytomers 4, 7 and 11, which illustrate the contrasting behaviour of lower and upper phytomers: phytomers 4–6 showed a higher R₂ and a longer duration of linear extension in HD than in ND. For phytomers 7–9, which were also longer in HD than in ND, the only difference in the kinetics of extension was a longer duration of the linear phase of extension in HD—resulting in the greater final length. The higher phytomers, which were shorter in HD, showed a reduced RER in the exponential phase, delayed onset of linear extension and a higher LER during this phase, with the end of extension taking place nearly simultaneously in both treatments. In this case, the shorter duration of the linear extension phase in HD more than compensated for the higher rate of linear extension and resulted in the reduced final length.

Fig. 5.

Extension of lamina 4 (triangles), 7 (diamonds) and 11 (circles), for ‘Déa’ at normal density (open symbols) and high density (filled symbols). Symbols are for the measurements, and lines show the model simulations with parameters fitted.

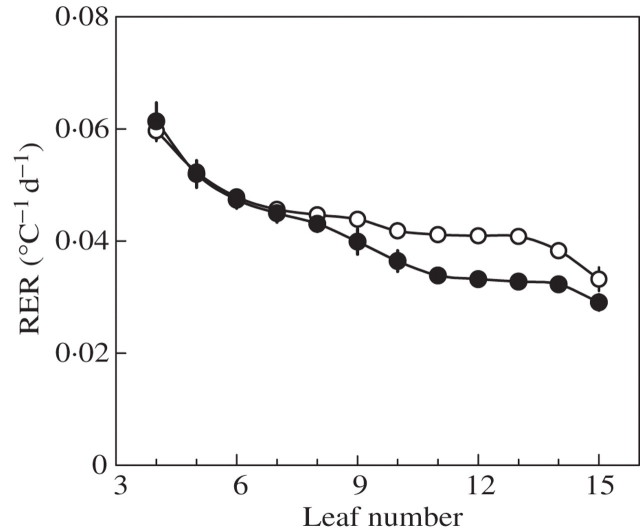
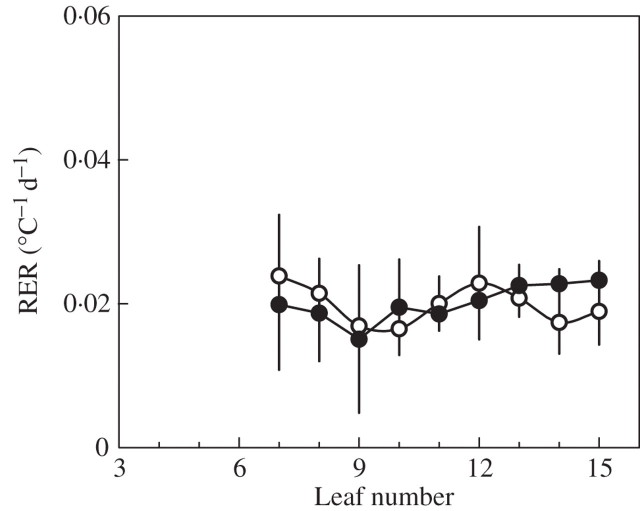
The RER during exponential extension is shown in Fig. 6. In both treatments R₁ decreased with leaf number, with a plateau for phytomers 10–13 (ND) or 11–14 (HD). R₁ did not differ between treatments for lower phytomers, whereas the decrease was much greater in HD than in ND for phytomers 8–11. Consequentially, R₁ at the plateau was lower in HD (0·032 °C⁻¹ d⁻¹) than ND (0·041 °C⁻¹ d⁻¹). In both cases, the R₁ of the topmost leaf was below that of the plateau.

Fig. 6.

Relative extension rate of laminae during the exponential phase (R₁). Data are for ‘Déa’ at normal density (open circles) and high density (filled circles). Vertical bars show confidence intervals (±2 s.e.).

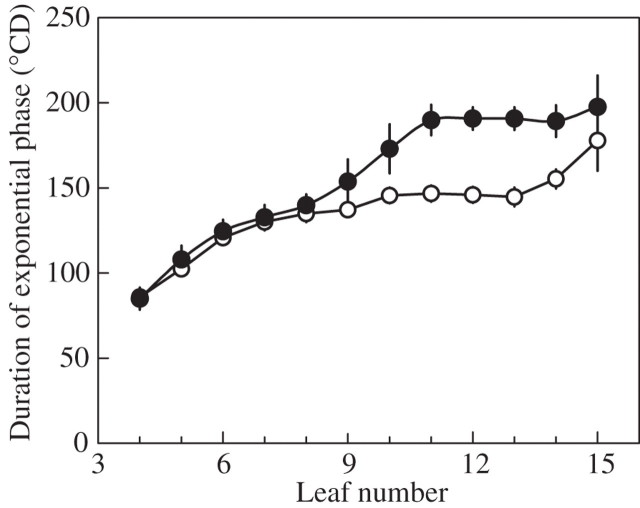
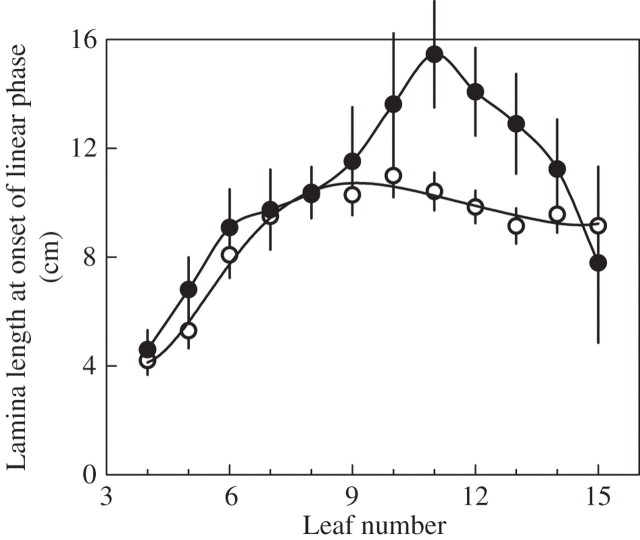
The duration of the exponential phase (Fig. 7) increased with leaf number, then reached a plateau. However, the increase above leaf 8 was very small in ND and the plateau was achieved by leaf 10, whereas the sharp increase in duration continued up to leaf 11 in the HD treatment. As a consequence, lamina length (L₁) at the end of the exponential phase followed a pattern (Fig. 8) very different from that of R₁, L₁ increasing in a similar way for both treatments up to and including leaf 9, then reaching a plateau in ND, but increasing sharply in HD up to leaf 11.

Fig. 7.

Duration of the exponential phase of laminae extension. Data are for ‘Déa’ at normal density (open circles) and high density (filled circles). Vertical bars show confidence intervals (±2 s.e.)

Fig. 8.

Length of laminae at onset of the linear phase. Data are for ‘Déa’ at normal density (open circles) and high density (filled circles). Vertical bars show confidence intervals (±2 s.e.).

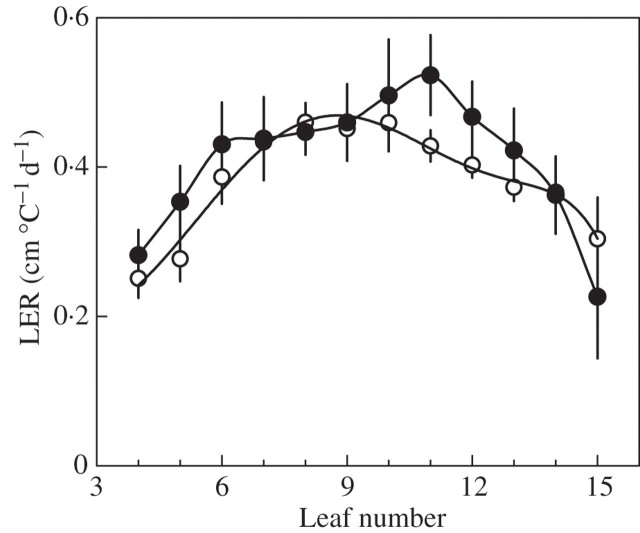
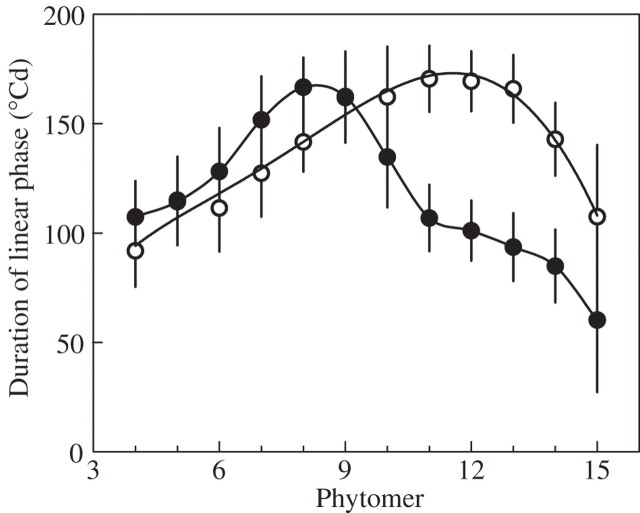
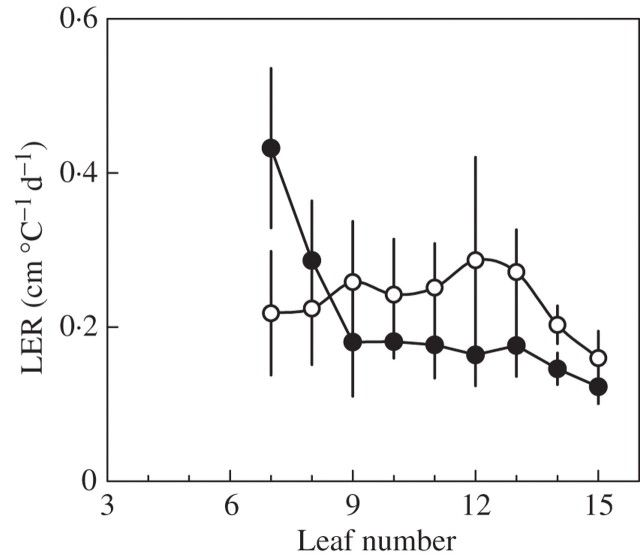
The LER and duration of the linear phase are shown in Figs 9 and 10, respectively. For phytomers 4–6, R₂ was higher in HD than in ND. For phytomers 7–9, R₂ was the same in both treatments, and an increased duration of linear extension was responsible for longer laminae in the HD treatment. For phytomers 10–13, R₂ was higher in HD, the difference being significant for leaves 11 and 12; however, the duration of extension decreased dramatically with leaf number. As a consequence, laminae were shorter in HD, despite some compensation due to the increased rate of extension.

Fig. 9.

Linear extension rate of laminae during the linear phase (R₂). Data are for ‘Déa’ at normal density (open circles) and high density (filled circles). Vertical bars show confidence intervals (±2 s.e.).

Fig. 10.

Duration of the linear phase of extension of laminae. Data are for ‘Déa’ at normal density (open circles) and high density (filled circles). Vertical bars show confidence intervals (±2 s.e.).

Kinetics of sheath extension

The extension kinetics of sheaths 6 and above were fitted with an exponential + linear model, in which a discontinuity in the rate of extension was permitted at the transition between exponential and linear phases. This discontinuity occurred for sheath lengths in the range 1·5–3 cm, which is approximately the size of the epidermal division zone alone (Tardieu et al., 2000). This means that phase 2 of sheath extension represents mainly the trajectory of the ligule in the region of cell division, and phase 2 includes most of the trajectory of the ligule in the region of cell elongation, and thus the rate of extension is not likely to be constant during this stage. In this respect, the two phases of the sheath extension model do not correspond to the phases in lamina extension.

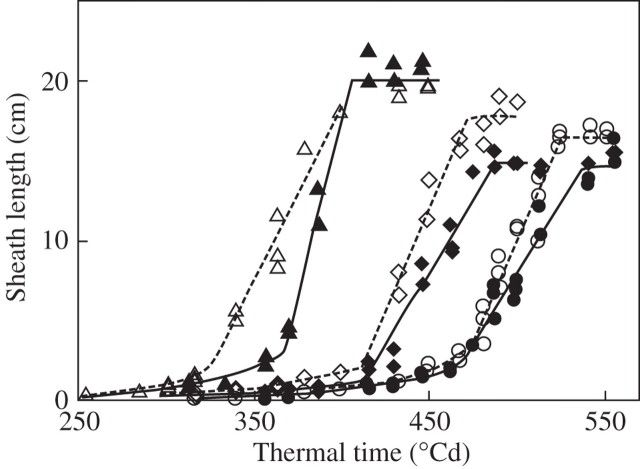
The extension of sheaths 7, 9 and 11 (Fig. 11) illustrates the range of kinetics found for all phytomers studied. The sheath of leaf 7 achieved a size of 1 cm almost synchronously in both treatments. However, in ND, the extension accelerated rapidly when sheaths reached 1 cm, whereas for HD this acceleration took place 50 °Cd later (sheath length approx. 2 cm). The same occurred for leaf 6 (not shown). For lower phytomers, fewer data were available, but they are compatible with the idea that (a) early development of the sheath (0·3–1 cm) was similar in both treatments; and (b) the change to fast extension took place later in HD than in ND—when the sheath was longer. A different pattern appears for phytomers 8–10, with early sheath development delayed in HD compared with ND but fast extension taking place simultaneously in both treatments. For phytomers 11 and above, the kinetics of sheath extension were identical in both treatments from the first date of accurate measurement up to a size of 5–8 cm, after which sheath expansion took place at a lower rate in the HD treatment.

Fig. 11.

Extension of sheaths 7 (triangles), 9 (diamonds) and 11 (circles) for ‘Déa’ at normal density (open symbols) and high density (filled symbols). Symbols are for the measurements, and lines show the model simulations with parameters fitted.

There was no obvious trend for the R₁ of sheaths with leaf number (Fig. 12), and differences between treatments were much smaller than the confidence intervals. This contrasts with what was observed on laminae (Fig. 6).

Fig. 12.

Relative extension rate of sheaths during the exponential phase (R₁). Data are for ‘Déa’ at normal density (open circles) and high density (filled circles). Vertical bars show confidence intervals (±2 s.e.).

There were quite large uncertainties in the estimation of linear rate of extension for sheaths (Fig. 13), partly because few data were collected due to the short duration of the period of fast sheath extension. This also supports the idea that a linear model is probably not sufficient to describe the measured patterns fully.

Fig. 13.

Linear extension rate of sheaths during the linear phase (R₂). Data are for ‘Déa’ at normal density (open circles) and high density (filled circles). Vertical bars show confidence intervals (±2 s.e.).

Timing of fast extension in sheath and laminae

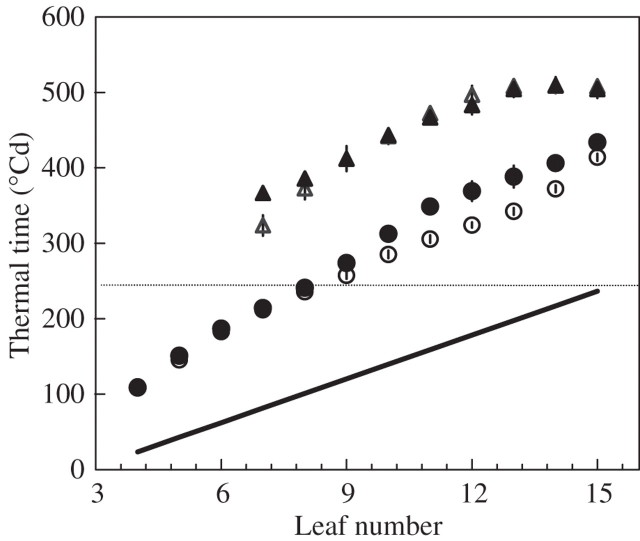
The duration of lamina linear extension, which was the main determinant of the difference in lamina size between treatments, is in fact determined by the delay between the onset of fast linear extension of the lamina and that of the sheath. Figure 14 shows the timing of the transition to fast extension of the laminae and sheaths along the shoot. The initiation of phytomers occurred at the same rate in both treatments. The time interval between laminae of leaves 4–8 entering the fast extension phase was longer than the plastochron, and identical in both treatments. Differences between treatments occurred from laminae 9 and 10 onwards, which were also the lowest laminae to begin fast expansion after panicle initiation. The onset of fast expansion for these two laminae was delayed in HD compared with ND. As for leaf appearance (Fig. 2), higher laminae entered the fast expansion phase at the same rate in both treatments, the delay created in HD treatment just after panicle initiation being conserved.

Fig. 14.

Thermal time from seeding to the start of linear extension of sheaths (triangles) and laminae (circles). Open symbols are for normal density and filled symbols are for high density. Vertical bars show confidence intervals (±2 s.e.) when larger than the size of the symbols. The bold line shows the time course of leaf initiation and the horizontal line indicates the time of panicle initiation.

The onset of fast extension for the sheath of phytomer 7 was delayed in HD compared with ND. A small difference (15 °Cd), which was not significant, also existed in the estimates for phytomer 8. The original data actually suggest a higher difference for this phytomer, and that the accuracy of the estimate is hampered by the linear approximation for phase 2. For phytomer 10 and higher, the similar estimates for onset of fast extension in both treatments reflect the synchronous time course of extension.

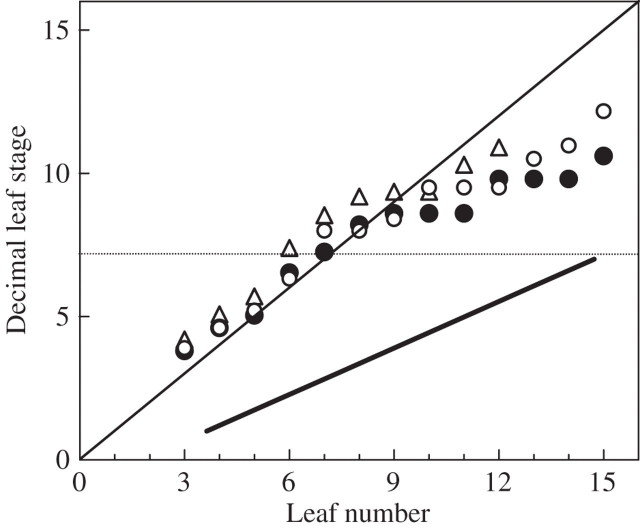
Figure 15 shows the decimal stage at which sheaths could first be measured in the present experiments. These first measures were taken when the ligule was sufficiently delineated that observation was without ambiguity, and corresponded to a sheath length typically between 1 and 3 mm. This is after the time of ligule differentiation, because of the sampling interval, and also because it was not initially the aim of the present study to establish the timing of sheath discernibility. However, the figure shows that up to leaf 8 the timing of the first measurements of sheath paralleled that of leaf appearance. This was not true of the sheaths of upper phytomers. Generally, sheaths 9 and 10 could be measured on the same date, very shortly after sheath 8 (although they were smaller), and the rate at which sheaths of upper phytomers could be measured was higher than the rate of leaf emergence—tending to parallel that of leaf initiation.

Fig. 15.

Decimal leaf stage (DLS, y-axis) at which the sheath for a given leaf (x-axis) was noted for the first time in these experiments. Data are for ‘Déa’ at normal density (open circles) and high density (filled circles), and for ‘Nobilis’ at normal density in 1998 (triangles). The 1 : 1 line is shown as a reference corresponding to the case when sheaths would be distinguished exactly at leaf appearance. The bold line shows the decimal leaf stage at the times phytomers were initiated, and the horizontal line shows the decimal leaf stage at panicle initiation.

DISCUSSION

The effect of density was perceptible very early in the plants' development, as differences between treatments were apparent from the lengths of the sheath and lamina of the first leaf. This means that the effects of density were already present before the appearance of the collar of the first leaf, at which time the leaf area index was approx. 0·013 in the ND treatment and 0·040 in the HD treatment. A signal likely to produce an effect at such a low leaf area index is the perception of far-red light reflected by neighbouring plants (Ballaré, 1999; Maddonni et al., 2002). The leaf area index of 0·04, sufficient to produce a response in leaf extension, was obtained in the ND treatment at DLS 5·0, when plants had two collared leaves. Thus, it is expected that in ND also, extension of at least phytomers 3 and above occurred in environmental conditions able to produce a response to density.

Sheaths 1–6 and laminae 1–8 were longer in HD than in ND. There was no effect of treatment on the RER of those leaves during exponential growth. Consistently, there was no difference in the rate of leaf initiation. For leaves 3–6, lamina R₂ and the duration of fast extension were higher in HD than in ND, whereas for leaves 7–8 there was no difference in R₂: these laminae were longer in the HD treatment only because they grew for longer, relating to the fact that the onset of fast sheath extension was delayed. Even if it is probably not representative of all lower leaves, the behaviour of leaves 7 and 8 is of special interest because, amongst the lower leaves, their final length differed the most between treatments.

Skinner and Nelson (1995) reviewed partial evidence that in grasses, emergence of the leaf tip may trigger the differentiation of the sheath. Putative mechanisms include light signals or change in gaseous concentration, similar to as discussed by Richardson et al. (2005) for the relationship between cuticular wax deposition and emergence. They are evidence that both sheath differentiation and cuticular wax deposition occur slightly before visual appearance of the leaf tip, and this could be because the visual appearance is somewhat delayed compared with the moment the tip emerges above the highest ligule. Alternatively, light piping in plant tissue (Sun et al., 2005) may result in a signal correlated with, but anticipating, leaf emergence. Such triggers would explain how the size of the sheath tube regulates that of the leaves that grow within. Becraft and Freeling (1991) and Freeling (1992) proposed a model in which the cells in the maize primordium pass through a series of competence stages, and their sheath/blade fate is determined by the competence stage they have acquired at the moment they receive a signal coming from the midrib. The progress through competence stages can be dissociated from the growth of the primordium, thus modifying the placement of the ligule (Muehlbauer et al., 1997). These authors do not discuss the precise nature of the signal, but they observed the differentiation of the ligule on leaf 5 when it is between five and six plastochrons old, which corresponds almost exactly to the moment of tip emergence, consistent with a previous report on maize by Sharman (1942). The observation in the present experiment that in both treatments the ability to observe the ligule of a given leaf (for early leaves) paralleled the timing of the leaf's emergence further supports the idea of tip emergence as a candidate for triggering this signal.

Similarly, the positive effect of sheath n on the length of sheath n + 1 could be because the emergence of a leaf's ligule is a signal for the end of sheath extension (Sharman, 1942; Dobrynin, 1960; Fournier and Andrieu, 2000). In the present data, a relationship was observed between the length of sheath n and the lengths of sheath and lamina n + 1, and this relationship was the same in both ND and HD treatments. This supports previous findings (Davies, 1983, Wilson; 1985; Casey et al., 1999) that, for lower phytomers, the length of the sheath tube within which a leaf is growing determines the final length of the lamina and the sheath. It suggests that the difference between the two density treatments for the length of leaves 1–8 may have partly originated from continued propagation, from leaf to leaf, of an effect which differed between treatments in the early stages, i.e. during the growth of a small number of phytomers. As discussed earlier, given the low leaf area indices for which responses to density have been observed, leaves 3 and above in the ND treatment did grow in an environment able to promote a response to density, and thus may be not essentially different from that in the HD treatment. This may explain why the greater length of leaves 7–8 was obtained without an increase in the rate of extension, as would be expected from a direct response to far-red perception.

A different pattern gradually emerged for laminae 10 and above, which were progressively shorter in HD than in ND. In HD, these laminae had a lower RER during the exponential growth phase, but a comparatively larger size at the onset of fast extension, as the onset of fast extension was delayed compared with that in ND. On the other hand, sheath development for these leaves was synchronous in the ND and the HD treatment, from the earliest time at which they could be observed up to a size of several centimetres. For HD, the delayed onset and synchronous conclusion of the fast extension phase resulted in a shorter duration, and thus in a shorter final length despite a faster rate of linear extension.

There is bibliographic evidence for differences in the processes leading to the formation of ligule and to the sheath/blade fate of cells between the lower and upper leaves. Harper and Freeling (1996) report that the liguless1 and liguless2 mutations of maize prevent the formation of the ligule (and thus the distinction between sheath and blade regions) in the lower leaves but not in the upper ones. Sylvester et al. (1990) show a distinct sheath and blade on a maize leaf 10 at stage P3, when the leaf is around 1 mm long and thus long before leaf emergence. In their experiment, the plants had a total of between 12 and 14 leaves, meaning that these observations were taken close to panicle initiation.

In the present work, two other features differed between sheaths of upper phytomers compared with lower ones: (a) ligules became distinguishable on several leaves within a short time period, although the corresponding sheaths had different lengths; and (b) after this short period, the rate of appearance of distinguishable ligules on higher leaves was close to that of leaf initiation. These features were observed some time after panicle initiation, but the ability to distinguish ligules was hampered because measurements were taken with a stereoscopic microscope using a limited magnification (10×); so the changes took place sooner, and probably very close to the time of panicle initiation. Similar results are shown in Paysant-Leroux (1998), who observed that the rate at which new sheaths could be discerned after panicle initiation was approximately twice that observed before panicle initiation. A possible scheme explaining this would be that at panicle initiation, there is a change in the rule for sheath/blade differentiation, which would then become based on the age of the leaf, instead of following leaf emergence. The rate of leaf initiation is approximately twice that of tip emergence, so such a rule would explain why the rate of sheath differentiation doubles. Because panicle initiation was synchronous in both treatments, this would also explain why no effect of density was found in the timing of sheath differentiation in higher phytomers.

Two other distinct features occurred shortly after panicle initiation: the difference in the R₁ of leaves between treatments started with leaves 9 and 10, and the appearance of leaves 9 and 10 was consistently delayed in the HD treatment compared with the ND treatment. It could be that these effects, apparently increasing over phytomers, actually reflect a step change in leaf R₁ occurring at panicle initiation, the gradual appearance reflecting the amount of time each leaf spent in phase 1 before and after panicle initiation (leaf 8 completed phase 1 very shortly after panicle initiation, and was unaffected). This may therefore be related to a global change in plant behaviour in relation to panicle initiation, an event that is known to promote major changes, such as stem extension. Alternatively, the leaf area index in HD reached 1·0 around panicle initiation, so this also corresponds to a period where there was significant competition for light between plants. Experiments with a more detailed time resolution and over a wider range of densities would be necessary to draw conclusions on the character (whether step or gradual) of this change in R₁ and whether it is more closely associated with increasing competition for light or with plant development.

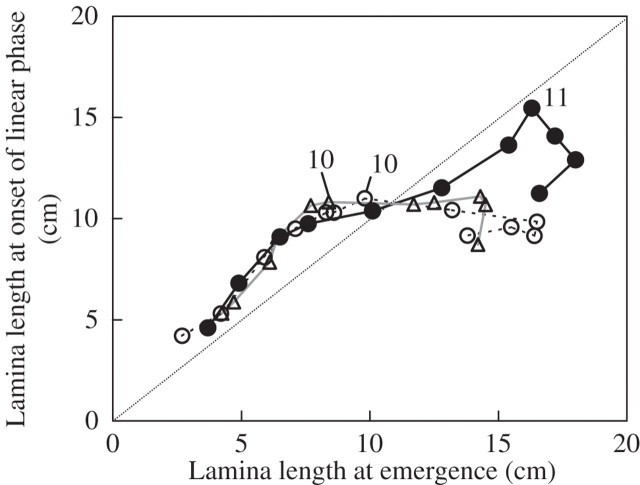
Finally, the lower R₁ of upper leaves appeared to be related to their shorter length, but the relationship was indirect, as it resulted from the delay in the onset of fast linear extension that was associated with the lower RER. R₁ and the duration of the first phase of extension varied in the opposite way, such that the leaf length, L₁, at the onset of fast extension was similar or higher in HD than in ND. The mechanisms leading to these compensations are not understood; however, in grasses, the time course of the transition from exponential to linear extension parallels that of tip emergence (Skinner and Nelson, 1995; Lafarge and Tardieu, 2002; Fournier et al., 2005), making the tip emergence a candidate trigger for this transition. In previous studies, tip emergence was not characterized with a high accuracy. Here the detailed kinetics of blade, sheath and internode extensions were used to relate L₁ to the size of the leaf at the time of its emergence, the criterion being that the height of a leaf tip reaches that of the highest ligule. This occurs long before leaf tip is visible by an external observer. Figure 16 shows that L₁ correlates with leaf length at emergence, for the series of phytomers (1–10 in ND and 1–11 in HD) for which L₁ increases with leaf number. Thus a possible control by the length of the sheath tube of the size at which the onset of fast extension occurs for lower leaves could explain the high value of L₁ observed for leaves 9–11 in the HD treatment. For phytomers above 10 (ND) or 11 (HD), the pattern of L₁ no longer correlates with the length at emergence; as shown in Fig. 6 for these leaves, there is a quasi constant duration of the exponential phase, independent of the RER.

Fig. 16.

Length of a leaf at the time of onset of linear extension, plotted against the length of the same leaf at the time the leaf tip emerges from the sheath tube. Data are for ‘Déa’ at normal density (open circles, leaf number 10 is labelled) and high density (filled circles, leaf number 11 is labelled), and ‘Nobilis’ at normal density in 1998 (triangles, leaf number 10 is labelled).

CONCLUSIONS

The present results extend and clarify previous observations on the responses of maize leaf length to density. High plant density resulted in longer sheaths and laminae for lower and intermediate leaves, and the effect existed from the sheath of the first leaf onwards. On the other hand, the lengths of laminae 10 and above were shorter in the HD treatment. The greater length of leaves 3–5 in the HD treatment originated from both an extended duration and a higher rate of linear extension compared with the ND treatment. For all higher leaves, the effects originated mainly from differences in the duration of lamina linear extension, resulting from asynchronies between the onset of lamina and sheath fast extension. The observations support the idea that, before panicle initiation (a) triggers linked to tip emergence are responsible for regulating sheath differentiation and the duration of the phases of lamina extension; and (b) triggers related to collar emergence are responsible for propagating differences created on early phytomers along the shoot. After panicle initiation, tip emergence no longer appeared to trigger sheath formation, which rather followed a repetitive scheme based on the age of the leaf. This scheme was not affected by density treatment, whereas the timing of lamina fast extension was delayed in the HD treatment. This asynchrony determined the reduced length of the upper laminae in HD treatment.

Interestingly, this also provides a mechanism by which the typical Bell pattern for the length of successive leaves along the shoot is produced. As stressed by Fournier et al. (2005), the co-ordination of sheath differentiation with tip emergence can result only in an ever-increasing length of phytomers along the shoot. The accelerated rate of sheath differentiation after panicle initiation provides a mechanism for explaining the plateau in leaf length for the middle phytomers.

The approximation that developmental events follow a constant schedule in thermal time is central in crop models, although some studies have investigated how other global environmental factors (e.g. photoperiod) could modify such a schedule. Within such a frame, environmental regulation of organ size is supposed to act through change in the rate of extension. In contrast, this work gives additional support to the view that signals linked to leaf emergence events play a role in the timing of development, resulting in a flexible timing, and this regulation should be further investigated in order to understand the plasticity of organ size in response to environmental conditions.