In Silico Analysis of Nuclei in Glioblastoma using Large-scale Microscopy Images Improves Prediction of Treatment Response

Abstract

In this paper, we present a complete and novel workflow for quantitative nuclear feature analysis of glioblastoma using high-throughput whole-slide microscopy image processing as it relates to treatment response and patient survival. With a complete suite of computer algorithms, large numbers of micro-anatomical structures, in this case nuclei, are analyzed and represented efficiently from whole-slide digitized images with numerical features. With regard to endpoints of treatment response, the computerized analysis presents a better discrimination than traditional neuropathologic review. As a result, this analysis method shows potential to facilitate a better understanding of disease progression and patients’ response to therapy for glioblastoma.

I. INTRODUCTION

The term in silico broadly refers to those experiments carried out on computers for simulation. The recent availability of high-throughput and high-resolution instruments has given rise to large sets of imaging data (e.g. microscopy imaging), clinical information (e.g. patient survival, response to treatment, etc.) and molecular signatures, (e.g., genomics and proteomics) that can be harnessed for biomedical research. These datasets provide detailed, multi-dimensional views of biological systems and functions. However, progress on comprehensive analysis integrating multi-type and multiscale data lags behind the pace of data generation. As a result, we initiated efforts to develop computerized analysis tools that can facilitate hypothesis-driven, biomedical translational studies on human gliomas in the In-Silico Brain Tumor Research Center (ISBTRC) [1].

Diffuse gliomas are the most common primary brain tumors of the central nervous system. They are notorious for rapid clinical progression and nearly uniform fatality [2]. Although a large number of research projects have focused on this disease, understanding of the biological driving forces and factors that underlie differential response to therapy and survival remains limited [3]. In an effort to address these issues, we initiated an integrated exploration of the complementary, multi-modal data on glioblastomas (GBMs) from cohorts of patients collected in large-scale efforts by The Cancer Genome Atlas (TCGA) project [4]. Due to the large data volume for analysis, traditional analysis by manual labor is replaced with in silico experiments executed by high throughput computational infrastructure with specifically designed analysis algorithms. This class of in silico studies, referred to as multi-scale integrative investigations, aims to measure and quantify biomedical phenomena in a way that accounts for multiple biological, spatial, and in some cases temporal scales.

In this paper, we describe an exploratory study on whether phenotypic information from nuclear morphology in digital microscopy images correlates with treatment responses or survivals for patients with GBMs. We present our methodology for 1) computation of quantitative features from nuclei in whole-slide microscopy images with a parallel computational infrastructure; 2) representation and classification of patient slides using nuclear features; and 3) use of imaging features for therapeutic response and survival. We demonstrate that computerized analysis of nuclear features derived from imaging data can discriminate groups with significant survival differences in response to therapy that are not observed with qualitative visual assessments by human reviewers.

II. IMAGE PROCESSING FOR NUCLEI CHARACTERIZATION

A. Importance of Nuclear Analysis

Based on pathologic criteria of the World Health Organization (WHO), gliomas can be broadly categorized into three classes: astrocytoma, oligodendroglioma, and mixed oligoastrocytoma [5]. These tumors behave differently clinically and are treated differently. Oligodendrogliomas and oligoastrocytomas tend to grow more slowly and have longer survivals, grade-for-grade, than astrocytomas. Nuclei of these three classes have distinct characteristics that are relied upon heavily for morphology-based classification. For example, nuclei that are round in shape, small in size, have negligible cell-to-cell variability and uniform nuclear texture are typical of oligodendroglioma. By contrast, nuclei of astrocytoma are elongated and irregular in shape with an uneven, rough nuclear texture due to the clumping of chromatin. However, many gliomas either contain mixtures of these nuclei or have intermediate forms. Representative examples of astrocytic and oligodendroglial nuclei, as well as those from the continuum between the two extremes are presented in Fig. 1. Nuclei with either variable combinations of oligodendroglioma and astrocytoma components or with morphologically ambiguous forms make the accurate and reproducible classification of gliomas challenging. By providing tools to segment, describe and classify nuclei, not only can we shed light on the morphologic spectrum of the diffuse gliomas, but also better understand the correlative strength of phenotypic data with response to therapy and patient survival.

Fig. 1.

The spectrum of nuclear features in glioma tumors is presented. Between the pure oligodendroglial and astrocytic nuclei there exists a spectrum of nuclei with mixed characteristics.

To attain discriminating morphologic data on nuclei, we developed a computerized analysis workflow for identifying, characterizing, and classifying nuclei in microscopic images of Haematoxylin and Eosin (H&E) stained gliomas. The resulting nuclear analysis is then used for further correlation with treatment response and patient survival. In Fig. 2, we illustrate this analysis framework with its individual steps discussed below in detail.

Fig. 2.

The nuclei analysis schema, consisting of image tiling, segmentation, feature computation, and classification, is presented.

B. Parallel Image Processing

Each whole-slide image included in the TCGA dataset can exceed 2GB in size. Due to large image size, data structures and intermediate results computed during whole slide image analysis may exceed available main memory on a machine. Moreover, processing a large image slide on a single machine can be slow. For these reasons, we partition each whole slide image into non-overlapping regions to permit parallel analysis. After careful study of hardware specifications and image properties, we selected an appropriate region tile size of 4096×4096 pixels. Meanwhile, the spin-off of whole-slide tiling makes it possible for us to leverage parallel computation power to its full extent. We process images on a high-performance computation infrastructure with a cluster of computer nodes that is used for executing jobs simultaneously. This infrastructure configuration currently consists of seven Dell 1950 1U rack mount units. Each unit is configured with Dual Xeon E5420 CPUs running with four cores at 2.5Ghz for a total of eight cores per node.

C. Nuclei Detection

The first stage of nuclear analysis is the identification and segmentation of all brain tumor nuclei present in digital slides [6]. In an effort to solve issues mostly arising from variations in image intensity, color, texture, and data scale, we employ a method that accommodates the identification of nuclei with distinct characteristics. The first module in this method is the recognition of non-tissue and red blood cell regions. The percentage of areas occupied either by blank spaces or red blood cells is computed to determine whether a given tile contains sufficient material for analysis. We then apply mathematical morphology operations to the tile for normalizing background regions degraded by artifacts arising from tissue preparation and the scanning process. This operation makes it possible to separate the foreground substantially from the normalized background with straightforward user-defined threshold mechanisms. Clumped nuclei are subsequently segregated using the watershed technique [7]. Finally, detected objects not satisfying either area or shape constraints are filtered out from the identified nuclei set, making the resulting nuclei set more uniform.

D. Nuclei Characterization and Representation

A diverse, yet complementary set of nuclear features is computed to characterize the segmented nuclei. Each individual nucleus is described using features from four broad categories: nuclear morphometry, region texture, intensity, and gradient statistics. As nuclear morphology is informative for distinguishing astrocytic and oligodendroglial cell differentiation, morphometric features such as the degree of elongation, size, and regularity are included. Nuclear texture information is also captured using multiple texture descriptors, as there is significant variation in texture across nuclei of distinct categories due to the clumping of chromatin. A complete list of features is presented in [6]. Additionally, we apply the same set of texture and gradient features to neighboring areas surrounding nuclear regions and use these features derived from “cytoplasm” regions to strengthen the representation power.

E. Nuclei Classification

Since it is critical to capture the full spectrum of glioma nuclei both within each tumor and from all disease types, we classify by their feature descriptors with a 10-class classification process. Since diffuse gliomas can be viewed as mixtures of oligodrengroglioma, astrocytoma, and intermediate morphology elements with variable weights, we assigned to each nucleus a score, i.e. a class label, defined as an integer ranging from 1 to 10, with 1 representing a classic oligodendroglioma and 10 a classic astrocytoma. The values in-between represent nuclei exhibiting nuclear features across the oligodrengroglioma-astrocytoma continuum. Since we define 10 different nuclear classes for recognition, it is ideal when the regression analysis, in which a large body of techniques closely tied to machine learning can be utilized for nuclear score computation [8].

Regression analysis is typically used for exploring the relationship between a dependent variable and a set of independent variables [9]. Meanwhile, it is also widely used for predicting a response variable from a set of explanatory variables, given the regression function. In our study, the generalized linear regression function is used because of the following: First, linear models are straightforward and therefore appropriate for revealing the dominant patterns between nuclear score and features. Second, linear models are less subject to over-fitting problems than non-linear ones, since they do not take into account the sensitive effects of cross-terms. However, it is well known that linear least-square estimates are heavily subject to either outliers or heavy-tailed error distribution. Therefore, we use the iteratively reweighted least-square criterion (IRLS) as the remedy to mitigate the influence from outlier data [10]. With this approach, we now aim to minimize the following cost function:

$$E(\beta )=\sum _{i=1}^{N}f(y_i-x_i^T\beta )$$ (1)

where $x_i=\left[\begin{array}{ccccc}1& x_{i1}& x_{i2}& \cdots & x_{ip}\end{array}\right]$ is a vector of predictors from the i-th observation, y_i is the response to x_i, and β is the set of p+1 coefficients to be determined; f (·) is a function that evaluates the contribution of each residual to the overall cost function. In our study, we choose f (·) to be the bi-square objective function, as the associated weight function decreases sharply when residual departs off 0. The final solution can be produced by an iterative computation process described as follows:

$${\beta }^{(i)}={\left(X^T{W}_B^{(i-1)}X\right)}^{-1}{X}^T{W}_B^{(i-1)}Y$$ (2)

where $Y={\left[\begin{array}{cccc}{y}_1& y_2& \cdots & y_n\end{array}\right]}^T$ is the response vector;W_B is a diagonal matrix determined by residuals that, in turn, depend on the estimated parameters. Circularly, the parameters rely on the weight functions. As a result, an iterative computation process gradually yields a stabilized coefficient vector.

III. EXPERIMENTAL RESULTS

Our dataset is drawn from TCGA project on GBMs. GBMs are considered to be grade IV astrocytic neoplasms, but they may contain a variable degree of oligodendroglioma as well. These GBMs have digitized pathology images with a rich set of annotations generated by seven TCGA consortium neuropatholgists. These annotations describe, among many features, the degree of oligodendroglioma present as 0 (none), 1+ (present) or 2+ (abundant). All digitized slides included in the dataset are the H&E stained sections of GBMs that were formalin-fixed and paraffin-embedded. In aggregate, more than 22 million neoplastic nuclei in 428 whole slides scanned at 20x magnification from 162 patients were analyzed with the aforementioned image processing pipeline. With the aforementioned computer cluster, the execution time cost is less than 36 hours. A typical slide region overlaid with analyzed nuclear boundaries and score ranges is presented in Fig. 3.

Fig. 3.

A typical image region is presented with overlaid nuclear boundaries in blue, green and red, representing nuclear score intervals of [1~3], [4~6], and [7~10], respectively.

In order to find the best set of feature descriptors for nuclear representation, an experienced neuropathologist assigns nuclear scores to a set of nuclei selected in a way such that they cover the entire oligo-astro spectrum. With this set of scores, we begin the discovery of discriminating features by computing correlation of each feature and the score. The top eight features exhibiting high correlation with the nuclear score are selected as candidates for further selection. This is followed by a greedy search on all possible combinations of k features from this feature subset, where k = 1, 2, …, 8. This yields 255 distinct combinations of features to search with. The best feature subset is identified by minimizing the following cost function:

$$C=\sum _{i=1}^N{\left|\right|s_i-{\widehat{s}}_i(\omega )\left|\right|}_1$$ (3)

where ω is a set of selected features; N is the number of nuclei with scores from the neuropathologist; s and ŝ are the human-assigned and computer-estimated nuclear score, respectively.

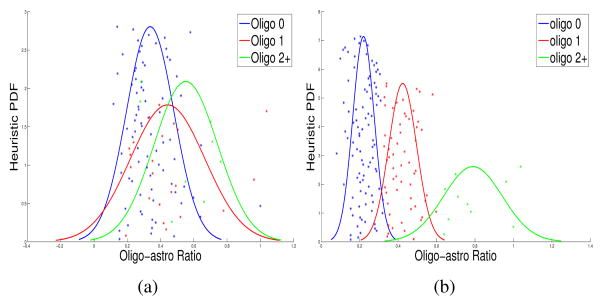
Using the best feature subset, we find the best linear regression model with equation (2). With the best linear regression model, we can compute the nuclear scores for all nuclei identified in 428 slides, in turn. To follow the same way TCGA glioma slides were visually classified by a panel of seven TCGA certified neuropathologists in terms of the degree of oligo-component present, we compute the ratio of the number of oligo-nuclei (with nuclear score in [1~3]) to that of astro-nuclei (with nuclear score [5~10]) from slides for each patient and cluster with k-means algorithm the patient oligo-to-astro ratios into three oligo-component clusters: namely, oligo-0, (i.e. lack of oligo-component), oligo-1+, (i.e. intermediate level of oligo-component), and oligo-2+, (i.e. abundant oligo-component). In Fig. 4 (a), we present the resulting scatter plots and the heuristic Gaussian probability density functions of the oligo-to-astro ratios associated with 162 patients grouped by the three oligo-component categories visually reviewed by the TCGA neuropathologists. With oligo-0 and oligo-2+ populations, the resulting p-value for the two-sample t-test is 7.78e–3. In Fig. 4 (b), populations of patients are categorized with the oligo-component group labels from the unsupervised k-means algorithm. With oligo-0 and oligo-2+ populations, the resulting p-value for the two-sample t-test is 3.75e–7.

Fig. 4.

Scatter plots and estimated Gaussian PDFs are presented with oligo-astro ratios of patients classified as oligo-0 (blue), oligo-1 (red), and oligo-2+ (green), by (a) TCGA neuropathologists; (b) K-means clustering method.

With these two different oligo-component classification results, we further investigate the clinical significance of the oligo-component by correlating with the response to therapy and survivals. In Table 1, we present the p-values of the Log-Rank test [11] with the patient survival data of different oligo-component groups determined by 1) the TCGA neuropathologists’ visual assessment, and 2) the unsupervised clustering process on the oligo-to-astro ratios. The result shown in Table I suggests that no Log-Rank test yields statistical significance with the survival data. Additionally, the p-values associated with human-reviewed and algorithm-produced oligo-component groups are very similar in most cases. In Table II, we summarize the p-values of the Log-Rank test with the survival outcomes of patients of different oligo-component groups that are treated with different therapies, i.e. aggressive vs. normal. It is noted that patients in oligo-0 group classified both by neuropathologists’ visual assessments and by machine-based clustering process present significant survival difference in response to different therapies, while patients in oligo-2+ cluster show significance in neither case. When patients only from either (oligo-1+) or (oligo-1+ and oligo-2+) group are studied, computer-based analysis shows significantly favorable response to aggressive therapy as compared to standard therapy. However, human-based grouping analysis fails to present such a separation of treatment response to these therapies. This finding suggests that the quantitative analysis does present more discrimination power than its qualitative counterpart. This is partly due to the fact that the quantitative analysis can be easily scaled-up without contaminating performance. As the training samples annotated by human experts are limited when compared with the total number of neoplastic nuclei in whole-slide images, human experts could identify oligo-astro nuclei in the small training set with high accuracy. However, neuropathologists’ performance could be substantially devastated when the scope of analysis is expanded to include all nuclei in whole-slide images. As opposed to neuropathologists, the compute-based process is not affected by the scale of the nuclear quantity. As a result, it is not surprising to see the computerized analysis achieves better discrimination power than neuropathologists, even though it were neuropatholgists who provided the annotated data with which computer-based algorithms were trained.

TABLE I.

WE PRESENT P-VALUES OF LOG-RANK TEST WITH SURVIVAL DATA FROM PATIENTS OF DIFFERENT OLIGO-COMPONENT GROUPS DETERMINED BY HUMAN VISUAL REVIEW AND K-MEANS CLUSTERINGMETHOD.

Oligo-Group	Oligo-Group	Visual Assessment	Unsupervised Clustering
0	(1, 2)	2.55e – 1	2.92e – 1
1	(0, 2)	1.64e – 1	2.41e – 1
2	(0, 1)	4.61e – 1	4.54e – 1
0	1	1.80e – 1	2.55e – 1
0	2	4.57e – 1	4.90e – 1
1	2	2.09e – 1	4.17e – 1

TABLE II.

WE PRESENT P-VALUES OF LOG-RANK TEST WITH SURVIVAL DATA FROM PATIENTS RECEIVING DIFFERENT TREATMENTS AND PRESENTING DIFFERENT OLIGO-COMPONENTS DETERMINED BY HUMAN VISUAL REVIEW AND K-MEANS CLUSTERING METHOD.

Oligo-Group	Visual Assessment	Unsupervised Clustering
0	5.40e – 5	3.02e – 3
1	2.79e – 1	6.41e – 3
2	6.06e – 2	5.37e – 2
(1, 2)	1.03e – 1	1.24e – 3

IV. CONCLUSIONS

This paper presents a correlative analysis of the degree of oligo-component in GBMs with treatment response and patient survival. As opposed to human visual reviewing process for classifying gliomas, we used quantitative nuclear features computed from imaging data with high-throughput microscopy image processing executed on a parallel computational infrastructure. In aggregate, more than 22 million nuclei were analyzed by the computer algorithms and used for oligo-component classification. When compared with a panel of neuropathologists, the computerized analysis results in better discrimination between GBMs with differing degrees of oligo-component, at least with regard to predicting response to therapy. This suggests that the in silico analysis method presented here is a promising approach to facilitate a better understanding of glioma progression and patient response to therapy.