Abstract
An image formation framework for ultrasound imaging from synthetic transducer arrays based on sparsity-driven regularization functionals using single-frequency Fourier domain data is proposed. The framework involves the use of a physics-based forward model of the ultrasound observation process, the formulation of image formation as the solution of an associated optimization problem, and the solution of that problem through efficient numerical algorithms. The sparsity-driven, model-based approach estimates a complex-valued reflectivity field and preserves physical features in the scene while suppressing spurious artifacts. It also provides robust reconstructions in the case of sparse and reduced observation apertures. The effectiveness of the proposed imaging strategy is demonstrated using experimental data.
INTRODUCTION
Imaging high contrast, spatially compact inclusions within a nominally homogeneous medium is important in domains ranging from nondestructive evaluation (NDE) to biomedical imaging. In NDE, such inclusions can indicate the presence of material defects, such as cracks.1 In medical imaging, these inclusions can be associated with objects such as shrapnel and kidney stones.2 For many of these tasks ultrasound is the imaging modality of choice due to its low cost, flexibility, and safety. However, conventional ultrasound imaging methods exhibit diffraction artifacts which can make imaging of distinct structures difficult, especially as there are often limited acoustic windows which result in poor data coverage. For example, one application where detecting strong, spatially compact inclusions in a weakly scattering background becomes challenging is detecting kidney stones using ultrasound imaging. A recent study on this application reports that ultrasound has a sensitivity of 76% with 100% specificity, indicating that about a quarter of the kidney stones could not be detected.3 A second application is the detection of needles and other medical instruments in ultrasound images where diffraction artifacts make the location and orientation of the instruments almost impossible to discern from the images.4, 5, 6
In this work, a new model-based framework for ultrasound imaging that estimates a complex-valued reflectivity field using single-frequency Fourier domain data is presented. It is demonstrated that the approach produces images with improved resolution and reduced diffraction artifacts. These gains are especially seen in challenging observation scenarios involving sparse and reduced apertures. The framework is based on a regularized reconstruction of the underlying reflectivity field using a wave-based linear model of the ultrasound observation process. The physical model is coupled with nonquadratic regularization functionals, exploiting prior knowledge that the underlying field should be sparse. In our previous work we have applied such sparsity-driven approaches to other wave-based, coherent imaging problems such as radar imaging.7 These nonquadratic functionals enable the preservation of strong physical features (such as strong scatterers or boundaries between regions with different reflectivity properties), and have been shown to lead to super-resolution-like behavior.8, 9 The resulting optimization problem for image formation is solved using efficient numerical algorithms. The new method is demonstrated using experimental ultrasound data.
A number of others have attempted to regularize the ultrasound image formation process. Ebbini et al.10 and Ebbini11 proposed optimal inverse filter approaches using singular value decomposition based regularization. These methods yield closed form solutions to ultrasound imaging problem. Carfantan and Mohammad-Djafari12 proposed a Bayesian approach for the nonlinear inverse scattering problem of tomographic imaging using microwave or ultrasound probing employing a generalized Gauss Markov random field (MRF) prior image model on the real and imaginary field components. They use a nonlinear observation model and show only two-dimensional simulated examples corresponding to transducer positions completely surrounding the object. Battle et al.13 coupled a linearized, physical-optics approximation with maximum entropy regularization applied to sparsely sampled multimonostatic sensing. They extended the maximum entropy method to account for the complex nature of the scattering field and apply it to the real and imaginary field components. They show experimental results. Husby et al.14 propose a deconvolution technique that estimates a real-valued reflectivity field based on a MRF model of the variance of the scattering field for diffuse ultrasound. The resulting optimization problem is computationally challenging and was solved using Markov chain Monte Carlo techniques. Lavarello et al.15 investigated the feasibility of a generalized Tikhonov technique. They use time-domain data and estimate a real-valued reflectivity field and perform performance analysis on simulated two-dimensional data. Viola et al.16 extended a passive sound navigation and ranging (SONAR) method to account for near field and broadband signals. Their method also uses time-domain data and estimates sparse, real-valued reflectivity fields; however, their method is computationally unattractive, requiring the use of a supercomputer. Although, they are not in the class of regularization methods, Capon (Ref. 17) and MUSIC (Ref. 18) beamformers are well known methods used in acoustic localization in sparse reflectivity fields and have been shown to perform well in scenarios involving isolated point targets, but are not directly applicable to scenarios involving extended targets.
This paper develops the methods presented in Refs. 7, 19 for the ultrasound imaging problem. There are a number of aspects of this paper that differentiate it from the existing literature. The proposed framework can seamlessly handle complex-valued, single-frequency Fourier domain data and estimates a complex-valued reflectivity distribution. The proposed method uses a Sobolev-type functional incorporating simultaneous penalties on the magnitude of the underlying complex reflectivity field as well as the gradient of this magnitude. This enhanced dual penalty functional contrasts those used in Refs. 12, 13, 14, 15, 16. Further, the corresponding optimization algorithms provide a straightforward and efficient solution when complex fields are used with penalties on the gradient of the magnitude, thus avoiding the need for general and expensive Monte Carlo sampling techniques,14 expanded field definitions,13 or specialized computational hardware.16 Finally, the new method is used to process experimental data and verify the anticipated improvement in image quality compared to conventional synthetic aperture focusing technique (SAFT). Results from the experiments show how the proposed approach can provide improved resolution, reduced artifacts, and robustness to data loss as compared to conventional imaging methods.
OBSERVATION MODEL FOR ULTRASOUND SCATTERING
The observation model used for ultrasound scattering is based on a linearization of the scalar wave equation, as developed in Refs. 13, 20, and is summarized here. The free space Green’s function is used to model the scattered field in space in response to a point source of excitation,
| (1) |
where r and denote the source location and the observation location in three-dimensional space, respectively, and k is the wavenumber. It is assumed that imaging is carried out with a single element transducer acting in pulse-echo mode, that is, only backscatter data are collected and that the transducer can be moved to a number of different locations. For this initial work it is assumed that the background is homogeneous and the wave suffers no scattering until an impenetrable scatterer is encountered. This assumption is reasonable from cases of strong reflectors of acoustic energy, e.g., shrapnel or kidney stones in the body and or cracks in nondestructive evaluation, where the scattering from the background medium is weak in comparison to the target. This is equivalent to the Born approximation and one can linearize the Lippmann–Schwinger equation using Born approximation to obtain the following observation model:21
| (2) |
where denotes the observed data and denotes the underlying, unknown backscatter function, which we will refer to as the reflectivity field and which for generality is taken to be complex valued.22 Complex-valued reflectivity fields are common in coherent imaging and allow the observation model 2 to capture the impedance of surfaces where the underlying material has a layered structure, for example, shrapnel from bullets where the jacket and internal alloy are different, or the lamellar structure of kidney stones. In Eq. 2, c is a constant scaling factor that depends on the wavenumber, electro-mechanical coupling, and other calibration factors and it is assumed that throughout this work. Note that squaring the Green’s function captures the two-way travel from the transducer to the target and back. Also note that the above-mentioned observation model involves essentially a shift invariant point spread function. The model is discretized and the presence of measurement noise is taken to be additive to obtain the following discrete observation model:
| (3) |
where y and n denote the measured data and the noise, respectively, at all transducer positions; f denotes the sampled unknown reflectivity field; and T is a matrix representing the discretized version of the observation kernel in Eq. 2. In particular, each row of T is associated with measurements at a particular transducer position. The entire set of transducer positions determines the nature of the aperture used in a particular experiment, and the matrix T carries information about the geometry and the sparsity of the aperture.
SPARSITY-DRIVEN ULTRASOUND IMAGING
Imaging problem formulation
Given the noisy observation model in Eq. 3, the imaging problem is to find an estimate of f based on the measured data y. The conventional ultrasound imaging method of SAFT essentially corresponds to using , the Hermitian adjoint of the operator T, to reconstruct the underlying field f,
| (4) |
SAFT has no explicit or implicit mechanisms to deal with low quality and limited data; hence it yields images with diffraction artifacts and low resolution in such scenarios.
In contrast, the method presented here obtains an image as the minimizer of a cost or energy functional that takes into account both the observation model 3 as well as terms reflecting prior information about the complex-valued field f. One type of generic prior information that has recently been successfully applied in a number of imaging applications, such as astronomical imaging,23 magnetic resonance imaging,24 and computer assisted tomography,25, 26 involves the sparsity of some aspect of the underlying field. In the context of ultrasound imaging, such sparsity priors can be a valuable asset since in many applications of interest the underlying field should be fairly sparse in terms of both the location of inclusions as well as the boundaries between such inclusions and the homogeneous medium. Overall, the proposed method produces an image as the solution of the following optimization problem, which will be called sparsity-driven ultrasound imaging (SDUI):
| (5) |
where the objective function has the following form:
| (6) |
In Eq. 6, denotes the -metric (for it is also a norm), D is a discrete approximation to the derivative operator or gradient, denotes the vector of magnitudes of the complex-valued vector f, and , are scalar parameters that will be discussed in the following. Here, D was implemented using first order differences in horizontal, vertical, and diagonal directions. The formulation 5, 6 starts from the measured acoustic waveforms and is not simply a postprocessing of a formed image.
The first term in Eq. 6 is a data fidelity term, which incorporates the Green’s-function-based observation model 2, and thus information about sensing geometry, e.g., aperture. The second and third terms in Eq. 6 are regularizing constraints that incorporate prior information regarding both the behavior of the field f and the nature of features of interest in the resulting reconstructions. By choosing these terms favor sparsity in their arguments.27 In particular, the sparsity favoring behavior of the second term preserves strong scatterers while suppressing artifacts. Similar objectives have been previously achieved in the context of nuclear magnetic resonance spectroscopy,28 astronomical imaging,29 and ultrasound imaging using maximum entropy methods.13 The third term has the role of smoothing homogeneous regions while preserving sharp transitions, such as those between cracks and background or kidney stone and the tissue. Such constraints have been applied in real-valued image restoration and reconstruction problems by using constraints of the form .30, 31 However, straightforward independent application of such a term to the real and imaginary parts of the complex-valued field f does not directly control the behavior of the magnitude,32 which is what is typically desired. Here, the gradient is applied to the magnitude of the field through use of the prior term , which directly imposes coherence on the magnitude of f while preserving discontinuities in the magnitude. The values of the scalar parameters and determine the relative emphasis on the regularizing sparsity constraints. Unfortunately, the resulting cost function in Eq. 5 is nonquadratic, and thus its minimization is nonlinear and potentially challenging. For its solution we adopt the efficient optimization method developed in Ref. 7 in the context of synthetic aperture radar, which is summarized next.
Solution of the optimization problem
In order to avoid problems due to the nondifferentiability of the metric around the origin when , we use the following smooth approximation to the metric in Eq. 6:
| (7) |
where is a small constant, K is the length of the complex valued vector z, and is the element of z. Using the approximation in Eq. 7, we obtain a modified cost function,
| (8) |
Note that as . The minimization of or does not yield a closed-form solution for f in general so numerical optimization techniques must be used. We employ the quasi-Newton method developed in Ref. 7 that accounts for the complex-valued nature of the ultrasound imaging problem and the associated prior terms. The gradient of the cost function is expressed as
| (9) |
where
| (10) |
| (11) |
and denotes the phase of the complex number . The symbol denotes a diagonal matrix whose ith diagonal element is given by the expression inside the square brackets. We use as an approximation to the Hessian in the following quasi-Newton iteration:
| (12) |
After substituting Eq. 9 into Eq. 12 and rearranging, the following fixed point iterative algorithm can be obtained:
| (13) |
The iteration 13 runs until , where δ is a small positive constant. It was shown in Ref. 33 that this algorithm can be interpreted as a so-called half-quadratic algorithm, with guaranteed convergence to an estimate that is at least a local minimum of the cost function.
The key step in the iterative algorithm 13 is the solution of a linear set of equations for the updated estimate . The matrix is sparse due to the observation that although T is not a sparse matrix in general, is usually sparse and sparsity of the second and third terms in is easier to recognize. The sparse structure of is well matched to efficient iterative solution by methods such as the preconditioned conjugate gradient (CG) algorithm,34 which is what we use here. The CG iterations are terminated when the norm of the relative residual becomes smaller than a threshold . Overall then, there is an outer iteration where is updated and an inner iteration where Eq. 13 is solved for a given using an efficient iterative solver.
EXPERIMENTS AND RESULTS
For the imaging experiments, two-dimensional cross sections of target objects were reconstructed using two methods: SAFT, Eq. 4, and the proposed SDUI method. Two different object types were imaged. First, circular metal rods made of either aluminum or steel were used for resolution studies. The second type of object was a more complicated aluminum U-shaped channel, as used in Ref. 13. In both cases the objects were aligned with their cross section parallel to the array plane.
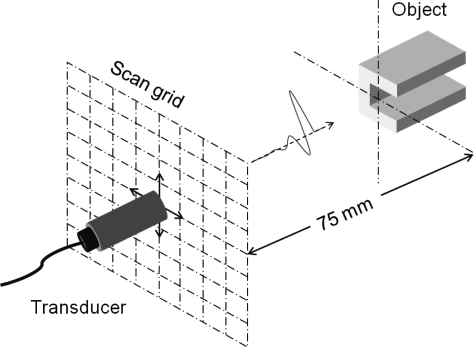
Ultrasound experiments were carried out in a tank of water (2 × 1 × 1 m). A broadband single-element unfocused transducer (HI-6743, Staveley, East Hartford, CT) with a diameter of 4.81 mm and a nominal center frequency of 500 kHz was employed. It was excited in pulse-echo mode using a pulser-receiver (Model 5800, Olympus-NDT, Waltham, MA) and the echo waveforms recorded on a digital oscilloscope with a sampling rate of 50 MHz. The target (rod or channel) was held fixed in the tank. The transducer was mounted to a computer controlled positioning system and was initially placed at a distance of 75 mm from the target. The transducer was then scanned in a raster pattern in a plane parallel to the cross section of the target and pulse-echo data recorded at each location, i.e., in a multimonostatic arrangement. The imaging setup is illustrated in Fig. 1. In the case of a single object, the scan plane covered a square with a side of 64 mm with 1 mm separation between each scan location, while in the case of multiple objects, it covered a square with a side of 96 mm with 1.5 mm separation between each scan location. In both cases a full scan forms a grid with a total of 4096 scan locations. The echo data were time gated from 90 to 170 in order to isolate the reflected signals from other signals, reflections from the target holder and the tank walls. The time-gated received signal was transformed to the frequency domain. In all experiments, the peak of the echo spectra was found to be around 320 kHz. Data from this single frequency were used in the image formation, which corresponds to a wavelength of 5 mm in water. For the transducer employed, the Rayleigh distance at 320 kHz was 3.9 mm and the far-field −6 dB half-angle beam width was 43.5°. At the imaging range of 75 mm the beam width corresponded to a lateral beam extent of 142 mm. The expected lateral resolution of SAFT is half the diameter of the transducer, mm.35
Figure 1.
(Color online) Illustration of the imaging setup: A broadband single-element unfocused transducer performs a raster scan in a plane parallel to the cross section of the object. At each scan location the transducer sends an acoustic pulse and then detects the echo. For all experiments, the initial distance between the object and transducer was set to be 75 mm.
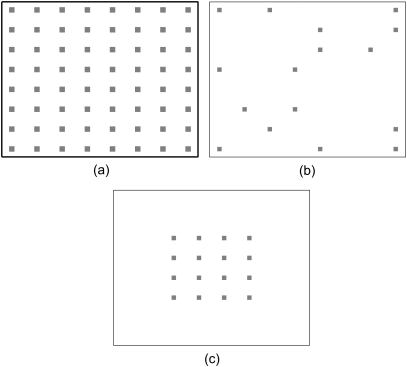
For each experiment, reconstructions were carried out for three data scenarios. The first is referred to as the full data scenario where data from all 4096 scan locations on the grid were employed. The second, referred to as a sparse aperture, corresponded to a subset of the locations chosen with random and irregular sampling over the full support of the grid. The sparse apertures reported here include , , , and of all scan locations. The third scenario, referred to as a reduced-support aperture, consisted of the same number of locations as the sparse aperture but the locations were restricted to squares with sides that were , , , and of the full aperture, i.e., a reduction in each dimension reduces the total number of scan locations by 0.5 × 0.5 = 0.25. These notions are illustrated schematically in Fig. 2. The motivation in choosing the two degraded scenarios was to contrast the effects of the amount of data available and the size of the aperture on the reconstruction. In particular, in reduced aperture scenarios, the resolution of SAFT is expected to degrade as the aperture size, 64 or 96 mm, for the full data scenario is smaller than the lateral width of the beam, 142 mm, hence reducing the aperture will remove signals with information about the target.
Figure 2.
Illustration of data acquisition scenarios being considered. (a) Full aperture case for an grid of scan locations. (b) Sparse aperture case: The data are collected from the marked locations that are irregularly and randomly distributed over the full support of the grid. (c) Reduced aperture case: Marked scan locations concentrated in the center of the full aperture are obtained by uniformly decreasing the aperture support in each dimension.
For all reconstructions with SDUI, a value of was used in the penalties of Eq. 6 or Eq. 7 and the regularization parameters, and , were chosen to yield reconstructions judged best by visual inspection. The sensitivity of the reconstruction to these regularization parameters is discussed in Sec. 4C. The smoothing parameter in Eq. 7 was set to be , which was observed to be small enough not to affect the behavior of the solutions. For all the experiments the SDUI method was initialized with a field of zeros and the tolerances for ending the iterations were .
Experiments with rods
The aim of these experiments was to demonstrate the resolution improvement and signal-to-noise ratio enhancement capabilities of SDUI compared to SAFT. Four cylindrical rods of different materials and diameters were used. Three rods were made of 316 stainless steel with diameters of approximately 9.5, 4.8, and 3.2 mm. The fourth rod was made of 6061 aluminum with a diameter of 3.2 mm. The performance of the imaging algorithms was first studied with single rods and then with pairs at various separations.
Single rod results
For all rods, reconstructions were created with the full data and then the sparse and reduced apertures at and of the full data. The results were quantified using full width at half maximum (FWHM) as an estimate of the diameter by calculating the average of FWHM values for horizontal and vertical cross sections passing through the center of the reconstruction. Similar results were obtained for all four rods and therefore only results pertaining to the 3.2 mm stainless-steel rod are presented here. Figure 3 shows the reconstructions by SAFT and the SDUI method using the full data and 6.25% and 3.5% sparse aperture data. Overall the proposed SDUI method suppressed the artifacts and reconstructed smooth object and background regions with clearly defined boundaries between them. Furthermore, the SDUI method showed robustness to data sparsity relative to the conventional ultrasound imaging method of SAFT, which had increased artifacts as data became more sparse.
Figure 3.
Images of the 3.2 mm steel rod using full and sparse aperture data. Reconstructions by SAFT using (a) full data, (c) 6.25% sparse data, and (e) 3.5% sparse data. Reconstructions by the SDUI method using (b) full data with , , (d) 6.25% sparse data with , , and (f) 3.5% sparse data with , . All dimensions are in millimeters.
In Fig. 4 the equivalent results are shown for the reduced aperture cases. In this case the data were reduced by reducing the aperture support, which should lead to resolution loss. This is clearly demonstrated by the conventional SAFT-based images. As the aperture was progressively reduced the apparent size of the reconstructed object increased as the effective point spread function of the array increased. Significant blurring occurred in these reduced aperture SAFT-based images, that is, the boundary of the rod did not appear as a sharp transition in the image. In contrast, the SDUI-based reconstructions retained their ability to focus the object as the aperture was reduced, producing a clear object image with sharp boundaries.
Figure 4.
Images of the 3.2 mm steel rod using full and reduced aperture data, corresponding to expected loss of resolution. Reconstructions by SAFT using (a) full aperture, (c) 6.25% reduced aperture, and (e) 3.5% reduced aperture. Reconstructions by the SDUI method using (b) full aperture with , , (d) 6.25% reduced aperture with , , and (f) 3.5% reduced aperture with , . All dimensions are in millimeters.
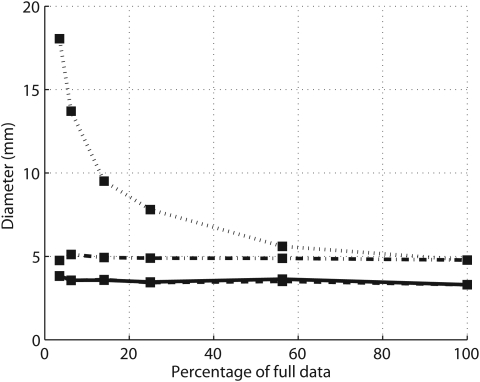
Figure 5 displays the apparent diameters obtained from the reconstructions of the 3.2 mm steel rod as a function of the amount of data used for both the reduced and sparse aperture data cases. It can be seen that the diameters obtained from SDUI reconstructions are approximately 3.5 mm as the amount of data is varied. In contrast, the apparent size obtained from the SAFT-based reconstructions are significantly larger than the true size (at least 4.7 mm). Further, in the reduced aperture cases this diameter grows dramatically as the aperture support is reduced, reflecting a loss of resolution with smaller aperture.
Figure 5.
Estimated diameter values of the 3.2 mm steel rod. SAFT sparse (dashed and dotted line), SAFT reduced (dotted line), SDUI sparse (solid line), SDUI reduced (dashed line). The curves, SDUI sparse and SDUI reduced, overlay each other.
Two rod results
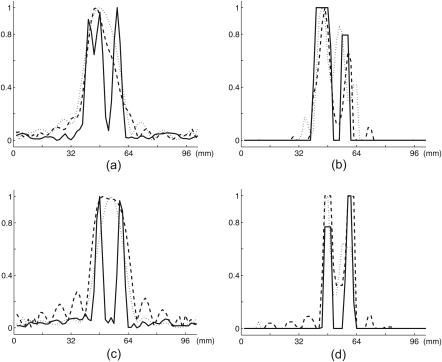
Experiments were then carried out using two different diameter rods at different separations to investigate the ability of conventional SAFT and the SDUI method to resolve closely spaced objects. Results are just shown for reduced aperture scenarios as the sparse aperture data scenarios were similar to the single rod case and so are not presented here. Figure 6 shows reconstructions by SAFT and SDUI of the 9.5 and the 4.8 mm steel rods separated by 5 mm using the full data, 6.25%, and 3.5% reduced aperture data. As 5 mm separation corresponds to two times the expected lateral resolution of SAFT, it can be seen that both methods separated the two rods in the full data case; however, for the reduced data cases SAFT was unable to resolve the rods whereas the SDUI method succeeded to resolve the rods. In Figs. 7a, 7b, the normalized cross sections of the two rod reconstructions of Fig. 6 are presented for a line passing through the center of both rods. As the aperture was reduced, conventional SAFT failed to resolve the two rods and instead merged them into a single object. In contrast, the SDUI method was able to resolve the two objects even as the aperture was reduced.
Figure 6.
Images of the 9.5 and the 4.8 mm steel rod at 5 mm separation using reduced aperture data, corresponding to expected loss of resolution. Reconstructions by SAFT using (a) full aperture, (c) 6.25% reduced aperture, and (e) 3.5% reduced aperture. Reconstructions by the SDUI method using (b) full aperture with , , (d) 6.25% reduced aperture with , , and (f) 3.5% reduced aperture with , . All dimensions are in millimeters.
Figure 7.
Cross sections of the reconstructions of Fig. 6. (a) SAFT, (b) SDUI, and the 3.2 mm steel and the 3.2 mm aluminum rod at 10 mm separation (c) SAFT, (d) SDUI. SAFT reconstructions using full aperture (solid line), 6.25% reduced aperture (dashed line) and 3.5% reduced aperture (dotted line). SDUI reconstructions using full aperture (solid line), 6.25% reduced aperture (dashed line) and 3.5% reduced aperture (dotted line).
Finally, in Figs. 7c, 7d cross sections are shown from the reconstructions of the 3.2 mm stainless-steel rod and the 3.2 mm aluminum rod when they were placed 10 mm apart. As in the case of the two steel rods, conventional SAFT method blurred the two rods together as the aperture was reduced while the proposed SDUI method resolved the two rods.
Experiments with the channel
The aim of this experiment was to demonstrate the resolution and signal-to-noise ratio enhancement capabilities of the SDUI method by using a more structured object rather than simple rods. In addition, this experiment is used to show that including the gradient-based regularization term in the formulation of SDUI 6 can produce significantly improved reconstructions. The channel used in this experiment is made of 6061 aluminum and has a U-shaped cross section with each side 12 mm long and a thickness of 2.4 mm. The comparison of the images formed by SDUI and SAFT will be quantified using a target-to-clutter ratio (TCR) metric adapted from Ref. 32, which is a measure of the signal in the target region relative to the signal from the background region. It can be expressed in decibels as follows:
| (14) |
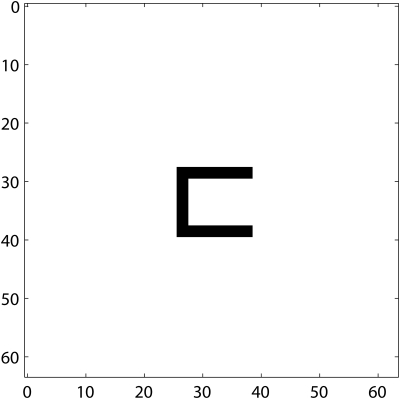
where denotes the pixels of the reconstructed image and T and C denote target and clutter (background) patches in the image, respectively. Since TCR is a ratio of target pixels to clutter pixels it does not depend on the relative amplitude of the reconstructed images, making it favorable to compare images reconstructed by two different methods. However, TCR requires the labeling of the image into target and background regions, which is not immediately available in real data cases. To overcome this problem, the theoretical location and shape of the cross section of the channel based on the physical dimensions of the scan plane and the channel itself were used. The cross section of the channel is illustrated in Fig. 8.
Figure 8.
Location and shape of the cross section of the U channel. All dimensions are in millimeters.
The full data reconstructions by SAFT and SDUI were nearly identical and well represented the channel; therefore, results are only shown for the reduced data cases, where the image reconstructions were more challenging. Figure 9 shows reconstructions by SAFT and SDUI of the channel using and sparse aperture data. As before, it can be observed that reconstructions by SAFT exhibited diffraction artifacts and inhomogeneities in the object and the background regions. Although the channel can be observed in both sparse aperture SAFT reconstructions, diffraction artifacts were stronger for the 6.25% case and hence it became more difficult to distinguish the object from the background. Reconstructions by the SDUI method that omit the gradient-based regularization term are shown in Figs. 9b, 9d for the same two sparse data cases. While these reconstructions successfully suppressed many of the diffraction artifacts, they yielded irregular, pointy object regions making it hard to recognize the underlying structure. In contrast, the complete SDUI reconstructions that include the gradient-based regularization term displayed robustness to data loss and yielded an accurate representation of the channel with excellent artifact suppression and greater uniformity across the target and background regions in spite of the loss of data.
Figure 9.
Images of the channel using sparse aperture data. Reconstructions by SAFT using (a) 14.06% sparse data and (d) 6.25% sparse data. Reconstructions by the SDUI method with using (b) 14.06% sparse data with and (e) 6.25% sparse data with . Reconstructions by the SDUI method using (c) 14.06% sparse data with , and (f) 6.25% sparse data with , . All dimensions are in millimeters.
Figure 10 compares results from SAFT and SDUI using , and reduced aperture data. Note that the reduction of the aperture in this manner corresponds to reducing the spatial resolution of the configuration. With reduced aperture data both methods reconstructed a shape that captured the concavity in the channel, though the SAFT-based image was significantly blurred, while the SDUI-based image retained sharpness of the U shape. With reduced aperture data the SAFT-based image was unable to capture the concavity of the channel, but the SDUI image retained the concavity, though the shape was starting to degrade. With reduced aperture data neither of the two methods was able to capture the U shape of the channel.
Figure 10.
Images of the channel using reduced aperture data. Reconstructions by SAFT using (a) 25% reduced aperture, (c) 14.06% reduced aperture, and (e) 6.25% reduced aperture. Reconstructions by the SDUI method using (b) 25% reduced aperture with , , (d) 14.06% reduced aperture with , , and (f) 6.25% reduced aperture with , . All dimensions are in millimeters.
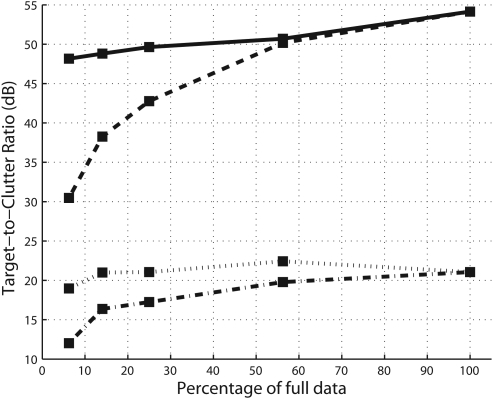
Figure 11 shows the TCR as a function of the fraction of data used in the reconstruction for both the reduced and sparse data sets. It can be seen that the TCR values for the SDUI reconstructions are 12–36 dB better than those for the SAFT reconstructions.
Figure 11.
Quantitative comparison of SAFT sparse (dashed and dotted line), SAFT reduced (dotted line), SDUI sparse (solid line), SDUI reduced (dashed line) using target-to-clutter ratio.
The effect and selection of regularization parameters
Our aim in this section is to present some general guidance on the selection of the values and as well as some insight into their effect and sensitivity. Recall that scales the term that emphasizes preservation of strong scatterers whereas scales the gradient of the image and emphasizes smoothness and sharp transitions. Therefore, if the object features of interest are below the size of a nominal resolution cell, that is they should appear as “points,” then they can be accentuated by choosing . This case leads to sparse reconstructions and can produce super-resolution. If instead the object features of interest span multiple pixels, and thus form regions, these homogeneous regions can be recovered with sharp boundaries by choosing . In this work, the regularization parameters were chosen manually on a case-by-case basis. Automated selection of multiple regularization parameters is a field in its own right (see Refs. 36, 37, 38) and is beyond the scope of the work presented here.
The sensitivity of SDUI reconstructions to regularization parameter selection was carried out for the case of the 3.2 mm steel and the 3.2 mm aluminum rod separated by 10 mm imaged with 6.25% reduced aperture data. The parameters that were chosen manually, that is the values that were judged by eye to give the “best” reconstructions, are denoted and and have values of 5 and 0.4, respectively. Reconstructions were then carried out corresponding to regularization parameters that varied over 2 orders of magnitude from the manually selected values, i.e., and . The reconstructions are shown in Fig. 12. The images along the main diagonal are robust to changes in the regularization parameters with both rods clearly visualized. The images in the upper right-hand side of Fig. 12, where dominates, show distinct scatters but the size of each rod is lost. The images in the lower left-hand side, where dominates, resulted in the rods merging together into one homogeneous object. These results are consistent with how the regularization parameters should control the image formation.
Figure 12.
SDUI reconstructions of the 3.2 mm steel and the 3.2 mm aluminum rod separated by 10 mm reconstructed from 6.25% reduced aperture data for various choices of the regularization parameters. All dimensions are in millimeters.
CONCLUSIONS
A new method, namely SDUI, for ultrasound image formation has been described that offers improved resolvability of fine features, suppression of artifacts, and robustness to challenging reduced data scenarios. The SDUI method makes use of a physical wave-based linear model of the ultrasound observation process coupled with nonquadratic regularization functionals that incorporate the prior information about the behavior of the underlying complex-valued field and its magnitude. The complex nature of the field is handled in a natural way. The resulting nonlinear optimization problem was solved through efficient numerical algorithms exploiting the structure of the SDUI formulation.
The SDUI method was applied on ultrasound pulse-echo data from metal targets in water. The results from SDUI were compared with conventional SAFT. Challenging data collection scenarios, sparse and reduced apertures, were used to test the robustness of the conventional and the proposed method. In sparse aperture scenarios conventional SAFT suffered excessive diffraction artifacts, whereas the SDUI method successfully suppressed the diffraction artifacts and yielded an accurate representation of the underlying reflectivity field. In reduced aperture scenarios, as the aperture support was reduced SAFT suffered resolution loss and was unable to resolve closely spaced objects, whereas SDUI showed super-resolution-like behavior and resolved closely spaced objects most of the time. Examination of the limits of the super-resolution capabilities of SDUI, e.g., in terms of the number of point objects that can be localized and resolved given a particular amount of data, could be a topic for future work. Such an analysis could benefit from recent and ongoing work and theoretical results in the domain of compressed sensing.39, 40
The performance of the SDUI method was tested using strong, spatially compact inclusions in a homogeneous background using single-frequency Fourier domain data. It has been observed that the proposed method exhibits better TCR than conventional imaging, suggesting that it might perform well in limited contrast scenarios, such as those involving weakly inhomogeneous backgrounds. In such scenarios, the proposed approach could produce solutions with less data fidelity than the homogeneous background case, due to the nature of the regularizing constraints. Such data mismatch errors are allowed and balanced with regularization errors in the optimization-based framework. More severe mismatches due to model errors involving phase aberration and attenuation effects encountered in biomedical applications may require more complex forward models or explicit treatment of model uncertainty. Based on all of these observations, ultrasound imaging applications that aim to detect and/or localize strong, spatially compact inclusions in a weak scattering background such as detection of kidney stones and localizing medical instruments are potential applications for the proposed method. Also, results obtained from sparse aperture data scenarios suggest that SDUI can alleviate the motion artifact problem observed when SAFT is used in medical imaging. The performance of the SDUI could be likely enhanced using multifrequency data where the choice of number of frequency components and the appropriate weightings will be key factors to consider. Three-dimensional reconstructions can be either performed by sequential reconstructions at a series of depths or alternatively, a larger inverse problem can be posed by reconstructing the reflectivity field with spatial smoothness constraints between successive slices where in the latter case memory issues can arise depending on the problem size.
ACKNOWLEDGMENTS
The authors would like to thank Dr. Emmanuel Bossy for assistance on the experimental setup. This work was supported in part by the Bernard M. Gordon Center for Subsurface Sensing and Imaging Systems under the Engineering Research Centers Program of the National Science Foundation (Award No. EEC- 9986821), by the National Institutes of Health (Award No. RC1 DK087062), and by the Scientific and Technological Research Council of Turkey under Grant No.105E090.
Portions of this work were presented in “Sparsity-driven sparse- aperture ultrasound imaging,” International Conference on Acoustics, Speech and Signal Processing, Toulouse, France, May 2006.
References
- Nondestructive Evaluation: Theory, Techniques, and Applications, edited by Shull P. J. (CRC Press, Boca Raton, FL, 2002), pp. 1–15. [Google Scholar]
- Chuong C., Zhong P., and Preminger G., “Acoustic and mechanical properties of renal calculi: Implications in shock wave lithotripsy,” J. Endourol. 7, 437–444 (1993). 10.1089/end.1993.7.437 [DOI] [PubMed] [Google Scholar]
- Passerotti C., Chow J. S., Silva A., Schoettler C. L., Rosoklija I., Perez-Rossello J., Cendron M., Cilento B. G., Lee R. S., Nelson C. P., Estrada C. R., Bauer S. B., Borer J. G., Diamond D. A., Retik A. B., and Nguyen H. T., “Ultrasound versus computerized tomography for evaluating urolithiasis,” J. Urol. 182, 1829–1834 (2009). 10.1016/j.juro.2009.03.072 [DOI] [PubMed] [Google Scholar]
- McGahan J. P., “Laboratory assessment of ultrasonic needle and catheter visualization,” J. Ultrasound Med. 5, 373–537 (1986). [DOI] [PubMed] [Google Scholar]
- Nelson T. R., Pretorius D. H., Hull A., Riccabona M., Sklansky M. S., and James G., “Sources and impact of artifacts on clinical three-dimensional ultrasound imaging,” Ultrasound Obstet. Gynecol. 16, 374–383 (2000). 10.1046/j.1469-0705.2000.00180.x [DOI] [PubMed] [Google Scholar]
- Huang J., Triedman J. K., Vasilyev N. V., Suematsu Y., Cleveland R. O., and Dupont P. E., “Imaging artifacts of medical instruments in ultrasound-guided interventions,” J. Ultrasound Med. 26, 1303–1322 (2007). [DOI] [PubMed] [Google Scholar]
- Cetin M. and Karl W., “Feature-enhanced synthetic aperture radar image formation based on nonquadratic regularization,” IEEE Trans. Image Process. 10, 623–631 (2001). 10.1109/83.913596 [DOI] [PubMed] [Google Scholar]
- Donoho D. L., “Superresolution via sparsity constraints,” SIAM J. Math. Anal. 23, 1309–1331 (1992). 10.1137/0523074 [DOI] [Google Scholar]
- Geman D. and Reynolds G., “Constrained restoration and the recovery of discontinuities,” IEEE Trans. Pattern Anal. Mach. Intell. 14, 367–383 (1992). 10.1109/34.120331 [DOI] [Google Scholar]
- Ebbini E., Li P.-C., and Shen J., “A new SVD-based optimal inverse filter design for ultrasonic applications,” Proc.-IEEE Ultrason. Symp. 2, 1187–1190 (1993). [Google Scholar]
- Ebbini E., “k-space based regularization of a new pulse-echo image reconstruction operator,” in Proceedings of the International Conference on Image Processing, ICIP 1999 (1999), Vol. 3, pp. 886–890.
- Carfantan H. and Mohammad-Djafari A., “A Bayesian approach for nonlinear inverse scattering tomographic imaging,” IEEE Int. Conf. Acoust., Speech, Signal Process. 4, 2311–2314 (1995). [Google Scholar]
- Battle D., Harrison R., and Hedley M., “Maximum entropy image reconstruction from sparsely sampled coherent field data,” IEEE Trans. Image Process. 6, 1139–1147 (1997). 10.1109/83.605411 [DOI] [PubMed] [Google Scholar]
- Husby O., Lie T., Lango T., Hokland J., and Rue H., “Bayesian 2D deconvolution: A model for diffuse ultrasound scattering,” IEEE Trans. Ultrason. Ferroelectr. Freq. Control 48, 121–130 (2001). 10.1109/58.895918 [DOI] [PubMed] [Google Scholar]
- Lavarello R., Kamalabadi F., and O’Brien W., “A regularized inverse approach to ultrasonic pulse-echo imaging,” IEEE Trans. Med. Imaging 25, 712–722 (2006). 10.1109/TMI.2006.873297 [DOI] [PubMed] [Google Scholar]
- Viola F., Ellis M., and Walker W., “Time-domain optimized near-field estimator for ultrasound imaging: Initial development and results,” IEEE Trans. Med. Imaging 27, 99-110 (2008). 10.1109/TMI.2007.903579 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Capon J., “High-resolution frequency-wavenumber spectrum analysis,” Proc. IEEE 57, 1408–1418 (1969). 10.1109/PROC.1969.7278 [DOI] [Google Scholar]
- Schmidt R., “Multiple emitter location and signal parameter estimation,” IEEE Trans. Antennas Propag. 34, 276–280 (1986). 10.1109/TAP.1986.1143830 [DOI] [Google Scholar]
- Cetin M., Karl W. C., and Willsky A. S., “Edge-preserving image reconstruction for coherent imaging applications,” in Proceedings of the 2002 International Conference on Image Processing (IEEE, New York, 2002), Vol. 2, pp. II-481–II-484.
- Battle D., “Maximum entropy regularisation applied to ultrasonic image reconstruction,” Ph.D. thesis, University of Sydney, Australia, 1999. [Google Scholar]
- Novotny L. and Hecht B., Principles of Nano-Optics (Cambridge University Press, New York, 2006). [Google Scholar]
- Mu Z., Plemmons R. J., and Santago P., “Iterative ultrasonic signal and image deconvolution for estimation of the complex medium response,” Int. J. Imaging Syst. Technol. 15, 266–277 (2005). 10.1002/ima.v15:6 [DOI] [Google Scholar]
- Starck J.-L. and Bobin J., “Astronomical data analysis and sparsity: From wavelets to compressed sensing,” Proc. IEEE 98, 1021–1030 (2010). 10.1109/JPROC.2009.2025663 [DOI] [Google Scholar]
- Lustig M., Donoho D., and Pauly J. M., “Sparse MRI: The application of compressed sensing for rapid MR imaging,” Magn. Reson. Med. 58, 1182–1195 (2007). 10.1002/mrm.v58:6 [DOI] [PubMed] [Google Scholar]
- Cao N., Nehorai A., and Jacobs M., “Image reconstruction for diffuse optical tomography using sparsity regularization and expectation-maximization algorithm,” Opt. Express 15, 13695–13708 (2007). 10.1364/OE.15.013695 [DOI] [PubMed] [Google Scholar]
- Yu H. and Wang G., “Compressed sensing based interior tomography,” Phys. Med. Biol. 54, 2791–2805 (2009). 10.1088/0031-9155/54/9/014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Donoho D., Johnstone M. I., Hoch C. J., and Stern S. A., “Maximum entropy and the nearly black object,” J. R. Stat. Soc. Ser. B (Methodol.) 54, 41–81 (1992). [Google Scholar]
- Sibisi S. and Skilling J., “Maximum entropy signal processing in practical NMR spectroscopy,” Nature (London) 311, 446–447 (1984). 10.1038/311446a0 [DOI] [Google Scholar]
- Gull S. and Daniell G., “Image reconstruction from incomplete and noisy data,” Nature (London) 272, 686–690 (1978). 10.1038/272686a0 [DOI] [Google Scholar]
- Charbonnier P., Blanc-Feraud L., Aubert G., and Barlaud M., “Deterministic edge-preserving regularization in computed imaging,” IEEE Trans. Image Process. 6, 298–311 (1997). 10.1109/83.551699 [DOI] [PubMed] [Google Scholar]
- Vogel C. and Oman M., “Fast, robust total variation-based reconstruction of noisy, blurred images,” IEEE Trans. Image Process. 7, 813–824 (1998). 10.1109/83.679423 [DOI] [PubMed] [Google Scholar]
- Cetin M., “Feature-enhanced synthetic aperture radar imaging,” Ph.D. thesis, Boston University, 2001. [DOI] [PubMed] [Google Scholar]
- Cetin M., Karl W. C., and Willsky A. S., “Feature-preserving regularization method for complex-valued inverse problems with application to coherent imaging,” Opti. Eng. 45, 017003 (2006). 10.1117/1.2150368 [DOI] [Google Scholar]
- Barrett R., Berry M., Chan T. F., Demmel J., Donato J., Dongarra J., Eijkhout V., Pozo R., Romine C., and der Vorst H. V., Templates for the Solution of Linear Systems: Building Blocks for Iterative Methods, 2nd ed. (SIAM, Philadelphia, 1994), pp. 12–15. [Google Scholar]
- Gough P. T. and Hawkins D. W., “Unified framework for modern synthetic aperture imaging algorithms,” Int. J. Imaging Syst. Technol. 8, 343–358 (1997). [DOI] [Google Scholar]
- Vogel C. R., Computational Methods for Inverse Problems (SIAM, Philadelphia, 2002), pp. 97–126. [Google Scholar]
- Belge M., Kilmer M. E., and Miller E. L., “Efficient determination of multiple regularization parameters in a generalized L-curve framework,” Inverse Probl. Eng. 18, 1161 (2002). 10.1088/0266-5611/18/4/314 [DOI] [Google Scholar]
- Batu O. and Cetin M., “Parameter selection in sparsity-driven SAR imaging,” IEEE Trans. Aerosp. Electron. Syst. 47, 3040–3050 (2011). 10.1109/TAES.2011.6034687 [DOI] [Google Scholar]
- Candes E., Romberg J., and Tao T., “Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information,” IEEE Trans. Inf. Theory 52, 489–509 (2006). 10.1109/TIT.2005.862083 [DOI] [Google Scholar]
- Donoho D., “Compressed sensing,” IEEE Trans. Inf. Theory 52, 1289–1306 (2006). 10.1109/TIT.2006.871582 [DOI] [Google Scholar]