Use of an adaptive-bandwidth protocol to measure importance functions for simulated cochlear implant frequency channels

Abstract

The Articulation Index and Speech Intelligibility Index predict intelligibility scores from measurements of speech and hearing parameters. One component in the prediction is the frequency-importance function, a weighting function that characterizes contributions of particular spectral regions of speech to speech intelligibility. The purpose of this study was to determine whether such importance functions could similarly characterize contributions of electrode channels in cochlear implant systems. Thirty-eight subjects with normal hearing listened to vowel-consonant-vowel tokens, either as recorded or as output from vocoders that simulated aspects of cochlear implant processing. Importance functions were measured using the method of Whitmal and DeRoy [J. Acoust. Soc. Am. 130, 4032–4043 (2011)], in which signal bandwidths were varied adaptively to produce specified token recognition scores in accordance with the transformed up-down rules of Levitt [J. Acoust. Soc. Am. 49, 467–477 (1971)]. Psychometric functions constructed from recognition scores were subsequently converted into importance functions. Comparisons of the resulting importance functions indicate that vocoder processing causes peak importance regions to shift downward in frequency. This shift is attributed to changes in strategy and capability for detecting voicing in speech, and is consistent with previously measured data.

INTRODUCTION

Cochlear implant (CI) technology has provided remarkable benefits to many patients with profound hearing losses. At present, however, there is a wide variation in the abilities of individual patients to recognize CI-processed speech, and many CI users have difficulty understanding speech in adverse conditions. Patient-specific factors associated with these variations include (but are not limited to) duration of severe-to-profound hearing loss, age of implantation, residual hearing acuity and speech perception ability, and electrode placement, configuration, and mapping (Rubinstein et al., 1999; Gomaa et al., 2003; Leung, et al., 2005; Adunka et al., 2008; Finley and Skinner, 2008; Goupell et al., 2008; Rodidi et al., 2009). Studies of these factors and their effects tend to present results in the form of percent-correct recognition scores, which obscures the contributions of the individual electrodes and their associated frequency bands. These contributions are further obscured by electrode current spread, placement uncertainty, and other factors that can make it difficult for the audiologist to determine which tonotopic region a particular electrode excites. While imaging measures like multisection computed tomography scans (Ketten et al., 1998; Skinner et al. 2002) are useful for illustrating electrode placement, they are also costly and complicated, and unsuitable for routine clinical work. The purpose of the present study is to evaluate a new method for measuring the individual contributions of each electrode’s assigned frequency band to speech perception.

One promising approach for measuring individual electrode contributions is the correlational method (Lutfi, 1995; Doherty and Turner, 1996; Turner et al., 1998; Calandruccio and Doherty, 2007; Calandruccio and Doherty, 2008). In this approach, speech is filtered into several bands, each of which is corrupted by additive noise at a wide range of signal-to-noise ratios (SNRs) and presented to subjects in a speech recognition task. From these responses, point-biserial correlations between subject responses (scored as 1 if correct and 0 if incorrect) and SNRs are computed for each band. The individual band correlations, divided by the sum of all correlations, comprise a set of band weights ranging between 0 and 1. Large weights for a band imply larger contributions to intelligibility, while small weights imply smaller contributions to intelligibility. Mehr et al. (2001) used the correlational method to measure weightings for listeners with normal hearing and for implantees using a six-band cochlear implant system (CIS-Link, Med-El, Inc., Innsbruck, Austria) listening to consonant-vowel syllables. Measurements for the normal-hearing listeners filtered speech into the six frequency bands used by the Med-El processors; noise was then added to the speech in each band and the bands were recombined to produce broadband speech. Results showed that normal-hearing listeners placed approximately equal weight on each of the six bands, while weightings for individual implantees differed markedly from each other. A second experiment testing the effects of band removal on intelligibility confirmed that bands with high weightings made larger contributions to intelligibility than bands with lower weightings. These results suggest that measuring band weights is a viable approach for quantifying individual electrode contributions to speech perception. Nevertheless, Mehr et al. (2001) note that their procedure may not be efficient enough for clinical applications. They report that as many as 1200 trials were required to obtain statistically significant correlations in two or more bands, and cautioned that even greater numbers of trials might be required to obtain significance in systems with many more bands.

The inefficiency of the correlational approach is common among psychophysical procedures that characterize the subject’s responses over a wide range of stimulus levels in adherence to the classical “constant stimulus” paradigm (Fechner, 1860). This inefficiency is typically addressed by use of adaptive psychophysical procedures. Adaptive procedures use information from previous responses to steer stimulus levels toward threshold, rather than utilizing levels far above or far below threshold which may provide limited information (Treutwein, 1995; Leek, 2001). This approach is probably not appropriate for obtaining the band weights of Mehr et al. (2001), since their weights, being derived from point-biserial correlations, have a variance that is inversely proportional to the number of trials used (Tate, 1954). It can, however, be appropriate for the “importance functions” (IFs) used in Articulation Index (AI) calculations (French and Steinberg, 1947; Fletcher and Galt, 1950), which have been shown to give band weightings equivalent to those obtained for the correlational method with nonsense syllable stimuli (Calandruccio et al., 2008). The original IFs were comprised of data from intelligibility tests with normal-hearing subjects, using nonsense syllables processed by high-pass or low-pass filters with varied cutoff frequencies. The resulting subject data are plotted as percent-correct intelligibility versus filter cutoff frequency (a monotonic relationship), with the “importance” of a frequency region represented by the rate of change of intelligibility versus cutoff frequency. In principle, an adaptive procedure that varied the bandwidth of speech in an effort to target specific performance levels on intelligibility tests could be used to efficiently determine the shape of the IF; this function, in turn, could be used to produce the desired band weightings.

The feasibility of adaptive-bandwidth IF measurement has been investigated by Whitmal and DeRoy (2011). They conducted two experiments measuring recognition of vowel-consonant-vowel (VCV) nonsense tokens processed by low-pass filters (LPFs) and high-pass filters (HPFs). The filters’ cutoff frequencies were adapted using transformed up-down rules (Levitt, 1971) to target each of five percent-correct performance levels. Psychometric curves were fitted to the resulting data, which in turn were used to derive IFs for the VCV tokens. An analysis of the algorithm’s convergence properties indicated that a complete set of LPF and HPF data could be obtained for a typical subject within (at most) 400 trials—about one-third of those required for the six-channel implants in the Mehr et al. (2001) study. Moreover, the efficiency of the proposed method is (unlike the correlational approach) independent of the number of channels used, and can therefore be used with conventional implant systems that drive twenty or more electrodes. The objective of the present study was to see if the Whitmal/DeRoy adaptive-bandwidth method could be used to obtain channel weightings in a listening experiment with channel vocoders where the number and assignment of channels could easily be controlled. Such findings would inform use of the adaptive-bandwidth method in implant applications.

METHODS

Subjects

Thirty-eight subjects between the ages of nineteen and thirty-nine participated in this experiment (mean age: 22.32 years). All of the subjects were native speakers of English and passed a 20 dB HL hearing screening at 500, 1000, 2000, 4000, and 6000 Hz. None had participated in previous simulation experiments. Partial course credit or monetary compensation was given in return for participation in this experiment.

Materials

Stimuli consisted of the 23 consonants /b d ɡ p t k f θ v ð h s ∫ z ʒ t ∫ dʒ m n w l j r/, recorded in /a/C/a/ format for a study by Whitmal et al. (2007). The consonants were spoken by a female talker with an American English dialect and digitally recorded in a sound-treated booth (IAC 1604, New York, NY) with 16-bit resolution at a 22 050 Hz sampling rate. Average steady-state values for the first-formant (F1) and second-formant (F2) frequencies of /a/ utterances measured with praat, ver. 5.1.04 (http://www.praat.org) were 835.6 and 1357.9 Hz, respectively.

Signal processing

The signal processing methods utilized in this experiment consisted of tone vocoding and adaptive-bandwidth filtering as used by Whitmal and DeRoy (2011). These processes are described below.

Implant processing simulation

Recorded VCV tokens were either processed by one of three tone-excited channel vocoder systems implemented in matlab (Mathworks, Natick, MA), or left “unprocessed” (i.e., subjected to no further processing or reduction in bandwidth). Speech for vocoded conditions was filtered into contiguous frequency bands (using sixth-order Butterworth bandpass filters) in either the 50–6000 Hz or 100–6000 Hz range, with each band having equal width on an equivalent-rectangular-bandwidth (ERB) scale (Glasberg and Moore, 1990). (The two frequency ranges span 28.87 and 27.33 ERB-units, respectively.) Band selections were made with two goals in mind: avoiding floor and ceiling effects as the bandwidth was varied, and testing the effects of both carrier location and bandwidth. These goals resulted in vocoders using a larger number of bands than typically thought to be available to implant users (Dorman and Loizou, 1998; Friesen et al., 2001). Performance on these tasks therefore reflects ideal conditions where the loss of temporal fine structure is the primary challenge, and factors such as current spreading, spiral ganglion survival, and electrode mismatch do not worsen performance. Vocoders included the following:

• (1)Vocoder “V28” used 28 bands in the 100–6000 Hz frequency range, each 0.98 ERB-units wide. Previous research (Dorman et al. 2002; Baskent, 2006) suggested that performance for this number of channels, distributed evenly over all critical bands in the analysis range, would not be significantly different from that of unprocessed speech.
• (2)Vocoder “V16A” used 16 bands in the 100–6000 Hz frequency range, each 1.71 ERB-units wide. Informal pilot testing indicated that this vocoder’s speech was significantly less intelligible than that of V28, yet intelligible enough to avoid floor effects as the bandwidth was decreased.
• (3)Vocoder “V16B” used 16 bands in the 50–6000 Hz frequency range, each 1.80 ERB-units wide. This band assignment provides essentially the same spectral resolution as V16A, albeit with different carrier frequencies (see Table TABLE I.), and was included to test the sensitivity of the adaptive-bandwidth method to carrier location.

TABLE I.

Center frequencies (CF) and bandwidths (BW) for three experimental vocoder systems, expressed in Hz.

V28	Channel	1	2	3	4	5	6	7	8	9	10
	CF	118.2	156.7	199.4	246.8	299.5	358.0	423.0	495.2	575.4	664.4
	BW	36.4	40.5	44.9	49.9	55.4	61.6	68.4	76.0	84.4	93.8
	Channel	11	12	13	14	15	16	17	18	19	20
	CF	763.4	873.3	995.4	1131.0	1281.6	1448.9	1634.7	1841.2	2070.4	2325.1
	BW	104.1	115.7	128.5	142.7	158.5	176.1	195.6	217.3	241.3	268.0
	Channel	21	22	23	24	25	26	27	28
	CF	2608.0	2922.2	3271.3	3659.0	4089.6	4567.9	5099.3	5689.4
	BW	297.7	330.7	367.3	408.0	453.2	503.4	559.2	621.1
V16A	Channel	1	2	3	4	5	6	7	8
	CF	133.2	206.2	294.1	399.6	526.4	678.8	862.0	1082.2
	BW	66.4	79.8	95.9	115.2	138.5	166.4	200.0	240.3
	Channel	9	10	11	12	13	14	15	16
	CF	1346.8	1664.7	2046.9	2506.2	3058.2	3721.6	4518.8	5477.0
	BW	288.8	347.1	417.2	501.4	602.6	724.2	870.3	1046.0
V16B	Channel	1	2	3	4	5	6	7	8
	CF	79.9	146.0	226.3	323.9	442.3	586.1	760.7	972.8
	BW	59.7	72.5	88.1	107.0	129.9	157.7	191.5	232.6
	Channel	9	10	11	12	13	14	15	16
	CF	1230.2	1542.9	1922.5	2383.5	2943.2	3622.9	4448.2	5450.4
	BW	282.4	342.9	416.4	505.6	613.9	745.5	905.2	1099.2

Center frequencies and bandwidths for each of the processors are provided in Table TABLE I.. The envelope of each band was extracted via half-wave rectification and smoothing (using a second-order Butterworth low-pass filter with 30 Hz cutoff frequency), and used to modulate a pure tone located at the band’s center frequency. In previous work using a similar vocoder architecture (Qin and Oxenham, 2003; Whitmal et al., 2007), the smoothing bandwidth was the smaller of 300 Hz or half the vocoder channel bandwidth. More recent work (Stone et al., 2008; Souza and Rosen, 2009) has shown that tone vocoder performance depends strongly on envelope bandwidth, with wider bandwidths providing greater access to pitch information and better overall performance. A constant bandwidth of 30 Hz was subsequently used in all channels to avoid the confounding influence of varied envelope bandwidths on vocoder performance. The modulated tones for all bands were level-matched to the original in-band input signals and added electronically to produce a simulated implant-processed signal.

Adaptive-bandwidth filtering

Unprocessed and vocoded VCV stimuli were processed by 2047-th order digital FIR LPFs produced by the fir1 command in matlab. Filter cutoff frequencies ranged between 125 and 8000 Hz, with attenuation exceeding 80 dB for frequencies more than 200 Hz from the filter’s specified cutoff frequency. The rms level of the waveform was adjusted to match the rms level of the unfiltered waveform so that a constant level could be maintained throughout each adaptive run (Noordhoek et al., 1999). For large reductions in bandwidth, this operation results in a substantial gain increase. The filtered syllables were output from a computer’s sound card (SigmaTel Digital Audio, Austin, TX) to a headphone amplifier (Behringer ProXL HA4700, Bothell, WA) driving a pair of Sennheiser HD580 circumaural headphones. The presentation level for the sentences (65 dB SPL, measured as loaded by a flat-plate coupler) was calibrated daily using repeated loops of broadband random noise that was matched in average spectrum and level to the VCV tokens. The noise was played by the cool edit pro software package (Syntrillium Software, Phoenix, AZ) through the signal chain and measured with a Class 1 sound level meter (Quest SoundPro SE/DL, Oconomowoc, WI) prior to the first testing session of each test day.

Procedure

Subjects were tested in a double-walled sound-treated booth (IAC 1604, New York, NY) in a single session lasting approximately two hours, with breaks provided as needed. Each subject was randomly assigned to one of eight groups that listened to a specific combination of implant processing and adaptive filtering type (LPF or HPF). The filtered VCV tokens were presented to subjects by custom matlab software executed on a laptop computer inside the booth. After hearing each syllable, subjects selected the perceived VCV token from a list of 23 candidates provided by the software’s visual interface (described in detail by Whitmal et al., 2007). Before experimental data were recorded, two practice sets consisting of unfiltered tokens were presented to each subject. The first set consisted of unprocessed tokens (one presentation per individual token), and was used to familiarize the listener with the use of the interface. The second set consisted of tokens (two presentations per individual token) processed by the implant simulator assigned to that subject. Correct-answer feedback was provided after each trial. Data from these trials are not included in the experimental results.

The test session for each subject consisted of adaptive runs using transformed up-down responses (Levitt, 1971) to target performance levels of 84.1, 70.7, 50.0, and 29.3 percent-correct syllable recognition in increasing order of difficulty for both LPFs and HPFs, and 15.9 percent-correct for LPF runs only. This sequencing was intended to help subjects gradually adjust to increasingly difficult listening conditions (Dorman et al., 1997a; Dorman et al., 1997b). Initial testing indicated that scores for some subjects could not converge reliably to a 15.9% level for HPF vocoded conditions; this is addressed below in the Discussion. The filter cutoff frequency for each run was set initially at 1000 Hz and then varied based on the subject’s responses in accordance with one of the five response rules shown in Table TABLE II.. The step sizes for frequency changes were initially one octave for the first two reversals, 1/2-octave for the next two reversals, and 1/4-octave thereafter. A total of 161 tokens (i.e., seven repetitions of each VCV) were presented for each run, for a total of 805 tokens presented per LPF subject session and 644 tokens per HPF subject session. Both experiments used fewer trials than Whitmal and DeRoy (2011) did; nevertheless, several participants were unable to finish testing during their scheduled time and did not return to complete testing. Their results were excluded, leaving subject groups to consist of four, five, or six subjects as indicated in Tables 3, TABLE IV.. It should be noted that these trials were conducted immediately after the original trials of Whitmal and DeRoy (2011) and before their convergence analyses were conducted. It is likely that convergence could have been accelerated (and the number of required trials further reduced) if initial cutoff frequencies were set equal to their average values for normal-hearing listeners (Whitmal and DeRoy, 2011, Tables 2, TABLE III.).

TABLE II.

Adaptation strategies for performance targets (after Levitt, 1971).

Rule	Target level(%-correct)	Increase bandwidthafter observing…	Decrease bandwidthafter observing…
1	15.9	Four consecutive misses	Three or fewer misses followed by a correct guess
2	29.3	Two consecutive misses	One correct guess or one miss followed by a correct guess
3	50.0	Two misses in two or three consecutive trials	Two correct guesses in two or three consecutive trials
4	70.7	One miss or one correct guess followed by a miss	Two consecutive correct guesses
5	84.1	Three or fewer correct guesses followed by a miss	Four consecutive correct guesses

TABLE III.

Descriptive statistics for adaptive low-pass-filter measurements.

Percent-correct (%)
	Unprocessed(N = 5)		V28(N = 6)		V16A(N = 5)		V16B(N = 5)
Target %	Mean	SD	Mean	SD	Mean	SD	Mean	SD
15.9	17.33	1.62	16.80	1.28	16.92	1.23	15.21	0.80
29.3	29.41	1.13	30.11	1.30	29.51	1.57	28.50	2.62
50.0	49.71	2.31	50.44	1.89	49.53	2.69	49.90	1.57
70.7	69.00	1.33	69.55	1.07	70.41	0.72	71.08	1.80
84.1	83.43	0.71	82.32	0.78	82.12	1.63	81.33	4.68

Cutoff frequency estimate (kHz)
	Unprocessed		V28		V16A		V16B
Target %	Mean	SD	Mean	SD	Mean	SD	Mean	SD
15.9	0.417	0.070	0.442	0.073	0.466	0.124	0.442	0.111
29.3	0.718	0.170	0.742	0.095	0.712	0.144	0.757	0.083
50.0	1.500	0.387	1.445	0.098	1.527	0.238	1.497	0.145
70.7	1.856	0.110	2.029	0.185	2.596	0.418	2.402	0.174
84.1	3.432	0.193	2.932	0.727	4.422	1.057	4.277	1.298

TABLE IV.

Descriptive statistics for adaptive high-pass-filter measurements.

Percent-correct (%)
	Unprocessed (N = 4)		V28 (N = 5)		V16A (N = 4)		V16B (N = 4)
Target %	Mean	SD	Mean	SD	Mean	SD	Mean	SD
29.3	30.01	1.50	31.46	1.84	30.05	1.97	30.81	1.90
50.0	49.82	2.61	50.19	2.44	49.52	1.85	50.37	1.25
70.7	72.13	1.06	71.04	1.45	69.99	1.36	69.87	1.00
84.1	83.91	2.11	84.72	3.08	79.18	5.58	82.88	5.95

Cutoff frequency estimate (kHz)
	Unprocessed		V28		V16A		V16B
Target %	Mean	SD	Mean	SD	Mean	SD	Mean	SD
29.3	4.330	0.310	2.789	0.352	2.050	0.729	2.727	0.771
50.0	3.071	0.410	1.680	0.178	1.225	0.162	1.527	0.301
70.7	1.891	0.333	1.074	0.191	0.839	0.275	0.850	0.398
84.1	1.305	0.088	0.660	0.149	0.329	0.160	0.353	0.206

RESULTS

Statistical analysis of data from adaptive LPFs

Percent-correct scores were computed for each adaptive run by inspecting all trials from the fifth reversal onward and dividing the number of correct guesses by the total number of trials. The minimum number of trials used was 115; the maximum number used was 155. This restriction removed bias from initial parts of each run where the cutoff frequency estimate (CFE) was either too low or too high to approximate the target performance level well. Average percent-correct values (presented in Table TABLE III.) are very close to target levels for all vocoder types: the largest single deviation from any target is 2.77 percentage points (for V16B under rule 5), and all other deviations are smaller than 2.00 percentage points. This performance is consistent with that observed by Whitmal and DeRoy (2011). Differences in the vocoders’ adherence to target performance were evaluated by converting subject percent-correct scores to rationalized arcsine units, or “rau” (Studebaker, 1985). The rau-converted scores were then input to a repeated-measures mixed-model analysis of variance (ANOVA), with fixed main factors of target percent-correct level and vocoder type; subject identity was assumed to be a random factor. Among main factors, level (F[4,85] = 3959.32, p < 0.001) was statistically significant, whereas vocoder type was not (F[3,85] = 0.784, p = 0.506). The interaction between level and vocoder type was also not significant, further suggesting that subjects for the four conditions showed equal facility for meeting target levels.

CFEs for each subject were calculated by averaging the subject’s cutoff frequencies for all reversals from the fifth reversal onward. Average CFEs (shown in Table TABLE III.) are consistent across all vocoders for the 19.1, 29.3, and 50.0%-correct levels. For the 70.7 and 84.1%-correct levels, the V16A and V16B CFEs were (approximately) 0.3 to 0.5 octaves higher than the corresponding CFEs for unprocessed speech. CFEs were also examined as dependent variables in a repeated-measures mixed-model ANOVA, with target level and vocoder type as main factors. Both level (F[4,85] = 191.583, p < 0.001) and vocoder (F[3,85] = 6.1, p = 0.001) were statistically significant. Pair-wise comparisons conducted with Bonferroni adjustments confirmed that the unprocessed and 28-channel vocoders had significantly lower CFEs than the 16-channel vocoders.

Statistical analysis of data from adaptive HPFs

Percent-correct scores were computed for each adaptive HPF run as described above for LPF runs. The minimum number of trials used was 108; the maximum number used was 155. Average percent-correct values (presented in Table TABLE IV.) are again within 2.00 percentage points of target levels for all vocoder types, with two exceptions: V28 for rule 2 (above target by 2.14 points) and V16A for rule 5 (below target by 4.92 points). The latter difference represents a ceiling effect for that condition (discussed below); in other respects, performance is consistent with that observed by Whitmal and DeRoy (2011). Rau-converted scores were input to a repeated-measures mixed-model ANOVA with target percent-correct level and vocoder type as fixed main factors. As for the LPF runs, level (F[4,52] = 906.45, p < 0.001) was statistically significant and vocoder type was not (F[3,52] = 2.13, p = 0.108). The interaction between level and vocoder type was also not significant.

Average CFEs (shown in Table TABLE IV.) vary substantially across vocoders. For every performance level, less bandwidth was required for the unprocessed speech than for any of the vocoders. Average CFE differences ranged from 0.83 octaves (for V28) to 1.39 octaves (for V16A). A repeated-measures mixed-model ANOVA of CFEs showed that both level (F[3,52] = 56.83, p < 0.001) and vocoder (F[3,52] = 124.18, p < 0.001) were statistically significant factors. Pair-wise comparisons conducted with Bonferroni adjustments confirmed that CFEs for unprocessed speech were significantly higher than those for V16B and V28, which in turn were significantly higher than those for V16A.

Fitting of psychometric functions

IFs were derived using the method of Fletcher and Galt [1950; Eq. (5), p. 95], who showed that the nonsense-syllable intelligibility function1s(f) at a given LPF cutoff-frequency f was governed by the transfer function

$$s(f)=1-{10}^{-\mathit{AI}(f)/K},$$ (1)

where AI(f) is the Fletcher–Galt AI value for that LPF and K is a curve-fitting constant.2 At optimum listening levels, the AI for a given LPF with cutoff frequency f_c and its complementary HPF is solely dependent on the IF I(f):

$$\begin{array}{c}{\mathit{AI}}_{\mathit{LP}}\left(f_c\right)=1-{\mathit{AI}}_{\mathit{HP}}\left(f_c\right)=-K{\log }_{10}(1-s\left(f_c\right))={\int }_{f=0}^{f_c}I\left(f\right)\mathit{df}.\hfill \end{array}$$ (2)

By definition, the AI equals 0.5 at the “crossover” frequency where LPF and HPF psychometric curves for unprocessed speech intersect; this constraint, along with performance data, can be used to find K.

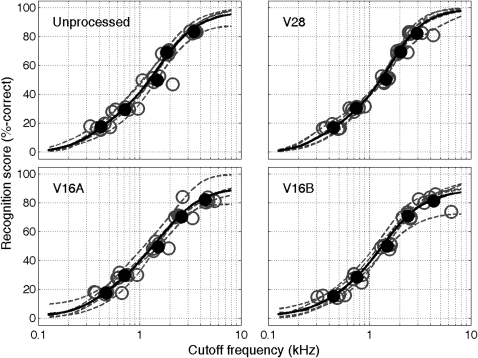
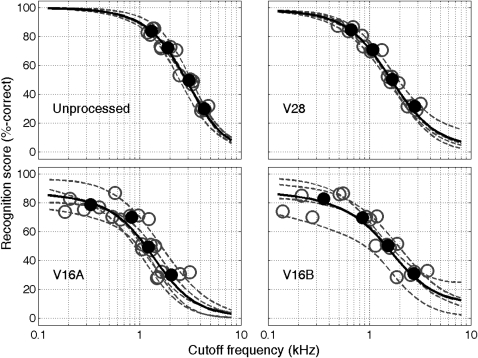
In Whitmal and DeRoy (2011), the intelligibility functions s(f) were derived from locally linearized psychometric curve estimates (Zychaluk and Foster, 2009) fitted to the ten rule-based performance/bandwidth data points obtained in LPF/HPF experiments with different cutoff frequencies. The rule-based recognition scores for the present study are shown in Figs. 12 (unfilled circles). In Whitmal and DeRoy (2011), the use of only these scores for curve estimates was facilitated by the fact that subject performance equaled 100%-correct at full bandwidth. Performance for subjects in the present study also approached 100%-correct in full-bandwidth conditions with unprocessed and 28-channel speech. However, several subjects were unable to achieve 100%-correct at full-bandwidth for 16-channel speech. Without data points corresponding to full-bandwidth vocoder conditions, the fitting algorithm extrapolated peak performance levels that were above the actual levels measured in the limited number of full-bandwidth trials for V16A and V16B. To address this shortcoming, two sets of curves were fitted for each subject. The first curves were fitted only to the rule-based data points, as in Whitmal and DeRoy (2011). The second curves were fitted to the percentages of correct token recognition achieved for each of the 25 cutoff frequencies used in the adaptive tracks. These curves (which reflect actual full-bandwidth performance) are denoted by dashed lines in Figs. 12. (For clarity, only the second set of curves is shown, since the two sets are substantially equal in the first set’s fitting range.) The averages of these curves for each cutoff frequency (denoted by solid lines) are also shown in Figs. 12. Maximum full-bandwidth performance was 99.7%-correct for unprocessed speech, 98.0%-correct for V28, 88.6%-correct for V16A, and 87.3%-correct for V16B. Values for the latter two conditions are close to the target for rule 5, reflecting a ceiling effect that may account for the lower performance values, higher variances, and broader bandwidths seen in Tables 3, TABLE IV.. Variability for V16A and V16B in HPF conditions is also considerably higher than for LPF conditions, a predictable result attributable to the lower slope of HPF psychometric functions (Taylor and Creelman, 1967; Kollmeier et al., 1988) and the higher variability of HPF speech (Miller and Nicely, 1955). Figure 3 displays the average curves for each of the LPF and HPF conditions.

Figure 1.

(Color online) Local linear psychometric curves fit to percent-correct recognition vs cutoff frequency data for VCV syllables, low-pass filtered in adaptive-bandwidth mode runs for four listening conditions. Unfilled circles and dashed lines represent (respectively) rule-based data points and psychometric curves fitted to recognition data at each cutoff frequency for individual subjects. Filled symbols and solid lines represent the average values for data points and psychometric curves.

Figure 2.

(Color online) Local linear psychometric curves fit to percent-correct recognition vs cutoff frequency data for VCV syllables, high-pass filtered in adaptive-bandwidth mode runs for four listening conditions. Format is identical to that of Fig. 1.

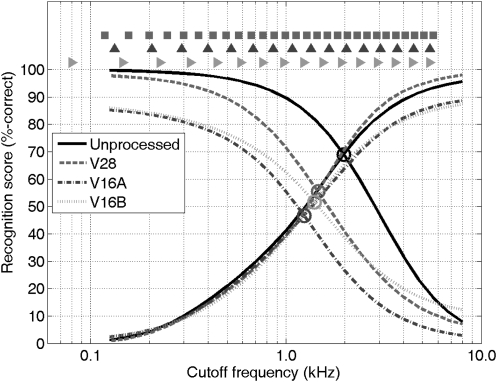
Figure 3.

(Color online) Average recognition scores (in percent-correct) for low-pass and high-pass filtered VCV syllables for unprocessed (solid lines) and vocoded speech. “Crossover” points for each listening condition are denoted by circles; locations of channel center frequencies for V28, V16A, and V16B are denoted (respectively) by squares, pyramids, and triangles at the top of the figure.

Use of the second set of curves may raise questions about the validity of attributing results to the rule-based curves. Hence, the second set of curves was tested with the pfcmp procedure of Wichmann and Hill (2001a, 2001b) to see whether they were significantly different from the first set in the performance region covered by the five rules. pfcmp uses Monte Carlo simulations to construct bivariate normal distributions of inter-curve threshold and slope differences; these are then used to test the null hypothesis that the threshold and slope parameters of the curves are identical. The original pfcmp procedure was modified to use the local linear fitting software of Zychaluk and Foster (2009). Hypothesis tests for each subject (using 2000 Monte Carlo trials) produced p-values ranging between 0.086 and 0.993 (average: 0.659) supporting the null hypothesis of equivalently-fitted curves.

The data of Fig. 3 indicate that vocoded speech is more dependent on content in low and midfrequency regions than unprocessed speech. This is particularly evident in the comparison between unprocessed and V28 conditions. The LPF psychometric curves for these two conditions are nearly identical, with performance increasing steadily as more high frequency content is added to the signal. In contrast, the HPF curves are very different: V28 performance decreases much more rapidly than unprocessed performance as low-frequency content is removed. This decrease appears to accelerate as bands above 600 Hz begin to be filtered out. Recognition scores for V16A and V16B follow a similar pattern, with V16A scores decreasing more rapidly than V16B scores, presumably because its most salient carriers are filtered out at lower frequencies than the V16B carriers. (The V16B carrier at 79.9 Hz seems to have little influence on recognition scores.)

The LPF/HPF differences described above are also evident in the vocoders’ crossover statistics. For unprocessed speech, the HPF and LPF curves intersect at 1975.2 Hz, where recognition scores equal 69.1%-correct. This score resembles the 67.1%-correct value measured by Whitmal and DeRoy at 2080 Hz. The more rapid decrease in HPF performance for V28, V16A, and V16B lowers their crossover frequencies by approximately one-half-octave (see Table TABLE V.). Their curves intersect near the 50%-correct level, indicating that the bands above and below crossover contribute less to intelligibility than the comparable bands in unprocessed speech. The lower crossover performance is also reflected in values of K, which is approximately 1.0 for unprocessed speech and about 60% higher for the vocoders. For Fletcher and Galt (1950), K was inversely proportional to a “proficiency factor” that described the relative capabilities of the talker and listener. In that sense, the 60% increase in K required for the vocoded speech reflects the decrease in listener proficiency evident in the vocoder subjects’ lower full-bandwidth scores.

TABLE V.

Crossover frequency statistics for intelligibility curves.

Listening condition	Crossover frequency (Hz)	Performance level (%-correct)	Fitting constant K
Unprocessed	1975.2	69.1	0.98
V28	1459.3	55.4	1.42
V16A	1239.4	46.7	1.83
V16B	1395.9	51.6	1.58

Derivation of importance functions

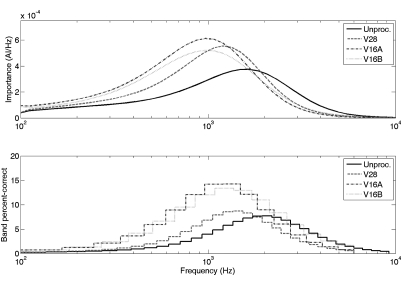
The intelligibility functions s(f) shown in Fig. 3 were converted into AI functions in accordance with Eq. 2. LPF curves used the relation ${\mathit{AI}}_{\mathit{LP}}\left(f_c\right)=-K{\log }_{10}(1-s\left(f_c\right))$: HPF curves used the relation ${\mathit{AI}}_{\mathit{HP}}\left(f_c\right)=1+K{\log }_{10}(1-s\left(f_c\right)).$ Derivatives of each AI function were then computed to calculate IFs, which are shown in the top panel of Fig. 4. The unprocessed-speech IF reaches its maximum value at 1661.1 Hz, while IFs for V28, V16A, and V16B reach their maximum values at values of (respectively) 1201.1, 967.64, and 967.64 Hz. Despite differences in location and skewness (2.61 for unprocessed speech, 3.78–4.25 for the vocoders), the four IFs concentrate similar amounts of importance (range 31.8–40.7 percentage points) into the octave band centered around their maximum values.

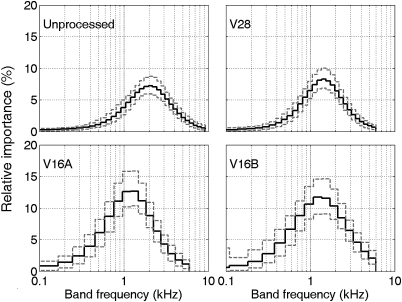
Figure 4.

(Color online) Top panel: Importance function for VCV syllables in AI units/Hz as derived from Eq. 2 for unprocessed (solid lines) and vocoded speech. Bottom panel: Importance functions for VCV syllables from top panel, recomputed in units of %-contribution per vocoder frequency channel for unprocessed and vocoded speech.

The bottom panel of Fig. 4 presents IFs in a band-oriented format analogous to the 1/3 rd-octave and octave-band versions reported by various authors (for example, see Pavlovic, 1994). Here, each continuous IF was integrated over each vocoder band to compute the bands’ percent-correct contributions. Maximum-importance bands for V28, V16A, and V16B are centered at 1448.9, 1346.8, and 1230.2 Hz (respectively). The apparent shift of these maxima to higher frequencies than continuous IFs maxima can be attributed to discretization, with increasing bandwidths at higher frequencies providing an offset. Skewness values for the band-wise IFs range between 0.80 and 1.08, denoting similar shapes; bands centered within one octave of each maximum-importance band contributed between 38.2 and 42.8 percentage points to intelligibility. Figure 4 also shows the unprocessed-speech IF as mapped onto an extended-bandwidth version of the V28 band configuration to allow comparison with the vocoder IFs. In this format, the unprocessed-speech IF’s maximum-importance band has shifted upwards to 2070.4 Hz, approximately one-half octave above those of the vocoder IFs. The unprocessed IF also exhibits higher resolution and/or higher importance above 2000 Hz than the vocoder IFs.

Analysis of phonetic feature reception

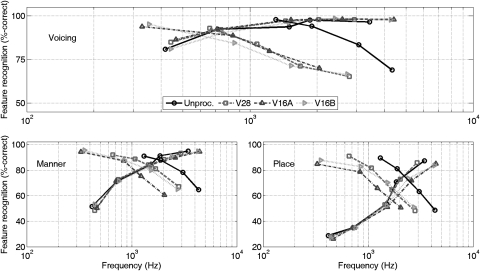
Previous studies reporting importance maxima shifts to lower frequencies (Hirsh et al., 1954; Pavlovic, 1994; DePaolis et al., 1996; Studebaker et al., 1987; Eisenberg et al., 1998) utilized unvocoded test materials with different phonemic content and/or higher message redundancy than nonsense syllables, and attributed the frequency shifts to these factors. In the present case, where the shift is produced by vocoding a single set of nonsense syllables, neither phonemic content nor redundancy can be responsible. A plausible alternative explanation is that the use of vocoding impairs perception of phonetic features. This hypothesis was tested by assembling feature confusion matrices for the subjects’ responses as described by Miller and Nicely (1955, p. 348) and computing the percentages of correct voicing, manner, and place-of-articulation feature classifications with respect to LPF/HPF cutoff-frequency. Results (displayed in Fig. 5) show that HPF-induced changes in voicing, manner and place perception also occur at lower CFEs when vocoding is introduced. To quantify these shifts, “crossover” levels and frequencies for each feature were estimated through linear interpolation of the HPF/LPF curves shown in Fig. 5; results are shown in Table TABLE VI.. Although all features show some downward crossover frequency shift under vocoding, the most noticeable shifts (on average, 1.29 octaves) are observed for voicing, with crossover frequencies located approximately one-third octave below F1. Crossover shifts for manner and place are much smaller in comparison (on average, 0.35 octaves).

Figure 5.

(Color online) Recognition (in %-correct) vs filter cutoff frequency of voicing (top panel), manner (lower left), and place (lower right) features for the consonants of unprocessed and vocoded VCV syllables after low-pass and high-pass filtering.

TABLE VI.

Crossover frequency statistics for phonetic features.

Phonetic feature	Listening condition	Crossover frequency (Hz)	Performance level (%-correct)
Voicing	Unprocessed	1669.6	95.5
	V28	718.3	91.6
	V16A	645.4	90.7
	V16B	682.4	88.1
Manner	Unprocessed	1731.9	88.7
	V28	1443.4	84.1
	V16A	1135.8	78.2
	V16B	1397.0	81.4
Place	Unprocessed	2279.0	75.2
	V28	1756.3	63.6
	V16A	1772.9	55.9
	V16B	1964.8	63.2

These shifts in feature crossover frequency probably reflect the effects of vocoding on the perception of voiced speech, which normally contains quasi-periodic segments with spectra having harmonically spaced components. Vocoding disrupts this harmonic spacing, and can also (as in the present study) remove periodic fine structure from envelope signals with low-bandwidth smoothing filters. Without these harmonic or temporal fine structure cues, listeners are forced to rely more heavily on secondary cues like voice onset times and formant transitions to detect voicing. (The latter are also vulnerable to vocoding: 16-channel speech exhibits stepwise formant transitions, rather than the smoother transitions found in natural and 28-channel speech.) These secondary cues suffice in favorable conditions: among all vocoded consonants, only those with low intensity at/above F2 (i.e., /l/, /θ/, and /ð/) had their recognition adversely affected at the 84.1% performance level. As the CFE increased, consonants distinguished by F1 and F2 transitions were attenuated in (approximate) order of formant locus frequency. Labial consonants with F1 transitions to/from lower frequencies (e.g., /b/, /p/, /v/, /w/) were among the first to be misidentified as F1 transitions were attenuated. Most of the other consonants were attenuated as the CFE moved between F1 and F2. This inter-formant frequency region contains consonant cues that include formant transition loci and nasal antiresonances, and may account for the maxima of the IFs being located here. Consonants that remained intelligible at the 29.3% performance level for the three vocoders were continuants with substantial output above F2 (e.g., /n/, /r/, /s/, and /∫/).

The loss of normal periodic structure also affects manner and place reception adversely. For unprocessed HPF speech, observed error patterns included conversions of stops to fricatives, fricatives to glides, affricates to stops, nasals to glides, and glides to fricatives. These patterns were largely replicated in vocoded speech (albeit at lower CFEs) with one major difference: as the CFE increased, vocoded speech was more likely to be classified as “nasal” than unprocessed speech. This tendency resulted in higher correct detection of nasals as well as higher nasal misclassification rates for stops. Possible contributing factors may include reduced output at low frequencies that mimics nasal antiresonances and the presence of high-frequency carriers that mimic formants. Place, typically the most fragile of the three features (Miller and Nicely, 1955), shows a crossover shift of less than 1/3 rd-octave and only minor changes in error patterns. The most notable difference between unprocessed and vocoded place perception is in reception of dental fricatives (defined here as /f/, /v/, /θ/, and /ð/), all of which are low in intensity and poorly represented by tonal carriers (Whitmal et al., 2007).

DISCUSSION

Implications for channel mapping

The results of this study indicate that listeners weight bands of unprocessed speech and vocoded speech in quiet very differently, even when the vocoded speech provides very good intelligibility. Subjects listening to unprocessed nonsense syllables assigned the highest importance to discrete bands in the 2000 Hz region, a result consistent with those of previous intelligibility studies (Kryter, 1962; ANSI, 1969; Humes et al., 1986; Studebaker and Sherbecoe, 1993; Pavlovic, 1994, ANSI, 1997). In contrast, subjects listening to vocoded speech assigned the highest importance to bands approximately one-half octave lower. Frequencies above 1500 Hz consequently became less important (even when high spectral resolution was maintained) and lower frequencies became more important. This is reflected by the asymmetry in LPF and HPF effects. In LPF conditions, subjects were able to obtain high recognition scores for V28 processing by adopting a strategy that placed more importance on low frequencies; no additional bandwidth was required at any performance level. Further losses in resolution imposed by V16A/V16B vocoders were mitigated by modest (0.3–0.5 octave) increases in bandwidth. In contrast, for HPF speech, the 84.1%-correct performance level was achieved for unprocessed speech with a 1.3 kHz CFE, a value (approximately) 1 octave above the corresponding V28 cutoff and (approximately) 2 octaves above the V16A and V16B cutoffs. These large bandwidth increases underscore the value of low frequency information.

The present work is consistent with studies that simulate the effects of “dead” cochlea regions on intelligibility by deactivating vocoder channels. For a 20-band vocoder, Shannon et al. (2002) and Baskent and Shannon (2006) showed that removing channels in the 1.0 kHz region reduced intelligibility of consonant, vowel, and sentence materials significantly more than removing channels in either the 2.4 or 5.0 kHz regions did. Garadat et al. (2010) studied a 20-band vocoder whose dead regions straddled those of Baskent and Shannon (2006) with partial overlap; their subjects also lost the most intelligibility when frequencies in the specified band were removed. Other band-removal studies using only six channels (Mehr et al., 2001; Kasturi et al., 2002) also assigned peak importance to this frequency region; however, the lack of importance function data for those low-resolution channel assignments makes direct comparison to the present data difficult. Additional support comes from studies of CI channel-mapping effects on intelligibility. Henry et al. (1998) suggested that intelligibility could be improved for individual subjects by making electrodes in the F1 and F2 spectral regions more discriminable. They also suggested that frequencies above 2680 Hz were primarily associated with noise burst cues that were less important to listeners. Fourakis et al. (2004, 2007) reported that users of the Nucleus 24 ACE systems obtained significantly better intelligibility for vowels when channels were reallocated from above 3000 Hz to an “F1” region below 1100 Hz and an “F2” region between 1100 and 2900 Hz.

Implications for measurement protocols

The objective of the present study was to evaluate the adaptive-bandwidth filtering method of Whitmal and DeRoy (2011) as a way to measure the importance of individual frequency channels for implant applications. To the extent that vocoder simulations model performance by implantees, these results confirm the feasibility of the approach. However, the present conditions and results differed from the original conditions and results of Whitmal and DeRoy for unprocessed speech, and compelled some small changes to the original Whitmal/DeRoy protocol. The implications of these changes are discussed below. In addition, the variability of the method for both unprocessed and vocoded speech is also assessed.

Removal of rule 1 for HPF speech

The original adaptive-mode measurements with unprocessed speech (Whitmal and DeRoy, 2011) met the rule 1 target (15.9%-correct) for HPF speech with a 4.89 kHz CFE. In initial tests for the present study, CFEs did not converge reliably to this target; they instead increased to 8000 Hz (the maximum value) and remained there for the duration of the adaptive run. To maintain that CFE, subjects must have been (and were) able to correctly identify at least one of four consecutive consonants. This unexpected result can be attributed to post-filtering level normalization, which was adapted from the speech recognition bandwidth threshold method of Noordhoek et al. (1999) to maintain a constant signal level. In the present experiment bandwidths narrow enough to produce low recognition scores require high gain to maintain a constant signal level. (For the 23 VCV tokens used here, high-pass filtering at 4.89 kHz mandates an average level change of 37.6 dB.) The effects of such gain changes were originally discounted, as the measurements of French and Steinberg (1947) show minimal changes in intelligibility as filtered unvocoded speech is raised above the optimum presentation level. However, the present results show that amplifying vocoded speech in this manner can make low-level envelope cues loud enough to contribute to intelligibility. This finding suggests that the use of level normalization should be re-evaluated for use in future trials.

Adjustment for ceiling effects

The VCV tokens used by Whitmal and DeRoy are highly intelligible when presented without filtering or vocoding applied (Whitmal et al., 2007). Performance for full-bandwidth presentation of these stimuli would be expected to approach 100%. In the present study, the V16A and V16B processors provided full bandwidth performance that approached the rule 5 target level (84.9%-correct). These performance levels were assessed from histograms constructed from thousands of subject trial responses—far more than the maximum of 40 trials per performance level recommended by Whitmal and DeRoy—as no series of full-bandwidth measurements had been scheduled. It is likely that rule 5 trials would have revealed little useful information at all if the full-bandwidth performance had been below that target level. This finding suggests that full-bandwidth measurements should be taken before adaptive trials to determine the performance range for the patient. Target performance levels could then be limited to those within the patient’s range, with nonuniform step sizes (Kaernbach, 1991) used as needed to converge on performance levels other than those specified by Levitt (1971). At the same time, the range of measurable performance levels could be increased by replacing the VCV tokens with the more easily recognized consonant-nucleus-consonant (CNC) word lists of Henry et al. (1998). Replacement would be straightforward: CNC words are also amenable to automated testing, and (despite their lexical content) follow a per-phoneme transfer function similar to that of Eq. 1.

Assessment of variability

Measurement reliability is an important consideration for any clinical procedure. In previous work, Whitmal and DeRoy (2011) showed that the proposed adaptive-bandwidth procedure provided repeatable, reliable measurements of rule-based filter cutoff frequencies and psychometric functions for both LPF and HPF speech. However, their assessment did not account for the high variability observed here with HPF psychometric functions for V16A and V16B. To evaluate the effects of this variability, adaptive trials were simulated for each of the listening conditions. For each simulated trial, the average psychometric curves of Figs. 23 were used to derive recognition probabilities for use in Bernoulli trials to simulate subject responses. These responses were used (as in the present experiment) to determine the CFE for the next simulated trial in accordance with the decision rules of Table TABLE I.. As in Whitmal and DeRoy (2011), average unprocessed CFE values of Tables 2, TABLE III. were used as initial values to reduce estimation bias. One thousand simulations (using three repetitions of the VCV token set) were run for unfiltered conditions and each of the nine rule/filter combinations. Psychometric curves were then fitted to each set of simulation data points to obtain bandwise IFs, which were then sorted to produce percentiles for each band. Figure 6 displays the IF value medians (solid line) and 95% central ranges (dashed lines) for each of the listening conditions. (The central range serves as an empirical confidence interval.) For each condition, the confidence intervals are widest near the mode of the importance function, equaling 2.8% for unprocessed speech, 3.2% for V28 speech, and 5.5% for both V16A and V16B. The higher variability of V16A and V16B is attributable to slope reductions in low-frequency regions of the HPF psychometric curves (Taylor and Creelman, 1967; Kollmeier et al., 1988).

Figure 6.

(Color online) Medians (solid line) and 95% central ranges (dashed lines) for importance function values in units of %-contribution per channel, derived from one thousand simulations of LPF and HPF adaptive bandwidth testing.

The confidence intervals reported above are larger than might be expected in traditional IF measurements. For example, Studebaker and Sherbecoe (1991) reported 95%-confidence intervals with maximum width of 1.8% for IF measurements for recordings of four W22 word lists. Their lower numbers, however, were acquired from repeated measurements of familiar words3 heard in 308 combinations of filtering and masking (using 10 different signal-to-noise ratios) with eight subjects listening in multiple two-hour sessions: a substantially larger effort than required with the present approach. Variability for the proposed method can be reduced by (a) using longer adaptive tracks, particularly for HPF data at low frequencies, or (b) using an adaptive test procedure with lower variability than the Levitt procedure. A promising framework for the latter approach is the theory of optimal experiments (Fedorov, 1972), in which a parametric model is fitted to the psychometric function by iteratively selecting stimulus parameters that reveal the maximum amount of information for (and reduce variance of) the model’s parameters. Remus and Collins (2008) showed that two adaptive procedures using optimal experiment design principles provided lower bias and faster convergence for threshold detection and intensity discrimination tasks than the Levitt procedure. Identifying a parametric model that fits the present data with low deviance might facilitate an optimal-experiment adaptive-bandwidth procedure that is more efficient than the present approach.

Limitations

The present study shows that subjects listening to speech from three vocoders placed more importance on the 1000–2000 Hz frequency region than subjects listening to unprocessed speech. The vocoders were specifically selected to produce uniform and favorable conditions for a new testing method (i.e., high performance at full-bandwidth, reduced ceiling and floor effects, fixed envelope bandwidths). This decision also restricts the generalizability of results. The numbers of channels used here are greater than the numbers of channels normally accessed by CI users (Dorman and Loizou, 1998; Friesen et al., 2001). This results in lower spectral smearing (particularly at high frequencies) than real-world listeners may experience. What’s more, the smoothing bandwidth used for envelope processing is narrower than normally used for CI users and simulation subjects (Wolfe and Schafer, 2010) and may provide less temporal fine structure than is normally available. This combination of factors will result in performance that will differ from that achieved by typical CI users or subjects in simulations more characteristic of implant usage. Data for these listeners and conditions can be obtained in future work, using the (necessary) modifications described above in Sec. 4B.

SUMMARY AND CONCLUSION

Importance functions (IFs) quantify the contributions of individual frequency bands to speech intelligibility. Previous research suggests that IFs might be suitable for quantifying contributions of bands associated with electrodes in cochlear implant systems. The present study used the adaptive procedure of Whitmal and DeRoy (2011) to measure IFs for both unprocessed speech and simulated implant-processed speech. Comparisons of these IFs indicate that vocoder processing shifts the peak speech importance region downward by approximately one-half octave, reflecting a change in strategy and capability for detecting voicing. Results are reliable and consistent with previous data, suggesting that the procedure is suitable for use in this application.