Three-dimensional biomechanical properties of human vocal folds: Parameter optimization of a numerical model to match in vitro dynamics

Abstract

The human voice signal originates from the vibrations of the two vocal folds within the larynx. The interactions of several intrinsic laryngeal muscles adduct and shape the vocal folds to facilitate vibration in response to airflow. Three-dimensional vocal fold dynamics are extracted from in vitro hemilarynx experiments and fitted by a numerical three-dimensional-multi-mass-model (3DM) using an optimization procedure. In this work, the 3DM dynamics are optimized over 24 experimental data sets to estimate biomechanical vocal fold properties during phonation. Accuracy of the optimization is verified by low normalized error (0.13 ± 0.02), high correlation (83% ± 2%), and reproducible subglottal pressure values. The optimized, 3DM parameters yielded biomechanical variations in tissue properties along the vocal fold surface, including variations in both the local mass and stiffness of vocal folds. That is, both mass and stiffness increased along the superior-to-inferior direction. These variations were statistically analyzed under different experimental conditions (e.g., an increase in tension as a function of vocal fold elongation and an increase in stiffness and a decrease in mass as a function of glottal airflow). The study showed that physiologically relevant vocal fold tissue properties, which cannot be directly measured during in vivo human phonation, can be captured using this 3D-modeling technique.

INTRODUCTION

The human voice signal originates in the larynx as a result of the three-dimensional (3D) oscillations of two opposing vocal folds. Healthy voice production is generally associated with symmetric, periodic vocal fold vibrations, while pathological voice production is generally associated with asymmetric, aperiodic vibrations. Unlike other voice disorders, functional dysphonia is an impairment of voice production which presents as follows: (1) it occurs in the absence of any known mucosal or neurogenic disease of the larynx,1, 2, 3 (2) it is observable only during phonation, and (3) it usually results in hoarseness.

Conventional examination methods, such as acoustical analysis of the voice signal, capture only the symptomatic information of laryngeal disease and are not able to uniquely determine properties of the voice source.4, 5, 6 Other visual inspection methods, such as videostroboscopy and videokymography, are limited by low temporal and spatial resolution.7, 8 To improve our understanding of basic mechanisms of human vocal fold vibration, enhanced mathematical and experimental techniques have been developed to better quantify vocal fold dynamics. Analysis of endoscopic high-speed (HS) digital recordings serves as basis for objective and quantitative measures of normal and pathological vocal fold vibrations.9, 10 Although endoscopic HS recordings can capture left-right asymmetries in vocal fold vibration, the corresponding observation is performed from a superior view where only the superior vocal fold dynamics along the longitudinal and lateral directions can be captured. The medial or more inferior parts of the vocal folds are therefore not visible. Such endoscopic, HS recordings of vocal fold dynamics have been used to optimize two- or other multi-mass-models in which only lateral vibrations of the vocal folds are considered.11, 12

During phonation, the vocal fold mucosal wave propagates primarily in a superior direction along the medial surface of the vocal folds.13, 14 Although Shaw et al. concludes that the mucosal wave differs considerably in normal voices,15 this conclusion was derived solely on the basis of endoscopic imaging. However, many of the complex 3D dynamics of the mucosal wave during phonation cannot be captured using endoscopic HS imaging (i.e., medio-lateral, inferior-superior, and anterior-posterior).16, 17, 18 Thus, it may be that the more complete dynamics of the mucosal wave obtained through direct imaging of the medial surface of the vocal folds will permit better differentiation of normal and pathological vibration patterns.

Hemilarynx studies may be used to capture the 3D vibrations of the vocal fold.9 In fact, the existence of the limitations of clinical endoscopy provided the primary impetus for our hemilarynx studies. Basically, an excised human larynx is used with one vocal fold removed to expose the medial surface of the opposite vocal fold. Microsutures are positioned on the vocal fold to track the 3D movements of the entire medial surface.17, 19, 20 To sufficiently duplicate these 3D vocal fold dynamics, a 3D-multi-mass-model (3DM) and corresponding optimization procedure were proposed in prior studies,21, 22 yielding preliminary insights into the biomechanical properties of the vibrating tissues along the medial surface of the vocal fold.

This work investigates physiologically relevant vocal fold tissue properties during phonation, which cannot be measured directly. For this purpose, the 3DM is optimized over a wide range of vocal fold conditions in the in vitro hemilarynx with variations in applied airflow, arytenoid adduction, and vocal fold elongation. The accuracy of the optimization procedure will be investigated. Spatial distributions of local effective mass and stiffness of the vocal fold will be detected and reported. Using statistical analysis, the dependencies of local effective mass and stiffness will be studied as a function of the input parameters. Thus this study will investigate the influence of applied airflow, arytenoid adduction, and vocal fold elongation adduction on the biomechanical parameters of the vocal folds. Finally, the application of the 3DM will also be used to evaluate the conclusions reported in other laryngeal tissue studies.20, 23, 24, 25, 26 Increased knowledge of the biomechanical parameters underlying laryngeal pathologies may facilitate clinical diagnosis of voice disorders, especially in the case of functional dysphonia.

METHODS

3D biomechanical model

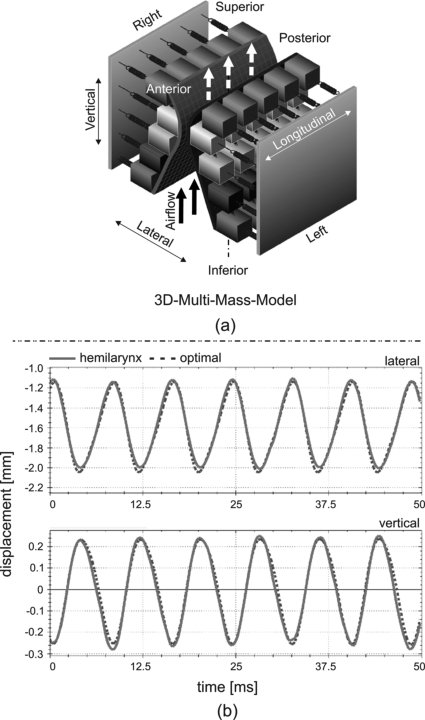
To model 3D vocal fold dynamics, a 3DM was developed previously.21 Within the 3DM, each vocal fold consists of five planes arranged from inferior to superior. Each plane contains five longitudinally coupled, mass-spring oscillators at each side, see Fig. 1a. During phonation, the subglottal pressure P^sub serves as the driving force and is approximated using Bernoulli’s law.11 Under the action of subglottal pressure, the masses located on both sides (left and right) are set into vibration. The 3DM dynamics may be modified by changing model parameters, such as spring stiffness (k_i,s), the masses (m_i,s) and rest positions $(x_{i,s}^r)$ of the oscillators, as well as the subglottal pressure (P^sub). Indices (i, s) denote the mass element i at the horizontal plane s. A detailed description of the 3DM can be found in Yang et al.21

Figure 1.

(Color online) (a) Schematic representation of the 3DM. Every vocal fold consists of five mass elements on each transverse plane. Each mass element is elastically connected to a rigid body by using an anchor spring. Also the mass elements are connected to their adjacent masses through springs in vertical and longitudinal directions.21 (b) Exemplary results of the optimized trajectories (dotted lines) of the mass elements m_3,3 located in the median cross section at the middle transverse plane on the right side of the model compared to the hemilarynx trajectories (solid lines) at the corresponding suture point. The longitudinal component is not shown here because the longitudinal displacement is relatively small ( ± 0.1 mm). The fundamental frequency is 120 Hz. The global normalized error (Γ) and correlation (k) are 0.09% and 88%, respectively. The local $(\Gamma ,\kappa )$ are (0.02, 99%) for lateral component and (0.11, 99%) for vertical component.

Optimization

To obtain 3DM vibrations (see Fig. 7 in Yang et al.)21 that matched measured human vocal fold vibrations as closely as possible (see Figs. 3 and 6 in Döllinger et al.),20 an optimization procedure was used to adjust model parameters.22 Within the optimization process, the model parameters (P^sub, m_i,s, k_i,s) were varied to reproduce the experimental trajectories. An objective function Γ was chosen to minimize the normalized error between the model-adapted 3D trajectories $c_{i,s}^M[n]$ and the experimental 3D trajectories c_i,s[n]. Due to anisotropy of the 3D vocal fold motions, heuristically chosen weighting coefficients for different dimensions, coronal cross sections, and transverse planes were applied to guarantee sufficient similarity between model and experimental dynamics. The non-convex objective function was regarded as the main challenge in the optimization procedure. To confront this issue effectively, combinations of global and local optimization techniques were applied. The optimization procedure was implemented along each side, each coronal cross section, and each horizontal plane within the 3DM. The basic idea was to gradually adapt the model parameters from a rough state to a more refined state, wherein increasing numbers of individual mass elements were considered. The optimization procedure has been validated by adapting 50 synthetic, laterally symmetric data sets with different glottal closure types in prior work.22 Similarities between the adapted 3D trajectories and the experimental 3D trajectories were judged according to two criteria: the normalized error function Γ and the correlation coefficient κ between the 3D trajectories. An example of such a comparison is shown in Fig. 1b. A detailed description of the optimization procedure is given in Yang et al.22

Application to hemilarynx experimental data sets

In this work, the optimization of the 3DM is applied to 24 hemilarynx experimental recordings. First, relationships between computed parameter values and experimental parameters will be presented to help assess the performance of the optimization procedure. Then the parameter values obtained by the optimization procedure will be discussed, including the computed distributions for the local effective mass and stiffness of the vocal fold. Finally, statistical analysis will be performed to investigate the dependence of the biomechanical properties of laryngeal tissues (i.e., as obtained from the optimization procedure) on parameters, such as glottal airflow, arytenoid adduction, and vocal fold elongation.

Hemilarynx experiments

The setup of the hemilarynx experiments is based on previous experiments with canine18, 27 and human hemilarynges.28, 29 The excised human larynx was obtained from a 76-year-old deceased male subject as provided by the autopsy unit of the UCLA Medical Center. The larynx was quick-frozen with liquid nitrogen and stored in a −20 °C freezer.17 It was slowly thawed before the experiments. This process has been shown to preserve the viscoelastic properties of the tissues.30 The trachea was mounted over a stainless steel cylindrical tube. A glass plate was attached at the top of the tube. To prevent air leaks, vacuum grease was applied between the anterior and posterior parts of the larynx and the glass plate.31 Vocal fold vibrations were induced by the airflow, which passed through the trachea and into the area between the glass plate and the vocal fold. A detailed sketch of the experimental setup can be found in Fig. 1 in Döllinger et al.20 To help quantify the 3D tissue trajectories captured by the HS recordings, surgical micro-sutures were uniformly distributed over the entire vocal fold surface.17 The vibrations were recorded with a HS digital camera [4000 Hz frame per second (fps), 512 × 512 pixels].17 A detailed description of the hemilarynx experiments and their analysis can be found in previous studies by Döllinger et al.31, 32

Experimental conditions

In the in vitro hemilarynx experiments, a variety of experimental conditions were implemented. First, to investigate sustained phonation, four levels of constant airflow were applied through the trachea and hemiglottis (i.e., area between the glass plate and the vocal fold) to induce vocal fold vibrations.17 The applied airflows U_g were 100, 200, 320, and 400 ml/s. Second, to modify the degree of vocal fold adduction, a suture pierced the arytenoid cartilage at the muscular process and coursed anteriorly to a pulley, at which varying weights M_p were attached (10, 20, 50 g). Third, to elongate the vocal fold, a suture pierced the thyroid cartilage and coursed anteriorly.20 Varying weights T_c were attached at the thyroid cartilage (10 and 20 g). All possible combinations of the above conditions were implemented. That is, for each data set (i.e., recording), each experimental setup differed from the other in U_g, M_p, and T_c. All together, 24 experimental conditions $E_{M_p,T_c}^{U_g}$ were implemented, see Table TABLE I. in the following Sec. 3.

TABLE I.

Optimization results for 24 hemilarynx experimental data sets: Objective function Γ and correlation coefficient k are optimization measures exhibiting the quality of the results. Corresponding experimental conditions $E_{M_p,T_c}^{U_g}$ include applied airflows U_g [ml/s], muscular process weights M_p [g], and thyroid cartilage weights T_c [g]. P^sub [cmH₂O] is the subglottal pressure applied in the experiments, while ${\hat{P}}^{\mathit{sub}}$ is the optimized value within the 3DM. Additionally, $\hat{f}$ [Hz] is the computed fundamental frequency, ${\hat{l}}_g$ [cm] is the computed length of vocal fold. The indices of recordings are defined in the hemilarynx experiments.17

Recordings	Γ	K (%)	$\hat{f}$	${\hat{l}}_g$	${\hat{P}}^{\mathit{sub}}$	Psub	f	Ug	Tc	Mp
H01	0.14	82	100	1.40	14.7	14	100	100	10	10
H03	0.11	80	120	1.42	21.4	21.7	120	200
H05	0.10	80	140	1.42	30.5	27.8	140	320
H07	0.10	80	140	1.42	32.6	29.2	140	400
H08	0.16	83	100	1.42	18.5	14.5	100	100	10	20
H10	0.12	85	120	1.43	22.3	23.5	120	200
H12	0.13	80	140	1.44	27.3	27.4	140	320
H14	0.13	82	140	1.42	34.8	31.7	140	400
H15	0.16	81	100	1.41	18.5	17.3	100	100	10	50
H17	0.15	84	120	1.42	21.1	24.2	120	200
H19	0.16	82	140	1.42	23.8	27.6	140	320
H21	0.16	81	140	1.43	26.3	28.8	140	400
H22	0.15	82	100	1.41	16.9	14	100	100	20	10
H24	0.09	88	120	1.44	21.5	22	120	200
H26	0.16	82	140	1.44	25.7	25.9	140	320
H28	0.14	81	140	1.44	26.9	29.3	140	400
H29	0.14	84	100	1.42	15.9	15.1	100	100	20	20
H31	0.15	82	120	1.43	22.4	23.4	120	200
H33	0.10	86	140	1.41	24.2	26.8	140	320
H35	0.09	80	140	1.44	26.9	29.5	140	400
H36	0.15	84	100	1.41	16.9	15.7	100	100	20	50
H38	0.10	84	120	1.43	20.1	22.6	120	200
H40	0.11	85	140	1.43	25.7	25.4	140	320
H42	0.11	82	140	1.42	28.5	28.7	140	400

To detect and further quantify the change of individual biomechanical vocal fold properties over the aforementioned experimental conditions (i.e., airflow, weight/force applied to muscular process to adduct the arytenoid, and weight/force applied to the thyroid elongate the vocal fold), the experimental data sets were collected over a time interval of 100 ms (i.e., 10–14 oscillation cycles for 100–140 Hz fundamental frequencies) of sustained phonation.17 A moving average filter was used to reduce measurement noise within the hemilarynx experimental data sets. To determine the distributions of parameters (i.e., mass, stiffness) within the 3DM, the positions of rigid bodies (serving as ventral/dorsal vocal fold extremes, see Fig. 2 in Yang et al.21) at anterior/posterior extremes were initialized to maintain a slight lateral separation from the glottal midline. Such initializations help to keep the glottal configurations as realistic as possible for studying the phonation onset status of the hemilarynx experiments.9, 17

Statistical analysis

Statistical analysis was performed to study the dependence of mass and stiffness on the various experimental conditions. To enable local spatial resolution of these changes across different experimental conditions, the mass and spring stiffness values were analyzed individually. This yielded 25 statistical tests for the parameters of mass and lateral stiffness, 20 statistical tests for vertical and longitudinal spring stiffness. Distributions of the computed vocal fold parameters (mass and stiffness) were verified to approximate a normal distribution across the 24 different recordings. Hence, we performed paired t-tests (left-tail, right-tail) for each parameter (i.e., increasing airflow, adduction forces, elongation forces). The significance level was chosen to be P = 0.05. The experimental conditions $E_{M_p,T_c}^{U_g}$ yielded the following comparisons for the statistical tests:

• Varying U_g with same M_p and same T_c: Because U_g is defined as 100, 200, 320, and 400 ml/s, the amount of comparisons is 36 [i.e., $(2\begin{array}{c}1\hfill \end{array})·(3\begin{array}{c}1\hfill \end{array})·(4\begin{array}{c}2\hfill \end{array})$]. Therefore for each parameter, there are 36 paired t-test elements, such as $E_{10,10}^{100}\to E_{10,10}^{200}$, $E_{10,10}^{100}\to E_{10,10}^{320}$, $E_{10,10}^{100}\to E_{10,10}^{400}$, $E_{10,10}^{200}\to E_{10,10}^{320}$, $E_{10,10}^{200}\to E_{10,10}^{400}$, $E_{10,10}^{320}\to E_{10,10}^{400}$, etc.

• Varying M_p with same U_g and same T_c: Because M_p is defined as 10, 20, and 50 g, the amount of comparisons is 24 [i.e., $(2\begin{array}{c}1\hfill \end{array})·(4\begin{array}{c}1\hfill \end{array})·(3\begin{array}{c}2\hfill \end{array})$]. That is to say, there are 24 paired t-test elements applied to analyze the influences of muscular process toward mass and stiffnesses in different regions of vocal fold. For example, $E_{10,10}^{100}\to E_{20,10}^{100}$, $E_{10,10}^{100}\to E_{50,10}^{100}$, $E_{20,10}^{100}\to E_{50,10}^{100}$, etc.

• Varying T_c with same U_g and same M_p: Because T_c is defined as 10 and 20 g, the amount of comparisons is 12 [i.e., $(3\begin{array}{c}1\hfill \end{array})·(4\begin{array}{c}1\hfill \end{array})·(2\begin{array}{c}2\hfill \end{array})$]. Therefore, there are 12 paired t-test elements applied to analyze the influences of thyroid simulation towards mass and stiffnesses in different regions of vocal fold. For example, $E_{10,10}^{100}\to E_{10,20}^{100}$, $E_{20,10}^{100}\to E_{20,20}^{100}$, $E_{50,10}^{100}\to E_{50,20}^{100}$, etc.

A Bonferroni correction was not introduced in the multiple testing because it is known to be a very conservative criterion for significance.33

RESULTS

Optimization accuracy

With regard to the hemilarynx experimental data sets, their fundamental frequencies, subglottal pressures, and optimization measures are summarized in Table TABLE I.. The achieved normalized error was lower than 0.16, and the corresponding correlation was higher than 80%. The average values of the objective function Γ and correlation κ over all 24 recordings were 0.13 ± 0.02% and 83% ± 2%, respectively. The computed subglottal pressure ${\hat{P}}^{\mathit{sub}}$ ranged between 11.8 and 32.6 cmH₂O. The normalized error of the computed subglottal pressure ${\hat{P}}^{\mathit{sub}}$ with respect to the applied subglottal pressure $P^{\mathit{sub}}$ was 8%, averaged over all recordings. The computed fundamental frequencies $\hat{f}$ for all recordings ranged between 100 and 140 Hz, which were derived and confirmed in both the time domain and the frequency domain. These computed fundamental frequencies were equal to the fundamental frequencies f measured in the hemilarynx experiments, see Table TABLE I..

Global parameters

The estimated vocal fold length ${\hat{l}}_g$ varied slightly between 1.40 and 1.44 cm. The mean value of the vocal fold length was computed to be 1.42 cm for T_c = 10 g, while the mean value of the vocal fold length was 1.43 cm for T_c = 20 g. The applied force at the muscular process (i.e., adduction) had no unique or no significant influence on either the computed or the measured subglottal pressure. In this work, the computed subglottal pressure ${\hat{P}}^{\mathit{sub}}$ was related to the airflow U_g. The computed subglottal pressure increased in a range of 6.5 to 17.9 cmH₂O, as the airflow increased from 100 to 400 ml/s. The increase in computed fundamental frequency $\hat{f}$ was dependent on the applied airflow U_g. In general, the elongation force applied to the thyroid cartilage yielded no change or decrease of subglottal pressure over the range of 1.0 to 7.9 cmH₂O, except for a slight increase at $E_{10,T_c,}^{100}$, $E_{50,T_c,}^{300}$, and $E_{50,T_c.}^{400}$.

Distribution of computed mass and stiffness of the vocal fold

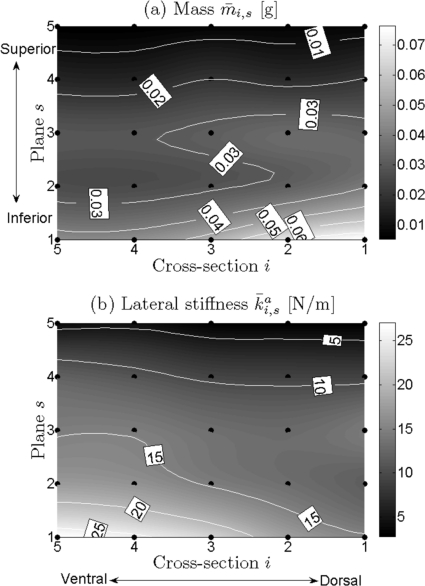
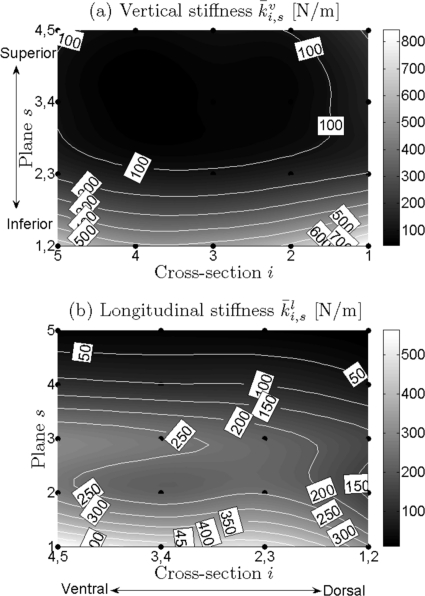
Maximum/minimum values of the optimized local mass, lateral stiffness, vertical stiffness, and longitudinal stiffness are shown in Table TABLE II.. Cubic 2D-data interpolations of the computed local mass and stiffness yielded continuous distributions between mass elements as shown within the following figures.

TABLE II.

Maximum and minimum of the optimized local mass m_i,s, lateral stiffness $k_{i,s}^a$, vertical stiffness $k_{i,s}^v$, and longitudinal stiffness $k_{i,s}^l$. These values are based on the applications of optimization procedure to 24 hemilarynx data sets. The unit of mass is [g]. The unit of stiffness is [N/m]. i = 1,…, 5 denote the dorsal cross section to the ventral cross section along the longi- tudinal direction. s = 1,…, 5 denote the inferior plane to the superior plane along the vertical direction.

	mi,s · 10−3	$k_{i,s}^a$	$k_{i,s}^v$	$k_{i,s}^l$
Max.	76.41	27.06	846.08	564.86
i	1	5	1	4,5
s	1	1	1,2	1
Min.	5.46	2.82	45.00	12.41
i	5	2	4	1,2
s	5	5	3,4	5

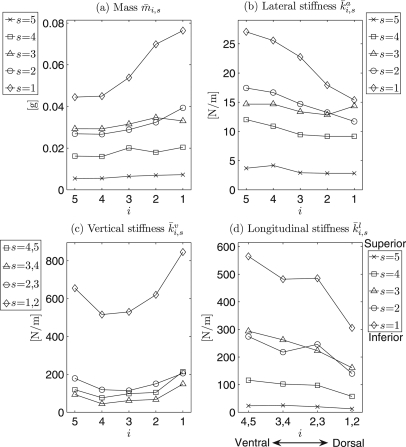
Due to space limitations, it is not possible to show all optimization results for each of the 24 recordings. However, a few representative examples will be given to illustrate the distributions and grand average values over mass ${\overline{m}}_{i,s}$ and stiffness ${\overline{k}}_{i,s}^a$, ${\overline{k}}_{i,s}^v$, ${\overline{k}}_{i,s}^l$ (Figs. 23). In all four charts, local mass and stiffness values significantly decreased along the vertical direction from inferior (s = 1) to superior (s = 5). Additionally, along the longitudinal direction [primarily at the median and inferior parts of vocal fold from ventral (i = 5) to dorsal (i = 1)], the following can be observed: an increase in mass; a decrease in lateral stiffness (i.e., anchor stiffness) ${\overline{k}}_{i,s}^a$; a slight decrease in vertical stiffness ${\overline{k}}_{i,s}^v$ from ventral to middle, followed by a subsequent increase from middle to dorsal; a decrease in longitudinal stiffness ${\overline{k}}_{i,s}^l$.

Figure 2.

(a) and (b) Charts for general distributions of local effective mass and local lateral stiffness of the vocal fold. They were averaged over all optimization results on the 24 experimental data sets. The black points are the positions of different mass elements distributed at vocal fold surface. Different gray levels correspond to different values of local mass/stiffness. Dark gray level to light gray level denotes small value to large value. The dotted lines are iso-lines.

Figure 3.

(a) and (b) Charts for general distributions of local vertical stiffness and local longitudinal stiffness of vocal fold, respectively. The same descriptions are shown in the caption of Fig. 2.

Distribution along the vertical direction

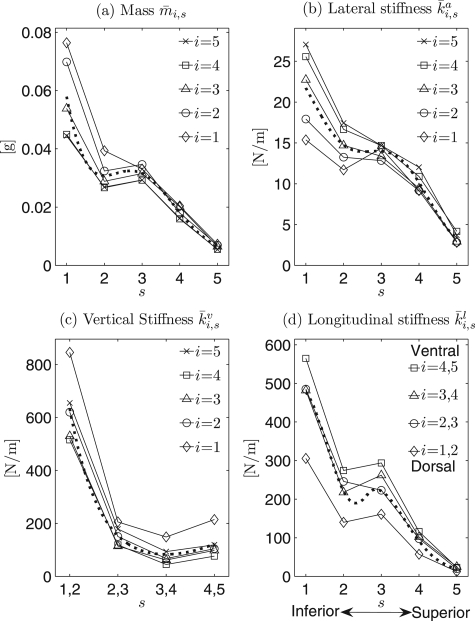
To further evaluate variations of the local mass and local stiffnesses along the vertical direction, comparisons between different horizontal planes s = 1,…, 5 were investigated, see Fig. 4.

Figure 4.

(a) to (d) Charts for comparisons of mass and stiffnesses between different horizontal planes s.${\overline{m}}_{i,s}$, ${\overline{k}}_{i,s}^a$, ${\overline{k}}_{i,s}^v$, and ${\overline{k}}_{i,s}^l$ denote the grand average values of mass, lateral stiffness, vertical stiffness, and longitudinal stiffness after applications of optimization procedure over all 24 hemilarynx experimental data sets, respectively. The dotted lines indicate the corresponding regressions for mass and different stiffness.

Mass.

In general, the effective mass values decreased from inferior (s = 1) to superior (s = 5) except for slight grooves located at the secondary inferior plane (s = 2), Fig. 4a. Similar variations occurred at each cross section (i =1,…, 5). For different horizontal planes (s = 1,…, 5) along the vertical direction, the mass values (averaged across all cross sections) ranged between 6.33 ± 3.12·10⁻³ and 57.90 ± 34.03· 10⁻³ g.

Lateral stiffness.

Figure 4b shows that lateral stiffness decreases from inferior to superior for all five cross sections (i = 1,…, 5). Along the vertical direction, the lateral stiffness values (averaged across all cross sections) for different planes ranged between 3.29 ± 2.59 and 21.74 ± 10.18 N/m.

Vertical stiffness.

In general, Fig. 4c shows that vertical stiffness nonlinearly decreased from inferior (s = 1, 2) to superior (s = 4, 5) across all five cross sections except for a slight increase from the superior planes (s = 3, 4) to the most superior planes (s = 4, 5). This general reduction trend yielded stiffness values (averaged across all cross sections) from 633.35 ± 365.04 to 122.64 ± 116.97 N/m along the vertical direction. The lowest value 83.24 ± 92.80 N/m was located between the two horizontal planes (s = 3, 4).

Longitudinal stiffness.

Similarly, over all cross sections, longitudinal stiffness generally decreased from inferior to superior. Only small grooves occurred at the secondary inferior plane (s = 2), see Fig. 4d. Along the vertical direction, the stiffness values (averaged across all cross sections) for different planes ranged between 20.15 ± 13.73 and 459.50 ± 262.75 N/m.

Additionally, Fig. 4 shows that maximum differences of mass/stiffness across different cross sections of the inferior vocal fold were greater and more discernible and than in superior regions with the exception of the vertical stiffness. Specifically, they were derived as 0.32 · 10⁻³ (inferior) and 1.80 · 10⁻³ g (superior) for mass, 11.69 (inferior) and 1.35 N/m (superior) for lateral stiffness, 330.60 (inferior) and 137.94 N/m (superior) for vertical stiffness, and 259.12 (inferior) and 12.58 N/m (superior) for longitudinal stiffness, respectively. Corresponding ratios of these differences between inferior and superior were 17.94 for mass, 8.66 for lateral stiffness, 2.40 for vertical stiffness, and 20.60 for longitudinal stiffness. The highest difference between cross sections occurred in the longitudinal stiffness distribution, while the lowest difference was in the vertical stiffness distribution.

Distribution along the longitudinal direction

To further examine the variations of mass and stiffnesses along the longitudinal direction, comparisons of their values across different vertical cross sections i = 1,…, 5 were made as follows (see Fig. 5):

Figure 5.

(a) to (d) Charts for the comparisons of mass and stiffness among different crosssections i. The descriptions are the same as Fig. 4.

Mass.

Along the longitudinal direction, the mass increased mostly at the median and inferior planes from ventral to dorsal especially at the inferior plane. Its highest value was located in the dorsal cross section i = 1 at the most inferior plane s = 1, while the lowest values were located in the ventral cross sections, see Fig. 5a. The mass values for the different cross sections ranged between 24.45 ± 16.50·10⁻³ and 35.29 ± 31.94·10⁻³ g.

Lateral stiffness.

Lateral stiffness decreased from ventral to dorsal, especially at the median and inferior planes. The dorsal cross section i = 1 generally yielded the lowest values, while the highest value usually occurred in the ventral cross section i = 5, see Fig. 5b. For different cross sections, the stiffness values ranged between 10.68 ± 5.68 and 14.98± 10.68 N/m.

Vertical stiffness.

Vertical stiffness decreased slightly from ventral to middle, and subsequently increased from middle to dorsal, especially at the inferior planes. A groove was generally situated at the middle cross sections, while both ventral and dorsal cross sections (i = 5 and i = 1) yielded the higher values [Fig. 5c]. For different cross sections, the values ranged between 201.16 ± 294.34 and 397.26 ± 552.54 N/m.

Longitudinal stiffness.

Figure 5d shows a near linear decrease in the longitudinal stiffness from ventral to dorsal, especially at the median and inferior planes. The highest values occurred in the ventral cross sections i = 4, 5, while the lowest values were found in the dorsal cross sections i = 1, 2. Along the longitudinal direction, longitudinal stiffness ranged from 254.44 ± 233.96 to 135.29 ± 169.18 N/m from ventral to dorsal, averaged across all planes.

Overall, in Figs. 5a–5d, neglecting small fluctuations, the values of local mass and stiffnesses at the superior planes exhibited nearly parallel horizontal lines with low variabilities, except for the vertical stiffness. Moreover, their variational tendencies (decrease/increase) became more and more significant near the most inferior plane. These results are summarized in Figs. 23: Along the longitudinal direction there were no remarkable variation tendencies at the superior planes except for the vertical stiffness.

Moreover, as compared with the mass and other stiffness values (e.g., lateral and longitudinal), the vertical stiffness inferiorly differed greatly with vertical stiffness values in other parts of the vocal fold, see Fig. 5c. The maximum vertical stiffness difference between the inferior and superior folds was 614.35 N/m, which occurred at the most ventral cross section (i = 5). The minimum difference was 395.93 N/m, which occurred at the dorsal cross section (i = 2). Likewise, all graphs in Fig. 5 were in agreement with Fig. 4, illustrating the variation tendencies of mass and stiffness differences, which decreased from inferior to superior along the vertical direction, in all cross sections.

Statistical analysis of computed mass and stiffness under different experimental conditions

Statistical analysis was performed on local changes of mass and stiffnesses evoked by different experimental conditions (e.g., increased airflow U_g, adduction forces at the muscular process M_p, and applied weights T_c at thyroid cartilage for elongation), as introduced in Table TABLE I..

An overview of the statistical tests is given in Table TABLE III.. The P-values, P_l for left-tail t-test, and P_r for right-tail t-test, have the following relationship: P_l = 1 − P_r. Three numbers (#-#-#) within each table cell can be used to heuristically reflect the dominant tendencies of the investigated parameters, as follows: a significant decrease (P_l < 0.05), a nonsignificant change (0.05 ≤ P_l ≤ 0.95), and a significant increase (P_l > 0.95, due to P_r = 1 − P_l). The sum of the three numbers represents the number of times each parameter was investigated within the 3DM: 25 times for mass, 25 times for lateral stiffness, 20 times for vertical stiffness, and 20 times for longitudinal stiffness due to the 25 mass elements connected to each other at one side within the 3DM. For example, 14-11-0 in Table TABLE III. indicates that 14 mass values significantly decreased with increasing airflow, while 11 mass values had no significant change, and no mass values significantly increased. Due to limitations of the hemilarynx experiment,17 the unique influence of simultaneously increasing airflow, adduction, and elongation could not be studied.

TABLE III.

Statistically relevant changes of mass and stiffnesses (stif.) under influences of increased airflow U_g, muscular process M_p, and thyroid simulation T_c after statistical left-tail and right-tail t-tests. Within each cell, the three numbers (#-#-#) denote significant decrease (P_l < 0.05) - nonsignificant change (0.05 ≤ P_l ≤ 0.95) − significant increase (P_l > 0.95, due to P_r = 1 − P_l). The sums of the three numbers represent the amounts of mass (25), lateral stif. (25), vertical stif. (20), longitudinal stif. (20).

Conditions	Mass	Lateral stif.	Vertical stif.	Longitudinal stif.
Ug	14-11-0	1-11-13	0-12-8	0-16-4
Mp	0-24-1	2-23-0	0-18-2	0-19-1
Tc	9-13-3	6-11-8	5-9-6	2-12-6

Table TABLE III. shows that increasing the airflow resulted in a decreased mass (14/25), an increased lateral stiffness (13/25), an increased vertical stiffness (8/20), and a slightly increased longitudinal stiffness (4/20). In comparison, the tendency of mass to increase, and the tendency of the different stiffnesses to decrease were not sufficiently significant. In other words, the larger the airflow, the smaller the vibrating mass and the higher the stiffness.

Moreover, for increased adduction forces, the mass and different stiffnesses did not significantly increase or decrease but exhibited large values indicative of nonsignificant changes: 24/25 for mass, 23/25 for lateral stiffness, 18/20 for vertical stiffness, and 19/20 for longitudinal stiffness.

Additionally, increased thyroid traction yielded slightly decreased mass (9/25), relatively increased stiffnesses like 8/25 for anchor, 6/20 for vertical, 6/20 for longitudinal. The increase tendency of mass (3/25) was not dominant. Also, 6/25, 5/20, and 2/20 indicated smaller significant decrease tendencies of anchor, vertical, and longitudinal stiffnesses, respectively, compared to corresponding increase tendencies (Table TABLE III.).

To visualize the P-values for mass and the different stiffnesses over distinct regions of the vocal fold, cubic 2D-data interpolation was applied to yield continuous surfaces of P-values over all of the mass elements within the 3DM, see Figs. 6–8, which was interpreted as follows.

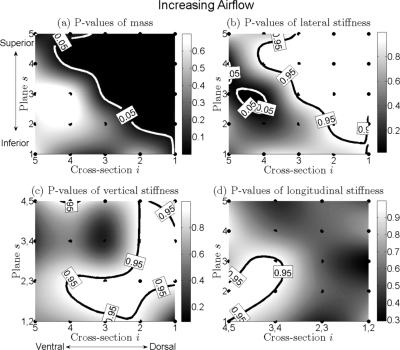
Figure 6.

(a) to (d) Charts for distributions of P-values of change of mass, lateral stiffness, vertical stiffness, and longitudinal stiffness of the vocal fold for increased airflow. They are on the basis of the optimization procedure to the 24 hemilarynx data sets. The black points are positions of different mass elements distributed across the vocal fold. Different gray levels correspond to different P-values of mass/stiffness. Dark gray level to light gray level denotes small value to large value. The black solid bold line indicates contour of P-value 0.95 (significant increase: P > 0.95), while the white solid bold line denotes contour of P-value 0.05 (significant decrease: P < 0.05).

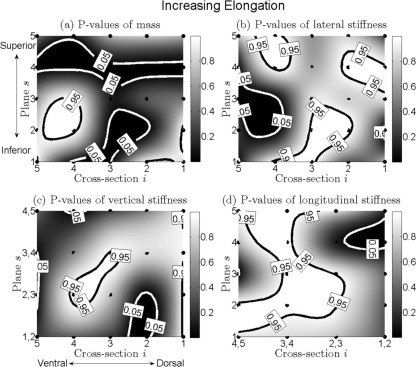
Figure 8.

(a) to (d) Charts for distributions of P-values of changing of mass, lateral stiffness, vertical stiffness, and longitudinal stiffness of the vocal fold for increased thyroid traction. Corresponding descriptions are shown in the caption of Fig. 6.

Increased airflow, Fig. 6

Mass.

The area that corresponded with a significant decrease in mass (which was more dark gray and bordered with a white contour of P-value 0.05) was located in the superior and dorsal part of the vocal fold [see Fig. 6a]. The remaining area corresponded to a nonsignificant change in mass. Overall, for increased airflow, a significant decrease of mass was dominant.

Lateral stiffness.

Conversely, in the superior and dorsal region of vocal fold, an area of significant increase was located which was shaded with more light gray and bordered with a black contour of P-value 0.95. A small ellipse with white contour was an area of significant decrease. Additionally, between the white contour and the black contour, an area of nonsignificant change was located. Overall, the tendency of lateral stiffness to increase was dominant [Fig. 6b].

Vertical and longitudinal stiffnesses.

For both stiffnesses, there were no areas of significant decrease. Only areas of significant increase and nonsignificant change existed, see Figs. 6c, 6d.

Increased adduction, Fig. 7

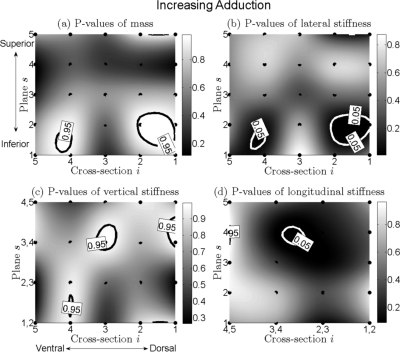
Figure 7.

(a) to (d) Charts for distributions of P-values of changing of mass, lateral stiffness, vertical stiffness, and longitudinal stiffness of the vocal fold for increased muscular process traction. Corresponding descriptions are shown in the caption of Fig. 6.

Mass.

The areas of significant increase, surrounded with black contours, were small as compared to the relatively large remaining areas of nonsignificant change, see Fig. 7a. Therefore the dominant tendency was that of nonsignificant change.

Lateral stiffness.

Similarly, only small areas of significant decrease were presented in Fig. 7b. The remaining area exhibited nonsignificant change. Thus, again, the dominant tendency was nonsignificant change.

Vertical and longitudinal stiffnesses.

For vertical stiffness, there were a couple of small areas of significant increase, see Fig. 7c. The dominant tendency of vertical stiffness was nonsignificant change. For longitudinal stiffness, only a small ellipse indicated significant decrease. Overall, the dominant tendency of longitudinal stiffness was nonsignificant change, see Fig. 7d.

Increased elongation force, Fig. 8

Mass.

The areas of significant decrease (bordered with white contours) were located not only at the superior plane s = 4 from ventral to dorsal but also at the nearly middle cross sections i = 2, 3, 4 from the inferior plane s = 1 to the medial plane s = 3, see Fig. 8a. Also, an ellipse of significant increase was located at the ventral and inferior region (s = 2, 3; i = 4, 5). Additionally, the dorsal and inferior boundaries of the vocal fold had a slightly significant increase.

Lateral stiffness.

Three areas of significant increase (with black contours) were located at the ventral-superior region (s = 4, 5; i = 4), the superior-dorsal region (s = 4; i = 1, 2), and the inferior-middle region (s = 1, 2; i = 2, 3, 4). The ventral-medial region (s = 2, 3; i = 4, 5) exhibited a significant decrease, see Fig. 8b.

Vertical and longitudinal stiffnesses.

For vertical stiffness, the middle-medial region exhibited a significant increase. Conversely, the remaining region (except superior-dorsal corner) tended to decrease, see Fig. 8c. For longitudinal stiffness, a large area of significant increase extended, meandering from the inferior planes s = 1, 2 to the most superior plane s = 5, see Fig. 8d. A small area of significant decrease was situated at the superior-dorsal corner.

DISCUSSION

In this work, the parameter optimization of a biomechanical model by matching its dynamics with measurements from in vitro experiments has proven to be an objective, quantitative method for computing biomechanical properties of human vocal folds. The presented quantification procedure (including experimental data collection, numerical modeling, and parameter optimization) served as an objective measure to determine physiologically relevant vocal fold properties during phonation.

Application to different hemilarynx data sets

To investigate the biomechanical properties of the vocal folds under different experimental conditions, the material parameters of the 3DM were optimized for 24 distinct data sets from hemilarynx experiments. The optimization procedure matched model trajectories with experimental 3D trajectories, yielding both low error (Γ = 0.13 ± 0.02) and a high correlation coefficient (k = 83% ± 2%), see Sec. 3A and Table TABLE I.. The measured subglottal pressure values during the experiments were elevated but remained within typical ranges reported in the literature for human phonation and exhibited variations consistent with conclusions about subglottal pressure in Refs. 34, 35, 36, 37. The normalized error (8% ± 6%) obtained by comparing the computed subglottal pressure ${\hat{P}}^{\mathit{sub}}$ with the measured subglottal pressure $P^{\mathit{sub}}$ suggests an acceptable reproduction quality. Over a specified range of glottal adductions and vocal fold elongations, a near linear relationship was observed between subglottal pressure and airflow during phonation (Sec. 3B). Briefly, the airflow increased significantly as the subglottal pressure increased. This result is consistent with the conclusions of Alipour et al.23, 38, 39, 40 and Jiang et al.28

The computed fundamental frequencies $\hat{f}$ were the same as the measured fundamental frequencies f, see Table TABLE I.. These results further demonstrate the reliability and the feasibility of the optimization procedure.

Overall, there was a slight increase in the length of the vocal fold (e.g., the mean value changed from 1.42 to 1.43 cm) with increased activation of the thyroid cartilage (i.e., T_c from 10 g to 20 g), see Table TABLE I.. However, while an increase in vocal fold length occurred, it was not sufficient to be considered statistically significant. This may be because the difference between 10 and 20 g was not sufficient to induce significant differences in length.

Distribution of local effective mass and stiffnesses

One goal of laryngeal studies is to uncover physiologically relevant tissue properties such as local effective mass and stiffness distributed over the entire vocal fold.25, 26, 41, 42 Stiffness and mass not only play a vital role in prephonatory glottal shaping but also exert a major influence on all aspects of 3D vocal fold dynamics. Such knowledge can enhance our understanding of vocal fold structure and provide novel biomechanical data to better inform physical and numerical models of the vocal folds. Therefore the goal of this research is to support surgical planning decisions, including identification of appropriate regions for incisions with the aid of predictive distributions of mass and stiffness within the entire vocal fold in order of scarring in locations which most adversely effect vibration.

Values and corresponding variations of effective mass and different stiffnesses are shown in Figs. 23. In general, further investigations over all 24 hemilarynx experimental data sets show that the lateral stiffness (lateral) is lower than stiffnesses in the other two directions (longitudinal, vertical), while the mean value of longitudinal stiffness is only slightly higher than vertical stiffness. This result further supports the conclusions by Alipour et al.43 that vocal fold tissue has stronger stiffness in the longitudinal direction than in the transverse direction. Furthermore, the local effective mass and stiffnesses (lateral, vertical, longitudinal) generally decrease from the inferior regions to the superior regions along the vertical direction. One physiological reason could be that there is a substantial variation in laryngeal tissue stiffness and density in the relatively stiff inferior region as compared to the relatively lax superior region.26 Additionally, this result supports the conclusions of Goodyer et al.26 that such changes in mass and stiffnesses may provide a more efficient transfer of energy across the air/tissue boundary by supporting the laminar rather than the turbulent flow. Indeed these inherently biomechanical variations of vocal fold tissues might facilitate the transfer of energy from the subglottal airflow to the mucosal wave.26, 44, 45

One finding (Fig. 4) that differs from Goodyer et al.26 is that the variations of mass and stiffness from inferior to superior along the vertical direction are not totally linear. For example, the vertical stiffness exhibits exponential regression [Figs. 4c, 5c]. However, an approximately linear variation occurs in the lateral stiffness (e.g., an increase of about 3.5 N/m per mm of distance) [Figs. 4b, 5b]. One possible reason could be that the study by Goodyer et al.26 was carried out using pig larynges, while our results were obtained on the basis of human hemilarynx experiments. In part, the variations in mass and longitudinal stiffness can be considered to be predominantly linear, when the grooves found in Figs. 4a, 4d are small enough to be negligible.

In addition, Fig. 4 shows that the variational range of parameters (mass or stiffness) in the inferior regions of the vocal fold are slightly higher than in the superior regions especially with regard to mass and longitudinal stiffness. These phenomena may be explained by the following two causes: First, the values of local parameters in the inferior regions are higher than in the superior regions. Second, the magnitude of parameter variations in the inferior regions is higher than in the superior regions because decrease/increase of parameters occurred mostly in the median and inferior regions (Figs. 23).

Additionally, in the superior regions of the vocal fold, mass, lateral stiffness, and longitudinal stiffness exhibited slight or nonsignificant variations along the longitudinal direction. The same was not true of vertical stiffness, see Fig. 5. This low variability of tissue properties may have been caused by the vocal ligament, which has fibrous tissues and firmly connects the thyroid cartilage to the vocal process of arytenoid cartilage within the superior vocal fold edges. However, in the median and inferior regions from ventral to dorsal, the following occurred with statistical significance: an increase in mass, an approximately linear decrease in lateral stiffness and longitudinal stiffness, and a nearly parabolic variation in vertical stiffness (e.g., a decrease followed by an increase) corresponding to ventral-middle-dorsal region (Fig. 5). Regarding the variations in mass and stiffness, it might be explained by the potentially anisotropic biomechanical properties and complex physiology of the vocal folds.46 The increase in mass was probably caused by the prominent muscular process in the dorsal region, which the cricoarytaenoideus posterior converges to insert into from behind, and the cricoarytaenoideus lateralis inserts into from the front.47 The relatively high lateral stiffness and longitudinal stiffness in the ventral region might be explained by the fact that the tissues closer to the fixed angle of the thyroid cartilage and the conus elasticus (connecting thyroid, cricoid, arytenoid cartilages to one another)47 are stiffer than in other regions because cartilage is stiffer than regular connective tissue.48 The parabolic decrease-increase variations in vertical stiffness might be caused by the relatively stiff supports at both longitudinal extremes, which are mounted on the angle of the thyroid cartilage at the ventral portion and the arytenoid cartilage at the dorsal portion. Nevertheless, more detailed investigations will be performed in future studies.

In this work, the variations in lateral stiffness and longitudinal stiffness (Figs. 2345) demonstrate that the vocal fold tissue was stiffer ventrally as opposed to dorsally. Further experimental studies using excised larynges are necessary to substantiate this finding. Another finding in Figs. 2345 is that the vertical stiffness decreased from the dorsal to the middle region of vocal fold, then subsequently increased from the middle to the ventral region of the vocal fold. This result might implicitly support previous empirical findings49 suggesting that the elastic mucosa is thickest in the middle region of the vocal fold with thinning noted both ventrally and dorsally, thus causing a lower stiffness in the middle region.

According to Fig. 5c, another point of interest is that there was a large difference between the vertical stiffness inferiorly, as compared to the other parts of the vocal fold, yielding an exponential recession curve as shown in Fig. 4c and a nonlinear change in Fig. 3a. This result implies that vertical stiffness has more nonlinear transition features in the vertical direction than the other stiffness components. It might be due partly to inherent, physiological tissue changes from the trachea to the glottis.

Variations of parameters under different experimental conditions

As presented in Sec. 2C2, 24 hemilarynx experimental data sets were studied. Each experimental condition was unique with respect to glottal airflow, adduction force, and elongation force.17 The corresponding initial conditions can also be found there. From a point of tissue-engineering research, investigating such influences can help improve our understanding of interactions between glottal airflow and the intrinsic laryngeal muscles. Statistical analysis has been implemented to investigate these influences. Three aspects are interpreted as follows.

Increasing airflow

Statistical analysis in Sec. 3D reveals that an increase in the applied airflow yielded a decrease in local mass and an increase in different local stiffness values, especially for lateral stiffness. These phenomena may be explained as follows: First, an increase in the applied airflow usually results in an increase in the fundamental frequency as demonstrated by Alipour et al.38, 39, 40 and Jiang et al.28 Second, the increased airflow may have induced an increase in acceleration and velocity of vocal fold dynamics.17, 50 Also, according to the physical laws among fundamental frequency, mass, and stiffness within the mass-spring oscillator,11 the fundamental frequency is directly proportional to square root of the stiffness and inversely proportional to the square root of the mass. That is to say, increasing the stiffness and decreasing the mass, by thinning the vocal fold through longitudinal stretching (i.e., contraction of the cricothyroid muscle with elongation of vocal folds), yields an increase in the vibration frequency. Also, to decrease the fundamental frequency, a decrease in stiffness and increase in mass may be performed due to contraction of the thyroarytenoid muscle with an increased concentration of the vocal fold. Therefore it can be deduced that mass decreases and stiffness increases as airflow increases. Additionally, for mass and lateral stiffness, the most significant variation area was located in superior and dorsal region of the vocal fold. This can be explained by the fact that tissue near the muscular process of the arytenoid cartilage might be potentially more sensitive, due to potentially greater forces exhibited in this region.

Increasing adduction

In general, increasing adduction forces yielded discernible but not sufficiently significant variations of local mass and stiffnesses as compared to the more dominant components of nonsignificant change, see Table TABLE III. and Fig. 7 (statistical analysis focusing on adduction). Because Sec. 4A and Döllinger et al.20 found that there was no significant relationship between subglottal pressure and adductory forces, in this case, increasing adduction did not result in an increase in fundamental frequency, which is dependent upon subglottal pressure.51, 52 Therefore, local mass and stiffnesses can not be easily changed during increase of adduction. Additionally, this result (Fig. 7) also implicitly supports the findings in Boessenecker et al.17 that adduction had no significant influence on displacements, velocities, and accelerations because increased adductory forces failed to increase airflow, which does yield increased velocities and accelerations of vocal fold dynamics.

Elongating vocal fold

Results in Fig. 8 as well as Table TABLE III. reveal that elongating the vocal fold can result in a significant decrease in mass along with a simultaneous increase in stiffnesses, especially longitudinal stiffness. This confirms the finding by Tao et al.25 that vocal fold elongation increases longitudinal tension, which in turn yields an increase in the effective spring constant of the vocal fold.53 These phenomena are consistent with Titze’s24 observation that human vocal folds (namely, vocal ligament) tense while elongating. That is, the vocal folds can be virtually limp when short but impressively tense when elongated.24 Furthermore, Titze emphasized that: “since lengthening a string has the effect of lowering pitch, tension must be increased at the same time to counteract the lengthening effect. In fact, according to physical law, tension must increase four-fold for a two-fold increase in length just to keep pitch the same.” Therefore, a stiff vocal ligament within the vocal fold plays an important role to achieve such function that is “increasing pitch by elongating a vocal fold.”24 Additionally, from a physical point of view, it is logical that elongating the vocal fold by longitudinal stretching yields a decrease in effective mass per unit volume along the longitudinal direction. That might be the reason why the significant reduction in area for mass occurred at the superior plane s = 4 from ventral to dorsal along the longitudinal suture course direction [Fig. 8a]. However, these results are not consistent with Tao’s et al.25 observation that vocal fold elongation failed to significantly change the effective mass of the vocal fold. One reason for this discrepancy could be that the comparisons of physiological parameters across different vocal fold elongation in Tao et al.25 reported total mass (i.e., m₁ + m₂ for the two-mass model) as opposed to spatial variations in mass. Such processes might tend to yield nonsignificant changes in mass. Because the effective mass is distributed throughout the 3D vocal fold tissues, variations in the effective mass may occur in different regions of the vocal fold [Fig. 8a], yielding various distribution of mass, while the total tissue mass may remain more or less constant.

Limitation

In the current work, from a computational point of view, enhancement of the optimization procedure is always possible even if its validation through different synthetic data sets and application to different experimental data sets exhibited sufficient accuracy so far. Because the optimization procedure is based on stochastic search algorithms,22 and because the inverse problem is non-convex (i.e., one global minimum with additional local minima), and because an analytic solution of the system of ordinary differential equations does not exist,21 the optimization solution cannot be said to be unique or necessarily yield a global minimum.22 Additionally, because only a single hemilarynx was utilized in this study, an analysis of the experimental data sets yielded in this single subject study will not allow generalized conclusions to be reached. Put another way, the biomechanical values yielded by the optimization procedure must be considered preliminary. Nevertheless, statistical analysis of influences from applied airflow, adductory forces function, and elongation forces revealed variations in the biomechanical properties of the vocal folds, which were largely consistent with conclusions reached in previous studies. At the same time, extending the study to optimize over a more extensive range of experimental 3D vocal fold dynamics may be beneficial to study the full range of life-like conditions exhibited in both normal and disordered voice. This would provide an opportunity to more fully investigate the morphological tissue alterations associated with many types of vocal dysphonia, including scarring. In the simplified model of 3D vocal fold dynamics utilized in this study, the layered structure of vocal fold tissues was not differentiated in the medial-lateral direction. Extending the number of mass elements in the medial-lateral direction would be necessary to overcome this limitation. Also, in this work, tissue parameters (mass, stiffness) were optimized for a specific mass-spring-oscillator model. Unfortunately, the biomechanical properties for this model are not directly generalizable to parameters of continuum vocal folds of vocal fold vibration (e.g., shear modulus, elastic modulus, Poisson ratio, etc., for the case a transversely isotropic continuum). In future work, it may be significant to extend these optimization procedures to such continuum models as well.54 In general, the current study represents a significant methodological step toward understanding the 3D biomechanical properties of the human vocal folds during phonation. It provides clinicians and scientists with valuable methodologies for laryngeal diagnosis, including but not limited to the following: the differentiation of healthy and pathological voice production, quantification of asymmetries between the left and right vocal folds, identifying and characterizing specific pathological regions of the vocal folds, evaluation of phonosurgical success through both pre- and post-operative analysis of 3D tissue properties.

SUMMARY

An optimization of the 3DM was applied to 24 experimental hemilarynx data sets, which differed from each other in terms of airflow, adductory forces, and elongation forces. The optimization procedure yielded estimates of the biomechanical properties of vocal fold tissues. With regard to the hemilarynx experiments, low normalized error and high correlation between model-optimized dynamics and experimental vocal fold dynamics ensured the reliability and capability of the applications. Novel distributions of the local effective mass and stiffness within the entire vocal fold were uncovered in Sec. 4A1, e.g., mass and stiffness in the superior regions were smaller than in the inferior regions, etc., which was largely consistent with the results of prior laryngeal studies26, 43 but also provided additional detail. By using statistical analysis to investigate the variations in the optimized model parameters across different experimental conditions, additional information regarding the biomechanical properties of laryngeal tissues was extracted (Sec. 3D), e.g., an increase in tension resulted from an increase in vocal fold elongation, an increase in stiffness and a reduction in mass resulted from an increase in glottal airflow, etc. These findings were consistent with the conclusions of other laryngeal tissue studies24, 25, 53 and further established the credibility of the proposed optimization procedure.

In future studies, the 3DM will be optimized over a more extensive range of 3D vocal fold dynamics extracted from in vitro or in vivo human larynges. To enable extraction of 3D vocal fold dynamics from endoscopic recordings, a HS camera with laser-dot projection system is currently under development.55 It is hoped that this development will facilitate our long-term goal of extending these optimization procedures to clinical applications, e.g., to use the optimized parameters from the 3DM as an objective measure to guide both conventional voice therapy and surgical interventions.