Applications of non-uniform sampling and processing

Abstract

Modern high-field NMR instruments provide unprecedented resolution. To make use of the resolving power in multidimensional NMR experiment standard linear sampling through the indirect dimensions to the maximum optimal evolution times (~ 1.2 T₂) is not practical because it would require extremely long measurement times. Thus, alternative sampling methods have been proposed during the past twenty years. Originally, random non-linear sampling with an exponentially decreasing sampling density was suggested, and data were transformed with a maximum entropy algorithm (Barna et al., 1987). Numerous other procedures have been proposed in the meantime. It has become obvious that the quality of spectra depends crucially on the sampling schedules and the algorithms of data reconstruction. Here we use the forward maximum entropy (FM) reconstruction method to evaluate several alternate sampling schedules. At the current stage, multidimensional NMR spectra that do not have a serious dynamic range problem, such as triple resonance experiments used for sequential assignments, are readily recorded and faithfully reconstructed using non-uniform sampling. Thus, these experiments can all be recorded non-uniformly to utilize the power of modern instruments. On the other hand, for spectra with a large dynamic range, such as 3D and 4D NOESYs, choosing optimal sampling schedules and the best reconstruction method is crucial if one wants to recover very weak peaks. Thus, this article is focused on selecting the best sampling schedules and processing methods for high-dynamic range spectra.

Introduction

The introduction of pulsed NMR and Fourier transformation of the time domain data has revolutionized NMR spectroscopy (Ernst and Anderson, 1966). The routine application of this technology became possible with the fast Fourier transformation (FFT) algorithm (Cooley and Tukey, 1965). It requires time domain data to be sampled in linear increments to enable its application. This technology has dominated NMR spectroscopy ever since. The sampling procedures used are called linear or uniform sampling. With the availability of higher field magnets and considering the low sensitivity of biological samples new ideas have come up to depart from uniform sampling and use new processing methods to enhance the capabilities of NMR spectroscopy, in particular of biological macromolecules.

The first proposal to abandon linear sampling was made by Barna et al. who suggested to place the sampling points in the indirect dimension with exponentially decreasing separation and transforming the spectra with a maximum entropy algorithm (Barna et al., 1987) developed by Skilling at al. (Sibisi et al., 1984). This proposal has found many followers since and numerous sampling methods and data processing procedures have been proposed. The approach has been further developed with the Maximum Entropy (MaxEnt) reconstruction tool using a different algorithm (Hoch, 1989), and many applications and implementations have followed (Schmieder et al., 1993; Schmieder et al., 1994; Schmieder et al., 1997; Shimba et al., 2003; Rovnyak et al., 2004a; Rovnyak et al., 2004b; Sun et al., 2005a; Sun et al., 2005b) (Frueh et al., 2006). The principle advantages of non-uniform sampling are increasingly recognized (Tugarinov et al., 2005). Besides Maximum Entropy reconstruction, other methods are used for processing non-uniformly recorded spectra, such as the maximum likelihood method (MLM) (Chylla and Markley, 1995), a Fourier transformation of non-uniformly spaced data using the Dutt-Rokhlin algorithm (Marion, 2005), and multi-dimensional decomposition (MDD) (Korzhneva et al., 2001; Orekhov et al., 2001; Gutmanas et al., 2002; Orekhov et al., 2003; Hiller et al., 2009). Several other methods have been presented to allow for a rapid acquisition of NMR spectra with suitable processing tools, including radial sampling and GFT (Kupce and Freeman, 2004a; Kupce and Freeman, 2004b); (Kim and Szyperski, 2003; Coggins et al., 2005; Venters et al., 2005; Coggins and Zhou, 2006; Kazimierczuk et al., 2006a; Kazimierczuk et al., 2006b; Coggins and Zhou, 2008).

While there is still much research to be done to find optimal non-uniform sampling schedules and processing methods the large benefits are already quite obvious. Nevertheless, most laboratories still acquire multidimensional NMR data with the traditional uniform acquisition schedules and process data with the FFT algorithm. This is despite the fact that linear sampling of 3D and 4D NMR data at modern high-field NMR spectrometers can only cover a fraction of the indirect time domains, and the resolution power of the new instruments is often largely wasted.

Here we analyze the benefits of non-uniform sampling for NMR spectroscopy on challenging biological macromolecules. The application of NUS has been well established with spectra that have no dynamic range problem, such as triple resonance experiments as described previously (Frueh et al., 2006; Hyberts et al., 2009). This allows recording of multidimensional triple resonance spectra at resolutions matching the resolving power of modern high-field instruments in a reasonable time. The current challenge of NUS approaches is more for experiments with high dynamic range problems, such as 3D and 4D NOESY spectra. Thus, the following is more concerned with this aspect. Below we discuss (i) procedures towards finding optimal sampling methods using point spread functions. (ii) We analyze the variation of performance due to the selection of the seed numbers used for creating random sampling schedules in different densities. (iii) We compare different sampling schedules when using just straight FFT for reconstruction. (iv) We analyze the variation of the performance depending on the stochastic type of noise. (v) And finally, we compare the use of different sampling schedules on an experimental 3D NOESY spectrum. Since the benefits of NUS depend on the processing methods we start out with a discussion of several processing principles but compare different sampling strategies primarily with the FM reconstruction procedure developed in our laboratory (Hyberts et al., 2007).

The forward maximum entropy (FM) reconstruction relative to other procedures

The purpose of this manuscript is to compare different sampling schedules. We do this using the FM reconstruction procedure described in detail previously (Hyberts et al., 2007; Hyberts et al., 2009). In short, FM reconstruction is a minimization procedure that obtains the best spectrum consistent with the non-uniformly sampled time domain data set by minimizing a target function Q(f), which is a norm of the frequency spectrum, such as the Shannon entropy S, or simply the sum of the absolute values of all spectral points. Initially, all data points not recorded are set to zero. This initial time domain data set is Fourier transformed yielding the initial Q(f). Each of the time domain data points that were not recorded are then altered somewhat and transformed independently to create a whole set of somewhat perturbed spectra and hence Q(f+δ_i) for each of the altered time domain data points. The relation between Q(f) and Q(f+δ_i) for each i defines the gradient Δ, and a Polak Riviere conjugate gradient minimization of the target function Q(f) with respect to the values of the missing time domain data points is carried out. This procedure minimizes Q(f) of all frequency-domain data points while only altering the non-measured time-domain data points.

The only variable in this procedure is the choice of the target function; we prefer to use the sum of the absolute values of the frequency domain data points, and the number of iterations to be carried out. Below we use this FM reconstruction procedure for comparing different sampling schedules.

Description of the software and computer hardware

The FM reconstruction program has been described previously (Hyberts et al., 2009) but some key aspects and recent developments are summarized here. The program requires a gradient for the minimization algorithm. Since the points that vary are in the time-domain, and the target function is defined in the frequency-domain, each calculation of a partial derivative requires a forward Fourier Transform of the deviation in the time-domain to the frequency-domain. A couple of considerations are immediately possible: first, contemplating that FFT is linear, i.e, FFT(t₁+ t₂) = FFT(t₁) + FFT(t₂); the set t₁ corresponding to the present set of values of the time-domain data and the set t₂ corresponding to a small value at the particular point i to which the partial derivative address, zero elsewhere; the FFT for the present set t₁ and the alteration set can be made separately. Hence, the FFT for the present set t₁ can be made once for all partial derivatives in the gradient. Second, as the set only describes one point, a FFT is not required since the transform is already known as a sinusoidal wave in the frequency domain. Third, if it is possible to store the result in memory for all indices of the gradient, this will also reduce the execution time to a certain extent.

The execution time for each partial derivative of the gradient with above considerations will be of O(n_max), where n_max is the number of points in the trial spectrum. This is due to the fact that a summation of all altered data points in the frequency domain is made for the target function Q(f). With n_variable data points in the time-domain, the execution time of one conjugate gradient iteration is hence proportional to n_variable × n_max. It follows that the time for re-construction will be quadratic in n, or O(n²), depending both on the number of points to be reconstructed and on the size of the reconstructed data. The total time for a complete reconstruction is hence further proportional to the number of iterations (n_iterations) of the conjugate gradient iteration and proportional to the number of points kept of the processed uniformly sampled dimension(s) (n_processed). The latter usually refers to the kept points after processing the direct dimension and extracting the area of interest, but it may also include the result after processing an indirect dimension that was not obtained non-uniformly.

Except for making the calculation of the gradient as efficient as possible, two approaches for parallelization are possible: (A) farming of the individual calculations for the points kept of the processed uniformly sampled dimension(s) (n_processed), and (B) internal parallelization of each of the partial derivatives (n_variable × n_max).

We constructed a program termed mpiPipe, to farm the individual calculations according to (A) above. It does the following: (a) Initiating and connecting with the other processing nodes. (b) Receiving data according to NMRPipe specifications. (c) Once initiating is done, the head node engages each external processor with a job; (i) a task identifier is sent to the external processor, (ii) a static command operation is sent to the processor, (iii) a unique job order is assigned and kept, allowing asynchronous work flow, (iv) the data are prepared and sent, (v) a non-blocking receive is requested. (d) Once a processor node has completed its task, the head node receives it and new data are delegated. (e) Once all processed data have been received from the processing nodes, the processed data are moved from the internal storage to the output pipe according to NMRPipe specifications. Notable, the mpiPipe program may be used for most types of NMRPipe processing on a cluster or a farm via MPI (Message Passing Interface).

As an alternative to using MPI, simple queuing to a cluster is also actively used. As NMRPipe is built on a 2D principle, we are typically using MPI for 1-dimensional reconstruction of e.g. 2D HSQC spectra, whereas the more approachable use of a queuing system comes in question for multi-dimensional reconstructions, such as of triple resonance and 4-dimensional spectra. Presently, we are using a 32-node cluster, each equipped with 2 dual 3.0 GHz core Xeon processors with a total of 128 cores.

In order to approach an internal parallelization along option B above, specific hardware is required. Fortunately, recent developments within the field of HPC (High Performance Computation) have lead to the option of programming GPUs with high numbers of cores. Using CUDA C language, we re-wrote the appropriate calculation of the gradient. Applying the code on a NVIDIA 240 core Tesla C-1060 computer, we find that we can get a speedup of a factor 90 comparing to one core of a 3.0 Xeon processor. Practically, this means using a workstation equipped with four of these cards (a total of 960 cores), we have achieve a speedup of a factor of 3 relative to our 128-core cluster. Presently, the 448 core Tesla C-2050 has been released, where each card is a factor of 3 faster than its predecessor. Equipping a workstation with four of these cards hence yielded a single node computer that is nearly 10 times faster than our 128 cpu cluster at a fraction (around a 1/10^th) of its cost.

Alternatively to using the high-end of these workstations and graphic cards, a smaller work station can be employed that is capable of using a graphics card comparable to the C-2050, such as the GTX-460, at a cost of less that $1,000. This would yield a speed comparable or faster than our 128 cpu cluster. When working with Open CL, it is also possible to use the ATI graphic-cards. We have found that this yields a performance comparable to the NVIDIA C-1060 card.

Principles of non-uniform sampling

Noteworthy, one could say that a form of non-uniform sampling was applied prior to the introduction of Fourier transform NMR in routine continuous wave spectroscopy when only the interesting parts of the spectra were scanned. With the introduction of pulsed NMR a set of uniformly sampled equidistant data points spaced by the dwell-time were to be acquired for proper input to the Fast Fourier Transform (FFT) algorithm. This was soon amended with zero filling, which can be considered a new general form of non-uniform sampling.

With the introduction of 2D and generally nD NMR, the number of increments is growing exponentially with t⁽ⁿ⁻¹⁾ whereas the information content remains restricted. This means that higher dimensional spectra contain a larger fraction of empty frequency-domain areas with only noise to spread out the signals. While this allows for better identification of signals due to reduced overlap it is paid for by the need of recording more increments and thus longer measuring times.

The desire of reducing the experimental time has revoked the idea of non-uniform sampling. Is it possible to design a sampling strategy, which does not necessarily inherit the requirement of equidistant data points, in order to reduce the total acquisition time and maintain the ability to distinguish otherwise overlapped signals? If this is the case, can one re-use the saved time and acquire more scans for the measured increments in order to gain sensitivity while maintaining resolution?

As indicated before, the use of FFT requires uniformly sampled equidistant data points. If it is desired to preserve a traditional looking spectrum, the non-obtained data points have hence to either be left zero (as with zero filling), or the values of the data points have to be emulated or reconstructed prior to Fourier transformation.

A non-trivial issue with implementing non-uniform sampling is that the traditional test functions for the Fourier Transform (i.e., the set of sinusoidal functions), or even a subset of them, are no longer orthogonal. This leads to artifacts via a mechanism called signal leaking. This does in fact occur for uniform sampling as well: when a signal’s frequency is not one of the sinusoidal test-functions, signal leakage is manifested in so-called sinc-wiggles. Since sinusoidal functions no longer provide an orthogonal set when non-uniform sampling is used signal leaking occurs even when the acquired signal is one of the sinusoidal functions traditionally displayed in a spectrum. In the frequency domain, these leakage artifacts are viewed as the so-called Point-spread function. They can easily overshadow the noise, especially when strong signals are present. This is particularly serious in NMR spectra with a large dynamic range. It is hence imperative for nonuniform sampling methods to use schedules where the set of test functions deviates least from being orthogonal.

The point-spread function for evaluation of sampling schedules

Intrinsic to all non-uniform sampling is the selection of a sampling schedule. Choosing an optimal schedule is central to the faithful reconstruction of the true spectra from NUS data. Randomly selecting 256 out of 1024 points can be done in $\left(\begin{array}{c}1024\\ 256\end{array}\right)$ ways, or more than 10²⁴⁸ combinations. A more modest selection, 64 out of 256 data points, yields already 10⁶¹ combinations. Theoretically, sampling through all of these possibilities would give us some schemes that were obviously not to be considered, such as selecting just the first 256 data points, or picking every fourth point. Here we use random or weighted random selection of sampling points, relying on a random number generator, such as the UNIX drand48 or equivalent, which only promise a randomization to 2⁴⁸ ways, or just above 10¹⁴ combinations. Each of these alternative schedules would be generated with a unique seed value. Note: as we are utilizing a pseudo-random generator, the sequence of random numbers is completely determined by its seed value.

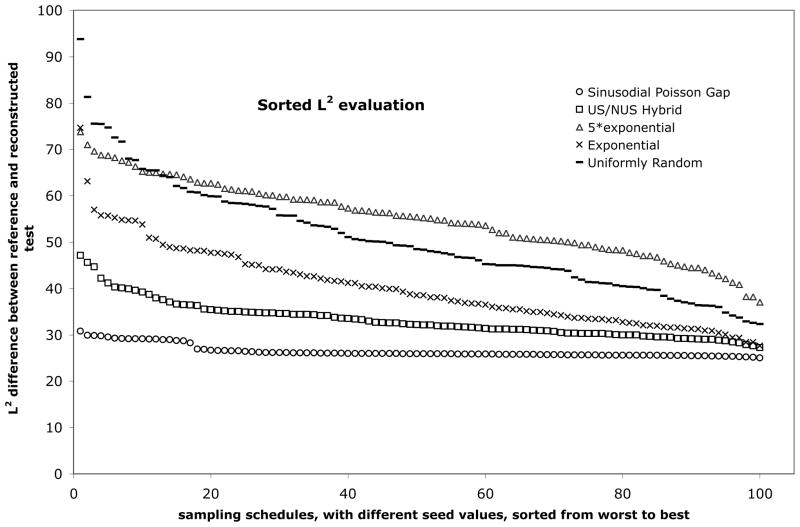
To predict the performance of a sampling schedule we rely on the point spread function. We create a synthetic exponentially decaying signal, select a subset of points with a sampling schedule and create a spectrum with the FM reconstruction algorithm. The spectrum is then compared with that obtained by FFT from the full uniformly sampled free induction decay, and the difference is expressed in terms of a L² norm. This is analogous to a χ² analysis, but the values are not normalized. As we have reported previously, the performance of the sampling schedule (lowest L² norm) depends on the value of the initial random seed number (Hyberts et al., 2010). This is shown in Fig. 1, where we evaluate different sampling schedules with the point-spread function using 100 different seed numbers. The resulting L² differences are sorted from worst (left) to best (right). Here we select 256 out of 1024 time domain data points, a 25% sampling schedule.

Figure 1.

Sorted L² norm evaluation of five sampling strategies for non-uniform sampling of NMR data. The L² norm ( $=\sqrt{{(f_i^{\mathit{ref}}-f_i^{\mathit{rec}})}^2}$) in this case describes the deviation between the reference spectrum (a singlet with no line-width) and the FM reconstructed equivalent, when selecting 256 of 1024 complex data points in the time domain based on particular sampling strategy and seed value. 100 seed values were used to create 100 specific sampling schedules for each sampling strategy. The L² values were hence sorted and the “best-of-100” (represented rightmost in the figure) and “worst-of-100” (represented leftmost) sampling schedules were identified for each strategy for further evaluation. (N.B. For practical use, only the “best-of-100” schedule would be of interest.)

Evaluating sampling schedules with the point-spread function

We first explore some typical sampling schedules that have been proposed in the literature.

(i) Uniformly random

Here 256 out of 1024 sampling points are selected randomly using the Unix random number generator with different seed numbers, but uniformly spread over the time axis. Fig. 1 shows that the deviation from the correct spectrum (L² norm) ranges from 95 (worst) to 32 (best). Thus, there is a large variation of fidelity depending on the pick of the seed number.

(ii) Exponentially weighted random sampling

A modification to the uniformly random sampling is the exponentially weighted random sampling scheme. The rational for this is that by decaying signals, the signal intensity is higher at the beginning of the FID, yielding better sensitivity. The probability function is altered in an exponential fashion, so that it picks more points for shorter rather than longer evolution times. Randomization is used similarly to the uniformly random sampling. It should be mentioned that those samplings created by exponentially weighting are a subset of the complete uniformly random one – the method only yields different results when a restricted subset is taken, such as a subset of 100 schedules as described above. Fig. 1 shows that the exponentially weighted sampling schedule yields L² differences between 74 (worst) and 28 (best). Thus, this schedule is less likely to make big mistakes and has a greater probability of creating high-fidelity reconstructions. However, the variation of fidelity is still very large.

(iii) 5*Exponential sampling

Whereas the exponential sampling strategy matches the decay of the signal, attempts of optimizing the weighting of the probability function has been suggested. As it is common to appodize the reconstructed FID, the actual decay is faster than given by a single T₂. “Over-weighting” the probability function up to 5 times has hence come in question.

To improve schedules we considered the results from these various sampling strategies and tried to elucidate what makes a generally “good” sampling schedule, i.e. those with fewer aberrations than “bad” sampling schedules. We observed that when there are larger and/or more gaps in the beginning of the sampling schedule, the resulting reconstructions yield “dips” or “trenches” around the reconstructed peak. This is especially a problem when working with spectra with high dynamic range. These are naturally more pronounced for the uniformly random schedules than for the exponentially weighted ones. By “over-weighting” the exponential probability the problem is less severe. This would initially lead to the conclusion that “over-weighting” the sampling schedule strategy is better. However, just like apodization, it trades resolution for sensitivity – working contrary to the idea of NUS. Also, by “over-weighting” the probability function, the sampling scheme is biased towards sampling the very beginning of the FID. This raises the question as to whether it may be just as good to simply acquire the first part of the schedule uniformly, essentially falling back to uniform sampling (US) with fewer data points. Fig. 1 demonstrates that the 5*exponential schedule exhibits the same worst-case scenario and disappointingly results in the worst overall performance.

(iv) US/NUS sampling

The considerations above have suggested that it may be good to sample the initial part uniformly (US), and then the rest of the schedule with NUS but in a uniformly-random point selection. As this introduces a discontinuity, many options are possible. For our search, we have typically sampled the first 1/8^th of the schedule with US and the subsequent 7/8^th with NUS and-uniformy random sampling point selection. Based on the point spread function analysis (Fig. 1) this schedule performs on average significantly better than the schedules discussed above. We find this strategy removes the artifacts, which manifest as “dips” or “trenches”. However, to use this strategy one needs to make decisions as to how long to linearly sample and how to weight the NUS period. Thus, the selection appears to be arbitrary and is in general hard to optimize; however, further optimization of this approach may be worthwhile.

(v) Poisson Gap sampling

As it is often desirable to use less or even much less than 50% sparsely sampling where the number of non-obtained data coordinates are larger than the obtained data coordinates, it is valuable to not only look at the distribution of points to be acquired, but to study the nature and distribution of the gaps created in the sampling schedule. Doing so we found that (1) large gaps are more detrimental to the fidelity of the reconstruction and (2) gaps located in the beginning as well as in the end of the schedule impact the ability of good reconstruction. (Note, as it is most common to apply an apodization prior to transforming the time domain data to the frequency domain, the impact of gaps at the end of the schedule is much less than that at the beginning.) In addition, (3) the distribution should be sufficiently random in order to satisfy the Nyquist theorem on average.

When analyzing the distribution of gaps in large uniform sampling schedules we find that the gap sizes approach a Poisson distribution with the average gap size of 1/sparsity minus one. Here the sparsity is the fraction of recorded versus non-recorded data points. Thus, for a sparsity of ¼, the average gap size would be 4−1 = 3. Our experience is that it is typically easier to find a “good” sampling schedule with high fidelity reconstruction when using 25% sparse sampling of 8k data points rather than with 25% sparse sampling of 256 data points. We hypothesize that this is due to the stochastic nature of smaller sets. We further hypothesize that our ability to find a “good” sampling schedule increases when adding the constraint of a general Poisson distribution of the gaps in the sampling schedule. Generally, considering the observation that large gap sizes are more detrimental in the beginning and in the end of the sampling schedule, we can vary the local average of gap sizes during the sampling schedule so that the sampling is denser in the beginning and the end of the schedule.. The selection of sampling points with Poisson Gap sampling has recently been described in detail (Hyberts et al., 2010). Fig. 1 shows that this sampling schedule is least dependent on the seed number and has on average the lowest L² values.

Performance of sampling schedules on a set of four peaks using FM reconstruction

So far, our analysis has been based on a single non-decaying signal without noise. This is certainly helpful to optimize the particular sampling schedule by entering different seed values into the underlying pseudo-random generator. However, it has little resemblance with the reality of NMR spectroscopy. In order to further evaluate the qualities of the above sampling strategies, we now simulate a set of four peaks that emulate a time domain acquisition to one T₂, (Figs 2 and 3), and we extract subsets of the data with the particular sampling schedules. Next we reconstruct the time domain data with the FM procedure and create the 2D spectra with FFT. Finally we add synthetic Gaussian noise and evaluate reconstruction performance. The synthetic spectrum consists of one intense and well-separated peak, and three weak peaks, two of them almost overlapping.

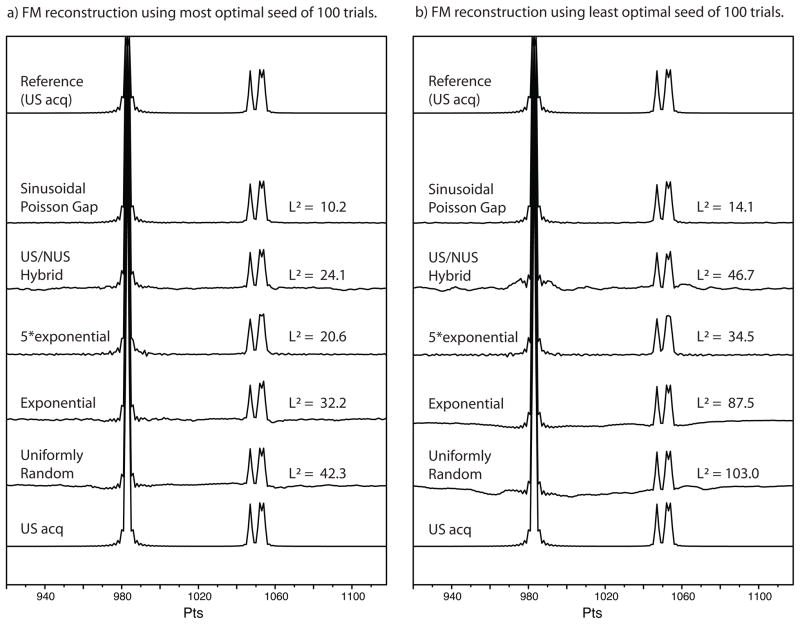
Figure 2.

Justification of prior selecting seed values and evaluation of sampling strategy based on a simulated spectrum with four signals, each simulated to been acquired to the equivalent of one T₂ and with no noise. (I.e., the simulated FID decays to 1/e.) The intensity of the leftmost signal is tenfold that to each of the three others. (a) FM reconstruction using the sampling schedule based on labelled sampling schedules and seed value found to be “best-of-100” from previous evaluation (figure 1.) and (b) FM reconstruction using the sampling schedule based on labelled sampling schedules and using the seed value found to be “worst-of-100” from previous evaluation. The experience is described in the text.

Figure 3.

Demonstration of initial state before FM reconstruction setting all non-obtained data values to zero, effectively using a discrete Fourier transformation (DFT) with the same sampling schedules as in Figure 2a. The residual between reconstructed and reference here describe the combined point spread function from the four signals.

Fig. 2 shows FM reconstructions using the five NUS schedules discussed above and compares the spectra with the reference (top). The bottommost spectrum, is a simulation of traditionally US acquired data for a 1024 complex data point FID, processed with cosine apodization, one set of zero filling and Fourier transformation. The leftmost signal has ten times the signal intensity of the three signals on the right. This is for evaluation of strong peaks, such as diagonal peaks in NOE spectroscopy (NOESY), and wherever a high dynamic range is exhibited. We chose a factor of 10 only for visibility purpose; we are aware that in real spectroscopy often a factor of 1000:1 appears. The two right most signals provide a doublet, barely visible using uniform sampling. This arrangement allows for easy inspection of reconstruction fidelity and ability to preserve resolution.

In the left hand panel we used the sampling schedule with the best seed number as found in the data shown in Fig. 1. At the right hand side we use the seed numbers of the least favorable reconstruction. Thus, the two panels span the range of reconstruction fidelity consistent with the analysis of Fig. 1. The performance of the sampling schedules is most different for the least favorable seed numbers.

The second trace from bottom (Uniformly Random) visualizes the same data as above, however, 256 of the 1024 complex data points in the FID were chosen in a uniformly random fashion and FM reconstructed prior to apodization and further processing. Clearly in both the “best” and the “worst” case, baseline abnormalities occur. These may not be detrimental in case of spectra with more uniform size of signals, where these abnormalities are easily hidden in the noise, but are cause for concern for spectroscopy when the signals exhibit a high dynamic range. The third section in both panels (Exponential) visualizes the situation using exponential decaying sampling instead of uniformly random sampling. The baseline abnormalities are less pronounced, yet still present. Over-weighting the sampling using 5 times the exponent (5*Exponential) provides a flat, but somewhat fluctuating baseline. However, the reduction of the base line abnormalities has come at the price of lower resolution. The result of the US/NUS hybrid method is provided in the fifth section. The strategy does indeed provide a better baseline in the “best” case, to no apparent loss of resolution, yet is obviously in need of optimization of the particular sampling/seed; this fact is made evident by comparing the “best” case (figure 2) with the “worst” case. Here the sinusoidal Poisson gap sampling exhibits the best results (trace 6 from the bottom). Only deeper inspection can find differences between the reconstructed and the original data. Even the displayed “worst” reconstruction looks better than any of the other “best” cases. The top traces repeat the bottom traces (US acq) for visual reference.

Fourier transformation of NUS data without reconstruction of missing points

As it has been discussed in the literature, we also compare the performance of straight Fourier transformation FFT on the NUS synthetic four-line spectrum in Fig. 3. We used the schedules obtained with the best seed numbers as in Fig. 2A and leave the missing time domain data points at zero value. The traces presented in Fig. 3 show that the artifacts due to the sampling schedules and lack of reconstruction are severe and mask the small peaks. However, the intense line is readily observable. Thus, straight Fourier transformation may be an option if one is only concerned with very intense peaks, such as methyl resonances in a protein, and weak peaks are of little concern. This treatment of NUS data may be useful for a quick inspection of a NUS data set to find out if an experiment has worked. However, it should be followed by a reconstruction effort to best retrieve the full information content of the NUS data.

Evaluation with noise, good and bad

Experimental NMR spectra always contain noise. To evaluate the more realistic situation of the mentioned sampling schedules we hence add noise to the above test spectrum of four signals. The noise is generated with the NMRPipe utility addNoise; we tune the rms-value of the noise to a realistic situation generating a set of 100 different Gaussian distributions with seed values ranging from 1 through 100. To the reference situation of the traditionally uniformly sampled FID, we also add noise, but with two-fold higher rmsd. This is to simulate the situation where equal time would be spent for data acquisition with uniform sampling and NUS. Since four-times more scans can be accumulated per increment when only one quarter of the increments are measured the noise-to-signal ratio in the time domain is two-fold higher in the uniformly sampled spectrum. It is worth mentioning that even though the noise added in the time domain is of Gaussian or white noise character, the resulting distribution of the noise in the frequency spectrum is not Gaussian. This is due to apodization as well as non-uniform distribution of the noise in the NUS test cases.

We generated 100 noise test cases for each sampling strategy. This is because the effect of noise is intrinsically non-predictive. Reconstruction will work well in one distribution of the noise and less in another. Also, even though the initial noise is the same for each test case and seed value, different points of the noise will be sampled when the sampling schedule is applied. For a fairer comparison, it is hence important not to draw a conclusion using just one set of noise.

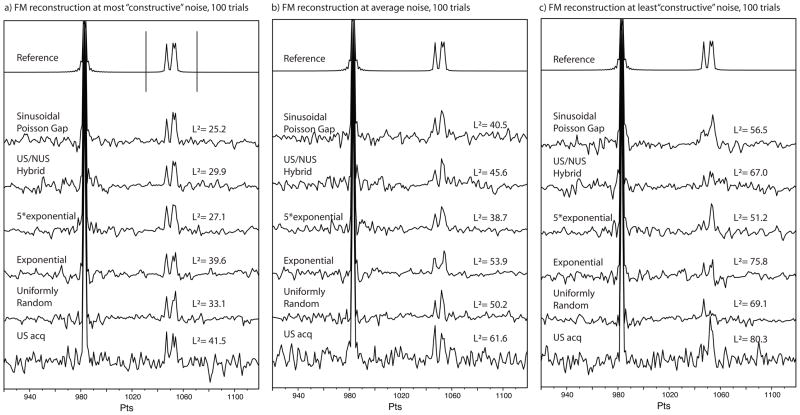
In order to distinguish better and worse reconstructions, again a L² norm is applied. If the norm were applied to the whole spectrum, only noise itself would be evaluated and would unfairly favor the NUS cases. Hence, we applied the L² norm evaluation only to a very restricted area around the three small signals of interest shown bracketed with two vertical bars in the top trace of Fig. 4a. The best-of-100, mean, and worst-of-100 reconstruction results based on this L² norm application are provided in Fig. 4a, b and c, respectively, and the calculated L² norms are given in the spectra.

Figure 4.

FM reconstruction of the test situation in figure 2a – with noise added. The Gaussian noise was generated 100 times, each time with a different seed value and added in the time-domain of the reference. The data was then sampled according to the various sampling schedules and FM reconstruction applied. In order to compare the situation of uniformly sampled data, the same noise was used, but with four fold rmsd in order to emulate equal time acquisition. As the evaluation is concentrated on the effect of the weaker peaks, only the data points 103 through 1072 were used for L² norm evaluation. (Marked with bars in the reference spectrum in (a)). As no prior knowledge about the noise, the result of the spectral presentation may vary from (a) when the noise is most cooperative, through (b) the average situation (median) to (c) where the noise is least cooperative.

Fig. 4a provides the considered best-of-100 results. The signals can easily be detected in each of the cases, and the splitting between the two adjacent signals can be seen to various degrees in all of the situations. The values of L² improve from the bottom to the top. Fig. 4b illustrates the case for average (mean) noise. The splitting between the two overlapping signals has mostly vanished, or cannot be fully confirmed based on surrounding noise. The more isolated signal of the three small peaks is present in all traces, except possibly in the exponential weighted case. The values of the L² norm vary more than for the best case. Here, the 5*exponential distribution performs best. Fig. 4c visualizes the situation when the reconstruction picks the least favorable noise set. For each of the sampling cases, the three small signals are hard to identify and barely resemble the spectrum without noise. The L² values are hence greater than in the mean- and the best-case scenarios. Note, the rightmost peak in the US spectrum, worst-case scenario, appears to have a shift in its position. However the strongest peak still lines up with the reference. Shift of signal positions is something that has been associated with NUS, but evidently occurs in uniformly sampled spectra as well when the S/N ratio (SNR) is low. Of the reconstructed NUS spectra, it seems that the US/NUS sampling schedule features a similar shift of the position; the situation is however not worse in the NUS reconstructed spectra than in the case of traditional uniform sampling. Of interest is that the traditional US acquisition (bottom traces) has a tendency to produce false positive peaks. Note that this analysis applies to the case when sampling is tested for equal measuring times for US and NUS. If NUS is used to reduce the total experimental time the difficulties with maintaining signal positions are proportionally greater.

The L² analysis is simplistic but provides an illustrative picture of the situation. A total of 42 frequency data points were used, reflecting about equal number of points representing signals in the reference spectrum and adjacent noise. There is however, a strong indication that the likeness to the reference spectrum is greater in the FM reconstructed NUS spectra than in a traditional US acquired spectrum. The spread between the best-case scenario (where the noise “cooperates”) and the worst-case scenario is greater than the differences in sampling strategy. Note that the particular sampling was optimized previously according to the method of using a single signal and no noise. There is however, a trend that the Sinusoidal Poisson gap sampling and the five times over-weighted exponential decay method are more faithful to the reference than the three other sampling strategies. The Sinusoidal Poisson Gap sampling strategy may offer better resolution, while the five times over-weighted strategy may produce somewhat better signal strength. Surprisingly, exponentially decaying sample weighting performs poorest in this evaluation.

Implementing NUS schedules in two indirect dimensions

Extending the probability weighted sampling strategies to two indirect dimensions is commonly done by creating a matrix and simply multiplying the weights from the two axes for probabilities of the individual points. The matrix is then converted into a one-dimensional object by taking the rows and concatenating them together. This is appropriate for all but the Poisson gap sampling strategy.

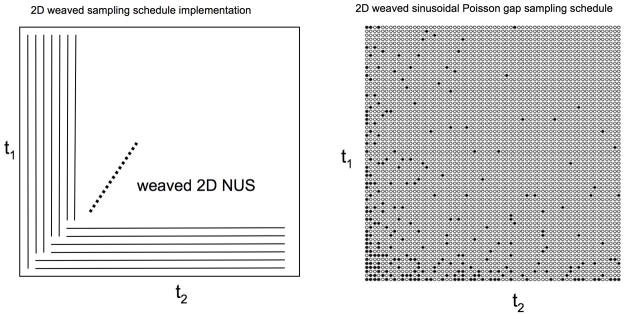
As Poisson gap sampling does not associate probabilities to a point but define a relation between points in a one-dimensional string, a different approach is required. We use individual strings “weaved” together, as outlined in Fig. 5, which allows us to cover two dimensions. First, a schedule with a desired weighting is implemented in one column followed by two rows and again two columns and so on (Fig. 5 left). What the figure does not reveal is that the strands have to be “pulled back” when a beginning is not occupied as a gap start is otherwise not defined. This approach truly “weaves” the strands together. An example created with the “weaved” Poisson gap sampling strategy is shown in Fig. 5 to the right.

Figure 5.

Weaved implementation of NUS Poisson gap sampling schedules in two indirect dimensions. First schedules are created with the selected schedule in the first t₁ column. This is followed by using the first two rows where the time points had not yet been selected. Subsequently, the next two columns are picked as indicated and so on.

Comparison of sampling schedules in two dimensions as used in 3D NMR spectra

In Fig. 6 we compare different sampling schemes for a matrix of nine synthetic peaks. Fig. 6A shows the 2D spectra without noise. The left panel shows the entire 2D spectrum; the subspectrum that contains the peaks and was analyzed with the L² norm is indicated with a box. The subspectrum consists of a 31 by 31 point section of the middle part of the total 128 by 128 frequency point grid where the 2D frequency domain is determined from a 64 by 64 (or 4k) hyper complex matrix in the time domain. The signals of the matrix have increasing relative intensities, starting at a value of 2 and ending with an intensity of 10. The order of intensities is written next to the peaks in the rightmost panel. The initial synthetic time-domain data set was created with the signals exponentially decaying to a value at point 64 of 1/e of its initial value in both dimensions to create 2D Lorenzian line shapes.

Figure 6.

Comparison of sampling schedules on a simulated spectrum of 2 indirect dimensions including Gaussian noise. Nine peaks of relative intensities 2 to 10 were created. A: Complete spectrum simulated. The central area containing the peaks is boxed and expanded in the panels of the rest of the figure. B: Contour plots of the central part plotted at two different starting levels of lowest contours. The contours are spaced by a factor of 1.5, and the relative intensity is indicated in the right-hand panel. C and D: Peak recovery with the best (C) and worst (D) of the 100 Gaussian noise sets. As best and worst noise sets we selected those that resulted in the lowest and highest L² values for the selected area containing the peaks. This indicates the quality range of peak recovery one can expect. The six panels in C and D correspond to the same total number of scans. Thus, 16 times more scans per increment can be collected for the NUS data. To take account of this we multiplied the added noise by a factor of four for the US spectra (top left panel). The simulations show that NUS recovers the peaks in the noisy spectrum significantly better than US when equal measuring times are considered. For all NUS schedules the best of 100 seed numbers were used as selected with minimizing the point spread function. (C)

Cosine apodization and zero filling to 128 points were applied to the time domain data prior to processing in both dimensions. A common exponential stack is used for plotting contour levels, and the multiplier from one level to the next is 1.5. The two panels in the middle and at the right are plotted with different lowest starting levels to visualize the different intensities. The plot denoted with *6.0 is plotted on 6 times higher minimal level than the right hand plot. Thus, four more levels should be visible for each peak in the rightmost plot relative to the center one.

To simulate an appearance of real spectra, 100 sets of Gaussian noise were created, each in a 64 by 64 hypercomplex matrix and added to the synthetic time domain data. In Figs. 6B and D, uniform sampling (top left) is compared with different non-uniform sampling schedules. We are interested in comparing the situation where equal measuring time is used for US and NUS. Thus, when only measuring 1/16^th of the increments, 16 times more scans can be acquired for each increment. For a fair comparison, and since noise adds non-coherently, we have added the same set of noise four times to the data set used to demonstrate US with FFT processing. Alternatively, we could have added 16 different sets of noise. Only one set of noise was added to the data sets used for simulating NUS and FM reconstruction. Five NUS strategies were evaluated, and in each case only 6.25% (1/16^th) of the grid points were selected according to the sampling strategies. In other words, 256 of 4096 hypercomplex time domain sampling points were used, selected based on sampling schedules optimized with the respective strategy and L² norm point spread function of a singlet without noise.

Each NUS data set selected for the seed number that gave the smallest L² value was combined with each of the 100 noise spectra and then FM reconstructed. The data were then processed with cosine apodization in both dimensions, including the uniformly sampled data, and an L² evaluation was made in the 31 by 31 point sub-area displayed in Fig. 6. The “best-of-100” (spectra with the smallest L² deviation from the reference) are shown in Fig. 6B. The “worst-of-100” are shown in Fig. 6C. The contours are plotted at the 1.0 level as defined in Fig. 6A except for the US panels (top left) where the noise was so overwhelming that the data had to be plotted at a minimum level six times the typical level for the NUS (*6.0).

The simulations presented in Fig. 6 show that with two indirect dimensions, NUS has quite significant benefits in terms of signal to noise and the ability to detect weak peaks. Among the sampling schedules, 5*Exponential and Sinusoidal Poisson Gap sampling outperform the other sampling schedules. At least seven, and potentially all nine, of the peaks can be observed in the above two cases, while US detects only four or five at best. This is consistent with a previous report that NUS can enhance sensitivity (Hyberts et al., 2010).

Comparison of NUS in a 3D NOESY spectrum

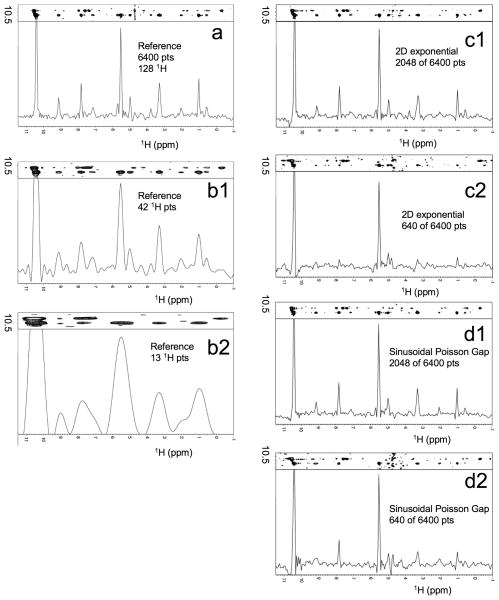
To evaluate sampling schedules on a 3D ¹⁵N dispersed NOESY spectrum of a protein we recorded high-resolution data sets on ¹⁵N labeled translation initiation factor eIF4E (Fig. 7). As a reference, the data was transformed with standard cosine apodization, zero filling and FFT. A representative slice and cross section along the indirect ¹H dimension are shown in Fig. 7a. Reducing the time domain data to 1/3 and 1/10 with uniform sampling obviously leads to low resolution in the indirect dimension as shown in Fig. 7b1 and 7b2. This is compared with NUS spectra following exponential weighting (Fig. 7c) and sinusoidal Poisson Gap sampling (Fig. 7d). The 2D sinusoidal Poisson Gap sampling schedule was created in a “weaved” fashion as indicated in Fig. 5.

Figure 7.

Comparison of alternative processing on a 3D ¹⁵N-NOESY-HSQC spectrum of human translation initiation factor eIF4e. (a) Uniformly sampled reference. The time domain data were acquired as 6400 hyper-complex points sampled in the two indirect dimensions (128 (H_indir) × 50 (¹⁵N)). The spectra were measured on a 700 MHz spectrometer with sweep widths of 9765 Hz and 2270 Hz, respectively. The t_max hence were 0.013 and 0.022 seconds each for the indirect proton and nitrogen dimensions, respectively, representing nearly an optimal situation for the nitrogen dimension, but not for the indirect proton dimension. Data were transformed with the standard FFT procedure after cosine apodization and doubling the time domain by zero filling. (b) Reducing the number of complex points to 42 (32%) (b1) and 13 (10%) (b2) in the indirect proton dimension, cosine apodization and zero filling results in low resolution spectra in the indirect dimensions. (c) FM reconstruction of 2048 (32%) (c1) and 640 (10%) (c2) data points sampled with an exponential weighting schedule in the two indirect dimensions. (d) FM reconstruction of 2048 (32%) (d1) and 640 (10%) (d2) sampled data points according to weaved sinusoidal Poisson gap sampling. For all spectra, equal number of scans were recorded per increment. Thus, the NUS spectra were acquired in one third and one tenth of the time used for the US spectrum, respectively.

The comparison of the NUS spectra with the reference shows that reduction of the number of acquired increments to 30% results in good quality spectra, comparable to the reference and reduction of measurement time to one third. This is highly significant considering the fact that typical US 3D NOESY spectra for proteins are recorded for several days. On the other hand, reduction of sampling points to 10% (Figs. 7c2 and 7d2) leads to loss of weak peaks. The NUS schedules of Fig. 7 use equal dilution of sampling in both indirect dimensions. It seems that less dilution in the proton dimension and a more drastic dilution in the heteronuclear (¹⁵N) dimension should be explored and might lead to superior results.

Discussion

Uniform sampling of multidimensional NMR spectra requires a large amount of measuring time if the resolution promised by high field spectrometers is to be fully utilized. Paradoxically, if one obtains a higher field magnet and maintains the same number of increments as on a lower field spectrometer, resolution is lost because one does not reach the same maximum evolution time as the dwell time is shortened. Thus, the spectroscopist has to record more increments to utilize the increased resolving power of the higher field instrument. Obviously, this requires more measuring time. Ideally, one wants to sample up to 1.2*T₂ of the respective coherence in each indirect dimension (Rovnyak et al., 2004b). This is an unacceptable situation, and replacing US with more economic alternatives has been a widely accepted goal of NMR development.

The first NUS approaches have used experimentally weighted random sampling methods and variations of random sampling. However, other NUS methods, such as radial sampling with projection reconstruction have been proposed (see introduction). Different algorithms have been used for reconstruction of NUS data, such as Maximum Entropy or Maximum Likelihood methods. It is beyond the scope of this article to exhaustively compare the different approaches. Here we use just the FM reconstruction software to compare the performance of different random sampling schedules where the randomness is skewed by weighting functions.

We have shown previously that the resolution of triple resonance experiments can be dramatically enhanced with random NUS in the indirect dimensions, and high-resolution 3D or 4D triple-resonance spectra of large proteins can be recorded within a few days, which would otherwise require months of instrument time with US (Frueh et al., 2009; Hyberts et al., 2009). This works rather well with triple resonance experiments where peaks have similar intensities and there is not much of a sensitivity and dynamic range issue. In fact, if there are primarily strong signals, such as methyl peaks in ILV labeled samples, a straight Fourier transformation of the NUS data where the missing data points are left at zero may faithfully retrieve the positions of the strongest peaks (see Fig. 3) but weaker signals are lost.

The focus of this manuscript is to evaluate different sampling schedules on samples that have a sensitivity issue, and we have evaluated sampling schedules assuming equal total measuring times. We investigated five sampling strategies: uniformly random, exponentially decaying random sampling, fivefold steeper decaying exponential weighting, a hybrid of US and NUS, and sinusoidal Poisson gap sampling. We find that the performance of any sampling schedule created with the help of a random number generator depends crucially on the original seed number. To determine optimal seed numbers we use the point-spread function, which determines the quality of the reconstruction by calculating the L² norm, the squared difference between a synthetic signal and the reconstruction using a particular sampling schedule.

Among all sampling schedules tested, we find that sinusoidal Poisson gap sampling depends least on the choice of the seed number but for the best seed numbers the different sampling schedules produce nearly identical results (Fig. 1). The different sampling schedules were then compared for situations without and with noise. Random noise has also to be created with seed numbers, and the noise can interfere with signals constructively (good noise) or destructively (bad noise). Thus, using both situations we have explored the range of reconstruction performances (Figs. 4 and 6).

To implement NUS schedules for Poisson gap sampling in two indirect dimensions we use a “weaved” selection by alternate picking of numbers in two columns followed by two rows and two columns and so on. Sampling times in each row or column are picked according to a desired sampling schedule. In this way we can evaluate sampling performance in two indirect dimensions. A similar weave NUS scheduling can be also used in higher dimensions.

Most of the evaluation of sampling schedules was done with simulated spectra and noise assuming equal total instrument time. This indicates that when using the time gained by not sampling all Nyquist grid points and using the time gained for measuring more transients for the sampled points one can obtain a better signal-to-noise ratio and detect peaks that are otherwise lost in the noise, which corresponds to a sensitivity gain (Fig. 6). This is consistent with a previous observation with ¹³C detected spectra (Hyberts et al., 2010).

Finally, we have compared different sampling schedules on an experimental ¹⁵N dispersed NOESY of a protein, where an equal numbers of scans were recorded per increment, and using NUS results in a shorter measuring time (Fig. 7). Here it is obvious that with 1/3 of the increments one can recover nearly the same quality spectrum as obtained with the three-fold longer US acquisition. It seems, however, that in heteronuclear-dispersed NOESY spectra it is worthwhile to maintain a higher sampling density in the ¹H dimension than in the heteronuclear dimension.