Model Selection for DCE-T1 Studies in Glioblastoma

Abstract

Dynamic Contrast Enhanced T₁-Weighted MRI (DCE-T1) using the contrast agent (CA) Gd-DTPA was performed on ten patients with glioblastoma (GBM). Nested models with as many as three parameters were employed to estimate plasma volume (v_p), or v_p and forward vascular transfer constant (K^trans), or v_p, K^trans, and the reverse vascular transfer constant (k_ep). These constituted Models 1, 2, and 3, respectively.

Model 1 predominated in normal non-leaky brain tissue, showing little or no leakage of CA. Model 3 predominated in regions associated with aggressive portions of the tumor, and Model 2 bordered Model 3 regions, showing leakage at reduced rates. In the patient sample, v_p was about four times that of white matter in the enhancing part of the tumor. K^trans varied by a factor of ten between the Model 2 (1.9 ×10⁻³ min⁻¹) and Model 3 regions (1.9 ×10⁻² min⁻¹). The mean calculated interstitial space (Model 3) was 5.5%.

In Model 3 regions, excellent curve fits were obtained to summarize concentration-time data (mean R² = 0.99). We conclude that the three parameters of the Standard Model are sufficient to fit DCE-T1 data in GBM under the conditions of the experiment.

Introduction

In fitting models to measurements, parsimony is an accepted heuristic; the simplest model that fits the data is usually accepted as the best model. The parameters of the simplest acceptable model are then taken as best summarizing the behavior of the system under study. One commonly used discriminant between models is the F-test. If nested models can be described, F-tests can be employed in a comparison of successively more complex models. This allows a reliable selection of the model and model parameters best fitted to the data, given the available signal-to-noise (S/N).

At a given level of S/N in T₁-weighted Dynamic Contrast-Enhanced (DCE-T1) studies in the brain, a number of possible conditions exist: 1. In normal brain, there is no detectable microvascular leakage of contrast agent (CA); 2. In some pathologies, it can be determined that the CA leaks from the microvasculature; 3. If enough CA leaks from the microvasculature at a high enough rate, it can be determined that the CA re-enters the microvasculature from the interstitial space. It has been proposed (1) that the standard model (SM) describing DCE-T1 studies in brain (2–5) is a nested model with either 1, 2, or 3 model parameters, corresponding to cases 1, 2, and 3 above. To this set of models, we add a model 0, where evidence of vascular filling with CA is absent. In the analysis, the F-statistic generated in cases 1, 2 and 3 can be directly compared to its reduced model alternative, thus allowing an unambiguous selection of model and model parameters best supported by the data.

This paper presents the results of DCE-T1 studies in 10 patients with treatment-naïve glioblastoma (GBM). For each voxel, dynamic MRI data was taken before, during, and after arrival of contrast agent (CA). This data was converted to a time trace of the change from baseline in the longitudinal relaxation rate, ΔR₁ (R₁ = 1/T₁). ΔR₁ was then used as a measure of the change of CA tissue concentration with time. For each voxel, the models of the previous section, Models 0, 1, 2, and 3 were fitted to the concentration-time curve, and the F-statistic comparing Model 0 (insufficient vascular filling) to Model 1 (vascular filling with no microvascular leakage), Model 1 to Model 2 (leakage without vascular reabsorption), and Model 2 to Model 3 (leakage with reabsorption) was calculated. Each F-statistic was thresholded at the 95% confidence level, and used as a mask to plot the parameters determined by the model. This produced almost complete maps of the plasma volume, v_p, maps of K^trans, the vascular forward transfer constant, in those areas that had leaky microvessels, and maps of k_ep, the vascular reverse transfer constant, in those areas that had high enough leakage rates to demonstrate vascular reabsorption.

Theory - Three Models plus one

There are four possible conditions for intravenously administered contrast agents (CAs) in cerebral tissue. The models corresponding to three of these conditions have been labeled Model 1, 2, and 3, respectively (1), because those are the number of parameters needed to model the pharmacokinetics of the CA in the system. In this paper, we have added Model 0 to describe the case where a voxel’s CA concentration is so low as to lack significant evidence of vascular filling. Note that the conditions of Model 3 cannot be true without the conditions of Model 2 first being true, Model 2 cannot be true without Model 1 first being true, and Model 1 cannot be allowed unless there is a detectable level of vascular filling. Thus, this system forms nested models in both the functional and statistical sense. This approach differs from the work in nested models of Brix et al (6) in that it starts from observed data and generates parsimonious models, and in its nesting scheme. We also note the innovative work of Sourbron (7) in extending DCE measurements to estimate blood flow as well as the parameters of vascular volume and leakage rates, and his demonstration that these extended models are useful in certain pathologies.

Modeling of leakage in the vascular system was first studied by Renkin (8) and Crone (9) in the single-capillary model, which estimated v_p, K^trans, and k_ep. Johnson and Wilson (10) later formulated the tissue homogeneity model, which added flow to the set of parameters in the model. The integral form of a matrix-based model that was mathematically equivalent to the Crone-Renkin single-capillary was first generated by Patlak (2,3) and reiterated by Tofts et al (4,5). This model has become known as the Standard Model (SM). The SM describes the concentration of CA in tissue after intravenous administration as follows:

$$C_t(t)=K^{\mathit{\text{trans}}}{\displaystyle {\int }_0^t}{e}^{-k_{\mathit{\text{ep}}}(t-\tau )}{C}_p(\tau )d\tau +v_p{C}_p(t),$$ [1]

where: C_p and C_t are the plasma and tissue concentrations of the indicator, K^trans is the unidirectional transfer rate constant of the indicator from plasma across the vascular endothelium and blood-brain barrier into the interstitial space, k_ep, is the transfer rate constant from the interstitial compartment to the vascular compartment, v_p is the fractional volume of the contrast agent’s vascular distribution space, usually thought to be the plasma distribution space. The plasma fractional volume and the blood fractional volume are related via the following relationship: $v_b=\frac{v_p}{1-\mathit{\text{Hct}}}$, where Hct is the hematocrit at the level of the microvasculature. In what follows, we assigned a value of 0.45 to Hct for all patients. The mean value of Hct for adult populations is 0.45 (11). Individual deviations from that value and variation due to the Fahraeus effect (12) will affect the value of K^trans proportional to the error in Hct.

If the transvascular transfer of the CA is bidirectionally passive, the two rate constants are related via the interstitial volume fraction: $v_e=\raisebox{1ex}{$K^{\mathit{\text{trans}}}$}\!\left/ \!\raisebox{-1ex}{$k_{\mathit{\text{ep}}}$}\right.$. Note, however, that in the computation of the parameters of the nested model (see below), v_e is a derived factor; k_ep is the rate constant that can be directly estimated from the tissue concentration-time curve.

Patlak and others introduced a method for linearizing the problem of curve fitting. In the original paper (2), it was demonstrated that a graph of the ratio C_t(t)/C_p(t) versus ${\displaystyle {\int }_0^t{C}_p}(\tau )d\tau /C_p(t)$ (generally this abscissa is called “stretch time”) yields a linear relationship, with a slope of K^trans and an ordinate intercept of v_p, or v_b if corrected for hematocrit. Such a graph has become known as the Patlak plot (2,13). If the full model of Equation 1 is to be analyzed in the same manner, the abscissa becomes ${\displaystyle {\int }_0^t{e}^{-k_{\mathit{\text{ep}}}(t-\tau )}{C}_p}(\tau )d\tau /C_p(t)$. This linearization is useful because it offers an easily visualized demonstration of the goodness of fit of the model to the observations.

Theory: The Observation Equation

If the change in longitudinal tissue relaxivity, ΔR₁ (R₁ = 1/T₁) is proportional to tissue concentration, the observation equation equivalent to Equation 1 is

$$(1-\mathit{\text{Hct}})\mathrm{\Delta }{R}_{1t}(t)=K^{\mathit{\text{trans}}}{\displaystyle {\int }_0^t}{e}^{-k_b(t-\tau )}\mathrm{\Delta }{R}_{1a}(\tau )d\tau +v_p\mathrm{\Delta }{R}_{1a}(t),$$ [2]

where R_1a is the longitudinal relaxation rate of all protons in the artery R_1t is the longitudinal relaxation rate of all protons in the tissue, and Δ refers to the subtraction of the pre-contrast rate from its post-contrast value.

The Calculation of ΔR₁ From SPGRE Data: In a spoiled gradient-recalled echo (SPGRE) DCE-T1 sequence, the signal intensity of any voxel will be as follows:

$$S_n(t)=\frac{M_0\text{sin}(\theta )e^{-{\mathit{\text{TE R}}}_2^{*}(t)}(1-e^{-{\mathit{\text{TR R}}}_1(t)})}{1-\text{cos}(\theta )e^{-{\mathit{\text{TR R}}}_1(t)}},$$ [3]

Where: S_n(t) is the signal intensity of the n^th image set in a DCE-T1 procedure, t is time, M₀ is the magnetization of the protons in the voxel, θ is the local tip-angle, TR is the repetition time between pulses, TE is the echo time – the time between the center of the excitation pulse and the center of the readout gradient - and R₂*(t) is the transverse relaxation rate in the voxel as a function of time (R₂* = 1/T₂*). The Appendix details the manner in which this relation can be used to calculate ΔR₁ during and after the arrival of CA.

Methods

MRI Studies

All studies were performed in a 3T GE Excite HD MR system (GE Healthcare, Waukesha WI) using a standard 8-channel phased-array RF coil and receiver. DCE-T1 studies were conducted in ten treatment-naïve patients with glioblastoma (GBM).

Prior to contrast agent (CA) administration, T₁ mapping was performed using DESPOT1 (14) and a 3D SPGRE sequence. Sequence parameters were as follows: TE/TR ~ 0.84/5.8 ms, flip angles, θ_i, of 2°, 5°, 10°, 15°, 20° and 25°, Asset number = 2, matrix of 256×128, FOV 240mm, sixteen 5 mm slices, no gap. This formed a set of signal intensities {S(θ_i)} that could be used to form a voxel-by-voxel least-squares estimate of M₀ and T₁, the two unknowns of Equation 3. The maps of T₁ were used to establish baseline pre-contrast values for the dynamic SPGRE procedure that followed.

The 3D SPGRE DCE-T1 sequence was then begun, with 70 image sets employing a 20° flip angle and other parameters as above. Total data acquisition proceeded for 6.8 min, about 5.9s per image set. About 20s after the start of the DCE-T1 sequence, Magnevist (Bayer Healthcare Pharmaceuticals, Wayne, NJ) in a dose of 0.1 mmol/kg was injected at a rate of 4 ml/sec. As detailed in the Appendix, ΔR₁(t) was calculated analytically for each voxel using the assumed value of the tip-angle, θ, the estimated pre-contrast value of T₁, and the ratio of the post-contrast to baseline pre-contrast MRI signal. If changes in R₂*(t) due to the arrival of CA could be ignored, Equation 3 could then be used to estimate the time trace of the change in R₁ (R₁=1/T₁), and that in turn was used as a measure of the CA concentration-time curve.

Numerical Methods – Processing

See Equation 3. The signal response with change in tip-angle was observed. TR and {θ_i} were known, although {θ_i} was probably not as well-known as TR. Using an object function of the squared residuals between the observed and modeled values of {S(θ_i)}, a Simplex search in the two variables M₀ and T₁ was used to form least-squares estimates at baseline. Following this, ΔR₁(t) was generated using the analytical process described in the Appendix.

Using the ΔR₁ concentration-time maps, an Arterial Input Function (AIF) for each patient was picked. Because there are a number of artifacts that might be introduced by the movement of blood through the image slice, and by T₂* signal loss, the AIF was adjusted by comparison to white matter in a normal area of the brain (15). An area of white matter was selected, and it was assumed that the plasma volume of the white matter(15,16) was 1%. The AIF was scaled so that the ratio of the integrated white matter concentration-time curve to that of the integrated AIF was 1%. Thus, all plasma volumes were measured relative to white matter plasma volume.

A nonlinear least squares optimization using the Levenberg-Marquardt (LM) Algorithm (17) was used to fit Model 3 to the experimental data, while the linear least-squares method was used for the linear models (Model 0, 1 and 2). Using the AIF described in the previous paragraph, the concentration-time data in all voxels were fitted with the linear models 0, 1, and 2. Model 1 was tested against model 0. If the F-test showed an advantage for Model 1, Model 2 was then tested against Model 1. If the F-test showed an advantage for Model 2, Model 3 (the full model) was then fitted to the data for further model comparison. To expedite the convergence rate of the fitting, the estimated parameters for the partial models in each step served as the initial values for fitting in the next step. Sum Squared Error (SSE) maps for the fitted parameters for all three models were calculated and used for statistical model comparison.

Statistical Tests – Model Comparisons

As in previous work, an “extra sum of squares analysis for nested variables” (1,18) was employed to examine which model best resolved the data. The ratio $\frac{S_e/{\nu }_e}{S_f/{\nu }_f}$ was computed, where S_e and S_f are summed-squared residuals (further described below), the subscript f refers to the higher-order model, and the subscript e refers to the extra variance accounted for by the higher-order model relative to the reduced, or partial, model. The degrees of freedom ν_e and ν_f are, in this case, 1 (for the number of extra parameters in the full model), and N-m, where N is the number of points on the clearance curve, and m is the number of parameters in the partial model (m = 1 and 2 for Models 1 and 2, respectively). It is further defined that S_e = S_p – S_f, where S_p is the sum of the squared residuals of the partial model, and S_f is the sum of the squared residuals of the higher-order model. For linear models with identical independently distributed (iid) errors that are normally distributed, the ratio $\frac{S_e/{\nu }_e}{S_f/{\nu }_f}$ is distributed as the F-statistic, F_ve,vf, with ν_e and ν_f degrees of freedom.

In the F-test, the null hypothesis is that the two samples of sum-squared residuals were drawn from the same pool. The failure of this hypothesis leads to acceptance of the higher-order model. The probability associated with the F-test (the p-value) is that of a Type I error, e.g., the probability of accepting Model 3 when the underlying truth is that of Model 2. In comparing model alternatives voxel-by-voxel, the confidence level (CL) was set at 95% for the main analysis. The effect of setting the CL at 90% was also examined.

Since it was unlikely that the errors of the fit of any model to typical concentration-time data in tissue would be iid and normally distributed (see the Discussion), the sampling distribution of the generated F-test was studied by selecting a region of normal tissue. It is known a priori that contrast agent does not leak into normal brain at any detectable rate, and therefore Model 1 must be true in normal brain. A large region in normal brain was selected (typically several thousand samples with around 60 time points each), and the distribution of the Model 1 versus Model 2 F-test statistic was plotted. A 95% confidence level (CL) for all F-tests was then generated from the sampling distribution’s estimate of the 95% CL for the Model 1 versus Model 2 F-test. The threshold for the 95% CL of all model tests was set according to this threshold.

The fitting procedures produced, at most, maps of v_p, K^trans, v_e, and F-tests for Model 0 vs. 1, Model 1 vs. 2, and Model 2 vs. 3 (F_0v1, F_1v2, and F_2v3, respectively). As noted, for the purpose of displaying the parametric maps, F_0v1, F_1v2 and F_2v3 were windowed at the 95% CL selected by an examination of F_1v2 in normal tissue. If the higher-order model was superior according to this criterion, its parameters were shown on the subsequent map of parametric estimates, with 0 displayed on the map of v_p in the event that F_0v1 was not significantly high, or the time trace of ΔR₁(t) could not be determined. This produced three parametric maps: a map of v_p for nearly every voxel of every slice studied, a map of K^trans in those voxels where either Model 2 or 3 was appropriate to the data fitting, and a map of v_e in those voxels where Model 3 was appropriate. In voxels where Model 0 prevailed, or where the fitting of Equation 3 did not converge for multiple time points, a value of 0 was plotted in the map of v_p. The parameter from the successful model was the one that was mapped, so the parametric map of v_p (for instance) included estimates from all four nested models. Lastly, a map of the regions where the four models prevailed was produced, with a signature included for non-convergent (NaN) voxels.

In each patient, the regions of interest (ROIs) defined by the three nonzero models were the basis for the summary of results. Results were summarized across all slices in which the tumor could be visualized. In regions where Model 2 held, K^trans and v_p were summarized across all slices and reported, and in regions where Model 3 held, K^trans, v_p, and k_ep (or v_e) were reported. Summaries for v_p in the core regions, i.e., those regions of Model 0, 1, or NaN that lay in the enhancing region of the tumor, were reported separately, either by reporting the counts of NaN and Model 0 voxels, or by reporting the average v_p in Model 1 regions.

As a descriptive statistic for each patient, concentration-time data from all the regions of the tumor that were identified as satisfying Model 3 criteria were summed, time point by time point, and the summed data were then least-squares fitted to the full model, thus producing a global estimate of K^trans, v_p, and k_ep for the summed data in regions where Model 3 prevailed. Using this estimate of k_ep, the data were then plotted as an extended Patlak plot (3), and the R² from the subsequent linear regression was calculated. This strategy was employed so that an intuitively clear presentation of the goodness of fit could be made, and also to examine the likelihood that a model with more elements might be usefully deployed. If, for instance, the data points that needed the most parameters (three) to explain their variation with time, had a linear regression that left some sizable fraction of variation unexplained, then a model with even more parameters – e.g., the shutter-speed model (19–21) - might be explored.

As for reporting other data and comparisons, mean ± standard deviation is given, and standard statistical tests are indicated where employed.

Results

Ten patients (5 male, 5 female) with treatment-naive GBM were studied. Patients ranged in age from 23 to 75 years. All except two patients had a single typical ring-enhancing lesion on their post-contrast MRI study. The remaining two patients had multi-centric enhancing lesions.

Pre-contrast S/N, measured as pre-contrast mean brain signal amplitude over noise amplitude, was about 15:1.

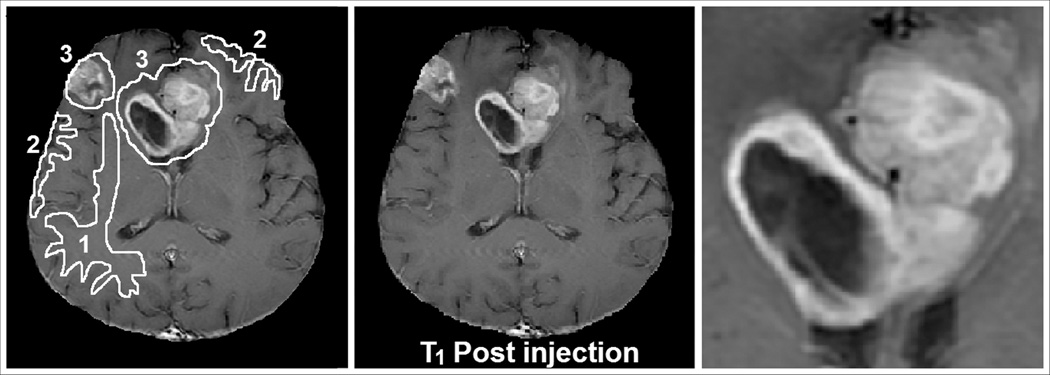
The left panel of Figure 1 displays a post-contrast T₁-weighted MRI of an image slice containing the largest aspect of a tumor in a 62 year old male who presented with headaches and seizures. The post-contrast MRI showed a bifrontal, heterogenously enhancing lesion with central necrosis extending across the corpus callosum. This is one of the two patients who had multi-centric lesions. Upon biopsy, the central lesion proved to be a GBM. The central panel of Figure 1 shows the regions of interest (ROIs) selected for tumor, grey, and white matter, and the right panel shows an enlarged detail of the central lesion.

Figure 1.

MRI of patient number 2 in Table 2. Center: Post-Contrast T1-Weighted image, Left: Regions of Interest 1= white matter, 2 = grey matter, 3 = tumorous tissue. Right: detail of central bifrontal lesion.

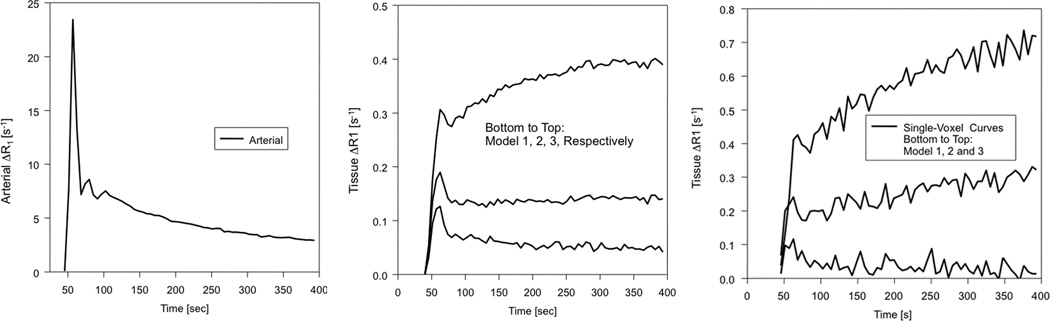
The left panel of Figure 2 shows a time trace of ΔR₁ in a voxel selected for an AIF in the patient of figure 1. This trace was produced by Equations A9 and A10 of the Appendix. The center panel exhibits the same trace in the summed data of regions associated with Models 1, 2, and 3 (to visualize these regions, see Figure 3). Finally, the right panel plots representative single-voxel data from Model 1, 2, and 3 regions. A visual inspection of the three tissue curves of this figure should provide assurance that the model selection algorithm is appropriate to the problem at hand. With some dispersion, the Model 1 voxel follows fairly well the uptake and long trailing curve of the input function, while the Model 2 and especially Model 3 curves deviate strongly from the clearance curve of the AIF. In fact, dispersion at the tissue level may well explain the deviation of the sampling distribution of the F-test from that of tabulated values based on normal distributions (see below).

Figure 2.

Left: Arterial Input Function as estimated by a concentration-time curve from a voxel in patient number 2 of Table 2. Center: tissue curves taken from Model 1, 2, and 3 regions. Bottom to top: regions in which Model 1, 2, and 3, respectively, were required. Right: representative voxels from the same Model 1, 2, and 3 regions.

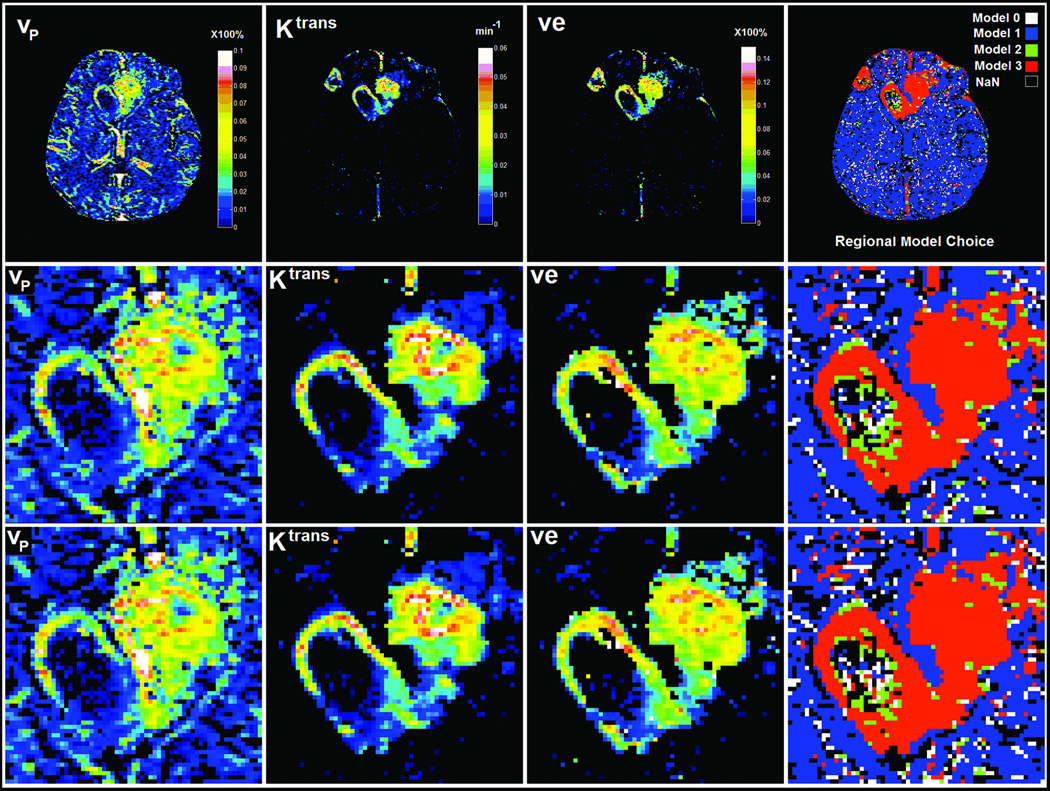
Figure 3.

The results of a typical analysis in the MRI slice shown in Figure 1. Top row shows parametric estimates in the full field of view, with the F-statistic threshold chosen at the 95% confidence limit. The bottom two rows show the corresponding detail in the central lesion when the F-test was windowed at the 95% (middle row) and 90% (bottom row) confidence limits. Left to Right: plasma volume, forward transfer constant, interstitial volume fraction, model selection windowed at the 95% (upper row) and 90% (lower row) confidence level. Noncovergent voxels are plotted as NaN, with a black signature. The parameters in each map are selected on the basis of the model mask, with Model 0 and nonconvergent (NaN) voxels both plotted as having a zero value. As a consequence of this model selection strategy, K^trans is not plotted in voxels where either Model 2 or 3 is not selected, and v_e, which is calculated from the ratio K^trans/k_ep, is not plotted in voxels where Model 3 is not selected.

Figure 3 shows the modeling results in this slice. The column labeled “Regional Model Choice” displays a map of regions where Model 0 (white), Model 1 (blue), Model 2 (green), and Model 3 (red) were the models of choice. Non-convergent voxels are plotted as black pixels, with 0 for all parameters. For the top two rows, the confidence level (CL) for selection of the higher-order model was set at 95%, as determined by the sampling distribution of F_1v2 in normal tissue. For the bottom row, the CL was set at 90%. In the column labeled v_p, the combined estimates of the plasma volume for all Models 0–3 are mapped, with the estimator for v_p chosen on the basis of the model selected. In the column labeled K^trans, the combined estimates of the transfer constant for Models 1 and 2 are mapped, again, with the estimator for K^trans chosen on the basis of the model selected. Finally, in the column labeled v_e, the estimate of the interstitial space provided by Model 3 is mapped.

In Figure 3 it is evident that, even in this central image slice showing the largest extent of the GBM, the great majority of voxels are free of CA leakage. Also evident is the appearance of loci in the ventricles and large vessels where Models 2 and 3 are selected; these must be ruled out as artifacts. In and around the tumor region, all three models are selected. In the detail chosen, shown in the bottom two lines of Figure 3, there are a relatively small number of non-convergent pixels. This demonstrates that a stable estimate of ΔR₁ versus time can usually be formed, and the data can be fitted with at least one of the available models. Regionally, Models 1 and 2 prevail in the necrotic core of the tumor, while Model 3 is selected in its peripheral and presumably highly vascular regions. Model 2 often borders Model 3 regions, providing a transition zone between the regions of very high leakage with vascular reabsorption and regions of no apparent leakage.

A 95% CL was chosen as a threshold for the model choice in the tumor ROI of patient number 2. The numbers of voxels and mean values for each of the three models is shown in Table 1. Note that the numbers for Model 1, 0, and NaN are only for the interiors of the lesion, i.e., those areas completely surrounded by a higher-order model. All plasma volumes are relative to an assumed white matter plasma volume of 1%. Mean v_p in the tumor core in Model 1 and Model 2 core regions was about twice that of white matter. In Model 3 regions v_p was about six times that of white matter. The mean value of K^trans increased ten-fold between regions where Model 2 held, and those where Model 3 held. Thus, the regions with Model 3 were presumably regions of the most aggressive tumor growth, with both increased vascular volume, and high leakage rates of the contrast agent. The interstitial volume calculated from $v_e=\raisebox{1ex}{$K^{\mathit{\text{trans}}}$}\!\left/ \!\raisebox{-1ex}{$k_{\mathit{\text{ep}}}$}\right.$, a quantity that could be estimated only in those voxels where Model 3 held, was estimated at about 6% in tissue that contained the most aggressive tumor growth, presumably showing a high cellular density.

Table 1.

Model Selection and Parameter Estimates from the Detail of Figure 2

Model	Voxels	Vp ±SD	Ktrans ±SD [Min−1]	Ve ±SD
(Core Only) NAN	117
(Core Only) Model 0	18
(Core Only) Model 1	131	0.022 ±0.070
Model 2	176	0.018±0.016	0.0015 ±0.0015
Model 3	1138	0.065 ±0.037	0.015±0.011	0.055 ±0.043

A note about the cutoff levels for the F-tests: for the patient studied, the value of the F-test at the sampling 95% CL was 10.4, and the 90% value was 7.0. For the group of 10 patients, the mean 95% CL was 22.39, with a range of 3.17 to 66.06, and the mean 90% CL was 12.84, with a range of to 1.64 to 43.33. These levels are well above the tabulated levels for a 95% CL (around 3.8) for an F-test of 1 and 60 degrees of freedom. Sources of this bias in the CL are considered in the Discussion.

See Table 2. As noted in the Methods, all of the tumor data from all of the slices where tumor could be visualized was used in these summaries. For instance in the patient chosen as an example, a total of 7316 voxels were found in the tumor area where Model 3 was the best-fit model at a CL of 95%. Note that in patient number 10, a patient with a relatively small lesion, no Model 3 regions could be found. Generally speaking, the trends already described continue, with vascular volume measuring about twice that of white matter in the enhancing regions of the tumor that contained Model 1 and Model 2 regions, and vascular volume in Model 3 regions being about four times that of white matter. K^trans was ten times higher in Model 3 regions than in Model 2 regions. The mean estimate of interstitial volume fraction, v_e, in regions where that parameter could be estimated, was about 8%, but with a relatively large coefficient of variation of 63%. It is beyond the scope of this paper to comment on the clinical correlates of these measures of vascular parameters, other than to note that GBM is notoriously heterogeneous in its pathology. That heterogeneity appears to be reflected in the maps produced, and in the wide range of parametric estimates produced by the analyses.

Table 2.

Summary of estimates of vascular parameters in ten patients studied serially. The parameters v_p and v_e are dimensionless fractional volumes for plasma volume and interstitial volume, respectively. The parameter K^trans has units of min⁻¹.

Pt	Slices	Model 0	Model 1 (Core)			Model 2			Model 3
		Voxels	Voxels	vp_ ± S.D	Voxels	vp ± S.D	Ktrans ± S.D [min−1]	Voxels	vp ± S.D	Ktrans ± S.D [min-1]	ve ± S.D	R2
1	7	44	238	0.0076±0.0050	4080	0.038±0.038	0.0023±0.0018	1719	0.042±0.019	0.030±0.011	0.128±0.057	0.9994
2	8	100	655	0.0337±0.0393	888	0.027±0.012	0.0016±0.0013	7316	0.061±0.034	0.013±0.009	0.057±0.033	0.9952
3	6	236	785	0.0300±0.0204	519	0.024±0.010	0.00079±0.00106	1711	0.045±0.018	0.0091±0.0046	0.050±0.047	0.9837
4	3	4	34	0.0381±0.0303	72	0.022±0.017	0.00077±0.00111	601	0.038±0.018	0.016±0.009	0.036±0.048	0.9935
5	7	104	358	0.0206±0.0248	564	0.033±0.027	0.0014±0.0015	1468	0.031±0.021	0.026±0.015	0.069±0.041	0.9901
6	7	192	408	0.0594±0.0515	511	0.028±0.020	0.00078±0.00168	1832	0.036±0.020	0.022±0.012	0.091±0.059	0.9755
7	5	292	310	0.0171±0.0127	554	0.013±0.008	0.00024±0.00058	1164	0.029±0.015	0.011±0.006	0.033±0.021	0.9923
8	6	34	547	0.0289±0.0276	1282	0.028±0.074	0.0026±0.0041	752	0.024±0.018	0.028±0.015	0.135±0.088	0.9967
9	5	0	21	-	456	0.026±0.022	0.0035±0.0025	316	0.029±0.011	0.023±0.008	0.087±0.032	0.9964
10	5	51	79	0.0096±0.0102	671	0.045±0.019	0.0053±0.0033	0	-	-	-
Mn±S.D				0.0213±0.0195	Voxels	0.028±0.025	0.0019±0.0019		0.037±0.019	0.019±0.010	0.076±0.048	0.9912

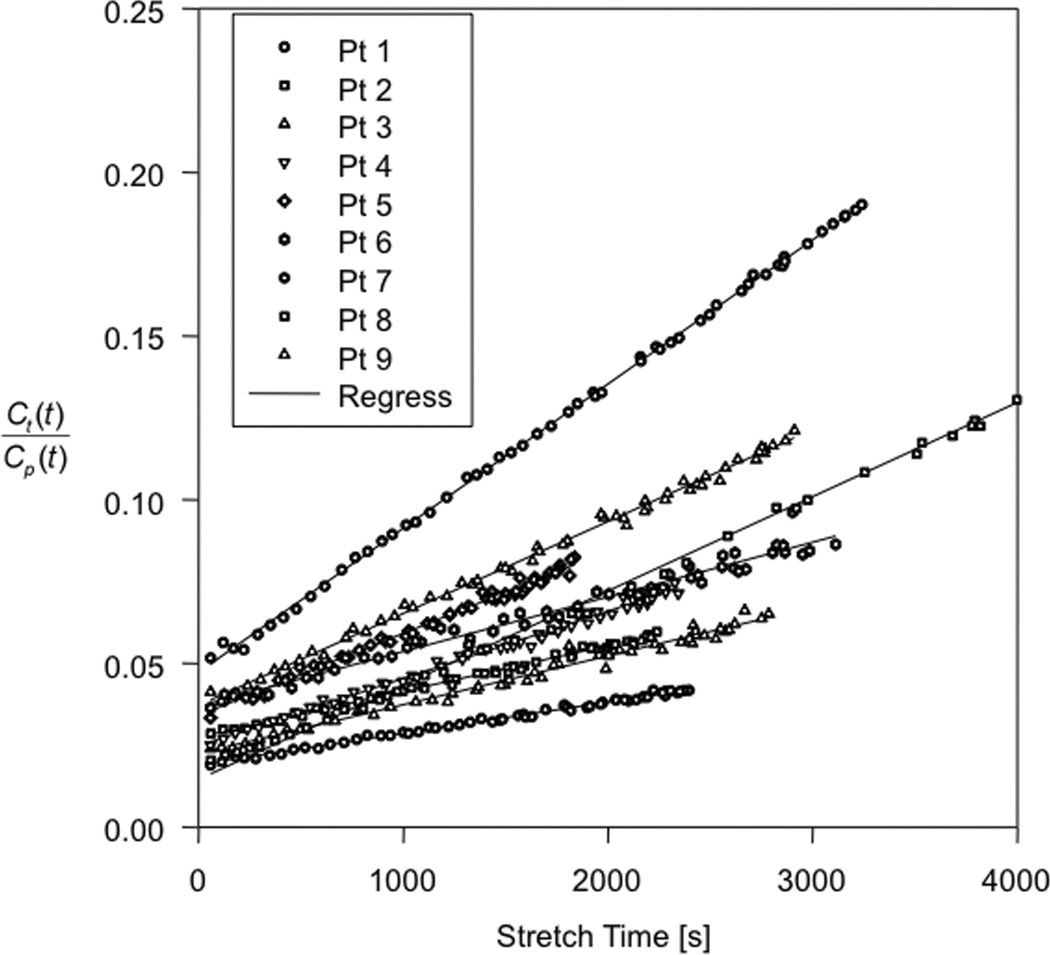
As described in the Methods, all of the concentration-time data from all of the Model 3 voxels in the region of the tumor was summed, and using the estimated arterial input function, was fitted to the extended Patlak model, thus producing a Model 3 fit to the summed concentration-time data from all of the voxels that, individually, needed to be fitted with all three parameters of the full SM. The curve fits of Figure 4 were produced, with coefficients of determination, R², reported in the last column of Table 2. Remarkably, the mean R² for nine patient studies with Model 3 regions was 0.991. Thus, in the region selected to require the highest number of parameters for fitting, on average 0.86% of the total variation of the dynamic change in the MRI signal was left unexplained by the SM.

Figure 4.

In nine patients with Model 3 regions, the data from the regions where Model 3 is valid is plotted as the extended Patlak Plot, with regression lines for each patient data set. This presents a visual verification of the robustness of the Model 3.

Discussion

Ten sequentially selected treatment-naive patients with diagnosis of GBM were studied with the intent of addressing the question of which model should be used for the study of vascular permeability in this very heterogeneous pathology. A set of nested models for the analysis of DCE concentration-time data that had proven useful in animal studies was employed, allowing an objective criterion for the voxel-by-voxel selection of the model most appropriate to the data. The heterogeneity of the pathology was reflected in the heterogeneity of the model selection, with three models appearing in substantial proportions, and in places that reasonably might reflect the underlying state of the tissue. In particular, Model 1 was selected in the great majority of tissue, where it was known a priori that there was no leakage of CA because the tissue was normal. In the necrotic core of the tumor, where a model could be selected, Models 1 and 2 were selected, possibly because the delivery of CA to the core was restricted by lack of flow. In the fast-growing rim, Model 3 was selected, sometimes bounded on the rim’s inner and outer surfaces by regions where Model 2 served best. Smoothly varying maps of parameters were generated, each in the regions where they could be estimated. This strategy assured the integrity of each of the parametric estimates, particularly insuring against indeterminacy in the parametric estimates of the higher-order models by requiring that, for each voxel, the experiment provided enough information to allow the appropriate number of parameters to be estimated. In the event that a parameter could not be estimated, its mapping was not performed, thus preventing any visual misinterpretation of the information that was available in the data.

A set of nested models in a linear system allows a firmly established theory to be applied to model selection. In the case at hand, the nesting of the models also constructs a physically intuitive narrative: the reverse transfer of CA from the interstitium to the vasculature (Model 3) cannot be measured unless the CA is first transferred in detectable amounts to the interstitium via forward leakage (Model 2), which in turn cannot take place unless the vasculature fills with CA (Model 1). Additionally, in parameters held in common between models (i.e., v_p between Models 1, 2, and 3, and K^trans between Models 2 and 3), it is evident that the parametric estimates tend to converge in value as evidence for the higher-order model decreases (1).

The nesting described is the only nesting that is physiologically reasonable. The commonly employed tactic of not considering plasma volume (i.e., setting v_p = 0) in the analysis clearly does not nest naturally in the SM.

There are numerous potential sources of systematic error in the data, beginning with uncertainties in measuring the arterial input function. Partial volume, inflow (and outflow) effects in this non-flow-compensated sequence are probably the most serious sources of artifacts. A tactic developed by Johnson et al (15), that of picking an AIF on the basis of shape (early arrival, well-defined recirculation bump, non-zero tail) and then normalizing the AIF to a white matter volume of 1% was chosen. Thus, all of the blood volumes reported are potentially biased to our choice of white matter volume. However, since DCE-T1 measures of volume may be biased low (22) due to restricted rates of water exchange across the blood-brain barrier (BBB), this tactic may have the effect of correcting an in-built bias. Contrariwise, because the rates of water exchange may, and probably do, vary upward with breakdown of the BBB, the vascular volumes in the tumor areas, relative to white matter vascular volumes, may be overestimated. This is a matter that would best be resolved by MRI measures of vascular volume that use a truly intravascular compound and contrast mechanisms that do not vary with the rate of water exchange across the vascular endothelium.

Another source of systematic error associated with the AIF may be jitter, lag, and limited resolution in its temporal sampling. Temporal requirements in DCE-MRI of breast cancer have been previously reviewed by Henderson (23), and also by Kershaw(24). Both of these papers modeled the consequences of limited temporal resolution in sampling of the arterial input function. Both demonstrated that a limited temporal resolution in measuring the AIF could bias parametric estimates of vascular parameters. Henderson specified that the AIF should be sampled at intervals of 1 s in order to limit biases in K^trans and v_e to less than 10%. Kershaw arrived at a similar conclusion, but found that under some circumstances, temporal requirements could be relaxed to 6 s intervals. In both papers, K^trans values were assumed to be of the order of 0.5 [min⁻¹]. At lower values of K^trans, the biases introduced by a slower temporal sampling of the AIF were much smaller (c.f. Figure 9 of Henderson). We note that our measured values of K^trans were at least ten times smaller than those assumed in Henderson or Kershaw’s modeling of breast tumors and consider that the biases introduced to K^trans by a 6-second sampling interval were probably not significant. In support of this opinion, note that a CT perfusion study using an iodinated contrast agent of similar molecular weight to Magnevist, with sampling at 1s intervals, arrived at values of K^trans and v_b in glioblastoma that were substantially in agreement with the values of this MRI DCE-T1 study (25).

As to the likelihood of making an MRI estimate of absolute cerebral blood volume, even with perfect knowledge of the exchange rate of water across the BBB, the uncertainties in the MRI-measured amplitude of the AIF listed in the previous paragraph, the dispersion in the shape of the AIF visible in the Model 1 trace of ΔR₁ versus time (Figure 2), and the timing lag between the AIF and its appearance in the microvasculature make this a tricky task. It may be possible to normalize the AIF to a large vein (e.g., the sagittal sinus), and thus relate all blood volume measures to venous blood, but without the approach described by Sourbron et al (7), the timing lag may still present a problem, particularly at the early time points of the study.

Since all calculations of R₁ depend on a knowledge of the tip angle, B₁ inhomogeneity is a pervasive source of systematic error, both in the pre-contrast estimates of R₁ via DESPOT1, and in the progressive saturation SPGRE estimate of ΔR₁ during and after contrast arrival in the tissue. Equations 3, A9, and A10 can be used to examine the effect of B₁ inhomogeneities on the time trace of ΔR₁ versus time, and on their further effect on the parametric estimates of the model. However, the matter of systematic errors is probably better addressed in a thorough study of the operating characteristics of estimates of vascular parameters, rather than a paper that considers model selection.

Another potentially serious artifact seldom addressed in the literature is the confounding effect of T₂* dephasing after the arrival of CA. We have conducted dual-echo gradient-echo experiments (data not shown) in animal models at 7T, and humans at 3T, that show a clear decrease in MRI signal in the tissue, and in blood due entirely to T₂* dephasing after injection of CA. While the echo times (0.84 ms) in the present experiment minimize this effect relative to the T₁ contrast, longer echo times can generate a reduction in the MRI tissue signal that has little to do with restricted transvascular water exchange and/or diffusion of CA in the interstitium.

The linear fitting of the highest-order model (Model 3) to the summed concentration time data that voxel-by-voxel demonstrated the highest-order variation yielded a very interesting result: in the worst fit, R² was 0.976, meaning that about 2.4% of the variation in the data could not be explained by the model. In the best fit, R² was 0.9994; at most 0.06% of variation in the data could not be explained by the model. These excellent fits were made on concentration-time data summed across multiple slices and numerous voxels containing a relatively large distribution of parametric values. Despite the numerous potential sources of error a remarkably good result in curve fitting was typically obtained. Thus, for summed areas it can be concluded that the largest number of parameters that can be simultaneously and reliably fit to the data of this experiment is three. This view should be qualified in that the result holds for GBM data with a temporal sampling rate, S/N, CA administration, and measurement duration such as presented in this work.

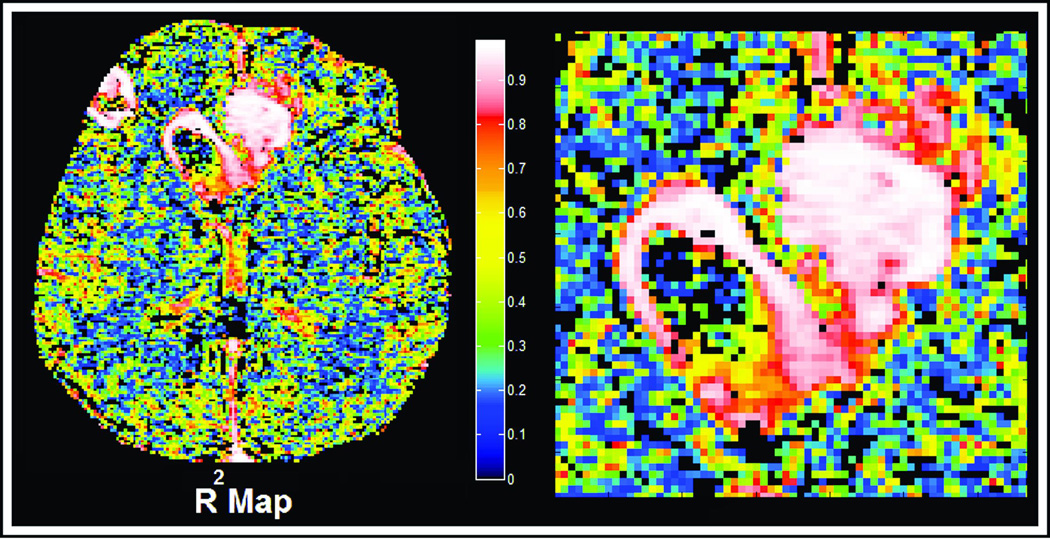
The possibility remains that there is some higher-order systematic time-varying behavior that averages out across the summed voxels. See Figure 5, where the individual values of R² are plotted for the patient and image slice shown in Figures 1 and 3. The maps of R² are uniformly high - in most cases above 0.9 in the regions where Model 3 prevails, and uniformly lower in the regions with lower-order models. There is an apparent correlation between areas of high R² and areas where high contrast-to-noise might be expected. Further, if models with more than three parameters could be supported in areas of high leakage, one would expect regions that had high values of K^trans and low values of R². However, it is evident from a comparison of Figures 3 and 5 that regions where K^trans is high are regions where R² is high. Therefore there is no support in Figure 5 for the existence of higher-order models. Again, this view must be qualified that the result holds for GBM data with temporal sampling rate, S/N, CA administration, and measurement duration such as presented in this work.

Figure 5.

Voxel-by-voxel maps of the R² of the successful model in patient number 2 of table 2. Referring to Figure 3, it is clear that the regions of high R² are strongly associated with Model 3 regions, and in general, that regions with higher contrast-to-noise are associated with higher R².

The very good fits of summed data using three parameters does undermine the utilization of higher-order models like the Shutter-Speed Model (SSM), since its full analysis (21) requires five parameters (v_p, K^trans, k_ep, and two water exchange rates). The SSM has been applied to studies of breast cancer, with interesting results (22,26,27), but seldom with more than three freely varied parameters, meaning that two of the model parameters have been fixed. In such a situation, it is axiomatic that the remaining freely varying parameters will arrive at biased estimates (c.f. chapter VII in Mood, Graybill, and Boes (28)).

The question of the cost of fitting extra parameters contrary to the principle of parsimony should be addressed. In fitting data in the presence of noise, the errors of estimation become highly covariant; employing too many parameters in model fitting will lead to a poor result in each of the parameters estimated. The results then depend on the nature and biases of the optimization procedure. In the extreme case, every optimization procedure will fail to find a best-fit set of estimates, and report this failure in a manner characteristic of the optimization procedure. However, even when an optimization procedure converges, if there is a lack of data (and/or S/N) sufficient to fit the model, the optimization program will produce a set of estimates that can be dependent on both the starting point of the optimizer, and on its characteristics. Since the fit to the data will be excellent, without a voxel-by-voxel estimate of the variance-covariance matrix, or alternatively, a model comparison to a reduced model, this kind of failure will not become apparent, but will lead to misleading results.

The 95% CLs, determined from the sampling distribution of the F-test in large numbers of normal voxels, were quite large, about six times larger than 95% CLs in tabulated F-tests. An inspection of the Model 1 time trace in Figure 2 demonstrates that, although there is no leakage in the tissue, dispersion in the intervening vasculature changes the shape of the input function. The model states that the shape of the AIF and tissue response will be the same, but with amplitudes dependent on the vascular volume. This is clearly not the case. The combination of low contrast-to-noise, dispersion, and possibly limited transvascular water exchange, appear to have increased the sampling distribution of the F-test in tissue that is known not to have a leaky microvasculature.

The tabulated F-tests are calculated under the assumption that the errors of measurement are normally distributed with mean 0, variance 1. An ROI was selected in normal brain of the patient of Figures 1, 3, and 5. A histogram of about 170,000 errors (2697 voxels, 63 time points each) in the estimate of v_b was calculated. If we assume that the errors are iid, we can use them to approximate the distribution of errors of the estimate of v_b in Model 1. This distribution, with a skew of 1.13, a kurtosis of about 6, and a mean value of −6.92 × 10⁻³, is not normally distributed, and should lead to a χ² distribution that is weighted toward its tail. This in turn should generate an F-test that is also weighted toward its tail, thus explaining the high value of the F-test for a CL of 95%.

We assumed that the sampling distribution of the F-test of Model 2 versus 1 in the normal area would be the sampling distribution of the F-test for Model 3 versus 2 in the leaky areas. The choice of CL was set at 95%. This was motivated in part by the intention to select the voxels that had the most evidence of higher-order variation (Model 3), to be further examined for evidence of an even higher-order model behavior. This CL implies a 5% probability of a Type 1 error; that is to say, on the average about 5% of the voxels identified as Model 3 are actually better fit by Model 2. In general usage, a Type 1 error is thought to be costly, and the 5% level is thought to be appropriate for avoiding the conclusion that the null hypothesis failed (in the sampling population) when in actuality it should not have failed. For the purposes of model selection in the DCE-T1 model, however, a 95% CL based on the assumption that the F-test sampling distribution is that of the Model 1 region may be too stringent. First, the selection of an erroneous higher-order model in a relatively small population of voxels, leading as it does to somewhat less stable estimates, may not prove costly in the overall evaluation of the image. Second, the sources of non-normality in the Model 1 region may not be as important in the Model 2 and 3 regions. The voxel-by-voxel map of R² suggests this, and suggests that the threshold of the Model 3 versus 2 F-test be adjusted downward.

The question of CL threshold, among other topics such as other model comparison tests (e.g., the likelihood-ratio test, or the related Akaike test that Brix et al (6) have used), variances, covariances, and biases of model estimates under various conditions can and should be addressed by an examination of the operating characteristics of model fitting in DCE-T1 data. That examination is, however, outside the scope of this paper, which concerns itself primarily with the question of model selection.

In conclusion, voxel-by-voxel model selection is the appropriate tactic for the analysis of DCE-T1 data in GBM. With the reservation that the detailed time-varying behavior of data on a voxel level might contain higher-order elements, the Standard Model, or its nested reduced models, can account for substantially all of the variation in summed DCE-T1 data, with biases to be expected in the estimate of vascular volume, but not in either transfer constant or interstitial space.

Appendix

The Calculation of ΔR₁ from Three-Dimensional T1-weighted Spoiled Gradient Echo MRI Data

We begin with Equation 3 of the main article:

$$S_t=\frac{M_0\text{sin}(\theta )e^{-{\mathit{\text{TE R}}}_2^{*}(t)}(1-e^{-{\mathit{\text{TR R}}}_1(t)})}{1-\text{cos}(\theta )e^{-{\mathit{\text{TR R}}}_1(t)}},$$ (A1)

Where S_t denotes the T₁-weighted signal intensity at time point t, and the other parameters are as stated in the paragraph associated with Equation 3.

For each voxel, there are two main phases for the signal: the pre-injection phase, and the post-injection phase. In order to set a baseline for the signal intensity prior to arrival of the CA in the tissue, the arrival time of the CA is determined by inspection, and the average of the points S_t, t < t_n is determined, where t_n is the time point of the last image before CA first appears in the tissue:

$${\mu }^{\mathit{\text{pre}}}=\frac{{\displaystyle {\sum }_{t=m}^n}{S}_t}{n-m+1},$$ (A2)

where m is the time point where the summation starts (usually the first or second time point of the data). Thus, μ^pre is the mean of the signal intensity before CA arrives. In this T₁-weighted acquisition, μ^pre is associated with the resting pre-contrast R₁ value, R₁(t≤t_n)

Let us now define a new parameter, α_t, the ratio of the baseline signal intensity to the post-injection signal intensity at time point t > t_n:

$${\alpha }_t=\frac{{\mu }^{\mathit{\text{pre}}}}{S_t},\mathrm{t}>{\mathrm{t}}_{\mathrm{n}}$$ (A3)

Equation 1 can be rewritten with the pre-injection T₁ and T₂^* values:

$$S_0=\frac{M_0\text{sin}(\theta )e^{-{\mathit{\text{TE R}}}_2^{*}(t\le t_n)}(1-e^{-{\mathit{\text{TR R}}}_1(t\le t_n)})}{1-\text{cos}(\theta )e^{-{\mathit{\text{TR R}}}_1(t\le t_n)}}.$$ (A4)

Since errors in MRI tissue are approximately normally distributed, μ^pre is an unbiased estimator for S₀:

$$S_0\approx {\mu }^{\mathit{\text{pre}}}.$$ (A5)

Assume that TE << T₂^*, and thus $e^{-{\mathit{\text{TER}}}_2^{*}}\approx 1$. In this case α_t can be approximated as:

$${\alpha }_t=\frac{(1-e^{-{\mathit{\text{TR R}}}_1(t\le t_n)})(1-\text{cos}(\theta )e^{-{\mathit{\text{TR R}}}_1(t>t_n)})}{(1-\text{cos}(\theta )e^{-{\mathit{\text{TR R}}}_1(t\le t_n)})((1-e^{-{\mathit{\text{TR R}}}_1(t>t_n)}))}$$ (A6)

Define the following:

$$\begin{array}{c}{E}^0=e^{-{\mathit{\text{TR R}}}_1(t\le t_n)}\hfill \\ E^t=e^{-{\mathit{\text{TR R}}}_1(t>t_n)}\hfill \\ E_t^{\mathrm{\Delta }}=\frac{E^t}{E^0}=e^{-\mathit{\text{TR}}[R_1(t>t_n)-R_1(t\le t_n)]}\hfill \end{array}$$ (A7)

Then Equation A6 can be written as:

$${\alpha }_t=\frac{(1-E^0)(1-\text{cos}(\theta )E_t^{\mathrm{\Delta }}{E}^0)}{(1-\text{cos}(\theta )E^0)((1-E_t^{\mathrm{\Delta }}{E}^0))}$$ (A8)

Solving for $E_t^{\mathbf{\Delta }}$:

$$E_t^{\mathrm{\Delta }}=\frac{(1-E^0)-{\alpha }_t(1-\text{cos}(\theta )E^0)}{{(E^0)}^2\text{cos}(\theta )({\alpha }_t-1)+E^0\text{cos}(\theta )-{\alpha }_t{E}^0}$$ (A9)

This yields an analytical solution for the change in R₁(t>n):

$$\mathrm{\Delta }{R}_1(t>n)=-\frac{1}{\mathit{\text{TR}}}\text{ln}\left(E_t^{\mathrm{\Delta }}\right)$$ (A10)

We note that others, particularly Li et al (29), have arrived at an analytical estimate of R₁ versus time after the injection of a contrast agent. However, in that paper’s method an a priori knowledge of the relaxivity of contrast agent in a particular tissue must be assumed, and a measure of proton density (M₀) must also be accomplished. It has been demonstrated(22), that the apparent tissue relaxivity of a contrast agent is dependent on the rate of transvascular water exchange, among other factors. This exchange rate probably does change in pathology. The analysis above does not require an assumption about the tissue relaxivity, or a calculation of M₀, and may avoid systematic errors associated with an assumption as to the relaxivity of the contrast agent in a particular tissue. On the other hand, note the sensitivity of expression A9 to an a priori knowledge of tip-angle, θ.