Loading Effect of Fibroblast-Myocyte Coupling on Resting Potential, Impulse Propagation and Repolarization: Insights from a Microstructure Model

Abstract

The numerous nonmyocytes present within the myocardium may establish electrical connections with myocytes through gap junctions, formed naturally or as a result of a cell therapy. The strength of the coupling and its potential impact on action potential characteristics and conduction is not well understood. This study uses computer simulation to investigate the load induced electrophysiological consequences of the coupling of myocytes with fibroblasts, where the fibroblast resting potential, density, distribution and coupling strength were varied. Conduction velocity (CV), upstroke velocity and action potential duration (APD) were analyzed for longitudinal and transverse impulse propagation in a two-dimensional microstructure tissue model, developed to represent a monolayer culture of cardiac cells covered by a layer of fibroblasts. The results show that: (1) At weak coupling (<0.25 nS), the myocyte resting potential was elevated, leading to CV up to 5% faster than control. (2) At intermediate coupling, the myocyte resting potential elevation saturated while the current flowing from the myocyte to the fibroblast progressively slowed down both CV and upstroke velocity. (3) At strong couplings (>8 nS), all the effects saturated. (4) APD₉₀ was usually prolonged by 0–20 ms (up to 60–80 ms for high fibroblast density and coupling) by the coupling to fibroblasts. The changes in APD depended on the fibroblast resting potential. This complex, coupling dependent interaction of fibroblast and myocytes also has relevance to the integration of other nonmyocytes in the heart, such as those used in cellular therapies.

Introduction

Nonmyocytes are numerous in the normal myocardial tissue (1, 30). Pathological proliferation of these cells, such as fibrosis, can result from structural changes associated with aging (9, 49, 54), mitral valve disease (8, 42) or congestive heart failure (11, 33). There is growing evidence that associates increased fibrosis with increased incidence of atrial fibrillation (AF) (12, 50, 56). It is not known, however, how fibrosis creates a substrate that facilitates AF. Some studies have suggested that the increased proliferation of fibroblasts and associated byproducts like collagen, acts to produce anatomic barriers that inhibit impulse conduction (24, 55, 56). Recent in vitro studies have shown that fibroblasts can electrically couple to myocytes and alter impulse conduction (15, 36, 43, 44). While the coupling of fibroblasts and myocytes has been observed in vivo, such as in the rabbit sinoatrial node (6), its occurrence in other parts of the heart and its possible functional impact are not yet known.

While fibroblast-myocyte coupling may not occur under normal or diseased conditions, there are a few studies that suggest that by enhancing coupling, through genetic manipulation, the readily available population of fibroblasts could be used to facilitate conduction in scarred or scarring tissue (26, 27). The use of nonmyocytes, such as skeletal myoblasts or mesenchymal stem cells has already been proposed to restore cardiac structure and function (35, 45). Recent clinical trials, however, have shown wide variability in the success of such therapy (35, 45). Mills et al. have related success to the quality of the myocyte-nonmyocyte electrical and mechanical interactions (35). As a result, it is important to understand how the coupling of myocytes with non-myocytes affects conduction and repolarization properties in tissue. Performing such study experimentally, however, is extremely challenging given the limited ability to manipulate gap junction conductance over a wide range.

To help characterize the nature of the myocyte-nonmyocyte electrical interactions, one can make use of the terminology introduced in Kohl et al. (29). Kohl et al. identified three types of possible connections: zero-sided, single-sided and double-sided connections. Zero-sided connections create obstacles leading to discontinuous impulse propagation (10, 17, 24, 55, 59). Single-sided connections correspond to myocyte-nonmyocyte electrical coupling through gap junctions. Because of this coupling, nonmyocytes may act as a current sink or source for the electrical activity of the myocytes and therefore disturb the propagation of the cardiac impulse, for instance by modulating its conduction velocity and maximal diastolic potential (21, 36) or by altering the firing rate of pacemaker cells (19, 31). Double-sided connections combine myocyte-nonmyocyte and nonmyocyte-nonmyocyte coupling to enable short-range conduction through bridges between otherwise uncoupled myocytes, as observed in the sinoatrial node (6) and in cell cultures (15). In addition to direct electrical connections, indirect interactions through the secretion of molecules have been described (32, 39, 60).

Only sparse data are available concerning the myocyte-fibroblast total coupling conductance. Rook et al. reported coupling conductances for myocyte-fibroblast cell pairs ranging from 0.31 to 8 nS (43, 44). In most of the cell culture preparations, and particularly in the intact heart, the value of this coupling remains largely unknown. Models have recently been developed to investigate the effect of myocyte-fibroblast coupling in cell pairs (31, 34), in a cable model with an insert of fibroblasts (19, 61), in a continuous 1-D model covered by a layer of fibroblasts (21, 46), and in a continuous 2-D model incorporating clusters of fibroblasts (56). While all these model studies considered the possible impact of coupling on conduction, none provided a thorough and systematic analysis of the effect over a wide range of coupling conductances.

In this paper, the influence of possible myocyte-fibroblast coupling on impulse propagation and tissue repolarization is investigated as a function of the coupling conductance. Because the nature of the connection in vivo is not known and likely complex, the effect of the coupling strength was studied here using a computer model of a single layer of normal cardiac cells covered by a layer of fibroblasts. This model of single sided connections represents several recent in vitro studies on fibroblast-myocyte interactions using engineered monolayers and has relevance to possible cell therapies using modified fibroblasts. Different microscale random and patchy fibroblast distributions were created to reproduce recent descriptions of tissue architecture and estimate their impact (24, 56). The advantage of using a computer model of realistic cellular architecture is that a wide range of coupling conductances can be considered, from a single connexon to strong coupling comparable to myocyte-myocyte connections. This range was intended to cover coupling conductances in in vivo cardiac tissues, in vitro experimental models, as well as tissue structures that might be engineered for cardiac therapy (14, 26, 27). The results of the simulations revealed that the effect of the fibroblast loading on conduction velocity and action potential morphology was non-monotonic and depended on the coupling strength, the distribution of fibroblasts and the fibroblast membrane properties.

Materials and Methods

Microstructure Model

Following the approach proposed by Spach et al. (53, 54, 55), a two-dimensional model representing the microstructure of a monolayer cardiac tissue, 8.64 by 2.88 mm in size, was created. Parameters corresponding to a canine atrium were selected whenever possible to ensure consistency (2, 41).

The cell membrane was represented by two parallel surfaces separated by 11 μm. The model was composed of 8354 randomly shaped cells generated using a technique similar to that of Hubbard et al. (18). The myocytes were discretized into segments of size 15 by 10 μm. Figure 1A shows a part of the tissue model. The average length of the myocytes was 156±29 μm (10-th to 90-th percentile range: 120 to 195 μm). This range corresponds to that reported by Spach et al. (55), namely 90 to 215 μm, and to the direct measurement (approximately 140 to 155 μm) on the confocal microscopy images of canine left atrial cells shown in Baba et al. (2). The cell width ranged from 10 to 30 μm, with a cross-sectional area 22 of 213±75 μm², similar to the value 212 μm² estimated by Spach et al. in human atrial cells (55). The large standard deviation comes from the cell width being limited to multiples of Δy=10 μm.

Figure 1.

Tissue architecture as represented in the model (bars = 200 μm). (A) Tissue structure: cell boundaries are shown as solid lines. (B) Cell-to-cell coupling: longitudinal end-to-end cell coupling (black stars), transverse coupling near the intercalated disk (gray circles) side-to-side coupling (gray diamonds). The light gray grid represents the intracellular discretization for the finite volume formulation. (C) Wavefront propagation initiated by a point stimulus in the control tissue. Isochrones are drawn every 0.25 ms.

The myocyte membrane kinetics was described by the Ramirez et al. model of canine atrial cell (41). Similarly to Spach et al. (55), the conductance of the sodium channel was increased by 50% in order to adjust the conduction velocity and upstroke velocity, while keeping the coupling conductance within reasonable range. The average area of active membrane per cell was increased to 10000±2600 μm² instead of the purely geometric value 6060±1576 μm² in order to approximate the irregular surface of the cell, as in previous studies (18, 54, 55). As a result, the equivalent surface-to-volume ratio was 3000 cm⁻¹ and the cell capacitance was 100±26 pF (10-th to 90-th percentile range: 70 to 138 pF), assuming a membrane capacitance per unit area of 1 μF/cm². The average capacitance is close to the experimental value 104.3±5.2 pF (range: 80 to 140 pF) measured by Baba et al. in adult left atrial cells (2).

Discrete cell-to-cell coupling was introduced to reproduce the gap junction distribution observed in adult cardiac tissue (55). These electrical connections were mainly located at end-to-end regions (intercalated disk), as shown on Fig. 1B. Additional sparse coupling covering 30% of the remaining cell lateral wall was added, following a Poisson distribution. The coupling conductance per unit contact area between the connected cell segments was set to 8.182 nS/μm² for both end-to-end and side-to-side connections. The resulting segment-to-segment coupling conductance was 0.9 μS (end-to-end; stars in Fig. 1B) and 1.35 μS (side-to-side, including in the intercalated disk; circles and diamonds in Fig. 1B). The side-to-side coupling is larger because the cell segments are anisotropic in shape (15 by 10 μm). The resistivity of the intracellular medium was assumed to be 200 Ω cm.

Three other microstructure models, composed of 8360±11 cells with the same geometrical and electrophysiological parameters, were created to estimate the sensitivity of the results with respect to the random tissue structure.

Incorporation of Fibroblasts

To study the influence of fibroblasts on impulse propagation, the two-dimensional tissue model was covered by a layer of fibroblasts, in a way similar to the experiments involving monolayers of cultured cells. Nine random fibroblast distributions were generated. These distributions, illustrated in Fig. 2B, differ by their fibroblast density (2, 4 and 8 fibroblasts per myocyte, covering respectively about 10, 20 and 40% of the tissue) and by their degree of randomness. For this purpose, a white-noise field was spatially filtered using a Gaussian filter (random Markov field) with a length scale of λ in the longitudinal direction and λ/6 in the transverse direction (where λ=0, 0.15 and 0.75 mm). The fibroblast distributions were obtained by identifying the 10%, 20% and 40% largest values in each of the filtered fields.

Figure 2.

(A) Steady-state current-voltage relationship for the MacCannell et al. fibroblast model. Solid curve: original model; dashed curve: voltage-dependent gates shifted by 15 mV and g_Kv set to 0.194 nS/pF; dashed-dotted curve: voltage-dependent gates shifted by 30 mV and g_Kv set to 0.155 nS/pF; (B) Fibroblast distributions used in this study: 3 fibroblast densities (2, 4, 8 fib/myo, from left to right) and 3 degrees of randomness (λ=0, 0.15 and 0.75 mm, from top to bottom). (C) This panel illustrates in a schematic tissue including 4 myocytes and 10 fibroblasts how the fibroblast distributions of panel B are used to create 2D tissue models incorporating a layer of fibroblasts.

One fibroblast was placed on top of each of the 15-by-10 μm segments forming the region covered by fibroblasts (black regions in Fig. 2B), as illustrated in Fig. 2C. The fibroblast and the segment of myocyte located right below were electrically coupled with a conductance g_c varying from 0.05 to 80 nS. Assuming a gap junction conductance of 30 pS (31, 43), these values correspond to 1.6 to 2700 gap junctions. This wide range was considered to cover both the physiological and the possible pathological or engineered cases, because the actual value of this coupling in vivo is unknown and even the existence of such coupling is debated. In cell culture experiments, values ranging approximately from 1 to 3 nS have been measured, estimated or inferred (23, 34, 36, 44). No fibroblast-fibroblast coupling was introduced in the model, although there are evidences of such coupling in vitro (15).

The electrophysiological properties of the fibroblasts were described by the MacCannell et al. fibroblast model (34). This membrane kinetics model incorporates a time-dependent K⁺ current (l_Kv) formulated using two gating variables, an inward-rectifying K⁺ current (l_K1), a Na⁺-K⁺ pump current (l_NaK), and a background Na⁺ current (l_bNa). Its resting potential (when isolated) is −49.4 mV. Two other versions were developed, which have a different resting potential. For that purpose, the voltage dependence of the gating variables of the current l_Kv was shifted by 15 mV and 30 mV. In order to keep the peak steady-state ionic current at the same value, the conductance g_Kv was reduced from 0.25 nS/pF to 0.194 nS/pF and 0.155 nS/pF respectively, leading to a resting potential of −36.8 mV and −24.5 mV, referred to as less negative fibroblast resting potentials. The three steady-state current-voltage relationships are displayed on Fig. 2A. The fibroblast capacitance was set to 6.3 pF, as suggested by MacCannell et al. (34). For a spherical fibroblast, this means that its diameter would be 14.2 μm (assuming a specific capacitance of 1 μF/cm²).

Mathematical Formulation and Implementation

Cardiac propagation in the microstructural model was simulated in the framework of the monodomain approximation. Since each fibroblast was coupled to only one cell segment and fibroblast-fibroblast coupling was ignored, the fibroblast equations were integrated into the myocyte equations extending the approach of Jacquemet et al. (21) to a two-dimensional tissue. As a result, the microstructural model can be formulated as a two-dimensional monodomain model with a fine discretization, highly heterogeneous and anisotropic diffusion at microscale, and including two membrane kinetics types (patch of myocyte and patch of myocyte+fibroblast).

A finite volume approach was used to discretize the intracellular space, each finite volume corresponding to a cell segment. Time integration was performed using a semi-implicit Crank-Nicholson scheme provided by the CardioWave software package (38) with a time step between 10 μs (depolarization) and 50 μs (repolarization). The linear system solver was based on the conjugated gradient method with an incomplete Cholesky preconditionner.

Simulation Protocols and Data Analysis

All simulations used the steady state as initial condition, in which the spatially varying myocyte-fibroblast interaction reached equilibrium. Due to some gating variables with large time constants (such as the gating variable s in the MacCannell et al. (34) model) and slow transient drifts in ionic concentration (28), simulating free evolution until the steady state is reached may be computationally expensive in large models. In addition, the steady state has to be recomputed for each myocyte-fibroblast coupling configuration and conductance. In this paper, the steady state was computed by solving numerically the full system with the time derivatives set to zero using a Newton-based approach, as described in previous papers (20, 22).

Longitudinal and transverse plane wave propagation was initiated by injecting intracellular current in the cells along the left or top border. The stimuli duration was 2 ms and its intensity was approximately 1.5 times threshold. The simulated time was 350 ms. This stimulation protocol was repeated for 16 values for g_c ranging from 0.05 to 80 nS (in addition to the control case g_c =0 nS), 3 fibroblast spatial distributions (λ=0, 0.15 and 0.75 mm), 3 fibroblast densities (2, 4 and 8 fibroblast par myocyte), and 3 fibroblast resting potential (−49.4, −36.8 and −24.5 mV), leading to a total of 866 simulations. For each simulated wavefront propagation, the activation time was measured at every computational node using a threshold at −40 mV and linear interpolation. The conduction velocity (CV) was computed by linear regression of these activation times. The nodes close to the boundary (<1 mm longitudinal and <0.4 mm transverse) were discarded.

In selected cases, an elliptical wavefront was initiated by stimulating (2 ms duration, 1.5 times threshold) four cells at the center of the tissue (see Fig. 1C). Because the CV of the wavefront varies with its curvature, longitudinal and transverse CV were estimated by linear interpolation around the isochrone located at mid-distance between the stimulus site and the tissue border.

The transmembrane potential was recorded at 87 sites forming a elliptic-shaped grid 3.84 by 1.44 mm in size. Upstroke velocity (dV/dt)_max, and action potential durations (APD), measured at 60% (APD₆₀), 70% (APD₇₀), 80% (APD₈₀) and 90% repolarization (APD₉₀), were extracted from each of these signals, and their mean values and standard deviations over the 87 measurement sites were computed.

Results

Propagation in the Absence of Fibroblast

To understand the loading effects of the fibroblasts, a simulation was first performed on the control tissue in the absence of fibroblasts to determine the CV under several conditions. A line stimulus was used to elicit planar wavefronts in the longitudinal and transverse directions. The longitudinal CV was 64.4 cm/s and the transverse CV was 29.3 cm/s, yielding a CV anisotropy ratio of 2.2. At the cellular level, propagation was affected by the discrete tissue architecture (see Fig. 1C). However, at the macroscopic scale, wavefront propagation was smooth and uniform. The upstroke velocity (dV/dt)_max was 136.6±2 V/s for longitudinal propagation and 136.9±4.5 V/s for transverse propagation. The longitudinal/transverse CV of an elliptical wavefront elicited by a point stimulus was 49.6/24.1 cm/s (ratio = 2.06). Elliptical propagation was slower than plane waves due to curvature effects. For the same reason, the anisotropy ratio was underestimated when computed from elliptical wavefronts, in agreement with Hubbard et al. (18).

The same protocol and analysis were applied to three other tissue models representing different realizations of the same microstructure statistics (cell shape, size, coupling, etc.). The statistics of the average electrophysiological properties measured were (mean±SD, n=4): longitudinal CV = 64.386±0.007 cm/s, transverse CV = 29.15±0.08 cm/s, anisotropy ratio = 2.209±0.006, longitudinal upstroke velocity = 136.6±0.07 V/s, transverse upstroke velocity = 137.0±0.3 V/s. Because of the consistency of these extracted parameters among the different realizations of the microstructure statistics, only one tissue was used to investigate the effects of including fibroblasts.

Because fibroblasts are expected to modulate the resting potentials of the myocytes to which they are coupled, a simulation was performed to evaluate the differences in CV induced by a change in the resting potential of the myocytes in the control tissue. Again using a line stimulus, planar longitudinal and transverse propagations were initiated under the initial condition of a less negative value for the myocyte membrane potential. The internal membrane variables (e.g. gating variables) were set to their steady-state value at the selected membrane potential. Table 2 reports the CV for an initial membrane potential ranging from −84 to −77 mV. Propagation was up to 5–6% faster when starting with a pre-depolarized state at −77 mV. The upstroke velocity, however, was identical to the control case. These values will serve as a reference to discuss the effect of coupling with fibroblast.

Table 2.

Conduction velocity for different initial conditions for the myocyte membrane potential in the control case.

Resting potential	long. CV	transv. CV
−84 mV	64.3 cm/s	29.2 cm/s
−83 mV	64.7 cm/s	29.4 cm/s
−82 mV	65.1 cm/s	29.6 cm/s
−81 mV	65.5 cm/s	29.7 cm/s
−80 mV	66.0 cm/s	30.1 cm/s
−79 mV	66.5 cm/s	30.4 cm/s
−78 mV	67.0 cm/s	30.7 cm/s
−77 mV	67.6 cm/s	31.0 cm/s

CV: conduction velocity; long.: longitudinal propagation; transv.: transverse propagation.

Steady-State Membrane Potential

It is expected that the initial conditions will depend on the density of fibroblasts and the fibroblast membrane properties. Simulations were performed to investigate the steady state membrane potential in the microstructure model loaded by fibroblasts with densities of 2 fib/myo, 4 fib/myo and 8 fib/myo. Figure 3 shows the average steady-state membrane potential of the myocytes and the fibroblasts as a function of the coupling conductance (g_c) between the two cell types for the three densities. At very low coupling conductance (g_c<0.1 nS), the steady-state membrane potential of each cell type is close to its intrinsic resting potential. At large coupling (g_c>10 nS), fibroblasts and myocytes equilibrate to the same steady-state membrane potential. Interestingly, the transition between these two regimes occurs around g_c=0.2 nS or equivalently 5 GΩ. This value corresponds to the typical membrane resistance of a fibroblast (7, 25, 30, 49).

Figure 3.

Steady-state myocyte (filled symbols) and fibroblast (open symbols) membrane potential as a function of the coupling conductance. The fibroblast density is 2 fib/myo (triangles), 4 fib/myo (diamonds) and 8 fib/myo (circles). The solid (resp. dashed) curves represent Eq. (1) fitted to the data points of myocyte (resp. fibroblast) membrane potentials. The fibroblast resting potential is (A) −49.4 mV, (B) −36.8 mV and (C) −24.5 mV. The resting potential of the myocyte and that of the fibroblast are shown as the lower and upper horizontal dotted lines respectively.

Although both the myocyte and the fibroblast models are active and have a non-linear current-voltage response, the results were compared to the simplest model involving two interacting linear passive cells. When a cell with resting potential V₁ and membrane conductance G₁ (myocyte) is coupled through a conductance G_c to a cell with resting potential V₂ and membrane conductance G₂ (fibroblast), then at steady state the membrane potential of cell 1 is:

$$V_1=\alpha V_{r,1}+(1-\alpha )V_{r,2}\text{where}\alpha =\frac{G_c+G_2}{(1+G_2/G_1)G_c+G_2}.$$ (1)

The formula for the steady-state membrane potential of cell 2 is obtained by permuting the indices 1 and 2. Equation (1) was fitted to all the series of data points (solid and dashed curves in Fig. 3) and the parameters G₁ and G₂ were estimated to check the consistency of the microstructure model with respect to the simple linear theory. The estimated membrane conductance of the fibroblast was found to be 0.027±0.003 nS/pF, which is close to the range 0.023 to 0.025 nS/pF computed from the fibroblast current-voltage relationship (shown in Fig. 2A) in the interval −84 to −77 mV. The estimated average conductance ratio G₂/G₁ (fibroblast/myocyte) was 0.026±0.003, which is of the same order of magnitude as the value 0.018 computed directly from the electrophysiological properties of the microstructure model. At low coupling (g_c < 0.3 nS or 10 gap junctions), the linear model slightly underestimates the differences in steady-state membrane potential between the fibroblast and the myocyte (see Fig. 3), due to the non-linearity of the current-voltage relationships. Despite the complexity of the microstructure model and its non-linear intrinsic properties, the simplest linear model still captures qualitatively the steady-state phenomena.

Comparison of Figs. 3A, B and C shows that making the intrinsic resting potential of the fibroblast less negative did not change significantly the steady-state membrane potential of the myocyte except when the coupling is very weak. At low coupling, the linear model predicts V₁ ≈ V_r,1+(G_c/G₁)(V_r,2−V_r,1), so that the steady-state potential of the myocyte is directly influenced by the fibroblast intrinsic resting potential but the global effect is small (g_c < 0.2 nS on Fig. 3). At high coupling, the linear model predicts the saturation at V₁ ≈ (G₁V_r,1 + G₂V_r,2)/(G₁ + G₂). In the interval −84 to −77 mV where the observed steady-state myocyte potentials lie, the three current-voltage relationships associated with each fibroblast resting potential are nearly identical (see Fig. 2A). As a result, the steady-state potential at high coupling is almost the same for the three-fibroblast models with different resting potentials.

Modulation of Impulse Propagation by Fibroblasts

As shown in Table 2, small changes in the initial resting potential of the myocytes act to increase the CV. The loading effect of the fibroblasts, however, will occur throughout the action potential and thus the overall impact on CV is expected to be more complex. Figure 4 presents the CV of longitudinal and transverse plane waves as a function of the myocyte-fibroblast coupling g_c for different fibroblast distributions and fibroblast resting potentials (note the logarithmic scale for the coupling). When the coupling g_c was smaller than about 2.7 nS, the CV was faster than the control case. At about g_c=0.3 to 0.4 nS, the increase in CV was maximal, but the speed-up was moderate (5% faster in both the longitudinal and transverse direction for 8 fib/myo). When g_c>2.7 nS, coupling with fibroblasts made the CV become significantly slower than the control case (up to 25% in the extreme case). Decreasing the intrinsic fibroblast resting potential from −49.4 mV to −24.5 mV did not significantly change the CV, except at low coupling (<1 nS), where the global effect was small anyway. The influence of fibroblast distribution on CV was observed only at high coupling (g_c> 10 nS). For a given fibroblast density, when the fibroblasts were randomly distributed in a uniform way, the CV was slightly, but consistently slower than when arranged in clusters. The presence of the fibroblasts also did not significantly affect the CV anisotropy ratio in the configurations studied: the CV anisotropy ratio (2.2 in the control case) was 2.200±0.005 for 2 fib/myo, 2.201±0.007 for 4 fib/myo and 2.205±0.005 for 8 fib/myo (averaged over all available simulations, n=144).

Figure 4.

Modulation of conduction velocity by fibroblasts as a function of the myocyte-fibroblast coupling for longitudinal (A,B,C) and transverse (D,E,F) propagation. The fibroblast resting potential is −49.4 mV in (A) and (D), −36.8 mV in (B) and (E), and −24.5 mV in (C) and (F). In each panel, the fibroblast density is 2 fib/myo (triangles), 4 fib/myo (diamonds) and 8 fib/myo (circles). The gray-level of the symbols denotes the fibroblast distribution: λ=0 mm (white), λ=0.15 mm (gray) and λ=0.75 mm (black). The dotted horizontal lines indicate the CV in the control case.

Analyzing elliptical wavefront propagation lead to qualitatively similar results. The longitudinal/transverse CV was 49.6/24.1 cm/s (ratio = 2.06). When the myocytes were randomly coupled to 4 fibroblasts (resting potential −24.5 mV) on average, the CVs of the elliptical wavefront were 50.4/24.9 cm/s (ratio = 2.02) for g_c=0.1 nS, 50.4/24.8 cm/s (ratio = 2.03) for g_c=1 nS, and 47.3/22.9 cm/s (ratio = 2.06) for g_c=10 nS. Propagation was slightly faster at low coupling and became slower at stronger coupling, the anisotropy ratio remaining relatively constant. However, the interplay between the changes in load due to the wavefront curvature and the fibroblasts makes it more difficult to separate the effects.

The fibroblast density also plays an important role in modulating CV. The relative change in CV was in good approximation proportional to the fibroblast density. The correlation coefficient (in absolute value), based on 4 samples (0, 2, 4 and 8 fib/myo), was >0.99, except in the region 2 nS < g_c < 3 nS (transition from positive to negative correlation), where it was >0.9. This suggested to display together all the CV-coupling relationships on a single graph (Fig. 5) in which CV is expressed in relative change divided by the fibroblast density (in fib/myo). All the data points corresponding to different fibroblast density, resting potential and distribution lie approximately on the same curve. Figure 5 reveals the (small) effect of the fibroblast resting potential at low coupling (g_c<0.4 nS). At high coupling, more dispersion in the changes in CV was observed, depending on the fibroblast density and distribution.

Figure 5.

Relative variation in CV (as compared to the control case) divided by the fibroblast density (in fib/myo) as a function of the myocyte-fibroblast coupling. All the data points of Fig. 4 are included in this graph using the same symbols. The solid curves correspond to the simulations with fibroblast potentials fixed at their initial condition, where the initial condition is computed assuming a fibroblast intrinsic resting potential of −49.4 mV (lower curve) and −24.5 mV (upper curve).

To explore the mechanisms leading to an increase of the CV at low coupling, the same simulations were run (in particular, starting from the same steady-state initial condition) with fibroblast membrane potentials clamped at their initial condition. In this case, fibroblasts act as a pure load. The resulting changes in CV are shown as solid lines on Fig. 5. These curves accurately follow the data points from the simulations with the full fibroblast model when g_c <2.5 nS, indicating that in this case the fibroblast membrane potential cannot follow that of the myocyte during the upstroke phase of the action potential. This simplified model, however, largely overestimates the reduction in CV at higher coupling when the fibroblast and myocyte membrane potential time-course becomes very similar.

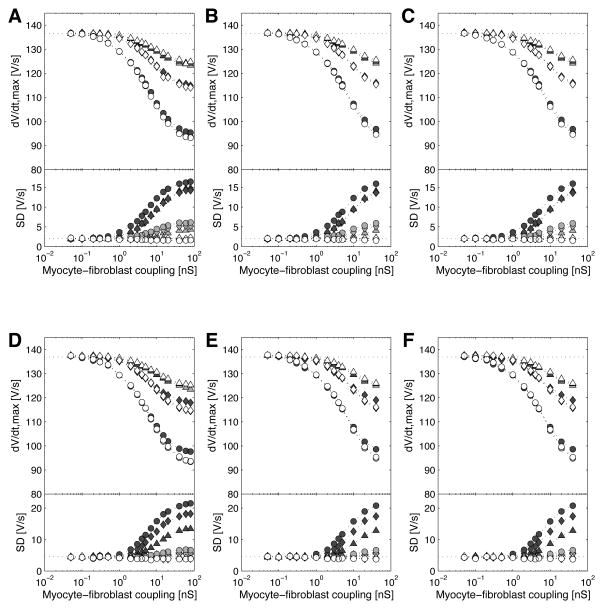
Figure 6 displays the upstroke velocity averaged over the 87 measurement sites, as well as its spatial dispersion (standard deviation of the 87 values), for longitudinal and transverse propagation, in a way corresponding exactly to Fig. 4. In the control case, the average upstroke velocity was 136.6±2.0 V/s for longitudinal propagation and 136.9±4.5 V/s for transverse propagation. Note that the average upstroke velocity is also an average over intracellular fluctuations (54). In all cases, the upstroke velocity decreased with increasing myocyte-fibroblast coupling as well as with increasing fibroblast density, or more generally with increasing load. Although CV was faster than control at low coupling, no increase in average upstroke velocity was observed at similar coupling. Nevertheless upstroke velocity was globally correlated with CV, as their correlation coefficient was 0.92 for longitudinal and 0.93 for transverse propagation. The dispersion of upstroke velocity demonstrates the local effect of the fibroblast distribution on impulse propagation. The standard deviation of upstroke velocity did not depend on coupling strength as long as the fibroblasts were randomly, but uniformly distributed over the tissue. When fibroblasts were arranged in clusters, local variations in upstroke velocity became much larger at coupling >1 nS. There was a negative correlation between upstroke velocity and the presence of a fibroblast coupled to the cell segment in which the membrane potential was recorded. Cell segments coupled to a fibroblast were associated with a significantly smaller (unpaired t-test with a significance level of 1%) local upstroke velocity in 5% (when λ=0 mm), 57% (when λ=0.15 mm) and 90% (when λ=0.75 mm) of the simulations with g_c>1 nS. The effect is therefore more pronounced in more heterogeneous fibroblast distributions.

Figure 6.

Upstroke velocity (dV/dt)_max as a function of the myocyte-fibroblast coupling for longitudinal (A,B,C) and transverse (D,E,F) propagation. In each panel, the top part shows the upstroke velocity (dV/dt)_max averaged over the 87 recording sites, and the bottom part shows its standard deviation (SD). Like in Fig. 4, the fibroblast resting potential is −49.4 mV in (A) and (D), −36.8 mV in (B) and (E), and −24.5 mV in (C) and (F). In each panel, the fibroblast density is 2 fib/myo (triangles), 4 fib/myo (diamonds) and 8 fib/myo (circles). The gray-level of the symbols denotes the fibroblast distribution: λ=0 mm (white), λ=0.15 mm (gray) and λ=0.75 mm (black). The dotted horizontal lines indicate the values in the control case.

Effect of Fibroblasts during Repolarization

As noted earlier, the fibroblasts load the myocytes differently throughout the action potential, due to their own intrinsic membrane dynamics. In the control tissue, the average APD₆₀ was 106.8±1.6 ms, the APD₇₀ was 131.9±1.5 ms, the APD₈₀ was 157.0±1.4 ms, and the APD₉₀ was 193.0±1.3 ms, where the values were averaged over the 87 measurement sites. Because the APDs measured during longitudinal and transverse propagation were not found to be significantly different (0.16±0.18 ms longer in the longitudinal case at all levels), the data presented result from simulations of longitudinal plane wave propagation.

Figure 7 illustrates the impact of loading on the action potential waveforms by showing examples of action potentials recorded at the center of a tissue with fibroblast density 4 fib/myo for different fibroblast resting potentials and coupling conductances. In general, coupling with fibroblast tends to lower the membrane potential in the phase 2 of the action potential and to raise it at the later stage of repolarization. The action potential amplitude is indeed decreased by about 1.7 mV when g_c=0.1 nS, 4.9 mV when g_c=1 nS, and 9.9 mV when g_c=10 nS. When the fibroblast resting potential is less negative (Fig. 7, B vs A and C vs B), the interval in which the membrane potential is lower than control tends to shrink. In extreme cases with a large fibroblast density, large coupling, and a fibroblast intrinsic resting potential of −24.5 mV (such as the dotted line on Fig. 7C), the APD prolongation can become considerable.

Figure 7.

Myocyte (A–C) and Fibroblast (D–F) membrane potentials recorded at the center of the tissue with a myocyte-fibroblast coupling of 0 nS (control case, solid curves), 0.1 nS (dashed curves), 1 nS (dash-dotted curves) and 10 nS (dotted curves). The fibroblast density is 4 fib/myo. The fibroblast resting potential is −49.4 mV in (A,D), −36.8 mV in (B,E), and −24.5 mV in (C,F). The horizontal dotted lines indicate the approximate location of the 60%, 70%, 80% and 90% repolarization levels (as these levels depend on the resting potential and action potential amplitude).

Figure 8 summarizes the changes in APD₆₀, APD₇₀, APD₈₀ and APD₉₀ (as compared to the control case) induced by coupling with fibroblast in all the simulations. When the intrinsic resting potential of the fibroblasts is −49.4 mV (panels A,D), APD shortens with increasing fibroblast density and coupling conductance, except at 90% repolarization level where this in only the case at lower coupling (g_c <0.1 to 1 nS). If the intrinsic resting potential of the fibroblasts is less negative, such as −36.8 (panels B,E) or −24.5 mV (panels C,F), APD can be significantly prolonged provided that a sufficient number of fibroblasts are present and the coupling is strong enough. The fibroblast distribution did not have a significant effect on the average APD. A non-negligible dispersion in APD occurs at strong coupling when λ=0.75 mm (non-uniform fibroblast distribution). This is due to spatial variations in steady-state potential (elevated baseline) and not in timing of repolarization.

Figure 8.

Changes in action potential duration (DAPD) due to coupling with fibroblasts. APDs were measured at 60% (panels A,B,C), 70% (panels D,E,F), 80% (panels G,H,I) and 90% repolarization level (panels J,K,L). Like in Fig. 4, the fibroblast resting potential is −49.4 mV in (panels A,D,G,J), −36.8 mV in (panels B,E,H,K), and −24.5 mV in (panels C,F,I,L). In each panel, the fibroblast density is 2 fib/myo (triangles), 4 fib/myo (diamonds) and 8 fib/myo (circles). The gray-level of the symbols denotes the fibroblast distribution: λ=0 mm (white), λ=0.15 mm (gray) and λ=0.75 mm (black). Standard deviations are indicated by error bars if larger than the symbol size. Data points corresponding to repolarization times >350 ms (simulation time) are not shown.

Discussion

This paper investigates how changes in the strength of coupling between myocytes and fibroblasts affect CV and APD. Three regimes for the coupling conductances were identified. When the coupling was smaller than the nonmyocyte membrane conductance, the conduction velocity was slightly enhanced through an elevation of the myocyte resting potential. For intermediate coupling, the CV and upstroke velocity of the action potential both decreased. For the strong coupling regime (>8 nS), all the effects saturated. Each of these regimes roughly corresponds to different physiological scenarios that might arise, in vivo and in vitro or as a consequence of cell manipulation.

Low Myocyte-Fibroblast Coupling

A combined analysis of Figs. 3, 5 and 8 suggests that the low myocyte-fibroblast coupling regime can be defined as g_c<0.25 nS. Assuming a gap junction conductance of 30 pS between the myocyte and the fibroblast (43), this is equivalent to the presence of up to 8 (fully functional) gap junctions. In this interval, the coupling conductance is at most of the order of the fibroblast membrane conductance (0.24 nS model around −80 mV for the MacCannell fibroblast). This regime is believed to be the closest to in vivo cardiac tissue (5, 16).

The myocyte membrane potential at steady state was found to be elevated above its intrinsic resting potential. In the low coupling regime, this elevation (up to 4 mV for a fibroblast density of 8 fib/myo) depended linearly on the myocyte-fibroblast coupling and on the fibroblast density (filled symbols on Fig. 3, shown in logarithmic scale). In contrast, the fibroblast steady-state membrane potential was more negative with increasing myocyte-fibroblast coupling (open symbols on Fig. 3). In the depolarization phase, the fibroblast membrane potential was not able to follow that of the myocyte because the coupling current was too weak, in agreement with our previous numerical study on a cable of mouse myocytes coupled with fibroblasts (21). As a result, the CV was approximately the same as that predicted from a model in which the fibroblast membrane potential was fixed to a constant value (symbols vs solid curves for g_c<0.25 nS in Fig. 5). Propagation was faster than in the control case by up to 5% for a fibroblast density of 8 fib/myo (Fig. 4). Making the fibroblast resting potential less negative strengthened the effect (Fig. 5). The variations in CV obtained by changing only the initial condition in the control tissue (also up to about 5%, see Table 2) suggest that in the low coupling regime, the changes in steady-state potential explain most of the effects of coupling with fibroblast on the depolarization process. These results are consistent with the experimental study by Miragoli et al. (36), in which CVs up to 10–15% faster than control and a less negative maximal diastolic potential were observed for monolayers with a low fibroblast density.

The effect of coupling with fibroblast on the repolarization process is more complex and depends on the fibroblast resting potential. As long as the myocyte membrane potential is more negative than the fibroblast membrane potential, the fibroblast acts as a current source. Otherwise, the fibroblast acts as a current sink. As a result, when the fibroblast resting potential was −49.4 mV (first column of Fig. 8 for g_c <0.25 nS), APDs were shorter since the myocytes were more depolarized than the fibroblasts during most of cardiac cycle. The effect was more pronounced for APD₆₀ (up to 27% reduction) than for APD₉₀ (less than 3% reduction), as illustrated by the examples shown on Fig. 7. Making the fibroblast resting potential less negative reversed the effect (column 2 and 3 of Fig. 8). When the fibroblast resting potential was −24.5 mV, only APD₆₀ and APD₇₀ were shorter than control. Only APD₆₀ was shorter than control (under the restriction that the fibroblast density is <8 fib/myo) for a fibroblast resting potential of −36.8 mV. In these cases APD₉₀ was significantly prolonged because during the late stage of repolarization, the coupling current slowed down the return to the steady-state value. Even with a coupling conductance of 0.1 nS (3.3 gap junctions per fibroblast on average), APD₉₀ was increased by 12% (resp. 28%) when each myocyte was coupled to 4 (resp. 8) fibroblasts with a resting potential of −24.5 mV (Fig. 8L).

Intermediate Myocyte-Fibroblast Coupling

The intermediate coupling regime corresponds to the transition zone (0.25 nS <g_c <8 nS) in which impulse propagation and action potential waveform are sensitive to fibroblast-myocyte coupling. This interval also matches the range of coupling conductances (0.31 to 8 nS) observed by Rook et al. in cell pairs (44) and may therefore be thought of as representing the effect of fibroblasts in cell culture experiments.

In this coupling regime, the steady-state potential of the myocyte does not depend a lot on the coupling g_c (solid curves in Fig. 3), so the speedup effect induced by the elevated resting potential saturates. On the other hand, the fibroblast steady-state potential is still significantly affected by the coupling g_c (dashed curves in Fig. 3). Consequently, with increasing values of g_c in this range, the current sink effect starts outperforming the current source effect, resulting in a decrease in CV (Fig. 5). This reduction in CV was associated with a decrease in upstroke velocity (Fig. 6). In contrast, in the control tissue, when the CV was slower due to a weaker myocyte-myocyte coupling, the upstroke velocity was larger. The underlying mechanism is therefore clearly different (current sink instead of lower coupling). This difference may affect the safety of propagation as a function of CV in the presence of fibroblasts (48).

The changes in APD induced by myocyte-fibroblast coupling varied a lot depending on the coupling conductance, fibroblast density and fibroblast resting potential. With 2 fib/myo at a resting potential of −49.4 mV, APD₉₀ did not differ significantly from control (Fig. 8J), while increasing fibroblast density to 4 fib/myo had a large effect on APD₉₀. In the intermediate coupling regime, with 4 fib/myo at a resting potential of −49.4 mV, −36.8 mV and −24.5 mV respectively, APD₉₀ were prolonged by approximately 0 to 20 ms, 30 to 60 ms and 40 to 80 ms. Note that the combination of extreme values for all the parameters (strongest coupling, highest fibroblast density, least negative fibroblast resting potential), considered here for the sake of completeness, may not be found in vitro or in vivo. In contrast, MacCannell et al. (34) found using the same fibroblast model that ventricular action potentials were shortened by up to 100 ms when coupled to 4 fibroblasts with a conductance of 3 nS. This suggests that the effect of fibroblasts on repolarization is action potential dependent. First, the capacitance and membrane conductance at rest of the myocyte play a major role in determining resting potential and near steady-state properties. Second, in the fibroblast model used, the steady-state fibroblast ionic current (Fig. 2A) is characterized by a peak around −20 mV. Its impact therefore depends on the time the myocyte action potential spends around that voltage, because the fibroblast follows the myocyte activity. When a long plateau phase exists, the effect tending to shorten the APD (in this phase, the membrane potential of the myocyte is higher than that of the fibroblast) is maximized (34). When the action potential shape is triangular (atrial cell) with a slow return toward the resting potential, the influence of the fibroblast during the last repolarization phase dominates and tends to prolong the APD. Another evidence for this voltage-dependent effect of fibroblasts on repolarization is the qualitative differences between the curves APD₆₀ and APD₉₀ as a function of coupling in Fig. 8, first column.

Strong Myocyte-Fibroblast Coupling

The strong coupling regime (g_c >8 nS) is characterized by the saturation of the main electrophysiological features describing impulse propagation (CV, APD and upstroke velocity) when expressed as a function of the coupling g_c. Note that, in Figs. 4 and 6, the logarithmic scale used for the horizontal axis masks the saturation. Although it is questionable whether such a strong coupling forms naturally in vivo or even in vitro, these conditions might be created in engineered tissues.

At strong coupling, the pair myocyte-fibroblast becomes, in some sense, equivalent to a single composite cell in which the capacitances and the ionic currents of the myocyte and coupled fibroblasts are summed. Assuming that the CV is inversely proportional to the square root of the membrane capacitance like in a cable (37), a rough estimate predicts that the CV would be decreased by a factor (1+6.3 pF/100 pF)^1/2 when g_c tends to infinity. This would correspond to a 3% decrease in CV for 1 fib/myo (18.5% for 8 fib/myo), a value close to that shown in Fig. 5 for g_c=80 nS. Therefore, for a given fibroblast density, there is a limit to the decrease in CV and to the changes in APD induced by fibroblasts through loading effects only. Additional effects may be observed if the coupled fibroblasts are embedded in the tissue and also create obstacles.

Limitations

This study has several limitations. First, not all of the ionic currents involved in fibroblasts or other nonmyocytes have been completely identified and characterized. MacCannell et al. (34) demonstrated that such differences (for instance, active versus passive fibroblast) could have a dramatic impact on myocyte-fibroblast interactions. A more comprehensive set of experimental measurements will enable more accurate model prediction (46). An alternative approach to facilitate the comparison between computer simulation and experiments would be to genetically engineer nonmyocytes in order to introduce known ion channels in it (14, 26, 27). This would enable the formulation of a dedicated nonmyocyte model with controllable properties.

Another limitation is that this study did not consider the effects of reduced coupling, uncoupling, microfibrosis, or random microscale obstacles (4, 17, 40, 55, 56, 57, 58, 59). These effects were purposely not incorporated in the model to focus only on the influence of fibroblast loading. These additional modifications of the microstructure are expected to have a major impact on the initiation and maintenance of reentry. In addition, these structural changes are often reported to be associated with aging, where ionic channels involved in both depolarization and repolarization are known to be altered (2). Because the effect of fibroblast on repolarization is action potential dependent, the age dependent changes in membrane kinetics may interact with structural changes and hence the overall change in electrophysiology is uncertain. The model described in this paper, however, provides a framework to investigate all of those factors.

Furthermore, the simulations were only in two dimensions, with a simple rectangular geometry and a random fibroblast distribution. The loading effects of the fibroblasts in three dimensions should be qualitatively similar, although quantitative differences are expected (58). Also, different configurations of fibroblast distribution have been found in vivo that combine diffuse and patchy fibrosis (56). The inclusion of such anatomical details would enable the analysis of the interactions between (micro-) structure and function in the context of fibrotic tissue. The size of the preparation, although much larger than the space constant of the tissue, may introduce some boundary effects on repolarization (3, 47).

While most cell culture experiments and cell therapy clinical trials involve ventricular cells, a model of adult atrial tissue was created, because a sufficiently coherent set of data was available for its development, and because of its possible significance to AF. The results obtained in this atrial tissue model are expected to apply to the ventricular myocardium, as suggested by qualitatively similar observations in continuous cables of mouse or rat ventricular cells (21, 46). The effects on APD were found to be action potential-dependent (21, 34, 46) and thus would not apply to a different cell type such as ventricular cells.

Finally, fibroblast-fibroblast electrical connections were ignored in this study. Although the coupling conductance is also largely unknown, it may be (at least in vitro) strong enough to enable delayed conduction across an obstacle formed by a cluster of fibroblasts (15). Because obstacles were not considered, the possible fibroblast-fibroblast coupling current is expected to be small, particularly in a diffuse fibroblast distribution where most of the fibroblasts do not have any direct neighboring fibroblast to interact with.

Physiological Significance

The relevance of this modeling study relies on the hypothesized existence of in vivo myocyte-fibroblast coupling at some stage of the development of fibrosis, which is still yet to be observed. However, this paper also opens a perspective on the impact of coupling (possibly facilitated by gene therapy) between myocytes and nonmyocytes used for cell therapy. The results involving basic mechanisms related to the resting potential and conduction velocity are expected to also apply in this case, provided that the average total capacitance of the nonmyocytes connected to a myocyte (fibroblast density x nonmyocyte capacitance) remains the same (21). When a more accurate electrophysiological description of these nonmyocytes will be available, specific simulations similar to those presented in this paper could be run to determine how much coupling is desirable or proarrhythmic in that case.

Table 1.

Myocyte-fibroblast coupling in the literature.

Reference	Coupling conductance
Cell cultures
Rook et al. (44)	0.31 to 8 nS
Computer models
Kohl et al. (31)	0.3, 0.6 and 0.9 nS
Vasquez et al. (61)	4.7 nS
Jacquemet (19)	0 to 60% of myo-myo coupling
MacCannell et al. (34)	1 to 3 nS
Tanaka et al. (56)	18.2% of myo-myo coupling
Jacquemet et al. (21)	0.09 to 4.05 nS
Sachse et al. (46)	0.1, 1, 10, and 100 nS
this present study	0.05 to 80 nS