The logic of ecological patchiness

Abstract

Most ecological interactions occur in environments that are spatially and temporally heterogeneous—‘patchy’—across a wide range of scales. In contrast, most theoretical models of ecological interactions, especially large-scale models applied to societal issues such as climate change, resource management and human health, are based on ‘mean field’ approaches in which the underlying patchiness of interacting consumers and resources is intentionally averaged out. Mean field ecological models typically have the advantages of tractability, few parameters and clear interpretation; more technically complex spatially explicit models, which resolve ecological patchiness at some (or all relevant) scales, generally lack these advantages. This report presents a heuristic analysis that incorporates important elements of consumer–resource patchiness with minimal technical complexity. The analysis uses scaling arguments to establish conditions under which key mechanisms—movement, reproduction and consumption—strongly affect consumer–resource interactions in patchy environments. By very general arguments, the relative magnitudes of these three mechanisms are quantified by three non-dimensional ecological indices: the Frost, Strathmann and Lessard numbers. Qualitative analysis based on these ecological indices provides a basis for conjectures concerning the expected characteristics of organisms, species interactions and ecosystems in patchy environments.

1. Introduction

Most theoretical analyses of consumer–resource dynamics are rooted in a macroscopic ‘mean field’ perspective. In this perspective, it is explicitly or implicitly assumed that there are one-to-one relationships between spatially averaged consumer and resource population densities and the spatially averaged rates at which those population densities change over time. In mean field models, quantitative (typically nonlinear) relationships between averaged populations and averaged rates—called functional responses—are hypothesized to determine the fundamental characteristics of ecological systems: stability versus oscillations or chaos; coexistence versus exclusion; resilience versus susceptibility to invasion or exploitation. This hypothesis lends mean field approaches a number of important strengths. Mean field models are analytically and numerically tractable; they offer clear experimental paths to quantifying key rates in the field or laboratory; and they have minimal requirements for spatially resolved data, which are sparse or wholly unavailable for most populations. On the strength of these advantages, mean field approaches have been widely successful and, in addition to their theoretical importance, are the basis of most ecological modelling applications to societal problems such as resource management, climate change and human health.

Despite this overall success, mean field models of consumer–resource interactions have important limitations. Ecological dynamics predicted by mean field models are often sensitive to subtle changes in functional responses, especially at low population densities [1]. Consequently, many mean field models invoke somewhat arbitrary assumptions at low densities, such as feeding or mortality thresholds [2]. Without these adjustments, the models could make spurious predictions like extinction in cases where the corresponding natural populations are robustly persistent. Some natural consumer populations thrive under mean resource concentrations that should, according to laboratory measurements, be insufficient to sustain them. As pointed out by Hutchinson [3] in his Paradox of the plankton and by many others, coexistence of multiple competitors for the same resource is ubiquitous in nature. In contrast, most mean field models suggest that competitive exclusion should be the norm—coexistence in mean field models typically occurs under relatively narrow conditions, which may become increasingly contrived as the number of competitors increases. Similarly, complex food webs are commonly stable in nature. However, May [4] and many others have observed that mean field models often predict that instability increases with complexity.

Some of these difficulties with mean field consumer–resource models likely result from subtle mischaracterizations or omissions of relationships between critical taxa or functional groups. These difficulties can be solved by tweaking existing models, with no need for major rethinking of model structure. However, some differences between ecological dynamics in nature and their representations in mean field models probably result from modes of ecological interaction—specifically, ecological dynamics involving causes and consequences of fine-scale spatial and temporal heterogeneity, or patchiness—that are ‘assumed away’ with the fundamental assumption of the mean field approach [5].

The presence and potential ecological importance of patchiness have historically been overlooked in many environments [6]. This is in part because quantifying patchiness frequently requires specialized spatio-temporal sampling schemes that are time-consuming, expensive or technically difficult. Marine environments provide good examples because they are difficult to sample and have typically been regarded as relatively uniform. However, recent studies have documented pronounced variability in consumers and resources at centimetre scales [7,8], metre scales [9] and 1–10 km scales [10]. Satellite imagery suggests that oceanic patchiness also occurs frequently on length scales of hundreds of kilometres [11]. In oceanographic timeseries, limiting resources exhibit fluctuations over several orders of magnitudes between successive sampling intervals [12] that are almost certainly accompanied by this kind of large-scale spatial patchiness. (See Ritchie [13] for terrestrial examples.) These observations and many others suggest that, in most ecological systems, pronounced spatial and temporal heterogeneity across a wide range of scales is more nearly the norm than the exception.

If most environments are strongly heterogeneous, it follows that most consumer–resource interactions occur under conditions that are locally very different from the mean [14]. It is reasonable then to ask, Under which conditions can the fundamental assumption underlying mean field consumer–resource models be justified? What systematic errors or ambiguities do mean field models introduce in our understanding of ecological dynamics, and how can they be resolved? These questions have motivated a variety of spatially explicit enhancements or alternatives to mean field ecological models (partial differential equations, individual-based models, fractal analysis, etc.) in which patchiness can be more explicitly and intuitively represented. Spatially explicit models have, in turn, stimulated detailed empirical and theoretical investigations of consumer movement in spatially heterogeneous resource distributions. These enhancements have provided dramatically more detailed and realistic representations of spatial and temporal fluctuations of consumers and resources in patchy environments. However, these representations come with increased technical complexity, proliferation of parameters and difficulties in interpretation. Hence, spatially explicit models sacrifice some of the benevolent traits that lend mean field models their broad utility.

The goal of this paper is to explore whether, using a heuristic analysis rather than a mathematically complex one, it is possible to derive logical expectations about consumer–resource interactions in patchy environments. If mean field models caricature real environments by spatially averaging heterogeneous resources into uniform shades of grey, this analysis adopts the complementary caricature: reducing heterogeneous landscapes in which local resources are lower or higher than the mean to black and white. The result is a greatly simplified and abstracted landscape in which areas devoid of resources are punctuated by saturating high-density resource patches.

Rather than consumption of resources being a nonlinear function of mean resource density, as in the mean field perspective, this ‘patchy resource’ perspective suggests that resource consumption is more directly a function of time spent in resource patches. Time spent in resource patches may be, but is not necessarily, quantitatively related to mean resource density. That is because in heterogeneous ecosystems, a given quantity of resources can be distributed in many ways—e.g. in patches that are closely spaced and long-lived, or in patches that are widely spaced and ephemeral—some of which provide higher access to resources than others by specific types of consumers.

This divergence between average density of resources and actual availability of those resources suggests that mean field models, at least in their usual forms, are insufficient to model patchy environments. However, the patchy resource perspective suggests an alternative approach, based on scaling and dimensional analysis. These methods are commonly used for consolidating parameters and distinguishing dominant mechanisms in the physical sciences but remain under-used in ecology.

2. Scaling consumer–resource patch dynamics

A useful starting point for this analysis is a trophic interaction in which a focal mobile consumer exploits a resource that is distributed as patches occurring randomly in time and space, within an otherwise empty landscape. Consumer–resource interactions are specified by a combination of organism- and landscape-level parameters (table 1). The key organism-level parameters are those characterizing consumers' movements (speed, s, and turning interval, τ) and demography (growth rate, σ, resource consumption rate, η and mortality rate, μ). At the landscape level, the trophic interaction is described by characteristic densities of resources, R, and consumers, C. R and C are rough metrics for what are ‘large’ or ‘small’ population densities, estimated from mean field models or empirical observations.

Table 1.

Organism-level and landscape-level parameters characterizing consumer–resource interactions on patchy landscapes, with associated timescales for consumer movement, reproduction and consumption.

parameter	interpretation
organism-level
s	consumer speed
τ	consumer turning interval
σ	consumer intrinsic rate of growth
η	consumer-specific consumption rate
μ	consumer mortality rate
landscape-level
T	resource timescale (patch duration)
L	resource length scale (distance between patches)
R	characteristic resource density
C	characteristic consumer density
consumer timescales
T	resource patch duration timescale
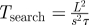	consumer search timescale (diffusive movement)
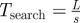	consumer search timescale (directed movement)
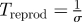	consumer reproduction timescale
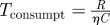	timescale of resource consumption

Resource patches are characterized at the landscape level by a timescale, T, representing the typical longevity of a resource patch. That is, T is the approximate time over which a resource patch decays (even in the absence of the focal consumers) owing to physical dispersion, removal by consumers or pathogens not explicitly represented in the model, or some other mechanism. Similarly, resource patches are characterized by a length scale, L, representing a typical separation distance between patches. We assume that environmental forcing creates resource patchiness in otherwise stable consumer–resource dynamics, and hence predictably determines T and L (see Brentnall et al. [14], for analysis of self-generated patchiness in an excitable media context). For example, in a marine environment, distinct values of T and L can be predicted for patches owing to environmental forcing by turbulence, tides, internal waves or storms.

Pursuing the patchy resource caricature, we now consider what combinations of organism-level and landscape-level parameters are likely to result in dramatically increased or decreased availability of resources to consumers. Such increases or decreases cause significant dynamic changes relative to the expectations of mean field theory. Three key mechanisms determine trophic interactions between the focal consumer and patchy resources: movement of consumers, as they seek out resource patches; reproduction of consumers, when sufficient resources are obtained to support it; and resource consumption, when consumers and resources coincide sufficiently in time and space. Each of these mechanisms can be associated with a timescale characterizing how much time is required for that mechanism to have significant trophic impacts.

When foraging for unpredictable patchy resources, consumer movements are most commonly modelled at the organism level as biased random walks. At large time and space scales, these random walks result in population movements governed by diffusion and (where relevant environmental gradients exist) taxis-type advection. If patches are detectable only at distances much smaller than L, then encounters with patches occur at rates determined primarily by the consumers' diffusion coefficient, D ≈ s²τ. The timescale for patch encounters—that is, the search time—is then T_search = L²/s²τ, where the L² dependence on distance between patches highlights the inefficiency of diffusive searching over large spatial scales [15]. Many organisms have been recently conjectured to employ other movement behaviours, particularly Lévy walks, in which the incidence of long movements is relatively much higher than classical random walks and in which encounter rates with widely spaced patches are consequently higher. In the extreme case of fully directed movement (i.e. always moving directly towards patches) foragers encounter patches with typical search time T_search = L/s. These estimates for diffusive and directed movements likely bracket search times for most foraging organisms (table 1). The corresponding timescale for consumer reproduction is much simpler, T_reprod = 1/σ. Finally, a characteristic density of consumers removes resources approximately at rate ηC; the timescale over which these consumers significantly impact a characteristic density of resources R is therefore T_consumpt = R/ηC.

These estimates of T_search, T_reprod and T_consumpt translate into a heuristic logic of ecological patchiness by considering their magnitudes in relation to the characteristic patch longevity, T. The importance of forager movement as a mechanism impacting consumer–resource interactions is given by a non-dimensional index, the Frost number [15]:

2.1

Large values of the Frost number (that is, ℱr ≫ 1) imply that patch longevity is relatively long, and search time is relatively short; this situation clearly implies that most consumers are able to spend most of their time in patches (table 2). Conversely, ℱr ≪ 1 means patch longevity is much shorter than search time, implying that most consumers spend most of their time searching for rather than exploiting patches. As with many physical applications of non-dimensional numbers, intermediate cases in which ℱr is neither much larger nor much smaller than unity are ambiguous, but potentially interesting because in these cases, environmental and organismal details can be decisive.

Table 2.

Definitions and interpretations of non-dimensional indices of consumer–resource interactions in patches, in terms of characteristic separation distance between patches, L, and patch duration, T.

name	definition	interpretation
Frost number, diffusive		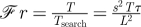ℱr ≫ 1 : consumers can move to patches
		ℱr ≪ 1 : consumers cannot move to patches
Frost number, directed		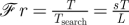ℱr ≫ 1 : consumers can move to patches
		ℱr ≪ 1 : consumers cannot move to patches
Strathmann number		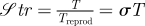𝒮tr ≫ 1: consumers can reproduce in a patch
		𝒮tr ≪ 1 : consumers cannot reproduce in a patch
Lessard number		ℒe ≫ 1 : consumers can consume patches
		ℒe ≪1 : consumers cannot consume patches

This logic extends to the other mechanisms of trophic dynamics with the definition of the Strathmann number,

2.2

and the Lessard number,

2.3

named in recognition of numerous contributions by Richard Strathmann and Evelyn Lessard to marine ecology. 𝒮tr ≫ 1 implies that patch longevity is much longer than consumer generation time; thus, significant consumer reproduction can occur within a single patch. A consequence is that, even if movement to patches is ineffective (i.e. ℱr ≪ 1), consumers may be aggregated within resource patches owing to explosive in-place reproduction. Conversely, 𝒮tr ≪ 1 implies that any given patch is likely to disappear before significant consumer reproduction can occur. Likewise, ℒe ≫ 1 implies that the time required by consumers to trophically impact patches is short compared with the timescale over which patches disappear owing to other removal mechanisms. Hence, ℒe ≫ 1 implies that consumers can heavily impact resource patches. Conversely, ℒe ≪ 1 implies that other removal mechanisms eliminate patches so quickly that consumers have little impact.

3. Implications for patchy populations

The rationale of §2 suggests a number of conjectures concerning the characteristics of ecosystems, species interactions and organisms likely to prevail in patchy environments. These conjectures are evidently speculative, but may warrant further theoretical or empirical investigation. In particular, these conjectures may prove interesting whether supported or contradicted by more detailed investigations, because they provide a reasonable and relatively simple array of testable predictions for a complex set of ecological interactions.

3.1. Conjectures for ecosystems in patchy environments

Non-dimensional indices are frequently used in the physical sciences to determine dynamic similarity, the basis of ‘scale models’. A conjecture following directly from §2 is that two consumer–resource interactions with equal values of ℱr, ℒe and 𝒮tr are dynamically similar. If so, one should function as a scale model of the other. Further, observations of complex dynamics that cannot be modelled directly can often be economically expressed in terms of non-dimensional indices, which form a greatly reduced parameter space in which to derive approximations or develop look-up tables. The conjecture follows that consumer and resource populations in patchy environments should be predictable functions of ℱr, ℒe and 𝒮tr. For example, factors by which standing populations deviate from mean field expectations could be parameterized as

3.1

potentially providing a correction factor for large-scale ecological models. Finally, non-dimensional indices provide a basis on which to form approximations in which variabilities in some mechanisms are retained while in others it is neglected. The conjecture follows that in consumer–resource interactions for which ℱr ≪ 1, 𝒮tr ≪ 1 or ℒe ≪ 1, metrics such as f are relatively insensitive to changes in the respective ecological mechanism (movement, reproduction or consumption).

3.2. Conjectures for species interactions in patchy environments

The rationale of §2 suggests threshold or ‘critical’ values of the order of magnitude,

which respectively delineate regions of parameter space in which movement, reproduction and consumption do or do not make significant contributions to consumer interactions with patchy resources (figure 1). For diffusive foragers, the locus of points for which ℱr_critical = 1 corresponds to a line of slope 2 on the log L–log T plane [15]; for directed foragers, the line has slope 1. Patches with characteristics T and L placing them above one of these lines are effectively available to the corresponding mobile consumers, while T and L values below the line are effectively unavailable. Extending this reasoning, 𝒮tr_critical = 1 corresponds to a horizontal line in the log L–log T plane (figure 1). Patches with T above this line are effectively available to consumers because consumers can reproduce explosively within them. Conversely, explosive reproduction is not possible within patches with T below this line. 𝒮e_critical = 1 also corresponds to a horizontal line; above this line, consumers have strong impacts, while below the line consumer impacts are weak (figure 2).

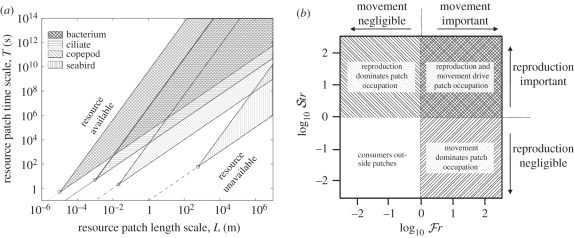
Figure 1.

Heuristic scaling of interactions between consumers and patchy resources, in terms of characteristic separation distance between patches, L, and patch duration, T. The critical Frost number, ℱr_critical ≈ 1, quantifies mobile consumers' abilities to move to transient resource patches (table 2). (a) On a plot of log₁₀ L versus log₁₀ T, this threshold translates to lines with slopes 2 and 1, respectively, for consumers with diffusive or directed foraging movements. For a given foraging movement type, patches above the corresponding line are accessible by movement, while those below the line are not. Cross-hatched areas indicate the consequences for patch accessibility of variations in foraging strategy: behavioural changes, e.g. from diffusive to Lévy or directed searches, shift limits from the upper edges of hatched areas to lower edges. Examples are shown corresponding to several hypothetical organisms (bacterium, s = 20 m s⁻¹, τ = 0.5 s; ciliate: s = 200 m s⁻¹, τ = 5 s; copepod: s = 1 cm s⁻¹, τ = 2 s; seabird: s = 10 m s⁻¹, τ = 60 s) illustrating how patches with particular length and timescales L and T may be accessible by movement to some consumers but not others. (b) The critical Strathmann number, 𝒮tr_critical ≈ 1, quantifies consumers' abilities to reproduce explosively within transient resource patches. Consumers with ℱr ≫ 1 and/or 𝒮tr ≫ 1 are likely to be aggregated inside patches, while other consumers are not.

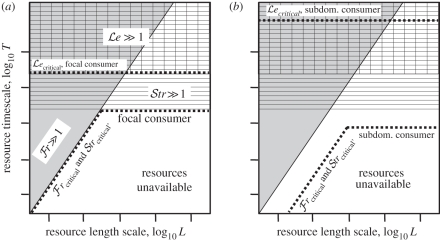
Figure 2.

Schematic of species interactions in a patchy resource environment. (a) For the focal species, grey indicates ℱr ≫ 1, the L–T region where the focal consumer can move to resource patches. Horizontal hatching indicates 𝒮tr ≫ 1, the L–T region where the focal consumer can reproduce in resource patches. Within the union of these two regions, patchiness increases access to resources for the focal consumers compared with a spatially uniform resource distribution; elsewhere, patchiness reduces availability. Vertical hatching indicates ℒe ≫ 1, the L–T region where the focal consumer can remove resource patches. Within the intersection of this region with the ℱr ≫ 1, 𝒮tr ≫ 1 region the focal consumer can be a dominant competitor; outside this intersection, exclusion of other consumers is unlikely. (b) A conjectured requirement is that to persist within this union despite competition from the dominant focal consumer, a subdominant consumer must have higher ℱr (i.e. a shorter T_search, indicated by ℱr_critical occurring at lower L and T) and/or higher 𝒮tr (i.e. a shorter T_reprod, indicated by 𝒮tr_critical occurring at lower T but lower ℒe (i.e. a longer T_consumpt, indicated by ℒe_critical occurring at higher T).

The conjecture follows that in a patchy resource distribution, a consumer species can persist only if its ℱr ≫ 1 and/or its 𝒮tr ≫ 1. That is, viable consumers must effectively exploit patches by at least one mechanism. A further conjecture is that a consumer of patchy resources can exclude competitors only if its ℒe ≫ 1; otherwise, it would have minimal impacts on resources and little competitive effect (figure 2). However, among different consumer species competing for a single patchy resource, only one species—the dominant consumer—can persist with ℒe ≫ 1. For multiple consumers to persist, all non-dominant consumers must have ℒe ≪ 1. Further, non-dominant consumers must have higher ℱr and/or higher 𝒮tr than the dominant competitor. The logic behind these conjectures is that, if the dominant competitor removes patches, persistent secondary consumers must have some means of exploiting patches before they disappear. This suggests an advantage over the dominant competitor in movement or reproduction. However, a secondary competitor with this advantage and high impacts on resources would not remain secondary, but instead exclude the dominant.

3.3. Conjectures for organisms in patchy environments

At the organism level, the conjectures about species interactions suggest that ℱr_critical and 𝒮tr_critical are functionally important performance metrics. Specifically, for dominant consumers that exploit patches by movement, ℱr ≈ 1 is a threshold for successful exploitation of resource patches. If movement is costly, a conjecture is that benefits and costs will be most favourably balanced by movement that meets but not does not greatly exceed this threshold. Analogously, 𝒮tr ≈ 1 is a growth/reproduction rate threshold for successful exploitation of resource patches. If rapid growth or reproduction is costly, favourable costs and benefits are conjectured to arise when growth or reproduction meets but does not exceed this threshold. Finally, if movement and rapid growth or reproduction are both costly, successful consumers are conjectured to have either ℱr ≫ 1 or 𝒮tr ≫ 1, but not both.